آنالیز تشخیصی خطی (LDA) در پایتون — راهنمای کاربردی

تحلیل یا «آنالیز تشخیصی خطی» (Linear Discriminant Analysis - LDA) یک روش آماری برای کاهش ابعاد یک مسئله و تشخیص دستهها بوسیله بیشینهسازی نسبت «پراکندگی بین گروهها» (Scatters between groups) به «درون گروهها» (Scatters within groups) است. رویکرد آنالیز تشخیصی خطی در واقع مشابه و وام گرفته از روشی است که «رونالد فیشر» (Ronald Fisher) برای تعیین میزان افتراق بین گروهها به کار برد و مبنایی برای تحلیل واریانس گردید. به همین دلیل گاهی به این تحلیل، «آنالیز افتراقی خطی» نیز میگویند.
در دیگر نوشته فرادرس با عنوان تحلیل تشخیص خطی فیشر (Fisher’s Linear Discriminant) — پیاده سازی در پایتون با نحوه عملکرد این تکنیک آماری آشنا شدهاید. در این نوشتار به بررسی گونه دیگری از تحلیل تشخیصی میپردازیم. البته به منظور پیادهسازی محاسبات و اجرای الگوریتمها از زبان برنامهنویسی پایتون استفاده خواهیم کرد. در نتیجه در طول این نوشتار با کدهایی از این زبان برخورد خواهیم داشت که برای روشن شدن نقش دستورات و شیوه اجرای الگوریتم توضیحاتی نیز ارائه خواهد شد.
از آنجایی که آنالیز یا تحلیل تشخیصی خطی، الهام گرفته از یکی دیگر از تکنیکهای آماری یعنی «تحلیل واریانس» (Analysis of Variance) است، خواندن مطلب تحلیل واریانس (Anova) — مفاهیم و کاربردها و تحلیل مولفه اساسی (PCA) — راهنمای عملی به همراه کد نویسی در پایتون و R به عنوان پیشنیاز این مطلب ضروری به نظر میرسد. همچنین خواندن مطلب احتمال پسین (Posterior Probability) و احتمال پیشین (Prior Probability) — به زبان ساده و تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده و بردار ویژه و مقدار ویژه — از صفر تا صد نیز خالی از لطف نیست.

آنالیز تشخیصی خطی (LDA)
هدف از انجام آنالیز تشخیص خطی، پیدا کردن یک «تصویر» (Projection) یا «تبدیل» (Transformation) است، که از این به بعد به آن $$w$$ میگوییم، روی مجموعه داده $$A$$ بطوری که بتواند نسبت «پراکندگی بین گروهها» (Between Class) را به «پراکندگی درون گروهها» (Within Class) دادههای تبدیل شده، حداکثر کند.
در این صورت اگر ماتریس $$A$$ را مجموعه دادههای اولیه $$d$$ بُعدی در نظر بگیریم، هدف از اجرای تحلیل یا آنالیز تشخیص خطی، پیدا کردن بردار یا ماتریس $$w$$ است که بتواند نسبت یاد شده را برای دادههای تبدیل یافته یعنی $$Y$$ بیشینه کند. این تبدیل یا تصویر در رابطه زیر دیده میشود.
$$\large Y=w^T A$$
از آنجایی که این تبدیل به صورت ترکیب خطی از سطرهای ماتریس $$A$$ نوشته میشود، این روش را «آنالیز تشخیصی خطی» (Linear Discriminant Analysis) مینامند. به این ترتیب به نظر میرسد که در هر بُعد از ماتریس $$A$$، که با $$X$$ نشان داده خواهد شد، به دنبال تبدیلی یا در واقع مضربی مانند بردار $$a$$ هستیم. به این ترتیب تبدیل حاصل که بوسیله عبارت $$Z=a^TX$$ نشان داده میشود، یک ترکیب خطی از $$X$$ است، به شکلی که دارای بیشینه مقدار واریانس بین گروهها نسبت به واریانس درون گروه را دارا است. از جهتی میتوان تکنیک LDA را به مانند روش «تحلیل مولفههای اصلی» (Principal Component Analysis - PCA) در نظر گرفت با این تفاوت که هدف از انجام تحلیل LDA پیدا کردن تبدیلی است که بیشترین تمایز را بین گروهها ایجاد کند در حالیکه هدف از PCA فقط کاهش بعد مسئله و ایجاد استقلال بین مولفهها است.
در ادامه به منظور آشنایی با نحوه انجام LDA، مفاهیم آماری و ریاضی مربوط به LDA را مرور میکنیم. هر چند این مفاهیم بیشتر جنبه ریاضی دارند ولی کاربردهای زیادی در ایجاد مدلهای آماری و بخصوص در یادگیری ماشین برای آنها بوجود آمده است، بطوری که امروزه بیشتر «تحلیلگرهای داده» (Data Scientist) باید از نحوه اجرا و پیادهسازی آن در نرمافزارها و زبانهای برنامهنویسی آگاهی داشته باشند تا قادر به حل مسئلههای شوند که دارای پارامتر یا متغیرهای زیادی هستند.
مفاهیم آماری مرتبط با تحلیل تشخیصی خطی
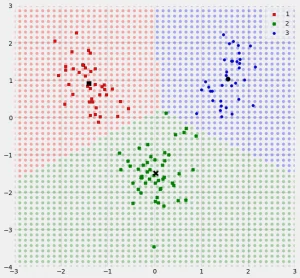
برای اینکه بیشتر و بهتر با مفاهیم و موضوع پراکندگی درون گروهی و بین گروهی آشنا شویم از تصویر زیر استفاده میکنیم و براساس آن، فرمولها و شیوه محاسبات مربوط به اندازهگیری پراکندگی درون گروهی با نماد $$S_W$$ و بین گروهی با نماد $$S_B$$ را معرفی خواهیم کرد.
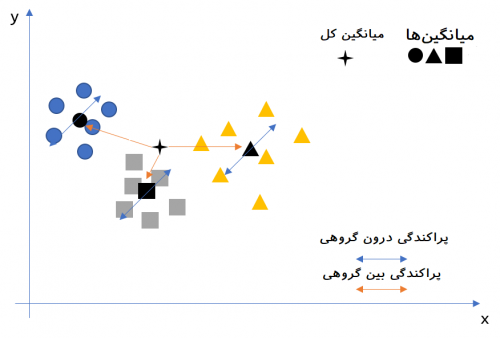
1- پراکندگی درون گروهی ($$S_W$$)
فرض کنید که مقدار مربوط به مشاهدات با $$x_j$$ و مرکز گروه $$c$$ نیز با $$\mu_c$$ نشان داده شده باشد. آنگاه نحوه محاسبه $$S_W$$ مطابق با رابطه زیر است.
$$\large S_W=\sum_{c}\sum_{x_j\in c}(x_j-\mu_c)(x_j-\mu_c)^T$$
مشخص است که در اینجا منظور از $$classes$$ در تصویر بالا، دستههای دایرههای آبی، مربعهای خاکستری و مثلثهای زرد هستند. همچنین $$x_j$$ نیز بردار مشاهدات را در هر کلاس یا گروه نشان میدهند. همانطور که در تصویر مشخص است مشاهدات دارای دو بُعد هستند به همین علت برای نمایش نقاط مربوط به مشاهدات از مختصات دو بُعدی دکارتی استفاده کردهایم که مولفه اول روی محور افقی و مولفه دوم نیز در محور عمودی قابل مشاهده و اندازهگیری است به این ترتیب نقاط دارای دو بُعد هستند.
این موضوع را هم در نظر بگیرید که میانگین این نقاط دو بُعدی برای گروه $$c$$ با $$\mu_c$$ مشخص شده است که آن هم یک مقدار دو بُعدی است. به این ترتیب اگر ۱۵ مشاهده از گروه یک موجود باشد، $$x_j$$ یک ماتریس $$15\times 2$$ است که دارای ۲ ردیف و ۱۵ ستون است و $$\mu_1$$ به صورت نقطه $$(m_1,m_2)$$ تشکیل میشود که $$m_۱$$ میانگین بروی مولفه اول و $$m_2$$ میانگین روی مولفه دوم است. در نتیجه آن را یک بردار $$1 \times 2$$ میتوان در نظر گرفت که دارای دو سطر و یک ستون است. به این ترتیب تفاضل آنها یعنی $$x_j-\mu_c$$ یک ماتریس $$15 \times 2$$ خواهد بود که ۱۵ ستون و ۲ سطر دارد. واضح است که در رابطه بالا منظور از $$^T$$ نیز ترانهاده بردار تفضلهای $$x_j-\mu_c$$ است. در نتیجه قرار است حاصل ضریب یک ماتریس $$15 \times 2$$ در یک ماتریس $$2 \times 15$$ بدست آید که حاصل یک ماتریس $$2 \times 2$$ خواهد بود.
از آنجایی هدف بیشینهسازی نسبت پراکندگی بین گروهی به درون گروهی است، به نظر میرسد که مقدار پراکندگی درون گروهی باید تا حد ممکن کاهش یابد تا نسبت مذکور به حداکثر مقدار خود برسد. به این ترتیب گروههای متجانس و همشکل ایجاد خواهد شد که دارای پراکندگی کوچکی خواهند بود در نتیجه مجموع پراکندگیهای درون گروهی برای همه دستهها کوچکترین مقدار را خواهد داشت. بنابراین گروههای آبی، زرد و خاکستری به نظر بهترین تفکیک برای دادهها خواهند بود.
همانطور که گفته شد ماتریس مقدارها یا $$A$$ از نقاط مربوط به مشاهدات و ابعادشان ساخته میشود. در این صورت $$(x_j-\mu_c)(x_j-\mu)^T$$ یک ماتریس $$2\times 2$$ را برای دادههای دو بُعدی مثال ما ایجاد خواهد کرد. بنابراین با جمع مقدارهای این ماتریسها برای همه دسته یا گروهها خواهیم داشت:
$$\large \begin{bmatrix}S_W(xx) & S_W(xy) \\S_W(yx) & S_W(yy) \end{bmatrix}$$
نکته: توجه داشته باشید که در این محاسبات ماتریس کوواریانس بدست نیامده است، بلکه فقط مجموع پراکندگیهای درون گروهی حاصل شده و در قسمتهای بعدی برای تجزیه پراکندگی کل استفاده خواهد شد. این کار درست به شکلی است که جدول تحلیل واریانس ساخته میشود.
پیادهسازی محاسبات در پایتون
به منظور محاسبه این ماتریسها و بدست آوردن $$S_W$$ و $$S_B$$ از کدهای پایتون استفاده خواهیم کرد. ابتدا به محاسبه $$S_W$$ خواهیم پرداخت. البته مطابق با تصویر قبلی، سه گروه از دستههای دایره، مربع و مثلث با رنگهای یاد شده ایجاد کردهایم و با توجه به مختصات دو بُعدی آنها، ماتریس پراکندگی درون گروهی را بدست آوردهایم. دادههای به کار رفته در درون کد قرار دارند و محاسبات براساس آنها صورت گرفته است.
1import numpy as np
2import matplotlib.pyplot as plt
3from matplotlib import style
4style.use('fivethirtyeight')
5np.random.seed(seed=42)
6# Create data
7rectangles = np.array([[1,1.5,1.7,1.45,1.1,1.6,1.8],[1.8,1.55,1.45,1.6,1.65,1.7,1.75]])
8triangles = np.array([[0.1,0.5,0.25,0.4,0.3,0.6,0.35,0.15,0.4,0.5,0.48],[1.1,1.5,1.3,1.2,1.15,1.0,1.4,1.2,1.3,1.5,1.0]])
9circles = np.array([[1.5,1.55,1.52,1.4,1.3,1.6,1.35,1.45,1.4,1.5,1.48,1.51,1.52,1.49,1.41,1.39,1.6,1.35,1.55,1.47,1.57,1.48,
10 1.55,1.555,1.525,1.45,1.35,1.65,1.355,1.455,1.45,1.55,1.485,1.515,1.525,1.495,1.415,1.395,1.65,1.355,1.555,1.475,1.575,1.485]
11 ,[1.3,1.35,1.33,1.32,1.315,1.30,1.34,1.32,1.33,1.35,1.30,1.31,1.35,1.33,1.32,1.315,1.38,1.34,1.28,1.23,1.25,1.29,
12 1.35,1.355,1.335,1.325,1.3155,1.305,1.345,1.325,1.335,1.355,1.305,1.315,1.355,1.335,1.325,1.3155,1.385,1.345,1.285,1.235,1.255,1.295]])
13#Plot the data
14fig = plt.figure(figsize=(10,10))
15ax0 = fig.add_subplot(111)
16ax0.scatter(rectangles[0],rectangles[1],marker='s',c='grey',edgecolor='black')
17ax0.scatter(triangles[0],triangles[1],marker='^',c='yellow',edgecolor='black')
18ax0.scatter(circles[0],circles[1],marker='o',c='blue',edgecolor='black')
19# Calculate the mean vectors per class
20mean_rectangles = np.mean(rectangles,axis=1).reshape(2,1) # Creates a 2x1 vector consisting of the means of the dimensions
21mean_triangles = np.mean(triangles,axis=1).reshape(2,1)
22mean_circles = np.mean(circles,axis=1).reshape(2,1)
23# Calculate the scatter matrices for the SW (Scatter within) and sum the elements up
24scatter_rectangles = np.dot((rectangles-mean_rectangles),(rectangles-mean_rectangles).T)
25# Mind that we do not calculate the covariance matrix here because then we have to divide by n or n-1 as shown below
26#print((1/7)*np.dot((rectangles-mean_rectangles),(rectangles-mean_rectangles).T))
27#print(np.var(rectangles[0],ddof=0))
28scatter_triangles = np.dot((triangles-mean_triangles),(triangles-mean_triangles).T)
29scatter_circles = np.dot((circles-mean_circles),(circles-mean_circles).T)
30# Calculate the SW by adding the scatters within classes
31SW = scatter_triangles+scatter_circles+scatter_rectangles
32print(SW)
33plt.show()توجه داشته باشید که در این کد، مقدارها به صورت زیر طبق سه ماتریس برای «مستطیلها» (Rectangles)، «مثلثها» (Triangles) و «دایرهها» (Circles) مشخص شدهاند. مقدارهای این ماتریسها در ادامه دیده میشود.
1('Rectangles= ', array([[ 1. , 1.5 , 1.7 , 1.45, 1.1 , 1.6 , 1.8 ],
2 [ 1.8 , 1.55, 1.45, 1.6 , 1.65, 1.7 , 1.75]]))
3('Triangles= ', array([[ 0.1 , 0.5 , 0.25, 0.4 , 0.3 , 0.6 , 0.35, 0.15, 0.4 ,
4 0.5 , 0.48],
5 [ 1.1 , 1.5 , 1.3 , 1.2 , 1.15, 1. , 1.4 , 1.2 , 1.3 ,
6 1.5 , 1. ]]))
7('Circles= ', array([[ 1.5 , 1.55 , 1.52 , 1.4 , 1.3 , 1.6 , 1.35 ,
8 1.45 , 1.4 , 1.5 , 1.48 , 1.51 , 1.52 , 1.49 ,
9 1.41 , 1.39 , 1.6 , 1.35 , 1.55 , 1.47 , 1.57 ,
10 1.48 , 1.55 , 1.555 , 1.525 , 1.45 , 1.35 , 1.65 ,
11 1.355 , 1.455 , 1.45 , 1.55 , 1.485 , 1.515 , 1.525 ,
12 1.495 , 1.415 , 1.395 , 1.65 , 1.355 , 1.555 , 1.475 ,
13 1.575 , 1.485 ],
14 [ 1.3 , 1.35 , 1.33 , 1.32 , 1.315 , 1.3 , 1.34 ,
15 1.32 , 1.33 , 1.35 , 1.3 , 1.31 , 1.35 , 1.33 ,
16 1.32 , 1.315 , 1.38 , 1.34 , 1.28 , 1.23 , 1.25 ,
17 1.29 , 1.35 , 1.355 , 1.335 , 1.325 , 1.3155, 1.305 ,
18 1.345 , 1.325 , 1.335 , 1.355 , 1.305 , 1.315 , 1.355 ,
19 1.335 , 1.325 , 1.3155, 1.385 , 1.345 , 1.285 , 1.235 ,
20 1.255 , 1.295 ]]))همانطور که در قبل گفته شد، حاصل اجرای کد فوق یک ماتریس دو بعدی خواهد بود که پراکندگی بین گروهی $$S_W$$ را نشان داده و نمودار نقطهها را هم رسم خواهد کرد. همانطور که انتظار داشتیم، نقاط از یکدیگر به خوبی تفکیکپذیر هستند. حال باید ببینیم که تکنیک LDA چگونه آنها را تشخیص میدهد.
1[[ 1.07646534 -0.05208045]
2 [-0.05208045 0.45007299]]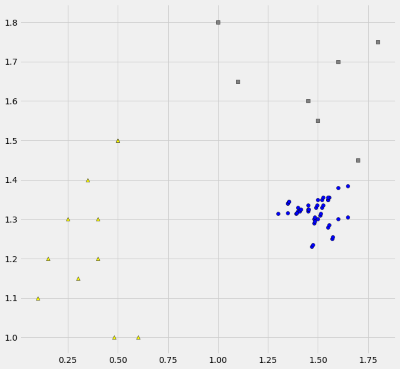
۲- پراکندگی بین گروهی ($$S_B$$)
همانطور که قبلا مشاهده کردیم، صورت کسری که باید بیشینه شود، برحسب $$S_B$$ نوشته شده است. به منظور محاسبه پراکندگی بین گروهی از رابطه زیر استفاده خواهیم کرد. به یاد دارید که در این حالت، در هر بار بررسی بیشینه بودن نسبت، مخرج ثابت در نظر گرفته میشود.
در نتیجه میانگین گروهها تغییر نخواهد کرد. ولی هر گاه گروهبندی تغییری داشته باشد، مراکز نیز تغییر کرده و مخرج کسر متفاوت خواهد بود.
$$ \large S_B=\sum\limits_{classes \in c} N_c(\mu_c-\mu)(\mu_c-\mu)^T$$
مشخص است که در این رابطه فاصله بین مراکز گروهها یا دستهها نسبت به مرکز یا میانگین کلی ($$\mu$$) اندازهگیری شده است بطوری که در مثال ما $$\mu$$ و $$\mu_c$$ ماتریسهای $$2 \times 1$$ هستند یعنی دو سطر و یک ستون دارند. در نتیجه حاصل ضریب عبارتهای $$(\mu_c-\mu)(\mu_c-\mu)^T$$ یک ماتریس $$2 \times 2$$ خواهد بود. همچنین باید توجه داشت که $$N_c$$ تعداد اعضای هر گروه یا دسته را نشان میدهد.
فرض کنید که پراکندگی کلی برای مشاهدات $$x$$ به صورت $$S_T$$ نامگذاری شده باشد. با توجه به مفهوم پراکندگی برحسب مربعات فاصله، خواهیم داشت:
$$\large S_T=\sum_x (x-\mu)(x-\mu)^T$$
در این حالت رابطه زیر بین پراکندگی درون گروهی و بین گروهی با پراکندگی کل وجود دارد.
$$\large S_T=S_B+S_W$$
زیرا با توجه به فرمول زیر به راحتی میتوان رابطه بالا را اثبات کرد.
$$\large (x-\mu)^2=(\mu_c-\mu)^2+(x-\mu_c)^2$$
بوسیله کدی که در ادامه قابل مشاهده است، رابطه بالا به خوبی نمایش داده شده است. این کد نموداری را برای یک نقطه مشخص کرده است که خط قرمز ترسیم شده، رابطه سمت چپ یعنی فاصله نقطه از میانگین کل را نشان میدهد. خط زرد رنگ نیز سمت راست معادله بالا را بیان میکند. از آنجایی که این مقدارها همگی به صورت مربع هستند، همانطور که دیده میشود براساس قاعده فیثاغورس، این دو خط با یکدیگر مساوی هستند. البته اثبات این مطلب نیز در ادامه و بعد از تصویر قابل مشاهده است.
1import numpy as np
2import matplotlib.pyplot as plt
3from matplotlib import style
4style.use('fivethirtyeight')
5np.random.seed(seed=42)
6x_j = np.array([3.5,4.5])
7mu = np.array([7,5])
8mu_k = np.array([4,3])
9fig = plt.figure(figsize=(10,10))
10ax0 = fig.add_subplot(111)
11ax0.set_xlim(-1,10)
12ax0.set_ylim(-1,10)
13for i in [x_j,mu,mu_k]:
14 ax0.scatter(i[0],i[1],s=50)
15ax0.annotate('x_j',x_j)
16ax0.annotate('mu',mu)
17ax0.annotate('mu_k',mu_k)
18ax0.annotate('(x_j - mu) = (mu_k - mu) + (x_j - mu_k)',np.array(mu)+np.array([1,1]))
19# Draw the position vectors
20for i in [x_j,mu,mu_k]:
21 ax0.arrow(0,0,i[0],i[1],head_width=0.01,width=0.05)
22
23# Draw the vectors
24ax0.arrow(mu[0],mu[1],(x_j-mu)[0],(x_j-mu)[1],head_width=0.05,width=0.1,color='yellow') # xj_minus_mu
25ax0.arrow(mu[0],mu[1],(mu_k-mu)[0],(mu_k-mu)[1],head_width=0.05,width=0.01,alpha=0.5,color='black') # mu_k_minus_mu
26ax0.arrow(mu_k[0],mu_k[1],(x_j-mu_k)[0],(x_j-mu_k)[1],head_width=0.05,width=0.01,alpha=0.5,color='black') # xj_minus_mu_k
27# If we now add up the vectors (mu_k-mu) and (x_j-mu_k) wee see that this vector alligns with the vector (x_k-mu)
28mu_k_minus_mu = mu_k-mu
29x_j_minus_mu_k = x_j-mu_k
30res = (mu_k-mu)+(x_j-mu_k)
31ax0.arrow(mu[0],mu[1],res[0],res[1],head_width=0.05,width=0.01,linestyle='-.',color='red')
32plt.show()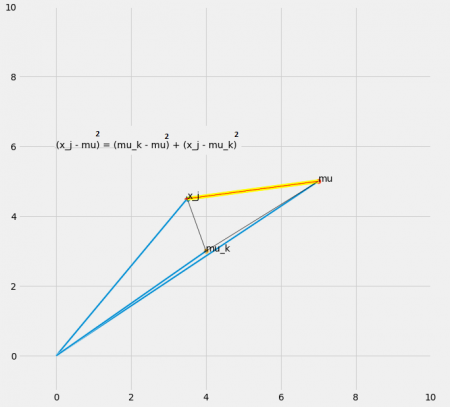
به منظور اثبات رابطه قبل، هنگام محاسبه $$S_T$$ مقداری $$\mu_c$$ را اضافه و کم میکنیم تا در مقدار پراکندگی کلی تغییری بوجود نیاید.
$$\large S_T = \sum_{c \in classes} \sum_{x\in c}(x -\mu_c + \mu_c-\mu)(x - \mu_c + \mu_c-\mu)^T$$
$$\large = \underbrace{\sumـ{c in classes} \sum_{x\in c}(x -\mu_c)(x -\mu_c)^T}_{S_W}+\sum_{c \in classes} \sum_{x\in c}(\mu_c -\mu)(\mu_c -\mu)^T$$
$$ \large = S_W + \underbrace{\sum_{c \in classes}N_c (\mu_c -\mu)(\mu_c - \mu)^T}_{S_B}$$
در رابطه آخر به علت اینکه جمع، روی مقدارهای $$x$$ بسته شده ولی داخل عبارت به آن بستگی ندارد، به صورت $$N_C$$ نوشته شده است. به این ترتیب کافی است پراکندگی کلی و پراکندگی درون گروهی را محاسبه کنیم و پراکندگی بین گروهها را براساس رابطهای که بینشان برقرار است بدست آوریم.
بیشینهسازی نسبت $$\dfrac{S_B}{S_W}$$
همانطور که قبلا اشاره شد، به دنبال ترکیبی خطی از مشاهدات هستیم که براساس آن بتوانیم نسبت $$\dfrac{S_B}{S_W}$$ را برای دادههای جدید و تبدیل یافته، بیشینه کنیم. البته مشخص است که دادههای تبدیل یافته، دارای بُعد کمتری نسبت به دادههای اصلی هستند. به این ترتیب به نوع کاهش بُعد در حل مسئله نیز رسیدهایم و با توجه به دادههایی با بُعد کمتر که در رابطه زیر تشکیل میشوند، میتوانیم تشخیص بهتری برای دسته یا گروهها ایجاد کنیم.
$$\large y= w^T x$$
از آنجایی که این تبدیل (ضرب) توسط بردار یا ماتریس $$w$$ روی همه نقطهها اثر میکند، میانگین گروه و میانگین کل نیز که به صورت $$\mu$$ و $$\mu_c$$ هستند نیز تحت تاثیر قرار میگیرند. این تغییرات و تبدیلات توسط تصویری که براساس کد زیر ایجاد شده است، به خوبی دیده میشوند.
1import numpy as np
2import matplotlib.pyplot as plt
3from matplotlib import style
4style.use('fivethirtyeight')
5np.random.seed(seed=42)
6mu = np.array([7,5]).reshape(2,1)
7mu_c = np.array([4,3]).reshape(2,1)
8fig = plt.figure(figsize=(10,10))
9ax0 = fig.add_subplot(111)
10ax0.set_xlim(-1,10)
11ax0.set_ylim(-1,10)
12# Plot the meshgrid
13X,Y = np.meshgrid(np.linspace(-1,10,num=12),np.linspace(-1,10,num=12))
14data = np.array([X.reshape(1,144),Y.reshape(1,144)]).reshape(2,144)
15ax0.scatter(X,Y)
16# Transform the data using w
17w = np.array([[0.5,0],[0,0.5]])
18data_trans = np.dot(data.T,w)
19mu_trans = np.dot(mu.reshape(2,1).T,w).reshape(2,1)
20mu_c_trans = np.dot(mu_c.reshape(2,1).T,w).reshape(2,1)
21ax0.scatter(data_trans[:,0],data_trans[:,1],alpha=0.8,color='grey',edgecolor='black')
22# Plot mu, mu_trans, mu_k, and mu_k_trans
23# Plot mu and mu_k
24for i in [mu,mu_c,mu_trans,mu_c_trans]:
25 ax0.scatter(i[0],i[1],s=80)
26ax0.annotate('mu',[mu[0],mu[1]])
27ax0.annotate('mu_c',mu_c)
28ax0.annotate('mu_c_transformed',mu_c_trans)
29ax0.annotate('mu_transformed',mu_trans)
30plt.show()اسامی mu ،mu_c به ترتیب میانگین و میانگین گروه c بوده و mu_transformed و mu_c_transformed نیز بیانگر میانگین و میانگین همان گروه با توجه به تبدیل فرضی هستند. همانطور که در کد میبینید ماتریس تبدیل به صورت دلخواه انتخاب شده و به شکل زیر نوشته شده است. یعنی این تبدیل، طول و عرض هر نقطه را نصف میکند.
1[[ 0.5 0. ]
2 [ 0. 0.5]]مطابق کد بالا دادههای مربوط به data به صورت زیر خواهد بود که مشخص است که ماتریس با ۲ سطر و 12 ستون است.
1[[ -1. 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. -1. 0.
2 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. -1. 0. 1. 2.
3 3. 4. 5. 6. 7. 8. 9. 10. -1. 0. 1. 2. 3. 4.
4 5. 6. 7. 8. 9. 10. -1. 0. 1. 2. 3. 4. 5. 6.
5 7. 8. 9. 10. -1. 0. 1. 2. 3. 4. 5. 6. 7. 8.
6 9. 10. -1. 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
7 -1. 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. -1. 0.
8 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. -1. 0. 1. 2.
9 3. 4. 5. 6. 7. 8. 9. 10. -1. 0. 1. 2. 3. 4.
10 5. 6. 7. 8. 9. 10. -1. 0. 1. 2. 3. 4. 5. 6.
11 7. 8. 9. 10.]
12 [ -1. -1. -1. -1. -1. -1. -1. -1. -1. -1. -1. -1. 0. 0.
13 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 1. 1. 1.
14 1. 1. 1. 1. 1. 1. 1. 1. 2. 2. 2. 2. 2. 2.
15 2. 2. 2. 2. 2. 2. 3. 3. 3. 3. 3. 3. 3. 3.
16 3. 3. 3. 3. 4. 4. 4. 4. 4. 4. 4. 4. 4. 4.
17 4. 4. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5.
18 6. 6. 6. 6. 6. 6. 6. 6. 6. 6. 6. 6. 7. 7.
19 7. 7. 7. 7. 7. 7. 7. 7. 7. 7. 8. 8. 8. 8.
20 8. 8. 8. 8. 8. 8. 8. 8. 9. 9. 9. 9. 9. 9.
21 9. 9. 9. 9. 9. 9. 10. 10. 10. 10. 10. 10. 10. 10.
22 10. 10. 10. 10.]]عناصر یا ستونهای سطر اول در ابتدا و عناصر یا ستونهای سطر دوم نیز در انتهای کادر بالا دیده میشوند. حال به بررسی نتیجه تبدیل میپردازیم. ماتریس تبدیل یافته به شکل زیر خواهد بود.
1[[-0.5 0. 0.5 1. 1.5 2. 2.5 3. 3.5 4. 4.5 5. -0.5 0. 0.5
2 1. 1.5 2. 2.5 3. 3.5 4. 4.5 5. -0.5 0. 0.5 1. 1.5 2.
3 2.5 3. 3.5 4. 4.5 5. -0.5 0. 0.5 1. 1.5 2. 2.5 3. 3.5
4 4. 4.5 5. -0.5 0. 0.5 1. 1.5 2. 2.5 3. 3.5 4. 4.5 5.
5 -0.5 0. 0.5 1. 1.5 2. 2.5 3. 3.5 4. 4.5 5. -0.5 0. 0.5
6 1. 1.5 2. 2.5 3. 3.5 4. 4.5 5. -0.5 0. 0.5 1. 1.5 2.
7 2.5 3. 3.5 4. 4.5 5. -0.5 0. 0.5 1. 1.5 2. 2.5 3. 3.5
8 4. 4.5 5. -0.5 0. 0.5 1. 1.5 2. 2.5 3. 3.5 4. 4.5 5.
9 -0.5 0. 0.5 1. 1.5 2. 2.5 3. 3.5 4. 4.5 5. -0.5 0. 0.5
10 1. 1.5 2. 2.5 3. 3.5 4. 4.5 5. ]
11 [-0.5 -0.5 -0.5 -0.5 -0.5 -0.5 -0.5 -0.5 -0.5 -0.5 -0.5 -0.5 0. 0. 0.
12 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.5 0.5 0.5 0.5 0.5
13 0.5 0.5 0.5 0.5 0.5 0.5 0.5 1. 1. 1. 1. 1. 1. 1. 1.
14 1. 1. 1. 1. 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5 1.5
15 1.5 1.5 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.5
16 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 2.5 3. 3. 3. 3.
17 3. 3. 3. 3. 3. 3. 3. 3. 3.5 3.5 3.5 3.5 3.5 3.5
18 3.5 3.5 3.5 3.5 3.5 3.5 4. 4. 4. 4. 4. 4. 4. 4. 4.
19 4. 4. 4. 4.5 4.5 4.5 4.5 4.5 4.5 4.5 4.5 4.5 4.5 4.5
20 4.5 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. ]]نمودار دادهها اصلی و تبدیل شده به همراه میانگینها در تصویر زیر قابل مشاهده است. البته تعداد ابعاد در اینجا کاهش نیافته است ولی مشخص است دادهها جابجا شدهاند.

با اعمال ماتریس تبدیل $$w$$ میزان پراکندگی درون گروهی مطابق رابطه زیر محاسبه خواهد شد.
$$\large S_W= \sum_{c \in classes}\sum_{x_j \in c}(w^T(x_j-\mu_c))(w^T(x_j-\mu_c))^T =w^T S_W w$$
از طرفی شیوه محاسبه پراکندگی بین گروهی نیز تغییر کرده و به شکل زیر درخواهد آمد.
$$ \large S_B=\sum_{c \in classes} N_c(w^T(\mu_c-\mu))(w^T(\mu_c-\mu))^T =w^T S_B w$$
به این ترتیب نسبت پراکندگی بین گروهی به درون گروهی به شکل زیر نوشته و محاسبه میشود.
$$ \large \dfrac{w^T S_B w}{w^T S_W w}$$
به منظور بیشینهکردن این کسر میتوان صورت کسر را حداکثر کرده و مخرج را ثابت در نظر گرفت. این قید را در محاسبات مدل لحاظ کرده و آن را به صورت زیر در میآوریم.
$$\large w^TS_Ww= K$$
به این ترتیب رابطه زیر را میتوان نوشت.
$$\large L=w^T S_B w-\lambda(w^T S_W w-K)$$
این حالت معادله را فرم لاگرانژی با پارامتر $$\lambda$$ مینامند، که قید در مدل نیز ظاهر شده است. برای حل این مسئله از روال معمول یعنی مشتقگیری و پیدا کردن نقاط اکسترمم استفاده میشود. در نتیجه رابطه زیر را برحسب مشتق خواهیم نوشت.
$$\large \frac{\delta L}{\delta w}=S_Bw-\lambda S_Ww=0$$
توجه داشته باشید که این معادله به صورت ماتریسی یا برداری است. در نتیجه این مشتق با بردار صفر برابر خواهد بود. به این ترتیب مقدار $$S_BW$$ برحسب $$S_Ww$$ بدست خواهد آمد.
$$ \large S_Bw=\lambda S_W w$$
جوابهای این معادله دقیقا همان فرم مقدارهای ویژه و بردارهای ویژه است. با شرط وجود داشتن معکوس ماتریس $$S_W$$ در این حالت خواهیم داشت:
$$\large S_W^{-1}S_Bw=\lambda w\\ \large (S_W^{-1}S_B-\lambda I)w=0$$
جوابهای این معادله، مقدارهای ویژه ($$\lambda$$) و بردارهای ویژه ($$w$$) برای ماتریس $$\large S_W^{-1}S_B$$ هستند که بوسیله تابع (numpy.linalg.eig(a در زبان برنامهنویسی پایتون قابل محاسبهاند.
نکته: البته برای محاسبه به روش دستی کافی است که $$\det(S_W^{-1}S_B-\lambda I)=0$$ را محاسبه کرده و $$\lambda$$ را بدست آوریم. با جایگذاری این مقدار در رابطه $$(S_W^{-1}S_B-\lambda\boldsymbol{I})\boldsymbol{w}=0$$ دستگاه معادلات خطی و بردارهای ویژه حاصل میشود. به این ترتیب بردار ویژه برای هر بعد ایجاد میشود. به این ترتیب امکان محاسبه دادههای تبدیل یافته بوجود آمده و ماتریس $$w$$ حاصل و تحلیل LDA صورت خواهد گرفت. از آنجایی که انجام این محاسبات توسط Numpy قابل انجام است، کد زیر را آورده و کل فرآیند انجام محاسبات برای LDA را بازنویسی کردهایم. گامهایی که در این کد دنبال شده است به قرار زیر هستند.
- استاندارد کردن دادهها به صورتی که میانگین آنها صفر و واریانس برابر با ۱ باشد. این عمل توسط محاسبه مقدارهای z برای آنها مقدور است. دستور standardScaler در کتابخانه sklearn.preprocessing برای انجام این کار مناسب است.
- محاسبه میانگین کل و میانگین برای هر گروه. این کار درون یک حلقه تکرار صورت گرفته است.
- محاسبه $$S_W$$ و $$S_B$$. برای انجام این محاسبات، از ضرب داخلی np.dot استفاده شده است.
- محاسبه بردار و مقدارهای ویژه $$S^{-1}_WS_B$$ به منظور پیدا کردن $$w$$ که نسبت $$\frac{\boldsymbol{w}^T S_B \boldsymbol{w}}{\boldsymbol{w}^T S_W \boldsymbol{w}}$$ را حداکثر کند. مقدار و بردارهای ویژه توسط دستور np.linalg.eig حاصل میشود.
- انتخاب k مقدار ویژهای که از بقیه مقدارهای ویژه بزرگتر هستند. با این کار میتوانیم ماتریس دادهها را از $$n \times d$$ به $$n \times k$$ تقلیل دهیم. مشخص است که ماتریس $$w$$ در این حالت دارای ابعاد $$d \times k$$ خواهد بود. ستونهای این ماتریس همان بردار ویژه هستند. معمولا با توجه به حساسیت مسئله مقدار k را از ۲ تا ۵ انتخاب میکنند. البته انتخاب مناسب برای این پارامتر میتواند توسط اعتبار سنجی متقابل نیز انجام شود.
- استفاده از ماتریس $$w$$ به منظور تبدیل دادهها و کاهش بعد و محاسبه $$Y$$.
استفاده از آنالیز LDA روی دادههای واقعی
مجموعه دادههای با نام vingar.txt دارای ۱۳ متغیر کمی و البته یک متغیر کیفی یا طبقهای است که مشاهدات را به سه گروه تقسیم میکند. میتوانید این فایل را از اینجا دریافت کنید.
میخواهیم به کمک آنالیز LDA این دادهها را به بهترین وجه به سه گروه تقسیم کرده و به جای استفاده از ۱۳ متغیر، به کمک تبدیل $$w$$، فقط از دادههایی با دو بُعد برای انجام این کار، بهره ببریم. کد زیر به این علت تهیه شده است.
1import pandas as pd
2import numpy as np
3import matplotlib.pyplot as plt
4from sklearn.preprocessing import StandardScaler
5import matplotlib.pyplot as plt
6from matplotlib import style
7from sklearn.model_selection import train_test_split
8style.use('fivethirtyeight')
9from sklearn.neighbors import KNeighborsClassifier
10# 0. Load in the data and split the descriptive and the target feature
11df = pd.read_csv('/vinegar.txt',sep=',',names=['target','Alcohol','Malic_acid','Ash','Akcakinity','Magnesium','Total_pheonols','Flavanoids','Nonflavanoids','Proanthocyanins','Color_intensity','Hue','OD280','Proline'])
12X = df.iloc[:,1:].copy()
13target = df['target'].copy()
14X_train, X_test, y_train, y_test = train_test_split(X,target,test_size=0.3,random_state=0)
15# 1. Standardize the data
16for col in X_train.columns:
17 X_train[col] = StandardScaler().fit_transform(X_train[col].values.reshape(-1,1))
18# 2. Compute the mean vector mu and the mean vector per class mu_k
19mu = np.mean(X_train,axis=0).values.reshape(13,1) # Mean vector mu --> Since the data has been standardized, the data means are zero
20mu_k = []
21for i,orchid in enumerate(np.unique(df['target'])):
22 mu_k.append(np.mean(X_train.where(df['target']==orchid),axis=0))
23mu_k = np.array(mu_k).T
24# 3. Compute the Scatter within and Scatter between matrices
25data_SW = []
26Nc = []
27for i,orchid in enumerate(np.unique(df['target'])):
28 a = np.array(X_train.where(df['target']==orchid).dropna().values-mu_k[:,i].reshape(1,13))
29 data_SW.append(np.dot(a.T,a))
30 Nc.append(np.sum(df['target']==orchid))
31SW = np.sum(data_SW,axis=0)
32SB = np.dot(Nc*np.array(mu_k-mu),np.array(mu_k-mu).T)
33
34# 4. Compute the Eigenvalues and Eigenvectors of SW^-1 SB
35eigval, eigvec = np.linalg.eig(np.dot(np.linalg.inv(SW),SB))
36
37# 5. Select the two largest eigenvalues
38eigen_pairs = [[np.abs(eigval[i]),eigvec[:,i]] for i in range(len(eigval))]
39eigen_pairs = sorted(eigen_pairs,key=lambda k: k[0],reverse=True)
40w = np.hstack((eigen_pairs[0][1][:,np.newaxis].real,eigen_pairs[1][1][:,np.newaxis].real)) # Select two largest
41# 6. Transform the data with Y=X*w
42Y = X_train.dot(w)
43# Plot the data
44fig = plt.figure(figsize=(10,10))
45ax0 = fig.add_subplot(111)
46ax0.set_xlim(-3,3)
47ax0.set_ylim(-4,3)
48for l,c,m in zip(np.unique(y_train),['r','g','b'],['s','x','o']):
49 ax0.scatter(Y[0][y_train==l],
50 Y[1][y_train==l],
51 c=c, marker=m, label=l,edgecolors='black')
52ax0.legend(loc='upper right')
53# Plot the voroni spaces
54means = []
55for m,target in zip(['s','x','o'],np.unique(y_train)):
56 means.append(np.mean(Y[y_train==target],axis=0))
57 ax0.scatter(np.mean(Y[y_train==target],axis=0)[0],np.mean(Y[y_train==target],axis=0)[1],marker=m,c='black',s=100)
58
59mesh_x, mesh_y = np.meshgrid(np.linspace(-3,3),np.linspace(-4,3))
60mesh = []
61for i in range(len(mesh_x)):
62 for j in range(len(mesh_x[0])):
63 date = [mesh_x[i][j],mesh_y[i][j]]
64 mesh.append((mesh_x[i][j],mesh_y[i][j]))
65NN = KNeighborsClassifier(n_neighbors=1)
66NN.fit(means,['r','g','b'])
67predictions = NN.predict(np.array(mesh))
68ax0.scatter(np.array(mesh)[:,0],np.array(mesh)[:,1],color=predictions,alpha=0.3)
69plt.show()توجه داشته باشید که در اینجا ۳۰٪ دادهها برای آزمایش استفاده شده است و ۷۰٪ آنها برای آموزش مدل به کار رفته است. خروجی مطابق با تصویر زیر خواهد بود. البته ابتدا توضیحاتی نیز توسط مفسر کد پایتون ظاهر میشود.
1/home/bernd/anaconda3/lib/python3.6/site-packages/ipykernel_launcher.py:21: SettingWithCopyWarning:
2A value is trying to be set on a copy of a slice from a DataFrame.
3Try using .loc[row_indexer,col_indexer] = value instead
4See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy
5/home/bernd/anaconda3/lib/python3.6/site-packages/sklearn/utils/validation.py:475: DataConversionWarning: Data with input dtype int64 was converted to float64 by StandardScaler.
6 warnings.warn(msg, DataConversionWarning)همانطور که در نمودار دیده میشود، سه گروه مجزا از یکدیگر توسط دو بعد تشکیل شده است. هر کدام از اعضای واقعی گروهها با علامت مربع، دایره و ضربدر مشخص شدهاند و نواحی مربوط به هر گروه که توسط LDA مشخص شده نیز با رنگهای قرمز و آبی و سبز دیده میشود.
آنالیز تشخیصی خطی با sklearn
برای اجرای آنالیز تشخیصی خطی در پایتون میتوانید از کتابخانه sklearn نیز استفاده کنید. روش ارائه دادهها در اینجا درست به مانند قبل است ولی میتوان با کدهای کمتری مدل آنالیز تشخیصی خطی را اجرا کرد.
باز هم در این قسمت دادهها به دو گروه آموزشی (Train) و آزمایشی (Test) تقسیم شدهاند. توجه داشته باشید که قبلا از اجرای این برنامه، فایل اطلاعاتی را بارگذاری کرده و آدرس محل آن را در قسمت pd.read_csv برنامه مشخص کنید.
1import pandas as pd
2import numpy as np
3import matplotlib.pyplot as plt
4from sklearn.preprocessing import StandardScaler
5import matplotlib.pyplot as plt
6from matplotlib import style
7from sklearn.model_selection import train_test_split
8style.use('fivethirtyeight')
9from sklearn.neighbors import KNeighborsClassifier
10from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
11# 0. Load in the data and split the descriptive and the target feature
12df = pd.read_csv('/vinegar.txt',sep=',',names=['target','Alcohol','Malic_acid','Ash','Akcakinity','Magnesium','Total_pheonols','Flavanoids','Nonflavanoids','Proanthocyanins','Color_intensity','Hue','OD280','Proline'])
13X = df.iloc[:,1:].copy()
14target = df['target'].copy()
15X_train, X_test, y_train, y_test = train_test_split(X,target,test_size=0.3,random_state=0)
16# 1. Instantiate the method and fit_transform the algotithm
17LDA = LinearDiscriminantAnalysis(n_components=2) # The n_components key word gives us the projection to the n most discriminative directions in the dataset. We set this parameter to two to get a transformation in two dimensional space.
18data_projected = LDA.fit_transform(X_train,y_train)
19print(data_projected.shape)
20# PLot the transformed data
21markers = ['s','x','o']
22colors = ['r','g','b']
23fig = plt.figure(figsize=(10,10))
24ax0 = fig.add_subplot(111)
25for l,m,c in zip(np.unique(y_train),markers,colors):
26 ax0.scatter(data_projected[:,0][y_train==l],data_projected[:,1][y_train==l],c=c,marker=m)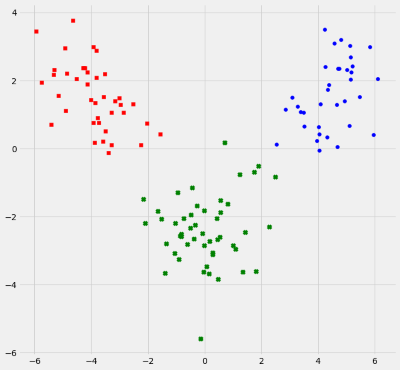
همانطور که میبینید نتیجه با این روش نیز درست به مانند قبل است. برای اجرای برنامه و یا کدهای پایتون میتوانید از نرمافزارهای مختلف در محیط وب یا روی رایانه شخصی خود استفاده کنید. اگر میخواهید بدون نصب هیچ برنامهای، در محیط وب کدهای پایتون را اجرا کنید از سایت بنیاد پایتون وارد پوسته اجرای پایتون شوید و کدهایتان را اجرا کنید. همچنین برای نصب مفسر پایتون در رایانه شخصی شاید استفاده از Canopy گزینه مناسبی باشد.
اگر مطلب بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای بهینه سازی چند هدفه
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- گنجینه آموزش های محاسبات هوشمند
- احتمال شرطی (Conditional Probability) — اصول و شیوه محاسبه
- تحلیل تشخیص خطی فیشر (Fisher’s Linear Discriminant) — پیاده سازی در پایتون
- تحلیل واریانس (Anova) — مفاهیم و کاربردها
^^