ماتریس مربعی و خصوصیات آن — از صفر تا صد

احتمالا در نوشتارهای دیگر مجله فرادرس، با ماتریس‌ها برخورد کرده‌اید. واضح است که ماتریس‌ها یک ساختار نمایش عددی هستند که بخصوص در بیان پدیده‌های «چند متغیره» (Multivariate) بسیار موثر عمل می‌کنند. در این بین «ماتریس مربعی» (Square Matrix) یکی از ماتریس‌های پرکاربرد در «جبر خطی» (Linear Algebra) و محاسبات ماتریسی محسوب می‌شود، زیرا بسیاری از عملگرها در جبر خطی توسط چنین ماتریس‌هایی صورت می‌گیرد.

اگر می‌خواهید در مورد اصطلاحات به کار رفته در این متن، اطلاعاتی بیشتری داشته باشید، پیشنهاد می‌شود که مطالب دیگر مجله فرادرس با عناوین ماتریس‌ها در ریاضی — به زبان ساده و ترانهاده ماتریس — به زبان ساده را بخوانید. همچنین خواندن نوشتارهای دترمینان یک ماتریس و محاسبه آن — به زبان ساده و اثر ماتریس (Trace) در جبر خطی — به زبان ساده نیز خالی از لطف نیست.

ماتریس مربعی چیست؟

قبل از آنکه به معرفی ماتریس مربعی بپردازیم، ماتریس‌ها را براساس تعداد سطر و ستون‌هایشان معرفی می‌کنیم.

همانطور که می‌دانید، ماتریس یک ساختار برای نمایش اعداد است که به صورت یک جدول در نظر گرفته می‌شود. این جدول دارای چندین سطر و ستون است. عناصر یا اعداد درون این جدول، «درایه» (Element) نامیده می‌شوند. برای مثال ممکن است یک ماتریس دارای ۳ سطر و۴ ستون باشد. چنین ماتریسی را ممکن است به صورت زیر نشان می‌دهیم و به آن یک ماتریس سه در چهار می‌گوییم.

$$ \begin{bmatrix}a & b& c & d \\ e & f & g &h
\\ i & j & k & l  \end{bmatrix} $$

واضح است که حروف a تا l می‌توانند با اعداد جایگزین شوند. البته معمولا برای نمایش یک ماتریس از شکل نمادین آن کمک می‌گیرند. برای مثال ماتریس $$A$$ را که از $$m$$ سطر و $$n$$ ستون تشکیل شده، به صورت زیر نشان می‌دهیم.

$$ \large A = [a_{ij} ]_{m \times n }, \;\;\; i = 1 , 2, \ldots ,m ; \;\; j = 1 , 2, \ldots , n $$

چنین ماتریسی را یک ماتریس $$m$$ در $$n$$ می‌گویند. واضح است که $$a_{ij}$$‌ درایه مربوط به سطر $$i$$ام و ستون $$j$$ام است. به حدودی که مقادیر $$i$$ و $$j$$ دارند، دقت کنید.

تعریف ماتریس مربعی

در ریاضیات، ماتریس مربعی (Square Matrix)، ماتریسی است که تعداد سطرها و ستون‌های آن برابر باشد. به این ترتیب یک ماتریس مربعی با ۴ سطر یا ستون به صورت زیر قابل نمایش است.

$$ \large A = \begin{bmatrix} a & b& c & d \\ e & f & g &h
\\ i & j & k & l \\ m & n & o & p \end{bmatrix} $$

به این ترتیب می‌توان چنین ماتریسی را به شکل زیر معرفی کرد.

$$ \large A_{n \times n} = [a_{ij}]_{n \times n } ,\;\;\; i , j = 1 , 2, \ldots , n $$

ماتریس‌های زیر همگی مربعی هستند.

$$ \large A = \begin{bmatrix} 1 & 0 \\
0 & 1 \end{bmatrix} $$

ماتریس مربعی $$2 \times 2 $$

$$ \large A = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0  \\ 14 & 2.55 & 1 \end{bmatrix} $$

ماتریس مربعی $$ 3 \times 3 $$

$$ \large A = \begin{bmatrix} 1 & -2 & 4 & 6 \\
8 & -\sqrt{2} & -\frac{3}{4} & -5
\\ 14 & 2.55 & 18 & -12.3 \\ 8.54 & \pi & 0 & 0 \end{bmatrix} $$

ماتریس مربعی $$4 \times 4 $$

چند ماتریس مربعی خاص

با توجه به ویژگی‌هایی که یک ماتریس مربعی می‌تواند داشته باشد، آن‌ها را به گونه‌های مختلفی طبقه‌بندی می‌کنند. در ادامه به بعضی از این گونه‌ها و همچنین ماتریس‌هایی از نوع خاص خواهیم پرداخت.

ماتریس قطری و ماتریس مثلثی

یکی از ویژگی‌های جالب در ماتریس مربعی، وجود «قطر اصلی» (Main Diagonal) است. عناصری که به صورت $$a_{ii}$$ باشند، درایه‌های قطر اصلی نامیده می‌شوند.

از طرفی بقیه عناصر چنین ماتریسی را درایه‌های «خارج قطر» (Off Diagonal) می‌نامند. واضح است که در این حالت، چنین درایه‌هایی به شکل $$a_{ij} , i \neq j $$ نمایش داده می‌شوند.

ماتریس قطری

چنانچه همه عناصر خارج از قطر یک ماتریس مربعی (خارج قطر)، صفر باشند، ماتریس حاصل را «ماتریس قطری» (Diagonal Matrix) می‌نامند. واضح است که ماتریس قطری حتما یک ماتریس مربعی است. در این حالت داریم.

$$ \large A = [a_ij]_{n \times n } , a_{ij} = 0 , \forall i \neq j $$

که برای $$n = 3$$، آن را به صورت زیر می‌توان نشان داد.

$$ \large {\begin{bmatrix} a_{11} & 0 & 0 \\ 0 & a_{22} & 0 \\ 0 & 0 & a_{33} \end{bmatrix}} $$

برای مثال ماتریس زیر یک ماتریس قطری است.

$$ \large A = \begin{bmatrix} 15 & 0 & 0 \\ 0 & 3 & 0  \\ 0 & 0 & 11 \end{bmatrix} $$

نکته: اگر همه درایه‌های یک ماتریس صفر باشد، آن را «ماتریس صفر» (Zero Matrix) می‌نامند. همانطور که می‌دانید، ماتریس همانی نقش عضو خنثی عمل ضرب ماتریسی را ایفا می‌کند. به همین ترتیب ماتریس صفر نیز عضو خنثی عمل جمع ماتریس‌ها است. البته توجه داشته باشید که ضرورتی بر مربعی بودن ماتریس صفر نیست.

$$ \large 0_{{{m,n}}} = {\begin{bmatrix} 0 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 \end{bmatrix}}_{{m\times n}} $$

به این ترتیب خواهیم داشت.

$$ \large 0_{m \times n} + A_{m \times n } = A_{m \times n } + 0_{m \times n}  = A_{m \times n} $$

ماتریس بالا مثلثی و پایین مثلثی

ماتریس مربعی را در نظر بگیرید که همه عناصر پایین قطر اصلی آن صفر باشند. چنین ماتریسی به «ماتریس بالا مثلثی» (Upper Triangular Matrix) شهرت دارد. زیرا حداقل یکی از عناصر بالای قطر اصلی، صفر نیست.

ساختار چنین ماتریسی برای $$n=3$$ به صورت زیر است.

$$ \large {\begin{bmatrix}a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & 0 & a_{33} \end{bmatrix}} $$

در مقابل اگر همه عناصر بالای قطر اصلی صفر باشند، ماتریس حاصل را «پایین مثلثی» (Lower Triangular Matrix) می‌گویند، زیرا حداقل یکی از عناصر زیر قطر اصلی، غیر صفر است. ماتریس زیر، نمایش یک ماتریس پایین مثلثی با سه ستون (یا سطر) است.

$$ \large {\begin{bmatrix}a_{11} & 0 & 0 \\ a_{21} & a_{22} & 0 \\ a_{31} & a_{32} & a_{33} \end{bmatrix}} $$

ماتریس همانی

ماتریس $$I_n$$ را یک ماتریس همانی می‌گویند اگر یک ماتریس قطری با مقادیر ۱ باشد. به این ترتیب همه درایه‌های قطر اصلی در این ماتریس برابر با ۱ بوده و عناصر خارج قطر، صفر هستند. ماتریس‌های زیر همگی ماتریس همانی محسوب می‌شوند.

$$ \large I_{1} = {\begin{bmatrix} 1 \end{bmatrix}},\ I_{2} = {\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}},\ \cdots ,\ I_{n} = {\begin{bmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots &0\\\vdots & \vdots &\ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{bmatrix}} $$

از آنجایی که حاصل‌ضرب این ماتریس در هر ماتریس دیگر، همان ماتریس را نتیجه می‌دهد، آن را «ماتریس همانی» (Identity Matrix) می‌نامند. به این ترتیب برای هر ماتریس $$m \times n $$‌ مثل $$A$$ داریم:

$$ \large A I_n = I_m A = A $$

ماتریس متقارن و ماتریس پادمتقارن

ماتریس $$A$$ را در نظر بگیرید. اگر جای سطرها را با ستون‌های چنین ماتریسی عوض کنیم، ماتریس دیگری ساخته می‌شود که به آن «ترانهاده» (Transpose) ماتریس اولیه می‌گویند که با نماد $$A^T$$ نمایش داده می‌شود.

حال اگر ماتریس مربعی $$A$$ با ترانهاده‌اش یعنی $$A^T$$ برابر باشد، ماتریس $$A$$ را «متقارن» (Symmetric) می‌گویند. واضح است که رابطه زیر بین ماتریس $$A$$ و $$A^T$$ برقرار است.

$$ \large  A =  A^T $$

مشخص است که ماتریس زیر یک ماتریس متقارن است.

$$ \large {\displaystyle A = {\begin{bmatrix} 1 & 7 & 3 \\ 7 & 4 & -5 \\ 3 & -5 & 6 \end{bmatrix}}} $$

همچنین اگر بین ماتریس $$A$$ و ترانهاده‌اش، رابطه‌ای به شکل زیر برقرار باشد،‌ ماتریس $$A$$ را «ماتریس پادمتقارن» (Skew-symmetric Matrix) می‌نامند.

$$ \large A =\ – \ A^T $$

با توجه به تعریف ارائه شده، ماتریس زیر یک ماتریس پادمتقارن خواهد بود.

$$ \large {\displaystyle A = {\begin{bmatrix} 1 & 2 & -45 \\ -2 & 0 & -4 \\ 45 & 4 & 0 \end{bmatrix}}} $$

زیرا داریم:

$$ \large {\displaystyle -A = {\begin{bmatrix} 1 & -2 & 45 \\ 2 & 0 & 4 \\ -45 & -4 & 0 \end{bmatrix}} = A^{\textsf {T}}} $$

نکته: در ماتریس‌ با عناصر مختلط که «ماتریس مختلط» (Complex Matrix)، نامیده می‌شود، تقارن با مفهوم «ماتریس هرمیتی» (Hermitian Matrix) جایگزین می‌شود.

ماتریس نرمال

ماتریس مربعی $$A$$ را «ماتریس نرمال» (Normal Matrix) می‌نامند، اگر حاصل‌ضرب ماتریس $$A$$ در ترانهاده آن از هر دو طرف برابر باشد. به این ترتیب خواهیم داشت:

$$ \large {\displaystyle A^{\mathrm {T} }A=AA^{\mathrm {T} }} $$

هر چند ضرب ماتریسی، خاصیت جابجایی ندارد ولی ضرب ماتریس نرمال در ترانهاده‌اش خاصیت جابجایی خواهد داشت. برای مثال ماتریس زیر را در نظر بگیرید.

$$ \large A = {\begin{pmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \end{pmatrix}} $$

ماتریس $$A$$ در این جا، یک ماتریس نرمال است، زیرا:

$$ \large AA^{T} = {\begin{pmatrix} 2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 2 \end{pmatrix}} = A^{T}A $$

اگر ترانهاده ماتریس $$A$$ را محاسبه کنید مشخص می‌شود که در اینجا $$A^T$$ به صورت زیر خواهد بود.

$$ \large A^T = {\begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 0 \\ 0 & 1 & 1 \end{pmatrix}} $$

ماتریس معکوس‌پذیر

در ریاضیات معکوس‌پذیری برای ماتریس‌های مربعی تعریف شده است. ماتریس $$B$$ را معکوس ماتریس $$A$$ گویند اگر حاصل‌ضرب ماتریسی آن‌ها، ماتریس همانی را نتیجه دهد. به این ترتیب داریم:

$$ \large {\displaystyle AB = BA = I_{n}} $$

اگر ماتریسی مثل $$B$$ وجود داشته باشد که در رابطه بالا صدق کند، آن را «ماتریس معکوس» (Inverse Matrix) ماتریس $$A$$ نامیده و با نماد $$A^{-1}$$ مشخص می‌کنند.

نکته: برای ماتریس‌های غیر مربعی، تعریف ماتریس معکوس نیز وجود دارد که به آن «ماتریس معکوس تعمیم یافته» (Generalized Inverse Matrix) گفته می‌شود. البته روش پیدا کردن و بعضی از خصوصیات آن با معکوس ماتریس مربعی متفاوت است.

ماتریس متعامد

اگر ماتریس مربعی با مقادیر حقیقی به شکلی باشد که سطرها و ستون‌های آن تشکیل «بردارهای متعامد واحد» (Orthogonal Unit Vector) یا بردارهای «اورتونرمال» (Orthonormal) بدهند،‌ ماتریس را «ماتریس متعامد» (Orthogonal Matrix) می‌نامند.

این ویژگی را به شکل دیگری نیز می‌توان نشان داد. ماتریس $$A$$ را متعامد می‌گویند اگر معکوس آن همان ترانهاده‌اش باشد. یعنی

$$ \large A^{\mathrm{T} } = A^{-1} \, $$

بنابراین داریم:

$$ \large A^{ \mathrm{T} } A = A A^{ \mathrm{T} } = I \,$$

نکته: هر ماتریس متعامدی، ضرورتا، معکوس‌پذیر بوده و معکوس آن ترانهاده ماتریس متعامد است. چنین ماتریسی را می‌توان یک ماتریس نرمال نیز نامید.

«دترمینان» (Determinant) ماتریس متعامد یا برابر با ۱- است یا ۱، در نتیجه تبدیل خطی تحت ماتریس متعامد با دترمینان مثبت، یک «دوران» (Rotation) و تحت ماتریس متعامد با دترمینان منفی، یک «انعکاس» (Reflection) خواهد بود.

توجه داشته باشید که مشابه ماتریس متعامد در ماتریس‌های مختلط، «ماتریس یکانی» (Unitary Matrix) است.

کاربرد ماتریس‌های مربعی

از ماتریس‌های مربعی، اغلب در بیان «تبدیلات خطی» (Linear Transformations) مانند «چرخش» (Rotation) یا «کشیدن» (Shearing) اشکالی که به صورت ماتریسی بیان شده‌اند، استفاده می‌شود.

برای مثال اگر $$R$$ یک ماتریس مربعی متناظر با چرخش و $$\nu$$ نیز «بردار ستونی» (Column Vector) مشخص‌کننده موقعیت یک نقطه باشند، آنگاه حاصل ضرب $$R \nu$$ نقطه‌ای را نشان می‌دهد که حاصل دوران نقطه $$\nu$$ است.

نکته: اگر بردار $$\nu$$ سطری باشد، آنگاه این عمل ضرب باید به صورت $$\nu R^T$$ انجام می‌شد که در آن $$R^T$$، «ترانهاده» (Transpose) ماتریس $$R$$ است.

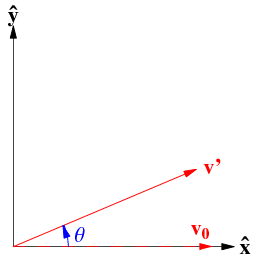
ماتریس چرخش یا دوران

نقطه یا برداری را در «مختصات دکارتی» (Cartesian Coordinates) در نظر بگیرید. واضح است که هر نقطه از این صفحه را به کمک یک بردار ستونی با دو سطر نشان خواهیم داد.

ماتریس دوران ۹۰ درجه‌ای برای چنین نقطه‌ای به صورت زیر و مطابق با یک ماتریس مربعی نوشته می‌شود.

$$ \large {\displaystyle \mathbf {A} = {\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}}}$$

همچنین اگر زاویه دوران برابر با $$\theta$$ باشد، «ماتریس دوران» (Rotation Matrix) به صورت زیر نوشته خواهد شد.

$$ \large {\displaystyle \mathbf {A} = {\begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix}}}$$

ماتریس انعکاس یا تقارن

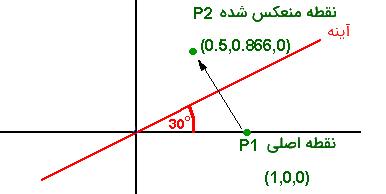
اگر بخواهیم یک نقطه را حول محور افقی (X-Axis) انعکاس داده و تصویر حاصل را مشاهده کنیم، باید بردار مربوط به نقطه را در ماتریس زیر ضرب کرده و مختصات نقطه یا نقاط جدید را در محور مختصات ترسیم کنیم.

$$ \large {\displaystyle \mathbf {A} = {\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}}} $$

اگر همین عمل را براساس محور عمودی (Y- Axis) انجام دهیم، احتیاج به ماتریسی به صورت زیر خواهیم داشت.

$$ \large {\displaystyle \mathbf {A} = {\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}}} $$

در نهایت اگر لازم باشد تصویر انعکاسی نقطه‌ای برحسب محوری با زاویه $$\theta$$ ایجاد شود، از «ماتریس انعکاس» (Reflection Matrix) زیر کمک خواهیم گرفت.

$$ \large {\displaystyle \mathbf {A} = {\begin{pmatrix}{\frac {1 – \tan ^{2}\theta }{\tan ^{2}\theta + 1}} & { \frac {2 \tan \theta }{ \tan ^{2}\theta + 1 }} \\ {\frac {2 \tan \theta }{\tan^{2}\theta + 1}} & {\frac {1 – \tan ^{2}\theta }{\tan ^{2}\theta + 1}} \end{pmatrix}}} $$

نکته: در ماتریس بالا، $$\tan \theta$$ شیب خط گذرنده از مبدا برای محور مورد نظر است.

خلاصه و جمع‌بندی

در این نوشتار با ماتریس مربعی و خصوصیات آن، آشنا شدید. همچنین چند نوع ماتریس مربعی که البته بسیار پر کاربرد نیز هستند، معرفی و ویژگی‌های آن‌ها مورد بررسی قرار گرفت. به علت خاصیت مربعی بودن این گونه ماتریس‌ها، استفاده و به کارگیری آن‌ها در جبر خطی و بخصوص «پردازش تصویر» (Image Processing) از اهمیت زیادی برخوردار است.