مشتق کسینوس – اثبات و فرمول مشتق Cos + مثال و تمرین

مثال ۱: محاسبه مشتق کسینوس ۳۰ درجه

مشتق $$ \cos \theta $$ را در $$ \theta = ۳۰ ^ {\circ } $$ به دست بیاورید.

مشتق کسینوس یک زاویه برابر با منفی سینوس آن زاویه است. به این ترتیب، داریم:

$$ \frac { d } { d x } \cos \theta = - \sin \theta $$

$$ \theta = ۳۰ ^ {\circ } $$

$$ \frac { d } { d x } \cos ( ۳۰ ^ { \circ } ) = \sin ( ۳۰ ^ { \circ } ) $$

سینوس ۳۰ درجه برابر است با:

$$ \sin ( ۳۰ ^ { \circ } ) = - \frac { ۱ } { ۲ } $$

در نتیجه:

$$ \frac { d } { d x } \cos ( ۳۰ ^ { \circ } ) = - \frac { ۱ } { ۲ } $$

در ادامه، به مرور اجمالی مشتق و معرفی فرمول کلی آن بر اساس تعریف حد می‌پردازیم. ابن مفاهیم در اثبات فرمول مشتق سینوس مورد استفاده قرار خواهند گرفت.

مشتق چیست؟

«مشتق» (Derivative)، شیب خط مماس بر منحنی تابع در یک نقطه مشخص را نمایش می‌دهد. این مفهوم، نرخ تغییرات نقطه‌ای تابع بر حسب یک متغیر است. به عنوان مثال، تصویر زیر را در نظر بگیرد. در این تصویر، بخشی از نمودار تابع $$ f ( x ) $$‌ (منحنی توپر) نمایش داده شده است. در نقطه $$ x $$، خطی را بر نمودار مماس می‌کنیم.

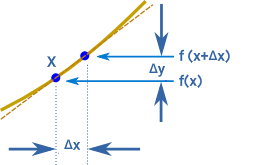
مشتق تابع $$ f ( x ) $$ در نقطه $$ x $$، شیب خط مماس در نقطه تماس با منحنی است. از آنجایی که امکان محاسبه دقیق شیب در یک نقطه وجود ندارد، از مفهوم حد استفاده می‌کنیم. بر اساس این مفهوم، فرمول کلی مشتق به صورت زیر نوشته می‌شود:

$$ \frac { \Delta y } { \Delta x } = \lim _ { \Delta x \to ۰ } \frac { f ( x + \Delta x ) - f ( x ) } { \Delta x } $$

فرمول های مشتق مهم + سوال با جواب و دانلود PDF

فیلم آموزش ریاضی پایه دانشگاهی در فرادرس

مشتق کسینوس چگونه به دست می آید ؟

مشتق کسینوس، شیب خط مماس بر منحنی این تابع مثلثاتی است. منحنی تابع کسینوس، همواره در بازه ۱- تا ۱ نوسان می‌کند.

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

تصویر زیر، منحنی تابع $$ \cos ( x) $$ را در بازه ۰ تا $$ ۲ \pi $$ (۰ تا ۳۶۰ درجه) نمایش می‌دهد.

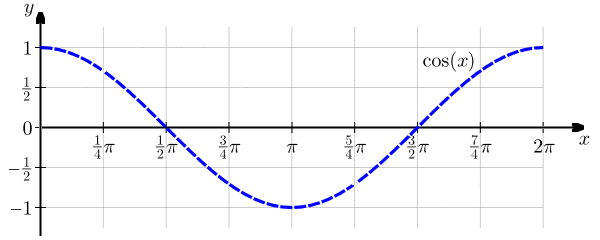
بر اساس تعریف، برای به دست آوردن مشتق cos در یک زاویه مشخص، باید شیب مماس بر منحنی تابع cos در آن زاویه را محاسبه کنیم. به عنوان مثال، مشتق کسینوس در زاویه $$ \pi $$ را در نظر بگیرید.

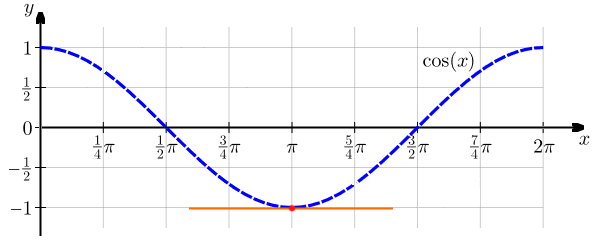
مماس بر منحنی کسینوس (مفهوم مشتق کسینوس)

همان‌طور که مشاهده می‌کنید، خط مماس بر منحنی تابع $$ \cos ( x ) $$ در نقطه $$ x = \pi $$، یک خط افقی است. به این ترتیب می‌گوییم مشتق $$ \cos ( \pi ) $$ برابر با صفر است. این نتیجه را با فرمول مشتق cos نیز بررسی می‌کنیم:

$$ \cos ^ { \prime } ( x ) = - \sin ( x ) $$

$$ \cos ^ { \prime } ( \pi ) = - \sin ( \pi ) $$

$$ \sin ( \pi ) $$ یا همان سینوس ۱۸۰ درجه برابر با صفر است. بنابراین:

$$ \cos ^ { \prime } ( \pi ) = ۰ $$

مثال ۲: مشتق کسینوس $$ \frac { \pi } { ۴ } $$

نسبت مشتق کسینوس $$ \frac { \pi } { ۴ } $$ به کسینوس $$ \frac { \pi } { ۴ } $$ را به دست بیاورید.

برای حل این مثال، ابتدا مشتق $$ \frac { \pi } { ۴ } $$ را تعیین می‌کنیم. بر اساس فرمول مشتق کسینوس، داریم:

$$ \frac { d } { d x } \cos ( x ) = - \sin( x ) $$

بنابراین:

$$ \frac { d } { d x } \cos \left ( \frac { \pi } { ۴ } \right ) = - \sin \left ( \frac { \pi } { ۴ } \right ) $$

سینوس $$ \frac { \pi } { ۴ } $$ یا همان سینوس ۴۵ درجه برابر با $$ \frac { \sqrt { ۲ } }{ ۲ } $$ است. به این ترتیب داریم:

$$ \frac { d } { d x } \cos \left ( \frac { \pi } { ۴ } \right ) = - \frac { \sqrt { ۲ } }{ ۲ } $$

از طرفی، کسینوس $$ \frac { \pi } { ۴ } $$ نیز با $$ \frac { \sqrt { ۲ } }{ ۲ } $$ برابری می‌کند. از این‌رو، برای نسبت مشتق کسینوس $$ \frac { \pi } { ۴ } $$ به کسینوس $$ \frac { \pi } { ۴ } $$ داریم:

$$
\frac { \frac { d } { d x } \cos \left ( \frac { \pi } { ۴ } \right ) }{ \cos \left ( \frac { \pi } { ۴ } \right ) } = \frac { - \frac { \sqrt { ۲ } }{ ۲ } }{ \frac { \sqrt { ۲ } }{ ۲ } } = -۱
$$

مقایسه مشتق کسینوس و سینوس

سینوس، یکی از توابع مثلثاتی اصلی است. مشتق این تابع از رابطه زیر به دست می‌آید:

$$ \frac { d } { d x } \sin ( x ) = \cos ( x ) $$

همان‌طور که مشاهده می‌کنید، مشتق سینوس برابر با کسینوس است. به عنوان مثال، مشتق تابع $$ y = \sin ( x ) $$ در نقطه $$ x = \pi $$ به صورت زیر محاسبه می‌شود:

$$ \frac { d } { d x } \sin ( \pi ) = \cos ( \pi ) $$

$$ \cos ( \pi ) $$ یا همان کسینوس زاویه ۱۸۰ درجه برابر با ۱ است. بنابراین داریم:

$$ \sin ^ { \prime } ( \pi ) = ۱ $$

مشتق سینوس – محاسبه و فرمول مشتق Sin + مثال و تمرین

تصویر زیر، نمودارهای دو تابع $$ \sin ( x ) $$ و $$ \cos ( x ) $$ را در بازه ۰ تا $$ ۲ \pi $$ نمایش می‌دهد.

سینوس و کسینوس به اندازه $$ \frac { \pi } { ۲ } $$ با یکدیگر اختلاف فاز دارند. بنابراین:

$$ \sin \left ( \frac { \pi } { ۲ } + \theta \right ) = + \cos ( \theta ) $$

$$ \cos \left ( \frac { \pi } { ۲ } + \theta \right ) = - \sin ( \theta ) $$

$$ \cos \left ( \frac { \pi } { ۲ } - \theta \right ) = \sin ( \theta ) $$

$$ \sin \left ( \frac { \pi } { ۲ } - \theta \right ) = \cos ( \theta ) $$

روابط بالا در اثبات فرمول مشتق کسینوس کاربرد دارند.

مثال ۳: محاسبه مشتق سینوس

تابع $$ f ( x ) $$ را در نظر بگیرید:

$$ f ( x ) = ۲ \cos ( x ) + \frac { ۱ } { ۳ } \sin ( x ) $$

مشتق این تابع را در $$ x = \frac { \pi } { ۶ } $$ به دست بیاورید.

تابع تابع $$ f ( x ) $$، حاصل جمع دو تابع مثلثاتی (سینوس و کسینوس) است. با توجه به قوانین مشتق‌گیری، مشتق جمع دو تابع با مجموع مشتق‌های آن دو تابع برابری می‌کند. به عبارت دیگر:

$$ ( u ( x ) + v ( x ) ) ^ { \prime } = u ^ { \prime } ( x ) + v ^ { \prime } ( x ) $$

یکی از توابع مورد سوال را برابر با $$ u ( x ) $$ و دیگری را برابر با $$ v ( x ) $$ قرار می‌دهیم و از آن‌ها مشتق می‌گیریم:

$$ u ( x ) = \cos ( x ) $$

$$ v ( x ) = \sin ( x ) $$

$$ u ^ { \prime } ( x ) = - \sin( x ) $$

$$ v ^ { \prime } ( x ) = \cos ( x ) $$

به این ترتیب، داریم:

$$ ( u ( x ) + v ( x ) ) ^ { \prime } = u ^ { \prime } ( x ) + v ^ { \prime } ( x ) $$

$$
( \cos ( x ) + \sin ( x ) ) ^ { \prime } = - \sin ( x ) + \cos ( x )
$$

صورت سوال، مشتق تابع در $$ x = \frac { \pi } { ۶ } $$ را از ما می‌خواهد. این مقدار را درون رابطه بالا قرار می‌دهیم:

$$ \frac { d } { d x } \left [ \cos \left ( \frac { \pi } { ۶ } \right ) + \sin \left ( \frac { \pi } { ۶ } \right ) \right ] = - \sin \left ( \frac { \pi } { ۶ } \right ) + \cos \left ( \frac { \pi } { ۶ } \right ) $$

$$ \frac { \pi } { ۶ } $$، زاویه ۳۰ درجه را نمایش می‌دهد. سینوس این زاویه برابر با $$ \frac { ۱ } { ۲ } $$ و کسینوس آن برابر $$ \frac { \sqrt { ۳ } } { ۲ } $$ است. بنابراین، داریم:

$$ \frac { d } { d x } \left [ \cos \left ( \frac { \pi } { ۶ } \right ) + \sin \left ( \frac { \pi } { ۶ } \right ) \right ] = - \frac { ۱ } { ۲ } + \frac { \sqrt { ۳ } } { ۲ } $$

$$ \frac { d } { d x } \left [ \cos \left ( \frac { \pi } { ۶ } \right ) + \sin \left ( \frac { \pi } { ۶ } \right ) \right ] = \frac { \sqrt { ۳ } -۱ } { ۲ } $$

در صورت تمایل به یادگیری بیشتر در رابطه با مشتق دیگر توابع مثلثاتی، مطالعه یکی دیگر از مطالب مجله فرادرس با عنوان «مشتق توابع مثلثاتی | به زبان ساده» را به شما پیشنهاد می‌کنیم.

مشتق توابع مثلثاتی | به زبان ساده

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

اثبات فرمول مشتق کسینوس

روش‌های مختلفی برای اثبات فرمول مشتق cos وجود دارد که در این بخش، به توضیح هر یک از آن‌ها خواهیم پرداخت.

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

اثبات فرمول مشتق cos با استفاده از تعریف حدی مشتق

تعریف حدی مشتق به صورت زیر نوشته می‌شود:

$$ \frac { \Delta y } { \Delta x } = \lim _ { \Delta x \to ۰ } \frac { f ( x + \Delta x ) - f ( x ) } { \Delta x } $$

$$ \frac { \Delta y } { \Delta x } $$، شیب خط مماس بر نمودار تابع $$ y = f ( x ) $$ در نقطه x یا همان $$ f ^ { \prime } ( x ) $$‌ را نمایش می‌دهد. برای اثبات فرمول مشتق کسینوس، رابطه بالا را بر حسب $$ y = \cos ( x ) $$ بازنویسی می‌کنیم:

$$
\cos ^ { \prime } ( x ) = \lim _ { \Delta x \to ۰ } \frac { \cos ( x + \Delta x ) - \cos ( x ) } { \Delta x }
$$

عبارت $$ \cos ( x + \Delta x ) $$، کسینوس جمع دو زاویه است. قوانین جمع و تفریق زوایا در مثلثات، می‌توان این عبارت را به صورت زیر نوشت:

$$
\cos ( x + \Delta x ) = \cos ( x ) \cos ( \Delta x ) − \sin ( x ) \sin ( \Delta x )
$$

عبارت‌های سمت راست را درون فرمول حدی جایگزین کرده و حد را به صورت زیر بازنویسی:

$$
\cos ^ { \prime } ( x ) = \lim _ { \Delta x \to ۰ } \frac { \cos ( x ) \cos ( \Delta x ) − \sin ( x ) \sin ( \Delta x ) - \cos ( x ) } { \Delta x }
$$

$$
\cos ^ { \prime } ( x ) = \lim _ { \Delta x \to ۰ } \frac { \cos ( x ) \cos ( \Delta x ) - \cos ( x ) } { \Delta x } - \lim _ { \Delta x \to ۰ } \frac { \sin ( x ) \sin ( \Delta x ) } { \Delta x }
$$

$$
\cos ^ { \prime } ( x ) = \lim _ { \Delta x \to ۰ } \frac { \cos ( \Delta x ) - ۱} { \Delta x } \cos ( x ) - \lim _ { \Delta x \to ۰ } \frac { \sin ( \Delta x ) } { \Delta x } \sin ( x )
$$

با توجه به قواعد حدگیری از توابع مثلثاتی، داریم:

$$
\lim _ { \Delta x \to ۰ } \frac { \cos ( \Delta x ) - ۱} { \Delta x } = ۰
$$

$$
\lim _ { \Delta x \to ۰ } \frac { \sin ( \Delta x ) } { \Delta x } = ۱
$$

این نتایج را درون فرمول قرار می‌دهیم:

$$
\cos ^ { \prime } ( x ) = ۰ \times \cos ( x ) - ۱ \times \sin ( x )
$$

$$
\cos ^ { \prime } ( x ) = ۰ - \sin ( x )
$$

$$
\cos ^ { \prime } ( x ) = - \sin ( x )
$$

به این ترتیب، اثبات کردیم که مشتق cos برابر با sin- است.

اثبات فرمول مشتق cos با استفاده از مشتق گیری زنجیره ای

یکی از روابط معروف در مبحث مشتق‌گیری، رابطه مشتق زنجیره‌ای است. قاعده مشتق زنجیره‌ای، به صورت زیر نوشته می‌شود:

$$
\frac { d } { d x } f [ g ( x ) ] =f' [ g ( x ) ] g' (x )
$$

بر اساس قوانین مثلثات برای زوایای تناوبی، می‌دانیم:

$$ \sin \left ( \frac { \pi } { ۲ } - \theta \right ) = \cos ( \theta ) $$

بنابراین:

$$
\frac { d } { d x } \cos ( x ) = \frac { d } { d x } \sin \left ( \frac { \pi } { ۲ } - x \right )
$$

با توجه به رابطه بالا، فرض می‌کنیم:

$$ \frac { \pi } { ۲ } - x = g ( x ) $$

به این ترتیب:

$$ \sin ( g ( x ) ) = f [ g ( x ) ] $$

برای استفاده از قاعده مشتق زنجیره‌ای، باید از توابع بالا مشتق بگیریم:

$$ g ^ { \prime } ( x ) = - ۱ $$

$$ f ^ { \prime } [ g ( x ) ] = \sin ^ { \prime } [ g ( x ) ] = \cos [ g ( x ) ] = \cos \left ( \frac { \pi } { ۲ } - x \right ) $$

توابع و مشتق‌هایشان را درون فرمول مشتق زنجیره‌ای قرار می‌دهیم:

$$
\frac { d } { d x } f [ g ( x ) ] =f' [ g ( x ) ] g' (x )
$$

$$
\frac { d } { d x } \sin \left ( \frac { \pi } { ۲ } - x \right ) = \cos \left ( \frac { \pi } { ۲ } - x \right ) \times ( - ۱ )
$$

$$
\frac { d } { d x } \sin \left ( \frac { \pi } { ۲ } - x \right ) = - \cos \left ( \frac { \pi } { ۲ } - x \right )
$$

بر اساس قوانین مثلثات، داریم:

$$ \cos \left ( \frac { \pi } { ۲ } - \theta \right ) = \sin ( \theta ) $$

$$ \sin \left ( \frac { \pi } { ۲ } - \theta \right ) = \cos ( \theta ) $$

به این ترتیب:

$$
\frac { d } { d x } \cos ( x ) = - \sin ( x )
$$

در نتیجه اثبات کردیم که مشتق کسینوس برابر با منفی سینوس است.

اثبات فرمول مشتق cos با استفاده از قاعده مشتق تقسیم

آخرین روشی که در این مقاله از مجله فرادرس برای اثبات فرمول مشتق کسینوس به آن می‌پردازیم، استفاده از قاعده مشتق تقسیم دو تابع است. این قاعده به صورت زیر نوشته می‌شود:

$$
\frac { d } { d x } \left [ \frac { f ( x ) } { g ( x ) } \right ] = \frac { f ^ { \prime } ( x ) g ( x ) – g ^ { \prime } ( x ) f ( x ) }{ g ^ ۲ ( x ) }
$$

بر اساس روابط بین نسبت‌های مثلثاتی، داریم:

$$ \cos ( \theta ) = \frac { ۱ } { \sec ( \theta ) } $$

بنابراین:

$$
\frac { d } { d x } \cos ( x ) = \frac { d } { d x } \left [ \frac { ۱ } { \sec ( x ) } \right ] $$

برای مشتق‌گیری از $$ \frac { ۱ } { \sec ( x ) } $$، صورت و مخرج را به عنوان دو تابع مجزا در نظر می‌گیریم:

$$ f ( x ) = ۱ $$

$$ g ( x ) = \sec ( x ) $$

مشتق این توابع عبارت هستند از:

$$ f ^ { \prime } ( x ) = ۰ $$

$$ g ^ { \prime } ( x ) = \sec ( x ) \tan ( x ) $$

توابع $$ f ( x ) $$ و $$ g ( x ) $$ را به همراه مشتق‌هایشان درون فرمول مشتق تقسیم قرار می‌دهیم:

$$
\frac { d } { d x } \left [ \frac { f ( x ) } { g ( x ) } \right ] = \frac { f ^ { \prime } ( x ) g ( x ) – g ^ { \prime } ( x ) f ( x ) }{ g ^ ۲ ( x ) }
$$

$$
\frac { d } { d x } \left ( \frac { ۱ } { \sec } \right ) = \frac { ۰ \times \sec ( x ) – \sec ( x ) \tan ( x ) \times ۱}{ \sec ^ ۲ ( x ) }
$$

$$
\frac { d } { d x } \left ( \frac { ۱ } { \sec } \right ) = \frac { ۰– \sec ( x ) \tan ( x )}{ \sec ^ ۲ ( x ) }
$$

$$
\frac { d } { d x } \left ( \frac { ۱ } { \sec } \right ) = - \frac { \tan ( x )}{ \sec ( x ) }
$$

$$
\frac { d } { d x } \left ( \frac { ۱ } { \sec } \right ) = - \frac { \frac { \sin ( x ) }{ \cos ( x ) } }{ \frac { ۱ } { \cos ( x ) } }
$$

$$
\frac { d } { d x } \left ( \frac { ۱ } { \sec } \right ) = - \sin ( x )
$$

به این ترتیب اثبات کردیم که مشتق cos برابر با sin است.

مثال ۴: اثبات مشتق تانژانت

با استفاده از مشتق سینوس و کسینوس، رابطه زیر را اثبات کنید:

$$ \frac { d } { d x } \tan ( x ) = \sec ^ ۲ ( x ) $$

بر اساس روابط بین نسبت‌های مثلثاتی، می‌دانیم که:

$$ \tan ( x ) = \frac { \sin ( x ) } { \cos ( x ) } $$

بنابراین:

$$
\frac { d } { d x } \tan ( x ) = \frac { d } { d x } \left [ \frac { \sin ( x ) } { \cos ( x ) } \right ] $$

به این ترتیب، برای تعیین مشتق تانژانت می‌توانیم از تقسیم سینوس بر کسینوس مشتق بگیریم. بر اساس قاعده مشتق تقسیم دو تابع، داریم:

$$
\frac { d } { d x } \left [ \frac { \sin ( x ) } { \cos ( x ) } \right ] = \frac { \cos ( x ) \frac { d } { d x } \sin ( x ) - \sin ( x ) \frac { d } { d x } \cos ( x ) } { \cos ^ ۲ ( x ) }
$$

$$
\frac { d } { d x } \left [ \frac { \sin ( x ) } { \cos ( x ) } \right ] = \frac { \cos ( x ) \cos ( x ) - \sin ( x ) ( - \sin ( x ) ) } { \cos ^ ۲ ( x ) }
$$

$$
\frac { d } { d x } \left [ \frac { \sin ( x ) } { \cos ( x ) } \right ] = \frac { \cos ( x ) \cos ( x ) + \sin ( x ) \sin ( x ) } { \cos ^ ۲ ( x ) }
$$

$$
\frac { d } { d x } \left [ \frac { \sin ( x ) } { \cos ( x ) } \right ] = \frac { \cos ^ ۲ ( x ) + \sin ^ ۲ ( x ) } { \cos ^ ۲ ( x ) }
$$

مجموع مربعات سینوس و کسینوس برابر با ۱ می‌شود. از این‌رو:

$$
\frac { d } { d x } \left [ \frac { \sin ( x ) } { \cos ( x ) } \right ] = \frac { ۱ } { \cos ^ ۲ ( x ) }
$$

$$
\frac { d } { d x } \left [ \frac { \sin ( x ) } { \cos ( x ) } \right ] = \sec ^ ۲ ( x )
$$

در نتیجه:

$$
\frac { d } { d x } \tan ( x ) = \sec ^ ۲ ( x )
$$

فرمول کلی مشتق کسینوس چیست ؟

فرم کلی تابع کسینوس به صورت زیر نوشته می‌شود:

$$ f ( x ) = a \cos( b x + c ) $$

فیلم آموزش ریاضی پایه – مرور و حل تست کنکور ارشد در فرادرس

b ،a و c، ضرایب ثابت هستند. با توجه به این فرم، رابطه مشتق کسینوس عبارت است از:

$$ f ^ { \prime } ( x ) = - a b \sin ( b x + c ) $$

مثال ۵: محاسبه مشتق کسینوس دو ایکس

مشتق $$ \cos ( ۲ x ) $$ را تعیین کنید.

برای به دست آوردن مشتق $$ \cos ( ۲ x ) $$، از فرمول کلی مشتق کسینوس استفاده می‌کنیم. بر اساس این فرمول، داریم:

$$ \frac { d } { d x } [ a \cos ( b x + c ) ] = - a b \sin ( b x + c ) $$

با توجه صورت سوال، داریم:

$$ a = ۱ $$

$$ b = ۲ $$

$$ c = ۰ $$

بنابراین، مشتق $$ \cos ( ۲ x ) $$ برابر است با:

$$ \frac { d } { d x } \cos ( ۲ x ) = - ۲ \sin ( ۲ x ) $$

عبارت $$ ۲ x $$ در $$ \cos ( ۲ x ) $$، تابعی از متغیر x است. بنابراین، $$ \cos ( ۲ x ) $$ یک تابع تو در تو محسوب می‌شود. مشتق این نوع تابع از فرمولی معروف به قاعده زنجیره‌ای به دست می‌آید. در بخش‌های بعدی به معرفی این فرمول و حل مثال‌های مرتبط با آن خواهیم پرداخت.

مشتق کسینوس توان دار چیست ؟

تابع $$ \cos ^ { n } ( x ) $$ را در نظر بگیرید. n، توان تابع کسینوس را نمایش می‌دهد. این توان می‌تواند مثبت یا منفی باشد.

فیلم آموزش ریاضی ۳ – پایه دوازدهم علوم تجربی در فرادرس

در صورت مثبت بودن n، مشتق $$ \cos ^ { n } ( x ) $$ با استفاده از قانون ضرب در مشتق‌گیری محاسبه می‌شود. با توجه به این قانون، برای دو تابع $$ f ( x ) $$ و $$ g ( x ) $$ داریم:

$$ \frac { d } { d x } [ f ( x ) g ( x ) ] = f ( x ) g ' ( x ) + g ( x ) f ' ( x ) $$

به عنوان مثال، $$ \cos ^ ۲ ( x ) $$ را در نظر بگیرید. این تابع را می‌توانیم به صورت ضرب کسینوس در کسینوس بنویسیم:

$$ \cos ^ ۲ ( x ) = \cos ( x ) \cos ( x ) $$

به این ترتیب، امکان تعیین مشتق $$ \cos ^ ۲ ( x ) $$ توسط فرمول مشتق ضرب دو تابع فراهم می‌شود. اگر توان n در $$ \cos ^ { n } ( x ) $$ منفی باشد، مشتق کسینوس توان‌دار از قانون تقسیم در مشتق‌گیری به دست می‌آید. بر اساس این قانون داریم:

$$ \frac { d } { d x } \left [ \frac { f ( x ) } { g ( x ) } \right ] = \frac { g ( x ) f' ( x ) - f ( x ) g' ( x ) } { g ^ { ۲ } ( x ) } $$

به عنوان مثال، $$ \cos ^ { - ۱ } $$ را در نظر بگیرید. این تابع مثلثاتی را می‌توانیم به صورت زیر بنویسیم:

$$ \cos ^ { - ۱ } ( x ) = \frac { ۱ } { \cos ( x ) } $$

به این ترتیب، به دست آوردن مشتق $$ \cos ^ { - ۱ } $$ به کمک فرمول مشتق تقسیم دو تابع امکان‌پذیر می‌شود. در ادامه، نحوه تعیین مشتق cos توان‌دار را با حل چند مثال توضیح می‌دهیم.

مثال ۶: مشتق کسینوس به توان دو

مشتق $$ \cos ^ ۲ ( x ) $$ را به دست بیاورید.

برای حل این مثال، ابتدا $$ \cos ^ ۲ ( x ) $$ را به صورت ضرب دو تابع کسینوس می‌نویسیم:

$$ \cos ^ ۲ ( x ) = \cos ( x ) \cos ( x ) $$

اکنون می‌توانیم مشتق $$ \cos ^ ۲ ( x ) $$ را با استفاده از فرمول مشتق ضرب توابع تعیین کنیم. این فرمول به صورت زیر نوشته می‌شود:

$$ \frac { d } { d x } [ f ( x ) g ( x ) ] = f ( x ) g ^ { \prime } ( x ) + f ^ { \prime } ( x ) g ( x ) $$

اگر یکی از کسینوس‌ها را برابر با تابعی مانند $$ f ( x ) $$ و کسینوس دیگر را برابر با تابعی مانند $$ g ( x ) $$ در نظر بگیریم، خواهیم داشت:

$$ f ( x ) = \cos ( x ) $$

$$ g ( x ) = \cos ( x ) $$

مشتق هر یک از توابع بالا عبارت است از:

$$ f ^ { \prime } ( x ) = - \sin( x ) $$

$$ g ^ { \prime } ( x ) = - \sin( x ) $$

توابع و مشتق‌هایشان را درون فرمول زیر قرار می‌دهیم:

$$ \frac { d } { d x } [ f ( x ) g ( x ) ] = f ( x ) g ^ { \prime } ( x ) + f ^ { \prime } ( x ) g ( x ) $$

$$
\frac { d } { d x } [ \cos ( x ) \cos ( x ) ] = \cos ( x ) [ - \sin ( x ) ] + \cos ( x ) [ - \sin ( x ) ] $$

$$
\frac { d } { d x } [ \cos ( x ) \cos ( x ) ] = - \cos ( x ) \sin ( x ) - \cos ( x ) \sin ( x )
$$

$$
\frac { d } { d x } [ \cos ( x ) \cos ( x ) ] = - ۲ \cos ( x ) \sin ( x )
$$

بر اساس روابط بین نسبت‌های مثلثاتی، داریم:

$$
\sin ( ۲ \theta ) = ۲ \sin ( \theta ) \cos ( \theta )
$$

بنابراین:

$$
\frac { d } { d x } [ \cos ( x ) \cos ( x ) ] = - \sin ( ۲ x )
$$

در نتیجه:

$$
\frac { d } { d x } \cos ^ ۲ ( x ) = - \sin ( ۲ x )
$$

مثال ۷: مشتق تقسیم کسینوس

مشق تابع زیر را تعیین کنید:

$$ f ( x ) = \dfrac { x } { \cos x } $$

برای حل این مثال، دو روش وجود دارد. در روش اول، ابتدا فرمول مشتق تقسیم دو تابع را می‌نویسیم و پس از تعیین توابع نظیر، از آن‌ها مشتق می‌گیریم:

$$
\frac { d } { d x } \left [ \frac { u ( x ) } { v ( x ) } \right ] = \frac { u ^ { \prime } ( x ) v ( x ) – v ^ { \prime } ( x ) u ( x ) }{ v ^ ۲ ( x ) }
$$

$$ u ( x ) = x $$

$$ v ( x ) = \cos ( x ) $$

$$ u ^ { \prime } ( x ) = ۱ $$

$$ v ^ { \prime } ( x ) = - \sin ( x ) $$

$$
\frac { d } { d x } \left ( \dfrac { x } { \cos x } \right ) = \frac { ۱ \times \cos ( x ) – ( - \sin ( x ) ) \times x }{ \cos ^ ۲ ( x ) }
$$

$$
\frac { d } { d x } \left ( \dfrac { x } { \cos x } \right ) = \frac { \cos ( x ) + x \sin ( x ) }{ \cos ^ ۲ ( x ) }
$$

می‌وانیم جواب بالا را به صورت زیر ساده‌سازی کنیم:

$$
\frac { d } { d x } \left ( \dfrac { x } { \cos x } \right ) = \frac { \cos ( x ) }{ \cos ^ ۲ ( x ) } +\frac { x \sin ( x ) }{ \cos ^ ۲ ( x ) }
$$

$$
\frac { d } { d x } \left ( \dfrac { x } { \cos x } \right ) = \frac { ۱ }{ \cos ( x ) } +\frac { x \sin ( x ) }{ \cos ( x ) } \times \frac { ۱ }{ \cos ( x ) }
$$

$$
\frac { d } { d x } \left ( \dfrac { x } { \cos x } \right ) = \sec ( x ) + x \tan ( x ) \sec ( x )
$$

روش دوم برای حل این مثال، تبدیل عبارت $$ \dfrac { x } { \cos x } $$ به $$ x \sec ( x ) $$ و مشتق‌گیری از آن با کمک قانون مشتق ضرب دو تابع است.

مشتق زنجیره ای کسینوس چیست ؟

ساده‌ترین فرم تابع کسینوس به صورت زیر نوشته می‌شود:

$$ f ( x ) = \cos ( x ) $$

فیلم آموزش ریاضی پایه دانشگاهی در فرادرس

به جای $$ x $$، تابعی مانند $$ g ( x ) $$ را درون کسینوس در نظر بگیرید:

$$ f ( g ( x ) ) = \cos ( g ( x ) ) $$

به تابع بالا، یک تابع تو در تو می‌گویند. مشتق این تابع از فرمول زیر به دست می‌آید:

$$ \frac { d } { d x } f \left [ g ( x ) \right ] = f ' \left ( g ( x ) \right ) g ' (x ) $$

مثال ۸: محاسبه مشتق کسینوس به توان ۲ به روش زنجیره‌ای

$$ \frac { d } { d x } \cos ^ ۲ ( x ) $$ را به کمک قاعده مشتق زنجیره‌ای به دست بیاورید.

بر اساس قاعده مشتق زنجیره‌ای داریم:

$$ \frac { d } { d x } f \left [ g ( x ) \right ] = f ' \left ( g ( x ) \right ) g ' (x ) $$

در مثال ۶، مشتق کسینوس به توان دو را با استفاده از قاعده ضرب تعیین کردیم. برای حل این مشتق توسط قاعده زنجیره‌ای، ابتدا تابعی مانند $$ g ( x ) $$ را در نظر می‌گیریم و آن برابر با تابع کسینوس ایکس قرار می‌دهیم:

$$ g ( x ) = \cos ( x ) $$

در مرحله بعد، تابعی مانند $$ f ( x ) $$ را در نظر می‌گیریم و آن را برابر با $$ x ^ ۲ $$ قرار می‌دهیم:

$$ f ( x ) = x ^ ۲ $$

اکنون، با توجه به فرضیات بالا، تابع تو در توی $$ f [ g ( x ) ] $$ را می‌نویسیم:

$$ f [ g ( x ) ] = g ^ ۲ ( x ) $$

از آنجایی که $$ g ( x ) = \cos ( x ) $$، داریم:

$$ f [ g ( x ) ] = \cos ^ ۲ ( x ) $$

به عبارت دیگر، $$ \cos ^ ۲ ( x ) $$ یک تابع تو در تو است که می‌توانیم مشتق آن را با استفاده از رابطه زیر به دست بیاوریم:

$$ \frac { d } { d x } f \left [ g ( x ) \right ] = f ' [ g ( x ) ] g ' (x ) $$

مشتق‌های درون رابطه بالا به صورت زیر تعیین می‌شوند:

$$ g ^ { \prime } ( x ) = \cos ^ { \prime } ( x ) = - \sin ( x ) $$

$$ f ^ { \prime } ( x ) = ( x ^ ۲ ) ^ { \prime } = ۲ x $$

$$ f ' [ g ( x ) ] = ۲ g ( x ) = ۲ \cos ( x ) $$

به این ترتیب:

$$
\frac { d } { d x } f \left [ g ( x ) \right ] = f ' [ g ( x ) ] g ' ( x )
$$

$$
\frac { d } { d x } \cos ^ ۲ ( x ) = ۲ \cos ( x ) \times [ - \sin ( x ) ] $$

$$
\frac { d } { d x } \cos ^ ۲ ( x ) = - ۲ \cos ( x ) \sin ( x )
$$

$$
\frac { d } { d x } \cos ^ ۲ ( x ) = - \sin ( ۲ x )
$$

همان‌طور که مشاهده می‌کنید، با استفاده از قاعده زنجیره‌ای نیز به جوابی مشابه جواب مثال ۶ رسیدیم.

مشتق کسینوس وارون چیست ؟

تابع وارون، توابعی هستند که معکوس توابع معمولی عمل می‌کنند. به عنوان مثال، تابع کسینوس و وارون آن (آرک‌کسینوس) را در نظر بگیرید:

$$ y = \cos ( x ) $$

$$ \arccos ( y ) = x $$

همان‌‌طور که می‌بینید، تابع وارون یا معکوس، با گرفتن خروجی تابع اصلی، ورودی را مشخص می‌کند. آرک‌کسینوس با $$ \cos ^ { - ۱ } ( y ) = x $$ نیز نمایش داده می‌شود.

تابع معکوس مثلثاتی — به زبان ساده

فیلم آموزش ریاضی مهندسی – مرور و حل مساله در فرادرس

مشتق کسینوس وارون عبارت است از:

$$ \frac { d } { d x } \arccos ^ { - ۱ } ( x ) = - \frac { ۱ }{ \sqrt { ۱ - x ^ ۲ } } $$

مشتق وارون کسینوس u نیز از رابطه زیر به دست می‌آید:

$$ \frac { d } { d x } \cos ^ { - ۱ } ( u ( x ) ) = - \frac { u ^ { \prime } ( x ) }{ \sqrt { ۱ - u ^ ۲ ( x ) } } $$

اثبات فرمول مشتق کسینوس وارون

به منظور اثبات فرمول مشتق کسینوس معکوس، ابتدا فرض می‌کنیم:

$$ y = \arccos ( x ) $$

بر اساس تعریف توابع وارون، داریم:

$$ \cos ( y ) = x $$

از دو طرف رابطه بالا بر حسب x مشتق می‌گیریم:

$$ \frac { d } { d x } \cos ( y ) = \frac { d } { d x } x $$

$$ \frac { d } { d x } \cos ( y ) = ۱ $$

y تابعی از x است. بنابراین، با توجه به قاعده زنجیره‌ای، حاصل عبارت سمت چپ رابطه بالا برابر خواهد بود با:

$$ - \sin ( y ) \cdot \frac { d } { d x } y = ۱ $$

بنابراین:

$$
\frac { d y } { d x } = - \frac { ۱ }{ \sin ( y )}
$$

بر اساس قوانین مثلثات، جمع مربعات سینوس و کسینوس برابر با ۱ می‌شود:

$$ \sin ^ ۲ ( y ) + \cos ^ ۲ ( y ) = ۱ $$

رابطه بالا را بر حسب $$ \sin ( y ) $$ بازنویسی می‌کنیم:

$$
\sin ^ ۲ ( y ) = ۱ - \cos ^ ۲ ( y )
$$

$$
\sin ( y ) = \sqrt { ۱ - \cos ^ ۲ ( y ) }
$$

در ابتدای اثبات، دیدیم که:

$$ \cos ( y ) = x $$

از این‌رو:

$$ \sin ( y ) = \sqrt { ۱ - x ^ ۲ } $$

$$
\frac { d y } { d x } = - \frac { ۱ }{ \sin ( y )}
$$

$$
\frac { d y } { d x } = - \frac { ۱ }{ \sqrt { ۱ - x ^ ۲ } }
$$

از آنجایی که $$ y = \arccos ( x ) $$، خواهیم داشت:

$$
\frac { d } { d x } \arccos ( x ) = - \frac { ۱ }{ \sqrt { ۱ - x ^ ۲ } }
$$

به این ترتیب، فرمول مشتق کسینوس وارون را اثبات کردیم.

مثال ۹: مشتق کسینوس اینورس

مشتق تابع زیر را تعیین کنید:

$$ f ( x ) = \cos ^ { - ۱ } ( ۳ x - ۱ ) $$

اگر $$ ۳ x - ۱ $$ را برابر با $$ u ( x ) $$ در نظر بگیریم، مشتق تابع بالا از رابطه زیر به دست می‌آید:

$$ \frac { d } { d x } \arccos u ( x ) = - \frac { u ^ { \prime } ( x ) }{ \sqrt { ۱ - u ^ ۲ ( x ) } } $$

$$
\frac { d } { d x } \arccos ( ۳ x - ۱ ) = - \frac { \frac { d } { d x } ( ۳ x - ۱ ) }{ \sqrt { ۱ - ( ۳ x - ۱ ) ^ ۲ } }
$$

$$
\frac { d } { d x } \arccos ( ۳ x - ۱ ) = - \frac {۳ }{ \sqrt { ۱ - ( ۹ x ^ ۲ + ۱ - ۶ x ) } }
$$

$$
\frac { d } { d x } \arccos ( ۳ x - ۱ ) = - \frac {۳ }{ \sqrt { ۱ - ۹ x ^ ۲ + ۱ + ۶ x } }
$$

$$
\frac { d } { d x } \arccos ( ۳ x - ۱ ) = - \frac {۳ }{ \sqrt { ۶ x - ۹ x ^ ۲} }
$$

$$
f ^ { \prime } ( x ) = - \frac {۳ }{ \sqrt { ۶ x - ۹ x ^ ۲} }
$$

مشتق کسینوس هیپربولیک چیست ؟

تابع کسینوس هیپربولیک عبارت به صورت زیر نوشته می‌شود:

$$ \cosh ( x ) $$

بیان این تابع بر اساس عدد اویلر عبارت است از:

$$ \cosh ( x ) = \frac { e ^ x + e ^ { - x } }{ ۲ } $$

مشتق کسینوس هیپربولیک با استفاده از رابطه زیر به دست می‌آید:

$$ \frac { d } { d x } \cosh ( x ) = \sinh ( x ) $$

$$ \frac { d } { d x } \cosh ( x ) = \frac { e ^ x - e ^ { - x } }{ ۲ } $$

به عبارت دیگر، مشق cosh برابر با sinh است. اگر به جای x، تابعی از x مانند $$ u ( x ) $$ را درون کسینوس هیپربولیک قرار دهیم، فرمول مشتق به شکل زیر درمی‌آید:

$$ \frac { d } { d x } \cosh [ u ( x ) ] = u ^ { \prime } ( x ) \sinh [ u ( x ) ] $$

مشتق کسینوس هیپربولیک وارون نیز با استفاده فرمول‌های زیر تعیین می‌شود:

$$ \frac { d } { d x } \cosh ^ { - ۱ } ( x ) = \frac { ۱ }{ \sqrt { x ^ ۲ - ۱ } } $$

$$
\frac { d } { d x } \cosh ^ { - ۱ } [ u ( x ) ] = \frac { u ^ { \prime } ( x ) }{ \sqrt { u ^ ۲ ( x ) - ۱ } }
$$

مشتق توابع هذلولوی و معکوس آن‌ها — از صفر تا صد

اثبات فرمول مشتق کسینوس هیپربولیک

به منظور اثبات فرمول cosh، ابتدا فرم اویلری آن را می‌نویسیم:

$$ \cosh ( x ) = \frac { e ^ x + e ^ { - x } }{ ۲ } $$

سپس، از دو طرف رابطه بالا مشتق می‌گیریم:

$$
\frac { d } { d x } \cosh ( x ) = \frac { d } { d x } \left ( \frac { e ^ x + e ^ { - x } }{ ۲ } \right )
$$

مشتق‌گیری را در سمت راست رابطه ادامه می‌دهیم:

$$
\frac { d } { d x } \cosh ( x ) = \frac { ۱ }{ ۲ } \left [\frac { d } { d x } \left ( e ^ x + e ^ { - x }\right ) \right ] $$

$$
\frac { d } { d x } \cosh ( x ) = \frac { ۱ }{ ۲ } \left [\frac { d } { d x } e ^ x + \frac { d } { d x } e ^ { - x } \right ] $$

مشتق تابع نمایی، از رابطه زیر به دست می‌آید:

$$ \frac { d } { dx } e ^ { f ( x ) } = f ' ( x ) e ^ { f ( x ) } $$

بنابراین:

$$
\frac { d } { d x } \cosh ( x ) = \frac { ۱ }{ ۲ } \left ( e ^ x - e ^ { - x } \right )
$$

$$
\frac { d } { d x } \cosh ( x ) = \frac { e ^ x - e ^ { - x } }{ ۲ }
$$

سمت راست رابطه بالا، همان $$ \sinh ( x ) $$ است. در نتیجه:

$$
\frac { d } { d x } \cosh ( x ) = \sinh ( x )
$$

مشتق e – به زبان ساده + مثال و حل تمرین

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

مثال ۱۰: مشتق کسینوس هیپربولیک

مشتق $$ \cosh ( x ^ ۴ - ۷ x ^ ۲ ) $$ را تعیین کنید.

برای به دست آوردن مشتق تابع مورد سوال، از فرمول زیر کمک می‌گیریم:

$$
\frac { d } { d x } \cosh [ u ( x ) ] = u ^ { \prime } ( x ) \sinh [ u ( x ) ] $$

بر اساس صورت سوال و رابطه بالا، داریم:

$$ u ( x ) = x ^ ۴ - ۷ x ^ ۲ $$

$$ u ^ { \prime } ( x ) = ۴ x ^ ۳ - ۱۴ x $$

بنابراین:

$$
\frac { d } { d x } \cosh ( x ^ ۴ - ۷ x ^ ۲ ) = \left ( ۴ x ^ ۳ - ۱۴ x \right ) \sinh \left ( x ^ ۴ - ۷ x ^ ۲ \right )
$$

مشتق مراتب بالاتر کسینوس چیست ؟

به تکرار مشتق‌گیری از خروجی‌های مشتق یک تابع، مشتق مراتب بالاتر گفته می‌شود. به عنوان مثال، مشتق اول و مراتب بالاتر تابعی مانند $$ y = f ( x ) $$ عبارت است از:

$$ \frac { d y } { d x } , \; \frac { d } { d x } \left ( \frac { d y } { d x } \right ) , \; \frac { d } { d x } \left ( \frac { d } { d x } \left ( \frac { d y } { d x } \right ) \right ) , \; ... $$

$$ \frac { d y } { d x } , \; \frac { d ^ ۲ y } { d x ^ ۲ } , \; \frac { d ^ ۳ y } { d x ^ ۳ } , \; ... $$

$$ f ^ { \prime } ( x ) , \; f ^ { \prime \prime } ( x ) , \; f ^ { \prime \prime \prime} ( x ) , \; ... $$

$$ y ^ { \prime } ( x ) , \; y ^ { \prime \prime } ( x ) , \; y ^ { \prime \prime \prime} ( x ) , \; ... $$

در بخش‌های قبلی با مشتق مرتبه اول کسینوس آشنا شدید. این مشتق به صورت زیر نوشته می‌شود:

$$ \frac { d } { d x } \cos ( x ) = - \sin ( x ) $$

اگر از $$ - \sin ( x ) $$ مشتق بگیریم، به مشتق مرتبه دوم کسینوس می‌رسیم:

$$
\frac { d } { d x } \left ( \frac { d y } { d x } \cos ( x ) \right ) = \frac { d y } { d x } [ - \sin ( x ) ] $$

می‌دانیم مشتق سینوس ایکس با کسینوس ایکس برابری می‌کند. بنابراین:

$$
\frac { d } { d x } \left ( \frac { d y } { d x } \cos ( x ) \right ) = - \frac { d y } { d x } [ \sin ( x ) ] $$

$$
\frac { d } { d x } \left ( \frac { d y } { d x } \cos ( x ) \right ) = - \cos ( x )
$$

به عبارت دیگر، مشتق مرتبه دوم کسینوس با منفی کسینوس برابر است. اگر مشتق‌گیری را برای مرتبه سوم و چهارم تکرار کنیم، به ترتیب به $$ \sin ( x ) $$ و $$ \cos ( x ) $$ می‌رسیم. در واقع، مشتق چهارم کسینوس با خودش برابر خواهد شد. این نتایج به همین ترتیب برای مشتق‌های مراتب بالاتر تکرار می‌شوند. بنابراین، مشتق‌های مرتبه هشتم، دوازدهم و دیگر مشتق‌‌های مرتبه ۴n از تابع $$ \cos ( x ) $$ برابر با $$ \cos ( x ) $$‌ خواهد بود.

مثال ۱۱: مشتق مرتبه دوم کسینوس

مشتق مرتبه دوم $$ \cos \left ( ۵ x ^ ۲ \right ) $$ را به دست بیاورید.

مشتق مرتبه دوم یک تابع ($$ \frac { d ^ ۲ } { d x } f ( x ) $$)، در دو مرحله تعیین می‌شود. مرحله اول، به دست آوردن مشتق مرتبه اول تابع است. برای تابع مورد سوال، این مشتق به صورت زیر نوشته می‌شود:

$$
\frac { d } { d x } \cos \left ( ۵ x ^ ۲ \right ) = - \sin \left ( ۵ x ^ ۲ \right ) \cdot \frac { d } { d x } \left ( ۵ x ^ ۲ \right )
$$

$$
\frac { d } { d x } \cos \left ( ۵ x ^ ۲ \right ) = - \sin \left ( ۵ x ^ ۲ \right ) \cdot ۱۰ x
$$

$$
\frac { d } { d x } \cos \left ( ۵ x ^ ۲ \right ) = - ۱۰ x \sin \left ( ۵ x ^ ۲ \right )
$$

به منظور تعیین مشتق مرتبه دوم $$ \cos \left ( ۵ x ^ ۲ \right ) $$، عملیات مشتق‌گیری را بر روی خروجی مشتق مرتبه اول (جواب بالا) تکرار می‌کنیم:

$$
\frac { d } { d x } \left [ - ۱۰ x \sin \left ( ۵ x ^ ۲ \right ) \right ] $$

جواب این مشتق با استفاده از قانون مشتق ضرب دو تابع به دست می‌آید. بنابراین، فرض می‌کنیم:

$$ u ( x ) = -۱۰ x $$

$$ u ^ { \prime } ( x ) = -۱۰ $$

$$ v ( x ) = \sin \left ( ۵ x ^ ۲ \right ) $$

$$ v ^ { \prime } ( x ) = ۱۰ x \cos \left ( ۵ x ^ ۲ \right ) $$

$$
\frac { d } { d x } [ u ( x ) v ( x ) ] = u ( x ) v ^ { \prime } ( x ) + u ^ { \prime } ( x ) v ( x )
$$

$$
\frac { d } { d x } \left [ - ۱۰ x \sin \left ( ۵ x ^ ۲ \right ) \right ] = -۱۰ x \left [۱۰ x \cos \left ( ۵ x ^ ۲ \right ) \right ] -۱۰ \sin \left ( ۵ x ^ ۲ \right )
$$

$$
\frac { d } { d x } \left [ - ۱۰ x \sin \left ( ۵ x ^ ۲ \right ) \right ] = -۱۰ \left [۱۰ x ^ ۲\cos \left ( ۵ x ^ ۲ \right ) + \sin \left ( ۵ x ^ ۲ \right ) \right ] $$

به این ترتیب، مشتق مرتبه دوم $$ \cos \left ( ۵ x ^ ۲ \right ) $$ را به دست آوردیم.

انتگرال کسینوس و رابطه آن با مشتق کسینوس چیست ؟

انتگرال، مفهومی است که به منظور تعیین مساحت زیر منحنی یک تابع مورد استفاده قرار می‌گیرد.

این مفهوم ارتباط بسیار نزدیکی با مشتق دارد. انتگرال کسینوس از رابطه زیر به دست می‌آید:

$$ \int \cos ( x ) d x = \sin ( x ) + C $$

اگر بازه انتگرال‌گیری معین باشد، ثابت عددی C از جواب انتگرال cos حذف می‌شود:

$$ \int \cos ( x ) d x = \sin ( x ) $$

به منظور درک بهتر مفهوم انتگرال کسینوس، مشتق‌های مرتبه اول تا سوم این تابع را در نظر بگیرید:

$$ \frac { d } { d x } \cos ( x ) = - \sin ( x ) $$

$$ \frac { d ^ ۲ } { d x } \cos ( x ) = - \cos ( x ) $$

$$ \frac { d ^ ۳ } { d x } \cos ( x ) = \sin ( x ) $$

انتگرال هر یک از عبارت‌های بالا برابر است با:

$$ \int - \sin ( x ) = - ( - \cos ( x ) ) = \cos ( x ) $$

$$ \int - \cos ( x ) = - \sin ( x ) $$

$$ \int \sin ( x ) = - \cos ( x ) $$

بر اساس نتایج به دست آمده می‌توان مشاهده کرد که انتگرال هر مشتق با مشتق مرتبه پایین‌تر خود برابری می‌کند. به عنوان مثال، انتگرال مشتق مرتبه سوم کسینوس با مشتق مرتبه دوم کسینوس برابر است. به همین شکل، انتگرال مشتق مرتبه دوم کسینوس با مشتق مرتبه اول کسینوس برابر می‌شود. به انتگرال، پادمشتق نیز می‌گویند.

مثال ۱۲: انتگرال جز به جز کسینوس

انتگرال $$ F ( x ) = e ^ x \cos ( x ) $$ را تعیین کنید.

برای تعیین انتگرال تابع مورد سوال، از روش انتگرال‌گیری جز به جز استفاده می‌کنیم. این روش، در به دست آوردن انتگرال ضرب دو تابع کاربرد دارد و فرمول آن به صورت زیر نوشته می‌شود:

$$ \int f ( x ) g ' ( x ) d x = f ( x ) g ( x ) - \int f ' ( x ) g ( x) d x $$

همان‌طور که مشاهده می‌کنید، در انتگرال جز به جز، فرض می‌کنیم تابعی مانند $$ f ( x ) $$ در مشتق تابع دیگری مانند $$ g ( x ) $$ ضرب شده است. بنابراین، برای استفاده از رابطه بالا، تابع $$ f ( x ) $$ باید مشتق‌پذیر و تابع $$ g ^ { \prime } ( x ) $$‌ انتگرال‌پذیر باشد. با توجه به قوانین انتگرال‌گیری جز به جز، مشتق‌گیری از توابع مثلثاتی نسبت به توابع نمایی اولویت دارد. از این‌رو، در این مثال داریم:

$$ f ( x ) = \cos ( x ) $$

$$ g ^ { \prime } ( x ) = e ^ x $$

برای تعیین تمام پارامترهای فرمول انتگرال جز به جز، از $$ f ( x ) $$ مشتق گرفته و از $$ g ^ { \prime } ( x ) $$‌ انتگرال می‌گیریم:

$$
f ^ { \prime } ( x ) = \frac { d } { d x } f ( x ) = \frac { d } { d x } \cos ( x ) = - \sin ( x )
$$

$$
f ^ { \prime } ( x ) = - \sin ( x )
$$

$$ g ( x ) = \int g ^ { \prime } ( x ) d x = \int e ^ x d x = e ^ x $$

$$ g ( x ) = e ^ x $$

با جایگذاری عبارت‌ها بالا در رابطه انتگرال‌گیری جز به جز خواهیم داشت:

$$
\int \cos ( x ) \cdot e ^ x d x = \cos ( x ) \cdot e ^ x - \int - \sin ( x ) \cdot e ^ x d x
$$

$$
\int \cos ( x ) \cdot e ^ x d x = e ^ x \sin ( x ) + \int e ^ x \sin ( x ) d x
$$

همان‌طور که مشاهده می‌کنید، انتگرال از درون رابطه حذف نشده و با یک الگوی مشابه دوباره در جواب ظاهر می‌شود. اگر انتگرال جدید را دوباره به روش جز به جز حل کنیم، به جواب زیر می‌رسیم:

$$
\int e ^ x \sin ( x ) d x = e ^ x \sin ( x ) - \int e ^ x \cos ( x ) d x
$$

نتیجه این انتگرال را در جواب اولیه قرار می‌دهیم:

$$
\int \cos ( x ) \cdot e ^ x d x = e ^ x \cos ( x ) + e ^ x \sin ( x ) - \int e ^ x \cos ( x ) d x
$$

در این مرحله از انتگرال‌گیری نیز مانند مرحله اول، انتگرال از درون جواب حذف نشده اما انتگرال سمت چپ معادله دقیقا در سمت راست تکرار می‌شود. بنابراین می‌توانیم انتگرال سمت راست را به سمت چپ ببریم:

$$
\int \cos ( x ) \cdot e ^ x d x + \int e ^ x \cos ( x ) d x= e ^ x \cos ( x ) + e ^ x \sin ( x )
$$

$$
۲ \int \cos ( x ) \cdot e ^ x d x = e ^ x \cos ( x ) + e ^ x \sin ( x )
$$

$$
\int \cos ( x ) \cdot e ^ x d x = \frac { e ^ x \cos ( x ) } { ۲ } + \frac { e ^ x \sin ( x ) } { ۲ }
$$

به این ترتیب، انتگرال $$ F ( x ) = e ^ x \cos ( x ) $$ را به دست آوردیم. روشی که در این مثال توضیح دادیم، روش بسیار خوبی برای به تعیین انتگرال توابعی است که طی مراحل انتگرال‌‌گیری، در جواب تکرار می‌شوند.

انتگرال جز به جز + آموزش فرمول و نمونه سوال با جواب

مشتق جزئی کسینوس

تابع زیر را در نظر بگیرید:

$$ f ( x , \; y ) = \cos ( x - y ) $$

$$ f ( x , \; y ) $$، تابعی از دو متغیر مستقل $$ x $$ و $$ y $$ است. مشتق این تابع، با استفاده از اصول مشتق‌گیری جزئی به دست می‌آید. در این روش، مشتق تابع بر حسب تمام متغیرهای مستقل تعیین می‌شود. به عنوان مثال، مشتق جزئی $$ \cos ( x - y ) $$ بر حسب $$ x $$ عبارت است از:

$$ \frac { \partial } { \partial x } [ f ( x , \; y ) ] = \frac { \partial } { \partial x } \cos ( x - y ) $$

$$ \frac { \partial } { \partial x } \cos ( x - y ) = \frac { \partial } { \partial x } ( x - y ) [ - \sin ( x - y ) ] $$

در صورت محاسبه مشتق بر حسب $$ x $$، پارامتر $$ y $$ به عنوان یک ثابت در نظر گرفته می‌شود. بنابراین:

$$
\frac { \partial } { \partial x } ( x - y ) = \frac { \partial } { \partial x } x - \frac { \partial } { \partial x } y = ۱ - ۰ = ۱
$$

در نتیجه:

$$
\frac { \partial } { \partial x } \cos ( x - y ) = ۱ \times [ - \sin ( x - y ) ] $$

$$
\frac { \partial } { \partial x } \cos ( x - y ) = - \sin ( x - y )
$$

مشتق جزئی $$ \cos ( x + y ) $$ بر حسب $$ y $$ نیز طی مراحل زیر به دست می‌آید:

$$ \frac { \partial } { \partial y } \cos ( x - y ) = \frac { \partial } { \partial y } ( x - y ) [ - \sin ( x - y ) ] $$

برای $$ \frac { \partial } { \partial y } ( x - y ) $$ داریم:

$$ \frac { \partial } { \partial y } ( x - y ) = \frac { \partial } { \partial y } x - \frac { \partial } { \partial y } y = ۰ - ۱ = - ۱ $$

در نتیجه:

$$
\frac { \partial } { \partial y } \cos ( x - y ) = - ۱ \times [ - \sin ( x - y ) ] $$

$$
\frac { \partial } { \partial y } \cos ( x - y ) = \sin ( x - y )
$$

مشتق جزئی — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

حل تمرین مشتق Cos

در این بخش، به منظور آشنایی بهتر و بیشتر با نحوه تعیین مشتق توابع کسینوسی، به حل چند تمرین متنوع می‌پردازیم.