مشتق و انتگرال سری توانی — به زبان ساده (+ دانلود فیلم آموزش رایگان)

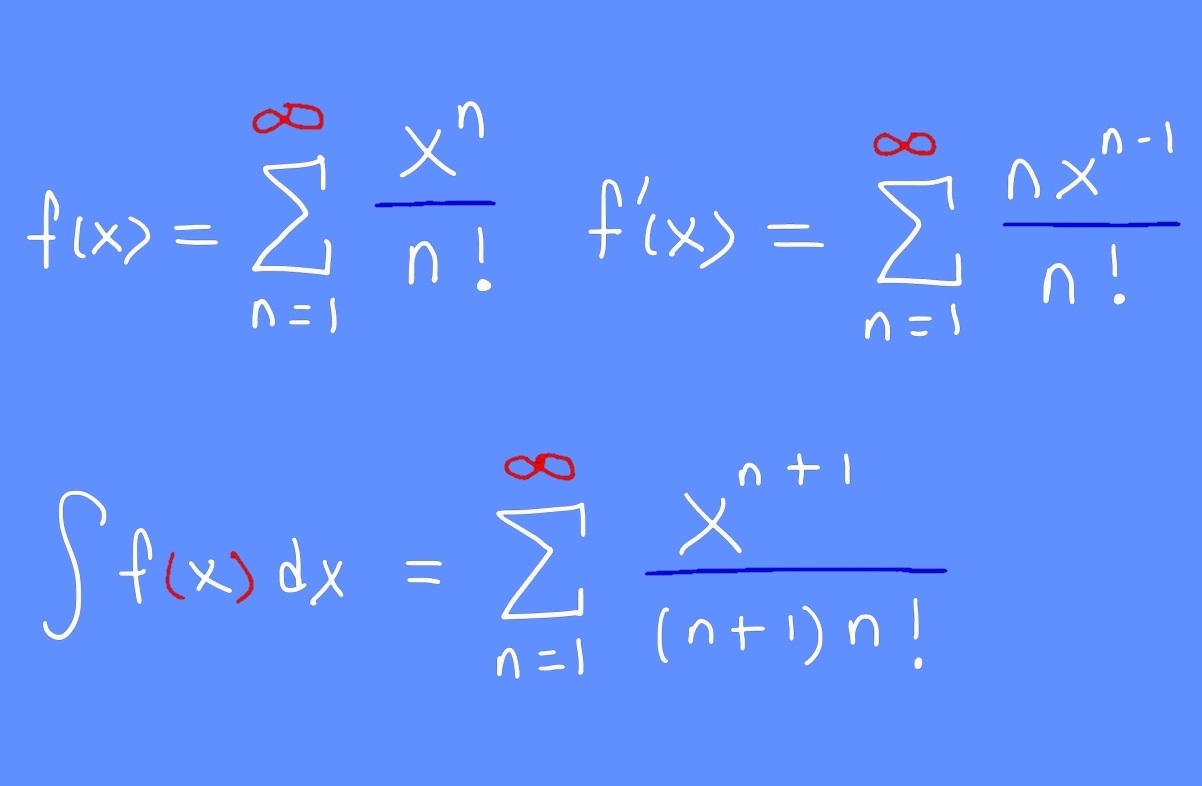
در مباحث قبلی مجله فرادرس، با سری‌ توانی آشنا شدیم و حل معادلات دیفرانسیل با استفاده از روش‌ سری توانی را بیان کردیم. دیدیم که سری توانی، کاربرد بسیار مهمی در حل معادلات دیفرانسیل دارد. در این آموزش از مجموعه آموزش‌های ریاضی مجله فرادرس، درباره مشتق و انتگرال سری توانی بحث خواهیم کرد.

مشتق و انتگرال سری توانی

سری توانی $$\sum \limits _ { n = 0 } ^ \infty { { a _ n } { x ^ n } }$$ را در نظر بگیرید که شعاع همگرایی آن $$R \gt 0$$ است. تساوی زیر را در نظر بگیرید:

$$\large { f \left ( x \right ) = \sum \limits _ { n = 0 } ^ \infty { { a _ n } { x ^ n } } } = { { a _ 0 } + { a _ 1 } x } + { { a _ 2 } { x ^ 2 } + \ldots , \; \; } \kern-0.3pt { \left | x \right | \lt R . }$$

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

فرض کنید در $$\left| x \right| \lt R$$ تابع $$f \left ( x \right ) = \sum \limits _ { n = 0 } ^ \infty { { a _ n }{ x ^ n } }$$ پیوسته باشد. از سری توانی می‌توان جمله به جمله در بازه همگرایی مشتق گرفت.

$$\large { f ’ \left ( x \right ) } = { \frac { d } { { d x } } { a _ 0 } + \frac { d } { { d x } }{ a _ 1 } x } + { \frac { d } { { d x } } { a _ 2 } { x ^ 2 } + \ldots } \\ \large = { { a _ 1 } + 2 { a _ 2 } x + 3 { a _ 3 } { x ^ 2 } + \ldots } = { \sum \limits _ { n = 1 } ^ \infty { n { a _ n } { x ^ { n – 1 } } } . }$$

همچنین می‌توان جمله به جمله از سری توانی در بازه همگرایی انتگرال گرفت. بنابراین، اگر $$– R \lt b \lt x \lt R$$، عبارت زیر برقرار است:

$$\large { \int \limits _ b ^ x { f \left ( t \right ) d t } } = { \int \limits _ b ^ x { { a _ 0 } d t } + \int \limits _ b ^ x { { a _ 1 } t d t } } + { \int \limits _ b ^ x { { a _ 2 } { t ^ 2 } d t } + \ldots } + { \int \limits _ b ^ x { { a _ n } { t ^ n } d t } + \ldots }$$

اگر از سری در بازه $$\left[ {0,x} \right]$$ انتگرال بگیریم، می‌توان نوشت:

$$\large { \int \limits _ 0 ^ x { f \left ( t \right ) d t } } = { \int \limits _ 0 ^ x { { a _ 0 } d t } + \int \limits _ 0 ^ x { { a _ 1 } t d t } } + { \int \limits _ 0 ^ x { { a _ 2 } { t ^ 2 } d t } + \ldots } + { \int \limits _ 0 ^ x { { a _ n } { t ^ n } d t } + \ldots } \\ \large = { { a _ 0 } x + { a _ 1 } \frac { { { x ^ 2 } } } { 2 } + { a _ 2 } \frac { { { x ^ 3 } } } { 3 } + \ldots } = { \sum \limits _ { n = 0 } ^ \infty { { a _ n } \frac { { { x ^ { n + 1 } } } } { { n + 1 } } } } + { C . }$$

مثال‌ها

در ادامه، چند مثال را بررسی می‌کنیم.

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

مثال ۱

نشان دهید تساوی زیر برقرار است.

$$\large { \frac { 1 } { { 1 + x } } = 1 – x + { x ^ 2 } } - { { x ^ 3 } + { x ^ 4 } – \ldots } = { \sum \limits _ { n = 0 } ^ \infty { { a _ n } { x ^ n } } \; \; } \kern-0.3pt{\text{,}\;\;\left| x \right | \lt 1 . }$$

حل: ابتدا سری توانی زیر را در نظر بگیرید:

$$\large { 1 + x + { x ^ 2 } } + { { x ^ 3 } + \ldots }$$

سری بالا، یک سری هندسی با قدر نسبت $$x$$ است. بنابراین، این سری در بازه $$\left| x \right| \lt 1$$ همگرا و مجموع آن برابر است با $${\large\frac{1}{{1 – x}}\normalsize}$$. اگر $$-x$$ را  به جای $$x$$ قرار دهیم، داریم:

$$\large { 1 – x + { x ^ 2 } } - { { x ^ 3 } + \ldots } = { \frac { 1 } { { 1 – \left ( { – x } \right ) } } } = { \frac { 1 } { { 1 + x } } \; \; } \kern-0.3pt{\text{,}\;\; \left | x \right | \lt 1 . }$$

بنابراین:

$$\large { \frac { 1 } { { 1 + x } } = 1 – x + { x ^ 2 } } - { { x ^ 3 } + { x ^ 4 } – \ldots } = { \sum \limits _ { n = 0 } ^ \infty { { { \left ( { – 1 } \right ) } ^ n } { x ^ n } } \; \; } \kern-0.3pt {\text{,} \; \; \left | x \right | \lt 1 . }$$

مثال ۲

سری توانی تابع کسری $$\large\frac{1}{{2 – x}}\normalsize$$ را به دست آورید.

حل: می‌توانیم تابع را به صورت زیر بنویسیم:

$$\large \frac { 1 } { { 2 – x } } = \frac { { \frac { 1 } { 2 } } }{ { 1 – \frac { x } { 2 } } } .$$

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

همان‌طور که می‌بینیم، عبارت بالا،‌ مجموع یک سری هندسی بی‌نهایت با جمله اول $${\large\frac{1}{2}\normalsize}$$ و قدر نسبت $${\large\frac{x}{2}\normalsize}$$ است:

$$\large { \frac { 1 } { 2 } + \frac { 1 } { 2 } \frac { x } { 2 } + \frac { 1 } { 2 } { \left ( { \frac { x } { 2 } } \right ) ^ 2 } } + { \frac { 1 } { 2 } { \left ( { \frac { x } { 2 } } \right ) ^ 3 } + \ldots } \\ \large = { \frac { 1 } { 2 } + \frac { x } { { { 2 ^ 2 } } } + \frac { { { x ^ 2 } } } { { { 2 ^ 3 } } } } + { \frac { {{ x ^ 3 } } } { { { 2 ^ 4 } } } + \ldots } = { \sum \limits _ { n = 0 } ^ \infty { \frac { { { x ^ n } } } { {{ 2 ^ { n + 1 } } } } } . }$$

سری توانی در $$\left| x \right| \lt 2$$ همگرا است.

مثال ۳

سری توانی $$\large\frac{{6x}}{{5{x^2} – 4x – 1}}\normalsize$$‌ را به دست آورید.

حل: ابتدا تابع را به کسرهای جزئی بسط می‌دهیم. تابع درجه دوم مخرج را می‌توان به صورت $$5{x^2} – 4x – 1= \left( {5x + 1} \right)\left( {x – 1} \right)$$ نوشت. بنابراین:

$$\large { \frac { { 6 x } } { { 5 { x ^ 2 } – 4 x – 1 } } } = { \frac { A } { { 5 x + 1 } } } + { \frac { B } { { x – 1 } } . }$$

با ضرب دو طرف تساوی بالا در $$5{x^2} – 4x – 1= \left( {5x + 1} \right)\left( {x – 1} \right)$$، خواهیم داشت:

$$ \large { { 6 x } = { A \left ( { x – 1 } \right ) } + { B \left ( { 5 x + 1 } \right ) , \; \; } } \Rightarrow<br /> { { 6 x } = { A x – A } + { 5 B x + B , \; \; } }\\ \large \Rightarrow<br /> { { 6 x } = { \left ( { A + 5 B } \right ) x } + { \left ( { – A + B } \right ) , \; \; } } \Rightarrow<br /> { \left\{ { \begin {array} { * { 2 0 } {l} }<br /> { A + 5 B = 6 } \\<br /> { – A + B = 0 }<br /> \end {array} } \right . . } $$

جواب دستگاه بالا، $$A=1$$ و $$B=1$$ است. بنابراین، تساوی زیر را خواهیم داشت:

$$\large { \frac { { 6 x } } { { 5 { x ^ 2 } – 4 x – 1 } } } = { \frac { 1 } { { 5 x + 1 } } } + { \frac { 1 } { { x – 1 } } } = { \frac { 1 } { { 1 + 5 x } } } - { \frac { 1 } { { 1 – x } } . }$$

دو کسر سمت راست تساوی بالا، مجموع سری‌های هندسی بی‌نهایت هستند:

$$\large { \frac { 1 } { { 1 + 5 x } } } = { \frac { 1 } { { 1 – \left ( { – 5 x } \right ) } } } = { 1 – 5 x + { \left ( { – 5 x } \right ) ^ 2 } } + { { \left ( { – 5 x } \right ) ^ 3 } + \ldots } = { \sum \limits _ { n = 0 } ^ \infty { { { \left ( { – 5 x } \right ) } ^ n } } , }$$

$$\large { \frac { 1 } { { 1 – x } } } = { 1 + x + { x ^ 2 } } + { { x ^ 3 } + \ldots } = { \sum \limits _ { n = 0 } ^ \infty { { x ^ n } } . }$$

بنابراین، بسط سری توانی تابع اصلی برابر است با:

$$\large { \frac { { 6 x } } { { 5 { x ^ 2 } – 4 x – 1 } } } = { \sum \limits _ { n = 0 } ^ \infty { { { \left ( { – 5 x } \right ) } ^ n } } – \sum \limits _ { n = 0 } ^ \infty { { x ^ n } } } \\ \large = { \sum \limits _ { n = 0 } ^ \infty { \left[ { { { \left ( { – 5 x } \right ) } ^ n } – { x ^ n } } \right]} } = { \sum \limits _ { n = 0 } ^ \infty { \left [ { { { \left ( { – 5 } \right ) } ^ n } – 1 } \right ] { x ^ n } } . }$$

مثال ۴

یک نمایش سری توانی برای تابع $$\ln \left( {1 + x} \right)$$ در $$\left| x \right| \lt 1$$ بیابید.

حل: در مثال ۱، بسط سری توانی زیر را به دست آوردیم:

$$\large { \frac { 1 } { { 1 + x } } } = { 1 – x + { x ^ 2 } } - { { x ^ 3 } + \ldots } = { \sum \limits _ { n = 0 } ^ \infty { { { \left ( { – 1 } \right ) } ^ n } { x ^ n } } , \; \; } \kern-0.3pt { \left | x \right | \lt 1 . }$$

با انتگرال‌گیری جمله به جمله در بازه $$\left[ {0,x} \right]$$، داریم:

$$\large { \ln \left ( { 1 + x } \right ) } = { \int \limits _ 0 ^ x { \frac { { d t } } { { 1 + t } } } } = { \int \limits _ 0 ^ x { \left ( { 1 – t + { t ^ 2 } – { t ^ 3 } + \ldots } \right ) d t } } \\ \large = { x – \frac { { { x ^ 2 } } } { 2 } + \frac { { { x ^ 3 } } } { 3 } } - { \frac { { { x ^ 4 } } } { 4 } + \ldots } = { \sum \limits _ { n = 0 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ n } { x ^ { n + 1 } } } } { { n + 1 } } } } = { \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ { n + 1 } } { x ^ n } } } { n } } . }$$

مثال ۵

انتگرال $$\int\limits_0^x {{\large\frac{{\ln \left( {1 + t} \right)}}{t}\normalsize} dt}$$ را به صورت یک سری توانی بنویسید.

حل: در مثال قبلی (مثال ۴)، بسط سری توانی تابع لگاریتمی را به دست آوردیم:

$$\large { \ln \left ( { 1 + t } \right ) } = { \sum \limits _ { n = 1 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ { n + 1 } } { t ^ n } } } { n } } } = { t – \frac { { { t ^ 2 } } } { 2 } + \frac { { { t ^ 3 } } } { 3 } } - { \frac { { { t ^ 4 } } } { 4 } + \ldots , \; \; } \kern-0.3pt{\left| t \right| \lt 1 . }$$

در نتیجه، می‌توانیم بنویسیم:

$$\large {\frac{{\ln \left( {1 + t} \right)}}{t} } = {\sum\limits_{n = 1}^\infty {\frac{{{{\left( { – 1} \right)}^{n + 1}}{t^{n – 1}}}}{n}} } = {1 – \frac{t}{2} + \frac{{{t^2}}}{3} }-{ \frac{{{t^3}}}{4} + \ldots }$$

با انتگرال‌گیری جمله به جمله از سری در بازه $$\left[ {0,x} \right]$$، خواهیم داشت:

$$\large \begin {align*} \int\limits_0^x {\frac{{\ln \left( {1 + t} \right)}}{t}dt} & = {\int\limits_0^x {\left[ {1 – \frac{t}{2} + \frac{{{t^2}}}{3} – \frac{{{t^3}}}{4} + \ldots } \right]dt} } \\ & = {x – \frac{{{x^2}}}{{2 \cdot 2}} + \frac{{{x^3}}}{{3 \cdot 3}} }-{ \frac{{{x^4}}}{{4 \cdot 4}} + \ldots } \\ & = {\sum\limits_{n = 1}^\infty {\frac{{{{\left( { – 1} \right)}^{n + 1}}{x^n}}}{{{n^2}}}} .} \end {align*}$$

مثال ۶

نمایش سری توانی تابع نمایی $$e^x$$ را بیابید.

حل: سری زیر را در نظر بگیرید:

$$\large { f \left ( x \right ) = \sum \limits _ { n = 0 } ^ \infty { \frac { { { x ^ n } } } { { n ! } } } } = { 1 + x + \frac { { { x ^ 2 } } } { {2 ! } } } + { \frac { { { x ^ 3 } }} { { 3 ! } } + \ldots }$$

که به ازای همه مقادیر $$x$$ همگرا است.

با مشتق‌گیری از تک تک جملات سری، داریم:

$$\large { f ’ \left ( x \right ) } = { \frac { d } { { d x } } 1 + \frac { d } { { d x } } x + \frac { d } { { d x } } \frac { { { x ^ 2 } } } { { 2 ! }} } + { \frac { d } { { d x } } \frac { { { x ^ 3 } } } { { 3 ! } } + \ldots } \\ \large = { 0 + 1 + x } + { \frac { { { x ^ 2 } } } { { 2 ! } } + \ldots } = { f \left ( x \right ) . }$$

بنابراین، تابع $$f(x)$$ در معادله $$f’ = f$$ صدق می‌کند. جواب عمومی این معادله به فرم $$f\left( x \right) = c{e^x}$$ است که در آن $$c$$ یک ثابت است. با جایگذاری مقدار اولیه $$f\left( 0 \right) = 1$$، مقدار $$c=1$$ به دست می‌آید. بنابراین، بسط سری توانی برای $$e^x$$ را می‌توان محاسبه کرد:

$$\large { f \left ( x \right ) = { e ^ x } = \sum \limits _ { n = 0 } ^ \infty { \frac { { { x ^ n } } } { { n ! } } } } = { 1 + x + \frac { { { x ^ 2 } } } { { 2 ! } } } + { \frac { { { x ^ 3 } } } { { 3 ! } } + \ldots }$$

مثال ۷

بسط سری توانی تابع سینوس هیپربولیک $$\sinh x$$ را بنویسید.

حل: از آن‌جایی که $$\sinh x = {\large\frac{{{e^x} – {e^{ – x}}}}{2}\normalsize}$$، می‌توان از نمایش سری توانی برای $$e^x$$ و $$e^{-x}$$ استفاده کرد.

در مثال قبل، فرمول زیر را محاسبه کردیم:

$$\large { { e ^ x } = \sum \limits _ { n = 0 } ^ \infty { \frac { { { x ^ n } } } { {n ! } } } } = { 1 + x + \frac { { { x ^ 2 } } } { { 2 ! } } } + { \frac { { { x ^ 3 } } } { { 3 ! } } + \ldots }$$

با قرار دادن $$-x$$ به جای $$x$$، داریم:

$$\large { { e ^ { – x } } = \sum \limits _ { n = 0 } ^ \infty { \frac { { { { \left ( { – x } \right ) } ^ n } } } { { n ! } } } } = { \sum \limits _ { n = 0 } ^ \infty { \frac { { { { \left ( { – 1 } \right ) } ^ n } { x ^ n } } } { { n ! } } } } = { 1 – x + \frac { { { x ^ 2 } } } { { 2 ! } } } - { \frac { { { x ^ 3 } } } { { 3 ! } } + \ldots }$$

در نهایت، بسط تابع سینوس هیپربولیک را می‌نویسیم:

$$\large { \sinh x = \frac { { { e ^ x } – { e ^ { – x } } } } { 2 } } = { \frac { 1 } { 2 }\left [ { \sum \limits _ { n = 0 } ^ \infty { \frac { { { x ^ n } } } { { n ! } } } } \right . } - { \left . { \sum \limits _ { n = 0 } ^ \infty { \frac { { { { \left ( { – x } \right ) } ^ n } }} { { n ! } } } } \right ] } \\ \large = { \frac { 1 } { 2 } \left [ { \left ( { 1 + x + \frac { { { x ^ 2 } } } { { 2 ! } } + \frac { { { x ^ 3 } } } { { 3 ! } } + \ldots } \right ) } \right . } - { \left . { \left ( { 1 – x + \frac { { { x ^ 2 } } } { { 2 ! } } – \frac { { { x ^ 3 } } } { { 3 ! } } + \ldots } \right ) } \right] } \\ \large = { \frac { 1 } { 2 } \left [ { 2 \left ( { x + \frac { { { x ^ 3 } } } { { 3 ! } } + \frac { { { x ^ 5 } } } { { 5 ! } } + \ldots } \right ) } \right ] } = { x + \frac { { { x ^ 3 } } } { { 3 ! } } + \frac { { { x ^ 5 } } } { { 5 ! } } + \ldots } = { \sum \limits _ { n = 0 } ^ \infty { \frac { { { x ^ { 2 n + 1 } } } } { { \left ( { 2 n + 1 } \right ) ! } } } . }$$