حل معادلات دیفرانسیل با سری توانی — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

در بخشهای قبل در مورد اصول معادلات دیفرانسیل، معادلات مرتبه اول و دوم صحبت کردیم. در این قسمت قصد داریم تا در مورد راه حلی بحث کنیم که در اکثر معادلات، کاربردی است.
گاهی اوقات پاسخ یک معادله دیفرانسیل را بهصورت سری توانی در نظر میگیرند. البته در مشتقات پارهای نیز با استفاده از روش جداسازی متغیرها، پاسخ معادله بهصورت یک سری در خواهد آمد. این مفهوم، دنبالهای است که به شکل حاصل جمع چندین عبارت در نظر گرفته میشود. در حالت کلی یک سری توانی بهصورت زیر بیان میشود:
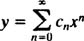
با جایگذاری چنین عبارتی در هر معادله دیفرانسیلی و محاسبه ضرایب موجود در سری، پاسخ معادله مفروض یافت خواهد شد. توجه داشته باشید این آموزش عمدتاً در قالب مثال بیان شده؛ بنابراین لطفا آنها را با دقت مطالعه فرمایید.

معادلات دیفرانسیل مرتبه اول
بهمنظور حل یک معادله دیفرانسیل مرتبه اول، سری توانی را به شکل زیر فرض کنید:
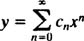
با جایگذاری این عبارت در معادله و محاسبه ثابتهای موجود در آن، سری مذکور به عنوان پاسخ معادله در نظر گرفته میشود.
مثال 1
سری توانی معادله زیر را بیابید.
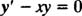
در قدم اول، پاسخ بهصورت زیر فرض میشود.
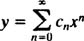
با جایگذاری این سری در معادله اصلی، عبارت زیر حاصل خواهد شد.
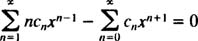
با باز کردن این سری در رابطه بالا، جملات آن بهصورت زیر نوشته میشوند.
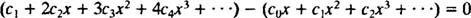
قدم بعدی مرتبسازی رابطه بر حسب درجه متغیرهای موجود در آن است. بنابراین جملات باز شده را بایستی بهشکل زیر نوشت.
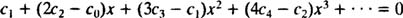
همانطور که احتمالا متوجه شدهاید، رابطه بالا از الگوی خاصی پیروی میکند. این الگو به شکلی است که در ادامه آمده.
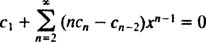
بهمنظور صادق بودن این رابطه برای تمامی xها، ضرایب درون سری بایستی صفر در نظر گرفته شوند. بنابراین:
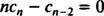
معادله بالا، یک رابطه حسابی بازگشتی است. لذا شکل بازنویسی شده آن بهصورت زیر بیان میشود.
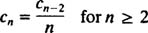
از آنجایی که محدودیتی برای c0 تعریف نشده، بنابراین مقدار آن تعریف نشده است. از طرفی همانطور که قبلا نیز بیان شد، تمامی عبارات سمت چپ معادله، به ازای هر متغیری بایستی صفر باشند؛ بنابراین مقدار c1 برابر با صفر بدست میآید. با توجه به رابطه بازگشتی بیان شده، داریم:
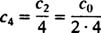
از طرفی برای عبارتهای فرد میتوان گفت:
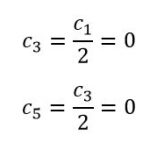
بنابراین تمامی عبارتهای فردِ (2n+1) این سری، صفر خواهند بود. با صفر قرار دادن آنها و جایگذاری عبارتهای زوج، میتوان سری را به شکل زیر و در قالب رابطهای بازگشتی بیان کرد.
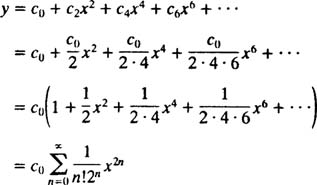
در نتیجه حالت نهایی معادله دیفرانسیل بهصورت زیر است.
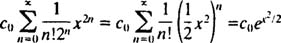
توجه داشته باشید که تمامی سریها را نمیتوان با الگوی مشخصی معلوم کرد.
مثال 2
معادله زیر را با استفاده از شرایط اولیه در نظر گرفته شده، حل کنید.
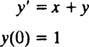
همانند مثال اول، عبارت کلی سری را در معادله مفروض جایگزین کرده و داریم:
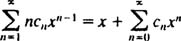
با مرتب کردن تمامی ضرایب در سمت چپ، میتوان گفت:
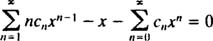
همانطور که میبینید چند جمله اول این سری به صورت زیر هستند.
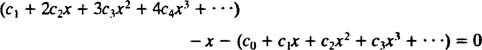
این جملات را بر اساس درجه متغریشان مرتب کرده و به شکل زیر مینویسیم.
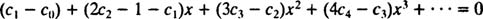
اگر دو جمله اول را در نظر نگیریم، مابقی جملات از الگوی زیر پیروی میکنند.
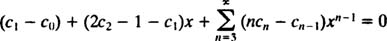
به منظور صادق بودن این معادله به ازای هر x، تمامی ضرایب آن بایستی صفر باشند. بنابراین میتوان گفت:
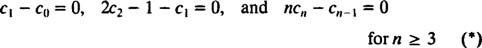
جمله آخر، یک تصاعد حسابی است که میتوان آن را بهشکل زیر بیان کرد.
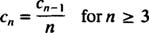
از معادله * این نتیجه گرفته میشود که c1 برابر با c0 و در معادله دوم، (c2=1/2(1+c1 است. بنابراین تصاعد حسابی به صورت زیر حاصل میشود.
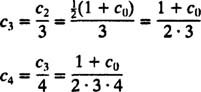
رابطه بالا به همین شکل، برای بقیه ضرایب نیز ادامه دارد. با جمع کردن تمامی این عبارات، سری توانی مد نظر بهصورت زیر قابل بیان است.
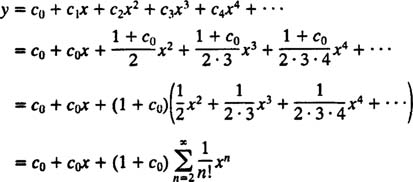
توجه داشته باشید که برای محاسبه c0 میتوان از شرط اولیه، بهشکل زیر استفاده کرد:
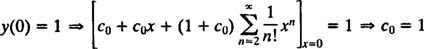
نهایتاً پاسخ معادله مقدار اولیه مفروض، بهصورت زیر بدست میآید:
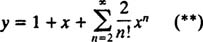
با توجه به بسط تیلور $$ e ^x$$، رابطه $$\sum _{n=2}^{\infty} \frac {1 } { n !} x ^ n =e ^ x - x -1 $$ را داریم. بنابراین، جواب معادله دیفرانسیل به صورت زیر خواهد بود:
$$ \large y = 1 + x + 2(e ^ x - x - 1 ) = -1-x +2e ^ x $$
معادله دیفرانسیل مرتبه دوم
به منظور حل یک معادله دیفرانسیل مرتبه دوم نیز میتوان از روش سری توانی استفاده کرد. همانطور که در بخشهای گذشته نیز بیان شد، یک معادله دیفرانسیل همگن خطی مرتبه دوم به شکل زیر قابل بیان است:
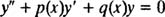
اگر هر دو تابع p و q در نقطه x0 مشتقپذیر باشند، تابع مربوطه نیز در آن نقطه تحلیلی است. به بیانی دیگر اگر هر کدام از این دو تابع در نقطه بیان شده، مشتقپذیر نباشند، به نقطه x0، «نقطه تکین» (Singular Point) تابع y گفته میشود. دقت کنید که در روشهایی که در این قسمت ارائه میکنیم توابع مربوطه، تحلیلی در نظر گرفته شدهاند.
مثال 3
سری توانی معادله شرایط اولیه تابع زیر را بیابید.
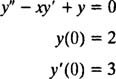
با فرض سری زیر:
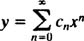
و جایگذاری آن در معادله اصلی خواهیم داشت:
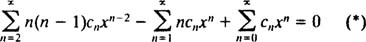
همانند مراحل انجام شده در مثال 1 و 2، ابتدا سری را باز میکنیم؛ سپس چند جمله اول آن را نوشته و بر حسب درجه متغیرهای x، مرتب میکنیم. با جایگذاری n+2 بجای n و نوشتن دوباره سری، خواهیم داشت:
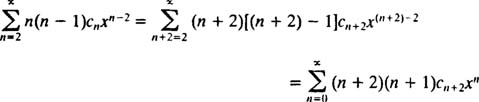
بنابراین معادله اصلی بهصورت زیر قابل بیان است.
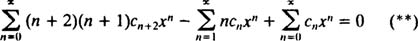
قدم بعدی نوشتن سمت چپ معادله است. در معادله بالا تعداد جملات سری در عبارت اول و سوم از صفر تا بینهایت تغییر میکند؛ این در حالی است که در عبارت دوم، اندیس n از 1 تا بینهایت در نظر گرفته شده است. همواره در حل معادلات دیفرانسیل، سریها را بایستی به نحوی نوشت که دارای اندیس ابتدا و انتهای یکسانی باشند. بدین منظور در عبارت اول و سوم، دو جمله اول را مطابق زیر مینویسیم.
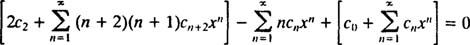
به منظور یکی کردن سریها، عبارت بالا را بهصورت زیر بیان میکنیم.
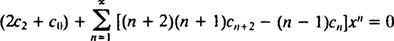
همانند مثالهای قبل، برای اینکه این معادله به ازای هر xای صادق باشد، بایستی تمامی عبارات سمت چپ آن را برابر با صفر قرار داد. در نتیجه، میتوان نوشت:
2c2+c0=0
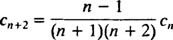
با توجه به دو عبارت ذکر شده در بالا، دو نتیجهگیری زیر حاصل میشود.
c2=-1/2c0
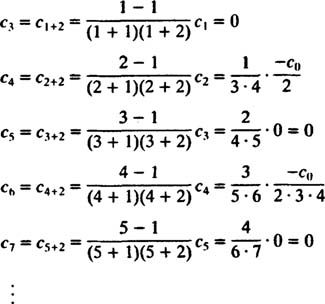
با دقت در این عبارت، الگوی کلی سری بهصورت زیر بدست میآید.
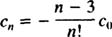
توجه داشته باشید که این رابطه برای nهای بزرگتر از 4 و زوج صادق است و تمام جملات به غیر از a1 صفر می شوند. بنابراین این رابطه معادل زیر خواهد بود:
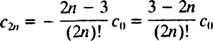
نهایتا سری توانی مد نظر، بهصورت زیر حساب خواهد شد.
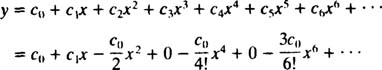
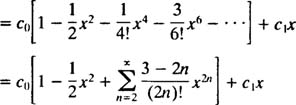
همانطور که از معادله دیفرانسیل مرتبه 2 انتظار میرفت، پاسخ مرتبط با آن شامل دو ثابت میشود که با استفاده از شرایط اولیه قابل محاسبه هستند. از آنجایی که y(0)=2 در نظر گرفته شده، با جایگذاری آن در معادله، مقدار c0 برابر با 2 و از شرط y′(0) = 3 عدد c1 برابر با 3 بدست میآید. نهایتا پاسخ معادله شرط اولیه مربوطه، بهصورت زیر قابل بیان است.
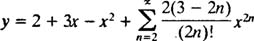
مثال 4
پاسخ سری توانی معادله زیر را بیابید.

پاسخ معادله را همانند مثالهای قبل، بهشکل زیر فرض میکنیم.
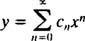
سپس با جایگذاری آن در معادله مربوطه خواهیم داشت:
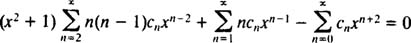
این عبارت را میتوان به صورت زیر نیز مرتب کرد.
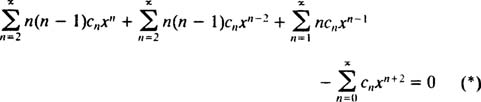
همانطور که در مثال قبل نیز بیان کردیم، تمامی توانهای x بایستی با هم برابر باشند؛ دلیل این کار جمع زدن تمامی عبارات در یک سری است. بدین منظور میتوان نوشت.
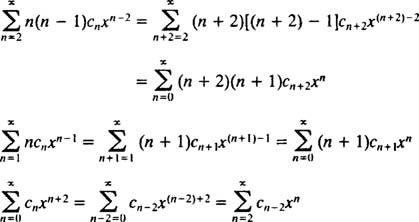
نهایتا این عبارت در قالب زیر بیان میشود.
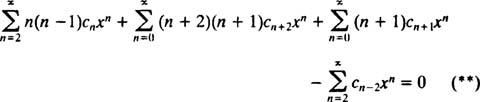
بنابراین معادله * بهصورت زیر قابل بازنویسی است.
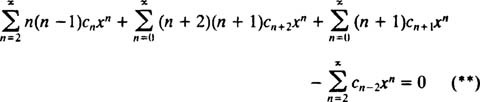
قدم بعدی این است که بایستی اندیس n در سریها، مشابه یکدیگر باشند. بدین منظور عبارت بالا بهشکل زیر بیان میشود.
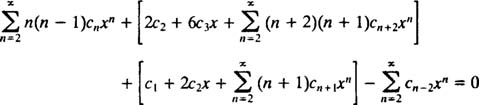
نهایتا بایستی تمامی عبارات در یک سری قرار گیرند. برای این کار، سری توانی بدست آمده، بهصورت زیر نوشته میشود.
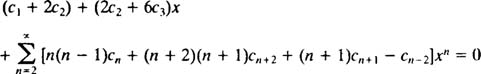
همانطور که قبلا نیز بیان شد، بهمنظور صادق بودن این عبارت در تمامی xها، کل ضرایب سمت چپ بایستی صفر باشند. با صفر قرار دادن این عبارتها، معادلات زیر حاصل میشوند.
2c2+c1=0
2c2+6c3=0
همچنین تصاعد حسابی که در ادامه آمده را میتوان از شرایط مرزی، بهصورت زیر استخراج کرد.
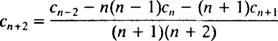
معادلات مربوط به ثابتها، پاسخهای زیر را در پی خواهند داشت.
c2=−½c1
c3=−⅓c2=−⅓(‐½c1)=⅙c1
بنابراین c4، c5 و c6 را میتوان بصورت زیر محاسبه کرد.
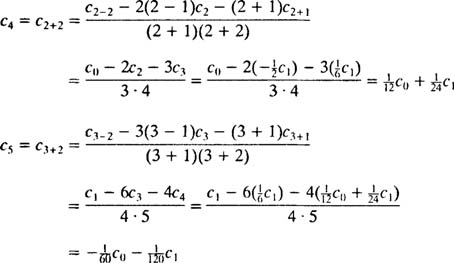
در نتیجه با محاسبه ضرایب، سری توانی مد نظر نیز به شکل زیر بدست میآید.
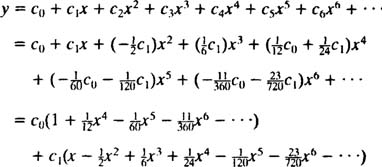











واقعا اموزش خوبی بود!
خداقوت.
سلام مجدد
من فیلم ها را نگاه کردم اما به حل مشکلم کمکی نکرد.در واقع من دو تا دنباله بازگشتی دارم یعنی یک anو یک an+1 که هر کدام از آن ها بر حسب an های دیگری هستند و من برای این که an ها را بتوانم ساده کنم مشکل دارم.
با سلام
آموزش های این سایت واقعا کاربردی و قابل فهمه خیلی ممنون
من یه سوالی داشتم اگه برای حل معادلات دیفرانسیل درجه اول و با استفاده از دنباله بازگشتی آن بخواهیم شعاع همگرایی را به دست بیاریم چگونه باید عمل کنیم؟
سلام.
احتمالاً آموزش «سری توانی — به زبان ساده (+ دانلود فیلم آموزش رایگان)» بتواند به شما کمک کند.
سپاس از همراهیتان.