در آموزشهای قبلی از مجموعه مقالات ریاضی مجله فرادرس، درباره مفهوم مشتق و روشهای مشتقگیری بحث کردیم و مباحثی مانند مشتق لگاریتم و تابع نمایی ، مشتق ضمنی ، مشتق جزئی ، مشتق زنجیرهای و مشتق جهتی را توضیح دادیم. در این آموزش، درباره مشتق توابع معکوس بحث خواهیم کرد.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
قضیه تابع معکوس
فرض کنید f ( x ) f(x) f ( x ) اکیداً یکنوا در بازه ( a , b ) (a, b) ( a , b ) x 0 x_0 x 0 f ’ ( x 0 ) ≠ 0 f’\left( {{x_0}} \right) \ne 0 f ’ ( x 0 ) = 0 x = φ ( y ) x = \varphi \left( y \right) x = φ ( y ) y 0 = f ( x 0 ) {y_0} = f\left( {{x_0}} \right) y 0 = f ( x 0 )
φ ’ ( y 0 ) = 1 f ’ ( x 0 ) . \large \varphi’\left( {{y_0}} \right) = \frac{1}{{f’\left( {{x_0}} \right)}}. φ ’ ( y 0 ) = f ’ ( x 0 ) 1 .
اثبات: فرض کنید متغیر y y y y 0 y _0 y 0 Δ y ≠ 0 \Delta y \ne 0 Δ y = 0 x x x x 0 x_0 x 0 Δ x \Delta x Δ x y = f ( x ) y = f\left( x \right) y = f ( x ) Δ x ≠ 0 \Delta x \ne 0 Δ x = 0
Δ x Δ y = 1 Δ y Δ x . \large \frac{{\Delta x}}{{\Delta y}} = \frac{1}{{\frac{{\Delta y}}{{\Delta x}}}}. Δ y Δ x = Δ x Δ y 1 .
اگر Δ y → 0 \Delta y \to 0 Δ y → 0 x = φ ( y ) x = \varphi \left( y \right) x = φ ( y ) y 0 y_0 y 0 Δ x → 0 \Delta x \to 0 Δ x → 0
lim Δ x → 0 1 Δ y Δ x = 1 lim Δ x → 0 Δ y Δ x = 1 f ’ ( x 0 ) . \large {\lim\limits_{\Delta x \to 0} \frac{1}{{\frac{{\Delta y}}{{\Delta x}}}} = \frac{1}{{\lim\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}}}} }
= {\frac{1}{{f’\left( {{x_0}} \right)}}.} Δ x → 0 lim Δ x Δ y 1 = Δ x → 0 lim Δ x Δ y 1 = f ’ ( x 0 ) 1 .
در این حالت، سمت چپ معادله به یک حد میل میکند که بنا به تعریف، برابر با مشتق تابع معکوس است:
lim Δ y → 0 Δ x Δ y = φ ’ ( y 0 ) . \large \lim\limits_{\Delta y \to 0} \frac{{\Delta x}}{{\Delta y}} = \varphi’\left( {{y_0}} \right). Δ y → 0 lim Δ y Δ x = φ ’ ( y 0 ) .
بنابراین، داریم:
φ ’ ( y 0 ) = 1 f ’ ( x 0 ) \large \varphi’\left( {{y_0}} \right) = \frac{1}{{f’\left( {{x_0}} \right)}} φ ’ ( y 0 ) = f ’ ( x 0 ) 1
یعنی مشتق تابع معکوس، معکوس مشتق تابع اصلی است.
مثالها
در این قسمت، برای آشنایی بهتر با نحوه محاسبه مشتق تابع معکوس و کاربرد آن، چند مثال حل شده را بررسی میکنیم.
مثال ۱
برای توابع زیر، مشتق تابع y = f ( x ) y = f\left( x \right) y = f ( x ) x = φ ( y ) x = \varphi \left( y \right) x = φ ( y )
(الف) y = x n \large y = \sqrt[\large n\normalsize]{x} y = n x
حل: ابتدا تابع معکوس تابع y = x n y = \sqrt[\large n\normalsize]{x} y = n x x x x y y y
y = f ( x ) = x n , ⇒ y n = ( x n ) n , ⇒ x = φ ( y ) = y n . \large {y = f\left( x \right) = \sqrt[\large n\normalsize]{x},\;\;}\Rightarrow
{{y^n} = {\left( {\sqrt[\large n\normalsize]{x}} \right)^n},\;\;}\Rightarrow
{x = \varphi \left( y \right) = {y^n}.} y = f ( x ) = n x , ⇒ y n = ( n x ) n , ⇒ x = φ ( y ) = y n .
با استفاده از قضیه تابع معکوس، داریم:
( x n ) ′ = f ’ ( x ) = 1 φ ’ ( y ) = 1 ( y n ) ′ = 1 n y n – 1 . \large {{\left( {\sqrt[\large n\normalsize]{x}} \right)^\prime } = f’\left( x \right) }
= {\frac{1}{{\varphi’\left( y \right)}} }
= {\frac{1}{{{{\left( {{y^n}} \right)}^\prime }}} }
= {\frac{1}{{n{y^{n – 1}}}}.} ( n x ) ′ = f ’ ( x ) = φ ’ ( y ) 1 = ( y n ) ′ 1 = n y n –1 1 .
اکنون عبارت y = x n y = \sqrt[\large n\normalsize]{x} y = n x
( x n ) ′ = 1 n y n – 1 = 1 n ( x n ) n – 1 = 1 n x n – 1 n ( x > 0 ) . \large {{\left( {\sqrt[\large n\normalsize]{x}} \right)^\prime } = \frac{1}{{n{y^{n – 1}}}} }
= {\frac{1}{{n{{\left( {\sqrt[\large n\normalsize]{x}} \right)}^{n – 1}}}} }
= {\frac{1}{{n\sqrt[\large n\normalsize]{{{x^{n – 1}}}}}}\;\;\;}\kern-0.3pt{\left( {x \gt 0} \right).} ( n x ) ′ = n y n –1 1 = n ( n x ) n –1 1 = n n x n –1 1 ( x > 0 ) .
(ب) y = arcsin x \large y = \arcsin x y = arcsin x
حل: تابع آرکسینوس ، معکوس تابع سینوس است. بنابراین، x = φ ( y ) = sin y x = \varphi \left( y \right) = \sin y x = φ ( y ) = sin y arcsin x \arcsin x arcsin x
( arcsin x ) ′ = f ’ ( x ) = 1 φ ’ ( y ) = 1 ( sin y ) ′ = 1 cos y = 1 1 – sin 2 y = 1 1 – sin 2 ( arcsin x ) = 1 1 – x 2 \large {{\left( {\arcsin x} \right)^\prime } = f’\left( x \right) }
= {\frac{1}{{\varphi’\left( y \right)}} }
= {\frac{1}{{{{\left( {\sin y} \right)}^\prime }}} } \\ \large
= {\frac{1}{{\cos y}} }
= {\frac{1}{{\sqrt {1 – {{\sin }^2}y} }} }
= {\frac{1}{{\sqrt {1 – {{\sin }^2}\left( {\arcsin x} \right)} }} }
= {\frac{1}{{\sqrt {1 – {x^2}} }}} ( arcsin x ) ′ = f ’ ( x ) = φ ’ ( y ) 1 = ( sin y ) ′ 1 = cos y 1 = 1– sin 2 y 1 = 1– sin 2 ( arcsin x ) 1 = 1– x 2 1
که در آن، − 1 < x < 1 -1 \lt x \lt 1 − 1 < x < 1
(پ) y = ln x \large y = \ln x y = ln x
حل: تابع لگاریتم طبیعی و تابع نمایی ، معکوس یکدیگر هستند. بنابراین، x = φ ( y ) = e y x = \varphi \left( y \right) = {e^y} x = φ ( y ) = e y x > 0 x \gt 0 x > 0 y ∈ R y \in \mathbb{R} y ∈ R
( ln x ) ′ = f ’ ( x ) = 1 φ ’ ( y ) = 1 ( e y ) ′ = 1 e y = 1 e ln x = 1 x \large {{\left( {\ln x} \right)^\prime } = f’\left( x \right) }
= {\frac{1}{{\varphi’\left( y \right)}} }
= {\frac{1}{{{{\left( {{e^y}} \right)}^\prime }}} }
= {\frac{1}{{{e^y}}} }
= {\frac{1}{{{e^{\ln x}}}} }
= {\frac{1}{x}} ( ln x ) ′ = f ’ ( x ) = φ ’ ( y ) 1 = ( e y ) ′ 1 = e y 1 = e l n x 1 = x 1
در محاسبات بالا، از e ln x = x {e^{\ln x}} = x e l n x = x
(ت) y = x + 1 3 \large y = \sqrt[\large 3\normalsize]{{x + 1}} y = 3 x + 1
حل: ابتدا معکوس تابع x = φ ( y ) x = \varphi \left( y \right) x = φ ( y ) y = f ( x ) y = f\left( x \right) y = f ( x ) x ∈ R x \in \mathbb{R} x ∈ R x x x y y y
y = x + 1 3 , ⇒ y 3 = x + 1 , ⇒ x = y 3 – 1. \large {y = \sqrt[\large 3\normalsize]{{x + 1}},\;\;}\Rightarrow
{{y^3} = x + 1,\;\;}\Rightarrow
{x = {y^3} – 1.} y = 3 x + 1 , ⇒ y 3 = x + 1 , ⇒ x = y 3 –1.
اکنون، مشتق f ’ ( x ) f’\left( x \right) f ’ ( x )
(ث) y = arccos ( 1 – 2 x ) \large y = \arccos \left( {1 – 2x} \right) y = arccos ( 1–2 x )
حل: تابع آرککسینوس، در بازه [ – 1 , 1 ] \left[ { – 1,1} \right] [ –1 , 1 ]
– 1 ≤ 1 – 2 x ≤ 1 , ⇒ − 2 ≤ – 2 x ≤ 0 , ⇒ 0 ≤ x ≤ 1. \large { – 1 \le 1 – 2x \le 1,\;\; }\Rightarrow {- 2 \le – 2x \le 0,\;\; }\Rightarrow
{0 \le x \le 1.} –1 ≤ 1–2 x ≤ 1 , ⇒ − 2 ≤ –2 x ≤ 0 , ⇒ 0 ≤ x ≤ 1.
تابع x = φ ( y ) x = \varphi \left( y \right) x = φ ( y )
y = arccos ( 1 – 2 x ) , ⇒ 1 – 2 x = cos y , ⇒ 2 x = 1 – cos y , ⇒ x = 1 2 – 1 2 cos y . \large {y = \arccos \left( {1 – 2x} \right),\;\;}\Rightarrow
{1 – 2x = \cos y,\;\;} \\ \large \Rightarrow
{2x = 1 – \cos y,\;\;}\Rightarrow
{x = \frac{1}{2} – \frac{1}{2}\cos y.} y = arccos ( 1–2 x ) , ⇒ 1–2 x = cos y , ⇒ 2 x = 1– cos y , ⇒ x = 2 1 – 2 1 cos y .
اکنون، مشتق تابع اصلی را با استفاده از مشتق تابع معکوس محاسبه میکنیم:
$$ \large \require {cancel}<br />
{{\left( {\arccos \left( {1 – 2x} \right)} \right)^\prime } = f’\left( x \right) }<br />
= {\frac{1}{{\varphi’\left( y \right)}} } \\ \large<br />
= {\frac{1}{{{{\left( {\frac{1}{2} – \frac{1}{2}\cos y} \right)}^\prime }}} }<br />
= {\frac{1}{{\frac{1}{2}\sin y}} = \frac{2}{{\sin y}} }<br />
= {\frac{2}{{\sqrt {1 – {\cos^2}y} }} } \\ \large<br />
= {\frac{2}{{\sqrt {1 – {\cos^2}\left( {\arccos \left( {1 – 2x} \right)} \right)} }} }<br />
= {\frac{2}{{\sqrt {1 – {{\left( {1 – 2x} \right)}^2}} }} }<br />
= {\frac{2}{{\sqrt {1 – \left( {1 – 4x + 4{x^2}} \right)} }} } \\ \large<br />
= {\frac{2}{{\sqrt {\cancel{1} – \cancel{1} + 4x – 4{x^2}} }} }<br />
= {\frac{\cancel{2}}{{\cancel{2}\sqrt {x – {x^2}} }} }<br />
= {\frac{1}{{\sqrt {x – {x^2}} }}.} $$
توجه کنید که مشتق، در نقاط مرزی x = 0 x = 0 x = 0 x = 1 x = 1 x = 1 y = f ( x ) y = f\left( x \right) y = f ( x )
(ج) y = 1 + x \large y = \sqrt {1 + \sqrt x } y = 1 + x
حل: این تابع، برای x > 0 x \gt 0 x > 0 x x x y y y
y = 1 + x , ⇒ y 2 = 1 + x , ⇒ x = y 2 – 1 , ⇒ x = ( y 2 – 1 ) 2 . \large {y = \sqrt {1 + \sqrt x } ,\;\;}\Rightarrow
{{y^2} = 1 + \sqrt x ,\;\;} \\ \large \Rightarrow
{\sqrt x = {y^2} – 1,\;\;}\Rightarrow
{x = {\left( {{y^2} – 1} \right)^2}.} y = 1 + x , ⇒ y 2 = 1 + x , ⇒ x = y 2 –1 , ⇒ x = ( y 2 –1 ) 2 .
اکنون مشتق تابع y = f ( x ) y = f\left( x \right) y = f ( x )
( 1 + x ) ′ = f ’ ( x ) = 1 φ ’ ( y ) = 1 [ ( y 2 – 1 ) 2 ] ′ = 1 2 ( y 2 – 1 ) ⋅ ( y 2 – 1 ) ′ = 1 2 ( y 2 – 1 ) ⋅ 2 y = 1 4 y ( y 2 – 1 ) . \large {{\left( {\sqrt {1 + \sqrt x } } \right)^\prime } = f’\left( x \right) }
= {\frac{1}{{\varphi’\left( y \right)}} }
= {\frac{1}{{{{\left[ {{{\left( {{y^2} – 1} \right)}^2}} \right]}^\prime }}} } \\ \large
= {\frac{1}{{2\left( {{y^2} – 1} \right) \cdot {{\left( {{y^2} – 1} \right)}^\prime }}} }
= {\frac{1}{{2\left( {{y^2} – 1} \right) \cdot 2y}} }
= {\frac{1}{{4y\left( {{y^2} – 1} \right)}}.}\qquad ( 1 + x ) ′ = f ’ ( x ) = φ ’ ( y ) 1 = [ ( y 2 –1 ) 2 ] ′ 1 = 2 ( y 2 –1 ) ⋅ ( y 2 –1 ) ′ 1 = 2 ( y 2 –1 ) ⋅ 2 y 1 = 4 y ( y 2 –1 ) 1 .
با جایگذاری تابع اصلی y y y
( 1 + x ) ′ = 1 4 y ( y 2 – 1 ) = 1 4 1 + x ( ( 1 + x ) 2 – 1 ) = 1 4 1 + x ( 1 + x – 1 ) = 1 4 x 1 + x ( x > 0 ) . \large {{\left( {\sqrt {1 + \sqrt x } } \right)^\prime } }={ \frac{1}{{4y\left( {{y^2} – 1} \right)}} }
= {\frac{1}{{4\sqrt {1 + \sqrt x } \left( {{{\left( {\sqrt {1 + \sqrt x } } \right)}^2} – 1} \right)}} } \\ \large
= {\frac{1}{{4\sqrt {1 + \sqrt x } \left( {\cancel{1} + \sqrt x – \cancel{1}} \right)}} }
= {\frac{1}{{4\sqrt x \sqrt {1 + \sqrt x } }}\;\;}\kern-0.3pt{\left( {x \gt 0} \right).} ( 1 + x ) ′ = 4 y ( y 2 –1 ) 1 = 4 1 + x ( ( 1 + x ) 2 –1 ) 1 = 4 1 + x ( 1 + x – 1 ) 1 = 4 x 1 + x 1 ( x > 0 ) .
(چ) y = arctan 1 x \large y = \arctan \frac{1}{x} y = arctan x 1
حل: تابع معکوس این تابع بهصورت زیر است:
y = arctan 1 x , ⇒ 1 x = tan y , ⇒ x = 1 tan y , x ≠ 0. \large {y = \arctan \frac{1}{x},\;\;}\Rightarrow
{\frac{1}{x} = \tan y,\;\;}\Rightarrow
{x = \frac{1}{{\tan y}},\;\;}\kern-0.3pt{\;\;x \ne 0.} y = arctan x 1 , ⇒ x 1 = tan y , ⇒ x = tan y 1 , x = 0.
اکنون مشتق تابع اصلی y = f ( x ) y = f\left( x \right) y = f ( x )
( arctan 1 x ) ′ = f ’ ( x ) = 1 φ ’ ( y ) = 1 ( 1 tan y ) ′ = 1 ( – 1 tan 2 y ) ⋅ 1 cos 2 y = – tan 2 y 1 cos 2 y . \large {{\left( {\arctan \frac{1}{x}} \right)^\prime } = f’\left( x \right) }
= {\frac{1}{{\varphi’\left( y \right)}} }
= {\frac{1}{{{{\left( {\frac{1}{{\tan y}}} \right)}^\prime }}} }\\ \large
= {\frac{1}{{\left( { – \frac{1}{{{{\tan }^2}y}}} \right) \cdot \frac{1}{{{{\cos }^2}y}}}} }
= { – \frac{{{{\tan }^2}y}}{{\frac{1}{{{{\cos }^2}y}}}}.} ( arctan x 1 ) ′ = f ’ ( x ) = φ ’ ( y ) 1 = ( t a n y 1 ) ′ 1 = ( – t a n 2 y 1 ) ⋅ c o s 2 y 1 1 = – c o s 2 y 1 tan 2 y .
با استفاده از اتحاد مثلثاتی 1 cos 2 y = 1 + tan 2 y \frac{1}{{{{\cos }^2}y}} = 1 + {\tan ^2}y cos 2 y 1 = 1 + tan 2 y
( arctan 1 x ) ′ = – tan 2 y 1 cos 2 y = – tan 2 y 1 + tan 2 y = – tan 2 ( arctan 1 x ) 1 + tan 2 ( arctan 1 x ) = – ( 1 x ) 2 1 + ( 1 x ) 2 = – 1 x 2 x 2 + 1 x 2 = – 1 1 + x 2 . \large {{\left( {\arctan \frac{1}{x}} \right)^\prime } = – \frac{{{{\tan }^2}y}}{{\frac{1}{{{{\cos }^2}y}}}} }
= { – \frac{{{{\tan }^2}y}}{{1 + {{\tan }^2}y}} } \\ \large
= { – \frac{{{{\tan }^2}\left( {\arctan \frac{1}{x}} \right)}}{{1 + {{\tan }^2}\left( {\arctan \frac{1}{x}} \right)}} }
= { – \frac{{{{\left( {\frac{1}{x}} \right)}^2}}}{{1 + {{\left( {\frac{1}{x}} \right)}^2}}} }
= { – \frac{{\frac{1}{{{x^2}}}}}{{\frac{{{x^2} + 1}}{{{x^2}}}}} }
= { – \frac{1}{{1 + {x^2}}}.} ( arctan x 1 ) ′ = – c o s 2 y 1 tan 2 y = – 1 + tan 2 y tan 2 y = – 1 + tan 2 ( arctan x 1 ) tan 2 ( arctan x 1 ) = – 1 + ( x 1 ) 2 ( x 1 ) 2 = – x 2 x 2 + 1 x 2 1 = – 1 + x 2 1 .
همانگونه که میبینیم، فقط علامت مشتق تابع y = arctan 1 x y = \arctan {\large\frac{1}{x}\normalsize} y = arctan x 1 y = arctan x y = \arctan x y = arctan x
(ح) y = x \large y = \sqrt x y = x
حل: این تابع، معکوس تابع سهمی x = φ ( y ) = y 2 x = \varphi \left( y \right) = {y^2} x = φ ( y ) = y 2
x = f ’ ( x ) = 1 φ ’ ( y ) = 1 ( y 2 ) ′ = 1 2 y = 1 2 x ( x > 0 ) . \large {\sqrt x = f’\left( x \right) }
= {\frac{1}{{\varphi’\left( y \right)}} } \\ \large
= {\frac{1}{{{{\left( {{y^2}} \right)}^\prime }}} }
= {\frac{1}{{2y}} }
= {\frac{1}{{2\sqrt x }}\;\;\left( {x \gt 0} \right).} x = f ’ ( x ) = φ ’ ( y ) 1 = ( y 2 ) ′ 1 = 2 y 1 = 2 x 1 ( x > 0 ) .
(خ) y = 2 x + 4 \large y = 2x + 4 y = 2 x + 4
حل: ابتدا تابع معکوس x = φ ( y ) x = \varphi \left( y \right) x = φ ( y ) y = f ( x ) y = f\left( x \right) y = f ( x )
y = 2 x + 4 , ⇒ 2 x = y – 4 , ⇒ x = y 2 – 2. \large {y = 2x + 4,\;\; }\Rightarrow {2x = y – 4,\;\;}
\Rightarrow {x = \frac{y}{2} – 2.} y = 2 x + 4 , ⇒ 2 x = y –4 , ⇒ x = 2 y –2.
بنابراین، مشتق f ’ ( x ) f’\left( x \right) f ’ ( x )
( 2 x + 4 ) ′ = f ’ ( x ) = 1 φ ’ ( y ) = 1 ( y 2 – 2 ) ′ = 1 1 / 2 = 2. \large {{\left( {2x + 4} \right)^\prime } = f’\left( x \right) }
= {\frac{1}{{\varphi’\left( y \right)}} }
= {\frac{1}{{{{\left( {\frac{y}{2} – 2} \right)}^\prime }}} }
= {\frac{1}{{1/2}} = 2.} ( 2 x + 4 ) ′ = f ’ ( x ) = φ ’ ( y ) 1 = ( 2 y –2 ) ′ 1 = 1/2 1 = 2.
مثال ۲
تابع y = x 5 + 2 x 3 + 3 x y = {x^5} + 2{x^3} + 3x y = x 5 + 2 x 3 + 3 x x = 1 x=1 x = 1
حل: در این مثال، یافتن یک توصیف برای تابع معکوس و مشتق آن، بسیار دشوار است. بنابراین، مشتق تابع اصلی را محاسبه، و پس از آن، مشتق تابع معکوس را در نقطه مورد نظر بهدست میآوریم.
y ’ = f ’ ( x ) = ( x 5 + 2 x 3 + 3 x ) ′ = 5 x 4 + 6 x 2 + 3. \large {y’ = f’\left( x \right) }
= {{\left( {{x^5} + 2{x^3} + 3x} \right)^\prime } }
= {5{x^4} + 6{x^2} + 3.} y ’ = f ’ ( x ) = ( x 5 + 2 x 3 + 3 x ) ′ = 5 x 4 + 6 x 2 + 3.
مقدار مشتق f ’ ( x ) f’\left( x \right) f ’ ( x ) x = 1 x= 1 x = 1
f ’ ( x = 1 ) = 5 ⋅ 1 4 + 6 ⋅ 1 2 + 3 = 14. \large f’\left( {x = 1} \right) = 5 \cdot {1^4} + 6 \cdot {1^2} + 3 = 14. f ’ ( x = 1 ) = 5 ⋅ 1 4 + 6 ⋅ 1 2 + 3 = 14.
مقدار خود تابع در نقطه x = 1 x = 1 x = 1
y ( x = 1 ) = 1 5 + 2 ⋅ 1 3 + 3 ⋅ 1 = 6. \large y\left( {x = 1} \right) = {1^5} + 2 \cdot {1^3} + 3 \cdot 1 = 6. y ( x = 1 ) = 1 5 + 2 ⋅ 1 3 + 3 ⋅ 1 = 6.
با استفاده از قضیه تابع معکوس، داریم:
φ ’ ( y = 6 ) = 1 f ’ ( x = 1 ) = 1 14 . \large {\varphi’\left( {y = 6} \right) }
= {\frac{1}{{f’\left( {x = 1} \right)}} = \frac{1}{{14}}.} φ ’ ( y = 6 ) = f ’ ( x = 1 ) 1 = 14 1 .
مثال ۳
تابع y = x 2 – x y = {x^2} – x y = x 2 – x x = 1 x=1 x = 1
حل: مشتق تابع اصلی بهصورت زیر است:
y ’ = f ’ ( x ) = ( x 2 – x ) ′ = 2 x – 1. \large {y’ = f’\left( x \right) }
= {{\left( {{x^2} – x} \right)^\prime } }
= {2x – 1.} y ’ = f ’ ( x ) = ( x 2 – x ) ′ = 2 x –1.
توجه کنید که نقطه x = 1 2 x = {\large\frac{1}{2}\normalsize} x = 2 1 x < 1 2 x < {\large\frac{1}{2}\normalsize} x < 2 1 x > 1 2 x > {\large\frac{1}{2}\normalsize} x > 2 1 φ 1 ( y ) {\varphi _1}\left( y \right) φ 1 ( y ) φ 2 ( y ) {\varphi _2}\left( y \right) φ 2 ( y ) y = f ( x ) y = f\left( x \right) y = f ( x ) x x x
y = x 2 – x , ⇒ x 2 – x – y = 0 , ⇒ D = 1 + 4 y , ⇒ φ 1 , 2 ( y ) = 1 ± 1 + 4 y 2 . \large {y = {x^2} – x,\;\;}\Rightarrow
{{x^2} – x – y = 0,\;\;}\Rightarrow
{D = 1 + 4y,\;\;} \\ \large \Rightarrow
{{\varphi _{1,2}}\left( y \right) }
= {\frac{{1 \pm \sqrt {1 + 4y} }}{2}.} y = x 2 – x , ⇒ x 2 – x – y = 0 , ⇒ D = 1 + 4 y , ⇒ φ 1 , 2 ( y ) = 2 1 ± 1 + 4 y .
مشتق تابع معکوس با فرمول زیر تعریف میشود:
φ ’ ( y ) = 1 f ’ ( x ) = 1 2 x – 1 ( x ≠ 1 2 ) . {\varphi’\left( y \right) = \frac{1}{{f’\left( x \right)}} }
= {\frac{1}{{2x – 1}}\;\;\;}\kern-0.3pt
{\left( {x \ne \frac{1}{2}} \right).} φ ’ ( y ) = f ’ ( x ) 1 = 2 x –1 1 ( x = 2 1 ) .
با جایگذاری عبارات صریح x = φ 1 ( y ) x = {\varphi _1}\left( y \right) x = φ 1 ( y ) x = φ 2 ( y ) x = {\varphi _2}\left( y \right) x = φ 2 ( y )
φ 1 ′ ( y ) = 1 2 ( 1 + 1 + 4 y 2 ) – 1 = 1 1 + 1 + 4 y – 1 = 1 1 + 4 y , \large {{\varphi _1}^\prime \left( y \right) = \frac{1}{{2 \left( {\frac{{1 + \sqrt {1 + 4y} }}{2}} \right) – 1}} }
= {\frac{1}{{\cancel{1} + \sqrt {1 + 4y} – \cancel{1}}} }
= {\frac{1}{{\sqrt {1 + 4y} }},} φ 1 ′ ( y ) = 2 ( 2 1 + 1 + 4 y ) –1 1 = 1 + 1 + 4 y – 1 1 = 1 + 4 y 1 ,
φ 2 ′ ( y ) = 1 2 ( 1 – 1 + 4 y 2 ) – 1 = 1 1 – 1 + 4 y – 1 = − 1 1 + 4 y . \large {{\varphi _2}^\prime \left( y \right) = \frac{1}{{2 \left( {\frac{{1 – \sqrt {1 + 4y} }}{2}} \right) – 1}} }
= {\frac{1}{{\cancel{1} – \sqrt {1 + 4y} – \cancel{1}}} }
= {-\frac{1}{{\sqrt {1 + 4y} }}.} φ 2 ′ ( y ) = 2 ( 2 1– 1 + 4 y ) –1 1 = 1 – 1 + 4 y – 1 1 = − 1 + 4 y 1 .
نقطه x = 1 x = 1 x = 1 y = 1 2 – 1 = 0 y = {1^2} – 1 = 0 y = 1 2 –1 = 0 φ 1 ( y ) {\varphi _1}\left( y \right) φ 1 ( y )
φ 2 ′ ( x = 1 ) = φ 2 ′ ( y = 0 ) = – 1 1 + 4 ⋅ 0 = – 1. \large {{\varphi _2}^\prime \left( {x = 1} \right) = {\varphi _2}^\prime \left( {y = 0} \right) }
= { – \frac{1}{{\sqrt {1 + 4 \cdot 0} }} = – 1.} φ 2 ′ ( x = 1 ) = φ 2 ′ ( y = 0 ) = – 1 + 4 ⋅ 0 1 = –1.
مثال ۴
مشتق معکوس تابع y = e x + 2 x + 1 y = {e^x} + 2x + 1 y = e x + 2 x + 1 x = 0 x =0 x = 0
حل: وقتی x = 0 x = 0 x = 0
y ( x = 0 ) = e 0 + 2 ⋅ 0 + 1 = 2. \large y\left( {x = 0} \right) = {e^0} + 2 \cdot 0 + 1 = 2. y ( x = 0 ) = e 0 + 2 ⋅ 0 + 1 = 2.
مشتق تابع y = f ( x ) y = f\left( x \right) y = f ( x ) x = 0 x = 0 x = 0
y ’ = f ’ ( x ) = ( e x + 2 x + 1 ) ′ = e x + 2 , \large {y’ = f’\left( x \right) = {\left( {{e^x} + 2x + 1} \right)^\prime } }
= {{e^x} + 2,} y ’ = f ’ ( x ) = ( e x + 2 x + 1 ) ′ = e x + 2 ,
y ’ ( x = 0 ) = f ’ ( x = 0 ) = e 0 + 2 = 3. \large {y’\left( {x = 0} \right) = f’\left( {x = 0} \right) }
= {{e^0} + 2 = 3.} y ’ ( x = 0 ) = f ’ ( x = 0 ) = e 0 + 2 = 3.
با استفاده از قضیه تابع معکوس، داریم:
φ ’ ( y = 2 ) = 1 f ’ ( x = 0 ) = 1 3 . \large {\varphi’\left( {y = 2} \right) }={ \frac{1}{{f’\left( {x = 0} \right)}} = \frac{1}{3}.} φ ’ ( y = 2 ) = f ’ ( x = 0 ) 1 = 3 1 .
مثال ۵
مشتق معکوس تابع y = sin ( x – 1 ) + x 2 y = \sin \left( {x – 1} \right) + {x^2} y = sin ( x –1 ) + x 2 x = ۱ x =۱ x = ۱
حل: ابتدا مقدار تابع اصلی و مشتق آن را در نقطه x = 1 x = 1 x = 1
y ( x = 1 ) = sin 0 + 1 2 = 1 , \large y\left( {x = 1} \right) = \sin 0 + {1^2} = 1, y ( x = 1 ) = sin 0 + 1 2 = 1 ,
y ’ ( x ) = f ’ ( x ) = [ sin ( x – 1 ) + x 2 ] = cos ( x – 1 ) + 2 x , \large {y’\left( x \right) = f’\left( x \right) }
= {\left[ {\sin \left( {x – 1} \right) + {x^2}} \right] }
= {\cos \left( {x – 1} \right) + 2x,} y ’ ( x ) = f ’ ( x ) = [ sin ( x –1 ) + x 2 ] = cos ( x –1 ) + 2 x ,
y ’ ( x = 1 ) = f ’ ( x = 1 ) = cos 0 + 2 ⋅ 1 = 3. \large {y’\left( {x = 1} \right) = f’\left( {x = 1} \right) }
= {\cos 0 + 2 \cdot 1 = 3.} y ’ ( x = 1 ) = f ’ ( x = 1 ) = cos 0 + 2 ⋅ 1 = 3.
بنابراین، میتوانیم مشتق تابع معکوس را بهصورت زیر بهدست آوریم:
φ ’ ( y = 1 ) = 1 f ’ ( x = 1 ) = 1 3 . \large {\varphi’\left( {y = 1} \right) }={ \frac{1}{{f’\left( {x = 1} \right)}} }
={ \frac{1}{3}.} φ ’ ( y = 1 ) = f ’ ( x = 1 ) 1 = 3 1 .
مثال ۶
مشتق معکوس تابع y = x 2 + 2 ln x y = {x^2} + 2\ln x y = x 2 + 2 ln x x = ۱ x =۱ x = ۱
حل: تابع اصلی y = f ( x ) y = f (x) y = f ( x ) x > 0 x> 0 x > 0
y ’ = f ’ ( x ) = ( x 2 + 2 ln x ) ′ = 2 x + 2 x > 0 x > 0. \large {y’ = f’\left( x \right) = {\left( {{x^2} + 2\ln x} \right)^\prime } }
= {2x + \frac{2}{x} \gt 0\;\;}\kern-0.3pt{\;\;x \gt 0.} y ’ = f ’ ( x ) = ( x 2 + 2 ln x ) ′ = 2 x + x 2 > 0 x > 0.
بنابراین، تابع اکیداً یکنوا است و تابع معکوس دارد. با استفاده از قضیه تابع معکوس، داریم:
φ ’ ( y ) = 1 f ’ ( x ) = 1 2 x + 2 x = 1 2 x 2 + 2 x = x 2 ( x 2 + 1 ) . \large {\varphi’\left( y \right) = \frac{1}{{f’\left( x \right)}} }
= {\frac{1}{{2x + \frac{2}{x}}} }
= {\frac{1}{{\frac{{2{x^2} + 2}}{x}}} }
= {\frac{x}{{2\left( {{x^2} + 1} \right)}}.} φ ’ ( y ) = f ’ ( x ) 1 = 2 x + x 2 1 = x 2 x 2 + 2 1 = 2 ( x 2 + 1 ) x .
در این حالت، تابع x ( y ) x\left( y \right) x ( y ) x = 1 x = 1 x = 1 y y y
y ( x = 1 ) = 1 2 + 2 ln 1 = 1 + 0 = 1. \large y\left( {x = 1} \right) = {1^2} + 2\ln 1 = 1 + 0 = 1. y ( x = 1 ) = 1 2 + 2 ln 1 = 1 + 0 = 1.
بنابراین، داریم:
φ ’ ( y = 1 ) = 1 f ’ ( x = 1 ) = 1 2 ( 1 2 + 1 ) = 1 4 . \large {\varphi’\left( {y = 1} \right) = \frac{1}{{f’\left( {x = 1} \right)}} }
= {\frac{1}{{2\left( {{1^2} + 1} \right)}} = \frac{1}{4}.} φ ’ ( y = 1 ) = f ’ ( x = 1 ) 1 = 2 ( 1 2 + 1 ) 1 = 4 1 .
مثال ۷
مشتق معکوس تابع y = x 3 – 3 x y = {x^3} – 3x y = x 3 –3 x x = − 2 x = -2 x = − 2
حل: مشتق این تابع بهصورت زیر است:
y ’ = f ’ ( x ) = ( x 3 – 3 x ) ′ = 3 x 2 – 3 = 3 ( x 2 – 1 ) , \large {y’ = f’\left( x \right) = {\left( {{x^3} – 3x} \right)^\prime } }
= {3{x^2} – 3 = 3\left( {{x^2} – 1} \right),} y ’ = f ’ ( x ) = ( x 3 –3 x ) ′ = 3 x 2 –3 = 3 ( x 2 –1 ) ,
با توجه به مشتق بالا میتوان گفت که تابع، سه بازه یکنوایی دارد:
تابع در بازه x ∈ ( – ∞ , – 1 ) x \in \left( { – \infty , – 1} \right) x ∈ ( –∞ , –1 )
تابع در بازه x ∈ ( – 1 , 1 ) x \in \left( { – 1, 1} \right) x ∈ ( –1 , 1 )
تابع در بازه x ∈ ( 1 , ∞ ) x \in \left( {1, \infty} \right) x ∈ ( 1 , ∞ )
میتوان تابع معکوس را در هر بازه بهدست آورد. همچنین، فرض میکنیم تابع معکوس متناظر با بازه اول، شامل نقطه x = − 2 x = - 2 x = − 2
مشتق تابع معکوس بهصورت زیر است:
φ ’ ( y ) = 1 f ’ ( x ) = 1 3 ( x 2 – 1 ) . \large {\varphi’\left( y \right) = \frac{1}{{f’\left( x \right)}} }
= {\frac{1}{{3\left( {{x^2} – 1} \right)}}.} φ ’ ( y ) = f ’ ( x ) 1 = 3 ( x 2 –1 ) 1 .
مقدار خود تابع، در نقطه x = − 2 x = -2 x = − 2
y ( x = – 2 ) = ( – 2 ) 3 – 3 ⋅ ( – 2 ) = – 8 + 6 = – 2. \large {y\left( {x = – 2} \right) }={ {\left( { – 2} \right)^3} – 3 \cdot \left( { – 2} \right) }
= { – 8 + 6 = – 2.} y ( x = –2 ) = ( –2 ) 3 –3 ⋅ ( –2 ) = –8 + 6 = –2.
بنابراین، مشتق تابع معکوس در نقطه مورد نظر بهصورت زیر خواهد بود:
φ ’ ( y = – 2 ) = 1 f ’ ( x = – 2 ) = 1 3 ⋅ ( ( – 2 ) 2 – 1 ) = 1 9 . \large {\varphi’\left( {y = – 2} \right) }={ \frac{1}{{f’\left( {x = – 2} \right)}} }
= {\frac{1}{{3 \cdot \left( {{{\left( { – 2} \right)}^2} – 1} \right)}} }
= {\frac{1}{9}.} φ ’ ( y = –2 ) = f ’ ( x = –2 ) 1 = 3 ⋅ ( ( –2 ) 2 –1 ) 1 = 9 1 .
مثال ۸
مشتق تابع معکوس y = 2 x 3 – 1 y = 2{x^3} – 1 y = 2 x 3 –1 x = 2 x=2 x = 2
حل: ابتدا مشتق تابع را محاسبه میکنیم:
y ’ = f ’ ( x ) = ( 2 x 3 – 1 ) ′ = 6 x . \large {y’ = f’\left( x \right) }
= {{\left( {2{x^3} – 1} \right)^\prime } = 6x.} y ’ = f ’ ( x ) = ( 2 x 3 –1 ) ′ = 6 x .
همانطور که میبینیم، علامت مشتق در نقطه x = 0 x = 0 x = 0 x < 0 x \lt 0 x < 0 x > 0 x \gt 0 x > 0 x = 2 x = 2 x = 2
φ ’ ( y ) = 1 f ’ ( x ) . \large \varphi’\left( y \right) = \frac{1}{{f’\left( x \right)}}. φ ’ ( y ) = f ’ ( x ) 1 .
با محاسبه y ( x = 2 ) = 2 ⋅ 2 3 – 1 = 15 y\left( {x = 2} \right) = 2 \cdot {2^3} – 1 = 15 y ( x = 2 ) = 2 ⋅ 2 3 –1 = 15
φ ’ ( y = 15 ) = 1 f ’ ( x = 2 ) = 1 6 ⋅ 2 = 1 12 . \large {\varphi’\left( {y = 15} \right) = \frac{1}{{f’\left( {x = 2} \right)}} }
= {\frac{1}{{6 \cdot 2}} = \frac{1}{{12}}.} φ ’ ( y = 15 ) = f ’ ( x = 2 ) 1 = 6 ⋅ 2 1 = 12 1 .
مثال ۹
مشتق تابع y = log 2 ( x 3 ) y = {\log _2}\left( {\frac{x}{3}} \right) y = log 2 ( 3 x )
حل: تابع y = f ( x ) = log 2 ( x 3 ) y = f\left( x \right) = {\log _2}\left( {\frac{x}{3}} \right) y = f ( x ) = log 2 ( 3 x ) x > 0 x \gt 0 x > 0 x = φ ( y ) x = \varphi \left( y \right) x = φ ( y )
y = log 2 ( x 3 ) , ⇒ x 3 = 2 y , ⇒ x = 3 ⋅ 2 y . \large {y = {\log _2}\left( {\frac{x}{3}} \right),\;\;}\Rightarrow
{\frac{x}{3} = {2^y},\;\;}\Rightarrow
{x = 3 \cdot {2^y}.} y = log 2 ( 3 x ) , ⇒ 3 x = 2 y , ⇒ x = 3 ⋅ 2 y .
با استفاده از قضیه تابع معکوس، داریم:
[ log 2 ( x 3 ) ] ′ = f ’ ( x ) = 1 φ ’ ( y ) = 1 ( 3 ⋅ 2 y ) ′ = 1 3 ⋅ 2 y ⋅ ln 2 = 1 3 ln 2 ⋅ 2 log 2 ( x 3 ) = 1 3 ln 2 ⋅ x 3 = 1 x ln 2 . \large {{\left[ {{{\log }_2}\left( {\frac{x}{3}} \right)} \right]^\prime } }={ f’\left( x \right) }
= {\frac{1}{{\varphi’\left( y \right)}} }
= {\frac{1}{{{{\left( {3 \cdot {2^y}} \right)}^\prime }}} } \\ \large
= {\frac{1}{{3 \cdot {2^y} \cdot \ln 2}} }
= {\frac{1}{{3\ln 2 \cdot {2^{{{\log }_2}\left( {\large\frac{x}{3}\normalsize} \right)}}}} }
= {\frac{1}{{3\ln 2 \cdot \frac{x}{3}}} = \frac{1}{{x\ln 2}}.} [ log 2 ( 3 x ) ] ′ = f ’ ( x ) = φ ’ ( y ) 1 = ( 3 ⋅ 2 y ) ′ 1 = 3 ⋅ 2 y ⋅ ln 2 1 = 3 ln 2 ⋅ 2 l o g 2 ( 3 x ) 1 = 3 ln 2 ⋅ 3 x 1 = x ln 2 1 .
که در آن، از اتحاد لگاریتمی زیر استفاده شده است:
a log a x = x \large {a^{{{\log }_a}x}} = x a l o g a x = x
مثال ۱۰
مشتق تابع y = arcsec x y = \text{arcsec }x y = arcsec x x = 2 x = \sqrt 2 x = 2
حل: از این حقیقت استفاده میکنیم که تابع آرکسکانت، معکوس تابع سکانت است. مشتق سکانت بهصورت زیر است:
( sec y ) ′ = tan y sec y = sin y cos 2 y . \large {{\left( {\sec y} \right)^\prime } = \tan y\sec y }
= {\frac{{\sin y}}{{{{\cos }^2}y}}.} ( sec y ) ′ = tan y sec y = cos 2 y sin y .
مقدار سکانت در نقطه y = π 4 y = {\large\frac{\pi }{4}\normalsize} y = 4 π
sec ( y = π 4 ) = 1 cos π 4 = 1 2 2 = 2 . \large {\sec \left( {y = \frac{\pi }{4}} \right) }
= {\frac{1}{{\cos \frac{\pi }{4}}} }
= {\frac{1}{{\frac{{\sqrt 2 }}{2}}} = \sqrt 2.} sec ( y = 4 π ) = cos 4 π 1 = 2 2 1 = 2 .
با استفاده از قضیه تابع معکوس، داریم:
( arcsec x ) ′ = f ’ ( x ) = 1 φ ’ ( y ) = 1 ( sec y ) ′ = 1 tan y sec y = cos 2 y sin y . \large {{\left( {\text{arcsec }x} \right)^\prime } = f’\left( x \right) }
= {\frac{1}{{\varphi’\left( y \right)}} }
= {\frac{1}{{{{\left( {\sec y} \right)}^\prime }}} }
= {\frac{1}{{\tan y\sec y}} }
= {\frac{{{{\cos }^2}y}}{{\sin y}}.} ( arcsec x ) ′ = f ’ ( x ) = φ ’ ( y ) 1 = ( sec y ) ′ 1 = tan y sec y 1 = sin y cos 2 y .
بنابراین، مشتق تابع arcsec x \text{arcsec }x arcsec x x = 2 x = \sqrt 2 x = 2
f ’ ( x = 2 ) = 1 φ ’ ( y = π 4 ) = cos 2 π 4 sin π 4 = ( 2 2 ) 2 ( 2 2 ) = 2 2 . \large {f’\left( {x = \sqrt 2 } \right) }
= {\frac{1}{{\varphi’\left( {y = \frac{\pi }{4}} \right)}} }
= {\frac{{{{\cos }^2}\frac{\pi }{4}}}{{\sin \frac{\pi }{4}}} }
= {\frac{{{{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2}}}{{\left( {\frac{{\sqrt 2 }}{2}} \right)}} }
= {\frac{{\sqrt 2 }}{2}.} f ’ ( x = 2 ) = φ ’ ( y = 4 π ) 1 = sin 4 π cos 2 4 π = ( 2 2 ) ( 2 2 ) 2 = 2 2 .
مثال ۱۱
مشتق تابع معکوس y = x ⋅ 3 x y = x \cdot {3^x} y = x ⋅ 3 x x > 0 x \gt 0 x > 0
حل: مشتق تابع دادهشده بهصورت زیر محاسبه میشود:
y ’ = f ’ ( x ) = ( x ⋅ 3 x ) ′ = x ’ ⋅ 3 x + x ⋅ ( 3 x ) ′ = 1 ⋅ 3 x + x ⋅ 3 x ln 3 = 3 x ( 1 + x ln 3 ) . \large {y’ = f’\left( x \right) = {\left( {x \cdot {3^x}} \right)^\prime } }
= {x’ \cdot {3^x} + x \cdot {\left( {{3^x}} \right)^\prime } } \\ \large
= {1 \cdot {3^x} + x \cdot {3^x}\ln 3 }
= {{3^x}\left( {1 + x\ln 3} \right).} y ’ = f ’ ( x ) = ( x ⋅ 3 x ) ′ = x ’ ⋅ 3 x + x ⋅ ( 3 x ) ′ = 1 ⋅ 3 x + x ⋅ 3 x ln 3 = 3 x ( 1 + x ln 3 ) .
مشتق فوق، برای x > 0 x \gt 0 x > 0 x = φ ( y ) v x = \varphi \left( y \right) v x = φ ( y ) v
φ ’ ( y ) = 1 f ’ ( x ) = 1 3 x ( 1 + x ln 3 ) . \large {\varphi’\left( y \right) = \frac{1}{{f’\left( x \right)}} }
= {\frac{1}{{{3^x}\left( {1 + x\ln 3} \right)}}.} φ ’ ( y ) = f ’ ( x ) 1 = 3 x ( 1 + x ln 3 ) 1 .
مثال ۱۲
مشتق تابع معکوس سینوس هیپربولیک y = arcsinh x y = \text{arcsinh } x y = arcsinh x
حل: توابع y = arcsinh x y = \text{arcsinh } x y = arcsinh x x = sinh y x = \sinh y x = sinh y
( arcsinh x ) ′ = f ’ ( x ) = 1 φ ’ ( y ) = 1 ( sinh y ) ′ = 1 cosh y . \large {{\left( {\text{arcsinh }x} \right)^\prime } = f’\left( x \right) }
= {\frac{1}{{\varphi’\left( y \right)}} }
= {\frac{1}{{{{\left( {\sinh y} \right)}^\prime }}} }
= {\frac{1}{{\cosh y}}.} ( arcsinh x ) ′ = f ’ ( x ) = φ ’ ( y ) 1 = ( sinh y ) ′ 1 = cosh y 1 .
اکنون از اتحاد زیر کمک میگیریم:
cosh 2 y – sinh 2 y = 1 \large {\cosh ^2}y – {\sinh ^2}y = 1 cosh 2 y – sinh 2 y = 1
با استفاده از این اتحاد، میتوانیم کسینوس هیپربولیک را برحسب سینوس هیپربولیک بنویسیم:
cosh 2 y – sinh 2 y = 1 \large {\cosh ^2}y – {\sinh ^2}y = 1 cosh 2 y – sinh 2 y = 1
cosh 2 y = 1 + sinh 2 y , ⇒ cosh y = 1 + sinh 2 y \large {{\cosh ^2}y = 1 + {\sinh ^2}y,\;\;}\Rightarrow
{\cosh y }
= {\sqrt {1 + {{\sinh }^2}y} } cosh 2 y = 1 + sinh 2 y , ⇒ cosh y = 1 + sinh 2 y
با توجه به اینکه sinh ( arcsinh x ) = x \sinh \left( {\text{arcsinh }x} \right) = x sinh ( arcsinh x ) = x
( arcsinh x ) ′ = 1 cosh y = 1 1 + sinh 2 y = 1 1 + sinh 2 ( arcsinh x ) = 1 1 + x 2 . \large {{\left( {\text{arcsinh }x} \right)^\prime } = \frac{1}{{\cosh y}} }
= {\frac{1}{{\sqrt {1 + {{\sinh }^2}y} }} } \\ \large
= {\frac{1}{{\sqrt {1 + {{\sinh }^2}\left( {\text{arcsinh }x} \right)} }} }
= {\frac{1}{{\sqrt {1 + {x^2}} }}.} ( arcsinh x ) ′ = cosh y 1 = 1 + sinh 2 y 1 = 1 + sinh 2 ( arcsinh x ) 1 = 1 + x 2 1 .
اگر این مطلب برای شما مفید بوده است و علاقهمند به یادگیری مباحث مشابه هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^
فیلم های آموزش مشتق توابع معکوس — از صفر تا صد (+ دانلود فیلم آموزش گام به گام) فیلم آموزشی مشتق توابع معکوس فیلم آموزشی حل چند مثال از مشتق توابع معکوس 
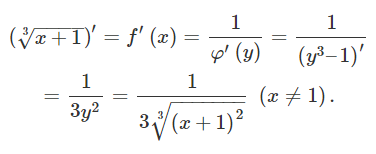













نظیر این قانون در انتگرال وجود داره؟
واقعا از سایت خوبتون تشکر می کنم خیلی مفید بود