دینامیک سازه چیست؟ — آشنایی با مبانی و مفاهیم | به زبان ساده

دینامیک سازه حوزه‌ای است که به مطالعه رفتار سازه‌های مهندسی در برابر بارهای دینامیکی می‌پردازد. این حوزه از مباحث مهم در مهندسی عمران، دریا و هوافضا محسوب می‌شود. در این مقاله، قصد داریم مبانی و مفاهیم اصلی دینامیک سازه را معرفی کنیم.

تئوری دینامیک سازه به چه زمانی باز می گردد؟

شروع مطالعه تئوری علم دینامیک، به قرن 17 میلادی (حدود قرن 11 شمسی) بازمی‌گردد. در این دوران، «ژوزف لوئی لاگرانژ» (Joseph-Louis Lagrange) با انتشار کتاب «مکانیک تحلیل» (Analytical Mechanics)، اصول تحلیل دینامیک در سیستم‌های خطی را پایه‌ریزی کرد. با پیشرفت علم و تکنولوژی، اصول تحلیل دینامیک به طور گسترده در ساخت سازه‌های مهندسی مختلف مورد استفاده قرار گرفت. این موضوع باعث توسعه و پیشرفت مداوم حوزه دینامیک سازه شد. امروزه، مهندسان با استفاده از تحلیل‌های دینامیکی می‌توانند سازه‌های پیچیده و بزرگ با هزاران درجه آزادی را طراحی کنند.

دینامیک سازه چیست و چه اهمیتی دارد؟

دینامیک سازه، حوزه‌ای تئوری و فنی است که به مطالعه خواص دینامیکی سیستم‌های سازه‌ای (دوره تناوب، فرکانس، حالت و میرایی) و تعیین عکس‌العمل سازه تحت بارگذاری دینامیک (نیروی داخلی، کرنش، جابجایی، سرعت، شتاب و غیره) می‌پردازد.

استاتیک نیز حوزه بسیار گسترده‌ای است که همیشه به عنوان اولین مسئله در طراحی یا تحلیل سازه مورد بحث قرار می‌گیرد. با این وجود، شکست سازه در اکثر مواقع به دلیل اعمال بیش از حد بارهای دینامیک رخ می‌دهد. به همین دلیل، تحلیل دینامیک سازه معمولا به عنوان معیار اصلی کنترل شرایط پایداری در طراحی سازه در نظر گرفته می‌شود؛ چراکه بارگذاری دینامیک نقش بسیار بیشتری در تخریب یا آسیب سازه دارد.

تخریب پل‌ها بر اثر وزش بادهای شدید یا تغییر شکل پایه‌ها و فونداسیون سازه بر اثر بارهای ضربه‌ای، نمونه‌هایی از تاثیر بارهای دینامیکی بر تخریب سازه‌های مهندسی هستند. در اغلب موارد، اجرای تحلیل‌های دینامیک برای مطالعه، طراحی و ارزیابی ایمنی سازه غیر قابل اجتناب است. دینامیک سازه، یکی از دروس تخصصی و از عنوان‌های مهم در کتاب های مهندسی عمران به شمار می‌رود.

بار دینامیک چیست و انواع آن کدام هستند؟

بارهای مختلف بر اساس تغییرشان نسبت به زمان، به دو نوع اصلی دینامیک و استاتیک تقسیم می‌شوند. بارهای دینامیک، بارهایی هستند که با گذشت زمان تغییر می‌کنند. به علاوه، این بارها باعث ایجاد نیروی اینرسی غیر قابل اجتناب در سازه می‌شوند.

از بارهای دینامیکی می‌توان به بار نوسانگر هارمونیک یا هماهنگ ساده، بارهای متناوب غیر هماهنگ، بار ضربه‌ای و بار نامنظم اشاره کرد. جدول زیر، تقسیم‌بندی کلی انواع بارهای دینامیک را نمایش می‌دهد. در ادامه، به معرفی این موارد می‌پردازیم.

بارهای دینامیک	بارهایی با مقدار مشخص	بارهای متناوب (هماهنگ ساده و ناهماهنگ)
		بارهای نامتناوب (ضربه‌ای و غیره)
	بارهایی با مقدار نامشخص (تصادفی)	بار ناشی از وزش باد
		بارهای لرزه‌ای
		بارهای نامشخص دیگر

بار متناوب چیست و چه انواعی دارد؟

در بارگذاری متناوب، اعمال بار برای دوره‌های طولانی‌مدت صورت می‌گیرد و شدت آن به طور پیوسته تغییر می‌کند. بارهای متناوب توسط ماشین‌آلات چرخشی، ترافیک، تندباد، امواج آب و ماشین‌آلات صنعتی به وجود می‌آیند. این بارها با عنوان دیگری مانند بارهای تکراری، چرخه‌ای و خستگی نیز شناخته می‌شوند.

بار هماهنگ ساده چیست و چه اهمیتی در دینامیک سازه دارد؟

بارهای هماهنگ ساده، بارهایی هستند که مقدار آن‌ها به صورت هارمونیک و متناوب تغییر می‌کند. نحوه تغییر این بارها را می‌توان با توابع هارمونیکی نظیر P(t)=P_Osinθt و P(t)=P_Ocosθt نمایش داد. تحلیل عکس‌العمل سازه در شرایط بارگذاری هماهنگ ساده از اهمیت بالایی برخوردار است.

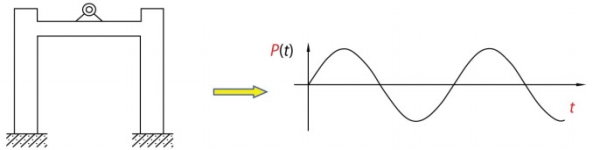
وجود این نوع بار در سازه‌های مهندسی، در کنار امکان نمایش بارهای متناوب غیر هماهنگ به صورت مجموعه‌ای از مولفه‌های هماهنگ ساده، اهمیت این بارهای دینامیکی را بیشتر می‌کند. در واقع، هر نوع بارگذاری متناوب را می‌توان به برهم‌نهی عکس‌العمل‌های ناشی از مولفه‌های هماهنگ ساده تبدیل کرد. علاوه بر این، عکس‌العمل‌های سازه در برابر بارهای هماهنگ ساده، بیانگر ویژگی‌های دینامیکی آن است. به همین دلیل، این نوع بار اهمیت بسیار زیادی در تحلیل دینامیک سازه دارد.

بار متناوب ناهماهنگ چیست؟

رفتار بارهای متناوب ناهماهنگ از توابع متناوب زمانی پیروی می‌کند. رفتار این بارها با توابع هماهنگ ساده متفاوت است. فشار هیدرودینامیک موج‌های آرام در پشت سد و نیروی پیشرانه ایجاد شده توسط پره‌های یک کشتی، به عنوان بارهای متناوب ناهماهنگ در نظر گرفته می‌شوند.

بار ضربه ای چیست؟

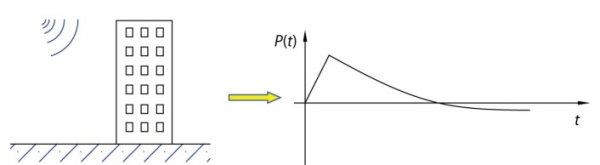
بارهای ضربه‌ای در هنگام برخورد دو شی به یکدیگر یا اصابت یک شی در حال سقوط به یک سازه ایجاد می‌شوند. مقدار این بارها در بازه‌های زمانی کوتاه به سرعت کاهش یا افزایش می‌یابد. بار ناشی از انفجار، سقوط و ترافیک سنگین وسایل نقلیه، مثال‌های خوبی از بارهای ضربه‌ای هستند.

بار دینامیکی نامنظم چیست؟

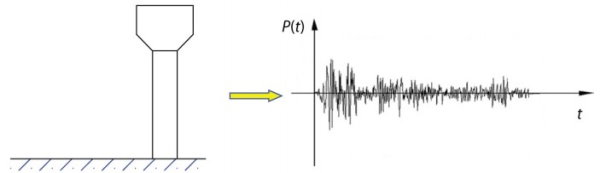
تعریف بارهای دینامیکی نامنظم با استفاده از روابط تحلیلی دشوار است. این بارها ماهیت پیچیده و مقدار، جهت‌گیری و محل قرارگیری نامشخصی دارند. از بارهای دینامیکی نامنظم شناخته‌شده می‌توان به بارهای ناشی از زلزله یا وزش باد اشاره کرد.

مفاهیم مور نیاز برای یادگیری دینامیک سازه چه هستند؟

به منظور آشنایی و درک بهتر دینامیک سازه، باید با مفاهیم و اصطلاحات رایج در این حوزه آشنا شد. در ادامه، به معرفی برخی از مهمترین مفاهیم دینامیک سازه می‌پردازیم.

جرم نقطه ای چیست و چه کاربردی در دینامیک سازه دارد؟

«جرم نقطه ای» (Mass Point)، یک موقعیت فرضی است که به منظور ساده‌سازی هندسه سازه و نمایش جرم آن توسط نقطه مورد استفاده قرار می‌گیرد. برای تعیین این پارامتر، اصول محاسبه مرکز جرم به کار برده می‌شود. جرم نقطه‌ای، کاربرد گسترده‌ای در ساده‌سازی حل مسائل دینامیک سازه و نمایش درجه آزادی دارد. اصلی‌ترین کاربرد این مفهوم در گسسته‌سازی هندسه سازه است.

درجه آزادی چیست و چه کاربردی در دینامیک سازه دارد؟

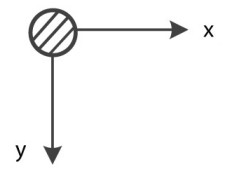
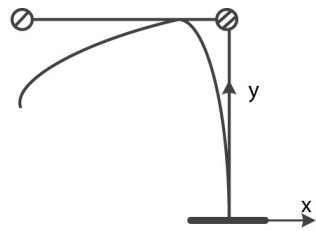
به تعداد پارامترهای هندسی مستقل مورد نیاز برای تعریف محل قرارگیری سازه متحرک (در حال ارتعاش)، درجه آزادی دینامیکی سازه گفته می‌شود. مفهوم درجه آزادی برای نوشتن معادلات حرکت مسائل دینامیک سازه مورد استفاده قرار می‌گیرد. تعداد درجات آزادی سازه ثابت نیست و با تغییر فرضیات محاسبات تغییر می‌کند. تصویر زیر، جرم منفردی را نمایش می‌دهد که دارای دو درجه آزادی بوده و می‌تواند در راستای محورهای X و Y حرکت کند.

تصویر زیر، یک تیر یکسرگیردار را نمایش می‌دهد. با صرفنظر کردن از اثر محوری، جرم سمت راست در این تیر قادر به حرکت در هر دو جهت و جرم سمت چپ فقط قادر به حرکت در جهت X است.

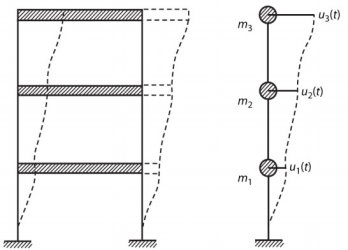
در تصویر زیر، یک تیر صلب نمایش داده شده است. در صورتی که مقدار صلبیت تیر را بی‌نهایت در نظر بگیریم، هر سه جرم معرف تیر دارای یک درجه آزادی با زاویه دوران θ خواهند بود.

تصویر زیر، یک قاب چهار لایه را نمایش می‌دهد. هر یک از جرم‌های معرف در این قاب می‌توانند در جهت افقی حرکت کنند. به این ترتیب، سازه دارای چهار درجه آزادی خواهد بود.

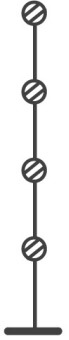
تعیین درجه آزادی و معادله حرکت (دیفرانسیل)، اولین مرحله در تحلیل دینامیک سازه است.

سیستم یک درجه آزادی چیست؟

سیستم‌های دارای یک درجه آزادی، ساده‌ترین سیستم‌های دینامیکی هستند. رفتار این سیستم‌ها از یک معادله دیفرانسیل درجه دو تبعیت می‌کند. در سیستم یک درجه آزادی می‌توان مسیر حرکت جسم را فقط با دو متغیر مکان و سرعت تعریف کرد.

آشنایی با ویژگی‌های دینامیکی و مسائل ارتعاشی در سیستم‌های یک درجه آزادی اهمیت بالایی دارد. از مهم‌ترین جنبه‌های مطالعاتی این سیستم‌ها می‌توان به دو مورد زیر اشاره کرد:

• سیستم‌های یک درجه آزادی بیانگر خصوصیات کلی یک سیستم دینامیک (کمیت‌های فیزیکی و مفاهیم اصلی تحلیل دینامیک سازه) هستند. این ویژگی، به یادگیری اصول دینامیک سازه کمک می‌کند.
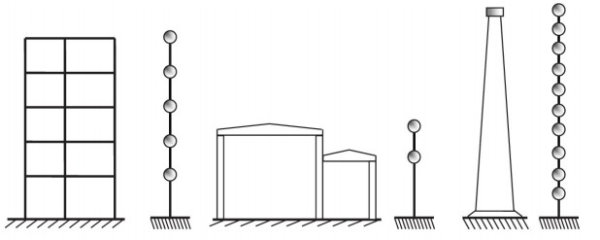
• بسیاری از مسائل دینامیکی واقعی (کارخانه یک طبقه و برج آب)، با استفاده از سیستم‌های یک درجه آزادی قابل تحلیل هستند.

تصویر زیر، دو مثال مکانیکی رایج در تحلیل دینامیک سازه با استفاده از سیستم یک درجه آزادی را نمایش می‌دهد.

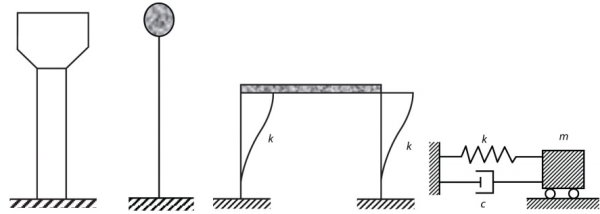
سیستم چند درجه آزادی چیست؟

امکان تبدیل اکثر سازه‌های مهندسی به سیستمی با یک درجه آزادی وجود ندارد. در این موارد، ساده‌سازی سازه به سیستمی با یک درجه آزادی باعث ایجاد خطای بزرگ در محاسبات می‌شود. توجه داشته باشید که مفهوم سیستم یک درجه آزادی با سیستم یک جرم نقطه‌ای متفاوت است. در تصویر زیر، جرم نقطه‌ای m می‌تواند در جهت‌های افقی و عمودی حرکت کند. به همین دلیل، این سیستم دارای چند درجه آزادی است.

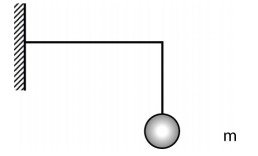
برای سیستم‌هایی با جرم غیرمتمرکز، به منظور نمایش دقیق‌تر عملکرد دینامیک سازه می‌توان سیستم را به چندین جرم نقطه‌ای ساده کرد. به عنوان مثال، برای کارخانه‌های یک طبقه با دو دهانه به ارتفاع‌های متفاوت (مثال دوم در تصویر زیر)، در نظر گرفتن دو جرم نقطه‌ای در سقف، روش مناسبی به منظور نمایش ساده‌تر سیستم است. در تصویر زیر، سه مثال از سیستم‌های چند درجه آزادی نمایش داده شده است.

نیروهای موجود در یک سیستم دینامیکی کدام هستند؟

یک سیستم دینامیکی، نمایش ساده‌ای از چندین سیستم فیزیکی است که توسط ویژگی‌هایی نظیر جرم، میرایی و صلبیت تعریف می‌شود. برای تمام سیستم‌های تحت بارگذاری دینامیک، جرم، الاستیسیته، هدررفت انرژی یا میرایی و بارهای خارجی، اصلی‌ترین مشخصات فیزیکی هستند. در ادامه، به معرفی این مهم‌ترین ویژگی‌های سیستم‌های دینامیک می‌پردازیم.

نیروی اینرسی یا لختی چیست؟

نیروی اینرسی، مقاومت سیستم در برابر تغییر سرعت است. جرم، یکی از ویژگی‌های بنیادی ماده است که در تمام سیستم‌های فیزیکی ظاهر می‌شود. مقدار این کمیت، از تقسیم وزن سازه بر شتاب گراش زمین به دست می‌آید. نیروی اینرسی در معادله دینامیکی حرکت، حاصل‌ضرب جرم در شتاب سیستم است:

$$F_{I}(t)=-mu^{''}(t)$$

• F_I(t)‎: نیروی اینرسی
• m: جرم
• ″u: شتاب

نیروی الاستیک چیست؟

نیروی الاستیک یا نیروی بازگرداننده، نیرویی است که باعث برگشت یک جسم تغییر یافته (شکل و اندازه) به حالت اولیه خود می‌شود. بهترین مثال برای درک نیروی الاستیک، فنر است. با فشردن فنر و رها کردن آن،‌ ابعاد فنر پس از مدتی به حالت اولیه خود بازمی‌گردد. نیروی مورد نیاز برای بازگشت فنر فشرده شده به حالت اول، به سختی و میزان جابجایی آن بستگی دارد.

سختی چیست؟

سختی، معیاری برای تعیین صلبیت (مقاومت در برابر تغییر شکل) است. این کمیت باعث افزایش صلبیت و کاهش اثرات دینامیکی می‌شود. معمولا، افزایش سختی سازه با افزایش ابعاد سطح مقطع،‌ کاهش ارتفاع یا استفاده از مواد سخت صورت می‌گیرد. با فرض خطی بودن رابطه بین نیرو و جابجایی، نیروی بازگرداننده فنر با عنوان نیروی بازگرداننده الاستیک شناخته می‌شود. این نیرو، از ضرب سختی فنر در جابجایی به دست می‌آید.

$$F_{S}(t)=-ku(t)$$

• F_S(t)‎: نیروی بازگرداننده
• k: سختی فنر
• (u(t‏‎‎‎‎: جابجایی

نیروی میرایی چیست؟

در فیزیک، کاهش و محدود کردن حرکت ارتعاشی (نوسان مکانیکی، امواج صوت و جریان الکتریکی) از طریق هدررفت انرژی، با عنوان «میرایی» (Damping) شناخته می‌شود. به عنوان مثال، کودکی که بر روی تاب مشغول بازی است را در نظر بگیرید. تا زمانی که به تاب فشار وارد شود، حرکت آن ادامه خواهد داشت. در طرف مقابل، اگر دیگر به تاب فشاری وارد نشود، تاب پس از چند حرکت نوسانی خواهد ایستاد. جرم و سختی از خصوصیات شناخته‌شده ماده و به سادگی قابل محاسبه هستند. با این وجود، میرایی با استفاده از روش‌های آزمایشگاهی و یا مقادیر تجربی به دست می‌آید.

در یک سیستم دینامیک، چندین نوع میرایی وجود دارد. میرایی ویسکوز یا میرایی ویسکوز خطی، رایج‌ترین سیستم مورد استفاده برای تحلیل دینامیک سازه است. در این سیستم، نیرو با سرعت سازه رابطه مستقیم دارد. این نوع میرایی، معرف خوبی برای نمایش میرایی در تحلیل اکثر سازه‌ها است. علاوه بر این، استفاده از میرایی ویسکوز باعث ساده‌سازی و تحلیل راحت‌تر مسئله با تقریب مناسب می‌شود. برای سیستمی با یک درجه آزادی، رابطه میرایی ویسکوز به صورت زیر خواهد بود:

$$
F_{D}(t)=-c \dot{u}
$$

• F_D(t)‎: نیروی میرایی
• c: ضریب میرایی
• $$\dot{u}(t)$$: سرعت جرم

منشا میرایی ویسکوز، هدررفت انرژی‌هایی مانند روغن‌کاری بین قطعات متحرک یک خودرو یا عبور سیال از یک حفره کوچک توسط پیستون در کمک فنرهای خودرو است. نیروی میرایی ویسکوز به طور مستقیم با نیروی بین دو انتهای وسیله میراگر ارتباط دارد. میرایی ویسکوز یکی از خواص ذاتی ماده است. این ویژگی، از مقاومت داخلی ذرات ماده در برابر حرکت بین لایه‌های مختلف به وجود می‌آید. انواع دیگر میرایی عبارت هستند از:

• «میرایی مجذور سرعت» (Velocity Squered Damping)
• «میرایی هیسترزیس» (Hysteresis Damping) یا «میرایی سازه‌ای» (Structural Damping)
• «میرایی مغناطیسی» (Magnetic Damping)

میرایی، هدررفت رفتن انرژی یک سازه در حال لرزش است. واژه هدررفت در دینامیک سازه، به معنی تبدیل انرژی از یک شکل به شکل دیگر و خارج کردن انرژی از سیستم در حال لرزش است. نوع تبدیل انرژی، به سیستم و مکانیزم فیزیکی مورد استفاده برای هدر رفت بستگی دارد. در اکثر سیستم‌های در حال لرزش، بخش قابل‌توجهی از انرژی به گرما تبدیل می‌شود.

در مجموع، جرم، معرف ماده سازنده سازه، نیروی اینرسی، مقاومت سازه در برابر تغییر سرعت، نیروی الاستیک، توانایی سازه در برگشتن به حالت اولیه، سختی، مقاومت سازه در برابر تغییر شکل، و میرایی، توانایی سازه در کاهش حرکت خود با گذشت زمان است.

دینامیک سازه در چه حوزه هایی کاربرد دارد؟

دینامیک سازه در حوزه‌های مختلفی مانند عمران، دریا، هوافضا و دیگر حوزه‌های مرتبط با سازه‌های مهندسی کاربرد دارد. در ادامه به معرفی برخی از این کاربردها می‌پردازیم.

کاربرد دینامیک سازه در مهندسی عمران چیست؟

هنگامی که یک ساختمان در معرض زلزله، باد، لرزش و دیگر بارهای دینامیک قرار می‌گیرد، مقدار، جهت‌گیری و محل اعمال بارها در مدت بارگذاری به میزان زیادی تغییر می‌کند. عکس‌العمل ساختمان در این شرایط با شرایط بارگذاری استاتیک متفاوت است.

تاثیر اعمال بارهای استاتیک بر روی یک ساختمان، عمدتا به صورت ایجاد نیروهای داخلی و تغییر شکل آن است. در صورتی که تاثیر بارهای دینامیک، حرکت شتاب‌دار ناشی از لرزش و کاهش حرکت به دلیل اثر میرایی است. بارهای دینامیکی علاوه بر تغییر شکل ساختمان، با ایجاد نیروی اینرسی ناشی از حرکت شتاب‌دار، ساختمان را وادار به نشان دادن عکس‌العمل در برابر نیروی داخلی، تغییر شکل، حرکت، جابجایی، شتاب و غیره می‌کنند.

ساختمان، یک سازه مهندسی است که از اتصال چندین عضو به یکدیگر تشکیل می‌شود. با توجه به مصالح مورد استفاده، این سازه به انواع بتنی، فولادی، چوبی و کامپوزیتی تقسیم می‌شود. کاربری، ظاهر، طراحی، الزامات اجرایی، مصالح و سطح مقطع سازه‌های ساختمانی بسیار متنوع است. هنگامی که یک ساختمان نامنظم در معرض تنش قرار می‌گیرد، فعل و انفعالاتی بین برخی از عضوهای نامنظم آن به وجود می‌آید. این فعل و انفعالات باعث پیچش سازه می‌شوند. در محل اتصال عضوهای نامنظم، تمرکز تنش و تغییرشکل رخ می‌دهد.

تمرکز تنش می‌تواند شکست سازه را در پی داشته باشد. به طور کلی، تحلیل یکنواخت بودن مقاومت جانبی ساختمان (عدم وجود نواحی تمرکز تنش) در شرایط بارگذاری زلزله، بارگذاری زلزله به همراه بارگذاری باد، بارگذاری مرده به همراه بارگذاری زنده و بارگذاری تصادفی ضروری است. علاوه بر این، انجام آزمایش‌های برجا نیز به درک بهتر ظرفیت باربری ساختمان کمک می‌کنند.

کاربرد دینامیک سازه در مهندسی دریا چیست؟

افزایش تقاضا برای استخراج نفت، گاز و مواد معدنی در سال‌‌های اخیر باعث رشد سریع حوزه مهندسی دریا شده است. مباحث مختلف زیادی در زمینه رابطه بین مهندسی دریا و دینامیک سازه وجود دارد.

دینامیک سازه‌های دریایی، برهم‌کنش بین موج و فونداسیون بستر دریا با سازه را مورد مطالعه قرار می‌دهد. در واقع، دینامیک سازه‌های دریایی، یک حوزه بین رشته‌ای است که دینامیک سازه، دینامیک خاک، زمین‌شناسی، اقیانوس‌نگاری، احتمالات ریاضی، روش‌های کامپیوتری، رویکردهای تجربی و دیگر حوزه‌ها را با هم ترکیب می‌کند.

بارهای دینامیکی سازه‌های دریایی به دو گروه بارهای طبیعی و مصنوعی تقسیم می‌شوند. بر اساس منشا بار، بارهای طبیعی را می‌توان به بارهای سیال، باد، زلزله و یخ‌های شناور تقسیم کرد. در طرف مقابل، بارهای دینامیکی مصنوعی (با منشا انسانی) به دلیل فعالیت‌هایی نظیر حفاری، حرکت کشتی یا دستگاه‌ها، استفاده از جرثقیل، انفجار و غیره به وجود می‌آیند. بارهای دینامیکی مصنوعی معمولا به عنوان بارهای سیال در نظر گرفته می‌شوند.

بارهای سیال توسط موج، جریان، گرداب، فرارفت، موج شکنا و غیره به وجود می‌آیند. منشا تشکیل موج، وزش باد بر روی سطح آب است. شکل سطح موج به منحنی سینوسی ایدئال در اعماق آب نزدیک و دامنه آن کوچک است. به طور کلی، دوره تناوب و ارتفاع به عنوان مشخصات اصلی موج در نظر گرفته می‌شوند.

بارهای زلزله و یخ شناور، از موارد بخصوص در دینامیک سازه‌های دریایی هستند. در حالت عادی از وجود این بارها صرف نظر می‌شود. با این وجود، قرارگیری سازه در نواحی مستعدد زلزله یا محدوده یخ شناور، اهمیت تحلیل این بارها را بالا می‌برد. علاوه بر این موارد، خستگی نیز یکی از مهمترین مسائل موجود در تحلیل سازه‌های دریایی است؛ چراکه احتمال اعمال بارهای چرخه‌ای بر روی این سازه‌ها بیشتر از سازه‌های روی زمین است. در بارگذاری‌های چرخه‌ای بلند مدت، رخ دادن ترک و گسترش آن حتی در شرایط بارگذاری کم نیز می‌تواند آسیب‌های جدی را به همراه داشته باشد.

در سازه‌های دریایی، مسائل دینامیکی مربوط به ساخت و نصب سازه وجود دارد. این مسائل با شرایط عادی متفاوت بوده و نیازمند رعایت الزامات ویژه هستند. عکس‌العمل دینامیکی سازه در شرایط پایداری شناوری، یدک‌کشی و غوطه‌وری در حین حمل و نقل، تحلیل شمع‌کوبی، بررسی تنش‌های محلی هنگام نصب کیسون بر روی فونداسیون غیریکنواخت و غیره از مسائل ویژه دینامیک سازه‌های دریایی محسوب می‌شوند. علاوه بر این، موارد دیگری نظیر پایداری فونداسیون، روانی خاک، عملکرد دینامیکی مواد، تمرکز تنش دینامیک، پلاستیسیته دینامیک، ترک‌خوردگی، اختلاف دما، سونامی، رانش زمین، تحلیل عدم قطعیت و استانداردهای تلورانس ارتعاش نیز از مسائلی هستند که در دینامیک سازه‌های دریایی مورد بررسی قرار می‌گیرند.

کاربرد دینامیک سازه در مهندسی هوافضا چیست؟

هواپیما، سازه‌ای است که بدنه آن اغلب در معرض بارهای دینامیکی مختلف قرار می‌گیرد. به همین دلیل، تحلیل لرزش‌ها و ضربه‌های وارده بر هواپیما برای بهبود عملکرد آن از اهمیت بالایی برخوردار است. میزان آسیب وارده بر این سازه هوایی به وضعیت حرکت، محیط فعالیت و خصوصیات دینامیکی آن بستگی دارد. از این‌رو، مقاومت دینامیکی به عنوان یک مسئله مهم در فرآیند طراحی و ساخت هواپیما تبدیل شده است.

با پیشرفت روش‌های تحلیل مقاومت سازه‌ای و آزمایش‌های هواپیما در سال‌های اخیر، کاربرد دینامیک سازه در حوزه طراحی هواپیما جهش قابل‌توجهی پیدا کرد. از مهمترین پیشرفت‌ها و دستاوردها در این زمینه می‌توان تحلیل دینامک سازه پیچیده هواپیما، شبیه‌ساز آزمایش دینامیکی، تکنولوژی طراحی آزمایش‌های لرزه‌ای برای هواپیماهای بزرگ، تحلیل شرایط محیطی تجهیزات هوایی، تحقیق بر روی دینامیک سازه هوایی کامپوزیت، پیش‌بینی صدای هواپیما و تحلیل زمانی خستگی آکوستیک را نام برد.

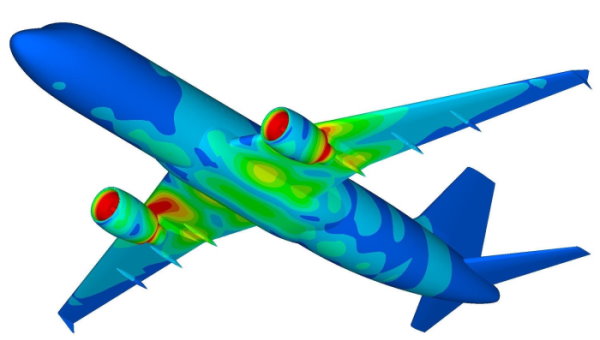
با تمام پیشرفت‌های حاضر، دینامیک سازه‌های هوایی یکی از حوزه‌های در حال توسعه مهندسی هوافضا محسوب می‌شود و مسائل حل نشده زیادی در این حوزه وجود دارد. به عنوان مثال، به دلیل پیچیدگی منبع ارتعاش، بارهای دینامیکی به طور دقیق قابل تعریف نیستند؛ به دلیل دشوار بودن شرایط مرزی، تحلیل عکس‌العمل دینامیک سازه‌های بزرگ و پیچیده به اندازه کافی دقیق نیست؛ و تعیین ویژگی میرایی سازه‌های پیچیده، دشوار است.

تحلیل دینامیک سازه با تحلیل استاتیک چه تفاوتی دارد؟

تحلیل دینامیک سازه، مجموعه محاسباتی است که به منظور ارزیابی عملکرد سازه در هنگام اعمال بارهای دینامیکی مورد استفاده قرار می‌گیرد.

این محاسبات در سازه‌های ساده به صورت دستی و در سازه‌های پیچیده با استفاده از نرم‌افزارهای عددی قابل انجام هستند. به طور کلی، مسائل دینامیک سازه دو تفاوت اصلی با مسائل استاتیک دارند:

1. تغییر بار نسبت به زمان: مقدار بارهای دینامیکی با زمان تغییر می‌کند. به همین دلیل، در حین محاسبه عکس‌العمل‌های دینامیک سازه باید چندین خروجی متوالی برای تمام زمان‌های موجود در تاریخچه زمانی را تعیین کرد. بنابراین، تحلیل دینامیک پیچیده‌تر و زمانبرتر از تحلیل استاتیک خواهد بود.
2. تاثیر نیروی اینرسی: به دلیل جابجایی سریع سازه هنگام مواجهه با بارهای دینامیک، باید ممان اینرسی را در تحلیل دینامیک در نظر گرفت. دلیل این موضوع، تاثیر جدی این پارامتر بر رفتار سازه در بارگذاری دینامیک و جهت‌گیری آن برخلاف شتاب است.

روش‌های محاسباتی نیمه استاتیک متعددی مانند «روش طیف پاسخ» (Response Spectrum Method) در طراحی لرزه‌ای، برای ساده‌سازی تحلیل سازه و تحلیل دینامیک سازه ارائه شده‌اند. با این وجود، اصول تئوری تمام این روش‌ها بر اساس دینامیک سازه بوده و اجرای تحلیل دینامیک برای بررسی دوره تناوب (پریود) طبیعی ارتعاش و حالت‌های درجه آزادی سیستم ضروری است.

مقایسه تحلیل استاتیک و دینامیک سازه را با مثال زیر ادامه می‌دهیم. تصویر سمت چپ، یک تیر ساده را نمایش می‌دهد که تحت بار استاتیک F قرار دارد. در این شرایط، نیروی خارجی F و عکس‌العمل‌های تکیه‌گاهی، تنها نیروهای اعمال شده بر تیر هستند. در تصویر راست، همان تیر تحت بارگذاری دینامیک قرار می‌گیرد. در این شرایط، تیر به سرعت جابجا می‌شود. از این‌رو، علاوه بر نیروی خارجی F و عکس‌العمل‌‌های تکیه‌گاهی، نیروی اینرسی نیز بر روی امتداد تیر توزیع خواهد شد. مقدار نیروی اینرسی به نحوه حرکت تیر، بستگی دارد.

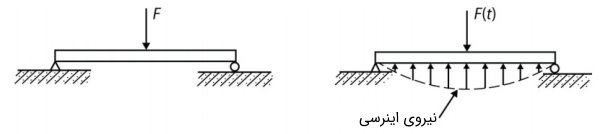
نکته جالب این است که نحوه حرکت تیر در این شرایط نیز به اندازه زیادی به ماهیت نیروی اینرسی بستگی دارد. وجود نیروی اینرسی، تحلیل رفتاری سازه را دشوار می‌کند. این پیچیدگی با افزایش نرخ بارگذاری بیشتر خواهد شد. عکس‌العمل سازه در برابر نیروهای اینرسی در این حالت بسیار شدیدتر از حالت استاتیک خواهد بود.

حل مسائل دینامیکی چگونه انجام می شود؟

محاسبات دینامیکی با در نظر گرفتن ضربه ناشی از نیروی اینرسی در تمام بازه‌های زمانی صورت می‌گیرند. وجود نیروی اینرسی، حل مسئله را دشوارتر می‌کند اما با درک صحیح و استفاده از روش‌های مناسب می‌توان پیچیدگی‌های موجود را ساده‌تر کرد. یکی از متداول‌ترین روش‌های ساده‌سازی و حل مسائل دینامیک سازه، روش گسسته‌سازی است.

گسسته سازی چیست و چه کاربردی در دینامیک سازه دارد؟

نیروی اینرسی، اصلی‌ترین دلیل عکس‌العمل سازه در برابر بارهای دینامیکی است. منشا این نیرو، به جرم سازه بازمی‌گردد. به همین دلیل، تعریف موقعیت مکانیکی و حرکت سازه با توجه به جرم آن، یکی از عوامل کلیدی در فرآیند تحلیل دینامیک خواهد بود. علاوه بر این، جرم سازه، محل قرارگیری و نحوه حرکت آن بر روی تعیین درجه آزادی دینامیکی و استاتیکی نیز تاثیرگذار است. در نتیجه، انتخاب صحیح درجه آزادی دینامیکی، اهمیت زیادی در تعریف دقیق نیروی اینرسی دارد.

تمام سیستم‌های سازه‌ای دارای جرم گسترده و بی نهایت درجه آزادی هستند. تحلیل دینامیک سازه‌ای با بی‌نهایت درجه آزادی کار بسیار دشواری است. به منظور جلوگیری از پیچیدگی محاسبات ریاضی در این نوع تحلیل، سازه مورد بررسی به سیستمی با درجه آزادی محدود تبدیل می‌شود. به این کار، فرآیند گسسته‌سازی سازه می‌گویند. از رایج‌ترین روش‌های گسسته‌سازی می‌توان به روش «جرم نقطه‌ای» (Lumped Mass)، «جابجایی تعمیم یافته» (Generalized Displacement) و «المان محدود» (Finite Element) اشاره کرد. گسسته‌سازی به عنوان روش اصلی تبدیل مسائلی با درجه آزادی نامحدود به مسائلی با درجه آزادی محدود محسوب می‌شود. در ادامه به معرفی روش‌های متداول گسسته‌سازی می‌پردازیم.

کاربرد روش جرم نقطه ای در تحلیل دینامیک سازه چیست؟

روش جرم نقطه‌ای یا جرم متمرکز، متداول‌ترین روش مورد استفاده در ساده‌سازی فرآیند تحلیل دینامیک سازه است. در این روش با استفاده از یک سری قوانین خاص، نقاطی از سازه به عنوان معرف رفتار آن انتخاب شده و سیستمی با درجه آزادی نامحدود به سیستمی با درجه آزادی محدود تبدیل می‌شود. تصویر زیر، مثالی از این تبدیل را با استفاده از روش جرم نقطه‌ای برای سازه‌ای با جرم گسترده نمایش می‌دهد. در این تصویر، جرم گسترده m توسط سه جرم نقطه‌ای m₂ ،m₁ و m₃ جایگزین شده است. با در نظر گرفتن جابجایی جانبی در سطح مقطع، تیر با جرم‌های نقطه‌ای دارای سه درجه آزادی جانبی خواهد بود.

تصویر زیر، مثال دیگری از تبدیل درجه آزادی نامحدود به درجه آزادی محدود را برای یک ساختمان سه طبقه نمایش می‌دهد. در این مثال، اگر جرم نیمی از ستون‌ها، دیوارها، کف و تیرهای هر طبقه را در مرکز کف طبقه متمرکز کنیم، تعداد درجات آزادی این ساختمان از بی‌نهایت به سه درجه آزادی کاهش می‌یابد.

کاربرد روش مختصات یا جابجایی تعمیم یافته در تحلیل دینامیک سازه چیست؟

مختصات تعمیم‌یافته، ‌پارامترهای مستقلی هستند که به منظور نمایش محل قرارگیری سیستم مورد استفاده قرار می‌گیرند. به کارگیری مختصات تعمیم‌یافته در سیستم تیر با جرم گسترده می‌تواند دقت محاسبات را افزایش دهد. به منظور حل معادلات دیفرانسیل معمولا از دنباله یا سری استفاده می‌شود. در دینامیک سازه می‌توان تغییر شکل سازه‌هایی نظیر تیر را با سری فوریه بیان کرد.

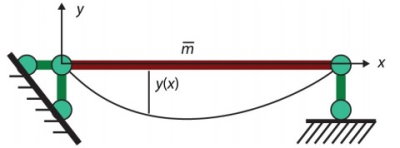
به عنوان مثال، سری فوریه برای تیر نمایش داده شده در تصویر بالا به صورت زیر است:

$$
y(x, t)=\sum_{i=1}^{N} b_{i} \sin \frac{n \pi x}{L}=\sum_{i=1}^{N} b_{i}(t) \sin \frac{n \pi x}{L}
$$

در این رابطه:

• L: طول تیر
• siniπx/L: تابع شکل (مجموعه‌ای از توابع مشخص که در شرایط مرزی یا محدوده شکل سازه صدق می‌کند.)
• b_i=b_i(t)‎: مختصات تعمیم‌یافته (مجموعه‌ای از پارامترهای قابل تعیین و تابعی از زمان است)

به دلیل مشخص بودن تابع شکل، تغییر شکل تیر توسط چندین مختصات تعمیم‌یافته تعیین می‌شود. در تحلیل دینامیک تئوری، تعداد درجات آزادی تیر ساده نامحدود خواهد بود. با این وجود، در تحلیل واقعی، فقط چند جمله اول سری فوریه مورد استفاده قرار می‌گیرند.

$$y(x, t)=\sum_{i=1}^{N} b_{i}(t) \sin \frac{n \pi x}{L}$$

به این ترتیب، سیستم تیر به یک سیستم با N درجه آزادی تبدیل می‌شود. عبارت تعمیم‌یافته برای بیان جابجایی سازه را می‌توان به صورت زیر نوشت:

$$
y(x, t)=\sum_{i=1}^{\infty} q_{i}(t) \varphi_{i}(x) \approx \sum_{i=1}^{N} q_{i}(t) \varphi_{i}(x)
$$

• q_i(t)‎: دامنه تابع شکل (مختصات تعمیم‌یافته)
• φ_i(x)‎: تابع شکل (تابع پیوسته‌ای که در شرایط مرزی صدق می‌کند)

در مثال تیر ساده، شرطی که تابع شکل باید در آن صدق کند عبارت است از:

$$
\varphi_{n}(\mathrm{O})=\varphi_{n}(L)=\mathrm{0}
$$

اگر تابع شکل، جابجایی سازه را نشان دهد، مختصات تعمیم‌یافته با جابجایی هم‌بعد خواهد شد. مختصات تعمیم‌یافته می‌تواند نمایش دهنده دامنه تابع شکل باشد اما جابجایی نمایش داده شده در این تابع واقعی نخواهد بود؛ زیرا جابجایی واقعی زمانی به دست می‌آید که تمام N جمله سری در محاسبات در نظر گرفته شده باشند.

کاربرد روش المان محدود در تحلیل دینامیک سازه چیست؟

«روش المان محدود» (Finite Element Method) یا به اختصار FEM، ترکیبی از روش‌های جرم نقطه‌ای و مختصات تعیم‌یافته است که برای حل مسائل استاتیک و دینامیک سازه مورد استفاده قرار می‌گیرد. در فرآیند FEM،‌ سازه به صورت مجموعه‌ای از نقاط (نقاط گره‌ای) تعریف می‌شود. جابجایی هر یک از نقاط گره‌ای، بیانگر وضعیت جابجایی نقطه متناظر آن در سازه واقعی است.

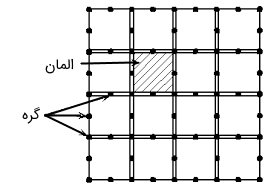
در فرآیند گسسته‌سازی FEM، با اضافه کردن جابجایی‌های فرضی به المان‌ها، منحنی تغییر شکل کل سازه در یک زمان مشخص به دست می‌آید. سپس منحنی‌های معرف شکل المان‌ها، به صورت تابع جابجایی یا درون‌یابی با چندین پارامتر مختلف تعریف می‌شوند. توابع جابجایی باید درون هر المان به صورت پیوسته و مطابق محدودیت‌های موجود در دو انتهای المان باشند. با توجه به این موارد، پارامترهای دخیل در تابع جابجایی را می‌توان توسط جابجایی گره‌ای تعریف کرد. به این ترتیب، سیستمی با درجه آزادی نامحدود به سیستمی با درجه آزادی محدود و جابجایی گره‌ای نامشخص تبدیل می‌شود.

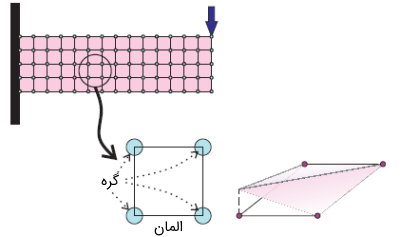
به عنوان مثال، یک تیر پیوسته را در نظر بگیرید. این تیر را می‌‌توان به N المان (قطعات تیر) تقسیم کرد. محل تقاطع المان‌های مجاور با عنوان نقاط گره‌ای شناخته می‌شود. پارامترهای جابجایی گره‌ای (جابجایی u و زاویه دوران θ) به عنوان مختصات تعمیم‌یافته سیستم مورد استفاده قرار می‌گیرند. این مدل المان محدود دارای شش مختصات تعمیم‌یافته با پارمترهای جابجایی زیر است:

$$
u_{1}, \theta_{1}, u_{2}, \theta_{2}, u_{3}, \theta_{3}
$$

توابع شکل نیز به صورت زیر هستند:

$$
\varphi_{1}, \varphi_{2}, \varphi_{3}, \varphi_{4}, \varphi_{5}, \varphi_{6}
$$

برای مدل گسسته تیر یکسرگیردار با N المان، در مجموع 2N مختصات تعمیم‌یافته وجود دارد. به علاوه، جابجایی تیر نیز توسط 2N مختصات تعمیم‌یافته و توابع شکل آن‌ها به صورت زیر قابل تعریف است:

$$
u(x)=u_{1} \varphi_{1}(x)+\theta_{1} \varphi_{2}(x)+\cdots+u_{N} \varphi_{2 N-1}(x)+\theta_{N} \varphi_{2 N}(x)
$$

به این ترتیب، یک تیر با درجه آزادی نامحدود به سیستمی با درجه آزادی 2N تبدیل می‌شود. فرآیند روش المان محدود، ویژگی‌های روش جرم نقطه‌ای و مختصات تعمیم‌یافته را به صورت زیر ترکیب می‌کند:

1. مشابه روش مختصات تعمیم‌یافته، در روش المان محدود از مفهوم تابع شکل استفاده می‌شود. برخلاف درون‌یابی کل سیستم (تعریف تابع شکل کل سازه) در روش مختصات تعمیم‌یافته، FEM از درون‌یابی منقطع (بین المان و الما‌ن‌های مجاور) استفاده می‌کند. به این ترتیب، رابطه تابع شکل در FEM، نسبتا ساده خواهد بود.
2. مانند روش مرکز جرم، مختصات تعمیم‌یافته FEM دارای پارامترهای فیزیکی واقعی است. این موضوع باعث سادگی و درک بصری فرآیند FEM می‌شود.

مقایسه روش های گسسته سازی در دینامیک سازه

از میان روش‌های مرکز جرم، مختصات تعمیم‌یافته و المان محدود، روش اول، ساده‌تر و کاربردی‌تر است. روش مختصات تعمیم‌یافته به انتخاب تابع شکل مناسب برای صدق کردن در شرایط مرزی جابجایی نیاز دارد. این مسئله، کاربرد روش مذکور را به سازه‌های ساده محدود می‌کند. به دلیل ترکیب ویژگی‌های دو روش اول در FEM، این روش به منظور تحلیل سازه‌های پیچیده و حل مسائل دینامیک سازه به طور گسترده مورد استفاده قرار می‌گیرد.

کاربرد معادله حرکت در تحلیل دینامیک سازه چیست؟

هدف از تحلیل دینامیک سازه، تعیین تاریخچه زمانی جابجایی برای سازه‌هایی است که بارهای اعمال شده بر آن‌ها در طول زمان تغییر می‌کند. در اغلب موارد، اجرای تحلیل‌های تقریبی با چند درجه آزادی می‌تواند دقت کافی را به همراه داشته باشد. بنابراین، می‌توان با ساده‌سازی مسئله، تاریخچه‌های زمانی مولفه‌های در نظر گرفته شده را تعیین کرد.

روابط ریاضی تعیین‌کننده جابجایی‌های دینامیک، با عنوان معادلات حرکت سازه شناخته می‌شوند. حل این معادلات، تاریخچه‌های زمانی مورد نیاز برای تحلیل دینامیک سازه را فراهم می‌کند. نوشتن معادله حرکت برای یک سیستم دینامیک، مهم‌ترین و گاهی اوقات دشوارترین مرحله تحلیل دینامیک سازه است. در ادامه، به معرفی روش‌های تعیین معادلات حرکت برای سیستم‌های دینامیک می‌پردازیم.

اصل دالامبر چیست و چه کاربردی در دینامیک سازه دارد؟

«اصل دالامبر» (D’Alembert’s Principle) یا اصل تعادل دینامیکی، فرم دیگر قانون دوم نیوتون است. در واقع این اصل، مسائل دینامیکی را به مسائل استاتیکی تبدیل می‌کند. بر اساس قانون دوم نیوتون، نیروی اعمال شده به یک جسم از حاصل‌ضرب جرم (m) در شتاب ($$\ddot{u}$$) به دست می‌آید:

$$
F=m \ddot{u}
$$

رابطه بالا را می‌توان به شکل زیر بازنویسی کرد:

$$
F-m \ddot{u}=0
$$

به عبارت دیگر، جرم بین اعمال نیروی واقعی (F) و نیروی فرضی ($$-m \ddot{u}$$) در تعادل است. نیروی فرضی در معادله تعادل بالا با عنوان نیروی اینرسی یا «نیروی موثر بازگشتی» (Reversed Effective Force) شناخته می‌شود.

اصل دالامبر، ابزار بسیار ساده‌ای برای حل مسائل دینامیک سازه است. این اصل، امکان بازنویسی معادلات حرکت به صورت معادلات تعادل دینامیکی را فراهم می‌کند. نیروی F می‌تواند به شکل‌ انواع مختلفی از نیروهای اعمال شده بر جسم، مانند محدودیت‌های الاستیکی (مقاومت در برابر جابجایی)، نیروهای ویسکوز (مقاومت در برابر حرکت) و نیروهای مستقل خارجی در معادله حرکت ظاهر شود. با این وجود، در صورت وجو نیروی اینرسی (نیروی مقاوم در برابر شتاب)، معادله حرکت به خوبی بیانگر تعادل تمام نیروهای اعمال شده بر جرم نخواهد بود. به همین دلیل، اصل دالامبر، فقط برای مسائل ساده گزینه مناسبی است.

اصل کار مجازی چیست و چه کاربردی در دینامیک سازه دارد؟

اگر سازه مورد تحلیل، دارای یک سیستم پیچیده و از چند نقطه جرمی یا چند جسم با ابعاد مشخص ساخته شده باشد، نوشتن معادلات تعادل تمام نیروهای اعمال شده بر آن دشوار خواهد بود. البته در بسیاری از موارد، امکان نوشتن معادلات نیروی‌های مختلف بر اساس درجه آزادی وجود دارد اما رابطه بین معادلات تعادل این نیروها مبهم است. در این حالت می‌توان از اصل کار مجازی به منظور تعیین معادلات حرکت استفاده کرد.

برای درک اصل کار مجازی، سیستمی از ذرات را در نظر بگیرید که تحت مجموعه‌ای از نیروهای خارجی در حالت تعادل قرار دارد. در صورتی که این سیستم در معرض هر نوع جابجایی مجازی (جابجایی مطابق با محدودیت‌های سیستم) قرار بگیرد، کار انجام شده توسط مجموعه نیروها صفر خواهد بود:

$$
\sum_{i=1}^{N}\left(F_{i}-m_{i} \ddot{u}_{i}\right) \cdot \delta u_{i}=0
$$

در رابطه بالا:

• i: عدد صحیح مورد استفاده برای نمایش ذره مورد بررسی
• F_i: نیروی کل اعمال شده (به غیر از نیروهای بازدارنده) بر ذره i ام
• m_i: جرم ذره i ام
• $$\ddot{u}_{i}$$: شتاب ذره i ام
• $$m_{i} \ddot{u}_{l}$$: تکانه ذره i ام
• δu_i: جابجایی مجازی ذره i ام (سازگار با محدودیت‌های سیستم)

مطابق این اصل، از بین رفتن کار انجام شده حین جابجایی مجازی مشابه مفهوم تعادل است. به این ترتیب، برای تعیین معادلات عکس‌العمل یک سیستم دینامیک، ابتدا باید تمام نیروهای اعمال شده بر ذرات سیستم را مشخص کرد. سپس، با اضافه کردن جابجایی مجازی متناسب با درجه آزادی و برابر قرار دادن کار انجام شده با صفر، معادلات حرکت به دست می‌آید.

مزیت اصل جابجایی مجازی این است که مولفه‌های موجود در کار مجازی به صورت کمیت‌های اسکالر نوشته می‌شوند و می‌توان آن‌ها را به صورت عددی به معادله اضافه کرد؛ در صورتی که نیروهای اعمال شده بر روی سازه ماهیت برداری دارند.

اصل همیلتون چیست و چه کاربردی در دینامیک سازه دارد؟

«اصل همیلتون» (Hamilton's Principle)، یکی از بنیادی‌ترین و مهم‌ترین اصول در حوزه مکانیک و ریاضی فیزیک است. مطابق اصل دالامبر، برای سیستم‌های ناپایستار (دارای مقاومت هوا، اصطکاک و دیگر نیروهای خروجی) متشکل از n ذره داریم:

$$
\sum_{i=1}^{N}\left(\mathbf{F}_{i}-m_{i} \frac{\mathrm{d}^{2} \vec{u}_{i}}{\mathrm{~d} t^{2}}\right) \cdot \delta \vec{u}_{i}=0
$$

توجه داشته باشید که در این اصل، نیازی به تعیین نوع نیرو (پایستار یا ناپایستار) و الزامات محدودیت‌ها (هولونومیک یا غیرهولونومیک) وجود ندارد. با بازنویسی اصل دالامبر خواهیم داشت:

$$
\sum_{i=1}^{N} \mathbf{F}_{i} \cdot \delta \vec{u}_{i}=\sum_{i=1}^{N} m_{i} \frac{\mathrm{d}^{2} \vec{u}_{i}}{\mathrm{~d} t^{2}} \cdot \delta \vec{u}_{i}
$$

اکنون، رابطه بالا را به صورت زیر می‌نویسیم:

$$
\sum_{i=1}^{N} m_{i} \frac{\mathrm{d}^{2} \vec{u}_{i}}{\mathrm{~d} t^{2}} \cdot \delta \vec{u}_{i}=\sum_{i=1}^{N} \frac{\mathrm{d}}{\mathrm{d} t}\left(m_{i} \frac{\mathrm{d} \vec{u}_{i}}{\mathrm{~d} t} \cdot \delta \vec{u}_{i}\right)-\sum_{i=1}^{N} m_{i} \frac{\mathrm{d} \vec{u}_{i}}{\mathrm{~d} t} \frac{\mathrm{d}}{\mathrm{d} t}\left(\delta \vec{u}_{i}\right)
$$

از آنجایی که $$\delta d \overrightarrow{\mathrm{u}} / d t=d(\delta \overrightarrow{\mathrm{u}}) / d t$$، می‌توانیم فرمول بالا را به صورت زیر بنویسیم:

$$
\sum_{i=1}^{N} m_{i} \frac{\mathrm{d}^{2} \vec{u}_{i}}{\mathrm{~d} t^{2}} \cdot \delta \vec{u}_{i}=\sum_{i=1}^{N} \frac{\mathrm{d}}{\mathrm{d} t}\left(m_{i} \frac{\mathrm{d} \vec{u}_{i}}{\mathrm{~d} t} \cdot \delta \vec{u}_{i}\right)-\delta T
$$

T در رابطه بالا، انرژی جنبشی سیستم است که از رابطه زیر به دست می‌آید:

$$
T=\frac{1}{2} \sum_{i=1}^{N} m_{i}\left(\frac{\mathrm{d} \vec{u}_{i}}{\mathrm{~d} t}\right)^{2}
$$

با قرار دادن رابطه انرژی جنبشی در فرمول قبلی، خواهیم داشت:

$$
\delta W=\sum_{i=1}^{N} \frac{\mathrm{d}}{\mathrm{d} t}\left(m_{i} \frac{\mathrm{d} \vec{u}_{i}}{\mathrm{~d} t} \cdot \delta \vec{u}_{i}\right)-\delta T
$$

به این ترتیب:

$$
\delta(W+T)=\sum_{i=1}^{N} \frac{\mathrm{d}}{\mathrm{d} t}\left(m_{i} \frac{\mathrm{d} \vec{u}_{i}}{\mathrm{~d} t} \cdot \delta \vec{u}_{i}\right)
$$

اکنون از رابطه بالا نسبت به زمان و در بازه t₀ تا t₁ انتگرال می‌گیریم:

$$
\int_{t_{0}}^{t_{1}} \delta(W+T) \mathrm{dt}=\sum_{i=1}^{N}\left[m_{i} \frac{\mathrm{d} \vec{u}_{i}}{\mathrm{~d} t} \cdot \delta \vec{u}_{i}\right]_{t_{0}}^{t_{1}}
$$

از آنجایی که هیچ تغییری در مختصات هیچ یک از مسیرهای حرکت در نقاط پایانی رخ نمی‌دهد ($$\left[\delta \vec{u}_{i}\right]_{t_{0}}^{t_{1}}=0$$)، رابطه بالا به فرم زیر درمی‌آید:

$$
\delta \int_{t_{0}}^{t_{1}}(W+T) \mathrm{dt}=0
$$

این رابطه با عنوان اصل همیلتون برای سیستم‌های ناپایستار شناخته می‌شود. اگر سیستم پایستار باشد، می‌توان بردار نیرو F(t) را به دو مولفه پایستار و ناپایستار تجزیه کرد:

$$
\mathbf{F}(t)=\mathbf{F}_{c}(t)+\mathbf{F}_{n c}(t)
$$

بنابراین، تابع انرژی پتانسیل V(t) باید به گونه‌ای تعریف می‌شود که بردار نیروی پایستار F_c(t) در رابطه بین مولفه‌ها صدق کند:

$$
\sum_{i} \mathbf{F}_{i} \cdot \delta \vec{u}_{i}=-\sum_{i} \frac{\partial V}{\partial \vec{u}_{i}} \delta \vec{u}_{i}=-\delta V
$$

به این ترتیب:

$$
\int_{t_{0}}^{t_{1}} \delta(T-V) \mathrm{dt}+\int_{t_{0}}^{t_{1}} \delta W_{n c} \mathrm{dt}=0
$$

با تعیین معادلات تمام ذرات و جمع آن‌ها می‌توان دریافت که در صورت محاسبه مقادیر انرژی جنبشی، انرژی پتانسیل و کار انجام شده، رابطه بالا برای هر سیستم پیچیده‌ای (خطی یا غیرخطی) معتبر خواهد بود. اصل بالا نشان می‌دهد که مجموع متغیرهای زمانی با انرژی پتانسیل و جنبشی مختلف و کار انجام شده توسط نیروهای ناپایستار در بازه t₁ تا t₂ برابر صفر است. با استفاده از این اصل می‌توان معادلات حرکت هر سیستمی را به طور مستقیم تعیین کرد. به طور کلی، استفاده از اصل همیلتون برای تعیین معادله حرکت شامل چهار مرحله زیر می‌شود:

1. بررسی دقیق جسم، تحلیل محدودیت‌ها، تعیین درجه آزادی سیستم و انتخاب مختصات مناسب
2. محاسبه انرژی پتانسیل و جنبشی سیستم
3. محاسبه حاصل جمع کار مجازی انجام شده توسط نیروهای ناپایستار
4. نوشتن معادله همیلتون به منظور تعیین معادله دیفرانسیل حرکت

مزیت اصل همیلتون این است که نیروهای اینرسی و الاستیک مورد استفاده قرار نمی‌گیرند و به ترتیب با متغییرهای انرژی جنبشی و پتانسیل جایگزین می‌شوند. در واقع، در اصل همیلتون به جای استفاده از کمیت‌های برداری، کمیت‌های اسکالر یا عددی مورد استفاده قرار می‌گیرند.

معادله لاگرانژ چیست و چه کاربردی در دینامیک سازه دارد؟

معادلات حرکت برای یک سیستم چند درجه آزادی را می‌توان به طور مستقیم توسط معادله همیلتون و با نوشتن رابطه انرژی جنبشی کل T، انرژی پتانسیل کل V و کار مجازی کل W_nc در قالب مجموعه‌ای از مختصات تعمیم‌یافته q₁ تا q_n به دست آورد.

برای اکثر سیستم‌های مکانیکی یا سازه‌ای، انرژی جنبشی، بر حسب مختصات تعمیم‌یافته به همراه مشتق مرتبه اول آن‌ها و انرژی پتانسیل، فقط بر حسب مختصات تعمیم‌یافته قابل تعریف است. علاوه بر این، کار مجازی صورت گرفته توسط نیروهای ناپایستار اعمال شده بر روی جابجایی‌های مجازی ناشی از تغییرات فرضی در مختصات تعمیم‌یافته نیز به صورت تابع خطی آن تغییرات بیان می‌شود. اگر بخواهیم جملات این پاراگراف را به صورت ریاضی بیان کنیم، خواهیم داشت:

$$
\begin{array}{c}
T=T\left(q_{1}, q_{2}, \ldots, q_{N} ; \dot{q}_{1}, \dot{q}_{2}, \ldots, \dot{q}_{N}\right) \\
V=V\left(q_{1}, q_{2}, \ldots, q_{N}\right) \\
\delta W_{n c}=Q_{1} \delta q_{1}+Q_{2} \delta q_{2}+\ldots+Q_{N} \delta q_{N}
\end{array}
$$

Q₁ تا Q_N: توابع نیروی تعمیم‌یافته مرتبط با مختصات q₁ تا q_N

با انتگرال‌گیری از معادلات بالا نسبت به t در بازه t₀ تا t₁، خواهیم داشت:

$$
\begin{array}{l}
\int_{t_{0}}^{t_{1}}\left(\frac{\partial T}{\partial q_{1}} \delta q_{1}+\frac{\partial T}{\partial q_{2}} \delta q_{2}+\ldots+\frac{\partial T}{\partial q_{N}} \delta q_{N}+\frac{\partial T}{\partial \dot{q}_{1}} \delta \dot{q}_{1}+\frac{\partial T}{\partial \dot{q}_{2}} \delta \dot{q}_{2}+\ldots+\frac{\partial T}{\partial \dot{q}_{N}} \delta \dot{q}_{N}\right. \\
\left.-\frac{\partial V}{\partial q_{1}} \delta q_{1}-\frac{\partial V}{\partial q_{2}} \delta q_{2}-\ldots-\frac{\partial V}{\partial q_{N}} \delta q_{N}+Q_{1} \delta q_{1}+Q_{2} \delta q_{2}+\ldots+Q_{N} \delta q_{N}\right) \mathrm{dt}=0
\end{array}
$$

از انتگرال‌گیری عبارت‌های دارای سرعت در رابطه بالا به رابطه زیر می‌رسیم:

$$
\int_{t_{0}}^{t_{1}} \frac{\partial T}{\partial \dot{q}_{i}} \delta \dot{q}_{i} \mathrm{dt}=\left[\frac{\partial T}{\partial \dot{q}_{i}} \delta \dot{q}_{i}\right]_{t_{0}}^{t_{1}}-\int_{t_{0}}^{t_{1}} \frac{d}{d t}\left(\frac{\partial T}{\partial \dot{q}_{i}}\right) \delta q_{i} \mathrm{dt}
$$

عبارت سمت راست در رابطه بالا برای تمام مختصات‌ها برابر صفر خواهد بود؛ چراکه δqi(t₀)=δqi(t₁)=0، شرط اولیه متغیرها است. با جایگذاری این رابطه در رابطه قبلی و مرتب کردن عبارت‌ها خواهیم داشت:

$$
\int_{t_{0}}^{t_{1}}\left\{\sum_{i=1}^{N}\left[-\frac{d}{d t}\left(\frac{\partial T}{\partial \dot{q}_{i}}\right)+\frac{\partial T}{\partial q_{i}}-\frac{\partial V}{\partial q_{i}}+Q_{i}\right] \delta q_{i}\right\} \mathrm{dt}=0
$$

از آنجایی که تمام متغیرهای δqi (از i=1 تا i=N) به صورت فرضی هستند، رابطه بالا تنها در حالت زیر برای شرایط کلی معتبر خواهد بود:

$$
\frac{d}{d t}\left(\frac{\partial T}{\partial \dot{q}_{i}}\right)-\frac{\partial T}{\partial q_{i}}+\frac{\partial V}{\partial q_{i}}=Q_{i}
$$

رابطه بالا با عنوان معادلات حرکت لاگرانژ شناخته می‌شود. این معادلات کاربرد گسترده‌ای در حوزه‌های مختلف مهندسی و علوم پایه دارد. به طور کلی، معادلات حرکت با استفاده از روش لاگرانژ طی چهار مرحله زیر به دست می‌آیند:

1. تشخیص سیستم و اشیا موجود در آن، تعیین درجه آزادی و انتخاب مجموعه مختصات تعمیم‌یافته مناسب
2. تعیین انرژی جنبشی و پتانسیل سیستم
3. یافتن نیروهای ناپایستار موجود در سیستم
4. به دست آوردن معادلات حرکت با جایگزینی مقادیر به دست آمده از مراحل قبل در معادلات لاگرانژ و ساده‌سازی روابط

مقایسه روش های تعیین معادله حرکت برای سیستم های دینامیک

در بخش‌های قبلی، چهار روش اصلی تعیین معادله حرکت برای سیستم‌های دینامیک را معرفی کردیم. روش تعادل مستقیم (اصل دالامبر)، یک روش ساده و بصری برای تعیین معادله حرکت است که به طور گسترده مورد استفاده قرار می‌گیرد. مهم‌تر از همه، این روش مفهوم تعادل دینامکی را بیان می‌کند.

روش تعیین معادلات تعادل در تحلیل استاتیکی سازه، به طور مستقیم برای مسائل دینامیکی تعمیم یافته است.در صورت توزیع گسترده جرم و الاستیسته درون سازه، استفاده از روش تعادل دینامیکی به منظور تعیین معادله حرکت دشوار خواهد بود. در این شرایط، به کارگیری اصل جابجایی مجازی (کار مجازی) گزینه مناسب‌تری است. در این اصل، به جای پارامترهای برداری از پارامترهای اسکالر برای تعیین معادله حرکت استفاده می‌شود.

اصل همیلتون نیز یکی دیگر از اصول تعیین معادله حرکت با استفاده از پارامترهای اسکالر است. در قضیه کار و انرژی، اگر از کار انجام شده توسط نیروهای ناپایستار (نیروی میرایی) صرفنظر شود، تمام محاسبات به صورت اسکالر خواهد بود.

استفاده از معادله لاگرانژ به منظور تعیین معادله حرکت، نسبت به دو روش قبلی متداول‌تر است. این روش شباهت زیادی به اصل همیلتون دارد. نیروی میرایی مورد استفاده در معادله لاگرانژ، توسط آزمایش‌های تجربی به دست می‌آید (مبنای محاسبه آن، صرفا تحلیل ریاضی و مکانیکی مواد و عضوهای سازه نیست). منشا اصلی میرایی مکانیکی محیط پیوسته، عمدتا خود محیط بوده و با میرایی دینامیکی سازه متفاوت است. منبع میرایی سازه، پیچیدگی زیادی دارد و به سادگی قابل تعریف نیست. با این وجود، مقدار ضریب تجربی آن را می‌توان با استفاده از اندازه‌گیری‌های آزمایشگاهی یا تجربی به دست آورد.