حل مسائل استوکیومتری — به زبان ساده + روش‌ و مثال

دغدغه بسیاری از دانش‌آموزان و دانشجویان حل مسائل استوکیومتری است، در صورتی‌که اگر با مفهوم استوکیومتری به خوبی آشنا شوید به راحتی می‌توانید از آن در حل مسائل کمک بگیرید. استوکیومتری بخش مهمی از شیمی را به خود اختصاص می‌دهد که با روابط کمی بین واکنش‌دهنده‌ها و فرآورده‌ها در واکنش‌های شیمیایی سر و کار دارد. ازجمله این روابط در مسائل استوکیومتری می‌توان به روابط میان جرم، تعداد مول، اتم، مولکول و یون‌های واکنش‌دهنده و فراورده‌ها اشاره کرد. حل مسائل استوکیومتری کمک می‌کند تا در صنعت یا آزمایشگاه‌ها بتوان به راحتی با جرم مواد اولیه یا تعداد مول‌ها در محلول سر و کار داشته باشیم. در این مطلب روش حل مسائل استوکیومتری در قالب ۸ نوع مسئله مهم به شما آموزش داده می‌شود و برای تسلط بیشتر برای هر کدام از این مسائل مثال‌هایی آورده شده است.

استوکیومتری چیست ؟

در زبان یونانی استوکیومتری به معنای عنصرسنجی یا قیاس‌سنجی است، بنابراین استوکیومتری به صورت مقیاسی برای عناصر تعریف می‌شود. در مجموع معنا و مفهوم استوکیومتری را می‌توان در جمله زیر خلاصه کرد:

« استوکیومتری مجموعه‌ای از روابط کمی میان جرم، تعداد مول و تعداد ذرات (اتم‌ها،‌ مولکول‌ها و یون‌ها)‌ واکنش‌دهنده و فراورده در معادله شیمیایی موازنه شده است.»

در آزمایشگاه و صنعت ممکن است سوالاتی از قبیل سوالات زیر پیش آید:

• چه مقدار اکسیژن نیاز است تا ایزوبوتان به طور کامل بسوزد؟ (توجه: طراحی این آزمایش باید به گونه‌ای باشد که آلودگی برای محیط زیست به وجود نیاید.)
• از یک سنگ معدن کوچک طلا چند گرم طلای خالص حاصل می‌شود؟
•  یک کارخانه‌ صنعتی برای تولید اسید سولفوریک در هفته به چه مقدار عنصر گوگرد نیاز دارد؟

همه این سوالات با استفاده از مفاهیمی ازجمله مول،‌ مولار و جرم مولی، غلظت قابل پاسخ است. به همین دلیل حل مسائل استوکیومتری اهمیت بسیار بالایی دارد.

موازنه در روش حل مسائل استوکیومتری

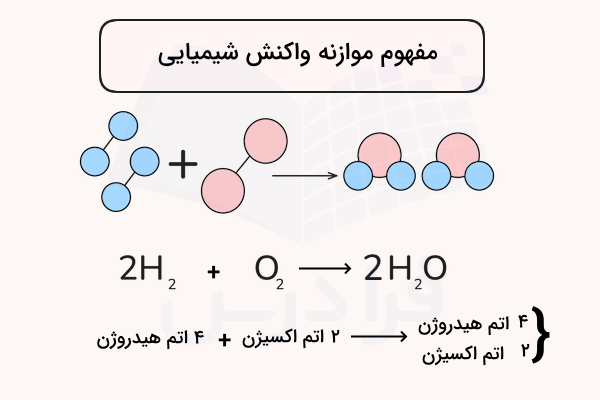
در مسائل مربوط به استوکیومتری فاکتوری به نام ضریب استوکیومتری نقش بسیار مهم و کلیدی را دارد زیرا به حل مسائل استوکیومتری کمک می‌کند. ضریب یا ثابت استوکیومتری بیانگر تعداد مولکول شرکت‌کننده در واکنش است. اگر به واکنش‌های موازنه شده نگاهی داشته باشید متوجه خواهید شد که تعداد برابری از هر مولکول در دو سمت واکنش وجود دارند.

به شکل زیر دقت کنید، مفهوم موازنه را نشان می‌دهد.

ضرایب استوکیومتری همان اعدادی هستند که قبل از هر مولکول در واکنش نوشته شده است. به همین دلیل اولین شرط برای حل مسائل استوکیومتری موازنه بودن واکنش‌های شیمیایی است. در حقیقت،‌ این ضرایب کمک می‌کنند تا نسبت مولی بین واکنش‌دهنده‌ها و فراورده‌ها مشخص شود.

واکنش‌ موازنه شده و نسبت‌ مولی

اندازه اتم‌ها و مولکول‌ها به قدری کوچک هستند که به همین خاطر در مقدار کوچکی از ماده تعداد آن‌ها بسیار بالاست. بنابراین،‌ برای نشان دادن اتم‌ها و مولکول‌ها در بالک ماده مفهوم مول به وجود آمد. یک مول از هر ماده شامل ۱۰^۲۳ × ۶/۰۲۲ تعداد اتم از آن ماده است. این عدد با نام عدد آووگادرو در شیمی شناخته می‌شود و نام آن از دانشمندی با همین نام گرفته شده است.

معادله واکنشی زیر را در نظر بگیرید:

$$Fe(s) + H_2O(l)\rightarrow Fe_3O_4(s) + H_2(g)$$

با توجه به معادله فوق در واکنش‌دهنده‌ها تعداد اتم‌های آهن $$(Fe)$$، هیدروژن $$(H)$$ و اکسیژن $$(O)$$ به ترتیب برابر ۱، ۲ و ۱ است. در حالی‌که مقادیر این عناصر به ترتیب در فراورده‌ها برابرند با ۳، ۲ و ۴ است. بنابراین با مقایسه این مقادیر در سمت چپ و راست واکنش متوجه می‌شویم که معادله شیمیایی فوق موازنه شده نیست.

البته توجه کنید که تعداد اتم‌های هیدروژن در دو طرف واکنش با هم برابرند. از مقایسه تعداد اتم‌ها در دو طرف واکنش می‌توان نتیجه گرفت که آهن را در سمت چپ واکنش باید در ۳ ضرب کرد.

برای موازنه کردن اتم اکسیژن اگر مولکول $$H_2O$$ در ۴ ضرب کنیم تعداد اکسیژن در دو طرف واکنش با هم برابر می‌شوند. اما از آنجا که این ضریب برای هه عناصر موجود در مولکول است در نتیجه تعداد هیدروژن برابر ۸ می‌شود و توازن بین اتم‌های هیدروژن را در این واکنش به هم می‌خورد. برای برقراری توازن مجدد کافی است که اتم هیدروژن را در سمت راست واکنش نیز در ۴ ضرب کنیم. به این صورت تعداد همه اتم‌ها در دو طرف واکنش فوق با هم برابر خواهند بود یعنی:

اتم آهن : ۳=۳

اتم هیدروژن: ۸=۸

اتم اکسیژن: ۴=۴

بنابراین حالت موازنه شده برای واکنش فوق به صورت زیر خواهد بود:

$$3Fe(s) + 4H_2O(l)\rightarrow Fe_3O_4(s) + 4H_2(g)$$

اغلب اوقات برای حل مسائل استوکیومتری به نسبت‌ مولی میان عناصر نیاز پیدا می‌کنیم،‌ منظور از نسبت مولی همان ضرایب استوکیومتری است. برای مثال در واکنش فوق نسبت مولی آهن به هیدروژن ۳ به ۸ است. به جرم یک مول از ماده به گرم، جرم مولی می‌گویند. جرم مولی یک مول از ماده از لحاظ کمی برابر جرم اتمی/مولکولی است به عنوان مثال واکنش فوق را در نظر بگیرید (حالت موازنه شده)، این واکنش به ما می‌گوید که:

۳ مول آهن با ۴ مول $$H_2O$$ واکنش می‌دهد و در اثر این واکنش یک مول $$Fe_3O_4$$ و ۴ مول $$H_2$$ تشکیل می‌شوند.

برای جرم مولی مولکول کافی است که جرم مولی هر اتم را در ضریب استوکیومتری خود ضرب کنیم (به همین دلیل باید برای حل مسائل استوکیومتری ابتدا باید آن‌ها را موازنه کرد). بنابراین با در نظر گرفتن اینکه جرم مولی آهن، هیدروژن و اکسیژن به ترتیب برابر ۵۶، ۱ و ۱۶ است. پس همین واکنش مفهوم دیگری را نیز می‌تواند به ما برساند:

۱۶۸ گرم آهن (۳×۵۶) با ۷۲ گرم $$H_2O$$ (۱×۲ + ۱۶×۱) واکنش می‌دهد تا ۲۳۱ گرم $$Fe_3O_4$$ (۵۶×۳ + ۱۶×۳ ) و ۸ گرم $$H_2$$ (۱×۲×۴) تولید شود.

چگونه مسائل استوکیومتری را حل کنیم

برای حل مسائل استوکیومتری ابتدا باید مسائل را دسته‌بندی کرد تا بتوان راحت‌تر روش حل هر یک را توضیح داد. اصولا بهترین راه برای روش حل مسائل استوکیومتری روش زنجیره‌ای است. در این قسمت این مسائل را به ۸ دسته کلی تقسیم‌بندی کردیم و روش حل هر یک را با ذکر مثال توضیح می‌دهیم. همچنین گاهی برخی از این ۸ نوع مسئله استوکیومتری با هم ترکیب می‌شوند که برای این نوع هم مثال آورده شده است.

۸ نوع مسئله مهم در حل مسائل استوکیومتری

تا این قسمت متوجه شدیم موازنه نقش اساسی و کلیدی را در حل مسائل اساسی دارد. مسائل استوکیومتری را به ۸ قسمت تقسیم می‌کنیم و حل هر کدام را به صورت جداگانه آموزش می‌دهیم تا با انواع مسائل استوکیومتری آشنا شوید.

1. عدد آووگادرو
2. جرم مولی
3. دما و فشار استاندارد (STP)
4. چگالی
5. محلول‌ها
6. درصد خلوص
7. بازده درصدی
8. گرمای واکنش (آنتالپی)

۱. عدد آووگادرو در مسائل استوکیومتری

همان‌طور که اشاره کردیم عدد آووگاردو نشان می‌دهد که در ۱ مول از هر ماده‌ای ۱۰^۲۳ × ۶/۰۲۲ اتم از آن ماده وجود دارد. در این قسمت به انواع مسائل استوکیومتری مربوط به عدد آووگادرو می‌پردازیم:

مثال ۱

۱۰^۲۷× ۲۵/۱۲۵ اتم کربن معادل چند مول کربن است؟

حل: برای حل این سوال باید با استفاده از عدد آووگادرو اتم‌ها را به مول تبدیل کرد:

$$\displaystyle 25.125\times10^{27}\text{atoms}\times \frac{1mol}{6.022\times10^{23}\text{atoms}}=4.17\times10^4mol$$

مثال ۲

چه تعداد اتم سدیم در سه مول از $$Na_2S$$ وجود دارد؟

حل: برای حل این سوال در ابتدا باید تعداد مول‌های سدیم را در این ترکیب بدست آوریم که با توجه به فرمول ترکیب می‌توان متوجه شد در هر مولکول Na_2S دو مول سدیم وجود دارد.

توجه: دقت داشته باشید در اینجا در هر مولکول $$Na_2S$$ دو مول سدیم وجود دارد. پس همه تعداد مول‌های سدیم را در عدد آووگادرو ضرب کنید. بنابراین حل استوکیومتری این مسئله به صورت زیر خواهد بود:

$$\displaystyle 3 mol Na_{2}S\times\frac{2mol Na}{1 mol Na_{2}S}\times\frac{6.022\times10^{23}\text{atoms Na}}{1 mole Na}=3.61\times10^{24}\text{atoms Na}$$

مثال ۳

چه تعداد اتم در ۱ مول از مولکول دو اتمی هیدروژن $$(H_2)$$ وجود دارد؟

حل: بسیاری از دانش‌آموزان و دانشجویان زمانی‌که با این چنین سوالاتی مواجه می‌شوند خیلی سریع پاسخ می‌دهند که ۱۰^۲۳ × ۶/۰۲۲ اتم. در صورتی‌که این پاسخ کاملا اشتباه است.

ابتدا باید مفهوم عدد آووگادرو را به خوبی درک کرده باشید تا بتوانید از آن در حل چنین سوالاتی کمک بگیرید، عدد آووگادرو تعداد ذرات (اتم، مولکول یا یون) را در ۱ مول نشان می‌دهد. در صورت سوال ذکر شده ۱ مول از مولکول دو اتمی هیدروژن، بنابراین در یک مول از $$(H_2)$$ تعداد ۱۰^۲۳ × ۶/۰۲۲ مولکول دو اتمی هیدروژن وجود دارد. با این حال سوال از ما تعداد اتم‌ها را در یک مول از مولکول دو اتمی هیدروژن $$(H_2)$$ می‌خواهد.

یک مول از $$(H_2)$$ دارای ۱۰^۲۳ × ۶/۰۲۲ مولکول و هر مولکول، دو اتم هیدروژن دارد در نتیجه عدد آووگاردرو را باید در ۲ ضرب کنیم. پاسخ این مسئله به صورت زیر است:

$$1mol H_2 \times \frac{6.022 \times 10^{23} moleculs H_2}{1 mole H_2}= 6.022 \times 10^{23} moleculs H_2$$

$$6.022 \times 10^{23} moleculs H_2 \times \frac{2 atoms H_2}{1 moleculs H_2 }= 1.2044 \times 10^{24} atoms H_2$$

۲. جرم مولی در مسائل استوکیومتری

جرم مولی بخش بزرگی از مسائل استوکیومتری را به خود اختصاص می‌دهد و از آنجا که در بیشتر حل مسائل استوکیومتری کاربرد آن از اهمیت بسیار بالایی برخوردار است. در این قسمت سعی شده به مهم‌ترین نمونه سوالات جرم مولی در مسائل استوکیومتری بپردازیم.

مثال۱

یک مول آب $$H_2O$$ چند گرم است ؟ $$(H=1\, O=16)$$

برای پاسخ به این سوال باید جرم مولی آب را داشته باشیم که برای این‌کار همان‌طور که در بالا توضیح دادیم جرم مولی هر عنصر را در ضریب استوکیومتری خود ضرب می‌کنیم. پس جرم مولی آب برابر است با:

$$2H+O= 2\times1+ 16= 18 g/mol$$

حال از طریق استوکیومتری یک مول از آب را برحسب گرم به دست می‌آوریم.

$$1mol H_2O \times\frac{18 g H_2O}{1 mol H_2O}= 18 g H_2O$$

مثال ۲

در اثر سوختن ۴۳/۳ گرم گلوکز چند گرم دی‌‌اکسید تولید می‌شود؟ واکنش سوختن گلوکوز در زیر آورده شده است. $$(C_6H_{12}O_6 = 180.2 g/mol)$$

$$C_6H_{12}O_6 (s) + O_2 (g) \rightarrow CO_2 (g) + H_2O (l)$$

حل: قبل از هر چیزی باید توجه کنیم که معادله شیمیایی موازنه شده است یا خیر که در مورد این سوال موازنه نشده است. معادله موازنه شده واکنش فوق به صورت زیر خواهد بود.

$$C_6H_{12}O_6 (s) + 6 O_2 (g) \rightarrow 6 CO_2 (g) + 6 H_2O (l)$$

حال نوبت تبدیل گرم گلوکز به مول آن می‌رسد برای این کار به صورت زیر عمل می‌کنیم:

$$45.3 \, g \, glucose \times {1 \, mol \, glucose \over 180.2 \, g \, glucose } = 0.251 \, mol \, glucose \nonumber$$

در این مرحله با در اختیار داشتن تعداد مول گلوکز و ضرایب استوکیومتری تعداد مول کربن دی‌اکسید را از طریق نسبت‌های مولی به دست می‌آوریم که به صورت زیر نشان داده شده است.

$$0.251 \, mol \, glucose \times {6 \, mol \, CO_2 \over 1 \, mol \, glucose } \nonumber= 1.51 \, mol \, CO_2 \nonumber$$

(یادآوری: ضرایب استوکیومتری همان تعداد مول‌ها در معادله واکنشی موازنه شده هستند.)

آخرین مرحله مربوط به تبدیل مول کربن دی‌اکسید به گرم آن است که به صورت زیر نمایش داده می‌شود (جرم مولی کربن برابر $$12 g/mol$$ است.

$$1.51 \, mol \, CO_2 \times {44.010 \, g \, CO_2 \over 1 \, mol \, CO_2} = 66.5 \, g \, CO_2 \nonumber$$

نکته: در حل مسائل استوکیومتری روشی برای نمایش همه راه‌حل‌های ذکر شده در بالا وجود دارد و نام آن روش زنجیره‌ای است. برای حل مثال فوق روش زنجیره‌ای به صورت زیر خواهد بود:

$$45.3 \, g \, glucose \times {1 \, mol \, glucose \over 180.2 \, g \, glucose} \times {6 \, mol \, CO_2 \over 1 \, mol \, glucose} \times {44.010 \, g \, CO_2 \over 1 \, mol \, CO_2} = 66.5 \, g \, CO_2 \nonumber$$

مثال ۳

از سوختن هیدروژن با اکسیژن مولکول گازی $$H_2O$$ تشکیل می‌شود و این واکنش شدیدا از نوع انفجاری است. همچنین مقدار انرژی که در اثر این واکنش رها می‌شود بسیار بالاست. از این سوخت طی همین واکنش شیمیایی در ناسا برای شاتل‌های فضایی استفاده می‌‌شود. مهندسین ناسا برای به دست آوردن مقدار دقیق هریک از واکنش‌دهنده‌ها برای به پرواز درآمدن شاتل‌های فضایی از روابط استوکیومتری استفاده می‌کنند.

حساب کنید که چند تن هیدروژن برای به پرواز در آمدن شاتل فضایی نیاز است تا ۱ تن اکسیژن را حمل کند. $$(1 ton = 1000 kg)$$. واکنش ترکیب هیدروژن با اکسیژن در زیر آورده شده است.

$$H_2 (g) + O_2 (g) \rightarrow H_2O (g) \nonumber$$

حل: توجه کنید که معادله فوق موازنه نشده است و باید آن را موازنه کرد. موازنه شده این واکنش به صورت زیر است:

$$2 H_2 (g) + O_2 (g) \rightarrow 2 H_2O (g) \nonumber$$

• مرحله ۱: طبق واکنش فوق ۲ مول هیدروژن با ۱ مول اکسیژن واکنش می‌دهد و ۲ مول گاز$$H_2O$$ را به وجود می‌آورد. در ابتدا باید مقدار تن اکسیژن را به گرم تبدیل کنیم.

$$1.00 \, ton O_2 \times { 1000 \, kg O_2 \over 1 ton O_2} \times {1000 \, g O_2 \over 1 kg O_2} = 10^6\, g \, O_2 \nonumber$$

• مرحله ۲: حال با استفاده از تبدیل گرم به مول تعداد مول اکسیژن را محاسبه می‌کنیم. هر مول اکسیژن برابر ۱۶ گرم است بنابراین یک مول از مولکول دو‌اتمی اکسیژن (۲×۱۶) دارای ۳۲ گرم است. تبدیل مول به گرم اکسیژن به صورت زیر است:

$$10^6 \, g \, O_2 \times {1 \, mol \, O_2 \over 32.00 \, g \, O_2} = 3.12 \times 10^4 \, mol \, O_2 \nonumber$$

• مرحله ۳: حال با استفاده از ضرایب استوکیومتری در معادله شیمیایی موازنه شده تعداد مول هیدروژن را می‌توان به صورت زیر به دست آورد.

$$mol \, H_2 = mol \, O_2 \times {2 \, mol \, H_2 \over 1 \, mol \, O_2} \nonumber$$

در رابطه فوق کافی است که مقادیر به دست آمده را جایگزین کنیم. تعداد مول اکسیژن برابر مقداری است که در مرحله ۲ به‌دست آمد و تعداد مول هیدروژن و اکسیژن در کسر نسبت مولی برابر ضرایب آن‌ها در معادله موازنه شده است. با جایگزین کردن این مقادیر در رابطه فوق داریم:

$$3.12 \times 10^4 \, mol \, O_2 \times {2 \, mol \, H_2 \over 1 \, mol \, O_2} = 6.24 \times 10^4 \, mol \, H_2 \nonumber$$

• مرحله ۴: اکنون با استفاده از تبدیل واحد مول به گرم برای هیدروژن، گرم آن را به دست می‌آوریم. جرم مولی هیدروژن برابر $$H=1 g/mol$$ است.

$$6.24 \times 10^4 \, mol \, H_2 \times {2 \, g \, H_2 \over 1 mol \, H_2} = 1.25 \times 10^5 \, g \, H_2 \nonumber$$

• مرحله ۵: در مرحله پایانی با استفاده از تبدیل واحد زیر گرم هیدروژن را به تن تبدیل می‌کنیم.

$$( 1.25 \times 10^5 \, g \, H_2 \times {1 \, kg \over 1000 \, g} \times {1 \, ton \over 1000 \, kg} = 0.125 \, ton \, H_2 \nonumber)$$

بنابراین شاتل فضایی باید به گونه‌ای طراحی شود که به ازای یک تن اکسیژن ۰/۱۲۵ تن هیدروژن حمل کند. از آنجا که برای واکنش با هر مول اکسیژن دو مول هیدروژن نیاز است بنابراین جرم مولی هیدروژن در مقایسه با جرم مولی اکسیژن باید هم کوچکتر باشد.

توجه: از آنجا که در شاتل‌های فضایی مقادیر بسیار مهم هستند و گاهی ممکن است ۰/۱ در نتیجه کار بسیار تاثیرگذار باشد محاسبات فوق در این زمینه با دقت بیشتری انجام می‌شود. مقادیر بالا معمولا گرد شده هستند و اینکه از تبدیل واحد کیلوگرم به تن و تن به کیلوگرم استفاده شد. اما در عمل در محاسبات میدانی از تبدیل واحد تن به پوند و پوند به گرم استفاده می‌شود $$(1 ton = 2000 lb)$$. با استفاده از این تبدیل واحد پاسخ نهایی برابر ۰/۱۲۶ تن هیدروژن‌ می‌شود. همان‌طور که می‌بینیم تفاوت این پاسخ با پاسخ بالا در ۰/۱ گرم است.

مثال ۴

سینابار (Cinnabar) یا «سیناباریت» (Cinnabarite) سنگ معدنی است که در آن ترکیب شیمیایی HgS وجود دارد که از آن برای تولید جیوه استفاده می‌شود. به دلیل اینکه یکی از اجزای اصلی این سنگ جیوه است جزء سنگ‌های معدنی خطرناک به شمار می‌رود زیرا جیوه به شدت سمی و خطرناک است. رنگ این سنگ معدنی قرمز بوده که به دلیل حضور جیوه است و در زمان‌های قدیم از آن به عنوان رنگدانه استفاده می‌شد.

واکنش زیر مربوط به تولید جیوه از HgS است.

$$HgS (s) + O_2 (g) \rightarrow Hg (l) + SO_2 (g) \nonumber$$

شیمیدان‌ها از ترکیب گوگرد جیوه با اکسیژن و طی واکنش گوگردزدایی (واکنش تشویه)، عنصر جیوه را تولید می‌کنند. فرار و سمی بودن جیوه این واکنش را خطرناک می‌کند به طوری‌که بسیاری از شیمیدان‌ها به دلیل قرار گیری در معرض این واکنش جان خود را از دست دادند.

به ازای ۱۰۰ گرم از سنگ معدنی سینابار چه مقدار جیوه می‌تواند توسط واکنش فوق حاصل شود؟

حل : در مرحله اول نگاهی به واکنش می‌اندازیم تا اطمینان حاصل کنیم معادله موازنه شده است یا خیر (این واکنش موازنه شده است). برای حل این سوال به روش استوکیومتری به شیوه زنجیره‌ای عمل می‌کنیم. در ابتدا گرم سینابار را به مول تبدیل کرده و با استفاده از ضرایب استوکیومتری و نسبت مولی، مول جیوه را بدست می‌آوریم. در نهایت مول جیوه را به گرم تبدیل خواهیم کرد.

$$100 g HgS \times \frac{1 mol HgS}{232.6 g HgS} \times \frac{1 mol Hg}{1 mol HgS} \times \frac{200.6 g Hg}{1 mol Hg}= 86.2 g Hg$$

گاهی در حل مسائل استوکیومتری با سوالاتی مواجه می‌شویم که ترکیبی از چندین نوع مسئله ازجمله جرم مولی و عدد آووگادرو است. به همین دلیل برای تسلط بیشتر بر حل مسائل استوکیومتری در این قسمت روش حل این چنین مسائلی را توضیح می‌دهیم.

مثال ۵

۱۰^۱۵ × ۵/۳۴ ذره اتان $$(\displaystyle C_2H_6)$$ چند گرم است؟

حل: برای حل این مثال باید از دو تبدیل واحد آووگادرو برای تبدیل ذره به مول و از تبدیل واحد مول به گرم استفاده کنیم تا مقدار گرم این تعداد ذره از اتان به دست آید، یعنی:

$$\displaystyle 5.34 \times 10^{15}\hspace{1 mm}particleshspace{1 mm}C_2H_6 \times \frac{1hspace{1 mm}molehspace{1 mm}C_2H_6}{6.022 \times 10^{23}\hspace{1 mm}particleshspace{1 mm} C_2H_6} \times \frac{30.0hspace{1 mm}ghspace{1 mm}C_2H_6}{1hspace{1 mm}molehspace{1 mm}C_2H_6}=2.66 \times 10^{-7}ghspace{1 mm}C_2H_6$$

مثال ۶

۱۰^-۳ × ۴/۳۷ گرم $$\displaystyle CH_3CH_2OH$$ برابر چند مولکول است؟

حل این سوال به صورت زیر است:

$$\displaystyle 4.37times 10^{-3}ghspace{1 mm}CH_3CH_2OH \times \frac{1hspace{1 mm}molehspace{1 mm}CH_3CH_2OH}{46hspace{1 mm}ghspace{1 mm}CH_3CH_2OH}\times\frac{6.022 \times 10^{23}\hspace{1 mm}moleculeshspace{1 mm} CH_3CH_2OH}{1hspace{1 mm}molehspace{1 mm}CH_3CH_2OH}=5.72 \times 10^{19}\hspace{1 mm}moleculeshspace{1 mm}CH_3CH_2OH$$

3. دما و فشار استاندارد در مسائل استوکیومتری

زمانی که در یک واکنش شیمیایی دما برابر صفر مطلق و فشار برابر یک اتمسفر باشد شرایط این واکنش شیمیایی را در دما و فشار استاندارد (Standard Tempreature and Pressure) یا به اختصار STP می‌گویند. شرایط STP برای گازهاست و در این شرایط یک مول از هر گاز ایده آل حجمی برابر 22/4 لیتر دارد.

از شرایط دما و فشار استاندارد برای حل مسائل استوکیومتری برای تبدیل مول به لیتر و برعکس استفاده بسیاری می‌شود البته لازم به ذکر است که این شرایط برای گازها صدق می‌کند.

مثال 1

3/2 لیتر گاز نیتروژن در شرایط استاندارد چند مول دارد؟

حل: در صورت سوال ذکر شده شرایط استاندارد به همین دلیل برای به دست آوردن تعداد مول از تبدیل واحد لیتر به مول می‌توان استفاده کرد:

$$3.2 lit N_2 \times \frac{1 mol N_2}{22/4 lit N_2}=0.143 lit N_2$$

مثال 2

تعداد مول گاز اکسیژن را با اطلاعات زیر محاسبه کنید.

• حجم گاز برابر 2/4 لیتر
• دمای گاز برابر 300 کلوین
• فشار گاز برابر 1/5 اتمسفر

حل: توجه داشته باشید در این مسئله خبری از شرایط استاندارد نیست زیرا دما برابر 300 کلوین و فشار برابر1/5 اتمسفر است. به همین دلیل نمی‌توان از تبدیل واحد در شرایط STP استفاده کرد زیرا این شرایط STP نیست. برای حل این سوال باید از رابطه زیر که برای گازهای ایده‌ال صدق می‌کند استفاده کرد.

$$PV=nRT$$

در رابط فوق:

n: تعداد مول‌های گاز

T: دمای گاز

V: حجم گاز

R: ئابت گازها که برابر $$0.082 L.atm/K^{-1}.mol^{-1}$$ است.

بنابراین تعداد مول‌های گاز براساس رابطه بالا به صورت زیر محاسبه می شود:

$$n= \frac{PV}{RT}$$

در رابطه فوق تمامی مقادیر را جایگزین می‌کنیم و تعداد مول هیدروژن را به صورت زیر به دست می‌آوریم.

$$\frac{1.5 \times 2.4}{0.082 \times 300}=\frac{3.6}{24.6}=0.146 mol O_2$$

مثال 3

حجم 10 گرم گاز هیدروژن در دمای صفر مطلق و فشار 1 اتمسفر چند میلی‌لیتر است؟

حل: از آنجا که شرایط این واکنش استاندارد است بنابراین برای به‌دست آوردن حجم گاز کافی است که گرم را به مول و بعد از آن مول را به لیتر تبدیل کنیم در این صورت حجم به دست می‌آید. پس:

$$10 g H_2 \times\frac{1 mol H_2}{2 g H_2}\times\frac{22.4 lit H_2}{1 mol H_2}= 112 lit H_2$$

توجه: به صورت سوال بار دیگر دقت کنید حجم گاز هیدروژن را در واحد میلی لیتر از ما خواسته است. در نتیجه باید پس از بدست آوردن لیتر هیدروژن طبق تبدیل واحد زیر آن را به میلی‌لیتر تبدیل کنید:

$$112 lit H_2\times\frac{10^3 ml lit H_2}{1 lit H_2}=112 \times 10^3 ml lit H_2$$

مثال4

در اثر واکنش 2 لیتر گاز اکسیژن با $$2H_2S$$ در دما و فشار استاندارد (STP) چه تعداد مولکول $$2SO_2$$ تشکیل می‌شود؟ واکنش مربوطه در زیر آورده شده است.

$${2H_2S}(g)+{3O_2}(g)⟶{2H_2O}(l)+{2SO_2}(g) \nonumber$$

حل: از آنجا که شرایط واکنش استاندارد است پس می‌توان لیتر گاز اکسیژن را به مول تبدیل کرد و با استفاده از ضرایب استوکیومتری و نسبت مولی، مول $$2SO_2$$ را بدست آورد. سپس مول را می‌توان با استفاده از عدد آووگادرو به تعداد مولکول آن تبدیل کرد. روش حل زنجیره‌ای در زیر آورده شده است.

$$2 lit O_2 \times \frac{1 mol O_2}{22.4 lit O_2} \times \frac{2 mol SO_2}{1 mol O_2} \times \frac{6.022 \times 10^{23} molecules SO_2}{1 mol SO_2}=$$

۴. چگالی در حل مسائل استوکیومتری

چگالی یا دانسیته نسبت جرم به حجم را نشان می‌دهد که با جرم رابطه مستقیم و با حجم رابطه عکس دارد. رابطه چگالی در زیر آورده شده است.

$$\rho= \frac{m}{v}$$

در رابطه فوق:

m: برابر جرم است.

V: برابر حجم است.

معمولا در حل مسائل استوکیومتری چگالی به عنوان یک واسطه عمل می‌کند و در حل سایر مسائل استوکیومتری مانند جرم مولی، حجم، شرایط استاندارد و به خصوص در محلول‌ها به عنوان یک تبدیل واحد کاربردی مورد استفاده قرار می‌گیرد. در این قسمت به مهم‌ترین مثال‌ها از کاربرد چگالی در حل مسائل استوکیومتری می‌پردازیم.

مثال 1

چه تعداد اتم هیدروژن در 500 میلی‌لیتر از آب در دمای اتاق وجود دارد؟ چگالی آب نیز برابر با $$1frac{g}{mL}$$ است. واکنش تشکیل آب از ترکیب اکسیژن با هیدروژن به صورت زیر نمایش داده شده است:

$$2H_2 + O_2rightarrow 2H_2O$$

حل: برای حل این سوال ابتدا باید حجم آب را از طریق چگالی به گرم و گرم را به مول تبدیل کرد. سپس با استفاده از ضرایب مولی از تعداد مول آب تعداد مول اکسیژن را به دست آوریم. در نهایت مول را با استفاده از عدد آووگادرو به تعداد اتم‌های تشکیل دهنده تبدیل می‌کنیم. بنابراین با استفاده از روابط تبدیل واحد داریم:

$$\displaystyle 500mL H_2O\times\frac{1g H_2O}{1mL H_2O }\times\frac{1mol H_2O}{18g H_2O} \times \displaystyle \frac{2mol H}{1mol H_2O} \times \displaystyle \frac{6.022 \times 10^{23}\text{atoms H}}{1mol}=3.35 \times 10^{25}\text{atoms H}$$

مثال 2

چگالی 20 گرم گاز کلر در شرایط STP چند گرم بر سانتی‌متر مکعب است؟ $$(Cl=35.5 g/mol)$$

حل: برای حل این سوال کافی است که حجم را به‌دست بیاوریم و جرم را که در صورت سوال داده شده است بر روی آن تقسیم کنیم. ا شرایط واکنش STP است. برای این کار به صورت زیر عمل می‌کنیم:

$$20 g Cl_2 \times \frac{1 mol Cl_2}{71 g Cl_2}\times\frac{22.4 lit Cl_2}{1 mol Cl_2}=6.30 lit Cl_2$$

کافی است که مقدار جرم را بر حجم ماده تقسیم کنیم. اما از آنجا که در صورت سوال ذکر کرده واحد چگالی گرم بر سانتی‌متر مکعب است پس باید حجم را به سانتی متر مکعب تبدیل کرد. برای این کار همان‌طور که در زیر نشان داده شده است در ابتدا لیتر را به متر مکعب و سپس متر مکعب را به سانتی‌متر مکعب تبدیل می‌کنیم. $$(1 lit= 10^{-3} m^3)$$.

$$448 lit\times\frac{10^{-3} m^3}{1 lit}\times\frac{10^6 cm^3}{1 m^3}= 448 \times 10^3 cm^3$$

اکنون با داشتن حجم در واحد سانتی‌متر مکعب و گرم گاز کلر به صورت زیر چگالی گاز کلر را برحسب سانتی‌متر مکعب به دست می‌آوریم:

$$rho_{cl}= \frac{20 g}{448 \times 10^3 cm^3}= 4.5 \times 10^{-5} g/cm^3$$

۵. مسائل استوکیومتری در محلول ها

در آزمایشگاه و صنعت محلول‌ها بسیار نقش مهمی دارند زیرا برای سنتز و تشکیل بسیاری از محصولات از محول‌سازی استفاده می‌شود. از طرفی برای محاسبات و غلظت محلول‌ها استفاده از روابط استوکیومتری کاربرد زیادی دارد. به همین دلیل به خاطر اهمیت بالای این موضوع در این قسمت مهم‌ترین مسائل استوکیومتری مربوط به محلول‌ها آورده شده است.

مثال 1

برای ساخت 500 میلی‌لیتر محلول سدیم هیدروکسید 0/10 مولار چند گرم سدیم هیدروکسید نیاز است؟

$$(Na=23\, O=16 \, H=1)$$

حل: در ابتدا باید جرم مولی سدیم هیدروکسید $$(NaOH)$$ را بدست آوریم:

$$Na+O+H= 23+16+1=40 g/mol$$

تعداد مول در یک حجم مشخصی از محلول را (به لیتر) مولاریته می‌گویند و آن را با M نشان می‌دهند.

$$M= \frac{n}{v}$$

بنابراین برای به‌دست آوردن تعداد مول، رابطه فوق به صورت زیر در می‌آید:

$$n=MV$$

پس طبق فرمول بالا اگر حجم محلول را به لیتر تبدیل کنیم و با داشتن مولاریته می توان تعداد مول سدیم هیدروکسید را در محلول بدست آوریم یعنی :

$$500 mL NaOH \times \frac{1 lit NaOH}{10^3 mL NaOH}= 0.5 lit NaOH$$

$$n_{NaOH}=0.1 \times 0.5=0.05 mol NaOH$$

در آخرین مرحله کافی است که با استفاده از جرم مولی سدیم هیدروکسید و مول آن به صورت زیر این جرم سدیم هیدروکسید را برای ساخت این محلول به‌دست آوریم.

$$0.05 mol NaOH\times\frac{40 g NaOH}{1 mol NaOH}= 2 g NaOH$$

به عبارتی برای ساخت 500 میلی‌لیتر محلول ۰/۱ مولار سدیم هیدروکسید باید 2گرم از پودر سدیم هیدروکسید را وزن کنید و در داخل بشر یا بالن ژوژه یا به طور کلی هر ظرف حجم‌دار بریزید سپس تا خط نشانه مربوط به 500 میلی‌لیتر یا سی‌سی، آب بریزید به این صورت محلول سدیم هیدروکسید ساخته می‌شود.

مثال 2

چه مقدار حجم از محلول 11 مولار هیدروکلریک اسید باید با آب رقیق شود تا 400 میلی‌لیتر محلول 3 مولار هیدروکلریک اسید ساخته شود:

حل: برای رقیق‌سازی و یا در حالت کلی به غلظت رساندن محلول‌ها از رابطه زیر استفاده می‌شود:

$$M_1V_1=M_2V_2$$

در رابطه فوق:

• $$M_1$$: مولاریته محلول اول
• $$M_2$$: مولاریته محلول دوم
• $$V_1$$: حجم محلول اول
• $$V_2$$: حجم محلول دوم

اگر محلول 11 مولار هیدروکلریک اسید را محلول شماره 1 و محلول 3 مولار را محلول شماره ۲ در نظر بگیریم در نتیجه مقدار حجم آبی که باید به هیدروکلریک اسید افزود تا رقیق شود را اندازه گیری می‌کنیم. پس طبق رابطه فوق یعنی $$V_1$$ مجهول است. مقادیر و اطلاعات داده شده در صورت سوال را در رابطه جایگزین می‌کنیم پس داریم:

$$11 \times V_1=3 \times 400$$

$$V_1=\frac{3 \times 400}{11}= 109 mL$$

پس باید به محلول 11 مولار هیدروکلریک اسید 109 میلی‌لیتر آب اضافه کرد تا به اندازه محلول 3 مولار رقیق شود.

مثال 3

در 0/5 مول اگزالیک اسید $$(C_2H_2O_4)$$ چه تعداد اتم کربن وجود دارد؟

حل: حل این مسئله هم مانند سایر مسائل مربوط به عدد اووگادرو در ترکیبات جامد است. برای پاسخ به این سوال کافی است که در ابتدا تعداد مول اگزالیک اسید را در عدد آووگادرو به صورت زیر ضرب کنیم تا تعداد اتم های آن به دست آید، پس داریم:

$$0.5 mole C_2H_2O_4 \times \frac{6.022 \times 10^{23} atoms C_2H_2O_4 }{1 mol C_2H_2O_4}= 0.5 \times 6.022 \times 10^{23}atoms C_2H_2O_4$$

از آنجا که در هر مولکول ترکیب اگزالیک اسید طبق فرمول شیمیایی آن دو اتم کربن وجود دارد بنابراین باید پاسخ فوق را در 2 ضرب کنیم. بنابراین تعداد اتم‌های کربن در 0/5 مول اگزالیک اسید برابر خواهد بود با:

$$0.5 \times 6.022 \times 10^{23}atoms C_2H_2O_4 \times 2=6.022 \times 10^{23}atoms C$$

۶. درصد خلوص در حل مسائل استوکیومتری

معمولا درصد خلوص برای صنایع و آزمایشگاه‌هایی که خلوص و نتیجه کار از حساسیت بالایی برخودار است بسیار مورد استفاده قرار می‌گیرد. در هر ترکیبی مقداری ناخالصی وجود دارد که تنها بخش خلوص آن در واکنش مورد نظر شرکت می‌کند. در ادامه با انواع مثال در رابطه با به کار بردن درصد خلوص در حل مسائل استوکیومتری بیشتر آشنا خواهیم شد.

مثال۱

درصد خلوص نمونه $$Mg(OH)_2$$ را در صورتی که ۲/۵۶۸ گرم از آن برای تیتراسیون نیاز به ۲۸/۴۵ میلی‌لیتر فسفریک اسید$$(H_3PO_4)$$ ۰/۶۶۹۵ مولار داشته باشد را محاسبه کنید.

اطلاعات مسئله: جرم مولی منیزیوم هیدروکسید برابر ۵۸/۳ گرم بر مول است. واکنش تیتراسیون منیزیم هیدروکسید با فسفریک اسید به صورت زیر است:

$$2H_3PO_4 + 3 Mg(OH)_2rightarrow 6H_2O +Mg_3(PO_4)_2$$

حل: برای پاسخ به این سوال در ابتدا باید وزن منیزیم هیدروکسید را به صورت زیر به دست آورید.

$$38.45 mL H_3PO_4 \times \frac{1 lit H_3PO_4}{10^3 mL H_3PO_4}\times\frac{0.6695 mol H_3PO_4}{1 lit H_3PO_4}\times\frac{3 mol Mg(OH)_2}{2 mol H_3PO_4}\times\frac{58.3 g Mg(OH)_2}{1 mol Mg(OH)_2}=2.251 g Mg(OH)_2$$

جرم منیزیم هیدروکسیدی که از رابطه فوق به‌دست آمد جرم خالص آن است زیرا در واکنش تنها ماده خالص در واکنش شرکت می‌کند. جرمی هم که در صورت سوال آورده شده مربوط به کل جرم ماده منیزیم هیدروکسید (خالص + ناخالص) است. فرمول درصد خلوص به صورت زیر نمایش داده شده است:

بنابراین با جایگزینی مقادیر در رابطه فوق و ضرب آن در ۱۰۰ درصد خلوص منیزیم هیدروکسید در تیتراسیون با فسفریک اسید به‌دست می‌آید، پس داریم:

$$\frac{2.251}{2.568} \times 100=87.7$$

مثال ۲

در صورت واکنش ۴ گرم آلومینا یا آلومینیوم اکسید $$(Al_2O_3)$$ با خلوص ۹۰ درصد با سدیم هیدروکسید چند اتم سدیم آلومینات $$(NaAlO_2)$$ وجود دارد؟

اطلاعات مسئله: جرم مولی سدیم، آلومینیوم و اکسیژن به ترتیب برابر ۲۳، ۲۷ و ۱۶ گرم بر مول است.

همچنین واکنش ترکیب آلومینیوم اکسید با سدیم هیدروکسید به صورت زیر است:

$$Al_2O_3.2H_2O(s) + NaOH(aq)\rightarrow NaAlO_2(aq) + H_2O(l)$$

 حل: برای حل این مسئله استوکیومتری باید از تبدیل واحد گرم به مول، ضرایب مولی، درصد خلوص و در نهایت عدد آووگادرو استفاده کنید.

یادآوری: قبل از اینکه شروع به حل کردن مسئله کنید به معادله شیمیایی نگاهی بیندازید در صورتی که معادله موازنه نشده بود باید آن را موازنه کرد. واکنش فوق موازنه شده نیست زیرا تعداد اتم‌های اکسیژن، هیدروژن و آلومینیوم در دو طرف واکنش با هم برابر نیستند. بنابراین نخستین گام موازنه کردن واکنش است که به صورت زیر نشان داده شده می‌شود:

$$Al_2O_3.2H_2O(s) +2 NaOH(aq)\rightarrow 2NaAlO_2(aq) + 3H_2O(l)$$

در ادامه برای به‌دست آوردن تعداد اتم‌های سدیم آلومینات به صورت زیر عمل می‌کنیم:

$$4 g Al_2O_3\times\frac{90 g Al_2O_3}{100 g Al_2O_3} \times \frac{1 mol Al_2O_3}{102 g Al_2O_3}\times\frac{2 mol NaAlO_2}{1 mol Al_2O_3} \times\frac{6.022 \times 10^{23} atomes NaAlO_2 }{1 mol NaAlO_2}= 4.2 times10^{22}atomes NaAlO_2$$

۷. بازده درصدی و مسائل استوکیومتری

مفهوم بازده درصدی در واکنش‌های شیمیایی به این معناست که در اثر ترکیب واکنش‌دهنده‌ها با هم چه مقدار فرآورده مورد نظر حاصل می‌شود. در مورد بازده درصدی نکاتی وجود دارد که خالی از لطف نیست به آن‌ها هم در این قسمت گریزی بزنیم، این نکات عبارتند از:

• در عمل واکنشی وجود ندارد که بازده درصد آن ۱۰۰ باشد به عبارتی امکان‌پذیر نیست که همه واکنش‌دهنده‌ها به فرآورده‌‌ها تبدیل شوند.
• در واکنش‌هایی که برگشت‌پذیر هستند نمی‌توان انتظار بازده درصد بالایی داشت زیرا فراورده‌ها به طور پوسته به واکنش‌دهنده‌ها تبدیل می‌شوند.
• برخی از محصولات ممکن است در اثر جداسازی و خالص‌سازی ازجمله فیلتراسیون و تقطیر جدا شوند.
• ممکن است در حین واکنش اصلی واکنش جانبی هم نیز رخ بدهد. واکنش جانبی یعنی واکنشی که در آن ماده یا ناخالصی در ماده با گاز در هوا واکنش می‌دهد.
• بازده عملی یعنی مقدار فراورده‌ای که در حقیقت از واکنش به دست می‌آید.
• بازده نظری یعنی مقدار فراورده‌ای که از محاسبات به صورت تئوری به دست می‌آید.
• برای به دست آوردن بازده درصدی باید طبق رابطه زیر عمل کرد:

مثال ۱

در اثر واکنش ۲ کیلوگرم نقره نیترات با پتاسیم یدید در صورتی‌که بازده درصد این واکنش ۶۰ درصد باشد چند کیلوگرم نقره‌ یدید به‌دست می‌آید؟ $$(Ag= 107.9\, N=14\, O=16\, k=39\, I= 126.9)$$. واکنش نقره نیترات با پتاسیم یدید به صورت زیر است.

$$AgNO3 + KI ⟶ AgI + KNO3$$

حل: این مسئله به صورت زنجیره‌ای به شکل زیر حل می‌شود (واکنش مورد نظر موازنه شده است):

$$2 Kg AgNO_3 \times \frac{1000 g AgNO_3}{1 Kg AgNO_3} \times \frac{1 mol AgNO_3}{ 169.9 g AgNO_3}\times\frac{1 mol AgI}{1 mol AgNO_3}\times\frac{234.8 g AgI}{1 mol AgI} \times \frac{1 kg AgI}{10^3 g AgI} \times \frac{60 kg AgI}{100 kg AgI}= 1.66 kg AgI$$

مثال ۲

واکنش مثال قبل را در نظر بگیرید. در اثر افزودن ۱۰ سانتی‌متر مکعب از محلول ۱ مول بر ۱ دسی‌متر مکعب نقره نیترات به محلول پتاسیم یدید طی واکنش جانشینی دوگانه رسوب نقره یدید تشکیل،‌ جداسازی و خشک می‌شود. وزن این رسوب برابر ۲ گرم اندازه‌گیری شد. در اثر این واکنش بازده درصدی رسوب نقره یدید را محاسبه کنید.

حل: برای این سوال در ابتدا مانند روش زیر تعداد مول نقره نیترات را با استفاده از مولاریته به دست آورید.

نکته: از آنجا که حجم در صورت سوال برحسب سانتی‌متر مکعب داده شده است پس باید حجم را در مولاریته به سانتی‌متر مکعب تبدیل کنیم تا زمانی که غلظت (مولاریته) برای به‌دست آوردن تعداد مول در حجم ضرب می‌شود هم واحد باشند و با هم ساده بشوند.

$$n_{AgNO_3}=1frac{mol}{dm^3}\times\frac{10^3 dm^3}{1m^3}\times\frac{1 m^3}{10^6 cm^3} \times 10=0.01 mol AgNO_3$$

از آنجا که نسبت مولی نقره نیترات و نقره یدید برابر ۱:۱ است بنابراین تعداد مول نقره یدید هم برابر ۰/۰۱ خواهد بود. حال با محاسبه جرم مولی نقره یدید و با داشتن تعداد مول آن می‌توان به کمک تبدیل واحد زیر مقدار تئوری جرم این رسوب را به دست آورد، پس داریم:

$$m_{AgI}= 0.01 mol AgI \times \frac{234.8 g AgI}{1 mol AgI}\simeq 2.35 g AgI$$

این مقداری که از واکنش فوق به دست آمده است برابر جرم تئوری بوده که در عمل این مقدار برابر ۲ گرم ماسبه شده است. حال از تقسیم مقدار عملی بر نظری بازده درصدی را به دست می‌آوریم پس خواهیم داشت:

$$\frac{2}{2.35} \times 100=85.1$$

۸. گرمای واکنش در مسائل استوکیومتری

واکنش‌های شیمیایی برای انجام دادن واکنش نیاز به دریافت انرژی دارند یا اینکه برخی از واکنش‌های شیمیایی گرما آزاد می‌کنند. در برخی از مسائل استوکیومتری گرمای واکنش نیز مطرح می‌شود به همین دلیل در این قسمت به مثال‌هایی در این رابطه می‌پردازیم.

مثال ۱

در اثر واکنش نیتروژن با هیدروژن برای تشکیل آمونیاک طبق واکنش زیر انرژی آزاد می‌شود. محاسبه کنید که در اثر واکنش ۲۲۲/۴ گرم نیتروژن با هیدروژن چند کیلوژول انرژی آزاد می‌شود؟

$$N_2(g) + 3 H_2(g) → 2 NH_3(g)\, ΔH = −91.8 kJ$$

برای حل این سوال مانند زیر عمل می‌کنیم:

$$224 g N_2\times\frac{1 mol N_2}{28 g N_2}\times\frac{-91.8 KJ}{1 mol N_2}= -729 KJ$$

مثال ۲

واکنش زیر را در نظر بگیرید:

$$N_2(g) + O_2(g) → 2NO(g) \, ΔH = 180.6 kJ$$

طبق واکنش فوق در صورتی که ۵۵۸ کیلوژول انرژی مصرف شود چند گرم اکسید نیتروژن می‌تواند تولید شود؟

حل:

$$558 \mathrm{~kJ} \times \frac{2 \mathrm{ mol NO}}{180.6 \mathrm{~kJ}} \times \frac{30.0 \mathrm{~g} \mathrm{NO}}{1 \mathrm{mol NO}}=185 \mathrm{~g} \mathrm{NO}$$

حل مسائل استوکیومتری به روش تناسب

یکی از روش‌های رایج برای حل مسائل شیمی روش تناسب است که اغلب در زمان‌های گذشته از آن استفاده می‌شد. اما اکنون به دلیل سریع بودن روش استوکیومتری این روش بیشتر مورد استفاده قرار می‌گیرد البته این بدان معنا نیست که از روش تناسب استفاده نمی‌شود. در ادامه چندین مثال آورده شده که حل آن‌ها به روش تناسب است تا با این روش نیز برای حل مسائل شیمی آشنا شوید.

مثال۱

واکنش زیر را در نظر بگیرید، از ترکیب چند گرم بوتان، ۱۰ گرم گاز کربن دی‌اکسید به وجود می‌آید؟

$$2C_4H_{10} + 13O_2rightarrow 8CO_2 + 10 H_2O$$

حل: برای حل کردن این موضوع می‌توان گفت که واکنش ۲ مول بوتان با اکسیژن، ۸ مول کربن دی‌اکسید تولید می‌کند و هر کربن دی‌اکسید برابر ۲۸ گرم است. از طرفی هر مول بوتان ۵۸ گرم دارد. بنابراین طبق این توضیحات حل این مسئله روش تناسب به صورت زیر خواهد بود:

در جدول بالا می‌بینیم که در ستون مربوط به بوتان ۵۸ گرم در تعداد مول آن یعنی ۲ ضرب می‌شود همین موضوع هم برای ستون مربوط به کربن‌دی اکسید هم اتفاق می‌افتد. در ردیف بعد مقدار گرمی که باید بوتان مصرف شود تا ۱۰ گرم گاز کربن‌دی‌اکسید به وجود آید به صورت مجهول نوشته می‌شود که در نهایت به صورت طرفین وسطین به صورت در می‌آید:

$$352 \times x= 112 \times 10$$

با توجه به رابطه فوق مقدار $$x$$ به صورت زیر محاسبه می‌شود:

$$x= \frac{112 \times 10}{352}=3/18 g$$

بنابراین از واکنش ۳/۱۸ گرم بوتان با اکسیژن، ۱۰ گرم کربن دی‌اکسید حاصل می‌شود.

مثال ۲

از ترکیب ۵ مول سولفید روی با اکسیژن طبق واکنش زیر چند گرم اکسید روی تشکیل می‌شود؟

$$2ZnS+3O_2→2ZnO+2SO_2$$

حل: برای حل این سوال نیز جدول تناسب رسم می‌کنیم و در هر ستون واحد مربوطه را قرار می‌دهیم. از آنجا که در صورت سوال مول سولفید روی را داده و برحسب گرم مقدار اکسید روی را می‌خواهد بنابارین در ستون مربوط به سولفید روی واحد مول و در ستون مربوط به سولفید روی واحد گرم را قرار می‌دهیم.

با طرفین وسطین کردن نسبت‌های تناسبی $$x$$ به صورت زیر محاسبه می‌شود:

$$$$2 times x= 79.5 times 2 times 5$$$$

از رابطه فوق مقدار $$x$$ برابر ۳۹۷/۵ گرم خواهد بود.

سایر مسائل استوکیومتری ازجمله چگالی،‌ عدد آووگادرو و غیره که در این مطلب به آن‌ها پرداخته شد به همین شکل به صورت تناسب می‌توانند حل شوند.

جمع بندی

استوکیومتری روابط کمی میان جرم، تعداد مول و تعداد ذره‌های تشکیل دهنده واکنش‌دهنده و فرآورده را در معادله شیمیایی که موازنه شده است را بررسی می‌کند. در این مطلب حل ۸ مسئله استوکیومتری ازجمله جرم مولی، عدد آووگادرو، چگالی را با ذکر مثال توضیح دادیم. همچنین مسائل استوکیومتری در شیمی را با ذکر مثال به روش تناسب حل کردیم. لازم به ذکر است که معمولا برای دقت و سرعت عمل بالا پیشنهاد می‌شود از روش زنجیره‌ای یا نردبانی برای مسائل استوکیومتری استفاده کرد. هرچند روش تناسب هم یک روش قدیمی و کاملا صحیح برای حل مسائل استوکیومتری به شمار می‌رود.

سوالات متداول در رابطه با حل مسائل استوکیومتری

در این قسمت به سوالات متداول در رابطه با حل مسائل استوکیومتری پاسخ داده شده است.

مسائل استوکیومتری به چه مسائلی می‌گویند؟

مسائل استوکیومتری مسائلی هستند که روابط کمی میان جرم،‌ تعداد مول و ذره‌های تشکیل دهنده مواد شرکت‌کننده در واکنش را بررسی می‌کنند و از طریق حل مسائل استوکیومتری می‌توان درصد خلوص، تعداد اتم‌های واکنش‌دهنده، بازده درصدی،‌ تعداد مول‌ها و جرم واکنش‌دهنده را به دست آورد. همچنین با استفاده از روابط استوکیومتری همه این مقادیر قابل تبدیل به هم هستند. یعنی می‌توان جرم مولی را به گرم و برعکس تبدیل کرد.

ثابت‌های استوکیومتری چه اعدادی هستند؟

ثابت‌های استوکیومتری که نقش بسیار مهمی را در حل مسائل استوکیومتری دارند همان ضرایب واکنش‌دهنده‌ها و فرآورده‌ها در معادله‌های شیمیایی موازنه شده هستند. این ضرایب یا ثابت‌ها تعداد مول‌های موادی را که در طی واکنش مصرف یا تولید می‌شوند را نشان می‌دهند.

نقش موازنه در حل مسائل استوکیومتری چیست ؟

در حل مسائل استوکیومتری اغلب به ضرایب یا ثابت های استوکیومتری نیاز داریم که برای داشتن آن‌ها باید معادله شیمیایی مذکور موازنه شده باشد. به همین دلیل موازنه نقش مهمی را در حل این چنین مسائل در شیمی ایفا می‌کند.

سریع ترین روش حل مسائل استوکیومتری چه روشی است ؟

معمولا سریع‌ترین و بهترین روش حل مسائل استوکیومتری روش زنجیره‌ای یا نردبانی است که با استفاده از تبدیل واحد داده‌ها به صورت زنجیره‌ای مسئله را حل می‌کند.