بازده درصدی واکنش در شیمی – به زبان ساده

مقدار نسبی واکنش‌دهنده‌ها و فرآورده‌هایی که در یک معادله شیمیایی موازنه شده وجود دارند را به طور معمول با نام «مقادیر استوکیومتری» (Stoichiometric Amounts) می‌شناسند. در بسیاری از موارد، در محاسبات مقادیر فرآورده‌های تولیدی، فرض بر این است که تمامی مقادیر مورد نیاز برای واکنش، با نسبت‌های استوکیومتری فراهم هستند. اما در این آموزش قصد داریم تا مواردی را بیان کنیم که در آن‌ها، چنین شرایطی برقرار نباشند و واکنش‌‌دهنده‌ها با نسبت‌های استوکیومتری حضور نداشته باشند. در این شرایط، بحث در خصوص بازده درصدی واکنش و مباحث دیگری همچون، بازده نظری و واکنش‌دهنده‌های محدود‌کننده و اضافی مطرح می‌شوند.

مقدمه‌ای بر بازده واکنش

در شیمی، بازده واکنش به مقدار فرآورده تولیدی در یک واکنش شیمیایی می‌گویند. «بازده مطلق» (Absolute Yield) را می‌توان در واحدهای گرم یا مول (بازده مولی) بیان کرد. بازده درصدی که با نام‌های بازده کسری و بازده نسبی نیز شناخته می‌شود، معیاری برای کارآمد بودن روش‌های سنتز است.

مقدار فرآورده‌ای که در هر واکنش شیمیایی بدست می‌آید، همواره کمتر از مقدار ماده مورد نیاز است، دلایل مختلفی برای این امر وجود دارد که برخی از آن‌ها به طور خلاصه در زیر آورده شده‌اند:

• بسیاری از واکنش‌ها به طور کامل انجام نمی‌شوند و واکنش‌دهنده‌ها همگی به فرآورده تبدیل نخواهند شد.
• ممکن است دو یا چند واکنش به طور همزمان اتفاق بیافتند و در نتیجه، مقادیری از واکنش‌دهنده‌ها به فرآورده‌هایی ناخواسته تبدیل شوند.
• در بسیاری از موارد، به هنگام جداسازی و خالص‌سازی فرآورده‌ها از مخلوط واکنش، هدررفت مواد از جمله فرآورده‌ها را خواهیم داشت.
• وجود ناخالصی در مواد واکنش‌دهنده را نیز می‌توان به عنوان عاملی مهم در کاهش بازده واکنش در نظر گرفت.

واکنش‌دهنده محدودکننده و اضافی

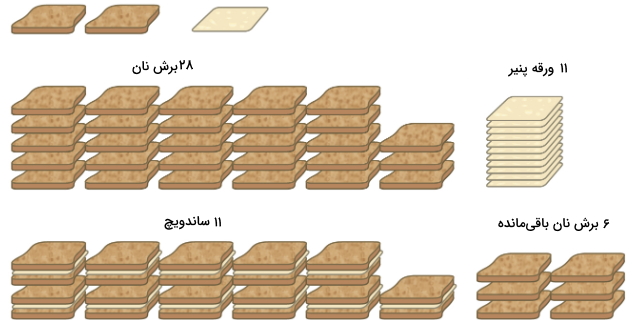
برای اینکه بخواهیم بازده واکنش را با زبانی بسیار ساده بیان کنیم، باید با مثال‌هایی ساده به ارائه این مطلب بپردازیم. فرض کنید بخواهیم به کمک نان تُست، ساندویچ‌های پنیری درست کنیم به گونه‌ای که با هر برش پنیر، نیاز به دو برش نان تست داشته باشیم. در اینصورت، رابطه کلی برای تهیه ساندویچ را به صورت زیر خواهیم نوشت:

۱ ورقه پنیر + دو برش نان تست = ۱ ساندویچ

به عبارت دیگر، نسبت‌های استوکیومتری برای تهیه این ساندویچ، به صورت ۲ به ۱ خواهند بود. فرض می‌کنیم که ۲۸ برش نان و ۱۱ ورقه پنیر داریم. با استفاده از مواد در دسترس، می‌توان ۱۱ ساندویچ تهیه کرد چراکه با مصرف هر ۱۱ برش پنیر، شش برش نان، اضافه می‌ماند. در این شرایط، می‌بینیم که تعداد ساندویچ‌های تهیه شده، توسط تعداد برش‌های پنیر محدود می‌شوند و برش‌های نان نیز در اینجا، با مقادیر اضافی وجود دارند.

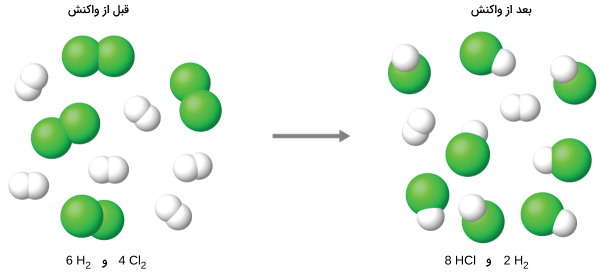
حال این مفهوم را در یک واکنش شیمیایی بررسی می‌کنیم. واکنش هیدروژن و کلر را در نظر بگیرید که به تولید هیدروژن کلرید ختم می‌شود:

$$\mathrm{H}_{2}(s)+\mathrm{Cl}_{2}(g) \longrightarrow 2 \mathrm{HCl}(g)$$

واکنش موازنه شده بالا نشان می‌دهد که هیدروژن و کلر با نسبت ۱ به ۱ با یکدیگر واکنش می‌دهند. اگر این واکنش‌دهنده‌ها، با مقادیر متفاوتی در یک واکنش حضور داشته باشند، یکی از آن‌ها به طور کامل به مصرف می‌رسد و در نتیجه،‌ تولید فرآورده، محدود به مقدار این واکنش‌دهنده خواهد بود. این واکنش‌دهنده موسوم به «واکنش‌دهنده محدود‌کننده» (Limiting Reactant) است و واکنش دهنده دیگر، «واکنش‌دهنده اضافی» (Excess Reactant) نام دارد.

فیلم آموزش فرآورده و واکنش‌ دهنده + ویژگی‌ و کاربرد (رایگان) در فرادرس

کلیک کنید

مشخص کردن واکنش‌دهنده‌های محدود‌کننده و اضافی در یک واکنش، نیازمند محاسبه مقادیر مولی و مقایسه آن‌ها با مقادیر استوکیومتری در معادله موازنه شده است. به طور مثال، فرض کنیم در واکنش بالا، ۳ مول $$H_2$$ و ۲ مول $$Cl_2$$ داشته باشیم. در نتیجه، نسبت هیدروژن به کلر به صورت نسبت ۳ به ۲ یا ۱/۵ به ۱، خواهد بود. این نسبت، بیشتر از نسبت ۱ به ۱ استوکیومتری است.

بنابراین، هیدروژن در این واکنش به صورت اضافی وجود دارد و کلر، محدود کننده واکنش خواهد بود. در این واکنش، تمامی ۲ مول کلر و همچنین، ۲ مول از ۳ مول هیدروژن به مصرف می‌رسند. در این شرایط، ۱ مول هیدروژن بدون واکنش باقی خواهد ماند.

روشی جایگزین برای تعیین واکنش‌دهنده محدود‌کننده، مقایسه مقدار فرآورده مورد انتظار در اثر واکنش کامل واکنش‌دهنده‌ها است. هر واکنش‌دهنده به طور جداگانه، بمنظور محاسبه مقدار فرآورده با نسبت‌های استوکیومتری مورد استفاده قرار می‌گیرد. واکنش‌دهنده‌ای که مقدار کمتری از فرآورده را تولید کند، به عنوان واکنش‌دهنده محدود‌کننده شناخته می‌شود. در مثال قبل، واکنش کامل هیدروژن، طبق محاسبات زیر، مقدار ۶ مول هیدروژن کلرید بدست می‌دهد:

$$\text { mol HCl }=3 \text { mol } \mathrm{H}_{2} \times \frac{2 \mathrm{mol} \mathrm{HCl}}{1 \mathrm{mol} \mathrm{H}_{2}}=6 \mathrm{mol} \mathrm{HCl}$$

همچنین، واکنش کامل کلر، ۴ مول هیدروژن کلرید تولید می‌کند.

$$\text { mol HCl }=2 \mathrm{mol} \mathrm{Cl}_{2} \times \frac{2 \mathrm{mol} \mathrm{HCl}}{1 \mathrm{mol} \mathrm{Cl}_{2}}=4 \mathrm{mol} \mathrm{HCl}$$

زمانی که ۴ مول هیدروژن کلرید تولید شود، به طور کامل،‌ تمامی مقادیر کلر به مصرف رسیده است. از آن‌جایی که مقادیر کافی هیدروژن برای تولید ۶ مول هیدروژن کلرید در دسترس بود، بنابراین، مقادیری اضافی از هیدروژن، بعد از مصرف کلر خواهیم داشت. در نتیجه، در واکنش بالا، کلر به عنوان واکنش‌دهنده محدودکننده و هیدروژن به عنوان واکنش‌دهنده اضافی در نظر گرفته می‌شوند.

مثال تعیین واکنش‌دهنده محدودکننده

ماده سیلیکون‌نیترید $$(Si_3N_4)$$، سرامیکی سخت با مقاومت دمایی بالا است که به عنوان جزئی از پره‌های توربین در موتورهای جت استفاده می‌شود. این ماده را بر اساس واکنش زیر تهیه می‌کنند:

$$3 \mathrm{Si}(s)+2 \mathrm{N}_{2}(g) \longrightarrow \mathrm{Si}_{3} \mathrm{N}_{4}(s)$$

اگر ۲ گرم $$si$$ و 1/5 گرم $$N_2$$ داشته باشیم، واکنش‌دهنده محدودکننده را تعیین کنید.

برای حل این سوال، ابتدا باید مقادیر داده شده را به مول تبدیل کنیم:

$$\begin{aligned} &\text { mol } \mathrm{Si}=2.00 \mathrm{g} \mathrm{Si} \times \frac{1 \mathrm{mol} \mathrm{Si}}{28.09 \mathrm{gSi}}=0.0712 \mathrm{mol} \mathrm{Si}\\ &\operatorname{mol} \mathrm{N}_{2}=1.50 \mathrm{g} \mathrm{N}_{2} \times \frac{1 \mathrm{mol} \mathrm{N}_{2}}{28.09 \mathrm{gN}_{2}}=0.0535 \mathrm{mol} \mathrm{N}_{2} \end{aligned}$$

حال، نسبت مولی $$Si$$ به $$N_2$$ را طبق رابطه زیر حساب می‌کنیم:

$$\frac{0.0712 \mathrm{mol} \mathrm{Si}}{0.0535 \mathrm{mol} \mathrm{N}_{2}}=\frac{1.33 \mathrm{mol} \mathrm{Si}}{1 \mathrm{mol} \mathrm{N}_{2}}$$

نسبت استوکیومتری $$Si$$ به $$N_2$$ نیز به صورت زیر خواهد بود:

$$\frac{3 \mathrm{mol} \mathrm{Si}}{2 \mathrm{mol} \mathrm{N}_{2}}=\frac{1.5 \mathrm{mol} \mathrm{Si}}{1 \mathrm{mol} \mathrm{N}_{2}}$$

با مقایسه این نسبت‌ها درمی‌یابیم که مقدار $$Si$$ که داریم، کمتر از مقدار استوکیومتری واکنش است و بنابراین، این ماده را به عنوان واکنش‌دهنده محدودکننده در نظر می‌گیریم. در روشی جایگزین، مقدار فرآورده تولیدی مورد انتظار را به ازای هر یک مقادیر واکنش‌دهنده، محاسبه می‌کنیم. بنابراین، طبق روابط زیر، میزان 0/0712 مول سیلیکیون (سیلیسیم)، 0/0237 مول سیلیکون‌نیترید تولید می‌کند:

$$\mathrm{mol} \mathrm{Si}_{3} \mathrm{N}_{4} \text =0.0712 \mathrm{mol} \mathrm{Si} \times \frac{1 \mathrm{mol} \mathrm{Si} \mathrm{N}_{4}}{3 \mathrm{mol} \mathrm{Si}}=0.0237 \mathrm{mol} \mathrm{Si}_{3} \mathrm{N}_{4}$$

درحالیکه با 0/0535 مول نیتروژن، 0/0268 مول سیلیکون‌نیترید به تولید می‌رسد:

$$\operatorname{mol} \mathrm{Si}_{3} \mathrm{N}_{4} \text =0.0535 \mathrm{mol} \mathrm{N}_{2} \times \frac{1 \mathrm{mol} \mathrm{Si}_{9} \mathrm{N}_{4}}{2 \mathrm{mol} \mathrm{N}_{2}}=0.0268 \mathrm{mol} \mathrm{Si}_{3} \mathrm{N}_{4}$$

از آن‌جایی که سیلیکون، موجب تولید مقدار کمتری از فرآورده می‌شود، در نتیجه این ماده،‌ واکنش‌دهنده محدودکننده خواهد بود.

بازده درصدی

به هنگام تعریف بازده واکنش باید دو تعریف «بازده حقیقی» (Actual Yield) و «بازده نظری» (Theoretical Yield) را بیان کنیم. مقدار فرآورده‌ای که ممکن است در یک واکنش، تحت شرایطی مشخص و با محاسبات استوکیومتری تولید شود، موسوم به بازده نظری واکنش است. مقدار فرآورده‌ای که در عمل به تولید می‌رسد را با نام بازده حقیقی (عملی) می‌شناسند. مقدار این بازده به طور معمول، کمتر از بازده نظری ذکر می‌شود.

دلایل مختلفی برای مقدار کمتر بازده حقیقی وجود دارند که از آن‌جمله می‌توان به این نکته اشاره کرد که برخی از واکنش‌ها به طور ذاتی، بهره خوبی ندارند و مواد واکنش‌دهنده، با شرکت در «واکنش‌های فرعی» (Side Reactions)، فرآورده‌های دیگری تولید می‌کنند. همچنین، برخی از واکنش‌ها به طور کامل انجام نمی‌شوند. این مورد را می‌توان در واکنش‌های اسید و بازهای ضعیف مشاهده کرد. این‌که در یک واکنش، چه میزان از بازده نظری تحقق پیدا کند را با «بازده درصدی» (Percent Yield) بیان می‌کنند و رابطه آن به صورت زیر است:

۱۰۰ × بازده نظری/ بازده عملی = بازده درصدی

بازده‌های عملی یا نظری را می‌توان به صورت مقادیر جرمی یا مولی نشان داد. همچنین اگر مواد به صورت گازی باشند، میزان بازده واکنش را می‌توان به صورت حجمی نیز بیان کرد چراکه در هر صورت، واحدهای ارائه شده، در صورت و مخرج کسر، حذف می‌شوند.

مثال

در واکنش 1/24 گرم $$CuSO_4$$ با مقدار اضافی از فلز روی، 0/392 گرم مس، طبق واکنش زیر به تولید می‌رسد. بازده واکنش (بازده درصدی) را حساب کنید.

$$\mathrm{CuSO}_{4}(a q)+\mathrm{Zn}(s) \longrightarrow \mathrm{Cu}(s)+\mathrm{ZnSO}_{4}(a q)$$

با توجه به صورت مساله درمی‌یابیم که $$CuSO_4$$، واکنش‌دهنده محدودکننده است و بازده نظری را می‌توان با روش بالا بیابیم. در ابتدا، مقدار گرم مس تولیدی از $$CuSO_4$$ را محاسبه می‌کنیم:

$$1.274 \mathrm{g} \mathrm{CuSO}_{4} \times \frac{1 \mathrm{mol} \mathrm{CuSO}_{4}}{159.62 \mathrm{g} \mathrm{CuSO}_{4}} \times \frac{1 \mathrm{mol} \mathrm{Cu}}{1 \mathrm{mol} \mathrm{CuSO}_{4}} \times \frac{63.55 \mathrm{gCu}}{1 \mathrm{mol} \mathrm{Cu}}=0.5072 \mathrm{gCu}$$

با استفاده از مقدار محاسبه شده بازده نظری و همچنین، مقدار بازده عملی در صورت مساله، بازده درصدی را حساب می‌کنیم:

$$\text {Percent Yield} =\left(\frac{0.392 \mathrm{g} \mathrm{Cu}}{0.5072 \mathrm{gCu}}\right) \times 100\\<br /> = 77.3 \text {%}$$

مثال

پتاسیم کلرات در حضور حرارت و کاتالیزور، طبق واکنش زیر تجزیه می‌شود:

$$2{KClO_3} \left( s \right) \rightarrow 2{KCl} \left( s \right) + 3 {O_2} \left( g \right)$$

در یک آزمایش، ۴۰ گرم پتاسیم کلرات را تا تجزیه کامل، حرارت داده‌ایم. میزان بازده نظری برای گاز اکسیژن را محاسبه کنید. با انجام آزمایش و جمع‌آوری گاز اکسیژن، درمی‌یابیم که میزان گاز اکسیژن تولیدی، ۱۴/9 گرم است. بازده درصدی واکنش را محاسبه کنید.

در ابتدا، بازده نظری، طبق روابط استوکیومتری محاسبه می‌شود. اما قبل از حل مساله، داده‌های سوال را فهرست می‌کنیم

• جرم $$KClO_3$$: $$40 g$$
• جرم مولی $$KClO_3$$: $$122.5 g / mol$$
• جرم مولی $$O_2$$: $$32.00 g/mol$$

با استفاده از روابط استوکیومتری، جرم فرآورده‌ها را از روی جرم واکنش‌دهنده‌ها محاسبه می‌کنیم:

$$\text{g} \: {KClO_3} \rightarrow \text{mol} \: {KClO_3} \rightarrow \text{mol} \: {O_2} \rightarrow \text{g} \: {O_2}$$

$$40.0 \: \text{g} \: {KClO_3} \times \frac{1 \: \text{mol} \: {KClO_3}}{122.55 \: \text{g} \: {KClO_3}} \times \frac{3 \: \text{mol} \: {O_2}}{2 \: \text{mol} \: {KClO_3}} \times \frac{32.00 \: \text{g} \: {O_2}}{1 \: \text{mol} \: {O_2}} = 15.7 \: \text{g} \: {O_2}$$

بنابراین، بازده نظری برای اکسیژن، 15/7 گرم است. در مرحله بعد، با استفاده از رابطه بازده درصدی می‌توان مقدار این عبارت را محاسبه کرد:

$$\text{Percent Yield} = \frac{14.9 \: \text{g}}{15.7 \: \text{g}} \times 100\% = 94.9\%$$

اگر این مطلب برای شما مفید بوده است، آموزش‌ها و مطالب زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس شیمی
• مجموعه آموزش‌های نرم‌افزارهای مهندسی شیمی
• آموزش محلول‌سازی در آزمایشگاه
• قانون هس — به زبان ساده
• فوگاسیته چیست؟ — به زبان ساده

^^