مقیاس یا طیف لیکرت و پیاده سازی در پایتون — راهنمای کاربردی

جمعآوری دادهها در تحلیلهای آماری یکی از مسئلههای جدی در آنالیز دادهها است. نحوه ثبت و امتیاز دهی به پاسخها در پرسشنامههایی که براساس متغیرهای کیفی ایجاد شدهاند، مبنایی برای ایجاد مقیاس یا طیفهای مختلف کد گذاری دادههای کیفی و تبدیل آنها به اعداد است. البته توجه داریم که تبدیل این مقادیر کیفی به عدد به معنی کمی کردن آنها نیست به همین علت نیز روشهای تحقیق و بررسی روی دادههای کیفی با کمی تفاوتهای زیادی دارند. در این میان، مقیاس یا طیف لیکرت (Likert Scale) در بین محققین از محبوبیت زیادی برخوردار است. در این نوشتار به بررسی مقیاس یا طیف لیکرت و پیاده سازی آن در پایتون خواهیم پرداخت.
همه طیفها و مقیاسهای عددی برای دادههای کیفی، دارای ترتیب (Order) هستند. به این معنی که از مقدار کوچک به بزرگ اهمیت مقادیر کیفی را مشخص میکنند. متاسفانه همه گویهها (سوالات) در پرسشنامهها دارای جهت یکسان در تعیین ویژگی مورد تحقیق نیستند. برای مثال ممکن است گویه اول رضایت از محیط کار را از کم به زیاد طبقهبندی کرده باشد و گویه دوم در مورد میزان استرس در محیط کار پرسشی مطرح کرده باشد. مشخص است که در گروه اول گویهها، مقدار ۱ نشان دهنده عدم رضایت است ولی در گروه دوم (مثلا استرس در محیط کار) مقدار ۱، نشان دهنده آسایش فرد در محیط کار است. به این ترتیب مشخص میشود که راستای پاسخها در این دو گونه سوال یکسان نیست. در چنین مواردی باید راستای پاسخها را در طیف و مقیاس اندازهگیری دادههای کیفی، یکسان و یکسو کنیم. در ادامه کدهایی از زبان پایتون را خواهید دید که برای انجام این امر تهیه شدهاند.
در این نوشتار پس از معرفی طیف لیکرت و رتبهبندی پاسخهای کیفی پرسشنامهها، با انواع طیف لیکرت نیز آشنا خواهیم شد. برای آشنایی بیشتر با اندازهگیری پایایی پرسشنامهها مطلب سنجش پایایی پرسشنامه با آلفای کرونباخ — شیوه محاسبه را مطالعه کنید. همچنین خواندن نوشتار جدول فراوانی برای دادههای کیفی و کمی — مثالهای کاربردی نیز خالی از لطف نیست.
طیف لیکرت
یکی از محبوبترین مقیاسهای کدگذاری دادههای کیفی به صورت عددی، طیف یا مقیاس لیکرت است. این مقیاس، توسط «رنیسی لیکرت» (Renisi Likert) محقق و دانشمند روانشناسی اجتماعی (Social Psychologist) در پایاننامه دکتری او در سال 1932 مطرح شد.
به کمک این طیف یا مقیاس، پاسخدهندگان به هر گویه، میزان موافقت خود را با موضوع مرتبط با گویه براساس سطوحی که از قبل تعیین شده، مشخص میکنند. این سطوح به صورت ترتیبی بوده و از کمترین تا بیشترین میزان توافق را نشان میدهند.

معمولا تعداد پنج سطح مختلف در طیف لیکرت در نظر گرفته میشود. البته هر چه تعداد سطوح بیشتر باشد، دقت اندازهگیری بالاتر خواهد رفت ولی این کار ممکن است پاسخدهنده را در انتخاب گزینه مناسب، دچار سردرگمی کند. از آنجا که بطور معمول، پنج حالت مختلف برای پاسخ در نظر گرفته شده، میانه آنها یعنی پاسخ سوم، میتواند مبنایی برای محاسبه میانه یا بیاثر بودن نظر پاسخدهنده باشد. در این حالت، طیف لیکرت پنج سطحی، میتواند گزینههای زیر را داشته باشد.
- کاملاً مخالفم
- مخالفم
- نظری ندارم
- موافقم
- کاملاً موافقم
در نهایت برای مشخص کردن امتیاز پاسخدهنده به «پرسشنامه» (Questionnaire)، مجموع یا میانگین مقادیر ثبت شده توسط طیف لیکرت برای گویهها را ثبت و مورد تحلیل قرار میدهند. گاهی ممکن است تعداد سطوح در طیف لیکرت، سه، چهار یا حتی هفت گزینه باشد. البته پرسشنامه با ۲ و حتی ۱۰ سطح نیز با مقیاس لیکرت وجود دارد. در ادامه به معرفی این دو گونه «چهار سطحی» و «پنج سطحی» از طیف لیکرت پرداخته و مزایا و معایب هر یک را بیان خواهیم کرد.
انواع طیف لیکرت
یکی از خصوصیات در طیفبندی و مقیاس لیکرت وجود فاصلههای یکسان بین گزینهها است. به این معنی که در مقیاسبندی لیکرت فرض میشود، فاصله بین گزینه «کاملاً مخالفم» و «مخالفم» با فاصله بین گزینه «نظری ندارم» و «موافقم» یکسان است. در مجموع، گزینههای طیف لیکرت، جملههایی هستند که پاسخ مخاطب را با دادن مقدار کمی (عددی) به هر یک از انتخابها، ارزیابی میکند. با همه ضعفها و اشکالاتی که در مورد طیف لیکرت وجود دارد، یکی از محبوبترین روشهای کمی سازی دادههای کیفی با «مقیاس فاصله ای» (Interval Scale) محسوب میشود.
طیف لیکرت چهار سطحی
مقیاس چهار سطحی لیکرت، در واقع مقیاسی است که حالت میانه ندارد. دلیل این امر آن است که پاسخدهنده مجبور است نظر خود را به صورت واضح بیان کند و در این بین هیچ گزینه خنثی و بیاثر مثل «نظری ندارم» دیده نمیشود. معمولا در بررسی و تحقیقات بازار، جمعآوری نظر مشتریان براساس طیف لیکرت چهار سطحی صورت میگیرد تا پاسخهای خاص دریافت شود.

مزایای استفاده از طیف لیکرت چهار سطحی به صورت فهرستوار در ادامه آورده شده است.
- در موارد خاصی که نظر و تمایل پاسخدهنده به موضوع مورد سوال، حساس و اساسی است، استفاده از مقیاس چهار سطحی لیکرت ایدهآل است.
- برای ثبت نظرات پاسخدهنده در مورد خدمات/محصولاتی که پاسخدهنده از آنها استفاده میکند، طیف لیکرت چهار سطحی مناسب است.
- معمولاً، تعداد سطوح مقیاسهای لیکرت فرد هستند و تنها در این مورد مقیاس لیکرت، چهار سطحی بوده و نقطه تعادل (خنثی) ندارد.
از معایب طیف لیکرت چهار سطحی میتوان به موارد زیر اشاره داشت:
- گاهی برای تحریف نتایج، از مقیاس لیکرت چهار سطحی استفاده میشود تا موضوعی خاص، مورد توجه قرار گیرد. زیرا هر چه تعداد سطوح کمتر باشند، امکان مطابقت نظر پاسخدهنده با یکی از گزینهها، سختتر و در نتیجه پاسخ، نادقیقتر خواهد بود. در نتیجه دقت در اندازهگیری ویژگی مورد نظر از طریق پرسشنامه کمتر خواهد شد.
- مقیاس چهار امتیازی یا چهار سطحی لیکرت، هنگامی که پاسخدهنده نظر خاصی ندارد، او را به یک انتخاب اجباری وادار میکند. هنگامی که مثلا اظهار نظری از طریق پرسشنامه سنجیده میشود، پاسخدهندهای که نظر خاصی ندارد، مجبور است در بین گزینههای «خیلی موافق»، «موافق»، «مخالف» و «خیلی مخالف»، یکی از گزینههای «موافق» یا «مخالف» را انتخاب کند که مشخص است هر کدام از آنها یک پاسخ ناصحیح محسوب میشوند.
- داده های مقیاس لیکرت پنج سطحی، دقیقتر از طیف یا مقیاس لیکرت چهار سطحی هستند زیرا انتخاب گزینه مناسب را از روی تصادف، کاهش میدهند.
- اگر پاسخدهندگان در موضوع مورد پرسش، نظری نداشته باشند، ممکن است به هیچ وجه جوابی را ثبت نکنند. در بسیاری از موارد، بهتر است بدانیم که آنها بیطرف بودهاند یا به اشتباه این طور به نظر رسیده است که به این سوال پاسخ ندادهاند.
طیف لیکرت پنج سطحی
مقیاس یا طیف لیکرت پنج سطحی شامل پنج گزینه برای پاسخ است. این پاسخها دارای یک گزینه خنثی بوده که در دو طرف آن گزینههایی مربوط به پاسخهای متوسط (On Average) و زیاد (Extreme) گنجانده شدهاند. مقیاس لیکرت پنج سطحی معمولاً برای اندازهگیری و سنجش رضایت مورد استفاده قرار میگیرد و به این ترتیب میتوان سطوح «بسیار راضی»، «راضی» «نظری ندارم»، «ناراضی» و «بسیار ناراضی» را برای آن در نظر گرفت.
مزایای استفاده از طیف لیکرت پنج سطحی در ادامه به صورت فهرستوار ذکر شده است:
- درک این مقیاس یا طیف برای پاسخدهندگان نسبت به طیف چهار سطحی آسانتر است.
- مقیاس پنج سطحی لیکرت برای مطالعات با دقت زیاد، مناسبتر است زیرا گزینه انتخابی به نظر پاسخدهنده نزدیکتر است.
- مقیاس لیکرت پنج سطحی، از لحاظ آماری دارای توزیع مناسبتر و نزدیک به توزیع نرمال خواهد بود.
از معایب طیف یا مقیاس لیکرت پنج سطحی میتوان به موارد زیر اشاره داشت:
- استفاده از این مقیاس، در بعضی مواقع نادرست است و ممکن است نتیجه تحقیق را گمراهکننده سازد.
- گاهی اوقات با استفاده از مقیاس لیکرت پنج سطحی نمیتوان نگرش نسبت به یک موضوع را به درستی اندازهگیری کرد.
- نتایج حاصل از مقیاس پنج سطحی لیکرت ممکن است با واقعیت منطبق نباشد.
معکوس کردن طیف لیکرت
بعضی اوقات، هنگام کار با پرسشنامههایی که از مقیاس لیکرت استفاده میکنند (مثلاً با سطوح کاملاً مخالفم، مخالفم، نظری ندارم، موافقم، کاملاً موافقم) لازم است امتیازدهی را معکوس کنیم. این امر بخصوص هنگامی که میخواهید پایایی پرسشنامه را تعیین کنید، بسیار ضروری است.
فرض کنید در یک پرسشنامه سوالاتی به صورت زیر مطرح شده است:
- خواندن کتاب هنگام مکالمه تلفنی در همان زمان، امری ساده و آسان است.
- وقتی موسیقی در اتاق پخش میشود، تمرکز روی خواندن مشکل است.
واضح است اگر پاسخها با طیف لیکرت باشند، و فردی به سوال اول، پاسخ «موافقم» را بدهد، نشان از تمرکز بالا برای انجام دو کار را دارد. به این ترتیب باید در پاسخ به سوال دوم نیز گزینه مخالفم را انتخاب کند. ولی هنگام جمعبندی و میانگینگیری از گویهها، اثر پاسخ سوال اول توسط پاسخ سوال دوم از بین میرود. زیرا جهت این سوالات، عکس یکدیگر هستند. بنابراین گاهی لازم است که با توجه به نحوه سوال و پاسخها، تغییری در ترتیب طیف لیکرت بدهیم. معمولا این تغییر را معکوس کردن طیف لیکرت مینامند.
در مورد سوالات با بیان مثبت، می توانیم آنها را با شیوه نمره «مخالف = ۱ ، مخالف = 2 ، خنثی = 3 ، موافق = 4 و به شدت مخالف = 5» مشخص کنیم. با این حال، برای سؤالات دارای بار منفی دیگر نمیتوان از همان سیستم امتیازدهی استفاده کرد. به این ترتیب لازم میآید که نمرات این گونه سؤالات را هنگام جمعبندی و یا امتیازدهی به پرسشنامه، معکوس کنیم. در این نوشتار برای انجام این امر از زبان برنامهنویسی پایتون کمک میگیریم. به تصویر زیر دقت کنید.
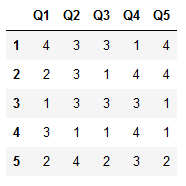
در تصویر ۱، پنچ گویه از ۵ فرد مورد پرسش قرار گرفته است با توجه به طیف لیکرت چهار سطحی (۱ = کم، ۲ = متوسط، ۳ = خوب و ۴ = عالی) میخواهیم با کد پایتونی که در ادامه مشاهده خواهید کرد، برای سوالات دوم، سوم و چهارم (Q2 و Q3 و Q4)، نمرهها را معکوس کنیم. یعنی مقدار 4 به ۱، ۲ به ۳، ۳ به ۲ و ۴ به ۱ تبدیل شوند.
کدهای معکوس کردن طیف لیکرت در پایتون
ابتدا، کتابخانههای مربوط به این برنامه را بارگذاری می کنیم. در اینجا از کتابخانههای random و pandas استفاده خواهیم کرد. برای معکوس کردن طیف لیکرت در امتیاز دهی معکوس، ابتدا دادههایی تصادفی تولید میکنیم. ولی برای کارهای عملی معمولا باید اطلاعات و نتایج پرسشنامه را از برنامهها یا محیطهای دیگر به پایتون وارد کنیم.
ممکن است منبع اطلاعاتی به صورت یک فایل اکسل یا مثلا اکسس باشد. برای اطلاع بیشتر در مورد نحوه ورود دادهها از اکسل به پایتون نوشتار کار با فایل های اکسل در پایتون — راهنمای مقدماتی را مطالعه کنید.
1from random import randint
2import pandas as pd
3
4def reverseScoring(df, high, cols):
5 '''Reverse scores on given columns
6 df = your data frame,
7 high = highest score available
8 cols = the columns you want reversed in list form'''
9 df[cols] = high - df[cols]
10 return df
11
12#Generate column names for the DataFrame (Question 1; Q1, and so on)
13colNames = ['Q' + str(i) for i in range(1,6)]
14
15#Generating data for the DataFrame
16data = [[randint(1,4) for i in xrange(5)] for i in xrange(1,11)]
17
18#Finally generating the DataFrame using Pandas
19dataf = pd.DataFrame(data, index=range(1,11), columns=colNames)
20
21#The Columns to be reversed
22cols = ['Q2', 'Q3', 'Q4']
23
24#Create a new DataFrame with reversed scores
25revFrame = reverseScoring(dataf, 5, cols)نتیجه اجرای این برنامه به صورت زیر خواهد بود. همانطور که مشخص است پاسخهای مربوط به سوالات دوم، سوم و چهارم در ستونهای Q2,Q3,Q4 معکوس شدهاند.
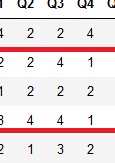
این نتایج در قالب یک مجموعه داده (DataFrame) ایجاد شده و برای تبدیل آن به یک فایل با فرمت csv، بهتر است از برنامه و کدهای زیر کمک بگیرید.
1#Saving your new dataframe as a csv (YOUR_FILENAME='filename.csv
2# & CHOSEN_SEPARATOR=',')
3to_csv(path_or_buf=YOUR_FILENAME, sep=CHOSEN_SEPARATOR)به این ترتیب یک فایل داده براساس نامی که در YOUR_FILENAME مشخص کردهاید، ایجاد خواهد شد. از این به بعد، فایل مورد نظر برای انجام تحقیقات و پژوهشهای آماری آماده است و میتواند برای محاسبه پایایی پرسشنامه، مورد بهرهبرداری قرار گیرد، زیرا همه گویهها دارای جهت یکسانی هستند.
نتیجه و جمعبندی
در این نوشتار با مقیاس یا طیف لیکرت آشنا شدیم و مقایسهای هم بین انواع آن ارائه کردیم. همچنین نحوه تغییر ساختار طیف لیکرت در زمانی که به جمعبندی و بررسی سوالات منفی و مثبت احتیاج باشد، نیز مورد بحث قرار گرفت. کدهایی هم با استفاده از زبان برنامهنویسی پایتون برای پیادهسازی این موضوع معرفی شد.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای آمار و احتمالات
- مجموعه آموزش های برنامهنویسی پایتون
- گنجینه آموزش های اکسل (Microsoft Excel)
- آموزش پایتون (Python) — مجموعه مقالات جامع وبلاگ فرادرس
- مجموعه آموزشهای نرمافزار مایکروسافت اکسل
- سنجش پایایی پرسشنامه با آلفای کرونباخ — شیوه محاسبه
^^