رگرسیون چندکی در پایتون — راهنمای کاربردی

«رگرسیون چندکی» (Quantile Regression)، یکی از روش‌های رگرسیون است که بخصوص در اقتصاد سنجی به کار گرفته می‌شود. همانطور که در دیگر نوشتارهای فرادرس با موضوع رگرسیون گفته شد، معمولا برای برآورد پارامترهای مدل رگرسیون خطی، از کمینه سازی خطای مدل به روش‌های مختلف استفاده می‌شود. در روش OLS شیوه مدل‌سازی معادله خط رگرسیونی به صورت برآورد میانگین یا امید ریاضی شرطی «متغیر پاسخ» (Response Variable) به شرط مشاهدات «متغیرهای پیشگو» (Predictor Variables) که گاهی متغیرهای مستقل نیز نامیده می‌شوند، صورت می‌گیرد.

$$\large \widehat{y}=E(Y|X)$$

در رگرسیون چندکی، به جای محاسبه میانگین شرطی متغیر پاسخ، از میانه یا چندک‌های شرطی متغیر پاسخ استفاده می‌شود.

به هر حال رگرسیون چندکی نیز یک حالت توسعه یافته از رگرسیون خطی است و زمانی که شرایط اجرای رگرسیون خطی وجود نداشته باشد، می‌توان از رگرسیون چندکی استفاده کرد.

برای آگاهی در زمینه محاسباتی رگرسیون خطی یک و چند متغیره بهتر است مطالب رگرسیون خطی — مفهوم و محاسبات به زبان ساده و رگرسیون خطی چندگانه (Multiple Linear Regression) — به زبان ساده را بخوانید. البته خواندن مطلب تحلیل واریانس (Anova) — مفاهیم و کاربردها نیز خالی از لطف نیست.

رگرسیون چندکی (Quantile Regression)

زمانی که توابع شرطی چندک‌های متغیر پاسخ مورد نیاز باشد، روش رگرسیون چندکی مناسب است. یکی از مزایای استفاده از رگرسیون چندکی نسبت به روش «معمول رگرسیون کمترین مربعات» (OLS)، پایداری در مقابل مقدارهای پرت (Outliers) یا دورافتاده است.

فیلم آموزش درس رگرسیون 1 – رگرسیون خطی در فرادرس

کلیک کنید

شکل و شیوه محاسبات رگرسیون چندکی با روش‌های معمول رگرسیونی کاملا متفاوت است. در روش رگرسیون معمولی (OLS) با استفاده از ضرب داخلی، به یک زیر فضا می‌رسیم و در عمل به کمک جبرخطی قادر به برآورد پارامترهای مدل رگرسیون خطی خواهیم شد. در حالیکه در رگرسیون چندکی چنین ساختاری وجود ندارد و روش حل مانند روش‌های برنامه ریزی خطی (روش سیمپلکس) است.

این روش توسط «راجر ویلیام کونکر» (Roger Willima Koenker) دانشمند آمریکایی در رشته اقتصاد سنجی در سال 1978 معرفی شد. او بعدها در سال ۲۰۰۵ کتاب Quantile Regression را در انتشارات کمبریج منتشر کرد که باعث شهرت و همه‌گیر شدن این روش رگرسیونی شد.

قبل از آنکه رگرسیون چندکی را مورد بررسی قرار دهیم، باید در مورد چندک‌ها و خصوصیاتشان اطلاعات بیشتری داشته باشیم.

چندک‌ها (Quantiles)

فرض کنید $$Y$$ یک متغیر تصادفی با تابع توزیع تجمعی $$F_Y(y)=P(Y\leq y)$$ است. چندک $$\tau$$ام متغیر $$Y$$ به صورت زیر تعریف می‌شود.

$$\large Q_{Y}(\tau)=F_{Y}^{-1}(\tau)=\inf\left\{ y:F_{Y}(y)\geq\tau\right\}$$

در اینجا $$\tau$$ مقداری بین 0 و ۱ در نظر گرفته می‌شود. به این ترتیب مشخص است که مثلا منظور از چندک 0.1، کوچکترین مقدار از مقادیر $$y$$ است که مقدار تابع توزیع تجمعی بزرگتر از 0.1 است. برای پیدا کردن چندک $$\tau$$ام از روشی که در ادامه معرفی می‌شود استفاده خواهیم کرد.  «تابع زیان» (Loss Function) را به صورت زیر در نظر می‌گیریم.

 $$\large {\displaystyle \rho _{\tau }(y)=y(\tau -\mathbb {I} _{(y<0)})}$$

منظور از $$\mathbb{I}_{(y<0)}$$ تابع نشانگر (Indicator Function) است. به این معنی که مقدار این تابع برای مقدارهای کوچکتر از صفر برابر با ۱ و برای بقیه مقدارها، صفر است. به این ترتیب برای پیدا کردن چندک، از کمینه‌سازی امید ریاضی $$Y-u$$ نسبت به $$u$$ استفاده می‌کنیم. بنابراین خواهیم داشت.

$$\large {\displaystyle {\underset {u}{\min }}E(\rho _{\tau }(Y-u))={\underset {u}{\min }}\left\{(\tau -1)\int _{-\infty }^{u}(y-u)dF_{Y}(y)+\tau \int _{u}^{\infty }(y-u)dF_{Y}(y)\right\}}$$

با استفاده از مشتق‌گیری و با فرض اینکه جواب برای کمینه‌سازی همان $$q_{\tau}$$ (چندک $$\tau$$ام) باشد، می‌توانیم بنویسیم.

$$\large 0=(1-\tau)\int_{-\infty}^{q_{\tau}}dF_{Y}(y)-\tau\int_{q_{\tau}}^{\infty}dF_{Y}(y)$$

در نتیجه با توجه به پاسخ معادله بالا، خواهیم داشت:

$$\large 0=F_{Y}(q_{\tau})-\tau$$

و در نتیجه مشخص است که:

$$\large F_{Y}(q_{\tau})=\tau$$

به این ترتیب می‌توانیم چندک $$\tau$$ام را مطابق با روشی که برمبنای کمینه‌سازی تابع زیان بیان شد بیابیم زیرا این رابطه بیانگر همان رابطه $$F_{Y}^{-1}(\tau)$$ است.

مثال

فرض کنید متغیر تصادفی گسسته $$Y$$ مقدارهای $$1,2,\cdots,9$$ را با احتمالات یکسان اختیار می‌کند. می‌خواهیم میانه این متغیر تصادفی را پیدا کنیم. در این حالت داریم $$\tau=0.5$$. از آنجایی که تابع احتمال یکنواخت و گسسته در نظر گرفته شده، احتمال رخداد هر یک از مقدارهای متغیر تصادفی برابر با $$\frac{1}{9}$$ است.

مقدار مورد انتظار (امید ریاضی) تابع زیان به صورت زیر در خواهد آمد.

$$\large L(u)=\frac{(\tau-1)}{9}\sum_{y_{i}<u}(y_{i}-u)+\frac{\tau}{9}\sum_{y_{i}\geq u}(y_{i}-u)\\ \large =\frac{0.5}{9}\left(-\sum_{y_{i}<u}(y_{i}-u)+\sum_{y_{i}\geq u}(y_{i}-u)\right)$$

اگر $$u=3$$‌ در نظر گرفته شود، مقدار $$L(u)$$ تقریبا برابر با رابطه زیر برابر خواهد بود.

$$\large {\displaystyle L(3)\propto \sum _{i=1}^{2}-(i-3)+\sum _{i=3}^{9}(i-3)=[(2+1)+(0+1+2+...+6)]=24}$$

اگر فرض کنیم که مقدار $$u$$ هر بار یک واحد افزایش می‌یابد، آنگاه مقدار امید ریاضی تابع زیان برای مقدارهای کمتر از ۴ به میزان $$(3)-(6)=-3$$ واحد کاهش خواهد یافت. در زمانی که $$u=5$$ باشد مقدار $$L(u)$$ بوسیله رابطه زیر محاسبه می‌شود.

$$\large L(5) \propto \sum_{i=1}^{4}i+\sum_{i=0}^{4}i=20$$

جدول زیر به بررسی مقدارهای  $$L(u)$$ برحسب مقدارهای مختلف $$u$$ پرداخته است. به این ترتیب مشخص است که میانه همان $$5$$ خواهد بود زیرا کمینه مقدار تابع $$L(u)$$ در این نقطه حاصل می‌شود.

چندک شرطی و رگرسیون چندکی

با مفهومی که از چندک و تابع زیان $$L(u)$$ درک کردیم، حالا می‌توانیم به چندک شرطی و رگرسیون چندکی بپردازیم. فرض کنید چندک شرطی $$Y$$‌ نسبت به متغیر $$X$$ را به صورت $$Q_{Y|X}(\tau)$$ نشان داده‌ایم. به کمک این رابطه رگرسیون یا مدل خطی رگرسیون چندکی را به شکل زیر بیان می‌کنیم.

$$\large Q_{Y|X}(\tau)=X\beta_{\tau}$$

به منظور برآورد پارامترهای این مدل خطی کافی است که تابع زیان معرفی شده را برحسب $$\beta$$ کمینه کنیم. بیان ریاضی این مسئله را به صورت زیر می‌نویسیم.

$$\large {\displaystyle \beta _{\tau }={\underset {\beta \in \mathbb {R} ^{k}}{\mbox{arg min}}}E(\rho _{\tau }(Y-X\beta ))}$$

حال این معادله منجر به برآورد پارامترهای $$\beta$$ به صورت زیر خواهد شد.

$$\large {\displaystyle {\hat {\beta _{\tau }}}={\underset {\beta \in \mathbb {R} ^{k}}{\mbox{arg min}}}\sum _{i=1}^{n}(\rho _{\tau }(Y_{i}-X_{i}\beta ))}$$

این مسئله کمینه‌سازی را به روش برنامه‌ریزی خطی می‌توان حل کرد. فرض کنید نمادهای زیر در نظر گرفته‌ شده‌اند.

 $$\large {\displaystyle \beta _{j}^{+}=\max(\beta _{j},0)}, \;\; {\displaystyle \beta _{j}^{-}=-\min(\beta _{j},0)}\\ \large {\displaystyle u_{j}^{+}=\max(u_{j},0)},\;\; {\displaystyle u_{j}^{-}=-\min(u_{j},0),\;\;}$$

با این نمادها در حقیقت تابع هدف در رگرسیون چندکی به شکل زیر قابل نوشتن است.

$$\large {\displaystyle {\underset {\beta ^{+},\beta ^{-},u^{+},u^{-}\in \mathbb {R} ^{2k}\times \mathbb {R} _{+}^{2n}}{\min }}\left\{\tau 1_{n}^{'}u^{+}+(1-\tau )1_{n}^{'}u^{-}|X(\beta ^{+}-\beta ^{-})+u^{+}-u^{-}=Y\right\}}$$

برای حل این مسئله می‌توان از «روش سیمپلکس» (Simplex Method) یا «روش نقاط داخلی» (Interior Point Method) استفاده کرد.

اجرای رگرسیون چندکی در پایتون

به منظور انجام محاسبات رگرسیون چندکی در پایتون باید از کتابخانه statsmodels و تابع QuantReg استفاده کنید. به همین منظور کتابخانه‌ها و ملزومات مربوط به استفاده از رگرسیون چندکی در پایتون در قطعه کدی که در ادامه قابل مشاهده است، قرار گرفته است.

فیلم آموزش رگرسیون لجستیک در یادگیری ماشین (رایگان) در فرادرس

کلیک کنید

توجه داشته باشید که در کدهای زیر منظور از quantile همان مقدار $$\tau$$ در فرمول‌ها و روابط بالا است.

1%matplotlib inline
2
3from __future__ import print_function
4import patsy
5import numpy as np
6import pandas as pd
7import statsmodels.api as sm
8import statsmodels.formula.api as smf
9import matplotlib.pyplot as plt
10from statsmodels.regression.quantile_regression import QuantReg
11
12data = sm.datasets.engel.load_pandas().data
13data.head()

در این بین از مجموعه داده Engel در کتابخانه statsmodels استفاده شده است. همانطور که خط آخر نشان می‌دهد، سطرهای اول مربوط به این مجموعه داده، با اجرای کد نمایش داده می‌شود. در ادامه بعضی از این مشاهدات قابل رویت هستند. مشخص است که این مجموعه داده مربوط به میزان درآمد و هزینه خوراک خانوار است.

1income	foodexp
20	420.157651	255.839425
31	541.411707	310.958667
42	901.157457	485.680014
53	639.080229	402.997356
64	750.875606	495.560775

اگر مقدار $$\tau$$ برابر با 0.5 در نظر گرفته شود، به رگرسیون چندکی، «مدل کمترین قدرمطلق خطا» (Least Absolute Deviation) نیز می‌گویند به این ترتیب در کد زیر مقدار q که نشان‌دهنده مرتبه چندک است برابر با 0.5 در نظر گرفته شده است.

1mod = smf.quantreg('foodexp ~ income', data)
2res = mod.fit(q=.5)
3print(res.summary())

مشخص است که ابتدا مدل توسط تابع smf.quantreg تولید شده و سپس با کمک mod.fit پارامترهای مدل برای q=0.5 برازش شده‌اند. خروجی این دستورات به صورت زیر خواهد بود.

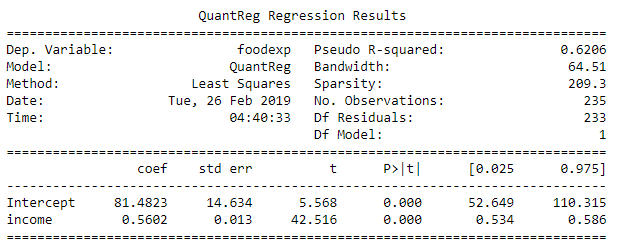
به منظور نمایش نتایج حاصل از رگرسیون چندکی، ابتدا باید داده‌ها را آماده کنیم که امکان نمایش آن‌ها در نمودار وجود داشته باشد. کدی که در ادامه مشاهده می‌کنید به این منظور تهیه شده است.

1quantiles = np.arange(.05, .96, .1)
2def fit_model(q):
3    res = mod.fit(q=q)
4    return [q, res.params['Intercept'], res.params['income']] + \
5            res.conf_int().loc['income'].tolist()
6    
7models = [fit_model(x) for x in quantiles]
8models = pd.DataFrame(models, columns=['q', 'a', 'b','lb','ub'])
9
10ols = smf.ols('foodexp ~ income', data).fit()
11ols_ci = ols.conf_int().loc['income'].tolist()
12ols = dict(a = ols.params['Intercept'],
13           b = ols.params['income'],
14           lb = ols_ci[0],
15           ub = ols_ci[1])
16
17print(models)
18print(ols)

در این برنامه برای راحتی و جداسازی نتایج حاصل از رگرسیون چندکی و رگرسیون معمولی، محاسبات مربوط به رگرسیون چندکی را در یک دیتافریم پانادس (Pandas DataFrame)  و نتایج حاصل از رگرسیون معمولی (OLS) را در ساختار داده‌ای دیکشنری (dictionary) قرار داده‌ایم. اجرای این کد نتایج را به صورت زیر نمایش خواهد داد.

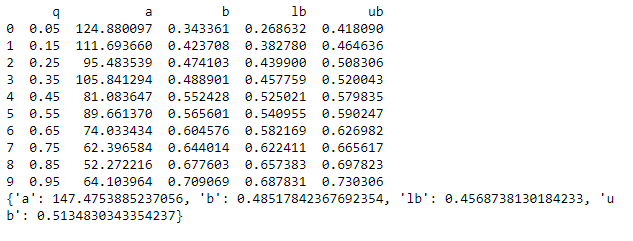
درصدها برای چندک‌ها از 0.05 تا 0.95 مشخص شده‌اند. البته به نظر می‌رسد که در کد، دامنه درصد برای چندک‌ها از 0.05 تا 0.96 است ولی از آنجایی که میزان افزایش برای آن‌ها 0.1 در نظر گرفته شده، هیچگاه به مقدار 0.96 نخواهیم رسید در نتیجه حداکثر مقدار برای $$\tau$$ در دامنه 0.05 تا 0.95 است. به این ترتیب صدک ۵ تا صدک ۹۵ ملاک ایجاد چندک‌ها خواهد بود. البته فاصله بین چندکها ۱۰٪ است. در خروجی، مقدار a عرض از مبدا و b شیب خط چندک مربوطه است. در نمودارهایی که بوسیله کد زیر ترسیم می‌شود ۱۰ نقطه اول بوسیله رگرسیون چندکی و همچنین رگرسیون خطی معمولی ترسیم و مقایسه می‌شوند.

1x = np.arange(data.income.min(), data.income.max(), 50)
2get_y = lambda a, b: a + b * x
3
4fig, ax = plt.subplots(figsize=(8, 6))
5
6for i in range(models.shape[0]):
7    y = get_y(models.a[i], models.b[i])
8    ax.plot(x, y, linestyle='dotted', color='grey')
9    
10y = get_y(ols['a'], ols['b'])
11
12ax.plot(x, y, color='red', label='OLS')
13ax.scatter(data.income, data.foodexp, alpha=.2)
14ax.set_xlim((240, 3000))
15ax.set_ylim((240, 2000))
16legend = ax.legend()
17ax.set_xlabel('Income', fontsize=16)
18ax.set_ylabel('Food expenditure', fontsize=16);

نمودار ترسیم شده به بررسی رابطه میزان درآمد و میزان سرانه خوراک پرداخته است. البته مشخص است که خطوط منقطع همان رگرسیون چندکی (Quantile Regression) و خط قرمز رنگ نیز رگرسیون خطی ساده (OLS) است. نقاط نیز به صورت دایره‌های آبی رنگ در نمودار دیده می‌شوند.

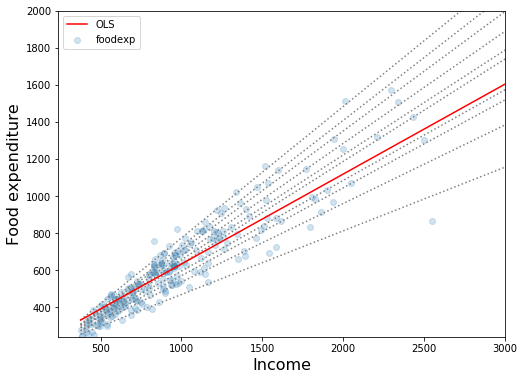
در ادامه به بررسی ضرایب مدل رگرسیونی چندکی می‌پردازیم. برای برآورد هر یک از چندک‌ها یک فاصله اطمینان ۹۵٪ نیز در نظر گرفته‌ایم. در نمودار زیر ۱۰ چندک (از چندک q=0.05 تا q=0.95) را ترسیم کرده‌ایم.

1n = models.shape[0]
2p1 = plt.plot(models.q, models.b, color='black', label='Quantile Reg.')
3p2 = plt.plot(models.q, models.ub, linestyle='dotted', color='black')
4p3 = plt.plot(models.q, models.lb, linestyle='dotted', color='black')
5p4 = plt.plot(models.q, [ols['b']] * n, color='red', label='OLS')
6p5 = plt.plot(models.q, [ols['lb']] * n, linestyle='dotted', color='red')
7p6 = plt.plot(models.q, [ols['ub']] * n, linestyle='dotted', color='red')
8plt.ylabel(r'$\beta_{income}$')
9plt.xlabel('Quantiles of the conditional food expenditure distribution')
10plt.legend()
11plt.show()

همانطور که در نمودار خواهید دید، میانگین برآورد پارامترها در روش OLS ثابت است در حالیکه در روش رگرسیون چندکی، شیب خط‌ها متفاوت است و در مثال ما برای چندک‌های پایین شیب زیاد و برای چندک‌های بالایی شیب کاهش می‌یابد. در بیشتر مواقع، نمودار ضرایب رگرسیون چندکی خارج از فاصله اطمینان برای ضرایب رگرسیونی OLS قرار می‌گیرند. خط مشکی در نمودار زیر نمایانگر ضرایب رگرسیون چندکی است و خط قرمز نیز میانگین ضریب رگرسیون OLS است. خط‌-نقطه‌ها نیز بیانگر فاصله‌های اطمینان برای هر دو گروه برآوردگرها هستند.

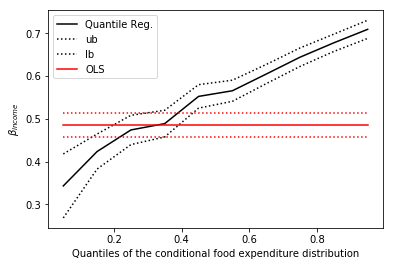
کاملا مشخص است که فاصله اطمینان برای ضرایب رگرسیون معمولی، ثابت است در حالیکه فاصله اطمینان برای ضرایب رگرسیون چندکی تابعی از درصد چندک است و با تغییر آن، طول فاصله اطمینان تغییر می‌یابد.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش های SPSS
• آموزش همبستگی و رگرسیون خطی در SPSS
• مجموعه آموزش‌های نرم‌افزارهای آماری
• آموزش یادگیری ماشین
• رگرسیون خطی — مفهوم و محاسبات به زبان ساده

^^