روشهای استاندارد سازی داده ها

قبل از انجام هر گونه تحلیلی روی دادهها، باید آنها را استاندارد کرد. بخصوص زمانی که دادهها چند بُعدی باشند. استفاده از دادههای استاندارد نشده ممکن است روی نتایج حاصل از تحلیلها اثر نامناسبی داشته باشد. به همین جهت در این نوشتار به روشهای استاندارد سازی داده ها خواهیم پرداخت.
استاندارد سازی داده
استاندارد سازی داده کمک میکند که اهمیت آنها به واحد اندازهگیریشان بستگی نداشته باشد. در نتیجه در مواردی مانند دادهکاوی و تحلیل دادههای چند متغیره از دادههای استاندارد شده استفاده میشود.
شایان ذکر است که استانداردسازی برای دادههای کمی و کیفی قابل اجرا است ولی در این نوشتار به بررسی روشهای استانداردسازی برای دادههای کمی میپردازیم و چند روش استانداردسازی را با هم مقایسه میکنیم.
نمره استاندارد Z1
برای تبدیل دادهها از توزیع نرمال به نرمال استاندارد از «نمره استاندارد» (Z-Score) استفاده میشود. حتی اگر دادهها توزیعی شبیه نرمال نیز داشته باشند باز هم تبدیل آنها به نمره استاندارد میتواند مفید باشد. رابطه بین نمره استاندارد و مقدار واقعی به صورت زیر است:
لازم به ذکر است در فرمول بالا نمره استاندارد برای داده است و میانگین و انحراف معیار برای دادهها است. با این کار ها دارای میانگین ۰ و واریانس ۱ میشوند.
اگر دادهها یک نمونه از جامعه آماری باشند، نمره استاندارد، براساس میانگین و انحراف استاندارد نمونهای محاسبه میشود.
در فرمول بالا نمره استاندارد برای داده است و میانگین و S انحراف معیار نمونه محسوب میشود. با این کار ها باز هم دارای میانگین ۰ و واریانس ۱ میشوند.
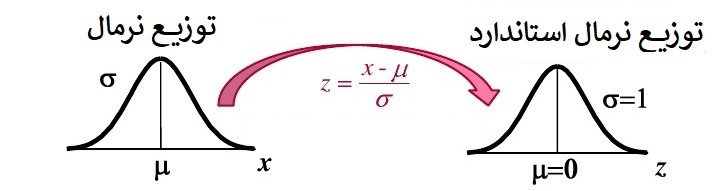
پس با این تبدیل میتوانید مقدارهایی تولید کنید که خصوصیات اصلی آنها مانند مرکز (میانگین) و مقیاس (واریانس) ثابت باشند. نمرههای استاندارد در بیشتر مواقع بین دو مقدار تا 3 قرار میگیرند.
به این ترتیب بعضی از نمرههای استاندارد، منفی (کوچکتر از میانگین) و بعضی مثبت (بزرگتر از میانگین) خواهند بود. اگر نمره استاندارد برای مقداری برابر با ۰ باشد، معلوم میشود که آن مقدار با میانگین برابر است.
همچنین از نمرات استاندارد برای مقایسه مقادیری استفاده میشود که ممکن است دارای واحدهای متفاوتی باشند.
مثال
امتیاز «مدرس الف» در دانشکده ریاضی برابر با 13 است. میانگین و انحراف استاندارد امتیازات در این دانشکده نیز به ترتیب برابر با ۱۰ و ۳ است. «مدرس ب» در دانشکده برق نیز دارای امتیاز ۱۵ است. ولی میانگین و انحراف استاندارد امتیازات در این دانشکده به ترتیب ۱۷ و ۴ است. برای مقایسه این دو مدرس توجه به امتیاز هر یک به تنهایی کافی نیست. باید مشخص شود که این امتیازات بر مبنای میانگین و انحراف استاندارد به چه ترتیب قرار میگیرند. برای آنکه بتوان تفاوت امکانات در هر دو دانشکده را نادیده گرفت (واحد اندازه امتیازات را از بین برد) از نمره استاندارد هر یک از مدرسین برای مقایسه استفاده میشود.
برای «مدرس الف» نمره استاندارد برابر با و برای «مدرس ب» نمره استاندارد برابر با است. با توجه به نمره استاندارد این دو مدرس مشخص است که «مدرس الف» از کارایی بیشتری برخوردار است.
مثال
دادههای مربوط به امتیاز 5 استاد دانشکده ریاضی و ۴ استاد دانشکده فیزیک در سطر دوم جدول قرار دارند. نمرههای استاندارد Z1 آنها نیز در سطر سوم جدول محاسبه شده است.
| دانشکده | استاد ۱- ریاضی | استاد ۲- ریاضی | استاد ۳- ریاضی | استاد ۴- ریاضی | استاد ۵- ریاضی | استاد ۱-فیزیک | استاد ۲- فیزیک | استاد ۳- فیزیک | استاد ۴-فیزیک |
| امتیاز | 12 | 13 | 11.5 | 10 | 8 | 12 | 5 | 8 | 9 |
| Z1 | 0.84 | 1.23 | 0.65 | 0.06 | -0.71 | 0.84 | 1.88 | -0.71 | -0.32 |
نکته: محاسبه میانگین و انحراف استاندارد برای Z۱ باید براساس مقدار امتیازات همه استادها انجام شود.
همانطور که دیده میشود استادهای دانشکده ریاضی دارای میانگین نمرات استاندارد بزرگتری هستند، پس استادهای این دانشکده توانمندتر هستند.
برای آشنایی بیشتر با نحوه محاسبه و خصوصیات میانگین، مطلب روش یافتن میانگین – به زبان ساده و برای انحراف معیار، مطلب واریانس و انحراف معیار — یک راهنمای جامع به زبان کاملاً ساده را مطالعه نمایید.
نمره استاندارد Z2
نمره استاندارد Z1 هم مرکز و هم مقیاس دادهها را ثابت میکند. ولی اگر هدف از استانداردسازی فقط یکسانسازی مقیاس باشد، میتوان از یک نمره بدون واحد به نام Z2 استفاده کرد که گاهی با عنوان «انحراف استاندارد اصلاح نشده وزنی» (Weighted Uncorrected Standard Deviation- USTD) نیز نامیده میشود. شیوه محاسبه آنها در ادامه آمده است.
میبایست اشاره کنیم که در این روش محاسباتی S انحراف استاندارد نمونه است.
از آنجایی که در مخرج کسر، انحراف معیار قرار دارد، این نسبت نشان میدهد که هر مقدار چند برابر انحراف معیار است، بدون آنکه نسبت به میانگین یا مرکز دادهها اصلاحی در نظر گرفته شود.
با این تبدیل، میانگین نمرات USTD یا Z2 برابر با و انحراف معیار آنها برابر با ۱ خواهد بود.

مثال
برای مثال مربوط به مدرسها با توجه به انحراف استاندارد هر دانشکده، نمره USTD «مدرس الف» برابر با و برای «مدرس ب» خواهد بود. باز هم به این ترتیب مشخص میشود که «مدرس الف» دارای امتیاز بیشتری است.
همچنین برای مثالِ استادان، نمرات استاندارد Z۲ در جدول زیر دیده میشود.
| دانشکده | استاد ۱- ریاضی | استاد ۲- ریاضی | استاد ۳- ریاضی | استاد ۴- ریاضی | استاد ۵- ریاضی | استاد ۱- فیزیک | استاد ۲- فیزیک | استاد ۳- فیزیک | استاد ۴- فیزیک |
| امتیاز | 12 | 13 | 11.5 | 10 | 8 | 12 | 5 | 8 | 9 |
| نمره استاندارد Z۲ | 4.66 | 5.05 | 4.47 | 3.89 | 3.11 | 4.66 | 1.94 | 3.11 | 3.50 |
نکته: محاسبه انحراف استاندارد برای Z2 باید براساس مقدار امتیازات همه استادها انجام شود.
با توجه به بزرگتر بودن متوسط نمرات دانشکده ریاضی، کارایی این دانشکده از دانشکده فیزیک بیشتر است.
ضمناً بر حسب نحوه محاسبه برای نمره استاندارد و میتوان مشاهده کرد که یک رابطه خطی به صورت زیر بین این دو برقرار است. در نتیجه میتوان یکی را بر مبنای دیگری محاسبه کرد.
نمره استاندارد Z3
بر اساس روش نمره استاندارد Z3، میتوان میزان نزدیکی هر یک از مقدارها را به حداکثر آنها به صورت نسبی بیان کرد. شکل محاسباتی برای آن نیز به صورت زیر است:
با این کار کران بالا برای نمرههای استاندارد Z3 برابر با ۱ خواهد بود.
اگر همه مقدارها مثبت باشند، این نسبت را به صورت درصدی نیز میتوان نشان داد. البته باید توجه داشت که برای مقدارهای منفی نمره استاندارد Z3 باید به شکلی محاسبه شود که درصد منفی ظاهر نشود. برای این کار کافی است مقدار مناسبی به همه دادهها بطور یکسان اضافه شود تا محاسبات منجر به تولید درصدهای مثبت شود. با این کار حدود نمرههای استاندارد بین ۰ تا ۱ خواهند بود.

مثال
با توجه به دادههای مثال استادهای دانشکده ریاضی و فیزیک، نمرههای استاندارد Z3 آنها در سطر سوم جدول محاسبه شده است.
| دانشکده | استاد ۱- ریاضی | استاد ۲- ریاضی | استاد ۳- ریاضی | استاد ۴- ریاضی | استاد ۵- ریاضی | استاد ۱- فیزیک | استاد ۲- فیزیک | استاد ۳- فیزیک | استاد ۴- فیزیک |
| امتیاز | 12 | 13 | 11.5 | 10 | 8 | 12 | 5 | 8 | 9 |
| نمره استاندارد Z3 | 0.92 | 1.00 | 0.88 | 0.77 | 0.62 | 0.92 | 0.38 | 0.62 | 0.69 |
با توجه به این اعداد مشخص است که در دانشکده ریاضی متوسط نمرههای استاندارد بیشتر از دانشکده فیزیک است. پس کارایی دانشکده ریاضی بهتر از دانشکده فیزیک محسوب میشود.
نکته: محاسبه مقدار حداکثر باید براساس مقدار امتیازات همه استادها انجام شود.
میانگین نمرههای استاندارد در این حالت برابر با و انحراف معیار آن نیز برابر با خواهد بود.
نکته: مقدار پراکندگی نسبی برای دادههای اصلی و نمرههای استاندارد Z3 تغییر نمیکند.
استفاده از نمره استاندارد Z3 باید با احتیاط انجام شود زیرا وجود یک مقدار خیلی بزرگ در مشاهدات، این نمره را برای بیشتر مقدارها کوچک میکند. این مقدار خیلی بزرگ، اغلب به «نقطه دور افتاده» (Outlier) معروف است.
نکته: از نمره استاندارد Z3 فقط در مواردی باید استفاده شود که دادههای کمی از نوع نسبی هستند. دادههای کمی از نوع نسبی در مقابل نوع فاصلهای قرار دارند. در این نوع داده صفر به معنی هیچ است در حالیکه داده فاصلهای، دادهای است که در آن صفر به صورت قراردادی در نظر گرفته میشود و به معنی هیچ نیست.
نمرههای استاندارد Z4 و Z5
اگر برای برآورد انحراف معیار از «دامنه تغییرات» (Range) در محاسبه نمره استاندارد Z2 استفاده شود، شکل محاسبه به صورت زیر خواهد بود.
همچنین اگر به جای فاصله از مرکز در رابطه Z1، فاصله از حداقل نمرات ملاک قرار گیرد، نمره استاندارد جدیدی به نام نمره استاندارد Z5 بوجود خواهد آمد.
با فرض اینکه مقدارها همگی مثبت باشند، نمره استاندارد Z5 بین ۰ تا ۱ تغییر خواهد کرد. البته یکی از نمرههای استاندارد حتما برابر با ۰ (برای مقدار حداقل) و یکی هم برابر با ۱ (برای مقدار حداکثر) خواهد بود.
میانگین نمرات استاندارد Z4 برابر و برای Z5 نیز برابر با خواهد بود. همچنین انحراف معیار هر دو نیز برابر است با .
مثال
برای دادههای مربوط به مثال استادها نمرات استاندارد Z4 و Z5 در سطر سوم و چهارم قرار گرفتهاند.
| دانشکده | استاد ۱- ریاضی | استاد ۲- ریاضی | استاد ۳- ریاضی | استاد ۴- ریاضی | استاد ۵- ریاضی | استاد ۱-فیزیک | استاد ۲- فیزیک | استاد ۳- فیزیک | استاد ۴-فیزیک |
| امتیاز | 12 | 13 | 11.5 | 10 | 8 | 12 | 5 | 8 | 9 |
| Z۴ | 1.50 | 1.63 | 1.44 | 1.25 | 1.00 | 1.50 | 0.63 | 1.00 | 1.13 |
| Z۵ | 0.88 | 1.00 | 0.81 | 0.63 | 0.38 | 0.88 | 0.00 | 0.38 | 0.50 |
با توجه به این اعداد مشخص است که در دانشکده ریاضی متوسط نمرههای استاندارد بیشتر از دانشکده فیزیک است. پس کارایی دانشکده ریاضی بهتر از دانشکده فیزیک محسوب میشود.
نکته: محاسبه مقدار حداکثر و حداقل باید براساس مقدار امتیازات همه استادها انجام شود.
درست به مانند نمره استاندارد Z3، نمرات استاندارد Z4 و Z5 نیز تحت تاثیر مقدارهای دور افتاده قرار خواهند گرفت. بنابراین هنگام استفاده از آنها باید وجود نقاط دور افتاده را بررسی کرد.
نکته: بین نمرههای استاندارد Z4 و Z5 یک رابطه خطی وجود دارد. بطوری که میتوان به شکل زیر یکی را برحسب دیگری محاسبه کرد.
نمره استاندارد Z6
اگر هر مقدار به حاصل جمع مقدارها تقسیم شود، یک نمره استاندارد شده بدست میآید که مجموع آنها برابر با یک و میانگینشان نیز برابر با است ولی واریانس این نمرهها مقدار ثابتی نیست. شکل محاسباتی برای Z6 به صورت زیر است:
مثال
براساس امتیاز استادها در مثال قبل، جدول زیر برای مقایسه نمرات استاندارد Z6 آنها تهیه شده است. (مجموع برای هر دانشکده به تفکیک محاسبه شده.)
| دانشکده | استاد ۱- ریاضی | استاد ۲- ریاضی | استاد ۳- ریاضی | استاد ۴- ریاضی | استاد ۵- ریاضی | استاد ۱- فیزیک | استاد ۲- فیزیک | استاد ۳- فیزیک | استاد ۴-فیزیک |
| امتیاز | 12 | 13 | 11.5 | 10 | 8 | 12 | 5 | 8 | 9 |
| Z6 | 0.35 | 0.38 | 0.34 | 0.29 | 0.24 | 0.35 | 0.15 | 0.24 | 0.26 |
با توجه به این مقدارها به نظر میرسد که استادهای دانشکده ریاضی از متوسط امتیازات بیشتری نسبت به استادهای دانشکده فیزیک برخوردارند.
نکته: محاسبه مجموع باید براساس مقدار امتیازات همه استادها انجام شود.
رتبه Z7
روش دیگر برای از بین بردن واحد اندازهگیری مقدارها، استفاده از رتبه دادهها است. اگر به جای استفاده از دادهها، رتبه آنها به کار گرفته شود، امکان مقایسه بین مقدارها با واحدهای اندازهگیری متفاوت بوجود میآید. چنانچه دادهها را از کوچک به بزرگ مرتب کنیم، مکان قرارگیری مقدارها، نشان دهنده رتبه آنها است.
مثال
براساس رتبه Z7 برای استادها در مثال قبل، جدول زیر برای مقایسه آنها تهیه شده است.
| دانشکده | استاد ۱- ریاضی | استاد ۲- ریاضی | استاد ۳- ریاضی | استاد ۴- ریاضی | استاد ۵- ریاضی | استاد ۱- فیزیک | استاد ۲- فیزیک | استاد ۳- فیزیک | استاد ۴-فیزیک |
| امتیاز | 12 | 13 | 11.5 | 10 | 8 | 12 | 5 | 8 | 9 |
| Z۷ | 7 | 9 | 6 | 5 | 2 | 7 | 1 | 2 | 4 |
با توجه به این مقدارها به نظر میرسد که استادهای دانشکده ریاضی از متوسط رتبههای بزرگتری نسبت به گروه فیزیک برخوردارند. پس دانشکده ریاضی دانشکده بهتری است.
نکته: محاسبه رتبهها باید براساس همه امتیازات انجام شود.
این روش برای استانداردسازی دادهها در مقابل نقاط دورافتاده مقاوم است و بیشتر در زمینههای آمار ناپارامتری به کار گرفته میشود. میانگین Z7 برابر با است و واریانس آن برابر با محسوب میشود.
اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزشهایی که در ادامه آمدهاند نیز برایتان کاربردی خواهند بود.
- مجموعه آموزش های SPSS
- مجموعه آموزش های Minitab
- روش یافتن میانگین – به زبان ساده
- واریانس و انحراف معیار — یک راهنمای جامع به زبان کاملاً ساده
- مجموعه آموزشهای نرمافزارهای آماری
- مجموعه آموزشهای علوم اقتصاد و مالی
^^













سلام در معادلات ساختاری مدل اندازه گیری با استفاده از داده های استاندارد داریم.محاسبه این استانداردبا فرمول زد معمولی است؟ممنونم
سلام و تشکر . چه فرقی بین استاندارد سازی دادهها و نرمال سازی دادهها وجود دارد ؟ سپاس
سلام دوست عزیز،
اغلب این دو واژه با یکدیگر و به یک معنی به کار میروند. منظور از استاندارد سازی و یا نرمال سازی، تغییر مقادیر به شکلی است که در یک بازه دلخواه تغییر کنند. برای مثال اگر به متن توجه کرده باشید، روش Z5 دادهها را در بازه ۱- تا ۱ قرار میدهد. از طرفی این روشهای استاندارد سازی، مقیاس اندازهگیری را از بین میبرند. برای مثال اگر داده ها براساس واحد کیلوگرم اندازهگیری شده باشند، زمانی که مقدار امتیاز Z score را برایشان محاسبه میکنید، واحدی برای نمایش بزرگی مقادیر وجود ندارد. این کار امکان مقایسه دادهها یا مقیاسهای مختلف (مانند کیلوگرم-تن و انس) را میدهد.
از طرفی نرمال سازی گاهی به همان معنی استاندارد سازی تعبیر شده و گاهی به معنی تبدیل توزیع دادهها به توزیع نرمال است. تبدیل کاکس باکس یکی از همین روشها محسوب میشود که دادههای چوله را به توزیع نرمال نزدیک میکند.
از این که همراه مجله فرادرس هستید سپاسگزاریم.
پیروز و تندرست باشید.
سلام
آیا می توان از مفهوم تئوری اطلاعات و آنتروپی شانون برای نرمال سازی داده ها استفاده کرد؟
سلام و درود به شما همراه مجله فرادرس،
همانطور که در مطلب نظریه اطلاع و بی نظمی — مفاهیم اولیه میتوانید بخوانید، ارتباط نزدیکی بین واریانس و اطلاع شانون وجود دارد. اگر از این جنبه به آنتروپی نگاه کنیم، میتوانیم برای استاندارد سازی در مخرج کسر مربوط به مقدار Z از اطلاع شانون (یا عکس آن) استفاده کنیم تا دادهها را استاندارد کنیم.
البته به نظر من باید هدف از انجام این کار مشخص باشد. در اکثر مواقع، استاندارد سازی باعث از بین رفتن واحد اندازهگیری شده و در نتیجه امکان مقایسه بین مقدارها با واحدهای متفاوت میسر میشود.
از اینکه به مطالب مجله فرادرس توجه دارید سپاسگزاریم.
تندرست و پیروز باشید.
سلام
لطفا منبع این مطالب رو هم ذکر کنید ممنون
سلام .میشه لطفا استاندارد سازی داده های کیفی هم بیان کنید به چه صورت هست ممنون میشم