رگرسیون کمترین زاویه (LAR Regression) — به زبان ساده

در «مدلهای خطی» (Linear Models)، روشهای رگرسیونی (Regression Methods) از اهمیت زیادی برخوردار هستند. در بسیاری از موارد به کمک این روشها قادر هستیم عمل برازش منحنی را بخصوص در زمینه «یادگیری ماشین» (Machine Learning) با دقت مناسب انجام دهیم. ولی وقتی ابعاد دادهها افزایش یابد، روشهای کلاسیک رگرسیون قابل استفاده نخواهند بود و در عمل به خاطر محدودیتهای محاسباتی برآوردیابی برای پارامترهای مدل خطی امکان پذیر نیست. در این مطلب به روشی خاصی به نام «رگرسیون کمترین زاویه» (Least Angle Regression) میپردازیم که بخصوص برای دادههای با «ابعاد بالا» (High Dimension) طراحی و در بیشتر بستههای زبانهای برنامهنویسی آماری مانند R و یا Python پیادهسازی شده است. در انتها نیز به کمک بسته نرمافزاری LAR، این روش را پیادهسازی میکنیم. برای آشنایی با شیوه محاسبات در رگرسیون خطی ساده بهتر است مطلب رگرسیون خطی — مفهوم و محاسبات به زبان ساده را مطالعه کنید.
رگرسیون کمترین زاویه (Least Angle Regression)
در سال 2004 «برد افرون» (Brad Efron) دانشمند آمار، طی مقالهای رگرسیون کمترین زاویه یا LAR را معرفی کرد. این روش بسیار شبیه رگرسیون «گام به گام پیشرو» (Forward Stepwise) عمل میکند.
در تحلیل رگرسیونی خطی چند متغیره، مدل به شکل زیر است:
در اینجا ، ضریب متغیر iام و نیز خطای تصادفی در نظر گرفته میشود. به پارامترهای ، گاهی ضرایب مدل رگرسیونی نیز میگویند. میدانیم که ها نیز متغیرهای مستقل یا توصیفی نامیده میشوند که دارای رابطه با متغیر پاسخ یعنی هستند.
در رگرسیون «گام به گام پیشرو» (Forward Step-wise)، تک تک متغیرها به صورت دنبالهای، به مدل اضافه میشوند. در هر مرحله، بهترین متغیر انتخاب شده و پارامترهای مدل برآورد میشود. متغیرهای بعدی نیز با توجه به تاثیری که در بهبود مدل خواهند داشت به همراه متغیرهای قبلی به مدل اضافه شده و مجموع مربعات خطا برای مدل محاسبه میشود. این کار تا ورود همه متغیرها به مدل ادامه پیدا میکند. با توجه به مربعات خطای بدست آمده برای هر مدل، مناسبترین مدل با توجه به «بیشبرازش» (Overfitting) انتخاب میشود.

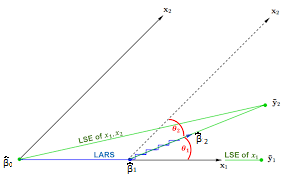
در رگرسیون کمترین زاویه، تقریبا همین روند برای انتخاب متغیرهای مدل به کار میرود. در ابتدا ضریب همه متغیرها (پارامترهای مدل) صفر در نظر گرفته میشود. یعنی در عمل هیچ مدلی با توجه به متغیرهای موجود وجود ندارد. در گام اول، متغیر مستقلی که بیشترین همبستگی با متغیر پاسخ را دارد در مدل وارد میشود. در روش LAR، به جای برآورد پارامترهای مدل رگرسیونی، ضریب متغیرها در جهت «مقدار حداقل مربعات» (Least-Squares value) از صفر دور شده و باقیماندهها برای دادهها محاسبه میشوند. همچنین حداقل مربعات خطا به منظور بررسی مدل مناسب به ثبت میرسند.
در گام بعدی، زمانی که متغیر دیگری، دارای بیشترین همبستگی با باقیماندهها باشد عمل افزایش ضریب متغیر قبلی در مدل متوقف شده و این متغیر وارد مدل میشود. به طور پیوسته مقدار ضریب متغیرهای موجود در مدل با توجه به جهت ضریب همبستگی که با متغیر پاسخ دارند از صفر دور میشوند. این گامها تا زمانی که همه متغیرها وارد مدل شوند ادامه پیدا میکنند.
همانطور که در تصویر بالا دیده میشود، ضریب و به شکلی انتخاب شدهاند که زاویه بین مقدارهای خطا و متغیر مستقل (معادل با ضریب همبستگی برای دادههای استاندارد شده) در هر مرحله کاهش مییابد. به همین علت این رگرسیون را کمترین زاویه مینامند.
این مراحل را میتوان در الگوریتم زیر مشاهده کرد.
الگوریتم رگرسیون کمترین زاویه
- استانداردسازی متغیرهای مستقل (پیشگو) به طوری که همه متغیرها دارای میانگین صفر و واریانس ۱ باشند. در این مرحله همه ضرایب برابر با صفر هستند یعنی داریم، و میزان خطا نیز به صورت محاسبه میشود.
- متغیر پیشگو براساس بیشترین همبستگی با باقیماندههای بدست آمده در مرحله قبل، انتخاب میشود.
- ضریب از صفر در جهت حداقل مربعات دور میشود تا زمانی که متغیر پیشگوی دیگری (مثلا ) بیشترین میزان همبستگی را نسبت به با باقیماندهها داشته باشد (منظور از ضرب داخلی و است که با توجه به استاندارد بودن متغیرها همان ضریب همبستگی بین آن دو خواهد بود).
- ضرایب و در جهت حداقل مربعات توام با باقیماندهها (یعنی ) تغییر میکنند تا متغیر دیگری مثل دارای بیشترین همبستگی با باقیماندهها بشود.
- این کار تا زمانی که همه متغیرها به مدل اضافه شوند تکرار میشود. با طی کردن این مراحل در انتها نیز برآورد پارامترهای مدل رگرسیون انجام پذیرفته است. تعداد تکرارها برابر است با که N تعداد مشاهدات و p نیز تعداد متغیرهای پیشگو است.
نکته: نسخهای از این الگوریتم نیز وجود دارد که با گذر مقدار برآورد پارامتر از صفر (تغییر علامت پارامتر مدل) آن را حذف میکند. این کار باعث میشود که تعداد پارامترهای مدل تقلیل یافته و مدل سادهتری بخصوص زمانی که باشد، بدست آید.
برای اجرای این الگوریتم، بستههایی در زبانهای R و Python وجود دارند که در این نوشتار فقط به بررسی و اجرای یکی از آنها در زبان برنامهنویسی R میپردازیم. «بسته» (Package) محاسباتی lars برای اجرای رگرسیون LAR در محیط R به کار گرفته میشود. کافی است این بسته را بارگذاری کنید تا به توابع مربوط به رگرسیون Lasso و LAR دسترسی داشته باشید. در این بسته مجموعه دادههای دیابت (Diabetes Dataset) نیز قرار دارد که از آن برای ایجاد مدل رگرسیونی LAR کمک میگیریم.
مثال
ابتدا مروری روی این مجموعه داده انجام میدهیم. برای این کار دستورات زیر را اجرا میکنیم.
1library(lars)
2data(diabetes)
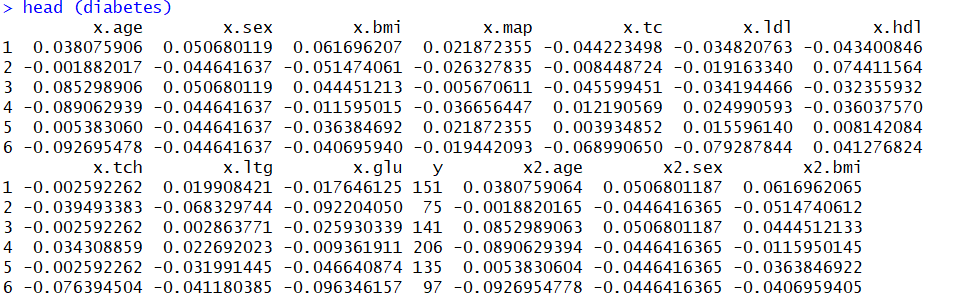
3attach(diabetes)با استفاده از دستور شش سطر اول از این دادهها مطابق با تصویر زیر نمایش داده میشود.
همانطور که قابل رویت است، متغیرهای مستقل با پیشوند x مشخص شدهاند و متغیر پاسخ نیز با y نامگذاری شده. در این مثال از متغیرهای دیگر مانند گروه x2 و ... در ایجاد مدل استفاده نشده است. مشخص است که متغیرهای مستقل، استاندارد شدهاند یعنی دارای میانگین صفر و واریانس ۱ هستند. حال به بررسی کد مربوط به رگرسیون کمترین زاویه میپردازیم. کدهای زیر به منظور تهیه یک مدل رگرسیونی برای دادههای دیابت با الگوریتم رگرسیون کمترین زاویه نوشته شدهاند.
1object <- lars(x,y,type="lar")
2object
3plot(object)
4larcoef=coef(object)
5detach(diabetes)دستور lars با توجه به متغیرهای x و y مدل رگرسیونی کمترین زاویه را با پارامتر اجرا کرده و خروجی را در object قرار میدهد. فرمان plot نیز خروجی تولید شده را به صورت نمودار ظاهر میسازد. برآورد پارامترهای مدل در هر مرحله نیز با دستور coef برای متغیر object تولید میشود.
خروجی که در متغیر object قرار گرفته را با وارد کردن نام این متغیر (همانطور که در سطر پنجم کد دیده میشود) میتوانید مانند تصویر زیر ظاهر کنید.
Call:
lars(x = x, y = y, type = "lar")
R-squared: 0.518
Sequence of LAR moves:
bmi ltg map hdl sex glu tc tch ldl age
Var 3 9 4 7 2 10 5 8 6 1
Step 1 2 3 4 5 6 7 8 9 10
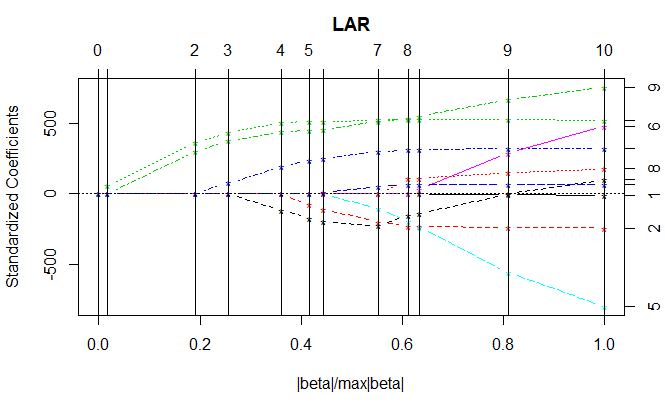
به این ترتیب با توجه به سطر Var دیده میشود که متغیر bmi (سومین متغیر) بیشترین همبستگی را با میزان دیابت داشته و با توجه به شماره ۱ در سطر Step، به عنوان اولین متغیر در مدل اضافه شده است. سپس متغیرهای بعدی به ترتیب به مدل وارد شده و متغیر age آخرین متغیری است که در آن حضور دارد. با توجه به اینکه دارای ۱۰ متغیر پیشگو هستیم، ده مرحله نیز برای اجرای الگوریتم LAR نیاز بوده است. چیزی که در این خروجی دیده نمیشود، برآورد برای پارامترهای مدل است. نمودار حاصل از خروجی برنامه ترتیب قرارگیری و حدودی برای ضرایب مدل رگرسیونی را ارائه میکند.
از آنجایی که برآورد پارامترهای مدل در رگرسیون LAR مرحله به مرحله انجام میشود، محور افقی نسبت قدر مطلق برآورد پارامتر به حداکثر قدر مطلق مقدار آن پارامتر (یعنی ) را در هر مرحله نشان میدهد. به همین علت آخرین مقدار در محور افقی برابر با ۱ خواهد بود. در محور افقی بالایی نیز مراحل الگوریتم مشخص شده است.
برای مثال در مرحله صفر همه ضرایب (پارامترهای مدل) صفر هستند. در مرحله اول متغیر bmi با شماره ۳ و سپس متغیر ltg با شماره ۹ وارد مدل میشوند. همچنین متغیر age با شماره ۱ در مرحله ۱۰ یعنی آخرین مرحله به مدل وارد شده است. ضمناً در هر مرحله نیز حدود ضرایب استاندارد مدل روی محور عمودی سمت چپ دیده میشود. برای مثال ضرایب مدل برای متغیر bmi و ltg در مرحله هفتم تقریبا برابر با ۵۰۰ خواهد بود.
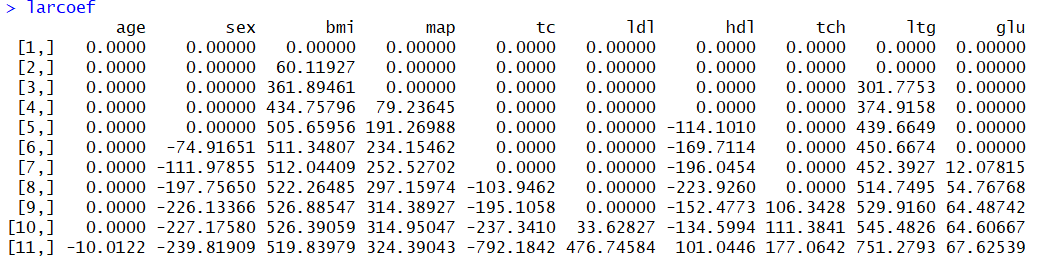
برای مشاهده مقدار دقیق پارامترهای مدل از دستور ceof از بسته lars استفاده میشود. ولی از آنجایی که مقدار این پارامترها در هر مرحله متفاوت است جدولی از برآورد پارامترها ارائه میشود که به صورت زیر خواهد بود.
باز هم دیده میشود که ضرایب متغیرها (پارامترهای مدل) در مرحله اول برابر با صفر بوده و به تدریج مقدار آنها در هر مرحله افزایش یافته و یا متغیر جدیدی به مدل اضافه میشود. البته توجه داشته باشید که این ضرایب با توجه به استاندارد کردن متغیرهای مستقل محاسبه شدهاند. همانطور که دیده میشود در مرحله آخر بزرگترین قدر مطلق ضریبها مربوط به متغیرهای tc، ltg و bmi و کمترین قدر مطلق مربوط به متغیرهای age و glu است.
حال به بررسی ضرایب رگرسیون خطی در حالت معمولی (Linear Least Square) میپردازیم. با استفاده از اجرای کدهای زیر، ضرایب مربوط به این مدل محاسبه میشوند.
1linearMod <- lm(y ~ x, data=diabetes) # build linear regression model on full data
2print(linearMod)نتایج حاصل مطابق تصویر زیر هستند.

همانطور که دیده میشود این ضرایب با ضرایب حاصل از رگرسیون کوچکترین زاویه (LAR) مطابقت دارند.
مزایا و معایب رگرسیون کمترین زاویه
با توجه به الگوریتم رگرسیون LAR میتوان مزایا زیر را برای آن برشمرد:
- محاسبات مربوط به برآورد پارامترهای مدل بسیار سریع و ساده هستند.
- این الگوریتم قابلیت استفاده در «اعتبار سنجی متقابل» (Cross Validation) را دارد و برای پیدا کردن تعداد متغیرهای بهینه مناسب است.
- اگر دو متغیر دارای همبستگی یکسانی با متغیر پاسخ باشند، ضرایب آنها نقریبا با نرخ یکسان افزایش مییابد.
- نتایج حاصل از رگرسیون LAR با نتایج حاصل از «رگرسیون لاسو» (Lasso Rergression) و دیگر شیوههای برآورد پارامترها در اکثر مواقع تطابق دارد.
- در زمانی که تعداد متغیرها بیش از تعداد مشاهدات باشد، این الگوریتم بسیار کارا بوده و به خوبی عمل برآورد پارامترها را انجام میدهد.
البته با توجه به تکراری بودن الگوریتم و استفاده از ملاک ضریب همبستگی، ممکن است وجود «نوفه» (Noise) در دادهها و همچنین وجود همخطی در متغیرهای مستقل نتایج حاصل از رگرسیون LAR را به انحراف بکشد.
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزش های SPSS
- مجموعه آموزش های داده کاوی یا Data Mining در متلب
- آموزش همبستگی و رگرسیون خطی در SPSS
- مهمترین الگوریتمهای یادگیری ماشین (به همراه کدهای پایتون و R) — بخش دوم: رگرسیون خطی
- آموزش یادگیری ماشین
- مجموعه آموزشهای نرمافزارهای آماری
- رگرسیون لاسو (Lasso Regression) — به زبان ساده
^^