انتقال جرم چیست؟ – از صفر تا صد

در مقالات قبلی مجله فرادرس پیرامون مسائل انتقال حرارت، از انتقال جرم صرف نظر کردیم. اما در کاربردهای واقعی، معمولاً در حین انتقال حرارت، انتقال جرم (Mass Transfer) نیز رخ میدهد. به عنوان مثال، حدود یکسوم گرمایی که از بدن یک فرد در حال استراحت تلف میشود، از طریق تبخیر است. انتقال جرم و انتقال حرارت از جنبههای مختلفی معادل یکدیگرند و بین معادلات آنها نیز ارتباط تنگاتنگی برقرار است. در این مقاله، روشهای انتقال جرم را مورد بررسی قرار داده و روابط اصلی آن را استخراج خواهیم کرد.
پیش از ورود به بحث انتقال جرم لازم است به این نکته توجه کنید که انتقال جرم و حرکت توده سیال (جریان سیال) دو مفهوم متفاوت هستند و نباید با هم اشتباه گرفته شوند. وجود دو ناحیه با ساختار شیمیایی متفاوت برای انتقال جرم ضروری است. به حرکت یک گونه (A Species) شیمیایی از ناحیهای با غلظت بیشتر به سمت ناحیهای با غلظت کمتر، انتقال جرم گفته میشود. در واقع، نیروی محرکه برای جریان سیال، اختلاف فشار است. حال آنکه برای انتقال جرم باید اختلاف غلظت وجود داشته باشد. به همین دلیل، نمیتوانیم در ماده همگن از انتقال جرم صحبت کنیم.
مقدمهای بر انتقال جرم
عدم توازن گونهای که در یک ماده قرار گرفته، باعث میشود توزیع آن گونه بارها و بارها تغییر کند تا توازن و برابری در آن برقرار شود. تمایل به این تغییر که از آن به عنوان نیروی محرکه هم یاد میشود، مکانیزمی را معرفی میکند که در بسیاری از پدیدههای انتقال نقش دارد.
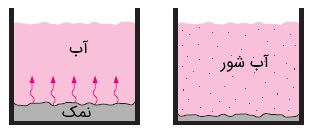
اگر غلظت هر گونه را برابر با مقدار آن گونه در واحد حجم تعریف کنیم، میتوانیم ادعا کنیم جریان گونه همیشه در جهت کاهش غلظت اتفاق میافتد. به عبارت دیگر و مطابق شکل بالا، جریان گونه از ناحیه غلیظتر به ناحیه رقیقتر برقرار است. هنگامی که مخلوطی از گازها یا مایعات دارای گرادیان غلظت، در محفظهای قرار داشته باشند، پدیده نفوذ (Diffusion) در مقیاس مولکولی از ناحیه با غلظت بالا به ناحیه دیگر رخ میدهد. سرعت جریان گونه با گرادیان غلظت که آن را به صورت تعریف میکنیم و همینطور مساحت مقطع عمود بر مسیر جریان متناسب است. در اینجا تغییرات غلظت در واحد طول و در جهت حرکت جریان سنجیده میشود.
در این رابطه، ضریب نفوذ ماده نامیده میشود و مقیاسی از سرعت نفوذ یک گونه در ماده است. علامت منفی نیز برای این است که اگر جریان در جهت مثبت برقرار شود، علامت آن مثبت باشد. توجه کنید که عبارت منفی است؛ زیرا غلظت در جهت جریان کاهش مییابد. اگر به خاطر داشته باشید، قانون فوریه در انتقال حرارت هدایتی، قانون اهم در رسانش الکتریکی و قانون نیوتن در ویسکوزیته، همگی به شکل رابطه تعریف شده بالا هستند.
برای درک بهتر فرآیند نفوذ، مخزنی را در نظر بگیرید که با کمک یک دیواره جداکننده، به دو قسمت مساوی تقسیم شده است. در ابتدا، نیمه سمت چپ مخزن، حاوی گاز نیتروژن است و در نیمه سمت راست نیز هوا (در حدود ۲۱ درصد از آن اکسیژن و مابقی نیتروژن است) وجود دارد. فشار و دما در هر دو نیمه مخزن یکسان هستند. همانطور که در شکل زیر مشاهده میکنید، مولکولهای اکسیژن و نیتروژن به ترتیب با دایرههای قرمز و سفید مشخص شدهاند.
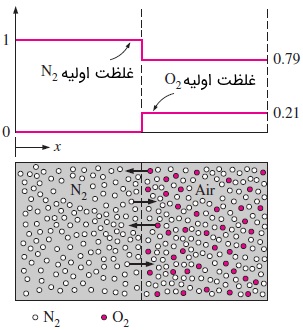
هنگامی که دیواره جدا کننده برداشته شود، مولکولهای در هوا و مولکولهای در نیمهای که از گاز نیتروژن پر بود نفوذ میکنند. پس از سپری شدن مدت زمان کافی، مخلوطی همگن از و خواهیم داشت. این فرآیند نفوذ جرمی را میتوان با در نظر گرفتن یک صفحه فرضی توضیح داد. این صفحه فرضی در شکل بالا با خطچین نشان داده شده است. مولکولهای گاز به صورت تصادفی حرکت میکنند و احتمال حرکت آنها به سمت راست یا سمت چپ با یکدیگر برابر است. به همین دلیل، در هر لحظه نیمی از مولکولهای قرار گرفته در هر سمت این خطچین، به سمت مخالف حرکت خواهند کرد. از آنجایی که غلظت در نیمه سمت چپ نسبت به سمت راست بیشتر است، تعداد مولکولهای که به سمت راست حرکت میکنند، نسبت به آنهایی که به سمت چپ میروند بیشتر است. در نتیجه، برآیند حرکت مولکولهای به سمت راست خواهد بود. از این رو، میگوییم به سمت راست منتقل شده است.
به طریق مشابه میتوانیم نشان دهیم که برآیند حرکت مولکولهای نیز به سمت چپ است و به همین دلیل میگوییم، به سمت چپ منتقل شده است. این فرآیند آنقدر ادامه مییابد تا غلظت و در سراسر مخزن یکنواخت شود و تعداد مولکولهای یا که به سمت راست حرکت میکنند، با تعداد مولکولهای همنوعشان که به سمت چپ میروند، مساوی شود. در این حالت، برآیند حرکت مولکولها از صفحه فرضی، صفر خواهد بود.
مولکولها در یک مخلوط گازی، به طور مرتب در حال برخورد با یکدیگر هستند و فرآیند نفوذ شدیداً به این برخوردها وابسته است. برخورد مولکولهای مشابه، اهمیت کمتری دارد. زیرا هر دو مولکول یکسان هستند و تفاوتی ندارد که کدام یک، از صفحه عبور کنند. اما برخورد مولکولهای غیر همسان میتواند روی سرعت نفوذ تأثیرگذار باشد. زیرا مولکولهای غیر همسان، جرم و در نتیجه، ممنتوم متفاوتی دارند. از این رو، مولکولهای سنگینتر در فرآیند نفوذ غالب خواهند بود. ضریب نفوذ و به دنبال آن، سرعت نفوذ گازها شدیداً به دما وابسته است. زیرا دما معیاری از سرعت متوسط مولکولهای گاز ارائه میدهد. بنابراین، سرعت نفوذ در دماهای بالاتر، افزایش مییابد.
انتقال جرم میتواند در مایعات و حتی جامدات نیز اتفاق بیفتد. به عنوان مثال، اگر یک لیوان آب را در اتاقی قرار دهید. پس از گذشت مدتی، به دلیل نفوذ مولکولهای آب در هوا، تمام آب تبخیر خواهد شد. این حالت، انتقال جرم مایع در گاز نامیده میشود. یک تکه یخ خشک ( جامد) به مرور زمان، کوچک و کوچکتر خواهد شد. زیرا مولکولهای در هوا نفوذ میکنند. این حالت، انتقال جرم جامد در گاز است. یک قاشق شکر ریخته شده در یک فنجان پر از چای، پس مدتی چای را شیرین میکند. زیرا مولکولهای شکر نسبت به مولکولهای آب سنگینترند و به راحتی در آنها نفوذ میکنند (انتقال جرم جامد در مایع).
حتی ممکن است انتقال جرم از گاز به مایع یا جامد هم صورت بگیرد. به عنوان مثال، نفوذ مولکولهای اکسیژن هوا در آب باعث میشود تا اکسیژن لازم برای جانداران زیر آب فراهم شود. آلایش یا داپینگ (Doping) نیمهرساناها برای ترانزیستور و حرکت مولکولهای آلاییده شده (Doped) در دماهای بالا درون نیمهرساناها هم نمونههایی از نوع انتقال جرم جامد در جامد است. شکل زیر مثالهایی از انواع انتقال جرم را نشان میدهد.
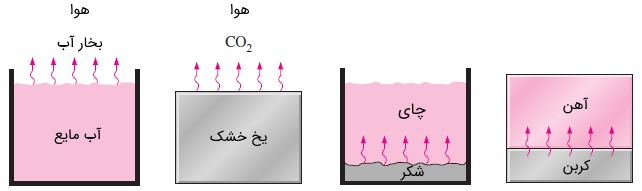
عامل دیگری که در فرآیند نفوذ تعیین کننده است، فاصله مولکولی (Molecular Spacing) نام دارد. به طور کلی هرچه این فاصله بزرگتر باشد، سرعت نفوذ بالاتر خواهد بود. بنابراین، سرعت نفوذ در گازها نسبت به مایعات و در مایعات نسبت به جامدات بسیار بیشتر است.
مقایسه انتقال جرم و انتقال حرارت
مکانیزمهای انتقال جرم و انتقال حرارت شباهت زیادی به یکدیگر دارند. به همین دلیل نیازی نیست تا زمان زیادی را برای یادگیری مباحث انتقال جرم اختصاص دهیم. در بسیاری از موارد میتوان از قرینههای موجود در مباحث انتقال حرارت برای درک بهتر مسائل انتقال جرم کمک گرفت. استفاده از این پلهای ارتباطی موجب میشود بتوانیم در تعداد زیادی از مسائل انتقال جرم برای گرفتن ایده، به دانش قبلی خودمان در زمینه انتقال حرارت رجوع کنیم. معکوس این ارتباط نیز برقرار است و با کمک دانش انتقال جرم میتوان مسائلی از انتقال حرارت را حل کرد. ماهیت جرم ذاتاً همان انرژی است و این دو، با کمک فرمول انیشیتین به یکدیگر تبدیل میشوند. در این رابطه، سرعت نور است. از این رو، جرم و حرارت دو شکل مختلف از انرژی هستند.
مفهوم دما در انتقال جرم و حرارت
نیروی محرکه برای انتقال حرارت، اختلاف دما است. در مقابل، نیروی محرک برای انتقال جرم هم اختلاف غلظت است. شاید بتوان دما را به عنوان معیاری برای «غلظت حرارت» در نظر گرفت. در این صورت، در ناحیهای با دمای بالا، تراکم و غلظت حرارت بالاست. شکل زیر را در نظر بگیرید. هم حرارت و هم جرم از ناحیههایی با غلظت بیشتر به ناحیههایی با غلظت کمتر انتقال مییابند. اگر بین دو ناحیه، هیچ اختلاف دمایی نباشد، انتقال حرارت نیز رخ نخواهد داد. به طور مشابه، اگر در گونه موجود در یک ماده، اختلاف غلظت وجود نداشته باشد نیز هیچ جرمی منتقل نمیشود.
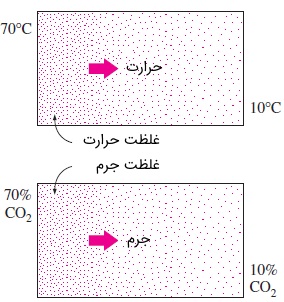
مفهوم رسانش در انتقال جرم و حرارت
همانطور که میدانید انتقال حرارت از سه طریق رسانش، جابجایی و تشعشع انجام میشود. اما برای انتقال جرم فقط دو روش رسانش (که نفوذ نامیده میشود) و جابجایی فراهم است و چیزی به اسم تشعشع جرم وجود ندارد. سرعت رسانش حرارت در جهت با گرادیان دمای در همان جهت متناسب است و قانون فوریه برای رسانش حرارتی نامیده میشود.
در رابطه بالا، ضریب رسانش حرارتی ماده و نیز سطح مقطع عمود به جهت انتقال حرارت است. به طور مشابه، سرعت نفوذ جرمی مربوط به گونه در یک ماده ایستا و در جهت ، با گرادیان غلظت در همان جهت متناسب است و با قانون نفوذ فیک (Fick's Law of Diffusion) تعریف میشود.
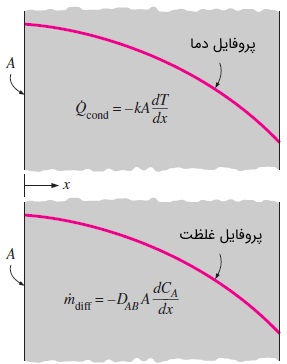
در رابطه بالا، ضریب نفوذ یا نفوذپذیری جرمی نامیده میشود و هم غلظت گونه در آن موقعیت از مخلوط است. میتوان نشان داد هر دو معادله دیفرانسیل مشابه هم هستند. بنابراین، پاسخ معادله دیفرانسیل مربوط به نفوذ جرمی از طریق پاسخ معادله رسانش حرارتی متناظر با آن قابل استخراج است. بدین منظور، باید به تشابه شرایط مرزی و ضرایب توجه شود.
مفهوم تولید گرما در انتقال جرم و حرارت
تولید گرما به تبدیل شکلی از انرژی مانند انرژی الکتریکی، شیمیایی یا هستهای به انرژی حرارتی گفته میشود. تولید گرما در ماده اتفاق میافتد و مشخصه آن نیز افزایش دما است. به طور مشابه، در برخی از مسائل انتقال جرم، واکنشهایی در داخل ماده رخ میدهد که نتیجه آن تولید یک فرآورده جدید است. بنابراین، تولید گونه، یک پدیده حجمی (Volumetric Phenomenon) است و سرعت تولید آن ممکن است در نقاط مختلف ماده با هم تفاوت داشته باشد.
این واکنشهای شیمیایی که درون ماده اتفاق میافتند، واکنشهای همگن نامیده شده و معادل تولید گرما به حساب میآیند. در مقابل، برخی واکنشهای شیمیایی دیگر، به دلیل تماس بین ماده و محیط اطراف، روی سطح ماده به وقوع میپیوندند. این واکنشها منجر به تولید گونهای در روی سطح ماده میشوند. مواردی از این قبیل، پدیده سطحی (Surface Phenomenon) نام دارند و باید مانند یک شرط مرزی با آنها رفتار شود. در مطالعات انتقال جرم چنین واکنشهایی، واکنشهای ناهمگون نامیده شده و با شار حرارتی از سطح معادل هستند.
مفهوم جابجایی در انتقال جرم و حرارت
انتقال حرارت جابجایی، شکلی از انتقال حرارت است که انتقال حرارت رسانشی (نفوذ مولکولی) و حرکت توده سیال را نیز شامل میشود. حرکت سیال موجب سرعت بخشیدن به انتقال حرارت میشود. زیرا سیال گرم نزدیک به سطح را کنار زده و سیال سرد را جایگزین آن میکند. در یک حالت حدی که در آن، حرکت توده سیال صفر میشود، جابجایی به رسانش تبدیل میشود. به طور مشابه، جابجایی جرمی (Mass Convection)، شیوهای از انتقال جرم است که بین سطح و سیال متحرک رخ میدهد و شامل نفوذ جرمی و حرکت توده سیال میشود. در اینجا هم حرکت سیال نقش زیادی در انتقال جرم دارد. زیرا سیال غلیظ نزدیک به سطح را کنار زده و آن را با سیال رقیق جایگزین میکند. در جابجایی جرمی، لایه مرزی غلظت (Concentration Boundary Layer) به شیوه مشابهی با لایه مرزی حرارتی تعریف میشود و اعداد جدید بدون بُعدی معرفی میشوند که قرینه اعداد ناسلت و پرانتل هستند.
سرعت انتقال حرارت جابجایی برای جریان خارجی را میتوان با استفاده از قانون سرمایش نیوتن بیان کرد.
در رابطه بالا، ضریب انتقال حرارت و هم اندازه سطح است. اختلاف دما در لایه مرزی حرارتی را نیز با نشان دادهایم. به طور مشابه میتوان سرعت جابجایی جرمی را نیز با رابطه زیر تعریف کرد.
در این رابطه، ضریب انتقال جرم و هم اندازه سطح است. همچنین اختلاف غلظت را در لایه مرزی غلظت با نشان دادهایم.
نفوذ جرمی چیست
براساس قانون نفوذ فیک که در سال ۱۸۵۵ میلادی معرفی شد، سرعت نفوذ یک گونه شیمیایی در نقطهای از یک مخلوط گازی (یا محلول مایع یا جامد) با گرادیان غلظت آن گونه در همان نقطه متناسب است. دو روش رایج برای بیان غلظت یک گونه وجود دارد؛ یکی غلظت جرمی و دیگری غلظت مولار.
غلظت جرمی
غلظت جرمی براساس چگالی بیان میشود و برابر با جرم در واحد حجم است. حجم کوچک را در قسمتی از یک مخلوط در نظر بگیرید. اگر چگالی جزئی هریک از گونهها () را در آن قسمت، با نشان دهیم، چگالی کل مخلوط در آن قسمت به صورت زیر نوشته میشود.
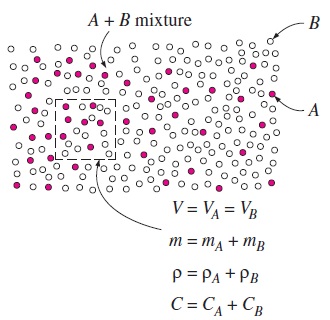
بنابراین چگالی مخلوط در هر قسمت با مجموع چگالی گونههای تشکیل دهنده آن در همان قسمت برابر است. غلظت جرمی را میتوان به صورت عددی بیبُعد و تحت عنوان کسر جرمی (Mass Fraction) و با نماد هم نشان داد. کسر جرمی هریک از گونهها به صورت زیر تعریف میشود.
توجه کنید که کسر جرمی هریک از گونهها میتواند عددی بین صفر و یک باشد. لازمه قانون پیوستگی جرم این است که مجموع کسر جرمی تمام گونههای تشکیل دهنده ترکیب، برابر با عدد یک باشد (). همچنین به خاطر داشته باشید که چگالی و کسر جرمی هر جزء تشکیل دهنده در مخلوط، در حالت کلی، در موقعیتهای مختلف تغییر میکند؛ مگر اینکه گرادیان غلظت صفر باشد.
غلظت مولار
غلظت مولار یا چگالی مولی برابر با مقداری از ماده برحسب کیلومول در واحد حجم است. بار دیگر، حجم کوچک را در قسمتی از مخلوط در نظر میگیریم. اگر غلظت مولار هریک از گونهها () را در آن قسمت، با نشان دهیم، غلظت مولار کل مخلوط در آن قسمت به صورت زیر نوشته میشود.
بنابراین، غظت مولار در هر قسمت از یک مخلوط، با مجموع غلظتهای مولار گونههای تشکیلدهنده آن در همان قسمت برابر است. همچنین میتوان غلظت مولار را به صورت عددی بدون بُعد و تحت عنوان کسر مولی بیان کرد.
در اینجا هم غلظت مولار هریک از گونهها میتواند عددی بین صفر و یک باشد و مجموع غلظتهای مولار تمام گونههای تشکیل دهنده هر مخلوط، برابر با یک است تا قانون پیوستگی جرم رعایت شده باشد (). جرم مربوط به تعداد مول را میتوان با کمک رابطه زیر و با استفاده از جرم مولی (یا جرم مولکولی) ماده () به یکدیگر مربوط ساخت.
ضمناً رابطه بالا در واحد حجمی به شکل تبدیل میشود. زیرا همانطور که میدانید، جرم هر یک کیلومول از ماده برابر با کیلوگرم است. در نتیجه، جرم کیلومول از آن ماده برابر با کیلوگرم خواهد بود. در نتیجه میتوانیم غلظتهای جرمی و مولار ماده را با رابطههای زیر به ترتیب برای هریک از گونهها و کل مخلوط، به یکدگیر تبدیل کنیم.
برای به دست آوردن جرم مولی مخلوط که با نشان داده شده است، میتوانیم به طریق زیر عمل کنیم.
رابطه بین کسرهای جرمی و مولی مربوط به هریک از گونههای این مخلوط نیز به صورت زیر است.
در این قسمت، دو روش برای بیان غلظت معرفی شد. همانطور که مشاهده کردید، هر دو روش با هم معادل هستند. از این رو، نوع خواستههای هر مسأله مشخص میکند که از کدامیک باید استفاده شود.
قانون نفوذ فیک
همانطور که میدانیم، سرعت نفوذ جرمی یک گونه شیمیایی در مادهای راکد و در یک جهت مشخص، با گرادیان غلظت محلی در همان جهت متناسب است. این رابطه خطی بین سرعت نفوذ و گرادیان غلظت در سال ۱۸۵۵ میلادی توسط فیک (Fick) به عنوان قانون نفوذ فیک و به صورت زیر تعریف شد.
شار جرمی گرادیان غلظت ثابت تناسب
ولی غلظت یگ گونه را در یک مخلوط گازی یا محلول مایع یا جامد، میتوانیم به چند شیوه از قبیل چگالی، کسر جرمی، غلظت مولار و کسر مولی بیان کنیم. پس قانون فیک را میتوان به چند روش ریاضی تعریف کرد. اما بهترین راه برای ارائه آن، به صورت گرادیان غلظت و برحسب کسر جرمی یا مولی است. یکی از فرمولهای متداول قانون فیک برای نفوذ گونه در مخلوط دوتایی و ایستای تشکیل شده از گونههای و در جهت به دو صورت زیر به ترتیب براساس غلظت جرمی و غلظت مولار نشان داده میشود.
در رابطههای بالا، شار جرمی نفوذی مربوط به گونه است و به صورت انتقال جرم از طریق نفوذ در واحد زمان و در واحد سطح مقطع عمود به جهت انتقال جرم تعریف شده و با واحد اندازهگیری بیان میشود. در رابطه بعدی نیز، شار مولی نفوذی است که به طریق مشابه و با واحد اندازهگیری تعریف میشود. شار جرمی یک گونه در یک موقعیت مشخص، با چگالی مخلوط در آن موقعیت متناسب است. توجه کنید که چگالی مخلوط دوتایی، برابر با و غلظت مولار آن نیز برابر با است و این مقادیر در حالت کلی، در قسمتهای مختلف مخلوط، متغیر است. بنابراین میتوانیم روابط زیر را بدین منظور بنویسیم.
ولی در حالت خاصی که چگالی و غلظت مولار مخلوط ثابت باشد، رابطههای قانون فیک به شکل زیر ساده میشوند.
فرض ثابت بودن چگالی یا غلظت مولار معمولاً در مورد جامدها و مایعات رقیق، معتبر است ولی در مورد مخلوطهای گازی یا محلولهای مایع غلیظ، درست نیست. برای کسب اطلاعات بیشتر در زمینه انتقال جرم و قانون فیک پیشنهاد میشود به بسته آموزش ویدیویی تحت عنوان آموزش انتقال جرم مراجعه کنید. در این بسته آموزشی، تمامی سرفصلهای انتقال جرم شامل قانون اول فیک، ضرایب نفوذ مولکولی و جذب و دفع گازها به صورت مشروح تدریس شده است. امیدواریم مطالعه مقاله حاضر و استفاده از بسته آموزش انتقال جرم در آموزش و یادگیری هرچه عمیقتر این مبحث، تأثیر مثبت داشته باشد. در ادامه این مقاله، مروری بر شرایط مرزی و همچنین انتقال جرم و حرارت به صورت همزمان داریم و چند مثال حل شده از این مفاهیم را ارائه خواهیم کرد.
مثال ۱: تعیین کسر جرمی با استفاده از کسر مولی
سؤال: ساختار اتمسفر استانداردِ خشک برحسب مول و به صورت درصد ، درصد و درصد داده شده است. کسر جرمی گونههای تشکیل دهنده هوا را محاسبه کنید.
پاسخ: جرم مولی مولکولهای ، و به ترتیب برابر با ، و کیلوگرم بر کیلومول است. در نتیجه جرم مولی هوا به صورت زیر محاسبه میشود.
حالا میتوانیم کسرهای جرمی گازهای تشکیل دهنده هوا را تعیین کنیم.
شرایط مرزی در انتقال جرم
همانطور که پیشتر هم گفتیم، معادله نفوذ جرمی، شباهت زیادی با معادله نفوذ حرارت (رسانش) دارد. در نتیجه برای تعیین توزیع غلظت هریک از گونهها در یک ماده، باید بتوانیم شرایط مرزی را نیز مقایسه کنیم. دو شرط مرزی متداول عبارتند از ۱) غلظت مشخص گونهها (که با دمای مشخص، معادل است) و ۲) شار مشخص گونهها (که با شار حرارتی مشخص، معادل است).
اما با وجود شباهت ظاهری، تفاوتی مهم بین دما و غلظت وجود دارد. دما لزوماً یک تابع پیوسته است ولی غلظت در حالت کلی اینطور نیست. به عنوان مثال، دمای دیوار و دمای هوا روی سطح دیوار، همیشه یکسان است. اما در سوی مقابل، بدیهی است که غلظت هوا در دو طرف سطح تماس آب -- هوا، تفاوت بسیاری دارد. در واقع، غلظت هوا در آب، نزدیک به صفر است. شکل زیر را در نظر بگیرید. غلظت آب در دو طرف سطح تماس آب -- هوا، حتی اگر آب در حالت اشباع باشد، با هم متفاوت است.
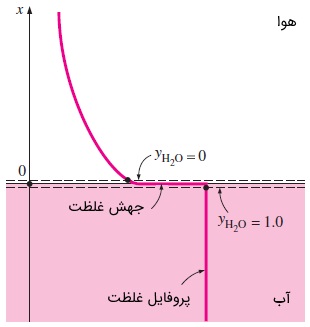
از این رو، هنگامی که میخواهیم یک شرط مرزی را تعیین کنیم، تعیین موقعیت به تنهایی کافی نیست و باید مشخص کنیم که در مورد کدام طرف سطح تماس صحبت میکنیم. بدین منظور، دو سطح فرضی را در دو طرف سطح تماس و با فاصله بینهایت نزدیک به آن، در نظر میگیریم.
با استفاده از قانون فیک، شرط مرزی شار ثابت برای گونه در حال نفوذ در مرز (در غیاب هرگونه مکش یا دمش) به صورت زیر تعریف میشود.
در رابطه بالا، و به ترتیب، شار مولی و جرمی گونه در مرز هستند. در حالتی خاص که شار جرمی برابر صفر شود ()، با سطحی نفوذناپذیر مواجه خواهیم بود که معادل رابطه زیر است.
برای اینکه بتوانیم شرط مرزیِ غلظت معلوم را لحاظ کنیم، باید غلظت گونه را در مرز بدانیم. اطلاعات لازم در این مورد را میتوان با استفاده از این اصل به دست آورد که در سطح تماس بین دو فاز از یک گونه، باید تعادل فازی برقرار باشد. در مورد سطح تماس هوا -- آب، مقادیر غلظت بخار آب در هوا را میتوان به راحتی و از طریق دادههای اشباع مانند مثال زیر تعیین کرد.
مثال ۲: کسر مولی بخار آب در سطح دریاچه
سؤال: با توجه به شکل زیر، کسر مولی بخار آب را در سطح دریاچهای که دمای آن $$\large 15\: ^\circ \text {C}$$
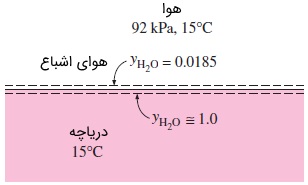
پاسخ: هوا و بخار آب را گازهای ایدهآل در نظر گرفته و از کسر مولی هوای محلول در آب صرف نظر میکنیم. با مراجعه به جداول ترمودینامیکی، فشار اشباع آب در دمای $$\large 15\: ^\circ \text {C}$$
با فرض گاز ایدهآل برای هوا و بخار آب، کسر مولی بخار آب در هوا در سطح دریاچه به صورت زیر تعیین میشود.
با صرف نظر از هوای محلول در آب، تمام دریاچه را آب مایع فرض میکنیم. اکنون میتوانیم کسر مولی آن را با تقریب به دست آوریم.
توجه کنید که غلظت مولار آب، بلافاصله در زیر سطح تماس هوا -- آب برابر درصد و بالافاصله در بالای آن، برابر درصد است. حتی با اینکه هوا در حالت اشباع فرض شده بود. بنابراین، ناپیوستگی مشهودی در غلظتها در مرز بین دو فاز وجود دارد.
انتقال جرم و حرارت به صورت همزمان
در عمل، بسیاری از فرآیندهای انتقال جرم به صورت همدما رخ میدهند. از این رو شامل هیچ انتقال حرارتی هم نمیشوند. ولی در برخی از کاربردهای مهندسی، مایعی تبخیر شده و بخار آن در گاز محیط اطراف نفوذ میکند. چنین فرآیندهایی، برای انجام عمل تبخیر نیازمند انتقال گرمای نهان تبخیر به مایع هستند. در نتیجه با انتقال همزمان جرم و حرارت مواجه هستیم.
به طور کلی، هر پدیده انتقال جرم که در حین آن، تغییر فاز (مانند تبخیر، تصعید، چگالش و ذوب) هم رخ دهد، همراه با انتقال حرارت خواهد بود. برای حل مسائلی از این دست، باید انتقال جرم و حرارت را به صورت همزمان در نظر گرفت. به عنوان مثالهایی از این پدیده میتوانیم به خشک شدن لباسها، سرمایش تبخیری، سرمایش از طریق تعریق، سرمایش با یخ خشک، احتراق قطرات سوخت و حتی پدیدههای روزمره مانند بارش برف و باران اشاره کرد. برخی از این نمونهها را در شکل زیر مشاهده میکنید.
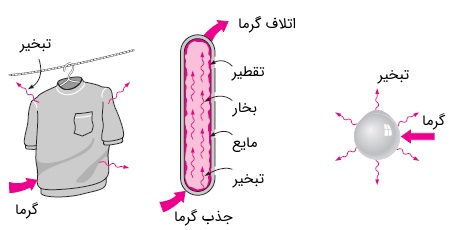
برای درک بهتر مکانیزم انتقال جرم و حرارت به صورت همزمان، تبخیر آب از یک استخر را در نظر بگیرید. فرض کنیم در ابتدا هوا و آب در دمایی یکسان قرار دارند. اگر هوا در حالت اشباع قرار داشته باشد (یعنی رطوبت نسبی برابر با $$\large \phi =100 \text {%}$$
تفاوت غلظت، نقش نیروی محرکه را برای انتقال جرم بازی میکند و موجب حرکت آب به سمت هوا خواهد شد. ولی اول باید تبخیر آب صورت بگیرد. بدین منظور، آب باید گرمای نهان تبخیر را جذب کرده باشد. در ابتدا تمام گرمای لازم برای تبخیر از آب نزدیک به سطح تماس دریافت میشود. زیرا هیچ اختلاف دمایی بین آب و هوای اطراف آن وجود ندارد و از این طریق هیچ انتقال حرارتی رخ نمیدهد. گرمایی که آب نزدیک به سطح تماس، به منظور تبخیر از دست میدهد، موجب کاهش دمای آن میشود. این موضوع باعث کاهش فشار اشباع و در نتیجه، کاهش غلظت بخار در سطح تماس خواهد شد.
از این رو، اختلاف دمایی در قسمت بالای آب و همینطور بین هوای اطراف و آب به وجود میآید. همین اختلاف دما برای انتقال حرارت از هوا و عمقهای پایینتر به سطح آب کافی است. به شکل زیر توجه کنید.
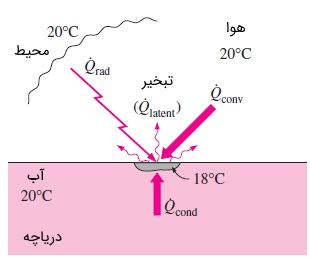
حالا فرض کنید سرعت تبخیر زیاد باشد. حالتی وجود دارد که در آن، نیاز به گرمای تبخیر نسبت به میزان گرمای قابل تأمین توسط عمقهای پایینتر آب و همچنین هوا بیشتر خواهد شد. اکنون، کمبود گرما موجب پایینتر آمدن دما در سطح آب میشود. این فرآیند تا جایی ادامه مییابد که گرمای نهان تبخیر با سرعت انتقال حرارت به سطح آب برابر شود. به محض پایدار شدن شرایط و دمای سطح، موازنه انرژی روی لایه نازکی از مایع در سطح را میتوان با رابطه زیر نشان داد.
در رابطه بالا، سرعت تبخیر و نیز گرمای نهان تبخیر آب در دمای سطح است. در این رابطه، تمام شیوههای انتقال حرارت از تمام چشمهها به سطح را در برمیگیرد و شامل جابجایی و تشعشع از محیط اطراف و رسانش از قسمتهای عمیقتر میشود. انرژی حرارتی منتقل شده از طریق رسانش میتواند هم ناشی از انرژی حرارتی محسوس در آب باشد و هم به دلیل استفاده از یک هیتر مقاومتی، یک کویل گرمایشی یا حتی رخداد واکنشهای شیمیایی در آب اتفاق بیفتد. معمولاً میتوان انتقال حرارت از توده آب به سطح و همچنین تشعشع از محیط را به دلیل ناچیز بودن در نظر نگرفت. از این رو، اتلاف حرارت از طریق تبخیر باید با گرمای دریافت شده از طریق روش جابجایی برابر باشد. به همین دلیل رابطه زیر را در نظر بگیرید.
از رابطه به دست آمده میتوانیم برای تعیین اختلاف دما بین مایع و گاز احاطه کننده آن در شرایط حالت پایدار استفاده کنیم. عدد لوئیس با نماد نشان داده شده است.
مثال ۳: سرمایش یک قوطی نوشابه با کمک تبخیر
سؤال: در یک روز داغ تابستانی، برای خنک کردن یک قوطی نوشابه، آن را ابتدا در یک پارچه خیس پیچیده و سپس مقابل یک پنکه قرار دادهایم. اگر دما و فشار محیط به ترتیب برابر با و $$\large 30\: ^\circ \text {C}$$
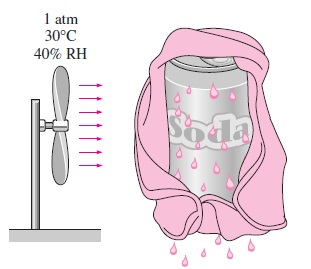
پاسخ: در چنین مسائلی، شار جرمی اندک است. به همین دلیل میتوانیم از ویژگیهای هوای خشک برای مخلوط در دمای میانگین استفاده کنیم. ولی دمای سطح مشخص نیست. دمای را برابر با $$\large 20\: ^\circ \text {C}$$
آب: و
هوای خشک: و
جرم مولی آب و هوا به ترتیب و کیلوگرم بر کیلو مول است. برای به دست آوردن دمای سطح نوشابه به شیوه زیر عمل میکنیم.
همانطور که میبینید، اگر عدد لوئیس را برابر با یک فرض میکردیم، احتمالاً دقت تا حد زیادی پایین میآمد. هوا روی سطح، در حالت اشباع است و در نتیجه، فشار بخار در سطح برابر با فشار اشباع آب در دمای سطح (یعنی ) است. فشار بخار هوا و دمای سطح به ترتیب زیر محاسبه میشود.
میتوانیم برای دقت بالاتر، تمام مراحل را با دمای سطح $$\large 19.4\: ^\circ \text {C}$$
مثال ۴: اتلاف گرما از حمام صنعتی آب داغ بدون پوشش
سؤال: استفاده از حمام آب داغ روباز در صنایع متخلف، دلایل بسیاری دارد. در کارخانهای که اسپری رنگ ساخته میشود، تست دمای قوطیهای رنگ تحت فشار، با مستغرق کردن آنها در آب داغ انجام میشود. در این حالت، دمای آب $$\large 50\: ^\circ \text {C}$$
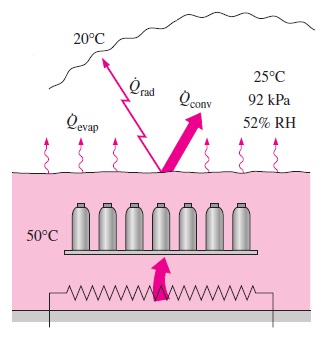
اگر شرایط میانگین کارخانه به صورت و $$\large 25\: ^\circ \text {C}$$
پاسخ: الف) اتلاف حرارت تشعشعی از آب به سطوح خارجی به صورت زیر محاسبه میشود.
ب) مخلوط هوا -- بخار آب، رقیق است و به همین دلیل میتوانیم از ویژگیهای هوای خشک در دمای میانگین، برای آن استفاده کنیم.
$$\large \left( T_ {\infty} \:+\: T_s \right) /2\:=\: \left( 25 \:+\: 50 \right) /2 \:=\: 37.5\: ^\circ \text {C}$$
ویژگیهای هوای خشک در دمای $$\large 37.5\: ^\circ \text {C}$$
همچنین ویژگیهای آب در دمای $$\large 50\: ^\circ \text {C}$$
هوا روی سطح در حالت اشباع است و در نتیجه، فشار بخار روی سطح با فشار اشباع آب در دمای سطح و مقدار برابر است. فشار بخار هوا را در فاصلهای دورتر از سطح آب، با رابطه زیر تعیین میکنیم.
هوا و بخار آب را به عنوان گازهای ایدهآل در نظر میگیریم و میدانیم فشار کل جو برابر با مجموع فشارهای بخار و هوای خشک است. از این رو، چگالی بخار آب، هوای خشک و مخلوط آنها در سطح تماس هوا -- آب به صورت زیر به دست میآید.
همچنین همین مقادیر را میتوان در فاصلهای دورتر از سطح تماس نیز محاسبه کرد.
مساحت و محیط سطح بالای حمام داغ به صورت زیر است.
به این ترتیب، طول مشخصه به دست میآید.
از آنجایی که مخلوط، همگن نیست، با استفاده از مقادیر چگالی (به جای دما) عدد گراشف را مشخص میکنیم.
در این مسئله جابجایی طبیعی، با سطحی داغ مواجه هستیم که رو به بالا قرار گرفته است. عدد ناسلت و ضریب انتقال حرارت جابجایی را تعیین میکنیم.
$$\large \text {Nu} \:=\: (0.15) (\text {Gr} \times \text {Pr}) ^{1/3} \:=\: (0.15) (2.125 \times 10^8 \times 0.7261) ^{1/3} \:=\: 80.45 \\~\\<br /> \large h_ {\text {conv}} \:=\: \frac {\text {Nu} \times k} {L} \:=\:\frac {(80.45) (0.02644\: \text {W/m. } ^\circ \text {C})} {0.3889\: \text {m}} \:=\: 5.47\: \text {W/m} ^2.\: ^\circ \text {C} \\~\\<br /> \large \dot {Q} _{\text {conv}} \:=\: h_ {\text {conv}} A_s (T_s \:-\: T_ {\infty}) \\~\\<br /> \large =\: (5.47\: \text {W/m} ^2.\: ^\circ \text {C}) (3.5\: \text {m} ^2) (50 \:-\: 25) ^\circ \text {C} \:=\: 479\: \text {W}$$
توجه کنید که عدد به دست آمده برای انتقال حرارت جابجایی طبیعی با مقدار انتقال حرارت تشعشعی قابل مقایسه است.
پ) در این قسمت از تشابه بین انتقال حرارت جابجایی و انتقال جرم به روش جابجایی استفاده میکنیم. برای تعیین ضریب انتقال جرم کافیست عدد را جایگزین کنیم. نفوذ جرمی بخار آب در هوا در دمای متوسط به صورت زیر است.
عدد اشمیت (Schmidt Number) را براساس تعریفش محاسبه میکنیم.
عدد شروود (Sherwood Number) و ضریب انتقال جرم به صورت زیر است.
حالا میتوانیم سرعت تبخیر و سرعت انتقال حرارت به وسیله تبخیر را به دست آوریم.
در پایان توجه کنید که جهت انتقال حرارت همیشه از دمای بالاتر به دمای پایینتر است. تمام شیوههای انتقال حرارت که تا اینجا محاسبه کردیم، در همین جهت بودند. به همین دلیل، نرخ کل اتلاف حرارت از آب به هوا و سطح اطراف به صورت زیر خواهد بود.
اگر قرار باشد حمام آب داغ را با کمک انرژی الکتریکی گرم کنیم، باید از یک هیتر مقاومتی با توان استفاده کنیم تا همین مقدار اتلاف حرارت را فراهم کند. همچنین ابعاد این هیتر هم باید بزرگتر باشد؛ زیرا اتلاف حرارت از دیوارههای جانبی و سطح زیرین و همینطور گرمای جذب شده از قوطیهای اسپری در دمای $$\large 50\: ^\circ \text {C}$$
در صورت علاقهمندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^












بسیار عالی مقاله بسیار خوبی برای آشنایی با انتقال جرم بود ممنونیم از شما و تلاش های شما
ممنون ، پایدار باشید
سلام و درود بر فرا درس….
در حیطه ای گام بر می دارید که پیشرفتِ شما سبب پیشرفت دیگران است… درود بر نهادِ خداجویتان… استفاده می کنم از تک تکِ مقالاتتان…
ضمن مطالعه ی این مقاله چون منبع اصلیشو مطالعه کرده بودم برای استفاده ی علمی تره سایر مراجعین به این مقاله به ذهنم رسید ضمن تشکر پیشنهاد کنم منبع مورد استفاده در مقاله هم معرفی و ذکر و قید بشه :
انتفال حرارت و جرم سنجل جلد 2 فصل آخر…
عالی تر از همیشه به سمت بی نهایت باشید
سلام، وقت شما بخیر؛
از اینکه با مجله فرادرس همراه هستید از شما بسیار سپاسگزاریم؛ منبع کلیه مطالب مجله در انتهای آنها و بعد از بخش مقالات پیشنهادی ذکر شده است.