انتقال حرارت هدایتی — از صفر تا صد

از دیدگاه ترمودینامیک، انتقال حرارت به عنوان فرآیندی دیده میشود که در آن، سیستم از یک حالت تعادل به حالت تعادل دیگری میرود. ترمودینامیک در مورد اینکه زمان این فرآیند چقدر طول میکشد، بحثی نمیکند. در حقیقت مبحث انتقال حرارت است که سرعت انتقال گرما را مورد توجه قرار میدهد. در این قسمت قصد داریم تا در مورد انتقال حرارت هدایتی بحث کنیم.
مهمترین عامل انتقال حرارت در یک سیستم، اختلاف دما بین دو نقطه از آن است. همانند اختلاف ولتاژ که منجر به ایجاد جریان الکتریکی میشود، اختلاف دما نیز دلیل ایجاد شار حرارتی است. مقدار کلی انرژی حرارتی منتقل شده Q در بازه زمانی Δt، برابر است با:
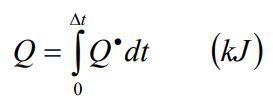
نرخ انتقال حرارت در واحد سطح که به آن شار حرارتی گفته میشود، برابر با مقدار زیر است.
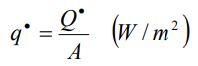
هدایت حرارتی پایا در صفحه تخت
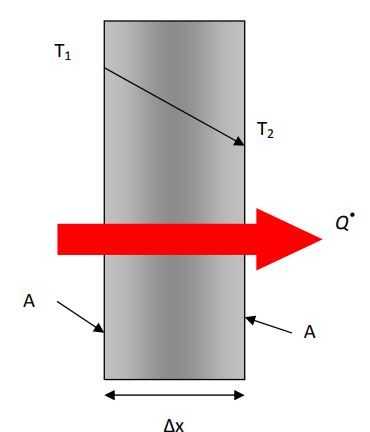
به جابجایی انرژی حرارتی که بین ذرات با انرژی بیشتر و ذرات با انرژی کمتر اتفاق میافتد، «هدایت حرارتی» (Conduction Heat Transfer) گفته میشود. صفحهای به ضخامت Δx=L و مساحت سطح A را در نظر بگیرید. تصور کنید که دمای یک سمت از صفحه T1 و دمای سمت دیگر آن T2 باشد.
بدیهی است که اختلاف دما در دو سمت این صفحه برابر با ΔT = T2 – T1 خواهد بود. دقت کنید که در این مسئله، انتقال حرارت به عنوان تنها شکل مبادله انرژی در نظر گرفته شده است؛ با این فرضیات میتوان تعادل انرژی را برای دیوار به صورت زیر نوشت:
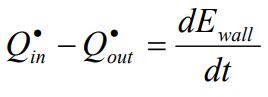
بنابراین در حالت پایا میتوان گفت:
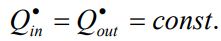
با استفاده از آزمایشات صورت گرفته، دیده شده که انتقال حرارت در یک دیواره تخت با مساحت سطح آن و اختلاف دمای دو سمت دیوار، رابطه مستقیم و با ضخامت آن، رابطه عکس دارد. بنابراین رابطه زیر را میتوان نتیجه گرفت.
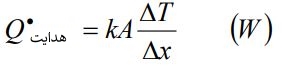
نسبت ثابت k، به عنوان ضریب هدایت حرارتی ماده شناخته میشود. در حالت حدی، که Δx→0، معادله انتقال حرارت فوریه به صورت زیر بیان میشود.
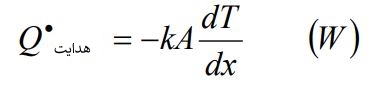
در این معادله عبارت dT/dx، گرادیان دما است که برابر با شیب نمودار آن در نظر گرفته میشود.
هدایت حرارتی
هدایت حرارتی، توانایی یک ماده در عبور دادن حرارت است. این خاصیت با دما تغییر میکند و با استفاده از آزمایش تعیین میشود. این ویژگی در بعضی از مواد در نزدیکی صفر مطلق، تغییرات بسیار زیادی دارد. به چنین موادی در این شرایط «ابررسانا» (Superconductor) گفته میشود.
مفهوم مقاومت حرارتی
معادله فوریه برای انتقال حرارتی پایا، در یک دیوار با سطح مقطع ثابت به صورت زیر است:
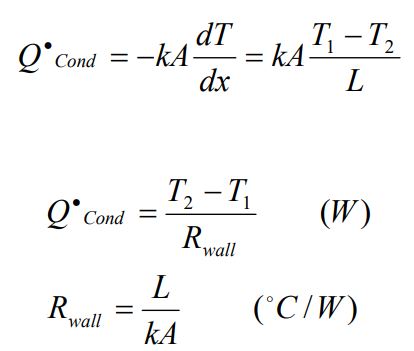
دیوارR مقاومت حرارتی دیوار در مقابل انتقال حرارت و یا به عبارتی سادهتر مقاومت هدایتی دیوار است. انتقال حرارت در صفحه رابط سیال و جامد، بر مبنای قانون سرمایش نیوتن به صورت زیر است:
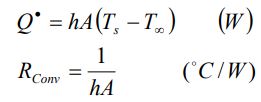
جابجاییR عبارت است از مقاومت حرارتی دیوار در مقابل انتقال حرارت جابجایی (در بخش دوم در مورد این نوع از انتقال حرارت بیشتر صحبت خواهیم کرد.) و یا به طور سادهتر، مقاومت جابجایی سطح است. تابش حرارتی از سطحی به مساحت A و دمای Ts، به محیطی با دمای ∞T برابر با مقدار زیر است.
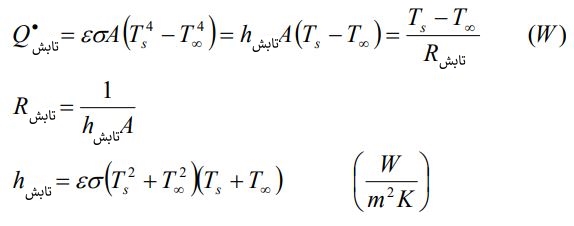
در معادله بالا σ =5.67x10-8 ثابت بولتزمن است. همچنین مقدار ε که «ضریب انتشار سطح» (Surface Emissivity) نامیده میشود، بین مقادیر صفر تا یک تغییر میکند. توجه کنید که تمامی مقادیر دما در این معادلات بر حسب کلوین هستند.
مجموعه مقاومتهای حرارتی
دو صفحه متوالی را مطابق شکل زیر در نظر بگیرید. فرض کنید انتقال حرارتی پایا در این دو صفحه اتفاق میافتد. دقت کنید که این دو صفحه از دو طرف تحت انتقال حرارت جابجایی قرار گرفتهاند.
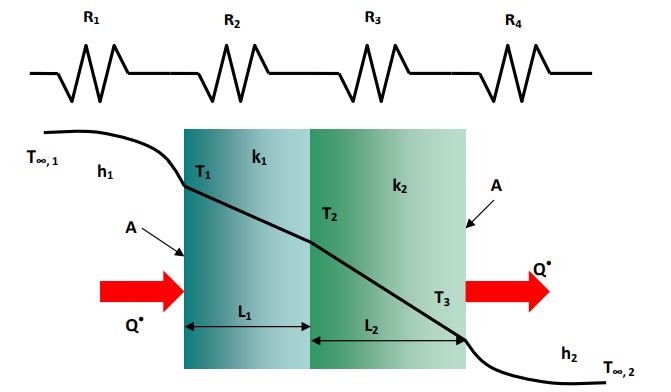
برای چنین سیستمی میتوان بیان کرد که نرخ انتقال حرارت هدایتی در دیوار شماره 1 = نرخ هدایت حرارت در دیوار 2 = نرخ جابجایی حرارتی از دیوار
همین مفهوم را میتوان در قالب فرمول و به صورت زیر نوشت.
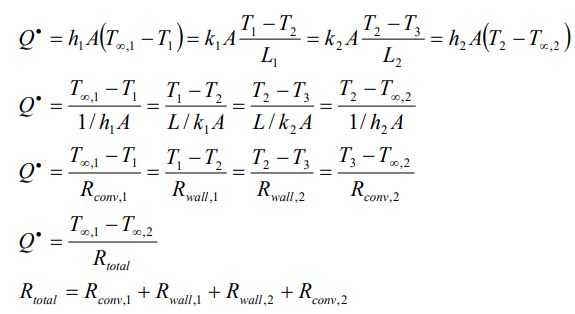
دقت کنید که در این معادله، A سطح ثابت برای دیوار تخت است. همچنین توجه کنید که مقاومتهای حرارتی به صورت متوالی هستند بنابراین میتوان آنها را همانند مقاومتهای الکتریکی با هم جمع کرد. نرخ انتقال حرارت در این دو دیوار برابر با Q=dT/R است. از مفهوم مقاومت حرارتی در عمل به صورت وسیع استفاده میشود.
مقاومت حرارتی در حالت موازی
دقت کنید که از مفهوم مقاومت حرارتی میتوان در حالاتی استفاده کرد که از چند لایه ماده به صورت موازی، سری یا سری–موازی، در کنار یکدیگر استفاده شده است. توجه داشته باشید که در اکثر مسائل مقاومت حرارتی، انتقال حرارت به صورت سه بعدی است اما به منظور درک بهتر از مثالهای یکبعدی استفاده میکنیم.
مثال 1
ترکیبی از لایههای سری و موازی را مطابق با شکل زیر در نظر بگیرید.
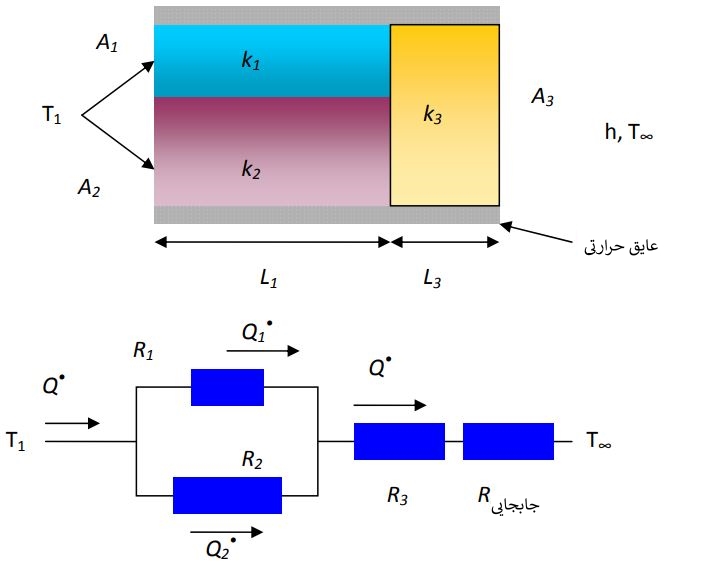
با فرض این که انتقال حرارت به صورت یک بعدی باشد، نرخ انتقال حرارت به صورت زیر محاسبه میشود.
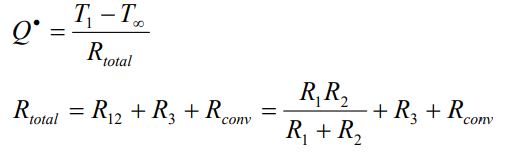
دقت کنید که در اکثر مسائل انتقال حرارت چند بعدی، دو فرض زیر به منظور محاسبه انتقال حرارت در نظر گرفته میشود:
- تمامی صفحات به صورت عمود بر محور x در نظر گرفته میشوند و دما فقط در یک جهت تغییر میکند.
- تمامی صفحاتی که به صورت موازی با محور x قرار گرفتهاند به صورت آدیاباتیک در نظر گرفته میشوند. بنابراین انتقال حرارت فقط در راستای x، اتفاق میافتد.
هدایت حرارتی در صفحات کروی و استوانهای
از مسائل مهم انتقال حرارت، که در صنعت نیز کاربرد بسیاری دارند، هدایت حرارتی در سطوحی است که الزاما به صورت تخت نیستند.
مثلا انتقال حرارت در لولههای خط گاز مربوط به پالایشگاهها عمدتاً به صورت عمود بر سطح است و در جهات دیگر تقریباً انتقال حرارتی صورت نمیگیرد. بنابراین این فرآیند را میتوان به شکلی پایا در نظر گرفت و دمای لوله نیز صورت تابعی از شعاع (T=T(r)) در نظر گرفته میشود. به منظور درک بهتر، سطحی به صورت استوانهای و مطابق با شکل زیر را در نظر بگیرید.
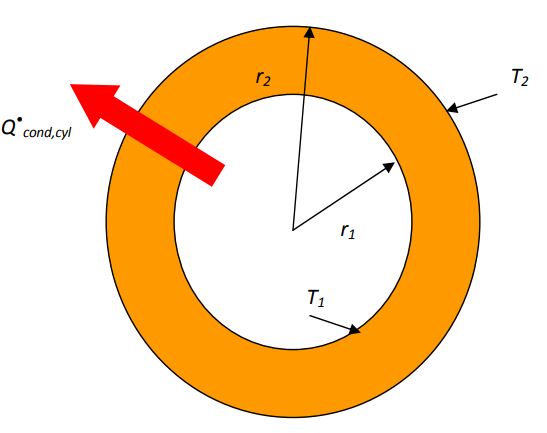
با توجه به اینکه انتقال حرارت فقط در راستای عمود بر صفحه انجام میشود میتوان قانون فوریه را به صورت زیر نوشت:
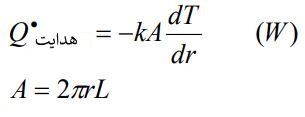
پس از انتگرالگیری از این معادله نرخ انتقال حرارت را به صورت زیر محاسبه میشود.
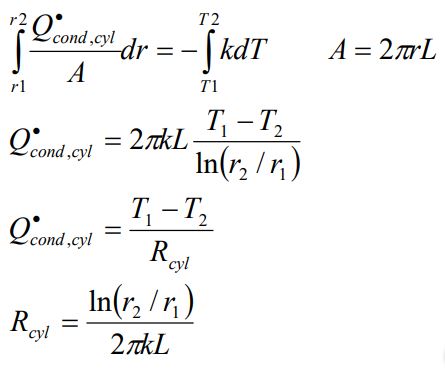
توجه داشته باشید که در این معادله، Rcyl مقاومت هدایتی استوانه است. دقت کنید که مقاومت جابجایی حرارتی برای هر دو سطح استوانهای و کروی برابر با Rconv= 1/hA است. در این فرمول برای استوانه، مساحت A برابر با 2πrL و برای کره، 4πr2 در نظر گرفته میشود.
مثال 2
بخار در دمای T∞,1 = 320 °C، در یک لوله آهنی (k=80 W/m.°C) با قطر داخلی D1=5 cm و قطر خارجی D2=5.5 cm (مطابق شکل زیر) جریان دارد. این لوله با استفاده از لایهای شیشهای (k=0.05 W/m.°C) با ضخامت 3 سانتیمتر عایق شده است. همچنین گرما با مکانیزم جابجایی و تابش، در دمای T∞,2 = 5°C و با ضریب جابجایی h2=18 W/m2°C از سیستم خارج میشود. ضریب انتقال حرارت جابجایی در داخل لوله را h1=60 W/m2K فرض کنید.
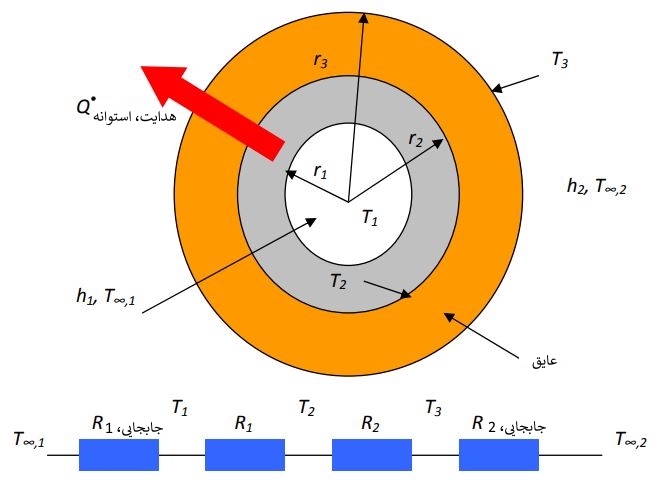
در ادامه قصد داریم تا نرخ حرارت خارج شده از بخار درون لوله و توزیع دما در کل پوسته استوانهای را به ازای یک متر از طول آن بیابیم. در قدم اول مساحتهایی محاسبه میشوند که انتقال حرارت جابجایی در معرض آنها اتفاق میافتد. بنابراین میتوان بیان کرد:
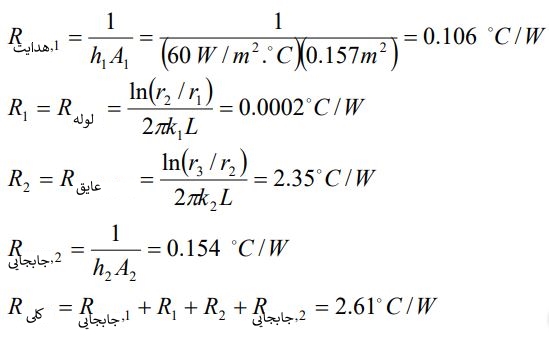
در ادامه نرخ حرارت خارج شده از بخار در حالت پایا با استفاده از رابطه زیر محاسبه میشود.
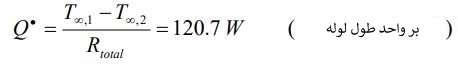
بنابراین کل حرارت خارج شده برای طول مدنظر را میتوان با ضرب کردن •Q در طول لوله محاسبه کرد. همچنین افت دما برای لوله و عایق را میتوان به صورت زیر به دست آورد:
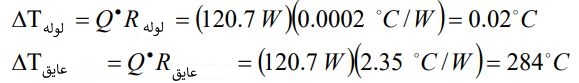
شعاع بحرانی عایق
احتمالا شما نیز متوجه شدهاید که در فرآیند عایق کاری هرچه از عایقی ضخیمتر استفاده کنیم، نرخ انتقال حرارت نیز کمتر خواهد شد.
از طرفی اضافه کردن عایق منجر به زیاد شدن سطح و در نتیجه افزایش انتقال حرارت میشود. بنابراین در حالت کلی که عایقکاری انجام میشود، ممکن است انتقال حرارت، افزایش و یا کاهش یابد. (شکل زیر)
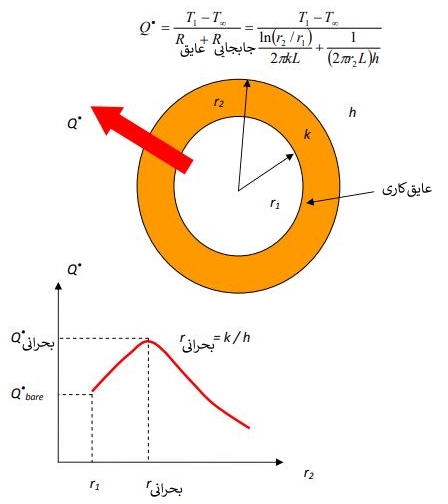
از نظر ریاضیاتی میتوان به تغییرات ماکزیممی از •Q بر حسب r2 دست یافت. بنابراین با صفر قرار دادن عبارت dQ•/dr2، شعاع بحرانی برای استوانه و کره به ترتیب برابر هستند با:
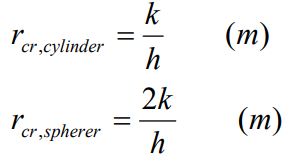
توجه داشته باشید که در اکثر کاربردها، این مقدار بحرانی بسیار کوچک است. بنابراین میتوان آب داغ و یا بخار را بدون نگرانی از سرد شدن، عایق کرد.
تولید حرارت در جامدات
به تبدیل شدن شکلهای مختلف انرژی به حرارت در یک محیط، تولید حرارت گفته میشود. این فرآیند در یک محیط منجر به افزایش دما در آن خواهد شد. به عنوان مثال انرژی به وجود آمده از مقاومت الکتریکی و یا حرارت ایجاد شده که به دلیل واکنشهای هستهای است، نوعی تولید حرارت محسوب میشوند. دقت کنید که معمولا نرخ تولید حرارت، در واحد حجم (W/m3) بیان میشود. در بیشتر کاربردها این دمای ماکزیمم است که به بررسی آن علاقهمند هستیم.
مکان دمای ماکزیمم (Tmax) در یک محیط جامد، به دور از لبه جسم که در دمای Ts نگه داشته شده، قرار دارد.
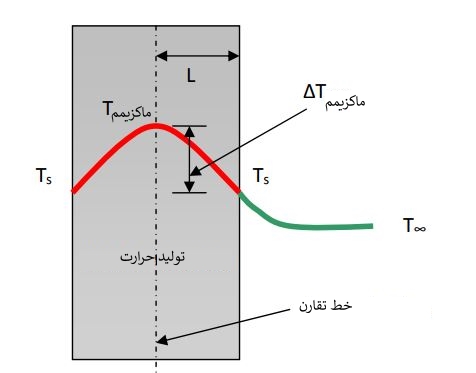
محیطی جامد را با سطح مقطع A، حجم V و ضریب هدایت حرارتی k در نظر بگیرید که در آن حرارت با نرخ •g بر واحد حجم تولید میشود؛ همچنین حرارت از لبه جسم که در دمای Ts قرار دارد خارج میشود. در حالت پایا میتوان قانون پایستگی انرژی برای این سیستم را به صورت زیر نوشت.
نرخ تولید انرژی در جامد = نرخ خارج شدن انرژی از جامد
بنابراین میتوان نوشت:
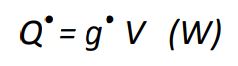
از طرفی با استفاده از قانون سرمایش نیوتن میتوان گفت:
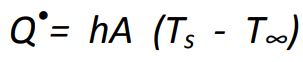
با ادغام دو رابطه بالا میتوان دمای سطح را به صورت زیر بدست آورد.
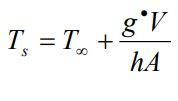
همچنین با استفاده از رابطه بالا میتوان دمای سطح تخت، استوانهای یا کروی با ضخامت 2L را به صورت زیر محاسبه کرد:
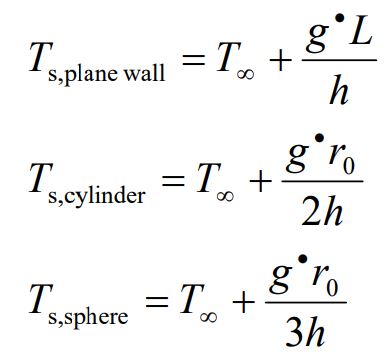
دقت کنید که این افزایش دما در دیواره به دلیل تولید حرارت در آن است. با استفاده از قانون فوریه میتوان دمای ماکزیمم را برای استوانه، صفحه تخت و کره با شعاع r0 به صورت زیر محاسبه کرد.

در بخشهای آینده در مورد شکلهای دیگری از انتقال حرارت بحث خواهیم کرد. در صورتیکه به مباحث مهندسی علاقهمند هستید، احتمالا آموزشهای زیر نیز میتواند برایتان مفید واقع شوند:
^^













سلام و خسته نباشید. ذهنمو مشغول کرده.
فرض کنیم که در لوله ای اب هست و زمستانه و دما منفیه. دمای نهایی اب داخل لوله در نهایت چقدره؟ ایا به عدد ثابت و بالاتری از دمای بیرون که منفیه میرسه و یعنی ممکنه اب اگر ساکن باشه یخ نزنه؟ یا اینکه نه دمای اب در نهایت به دمای بیرونی میرسه؟ خیلی ممنون.پاسخش برایم مهمه اگر شد یه مقاله با عدد واقعی بدین. ممنون میشم
سلام
چرا در مختصات استوانه ای برای محاسبه ی kond نمی توان از شار انتقال حرارت استفاده کرد
سلام کسی جواب این سوال رو میدونه؛میزان بازده حرارتی را در یک ورق آلمینیوم به ضخامت ۳ میل .عرض ۵ میلوطول ۱۰ میل که جوش شود به ورق فولادی با ضخامت ۳ میل.عرض ۵ میل و طول ۱۰ میلی متر.میزان پخش شدن حرارت را تا عرض ۴،۵ میل محاسبه کنید؟
درود اقای مهندس خسته نباشید لطفا مطالب را از سایت های خارجی کپی نکنید
چون ترجمه مطالب طوری انجام شده درک مطلب راحت نیست و اشکالاتی دارد بطوریکه ایجاد ابهام میکند و ضمنا از جهت امانتداری مرجع را ذکر کنید و هم اینکه خواننده بتوانند به مرجع مراجعه کند .
با سلام؛
منبع تمامی مطالب مجله فرادرس اگر ترجمه باشند در انتهای مطلب و پیش از نام نویسنده آورده شدهاند. منبع این مطلب نیز در انتها آورده شده است.
با تشکر از همراهی شما با مجله فرادرس
سلام وقت بخیر
اگر سطح خارجی سیلندر توخالی مقید شده باشه(مثلا جوش داده شده) و سیلندر تحت یک توزیع دمای خطی در راستای شعاعی قرار گرفته باشه چطور محاسبه میشه؟
سلام در نظر داریم یک مبدل حرارتی گاز به گاز برای استقاده از گاز اگزوز یک کارخانه طراحی کنیم.
دمای گاز حدود 500 درجه است و میخواهیم با ان هوای داغ برای قسمت دیگر کارخانه تولید کنیم.
به نظرم رسید برای خلاصی از فین تیوب از مشابه المان های بیضوی بخاری های گازی فن دار ( مثلا انرژی) استفاد کنیم. ایا مقطعی همانند ان مورد یا بیضی برای افزایش سطح مناسب است؟
r عایق چطوری حساب میشه؟
قانون فوریه در مواد غیر ایزوتروپیک هم کاش بررسی میشد.
چرا در قانون فوریه علامت منغی گذاشته میشود؟!
سلام. ببینید وقتی از dt صحبت میکنیم یعنی t2-t1 حالا چون ما بحث انتقال حرارت رو داریم ، زمانی حرارت از نقطه ی 1 به 2 منتقل میشه که نقطه ی اول دمای بیشتری داشته باشه حالا یا ما باید قبول کنیم دمای t2 بیشتره و با اینحال انتقال حرارت از 1 به 2 بوده که در این صورت قانون سرمایش نیوتن (دما از جسم گرم تر به جسم سرد تر منتقل میشود) نقض میشه یا باید یک منفی قرار بدیم که فرمول به حالت درست یعنی t1-t2 اصلاح بشه.
نتقال حرارت را از طریق دیواره ضخامت L و سطح A. در نظر بگیرید در چه شرایطی توزیع دما در دیوار مستقیم خواهد بود؟ بی زحمت جواب این سوال میدین
خیلی توضیحات خوب بود مرسی?