عدد ناسلت (Nusselt Number) — به زبان ساده
پیشتر در بلاگ فرادرس مفاهیم مرتبط با لایهمرزی و انتقال حرارت را توضیح دادیم. همچنین در مطلبی، مفاهیم مرتبط با عدد رینولدز ارائه شدند. در این مطلب قصد داریم تا عددی تحت عنوان عدد ناسلت را توضیح دهیم.
البته پیشنهاد میشود قبل از مطالعه این مطلب، مطالب انتقال حرارت هدایتی، جابجایی حرارتی و عدد رینولدز را مطالعه فرمایید.
مفهوم عدد ناسلت
در انتقال حرارت، عدد ناسلت نشان دهنده نرخ انتقال حرارت جابجایی به انتقال حرارت هدایتی است. بنابراین عدد ناسلتی که به ۱ نزدیک باشد، به معنای آن است که انتقال حرارت هدایتی و جابجایی به هم نزدیک هستند. اعداد ناسلت بزرگتر نشان دهنده انتقال حرارت جابجایی بیشتر هستند.
فرمول عدد ناسلت
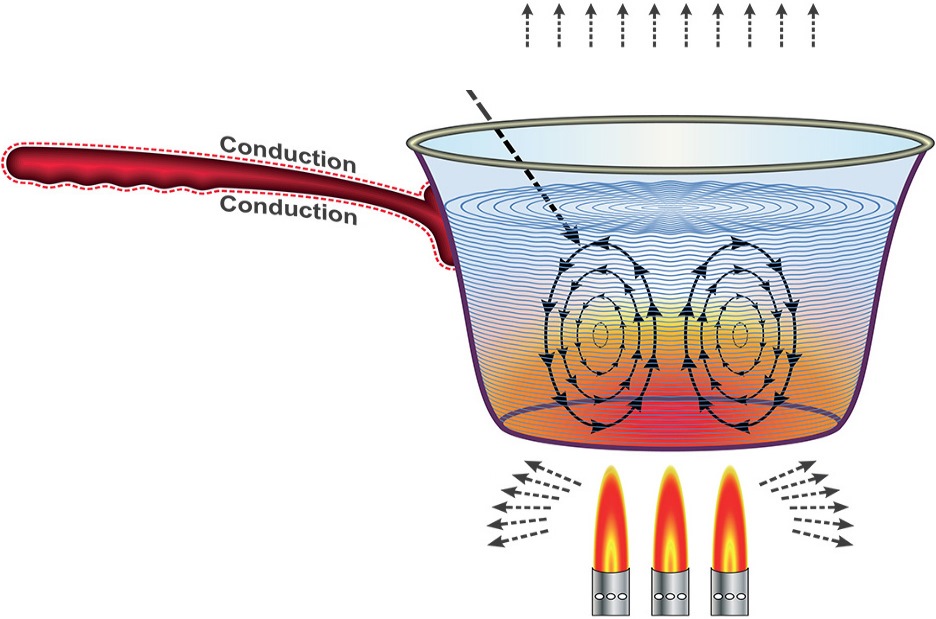
برای بدست آوردن عدد ناسلت، مطابق با شکل زیر فرض کنید جریانی به صورت لایهای روی سطحی تخت در حال عبور است.

همانطور که در شکل فوق نیز نشان داده شده، جریان آزاد در دمای $$ T _ \infty $$ و سطح در دمای $$ T _ s $$ قرار دارد. با توجه به متفاوت بودن دمای سطح و دمای سیال، لایهمرزی حرارتی تشکیل میشود. همچون لایهمرزی هیدرودینامیکی، در لایهمرزی حرارتی، دما از سطح تا لبه لایهمرزی متفاوت است. در این صورت نرخ انتقال حرارت جابجایی بین سطح و سیال برابر است با:
$$ \large { { Q } _ { y } } = h A \left ( { { T } _ { s } } - { { T } _ { \infty } } \right ) $$
توجه داشته باشید که در رابطه فوق، h برابر با ضریب انتقال حرارت جابجایی سیال است. بدیهی است که این میزان از انرژی منتقل شده از سطح با مکانیزم هدایت حرارتی در سیال عبور میکند. بنابراین با فرض اینکه ضریب هدایت حرارتی سیال برابر با k باشد، رابطه زیر را نیز میتوان برای انتقال حرارت رخ داده درون سیال عنوان کرد.
$$ \large { { Q } _ { y } } = - k A { \frac { \partial } { \partial y } } { { \left . \left ( T -{ { T } _ { s } } \right ) \right | } _ { y = 0 } } $$
با برابر قرار دادن هدایت و جابجایی حرارتی، داریم:
$$ \large - k A { \frac { \partial } { \partial y } } { { \left . \left ( T - { { T } _ { s } } \right ) \right | } _ { y = 0 } } = h A \left ( { { T } _ { s } } - { { T } _ { \infty } } \right ) $$
با مرتب کردن رابطه فوق، عبارت زیر بدست میآید.
$$ \large { \frac { h } { k } } = { \frac { { \left . { \frac { \partial \left ( { { T } _ { s } } - T \right ) }{ \partial y } } \right | } _ { y = 0 } } { \left ( { { T } _ { s } } - { { T } _ { \infty } } \right ) } } $$
عبارت سمت چپ در رابطه فوق را میتوان به صورت زیر بیبعد کرد.
$$ \large { \frac { h L } { k } } = { \frac { { \left . { \frac { \partial \left ( { { T } _ { s } } - T \right ) }{ \partial y } } \right | } _ { y = 0 } } { \frac { \left ( { { T } _ { s } } - { { T } _ { \infty } } \right ) } { L } } } $$
همانطور که میبینید سمت چپ عبارت فوق، نشان دهنده نسبت انتقال حرارت جابجایی به هدایت حرارتی است. به این نسبت عدد ناسلت گفته میشود. بنابراین نهایتا عدد ناسلت برابر است با:
$$ \large { \displaystyle \mathrm { N u } = { \frac { h } { k / L } } = { \frac { h L } { k } } } $$
عدد ناسلت در جابجایی آزاد
معمولا روابطی تجربی برای عدد ناسلت در شرایط مختلف ارائه شده است. ما در این مطلب روابط مربوط به عدد ناسلت را در دو حالت صفحه افقی و عمودی به طور جدا ارائه خواهیم داد.
جابجایی آزاد عمودی
همانطور که در شکل زیر نیز نشان داده شده، یک صفحه به صورت عمودی قرار گرفته و در آن جابجایی آزاد رخ میدهد.
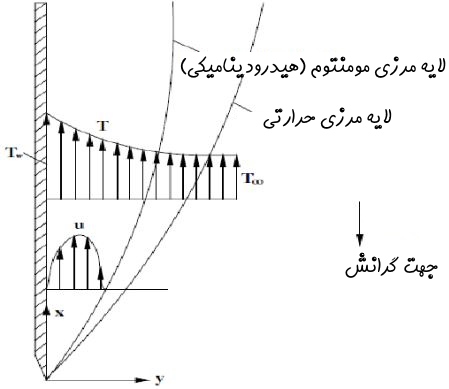
در جابجایی آزاد روی صفحه عمودی، چرچیل رابطه زیر را پیشنهاد میدهد.
$$ \large { \overline { \mathrm { N u } } } _ { L } \ = 0 . 6 8 + { \frac { 0 . 6 7 \, \mathrm { R a } _ { L } ^ { 1 / 4 } } { \left [ 1 + ( 0 . 4 9 2 /\mathrm { P r } ) ^ { 9 / 1 6 } \, \right ] ^ { 4 / 9 } \, } } \quad \mathrm { R a } _ { L } \leq 1 0 ^ { 9 } $$
در رابطه فوق Ra نشان دهنده «عدد رایلی» (Rayleigh Number) بوده و Pr «عدد پرانتل» (Prandtl) را نشان میدهد. عدد ریلی نیز به صورت زیر تعریف میشود:
$$ \large {\displaystyle \mathrm { R a } _ { x } = \mathrm { G r } _ { x } \mathrm { P r } = { \frac { g \beta } { \nu \alpha } } ( T _ { s } - T _ { \infty } ) x ^ { 3 } } $$
در رابطه فوق نیز نمادهای استفاده شده موارد زیر را نشان میدهند.
- x= طول مشخصه
- Rax: عدد رایلی در فاصله x
- Grx = عدد گراشوف در طول x
- Pr = عدد پرنتل
- g =شتاب گرانشی
- Ts = دمای سطح (دمای دیواره)
- $$T _ { \infty }$$ = دمای محیط اطراف (دمای سیال دور از دیواره)
- ν = ویسکوزیته سینماتیک
- α = ضریب نفوذ گرمایی
- β = ضریب انبساط حرارتی
جابجایی آزاد افقی
در این حالت در ابتدا عددی تحت عنوان طول مشخصه به صورت زیر تعریف میشود.
$$ \large L \ = { \frac { A _ { s } } { P } } $$
در رابطه بالا As برابر با مساحت سطح صفحه و P نشان دهنده محیط آن است. در شرایطی که سطح بالایی گرم در محیط سرد قرار گرفته یا سطح پایینی سرد در محیط گرم قرار گرفته عدد ناسلت با استفاده از روابط زیر بدست میآید.
$$ \large { \overline { \mathrm { N u } } } _ { L } \ = 0 . 5 4 \, \mathrm { R a } _ { L } ^ { 1 / 4 } \, \quad 1 0 ^ { 4 } \leq \mathrm { R a } _ { L } \leq 1 0 ^ { 7 } $$
$$ \large { \overline { \mathrm { N u } } } _ { L } \ = 0 . 1 5 \, \mathrm { R a } _ { L } ^ { 1 / 3 } \, \quad 1 0 ^ { 7 } \leq \mathrm { R a } _ { L } \leq 1 0 ^ { 1 1 } $$
همچنین در حالتی که سطح پایین، جسم گرم بوده و در محیطی سرد قرار گرفته یا سطح بالایی جسم سرد بوده و در محیطی گرم قرار گرفته، عدد ناسلت بهصورت زیر بدست میآید.
$$ \large {\displaystyle { \overline { \mathrm { N u } } } _ { L } \ = 0 . 5 2 \, \mathrm { R a } _ { L } ^ { 1 / 5 } \, \quad 1 0 ^ { 5 } \leq \mathrm { R a } _ { L } \leq 1 0 ^ { 1 0 } } $$
جابجایی اجباری روی سطح تخت
در این قسمت، قصد داریم تا روابط مربوط به عدد ناسلت روی صفحه تخت را مورد بررسی قرار دهیم. در ابتدا مطابق با شکل زیر، صفحهای تخت را در نظر بگیرید که جریان روی آن عبور میکند.
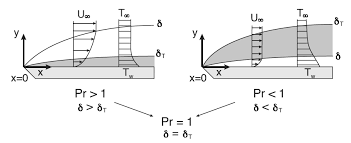
در این صورت عدد ناسلت در فاصله x از لبه برابر است با:
$$ \large \mathrm { N u } _ { x } \ = 0 . 3 3 2 \, \mathrm { R e } _ { x } ^ { 1 / 2 } \, \mathrm { P r } ^ { 1 / 3 } , ( \mathrm { P r } > 0 . 6 ) $$
با انتگرالگیری از رابطه فوق در فاصله ۰ تا x، مقدار متوسط ناسلت در این فاصله به صورت زیر بدست میآید.
$$ \large { \displaystyle \mathrm { { \bar { N u } } _ { x } } \ = { 2 } × 0 . 3 3 2 \, \mathrm { R e } _ { x } ^ { 1 / 2 } \, \mathrm { P r } ^ { 1 / 3 } , ( \mathrm { P r } > 0 . 6 ) } $$
به همین صورت مقدار متوسط این عدد روی کل صفحه، یعنی در فاصله ۰ تا L برابر با رابطه زیر بدست میآید.
$$ \large { \displaystyle \mathrm { { \bar { N u } } _ { L } } \ = { 2 } × 0 . 3 3 2 \, \mathrm { R e } _ { L } ^ { 1 / 2 } \, \mathrm { P r } ^ { 1 / 3 } , ( \mathrm { P r } > 0 . 6 ) } $$
جابجایی اجباری در جریان توربولانس درون لوله
در حالتی که جریانی به صورت توربولانس درون لوله برقرار باشد، رابطه زیر را میتوان برای عدد ناسلت بیان کرد.
$$ \large \mathrm { N u } _ { D } = { \frac { \left ( f / 8 \right ) \left ( \mathrm { R e } _ { D } - 1 0 0 0 \right ) \mathrm { P r } } { 1 + 1 2 . 7 ( f / 8 ) ^ { 1 / 2 } \left (\mathrm { P r } ^ { 2 / 3 } - 1 \right ) } } $$
این رابطه توسط «ﮔﻠﯿﻨﺴﮑﯽ» (Gnielinski) ارائه شده است. D برابر با قطر لوله است. توجه داشته باشید که در رابطه فوق، f برابر با ضریب اصطکاک دارسی است که در نمودار مودی برای لولههای مختلف با زبریهای متفاوت ارائه شده است. البته برای لولههای صاف که زبری آنها در نظر گرفته نمیشود میتوان از رابطه «پتکوف» (Petukhov) نیز به منظور محاسبه ضریب f استفاده کرد. این رابطه در ادامه ارائه شده است.
$$ \large f = \left ( 0 . 7 9 \ln \left ( \mathrm { R e } _ { D } \right ) - 1 . 6 4 \right ) ^ { - 2 } $$
توجه داشته باشید که رابطه ﮔﻠﯿﻨﺴﮑﯽ در بازههای مشخصی از اعداد پرانتل و رینولدز صادق هستند. این بازهها در ادامه بیان شدهاند.
$$ \large 0 . 5 \leq \mathrm { P r } \leq 2 0 0 0 $$
$$ \large 3 0 0 0 \leq \mathrm { R e } _ { D } \leq 5 \times 1 0 ^ { 6 } $$
در این مطلب مفاهیم کلی و روابط مهم مربوط به عدد ناسلت ارائه شدند. در آینده در مورد این عدد بیشتر صحبت کرده و مثالهایی از آن را ارائه خواهیم داد.
^^











سلام وقت بخیر
ببخشید مقادیر ناسلت متوسط برای جریان آشفته چقدر هست؟
با سلام
محاسبهی عدد ناسلت در شرایط آشفته در شرایط مختلف متفاوت است، سادهترین راه برای محاسبهی ناسلت استفاده از تشابه کلبرن است.
۱. در شرایطی که جابجایی اجباری، جریان آشفته، صفحهی تخت و دمای ثابتی در دیواره داشته باشیم عدد ناسلت برابر با:
Nu= 0.0296 Re^(4/5) pr(1/3)
خواهد بود.
توجه داشته باشید که جهت جریان در جهت x است.
۲. در شرایطی که جابجایی اجباری، جریان آشفته، صفحهی تخت داشته باشیم و شار روی دیواره ثابت باشد عدد ناسلت به مقدار ذیل خواهد بود:
Nu= 1.04Nu
درواقع میتوان گفت که عدد ناسلت موضعی تحت شرایط ذکر شده تنها 4 درصد از ناسلت موضعی در حالت دما ثابت بیشتر است.
پس در رابطهی دوم، سمت چپ رابطه ناسلت در حالت شار ثابت و سمت راست رابطه ناسلت در حالت دما ثابت[دیواره] میباشد.
۳. شرایط دیگری مشابه شرایط اول اما برای فلزات مایع وجود دارد که رابطهی ناسلت به شرح زیر خواهد بود:
Nu= 0.53pe^(0.5)
که در رابطهی فوق pe(عدد پکلت) چنین تعریف میشود:
Pe= Re . Pr
آیا ضریب هدایت k در فرمول ناسلت را برای سیال باید باتوجه به جنس و دمای سیال از جداول بدست آوریم؟
سلام وقت بخیر
درمورد عدد ناسلت روی کره، عدد 2 که توی فرمول هست از کجا ظاهر میشه؟؟؟
ممنون میشم پاسخ بدین
با سلام؛
عدد ۲ در فرمول مربوط به جابجایی اجباری روی سطح تخت، حاصل از انتگرالگیری رابطه است که در نهایت، جواب انتگرال در متن آورده شده است.
با تشکر از همراهی شما با مجله فرادرس
سلام ممنون از زحمات شما
مطالب تان خیلی خوبه
آیا این امکانش هست که سوال بپرسیم جواب ارسال کنید؟
به چه طریقی؟
مثلاً واتساپ و….
در این صورت برام اعلام فرمائید
ممنون از توضیحات شما