تعادل فازی در ترمودینامیک – از صفر تا صد

براساس تعریف، هنگامی که یک سیستم در تعادل باشد، با فرض ایزوله بودن سیستم از محیط پیرامونش، هیچ تغییری در آن رخ نمیدهد. اگر هیچ تغییری در فشار یک سیستم ایزوله ایجاد نشود، آن سیستم در تعادل مکانیکی است. اگر دمای آن عوض نشود، در تعادل گرمایی قرار دارد و بالاخره زمانی که از یک فاز به فاز دیگر، هیچ تبدیلی رخ ندهد، سیستم در تعادل فازی است.

همانطور که میدانید به حالتی از یک سیستم که تابع گیبس در دما و فشار مشخص، به مینیمم مقدار خود برسد، حالت تعادل گفته میشود. بنا به تجربه میدانیم که اگر لباس خیسی را در معرض هوای آزاد قرار دهیم، پس از مدتی در نهایت خشک میشود. قطرات آب نشسته روی شیشه عینک، کمکم تبخیر میشوند و اگر درپوشِ شیشه الکل را باز بگذاریم، رفته رفته از حجم الکل کاسته خواهد شد.
این مثالها نشان میدهند نیروی محرکهای بین دو فاز یک ماده وجود دارد که ماده را مجبور میکند از یک فاز به فاز دیگر تبدیل شود. بزرگی این نیرو به غلظت نسبی این دو فاز وابسته است. یک تیشرت کوچک، در هوای خشک با سرعت بیشتری نسبت به هوای مرطوب، خشک میشود. در واقع اگر رطوبت نسبی محیط ۱۰۰ درصد باشد، این لباس هرگز کاملاً خشک نخواهد شد. در این حالت هیچ انتقالی بین فاز بخاز و فاز مایع رخ نمیدهد و اصطلاحاً گفته میشود سیستم در تعادل فازی (Phase Equilibrium) است. با تغییر دما یا فشار، شرایط تعادل نیز به هم میخورد. در نتیجه، برای بررسی تعادل فازی باید دما و فشار را ثابت نگه داشت.
تعادل فازی برای سیستم تکجزئی
برای بررسی تعادل بین دو فاز یک ماده خالص مانند آب، مخلوط مایع اشباع و بخار اشباع را که در دما و فشاری مشخص با هم در تعادل هستند، در نظر بگیرید. تابع گیبس کل این مخلوط به صورت زیر نوشته میشود.

$$\large G\:=\: m_f g_f \:+\: m_g g_g$$
پارامترهای $$\large g_f$$ و $$\large g_g$$ به ترتیب، تابع گیبس فازهای مایع و بخار در واحد جرم هستند. حالا اعوجاجی را در نظر بگیرید که در طی آن، مقدار دیفرانسیلی از مایع ($$\large dm_f$$) در دما و فشار ثابت تبخیر شود. تغییر در تابع گیبس کل در این اعوجاج به صورت زیر است.
$$\large (dG) _{T,P} \:=\: g_f dm_f \:+\: g_g dm_g$$
توجه کنید که $$\large g_f$$ و $$\large g_g$$ در دما و فشار ثابت، تغییری نمیکنند. در حالت تعادل، رابطه $$\large (dG) _{T,P} =0$$ برقرار و با توجه به اصل پایستگی جرم، $$\large dm_g = -dm_f$$ نیز مفروض است. با ادغام این رابطهها، رابطه زیر حاصل میشود.
$$\large (dG) _{T,P} \:=\: (g_f \:-\: g_g) dm_f$$
اگر رابطه بالا را در حالت تعادل فازی برابر با صفر قرار دهیم، نتیجه زیر به دست میآید.
$$\large g_f \:=\: g_g$$
از این رو، دو فاز یک ماده خالص با یکدیگر در تعادل فازی هستند؛ اگر مقدار تابع گیبس مخصوص در هریک از فازها برابر باشد. همچنین در نقطه سهگانه (حالتی که در آن هر سه فاز با هم در تعادل هستند) تابع گیبس مخصوص برای هر سه فاز یکسان است. اما اگر $$\large g_f > g_g$$ شود چه اتفاقی خواهد افتاد؟ بدیهی است که در این لحظه، تعادل فازی برقرار نیست. بنا به قانون دوم ترمودینامیک، باید رابطه $$\large (dG) _{T,P}= (g_f - g_g) \:dm_f \leq0$$ برقرار باشد. در نتیجه، $$\large dm_f$$ منفی است. به عبارت دیگر، اندکی از مایع باید تبخیر شود تا $$\large g_f = g_g$$ برقرار شود. بنابراین، اختلاف تابع گیبس به عنوان نیروی محرکهای برای تغییر فاز عمل خواهد کرد؛ مانند اختلاف دما که نیروی محرکه انتقال حرارت است.
مثال ۱: تعادل فازی برای یک مخلوط اشباع
سؤال: نشان دهید که مخلوط آب در حالت مایع اشباع و بخار آب اشباع در دمای $$\large 120 ^\circ C$$، در تعادل فازی قرار دارند. مشخصات آب اشباع در دمای $$\large 120 ^\circ C$$ به صورت زیر است.
$$\large h_f \:=\: 503.81 \:kJ /kg \\~\\
\large s_f \:=\: 1.5279 \:kJ/ kg.K \\~\\
\large h_g \:=\: 2706.00:kJ /kg \\~\\
\large s_g \:=\: 7.1292 \:kJ /kg.K$$
پاسخ: از تعریف تابع گیبس به صورت زیر استفاده میکنیم.
$$\large g_f \:=\: h_f \:-\:T s_f \:=\: 503.81 \:kJ /kg \:-\: (393.15 \:K) (1.5279 \:kJ /kg.K) \\~\\
\large \Rightarrow ~~~ g_f \:=\: -\: 96.6 kJ /kg \\~\\
\large g_g \:=\: h_g \:-\: Ts_g \:=\: 2706.00 \:kJ /kg \:-\: (393.15 \:K) (7.1292 \:kJ /kg.K) \\~\\
\large \Rightarrow ~~~ g_g \:=\: -\: 96.8 kJ /kg$$
نتایج بالا تقریباً با هم برابرند و شرایط تعادل فازی با تقریب خوبی برقرار است.
قانون فازی گیبس
توجه کنید که ممکن است یک سیستم تکجزئیِ دو فازی در دماها (یا فشارهای) مختلفی در تعادل فازی قرار بگیرد. البته به محض اینکه دما ثابت شود، سیستم در حالت تعادل قرار گرفته و مقدار تمام مشخصههای شدتی هر فاز ثابت میشوند. بنابراین، هر سیستم دو فازی تکجزئی، فقط یک ویژگی مستقل دارد که آن ویژگی میتواند دما یا فشار باشد.
در حالت کلی، تعداد متغیرهای مستقل در سیستم چند فازی چند جزئی را میتوان با قانون فازی گیبس (Gibbs Phase Rule) تعیین کرد که به صورت زیر تعریف میشود.
$$\large IV \:=\: C \:-\: PH \:+\: 2$$
در رابطه بالا، تعداد متغیرهای مستقل با $$\large IV$$ نشان داده شده است. $$\large C$$ و $$\large PH$$ نیز به ترتیب تعداد جزءها و فازهای در تعادل را نشان میدهد. به عنوان مثال، برای سیستم تکجزئی ($$\large C =1$$) دو فازی ($$\large PH =2$$) که پیشتر در موردش بحث شد، فقط به یک ویژگی مستقل ($$\large IV =1$$) نیاز است. شکل زیر را در نظر بگیرید.

در نقطه سهگانه که مقدار $$\large PH =3$$ است، تعداد ویژگیهای مستقل برابر $$\large IV =0$$ خواهد بود. به عبارت دیگر، هیچ یک از ویژگیهای یک ماده خالص در نقطه سهگانه قابل تغییر نیست. همچنین براساس این قانون، هر ماده خالصی که به صورت تکفاز قرار داشته باشد ($$\large PH =1$$)، دارای دو متغیر مستقل است. یعنی برای تثبیت حالت تعادل یک ماده خالص تکفاز، به دو ویژگی شدتی و مستقل نیاز است.
تعادل فازی برای سیستمهای چندجزئی
بسیاری از سیستمهای چند فازی در عمل دارای دو یا بیش از دو جزء هستند. یک سیستم چند فازی چند جزئی در دما و فشار مشخص، هنگامی در تعادل فازی قرار دارد که در آن هیچ نیروی محرکهای بین فازهای مختلف در هیچ کدام از فازها وجود نداشته باشد.
بنابراین، برای تعادل فازی، تابع گیبس مخصوص مربوط به هر جزء باید در تمام فازها یکسان باشد.

به عبارت دیگر باید روابط زیر به ترتیب برای هر جزء برقرار باشد.
$$\large g_{f, \:1} \:=\: g_ {g, \:1} \:=\: g_{s, \:1} \\~\\
\large g_{f, \:2} \:=\: g_ {g, \:2} \:=\: g_{s, \:2} \\~\\
\large ................ \\~\\
\large g_{f, \:N} \:=\: g_ {g, \:N} \:=\: g_{s, \:N}$$
حالا به سراغ سیستمهای دو جزئی برویم که شامل دو فاز مایع و بخار در تعادل میشوند. این سیستمها معادل $$\large C= 2$$ و $$\large PH= 2$$ هستند. از این رو $$\large IV= 2$$ به دست میآید. به عبارت دیگر، یک سیستم دو جزئیِ دو فازی، دارای دو متغیر مستقل است و چنین سیستمهایی تنها در حالتی به تعادل میرسند که هر دو ویژگی شدتی مستقل، ثابت شود.
به طور کلی، ساختار سیستمهای دو جزئی دو فازی که در تعادل فازی هستند، در هر فاز یکسان نیست. یعنی کسر مولی هر جزء در هر فاز متفاوت است. این موضوع در شکل زیر نشان داده شده است. در اینجا، مخلوط دو فازی اکسیژن و نیتروژن در فشار $$\large 0.1\: MPa$$ قرار دارند. خط بخار در این نمودار، ساختار فاز بخار در دماهای گوناگون و در حالت تعادل است. خط مایع نیز همینکار را برای فاز مایع انجام میدهد. به عنوان مثال، در دمای $$\large 84 K$$ کسرهای مولی برابر $$\large 30$$ درصد نیتروژن و $$\large 70$$ درصد اکسیژن در فاز مایع و $$\large 66$$ درصد نیتروژن و $$\large 34$$ درصد اکسیژن در فاز بخار هستند. رابطههای زیر را در نظر بگیرید.
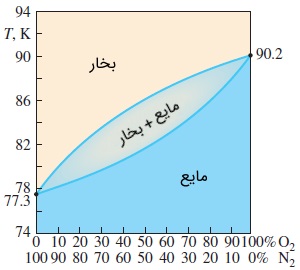
$$\large y_{f, \text { N}_2} \:+\: y_{f, \text { O}_2} \:=\: 0.30 \:+\: 0.70 \:=\: 1 \\~\\
\large y_{g, \text { N}_2} \:+\: y_{g, \text { O}_2} \:=\: 0.66 \:+\: 0.34 \:=\: 1$$
بنابراین به محض اینکه فشار و دما (دو متغیر مستقل) در یک سیستم دو جزئیِ دو فازی مشخص شود، ساختار هر فاز در تعادل را میتوان از روی نمودار فاز تعیین کرد که از طریق اندازهگیریهای آزمایشگاهی به دست میآید.
به این نکته توجه داشته باشید که دما، تابعی پیوسته است ولی کسر مولی در حالت کلی این گونه نیست. به عنوان مثال، دمای هوا و آب را روی سطح آزاد یک دریاچه در نظر بگیرید. این دو عدد همیشه با هم برابرند. اما بدیهی است که کسر مولی هوا در دو طرف سطح تماس هوا -- آب کاملاً متفاوت است. کسری مولی هوا در آب، مقداری تقریباً برابر صفر دارد. در سوی مقابل، کسر مولی آب هم در دو طرف این سطح تماس، متفاوت است. حتی زمانی که هوا در حالت اشباع باشد. از این رو، هنگامی که از کسر مولی در مخلوطهای دو فازی صحبت میکنیم، باید فاز مورد نظر مشخص شود.
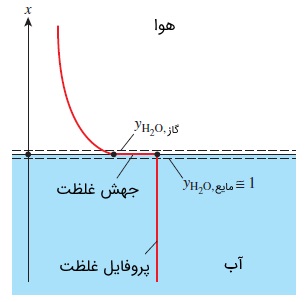
در بسیاری از کاربردهای عملی، فازهای یک مخلوط، در تعادل فازی نیستند؛ زیرا لازمه تعادل فازی این است که ماده از نقاط غلیظتر به نقاطی که غلظت کمتری دارند، منتشر شود. اما این فرآیند، بسیار زمانبر است. با این وجود، تعادل فازی همیشه در سطح تماس دو فاز از یک ماده برقرار است. در مورد سطح تماس هوا -- آب، کسر مولی بخار آب در هوا را میتوان به راحتی و با کمک دادههای اشباع به دست آورد. در ادامه این مقاله و در مثال ۲، این موضوع را بررسی خواهیم کرد.
این وضعیت در سطح تماس جامد -- مایع نیز برقرار است. در یک دمای مشخص، فقط میزان مشخصی از جامد را میتوان در یک مایع حل کرد. قابلیت انحلال جامد در مایع بر این اساس تعیین میشود که تعادل ترمودینامیکی بین جامد و محلول در سطح تماس برقرار باشد. قابلیت انحلال (Solubility)، به عنوان بیشترین مقدار جامد قابل حل در یک مایع در دمای مشخص تعریف میشود. در جدول زیر، اطلاعاتی در مورد قابلیت انحلال سدیم کلرید ($$\large NaCl$$) و کلسیم بیکربنات ($$\large Ca (HO_3)_2$$) در دماهای مختلف ارائه شده است.
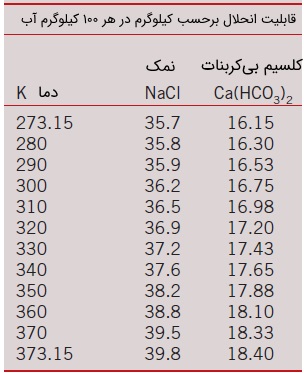
به عنوان مثال، قابلیت انحلال نمک طعام در آب در دمای $$\large 310K$$ برابر با $$\large 36.5$$ کیلوگرم در $$\large 100$$ کیلوگرم آب است. بنابراین، کسر جرمی نمک در آب شور اشباع به راحتی قابل محاسبه است.
$$\large mf_{\text {salt, liquid side}} \:=\: \frac {m_ {\text {salt}}} {m} \:=\: \frac {36.5 \:kg} {(100 \:+\: 36.5) \:kg} \:=\: 0.267$$
در حالی که کسر جرمی نمک در نمک خالص برابر با $$\large mf= 1.0$$ است. در بسیاری از فرآیندها، جذب گاز در مایع اتفاق میافتد. بسیاری از گازها، قابلیت انحلال بسیار کمی در مایعات دارند (مانند هوا در آب). برای چنین محلولهای رقیقی، کسرهای مولی ماده $$\large i$$ در فازهای گاز و مایع در سطح تماس، با هم نسبت مستقیم دارند. به عبارت دیگر، روابط زیر برقرارند.
$$\large y_ {i, \text {gas side}} \:\propto\: y_ {i, \text {liquid side}} \\~\\
\large P_ {i, \text {gas side}} \:\propto\: Py_ {i, \text {liquid side}}$$
زیرا در مخلوط گازهای ایدهآل در تعادل فازی رابطه $$\large y_i = P_i /P$$ برقرار است. این موضوع به عنوان قانون هِنری (Henry's Law) معروف بوده و به صورت زیر تعریف میشود.
$$\large y_ {i, \text {liquid side}} \:=\: \frac {P_{i, \text {gas side}}} {H}$$
$$\large H$$ در رابطه بالا، ثابت هِنری (Henry's Constant) است و به صورت حاصلضرب فشار کل مخلوط گازی در ثابت تناسب تعریف میشود. در یک ماده مشخص و در فشارهای کمتر از $$\large 5\: atm$$، ثابت هنری فقط تابعی از دما بوده و عملاً به فشار وابسته نیست. در مورد قانون هنری، نکات زیر را باید مد نظر قرار داد.
- غلظت گاز حل شده در یک مایع، با ثابت هنری نسبت عکس دارد. بنابراین، هرچه ثابت هنری بزرگتر باشد، غلظت گاز محلول در مایع نیز کمتر خواهد بود.
- ثابت هنری با افزایش دما، بالا میرود. با توجه به بند قبلی میتوان نتیجه گرفت غلظت گاز محلول با دما نسبت عکس دارد. به همین دلیل، با گرم کردن یک مایع، گازهای حل شده در آن، خارج میشوند.
- غلظت گاز حل شده در مایع، با فشار جزئی گاز متناسب است. از این رو، افزایش فشار گاز به افزایش میزان گاز حل شده در مایع میانجامد. از همین قابلیت در انحلال گاز $$\large \text {CO}_2$$ در نوشابههای گازدار استفاده میشود.
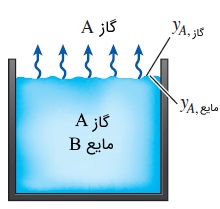
قانون هنری به محلولهای رقیق گاز در مایع محدود است. اما در عمل به شرایطی برمیخوریم که در آنها مقادیر زیادی گاز (یا جامد) در مایع حل شده است. در این مواقع، دیگر رفتار خطی قانون هنری معتبر نیست و کسر مولی گاز محلول در مایع را میتوان به عنوان تابعی از فشار جزئی گاز بیان کرد.
قانون رائول (Raoult's Law) که به صورت زیر تعریف میشود، رابطهای تقریبی برای کسر مولی یک ماده در دو طرف سطح تماس تعادل فازی ارائه میدهد.
$$\large P_ {i, \text {gas side}} \:=\: y_{i, \text {gas side}} P_{\text {total}} \:=\: y_{i, \text {liquid side}} P_ {i, \text {sat}} (T)$$
عبارت $$\large P_ {i, \text {sat}} (T)$$، فشار اشباع ماده $$\large i$$ را در دمای سطح تماس نشان میدهد و $$\large P_{\text {total}}$$ نیز فشار کل در سمت فاز گازی است. دادههای آزمایشگاهی قانون رائول در تمام هندبوکهای شیمی و برای محلولهای متداولی از قبیل محلول آب -- آمونیاک که به طور گسترده در سیستمهای تبرید جذبی کاربرد دارد، در دسترس است.
ممکن است گازها در مواد جامد حل شوند ولی پدیده انتشار در این مورد، پیچیدگیهای زیادی دارد. انحلال یک گاز میتواند مستقل از ساختار جامد باشد یا در سوی مقابل، وابستگی شدیدی به تخلخل داشته باشد. برخی از فرآیندهای انحلال مانند انحلال هیدروژن در تیتانیوم، که مشابه انحلال گاز $$\large \text {CO}_2$$ در آب است، برگشتپذیرند. در این موارد، برای اینکه مقدار گاز موجود در جامد، ثابت باشد، جامد باید در تماس با مخزن گاز باقی بماند. برخی دیگر از انواع انحلال، برگشتناپذیرند. به عنوان مثال، گاز اکسیژن حل شده در تیتانیوم، $$\large \text {TiO}_2$$ را روی سطح تشکیل میدهد و چنین فرآیندی به صورت خود به خود قابل برگشت نیست.
چگالی مولی ماده گازی $$\large i$$ حل شده در جامد و در سطح تماس را با $$\large \overline{ \rho}_ {i, \text {solid side}}$$ نشان میدهیم. این پارامتر با فشار جزئی $$\large P_ {i, \text {gas side}}$$ مربوط به ماده گازی $$\large i$$ در سمت گازی سطح تماس، متناسب است و از رابطه زیر تبعیت میکند.
$$\large \overline{ \rho}_ {i, \text {solid side}} \:=\: S \times P_{i, \text {gas side}} ~~~ ~~~ ~~~ (\text {kmol}/ \text {m} ^3)$$
در رابطه بالا، $$\large S$$ نماد قابلیت انحلال است. اگر فشار برحسب $$\large bar$$ اندازهگیری شود و غلظت مولی را با $$\large kmol$$ ماده $$\large i$$ در هر $$\large m^3$$ نشان دهیم، واحد سنجش قابلیت انحلال، برابر $$\large kmol /m^3$$ خواهد بود. اگر قابلیت انحلال گاز و ضریب انتشار آن در جامد را در یکدیگر ضرب کنیم، عددی به دست میآید که به آن تراوایی (Permeability) گفته میشود. تراوایی معیاری از توانایی گاز در نفوذ به داخل یک ماده جامد است و با ضخامت نسبت عکس دارد. برای بیان تراوایی از واحد اندازهگیری $$\large \text {kmol} / \text {s.m.bar}$$ استفاده میشود.
در انتهای این مقاله خوب است به این نکته اشاره کنیم که اگر در یک فرآیند، تصعید یک جامد خالص مانند یخ یا تبخیر یک مایع خالص مانند آب در محیطی متفاوت مانند هوا اتفاق بیافتد، کسر مولی (یا جرمی) ماده در فاز مایع یا جامد را میتوان برابر با $$\large 1.0$$ در نظر گرفت. در این حالت، فشار جزئی و در نتیجه، کسر مولی ماده در فاز گازی، به راحتی و با استفاده از دادههای اشباع در آن دما، تعیین میشود. همچنین، فرض تعادل ترمودینامیکی در کنار تعادل فازی در سطح تماس برای جامدات خالص، مایعات خالص و محلولها کاملاً منطقی است؛ مگر اینکه در سطح تماس، واکنشهای شیمیایی رخ دهد.
مثال ۲: کسر مولی بخار آب در بالای سطح دریاچه
سؤال: کسر مولی بخار آب را در سطح دریاچهای تعیین کنید که دمای آن $$\large 15\: ^ \circ \text {C}$$ است. مقدار به دست آمده را با کسر مولی آب درون دریاچه مقایسه کنید. فشار اتمسفر در سطح دریاچه برابر $$\large 92\: \text {kPa}$$ است. فشار اشباع آب را در دمای $$\large 15\: ^ \circ \text {C}$$، برابر با $$\large 1.7057\: \text {kPa}$$ در نظر بگیرید.
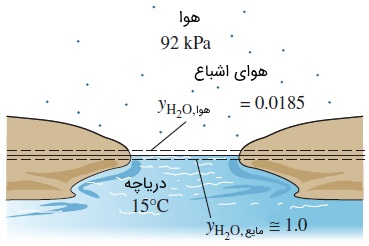
پاسخ: تعادل فازی در سطح آزاد دریاچه برقرار است و به همین دلیل، هوا در سطح آب و دمای سطح تماس، همواره در حالت اشباع قرار دارد. از این رو، فشار جزئی بخار آب در هوای روی سطح دریاچه، برابر با فشار اشباع آب در دمای $$\large 15\: ^ \circ \text {C}$$ است.
$$\large P_v \:=\: P_ {\text {sat} @ \text {15} ^\circ \text {C}} \;=\: 1.7057 \:\text {kPa}$$
کسر مولی بخار آب در هوای روی سطح دریاچه، به صورت زیر تعیین میشود.
$$\large y_v \:=\: \frac {P_v} {P} \:=\: \frac {1.7057\: \text {kPa}} {92\: \text {kPa}} \:=\: 0.0185$$
مقدار کمی هوا در آب حل شده است ولی میتوان از آن صرف نظر کرد. بنابراین، تمام دریاچه را آبِ مایع فرض میکنیم. به این ترتیب، کسر مولی به صورت زیر قابل محاسبه است.
$$\large y_{\text {water, liquid side}} \:\cong\: 1.0$$
توجه کنید که غلظت مولی آب، دقیقاً زیر سطح تماس هوا -- آب برابر با یک بوده و در بالای آن، به کمتر از $$\large 2$$ درصد میرسد. در نتیجه، پروفایل غلظت یک ماده در مرز فازها میتواند شدیداً ناپیوسته باشد.
مثال ۳: حجم هوای محلول در آب
سؤال: کسر مولی هوا را در سطح دریاچهای که دمایش $$\large 17\: ^\circ \text {C}$$ است، محاسبه کنید. فشار اتمسفر در سطح دریاچه برابر با $$\large 92\: \text {kPa}$$ است. فشار اشباع آب را در دمای $$\large 17\: ^\circ \text {C}$$ برابر با $$\large 1.96\: \text {kPa}$$ و ثابت هنری را برای هوای محلول در آب $$\large 290\: \text {K}$$ برابر با $$ \large H= 62,000\: \text {bar}$$ در نظر بگیرید.
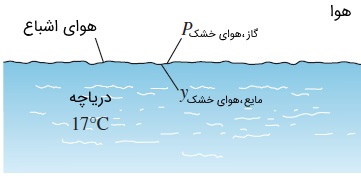
پاسخ: هم هوا و هم بخار را گاز ایدهآل فرض میکنیم. هوا در سطح آب به حالت اشباع رسیده است و در نتیجه، فشار جزئی بخار آب موجود در هوا در سطح دریاچه، برابر با فشار اشباع آب در دمای $$\large 17\: ^\circ \text {C}$$ است.
$$\large P_v \:=\: P_ {\text {sat @} \:17\: ^\circ \text {C}} \:=\: 1.96\: \text {kPa}$$
فشار جزئی هوای خشک به صورت زیر محاسبه میشود.
$$\large P_{\text {dry air}} \:=\: P\:-\: P_v \:=\: 92\:-\: 1.96 \:=\: 90.04\: \text {kPa} \:=\: 0.9004\: \text {bar}$$
توجه کنید از آنجایی که مقدار بخار در هوا بسیار اندک است، میتوانیم با تقریب خوبی (با خطای حداکثر دو درصدی) از فشار بخار صرف نظر کنیم. کسر مولی هوای موجود در آب، براساس قانون هنری به دست میآید.
$$\large Y_{\text {dry air, liquid side}} \:=\: \frac {P_ {\text {dry air, gas side}}} {H} \:=\: \frac {0.9004\: \text {bar}} {62,000\: \text {bar}} \:=\: 1.45 \:\times\: 10 ^{-5}$$
همانطور که انتظار میرفت، مقدار به دست آمده بسیار کوچک است. بنابراین، غلظت هوا در آب، بلافاصله در پایین سطح تماس هوا -- آب برابر با $$\large 1.45$$ مول در هر $$\large 100,000$$ مول است. ولی میدانیم که این مقدار اکسیژن برای ماهیها و سایر جانداران آبی کفایت میکند. این نکته را نیز در نظر داشته باشید که میزان هوای محلول در آب با افزایش عمق، کاهش مییابد؛ مگر اینکه تعادل فازی در تمام دریاچه برقرار باشد.
مثال ۴: انتشار گاز هیدروژن درون صفحهای از جنس نیکل
سؤال: صفحهای از جنس نیکل را در نظر بگیرید که درون مخزنی پر از گاز هیدروژن قرار گرفته است. اندازهگیری فشار و دمای گاز هیدروژن، به ترتیب اعداد $$\large 300\: \text {kPa}$$ و $$\large 358\: \text {K}$$ را نشان میدهد. در شرایطی که تعادل فازی برقرار شده باشد، چگالی مولی و چگالی جرمی هیدروژن را در صفحه نیکلی به دست آورید. قابلیت انحلال هیدروژن در نیکل در این دما، برابر $$\large 0.00901\: \text {kmol}/ \text {m} ^3.\text {bar}$$ است.
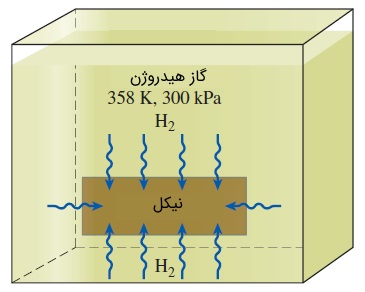
پاسخ: جرم مولی مولکول هیدروژن ($$\large \text {H}_2$$) برابر با $$\large M=2\: \text {kg} /\text {kmol}$$ است. با کمک رابطه زیر، چگالی مولی و سپس چگالی جرمی را به دست میآوریم.
$$\large \overline{\rho}_ {\text {H} _2, \text {solid side}} \:=\: S \times P_ {\text {H} _2, \text {gas side}} \\~\\
\large =\: (0.00901\: \text {kmol} /\text {m} ^3. \text {bar}) (3\: \text {bar}) \:=\: 0.027\: \text {kmol}/ \text {m}^3 \\~\\
\large \rho_ {\text {H} _2, \text {solid side}} \:=\: \overline{\rho}_ {\text {H} _2, \text {solid side}} M_ {\text {H}_2} \\~\\
\large =\: (0.027\: \text {kmol}/ \text {m}^3) (2\: \text {kg}/ \text {kmol}) \:=\: 0.054\: \text {kg}/ \text {m} ^3$$
به عبارت دیگر، پس از برقراری تعادل فازی، $$\large 0.027\: \text {kmol}$$ (معادل $$\large 0.054\: \text {kg}$$) از گاز هیدروژن در هر متر مکعب از صفحه نیکل وجود خواهد داشت.
مثال 5: ساختار فازهای مختلف در یک مخلوط
سؤال: در سیستمهای تبرید جذبی، مخلوط دو فازی و در حالت تعادل فازی آمونیاک مایع ($$\large \text {NH} _3$$) و آب ($$\large \text {H} _2 \text {O}$$) به وفور مورد استفاده قرار میگیرد. چنین مخلوطی را در دمای $$\large 40\: ^\circ \text {C}$$ و مطابق شکل زیر در نظر بگیرید. اگر ساختار فاز مایع از $$\large 70$$ درصد مولی آمونیاک و $$\large 30$$ درصد مولی آب تشکیل شده باشد، ساختار فاز بخار را در این مخلوط محاسبه کنید. فشار بخار در دمای $$\large 40\: ^\circ \text {C}$$ برای آب و آمونیاک به ترتیب برابر با $$\large P_{\text {H}_2 \text{O} ,\: \text {sat}} =7.3851\: \text {kPa}$$ و $$\large P_{\text {NH}_3,\: \text {sat}} =1554.33\: \text {kPa}$$ است.
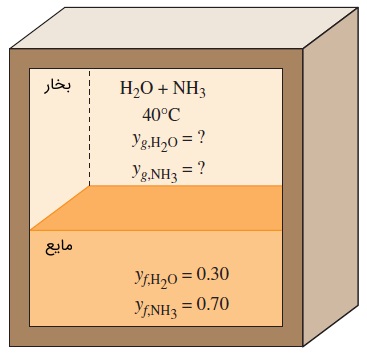
پاسخ: با استفاده از قانون رائول، مقادیر فشار بخار محاسبه میشوند.
$$\large P_{\text {H}_2 \text{O} ,\: \text {gas side}} \:=\: y_{\text {H}_2 \text{O} ,\: \text {liquid side}} \times P_ {\text {H}_2 \text{O} ,\: \text {sat}} (T) \:=\: 0.30 (7.3851\: \text {kPa}) \:=\: 2.22\: \text {kPa} \\~\\
\large P_{\text {NH}_3 ,\: \text {gas side}} \:=\: y_{\text {NH}_3 ,\: \text {liquid side}} \times P_ {\text {NH}_3 ,\: \text {sat}} (T) \:=\: 0.70 (1554.33\: \text {kPa}) \:=\: 1088.03\: \text {kPa}$$
حالا فشار کل مخلوط در تعادل فازی را به دست میآوریم.
$$\large P_{\text {total}} \:=\: P_ {\text {H}_2 \text {O}} \:+\: P_ {\text {NH}_3} \:=\: 2.22 \:+\: 1088.03 \:=\: 1090.25\: \text {kPa}$$
در نهایت، کسرهای مولی در فاز گازی به صورت زیر خواهند بود.
$$\large y_ {\text {H}_2 \text {O} ,\: \text {gas side}} \:=\: \frac {P_ {\text {H}_2 \text {O} ,\: \text {gas side}}} {P_ {\text {total}}} \:=\: \frac {2.22 \text {kPa}} {1090.25\: \text {kPa}} \:=\: 0.0020 \\~\\
\large y_ {\text {NH}_3 ,\: \text {gas side}} \:=\: \frac {P_ {\text {NH}_3 ,\: \text {gas side}}} {P_ {\text {total}}} \:=\: \frac {1088.03 \text {kPa}} {1090.25\: \text {kPa}} \:=\: 0.9980$$
همانگونه که مشاهده کردید، فاز گازی عموماً از آمونیاک تشکیل شده که همین عامل، کاربرد این مخلوط را در تبرید جذبی مناسب میسازد.
در صورت علاقهمندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- ترمودینامیک — از صفر تا صد
- قانون دوم ترمودینامیک - از صفر تا صد
- فرآیند احتراق یا سوختن — از صفر تا صد
- تعریف گرما و دما در ترمودینامیک — به زبان ساده
^^









