انتقال حرارت جابجایی — از صفر تا صد
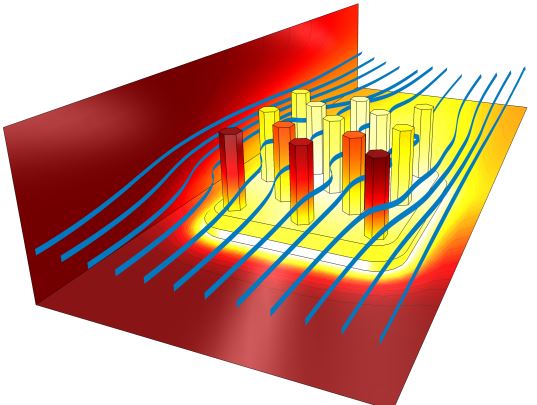
به انتقال حرارتی که همزمان با حرکت سیال اتفاق میافتد، انتقال حرارت به روش جابجایی (Convection Heat Transfer) گفته میشود. بسته به نوع فرآیند صورت گرفته، جابجایی حرارتی به دو دسته آزاد و اجباری تقسیم میشود.

در جابجایی آزاد، انرژی منتقل شده ناشی از عواملی طبیعی همچون نیروی ارشمیدس است. اما در جابجایی اجباری نیروهای خارجی مثل پمپ یا فن منجر به حرکت سیال میشود.
جابجایی اجباری
تحلیل انتقال حرارت جابجایی، به دلیل همزمان بودن فرآیند هدایت حرارتی و حرکت سیال، پیچیده است. توجه داشته باشید که هرچه سرعت سیال بیشتر باشد، نرخ انتقال حرارت نیز افزایش خواهد یافت.
همچنین میتوان سرعت انتقال حرارت جابجایی را با استفاده از قانون سرمایش نیوتن و در قالب فرمول زیر بیان کرد.
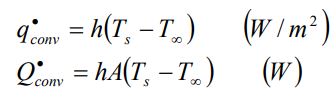
ضریب انتقال حرارت جابجایی h به خواص سیال، زبری سطح و نوع رژیم جریان (لایهای یا توربولانس) وابسته است.
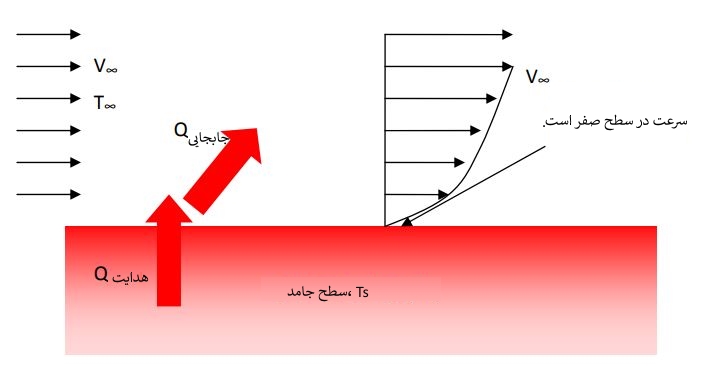
همانطور که در شکل نیز دیده میشود، سرعت سیال در سطح برابر با صفر (شرط عدم لغزش) در نظر گرفته شده. با این فرض میتوان نتیجه گرفت، در حالتی که سرعت سیال ناچیز باشد، انتقال حرارت صورت گرفته، فقط ناشی از هدایت حرارتی خواهد بود. بنابراین میتوان معادلات مربوط به انتقال گرما را به صورت زیر بیان کرد:
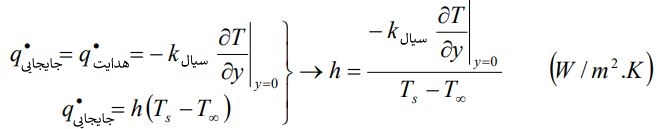
در حالت کلی ضریب انتقال حرارت جابجایی، در جهت جریان تغییر میکند. بنابراین به منظور بررسی حرارتی یک سیستم، از میانگین این ضریب در طول یک صفحه استفاده میشود.
لایه مرزی سرعت
جریانی را در طول یک صفحه در نظر بگیرید. فرض کنید سیال مد نظر با دمای ∞T و ∞U روی این صفحه حرکت میکند. (مطابق شکل)
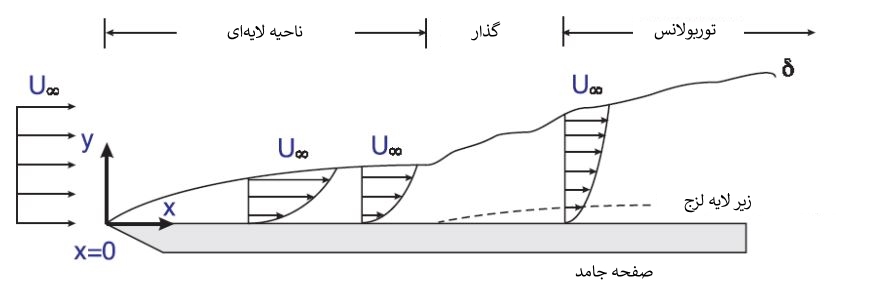
توجه داشته باشید که شرط عدم لغزش نیز در نظر گرفته شده؛ بنابراین سرعت سیال روی صفحه جامد برابر با صفر خواهد بود. در چنین سیستمی، ذرات سیال به صورت لایهای روی یکدیگر قرار گرفتهاند، در نتیجه لایههایی که با سرعت کمتری حرکت میکنند به وسیله اصطکاک، به لایههای بالاتر نیرو وارد کرده و سرعت آنها را کم میکنند. تاثیر این نیرو تا ارتفاع مشخصی از صفحه حس خواهد شد. در این منطقه، سرعت سیال متفاوت با ∞U است. به همین دلیل این ناحیه را «لایهمرزی» مینامند.
در لایهمرزی، اثرات ویسکوزیته حس میشوند. با توجه به مطالب بیان شده، میتوان تنش برشی روی سطح را با استفاده از رابطه زیر توصیف کرد.
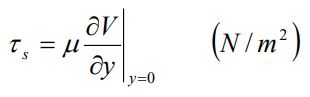
در این معادله، μ ویسکوزیته سینماتیکی سیال است که واحد آن بر حسب kg/m.s یا N.s/m2 بیان میشود. از نظر مفهومی، ویسکوزیته سیال بیان کننده مقاومت آن در مقابل حرکت است. مثلا ویسکوزیته عسل از آب بیشتر در نظر گرفته میشود. از نظر فیزیکی هم میتوان درک کرد که عسل به نسبت آب، سختتر جریان مییابد.

نیروی برشی را میتوان با تعریف مفهومی تحت عنوان ضریب اصطکاک توصیف کرد. با استفاده از این بیان، تنش برشی با استفاده از معادله زیر قابل بیان است.
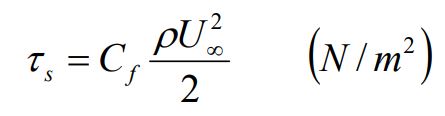
در این رابطه، Cf به عنوان ضریب اصطکاک در نظر گرفته میشود. توجه داشته باشید که در حالت کلی، بخشهای سیال را میتوان به سه ناحیه لایهای، گذرا و توربولانس تقسیمبندی کرد.
گروههای بیبعد
به منظور سادهتر کردن مسائل جابجایی حرارتی از تعاریفی تحت عنوان گروههای بی بعد استفاده میشود.
- ناسلت: نسبت انتقال حرارت جابجایی به هدایتی
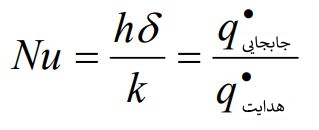
در این معادله δ طول مشخصه است که در موارد صفحه و استوانه به ترتیب برابر L و D در نظر گرفته میشود. - رینلدز: نسبت نیروی اینرسی به ویسکوز

- پرانتل: نسبت ضخامت لایه مرزی سرعت به حرارت

در این معادله خواص سیال عبارتند از:
لایه مرزی حرارتی
مشابه با لایهمرزی سرعت، لایهمرزی حرارتی نیز زمانی به وجود میآید که سیالی رو یک سطح جریان یابد. در این حالت ضخامت این لایه را با δt نشان میدهند.
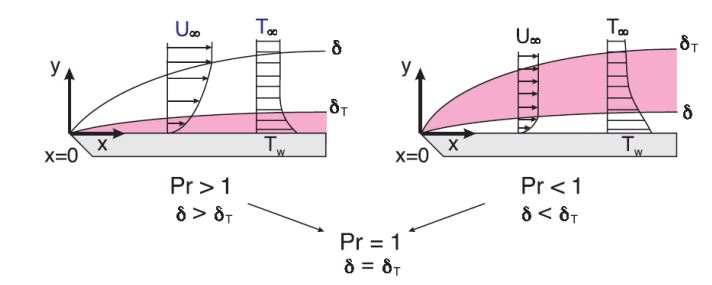
ضخامت نسبی لایهمرزی سرعت و حرارت توسط عدد پرانتل توصیف میشود. برای نمونه، موادی همچون فلزات مایع از عدد پرانتل پایینی برخوردار هستند.
جریان روی سطح تخت
ضرایب انتقال حرارت و اصطکاک را میتوان با حل معادلات پایستگی جرم، مومنتوم و انرژی بدست آورد. همچنین این مشخصات را میتوان به صورت آزمایشگاهی تعیین کرد. عدد ناسلت به صورت زیر تعریف میشود.
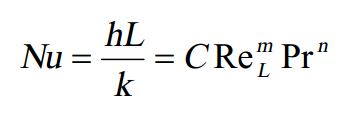
در این معادله C، m و n ثابت هستند و L به عنوان طول صفحه در نظر گرفته میشود. خواص سیال در دمایی تحت عنوان «دمای فیلم» در نظر گرفته میشوند. در واقع این دما برابر با میانگین دمای سیال و محیط است.
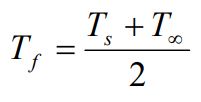
جریان لایهای
ضریب اصطکاک و ناسلت محلی در حالتی که جریان سیالی روی یک صفحه با دمای یکنواخت جریان مییابد، به صورت زیر در نظر گرفته میشود.
با این فرض که رینلدز بحرانی برابر با 500000 باشد، میتوان طول بحرانی (xcr) را با استفاده از رابطه زیر محاسبه کرد.
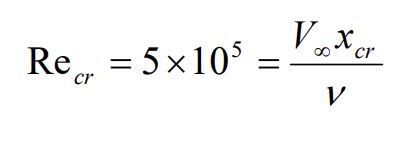
جریان توربولانس
ضریب اصطکاک و ناسلت محلی در مکان x، برای سیالی که روی یک سطح جریان دارد، با استفاده از رابطه زیر محاسبه میشود.
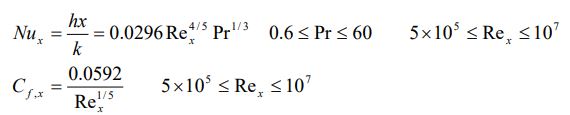
بنابراین مقادیر میانگین ناسلت و ضریب اصطکاک در مکان x به صورت زیر بدست میآیند.
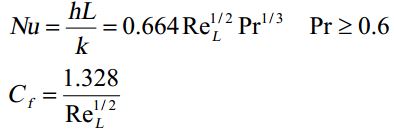
لایهمرزی جریان لایهای و توربولانس
فرض کنید سیالی روی یک صفحه جریان دارد. تصور کنید طول صفحه انقدر باشد که سیال از حالت لایهای به توربولانس تبدیل شود؛ در این حالت ضریب اصطکاک و ضریب انتقال حرارت جابجایی میانگین را میتوان به صورت زیر محاسبه کرد:
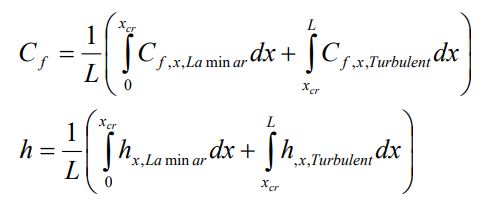
با فرض این که مقدار بحرانی رینلدز برابر با 500000 باشد، عدد ناسلت و ضریب اصطکاک میانگین، به صورت زیر محاسبه میشوند.
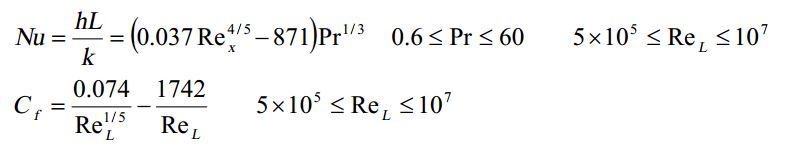
معادلات بالا با این فرض حاصل شده که دمای صفحه یکنواخت باشد. با این حال در اکثر مواردی که دما متغیر باشد نیز میتوانند کاربرد داشته باشند.
مثال 1
روغن موتور در دمای 60 درجه، روی یه سطح به طول 5 متر، دمای 20 درجه و با سرعت 2m/s جریان مییابد. (مطابق با شکل زیر)
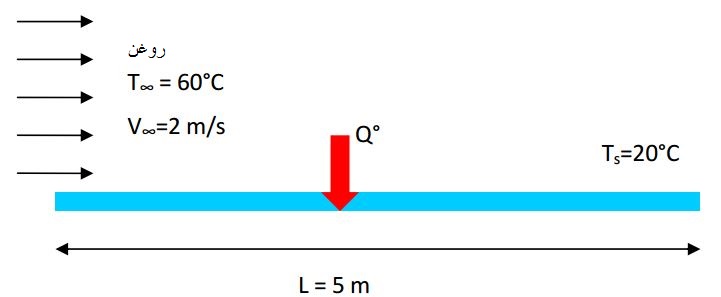
با فرض اینکه رینلدز بحرانی برابر با 500000 در نظر گرفته شود خواص روغن مفروض در دمای فیلم برابر هستند با:
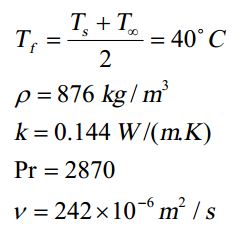
از طرفی عدد رینلدز برای یک صفحه تخت به صورت زیر محاسبه میشود:
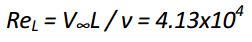
توجه کنید که این مقدار بسیار کمتر از عدد بحرانی رینلدز است. با توجه به خواص سیال و دمای فیلم، ضریب اصطکاک و نیروی درگ ناشی از آن برابر هستند با:
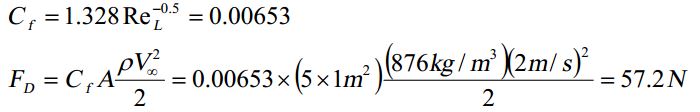
از طرفی عدد ناسلت و نهایتا انتقال حرارت را میتوان به صورت زیر محاسبه کرد.
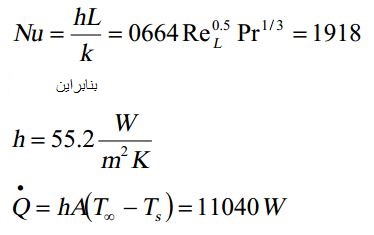
جریان روی استوانه و کره
طول مشخصه یک لوله دایروی یا کره، همان قطر خارجی آن است. با این فرض، عدد رینلدز به صورت محاسبه میشود.
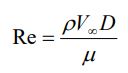
توجه داشته باشید که ریندلز بحرانی برای استوانه و کره برابر با 200000 است. در رینلدزهای پایین (Re<4) سیال به طور کامل به جسم متصل است و پدیده جدایی هیچگاه اتفاق نخواهد افتاد.
این در حالی است که در رینلدزهای بالاتر، جریان پس از اندکی چرخیدن روی استوانه (یا کره) از جسم جدا خواهد شد. پس از جدایی آن، گردابهای در پشت جسم تشکیل میشود که افزایش نیروی درگ را در پی خواهد داشت. به نقطهای که در آن جریان جدا میشود، نقطه جدایی (Seperation Point) گفته میشود.
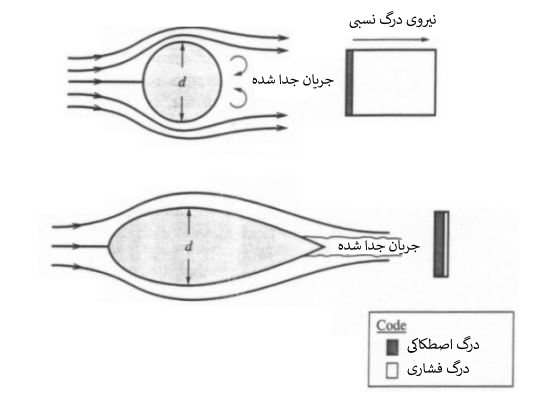
در طراحی اجسام پرنده همچون هواپیماها تلاش بر این است تا جدایی در زاویهای بیشتر اتفاق بیافتد چرا که دیرتر جدا شدن سیال، درگ کوچکتری را منجر میشود که مطلوب نظر طراحان است. نقطه جدایی در شکلهای زیر نشان داده شده.
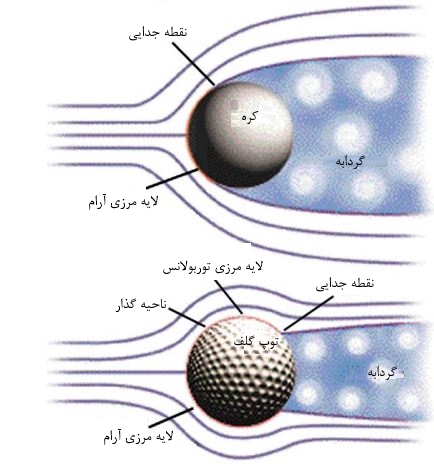
در حالتی که سیالی روی استوانه یا کره عبور میکند، زاویه جدایی جریان در حالت لایهای برابر با 80 و در حالت توربولانس این زاویه معادل 140 درجه است. همچنین ناسلت متوسط برای جریان عبوری روی استوانه توسط «چرچیل» (Churchill) و «برنشتاین» (Bernstein)، به صورت زیر ارائه شده.
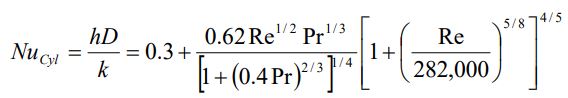
در این فرمول خواص جایگذاری شده در دمای فیلم (Tf = (Ts + T∞)/2) هستند. «ویتاکر» (Whitaker) نیز رابطه زیر را به منظور محاسبه ناسلت جریان روی کره، ارائه میدهد.
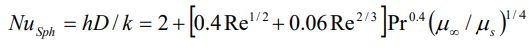
این رابطه در رینلدزهای بین 3.5 تا 80000 و پرانتل بین 0.7 تا 380 صادق است. همچنین توجه داشته باشید که خواص جایگذاری شده در دمای ∞T فرض شده و μs در دمای سطح در نظر گرفته میشود.
مثال 2
جریانی از هوا در دمای 23 درجه و با سرعت 10 متر بر ثانیه، روی کرهای از جنس مس با قطر 10 میلیمتر و با دمای 75 درجه عبور میکند. زمان مورد نیاز به منظور سرد شدن کره تا دمای 35 درجه چقدر است؟
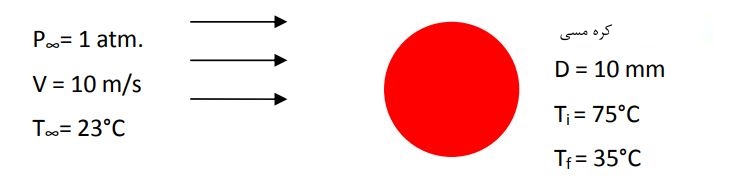
فرضیات:
1. دمای کره به صورت یکنواخت است.
2. از اثرات تابش صرف نظر شده.
خواص سیال و کره مفروض به شرح زیر هستند.
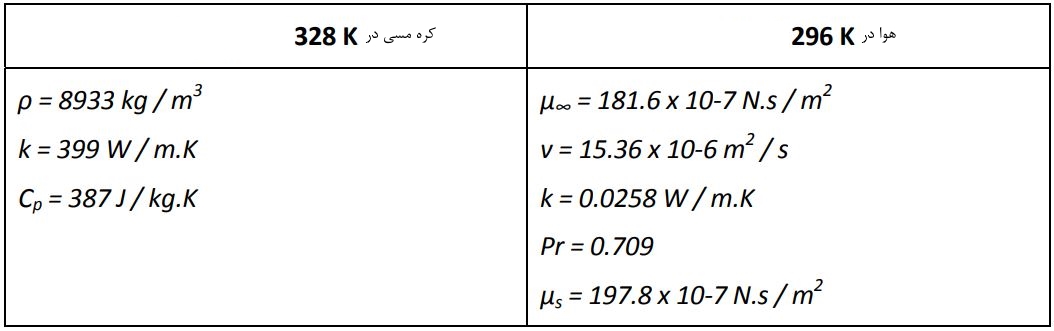
زمان مورد نیاز برای سردن شدن کره تا دمای 35 درجه با استفاده از مفهوم ظرفیت حرارتی و به صورت زیر قابل محاسبه است.
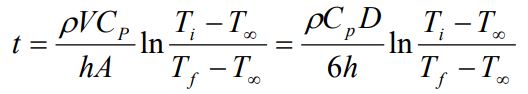
میتوان از رابطه ویتاکر نیز به منظور محاسبه h حول کره استفاده کرد. بنابراین:
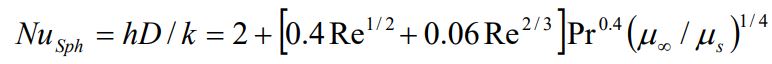
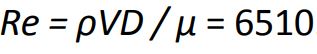

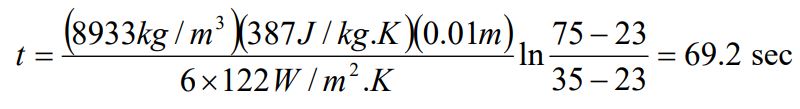
^^











سپاسگزارم. مطلب بسیار مفیدی بود
با سلام.
خیلی عالی بود. ممنون
انتقال حرارت دستی
سلام وقت تون بخیر از مطالب خوب تون سپاس گزارم بنده سوالی داشتم:
درون یک میکرو لوله که به جداره آن شار حرارتی وارد می شود رابطه ای برای دمای جداره با طول لوله پیدا کنید
اثبات روایط و از کدوم منبع میتونم مطالعه کنم ؟؟