انتقال حرارت تشعشعی — از صفر تا صد

پیشتر در وبلاگ فرادرس در مورد انتقال حرارت به روش هدایت و جابجایی حرارتی صحبت شد. در این قسمت قصد داریم تا در مورد روش سوم انتقال حرارت که تحت عنوان انتقال حرارت تشعشعی -یا همان تابشی- شناخته میشود، بحث کنیم.
«تابش» (Radiation) عبارت است از انتقال حرارتی که از طریق امواج الکترومغناطیسی صورت میگیرد. از آنجایی که این امواج با سرعت نور منتقل میشوند، بنابراین سرعت انتقال انرژی در این حالت نیز برابر با سرعت نور است. شاید به همین دلیل است که دستگاه مایکروویو غذا را با سرعت نور گرم میکند چرا که مکانیزم آن مبتنی بر انتقال حرارت تشعشعی است!
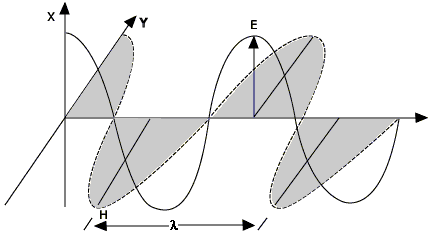
اولین بار مفهوم انتقال انرژی از طریق امواج الکترومغناطیسی توسط «جیمز کلارک ماکسول» (James Clerk Maxwell)، دانشمند اسکاتلندی مطرح شد. او نشان داد که انتقال انرژی نیز با سرعت نور اتفاق میافتد. معمولا امواج الکترومغناطیسی را بر اساس فرکانس و طول موجشان دستهبندی میکنند. ارتباط میان طول موج و فرکانس به صورت زیر است.
λ =c/ν
در رابطه بالا λ و ν به ترتیب برابر با طول موج و فرکانس هستند. همچنین مقدار c سرعت نور را نشان میدهد که اندازه آن برابر با ۱۰۸×۲.۹۹ متر بر ثانیه است. رابطه بالا نشان میدهد که طول موج و فرکانس رابطهای عکس با یکدیگر دارند. در حقیقت بزرگ بودن یکی از آنها کوچک بودن دیگری را معنی میدهد.
عدد بیان شده در بالا، سرعت نور در خلا را نشان میدهد. واقعیت این است که این مقدار در محیطهای مختلف متفاوت است. از این رو برای بدست آوردن سرعت نور در محیطی به جز خلا، از رابطه زیر استفاده میشود.
c = c0/n
در این رابطه n ضریب شکست محیطی است که میخواهیم سرعت نور را در آن بیابیم. برای هوا این ضریب را تقریبا برابر با ۱ و برای آب ۱.۵ در نظر میگیرند. توجه داشته باشید که فرکانس یک موج الکترومغناطیسی فقط به منبع انتشار آن وابسته است و به بستری که در آن، موج منتشر میشود، ارتباطی ندارد.
واحد فرکانس برابر با سیکل در ثانیه است. جالب است بدانید که برای بسیاری از پدیدهها میتوان از این مفهوم بهره برد. برای مثال همین الان که در حال خواندن این مطلب هستید، میتوانید عددی تحت عنوان تعداد کلمات خوانده شده در ثانیه را تعریف کنید. این عدد در حقیقت فرکانس مطالعه شما است! فرکانس یک موج میتواند از چند سیکل در ثانیه تا میلیونها سیکل در ثانیه متغیر باشد.
در ابتدای قرن بیستم، انیشتین نظریه جدیدی را در مورد انتشار امواج تابشی ارائه کرد. بر مبنای این تئوری، انتقال انرژی عبارت است از انتقال بستههایی از انرژی، که «فوتون» (Photon) نامیده میشوند. برای هر کدام از این بستهها میتوان فرکانسی برابر با ν [تلفظ این نماد نو است] تعریف کرد. با توجه به فرکانس اختصاص داده شده به آنها میتوان گفت انرژی هر کدام از این بستهها برابر با مقدار زیر است.
e = h×ν = hc/λ
در رابطه بالا h مقداری ثابت، برابر با34-۱۰×۶.۶۲۵ است که آن را «ثابت پلانک» (Planck's constant) مینامند. توجه داشته باشید که همواره در این فرض مقادیر c و h اعداد ثابتی هستند. از این رو میتوان گفت انرژی بستهها یا همان فوتونها، فقط به طول موج آنها وابسته است. از رابطه بالا میتوان فهمید که طول موج پایینتر به معنای انرژی بیشتر فوتون است. برای نمونه «امواج ایکس» (X-rays) و یا «گاما» (Gamma) دارای طول موج بسیار کمی هستند، از این رو دارای انرژی بالایی بوده و میتوانند بسیار مخرب باشند.

شکل زیر طیفی از طول موجهای مختلف را نشان میدهد. همانطور که در آن پیدا است، طول موج میتواند از ۱۰-۱۰ تا ۱۰۱۰ میکرومتر متغیر باشد. جالب است بدانید که امواج کیهانی کمترین طول موج و الکتریکی بیشتر طول موج را دارند.
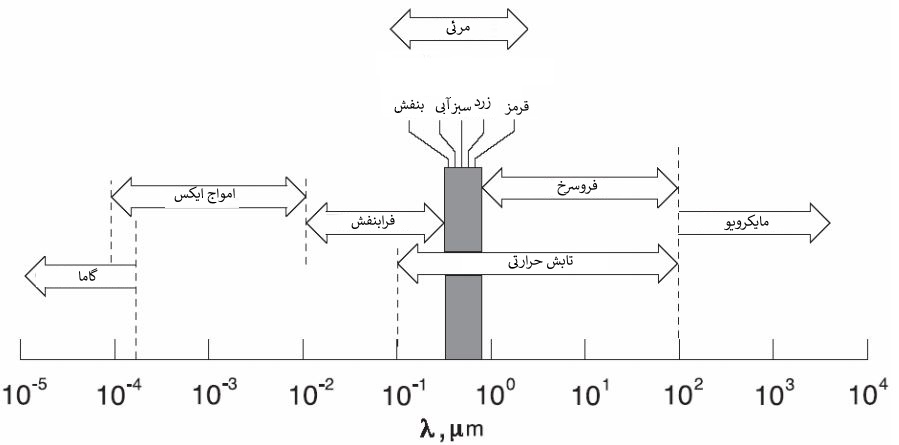
همانطور که در شکل مشخص شده، انتقال امواج حرارتی در طول موج بین ۱-۱۰ تا ۱۰۲ اتفاق میافتد. علت اصلی انتقال حرارت به روش تشعشع، حرکات دورانی و ارتعاشی مولکولها، اتمها و الکترونها است. در حقیقت مقدار دما برآیند این تحرکات را نشان میدهد. از این رو افزایش دما باعث افزایش نرخ انتقال حرارت تابشی میشود.
مفهومی که آن را با عنوان نور میشناسیم در حقیقت بخش مرئی از طیف الکترومغناطیسی است. شکل بالا نشان میدهد که طول موج نوری زیر مجموعه طول موج حرارتی است.
انتقال حرارت تشعشعی، پدیدهای حجمی است. البته برای اجسام ماتی همچون فلزات، تابش به صورت سطحی اتفاق میافتد. توجه داشته باشید که مشخصههای تابشی یک سطح میتواند با روکش کردن آن با لایههای جدید، انجام شود.
تابش جسم سیاه
به جسمی که کاملترین جذب کننده و ساطع کننده انرژی در یک طول موج خاص باشد، «جسم سیاه» (Black Body) گفته میشود. در یک دما و طول خاص هیچ جسمی نمیتواند بیشتر از جسم سیاه انرژی ساطع کند. از نظر تئوری یک جسم سیاه، انرژی را در تمامی جهات به طور یکنواخت جذب میکند. اما انرژی جذب شده، وابسته به جهت تابش موج رسیده به آن است.
میزان انرژی ساطع شده از یک جسم سیاه، در واحد زمان و در واحد سطح را میتوان با استفاده از قانون استفان-بولتزمن (Stefan-Boltzman) محاسبه کرد.
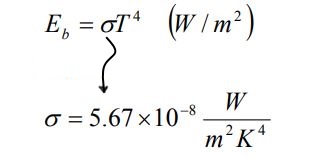
در رابطه بالا T دمای مطلق سطح جسم سیاه است که بر حسب کلوین بیان میشود. همچنین Eb را توان گسیل جسم سیاه مینامند. برای نمونه میتوان یک محفظه بسته که دارای حفرهایی کوچک است را مدلسازی خوبی برای جسم سیاه دانست. توان تشعشعی جسم سیاه برابر با میزان انرژی ساطع شده از آن در واحد زمان، سطح و طول موج است. این کمیت را با نماد Ebλ نشان میدهند. قانون توزیع پلانک بیان میکند که برای چنین جسمی رابطه میان Ebλ با دما و طول موج به صورت زیر است.

توجه داشته باشید که در واقعیت این رابطه برای محیط خلا و یا گاز صادق است. برای دیگر محیطها میتوان از C1/n2 به جای C1 استفاده کرد. n نیز همان ضریب شکست محیط است که در بالا به آن اشاره کردیم.
شکل زیر میزان انرژی ساطع شده از جسم سیاه را در دماها و طول موجهای مختلف نشان میدهد.
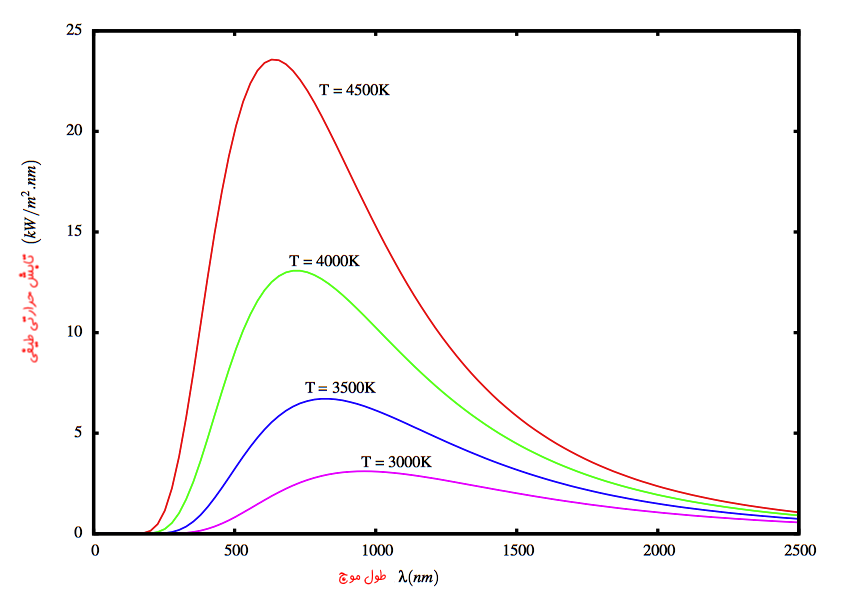
همچنین طول موجی که در آن بیشترین تشعشع اتفاق میافتد را میتوان با استفاده از «قانون جابجایی وین» (Wien’s displacement law)، از طریق رابطه زیر توصیف کرد.
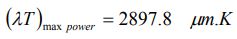
با انتگرالگیری از این معادله در تمامی طول موجها، میتوان توانایی انتشار انرژی جسم سیاه را بر حسب دمای سطح آن و به صورت زیر بدست آورد.
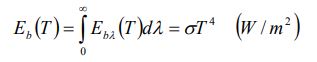
معادله بالا فرض میکند که یک جسم سیاه در دمای ثابت T قرار گرفته و در تمامی طول موجهای ممکن، انرژی ساطع کرده است. اما واقعیت این است که یک جسم خاص در بازهای محدود از طول موج، انرژی ساطع میکند. برای اینکه مجبور نباشیم معادله بالا را به صورت عددی حل کنیم، مقداری بیبعد را تحت عنوان تابع تابش جسم سیاه تعریف میکنیم که با نماد fλ نشان داده میشود. این کمیت که تابعی از دما است را میتوان با استفاده از انتگرال زیر محاسبه کرد.
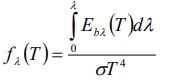
کمیت بالا نشان دهنده کسری از انرژی است که در طول موج بین 0 تا λ از جسم سیاهی با دمای T ساطع میشود. با توجه به اینکه صورت رابطه مربوط به fλ به شکل انتگرالی است، میتوان گفت:
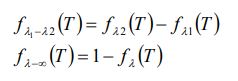
در کتب مختلف مقدار کمیت بالا در طول موجهای مختلف، محاسبه و جداولی برای آن ارائه شده است. برای نمونه جدول زیر مقدار fλ را در بازه بین ۲۰۰ تا ۲۰۰۰ - میکرومتر.کلوین - ارائه داده است.
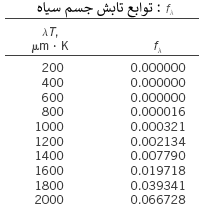
همچنین در شکل زیر میتوانید میزان انرژی ساطع شده در بازه λ۱ تا λ۲ را مشاهده کنید.
برای درک بهتر بیان بالا، به مثال ارائه شده در ادامه توجه فرمایید.
مثال ۱
دمای تنگستن موجود در لامپ در حدود ۲۵۰۰ درجه کلوین است. با فرض جسم سیاه بودن تنگستن، میزان انرژی ساطع شده توسط سیم، در طول موج مرتبط با نور مرئی چقدر است؟
طول موج نور مرئی در بین ۰.۴ تا ۰.۷۶ میکرومتر است. از این رو در ابتدا بایستی حاصلضرب λT را محاسبه کرد، سپس مقدار fλ مرتبط با آن را از جدول بالا خواند. بنابراین میتوان به ترتیب زیر عمل کرد.
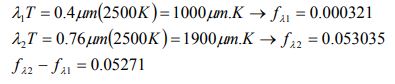
مقدار بالا نشان میدهد که تنها ۵ درصد از کل انرژی تابشی ساطع شده از سیم تنگستن در بازه نور مرئی است. در واقع نوری که ما از لامپ میبینیم، ۵ درصد کل انرژی ساطع شده از لامپ است.
ثابتهای تابشی
جسم سیاه میتواند مرجع خوبی برای بررسی مشخصههای تابشی یک سطح واقعی باشد.
گسيلندگی
به نسبت انرژی ساطع شده توسط یک سطح به انرژی ساطع شده توسط جسم سیاه که در دمایی یکسان قرار گرفتهاند، «گسیلندگی» (Emissivity) گفته میشود که با ε نشان داده میشود. واضح است که این مقدار همواره بین صفر و یک قرار میگیرد. این کمیت به ما نشان میدهد که خواص تابشی یک سطح واقعی به چه میزان به جسم سیاه نزدیک است [ضریب گسیلندگی برای جسم سیاه برابر با یک است]. از تعریف ارائه شده برای این مقدار پیدا است که میتوان این عدد را با استفاده از رابطه زیر محاسبه کرد.
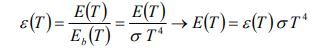
رابطه بالا گسیلندگی کلی یک سطح را نشان میدهد. اما در بعضی از تحلیلها از توانایی گسیلش سطح، در یک طول موج خاص استفاده میشود. در چنین شرایطی میتوان از مفهوم گسیلندگی طیفی بهره برد. گسیلندگی سطحی را با نماد ελ نشان میدهند و مقدار آن با استفاده از رابطه زیر قابل محاسبه است.
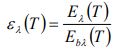
توجه داشته باشید که در هر دو مفهوم بالا دمای سطح واقعی و جسم سیاه برابر هستند. در رابطه بالا (Eλ(T توانِ تابشِ طیفی یک جسم سیاه است. در شکل زیر این مفهوم در قالب نمودار نشان داده شده. همانطور که در آن میبینید، توان تابشی یک سطح واقعی همواره کمتر از جسم سیاه است.
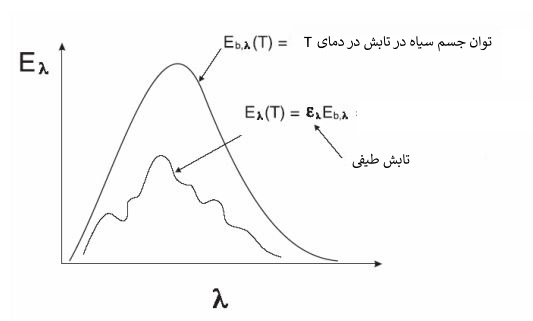
مشخصههای تابشی یک سطح
نرخ انتقال حرارت تشعشعی به ویژگیهای فیزیکی سطح نیز وابسته است. از این رو، به منظور سادگی محاسبات مربوط به تابش، سطوح مختلف در دستهبندیهای زیر قرار میگیرند.
سطح پخشکننده: به سطحی که خواص تابشی آن مستقل از جهت انتشار امواج باشد.
سطح خاکستری: به سطحی گفته میشود که خواص تابشی آن مستقل از طول موج تابش است.
ضریب انتشار یک سطح خاکستری را میتوان با استفاده از رابطه زیر محاسبه کرد.
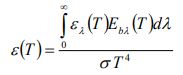
ضریب انتشار معرفی شده در معادله بالا به شدت به دمای T وابسته است.
جذب، بازتاب و شفافیت یک سطح
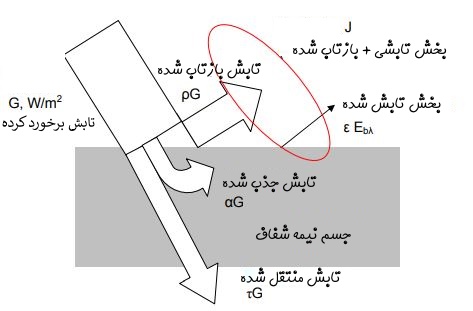
به میزان انرژی تابشی که به یک سطح میرسد، «پرتوافکنی» (Irradiation) گفته میشود که با نماد G نشان میدهند.
جذب (α): نسبت انرژی جذب شده به انرژی تابیده شده به یک سطح
بازتاب (ρ): نسبت انرژی بازتاب شده به کل انرژی تابشی وارد شده به سطح
شفافیت: نسبت انرژی عبوری به کل انرژی وارد شده به سطح
تشعشع خروجی (J): عبارت است از نسبت انرژی ساطع شده به کل انرژی وارد شده به یک سطح
میتوان خصوصیات ارائه شده در بالا را در قالب زیر بیان کرد:

با استفاده از قانون اول ترمودینامیک میدانیم که مجموع انرژیهای جذب شده، بازتاب شده و منتقل شده از سطح بایستی برابر با کل انرژی ورودی به آن باشد. از این رو میتوان این قانون را به شکل زیر بیان کرد:
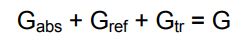
با تقسیم عبارت بالا به G، رابطه میان ضرایب بیان شده برای یک سطح، به شکل زیر بدست میآید.
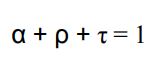
در شکلی که در ادامه آمده، هر کدام از این انرژیها، به تفکیک نشان داده شده است.
برای یک سطح مات مقدار τ برابر با صفر است. از این رو معادله بالا به شکل زیر در میآید.
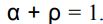
توجه داشته باشید که تعاریف ارائه شده در بالا در تمامی جهات و تمامی فرکانسها صادق هستند. ما همچنین میتوانیم این خواص را بر اساس خواص طیفی آنها بیان کنیم. برای نمونه میتوان G را به شکل زیر نوشت.

توجه کنید که ضریب جذبی α مستقل از دمای سطح است و به شدت به دمای منبعی وابسته است که امواج تابشی از سمت آن میآید. برای نمونه ضریب جذبی سقفی که از بتن باشد، نسبت به تابش خورشید برابر با ۰.۶ است. اما این ضریب نسبت به تابشی که از محیط اطراف میآید، برابر با ۰.۹ است.
قانون کیر شُهف
مطابق شکل زیر یک محفظه و یک سطح را در نظر بگیرید که در دمای یکنواخت T قرار گرفتهاند.
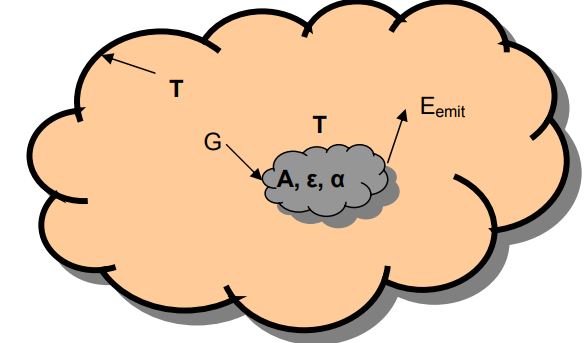
با فرض اینکه محفظه مفروض در تعادل ترمودینامیکی باشد میتوان کل انرژی رسیده به آن را به صورت زیر نوشت.
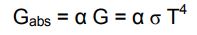
در این حالت میزان انرژی ساطع شده از آن نیز برابر با مقدار زیر است.
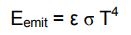
از آنجایی که جسم مفروض در تعادل ترمودینامیکی است بنابراین انرژی وارده شده و خارج شده از آن با یکدیگر برابر هستند. از این رو میتوان گفت:
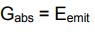
با توجه به رابطه بالا نتیجه مهم زیر حاصل میشود.
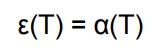
رابطه بالا بیان میکند که انرژی تابیده شده توسط یک سطح که در دمای T قرار گرفته، برابر است با کل انرژی تابشی جذبی که از جسم سیاهی با دمای T دریافت کرده است.
این قانون را میتوان به فرمت طیفی،به شکل زیر نشان داد.
تابش خورشیدی
به انرژی خورشیدی که به سطح اتمسفر زمین میرسد، ثابت خورشیدی گفته میشود که برابر با مقدار زیر است.

با توجه به این که مدار چرخش زمین به دور خورشید، بیضیگون است، مقدار ثابت خورشیدی در سال به میزان ۳.۴± درصد تغییر میکند. این عدد بسیار اندک است، از این رو مقدار تابش را تقریبا ثابت فرض میکنند.
سوال: به نظر شما چطور میتوان با توجه به معلوم بودن ثابت خورشیدی، دمای سطح خورشید را یافت.
از آنجایی که بین خورشید و اتمسفرِ زمین مادهای وجود ندارد، بنابراین تمامی انرژی ساطع شده از سطح خورشید به اتمسفر زمین میرسد. در نتیجه با فرض کردن خورشید به عنوان جسم سیاه میتوان دمای موثر سطح آن را یافت. بخشی از انرژی دریافت شده، توسط اتمسفر جذب شده و بخش دیگری از آن پراکنده میشود.
پخش شدن و بازتاب انرژی دریافت شده توسط اتمسفر، مقداری از ثابت خورشیدی را کم میکند.
ضریب دید
میزان انتقال حرارت تابشی بین دو صفحه، علاوه بر خواص تابشی دو سطح، به زاویه آنها نسبت به یکدیگر نیز مرتبط است. بدین منظور در انتقال حرارت تابشی از مفهومی تحت عنوان ضریب دید استفاده میشود. این عدد فقط به شرایط هندسی دو سطح وابسته است.
در محاسبات مربوط به ضریب دید، فرض میشود که انتقال حرارت تابشی به صورتی کاملا یکنواخت در تمامی سطح اتفاق میافتد. همچنین فرض بر این است که فضای میان سطوح، انرژی مبادله شده میان دو سطح را جذب و یا منعکس نمیکند.
- Fij برابر است با نسبت انرژی برخورد کرده به سطح j به انرژی ساطع شده از سطح i. با توجه به تعریف، میتوان گذارههای زیر را بیان کرد:
- ضریب دیدِ سطوح، بین ۰ و ۱ قرار دارند.
- 0=Fij به این معنی است که دو سطح یکدیگر را نمیبینند. از طرفی ۱=Fij به معنای این است که سطح j به طور کامل سطح i را پوشانده است.
- حرارت تابشی که به سطحی برخورد میکند، نیاز نیست الزاما توسط سطح مذکور جذب شود.
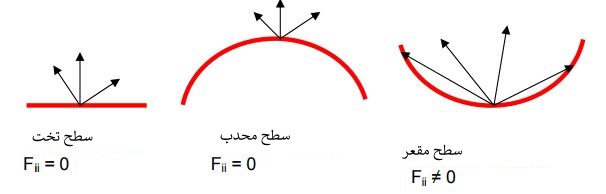
- Fii عبارت است از نسبت انرژی ساطع شده توسط یک سطح، به انرژی دریافت شده توسط همان سطح. از این رو برای سطوح تخت و محدب این ضریب برابر با صفر و برای سطوح مقعر این مقدار میتواند غیرصفر باشد. در شکل زیر مفهوم Fii نشان داده شده. همانطور که میبینید این مقدار ممکن است برای یک سطع مقعر غیرصفر باشد.
قوانین مربوط به محاسبه ضریب دید
در حالتی که انتقال حرارت تابشی بین N سطح اتفاق میافتد، به محاسبه N2 ضریب دید نیازمند هستیم. البته ممکن است یافتن تمامی ضرایب نیاز نباشد، چراکه با استفاده از روابط زیر میتوان با معلوم بودن چند ضریب، بقیه ضرایب را نیز محاسبه کرد.
قانون عکس ضرایب
میتوان نشان داد که رابطه بین ضریب Fij و Fji به صورت زیر است.
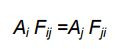
قانون جمع
در تحلیل مسائل مربوط به تابش، معمولا سطحی کاملا بسته را در نظر میگیریم. قانون پایستگی انرژی میگوید تمامی انرژی تولید شده توسط سطوح، به یکدیگر برخورد میکنند. از این رو برای مجموعهای که سطح بستهای را تشکیل میدهند، میتوان رابطه زیر را نوشت.
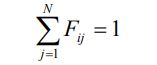
از طرفی رابطه بالا را میتوان برای i از ۱ تا N نوشت. در نتیجه این عبارت نشاندهنده N معادله است. از طرفی قانون عکس ضرایب نیز ۲/(N(N-1 معادله را به ما میدهد. بنابراین تعداد ضرایبی که برای چنین سیستمی بایستی محاسبه شود، برابر با عدد زیر است.
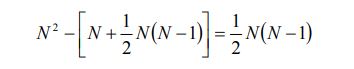
مثال ۲
ضرایب F12 و F21 را برای شکلهای زیر بیابید.
۱. کرهای به قطر D که در جعبهای مکعبی به طول L=D قرار گرفته است.
۲. صفحه موربی که درون لولهای با مقطع مربعی قرار گرفته.
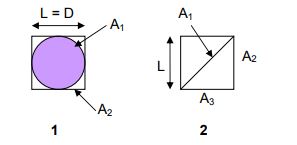
پاسخ مربوط به شکل ۱
در شکل ۱ تمامی انرژی که توسط کره ساطع میشود، توسط جعبه جذب میشود. بنابراین ۱ = F12 است. با استفاده از قانون عکس ضرایب و قانون جمع، میتوان گفت:
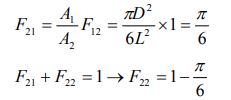
پاسخ مربوط به شکل ۲
با استفاده از قانون جمع میتوان گفت:
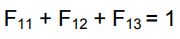
انرژی از سطح شماره ۱ به خودش برخورد نمیکند، بنابراین در معادله بالا میتوان F11 را برابر با صفر فرض کرد. همچنین با توجه به تقارن موجود در مسئله میتوان رابطه زیر را بیان کرد:
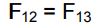
با حل دو معادله بالا مقادیر F12 و F13 برابر با ۰.۵ بدست میآیند. با یافت شدن F12 و استفاده از قانون عکس ضرایب میتوان F21 را به شکل زیر محاسبه کرد.
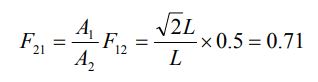
جذابیت اصلی انرژی تابشی به این دلیل است که مدلی از انتقال انرژی را ارائه میدهد که به وجود مادهای نیاز ندارد. در حقیقت اگر انتقال انرژی به این روش وجود نداشت، احتمالا زمین یخ زده بود!
«استیون هاوکینگ» (Stephen William Hawking)، دانشمند بریتانیایی، در دهه ۱۹۷۰ نظریهای تحت عنوان «تابش هاوکینگ» (Hawking Radiation) ارائه کرد. او میزان انرژی تابشی ساطع شده از یک سیاهچاله و همچنین نتایج آن را توضیح داد. این نظریه نشان میدهد که یک سیاهچاله میتواند از طریق تابش جرمش را تا حدی از دست بدهد که نهایتا از بین برود.

^^













با سلام ممکنه توضیح و درس مطالب بالا را به صورت صوتی و تصویری روی سایت بگذارید ممنون میشم چون من میخوام این مطالب و کنفراس بدم ممنون میشم
با سلام
لطفا بفرمایید چرا رادیاتورهای صنعتی نظیر رادیاتورهای ماشین – و کندانسورهای یخچال های معمولی و صنعتی را به رنگ سیاه در می اورند ؟ با این توضیحات شما بیشتر جذب کننده گرما هستند تا دفع کننده ؟
لطفا توضیحات لازم را ایمیل بفرمایید .
بسیار عالی
در خصوص تاثیر پذیری محیط و یا دوربین های ترموگراف و نوع دریافت این انرژی توسط اونها چطور؟ مقاله ای در این مورد وجود داره و یا منابعی برای خوندن ؟ میدونید منظورم چیه؟ در نظر بگیرید این تابشی که از سمت جسم به محیط اطا میشه و بسه به زاویه و فاصله و محیط و … به دوربین های ترموگراف و یا سنسورهای ir میرسه…. این مورد به چه عواملی بستگی داره؟ در این مورد میواستم بیشتر بخونم
سلام دستگاه ماکروویو با استفاده از ایجاد میدان الکترومغناطیس غذا را گرم میکند، به این صورت که اگر مولفه الکتریکی این امواج را به صورت سینوسی در نظر بگیریم ، قطب های الکتریکی موجود در غذا تحت تاثیر این میدان جابه جا میشوند که منجر به افزایش انرژی جنبشی ذرات غذا شده و نهایت غذا گرم میشود