ارتفاع چیست؟ – ارتفاع در اشکال هندسی به زبان ساده

هنگام نگاه کردن به یک برج، اولین چیزی نظر هر فرد را به خود جلب می‌کند، فاصله بین پایین‌ترین نقطه تا بالاترین نقطه آن است. به این فاصله، ارتفاع یا بلندی می‌گویند. ارتفاع در هندسه، جغرافیا، ستاره‌شناسی و حوزه‌های دیگر کاربرد دارد. در هندسه، فاصله عمودی یک راس (گوشه) تا ضلع مقابل آن، با عنوان ارتفاع شناخته می‌شود. به عنوان مثال، اگر از یک راس مثلث، پاره‌خطی را بر ضلع مقابل آن عمود کنیم، ارتفاع مثلث به دست می‌آید. در این آموزش، به طور کامل یاد می‌گیریم که مفهوم ارتفاع چیست و تعریف و محاسبه اندازه ارتفاع اشکال هندسی مختلف و تفاوت‌های آن‌ها را نیز بررسی می‌کنیم.

تعریف ارتفاع چیست؟

«ارتفاع» (Height یا Altitude)، فاصله عمودی بین یک نقطه یا شیء تا یک نقطه مرجع است. این کمیت، گسترش یا موقعیت عمودی را نمایش می‌دهد.

برای درک مفهوم ارتفاع، یک هواپیمای در حال پرواز را در نظر بگیرید. این هواپیما، در فاصله مشخصی از سطح زمین قرار دارد. به فاصله عمودی هواپیما تا سطح زمین، ارتفاع پرواز هواپیما می‌گویند.

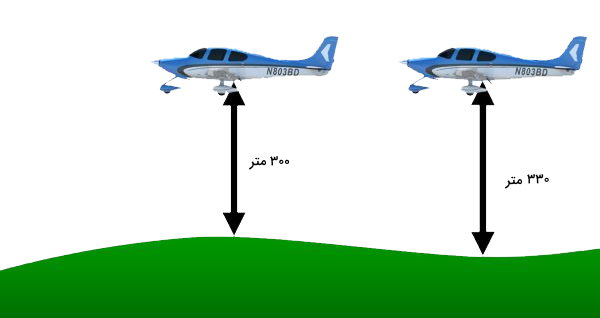
در تصویر بالا، سطح زمین را به عنوان مرجع اندازه‌گیری ارتفاع در نظر گرفتیم. به این ترتیب، ارتفاع پرواز هواپیما در موقعیت اول (سمت راست) برابر با ۳۳۰ متر و در موقعیت بعدی (سمت چپ) برابر با ۳۰۰ متر شد.

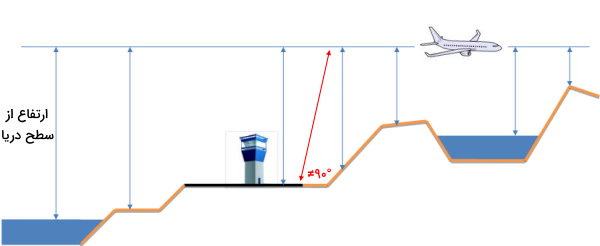
توجه داشته باشید که ارتفاع، همیشه فاصله عمودی (۹۰ درجه) یک نقطه یا شی تا مرجع اندازه‌گیری است. در تصویر بالا، فاصله نمایش داده شده با خط قرمز، ارتفاع هواپیما نیست؛ چراکه این خط، زاویه ۹۰ درجه ندارد. در طبیعت، بسیاری از پستی و بلندی‌های زمین را با ارتفاعشان می‌شناسند. به عنوان مثال، ارتفاع کوه دماوند برابر با ۵۶۰۹ متر است. به عبارت دیگر، فاصله عمودی قله این کوه (بالاترین نقطه آن) تا سطح دریا، برابر با ۵۶۰۹ متر است.

به تصویر کوه دقت کنید. احتمالا تصویر کوه شما را یاد یکی از شکل‌های هندسی معروف می‌اندازد. کوه‌ها، تقریبا شبیه به مثلث هستند. برای مثلث‌ها نیز مانند کوه‌ها، اندازه‌ای به عنوان ارتفاع تعریف می‌شود. تعریف ارتفاع اجسام واقعی با ارتفاع اشکال هندسی، شباهت‌ها و تفاوت‌هایی دارد. به منظور درک این تفاوت‌ها، در بخش بعدی، مفهوم ارتفاع در مثلث و دیگر اشکال هندسی را تعریف می‌کنیم.

ارتفاع در اشکال هندسی دو بعدی چیست ؟

تعریف ارتفاع در هندسه، به دوبعدی یا سه‌بعدی بودن اشکال بستگی دارد. به شکل‌هایی مانند مثلث، مربع، مستطیل، لوزی، متوازی‌الاضلاع، ذوزنقه و غیره، شکل‌های دوبعدی چندضلعی می‌گویند. ارتفاع چندضلعی، پاره‌خطی است که از یک راس تا ضلع مقابلش رسم می‌شود و با آن ضلع، زاویه راست (۹۰ درجه) می‌سازد. در این بخش، به معرفی ارتفاع چندضلعی‌ها به همراه حل مثال می‌پردازیم.

ارتفاع مثلث چیست ؟

ارتفاع مثلث، پاره‌خطی است که از راس‌های این شکل هندسی بر ضلع‌ها یا امتداد ضلع‌های آن عمود می‌شود. به ضلعی که ارتفاع بر آن عمود می‌شود، قاعده می‌گویند. هر مثلث، سه ارتفاع و سه قاعده دارد. تصویر زیر، ارتفاع و قاعده‌های یک مثلث را نمایش می‌دهد.

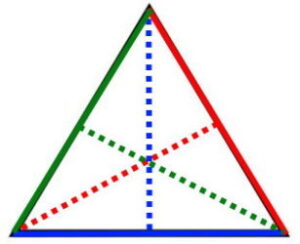
ارتفاع، برای محاسبه مساحت مثلث مورد استفاده قرار می‌گیرد. مساحت انواع مثلث از فرمول «ارتفاع ضربدر قاعده تقسیم بر ۲» به دست می‌آید. عبارت جبری فرمول مساحت مثلث به صورت زیر نوشته می‌شود:

$$A = \frac { ۱ } { ۲ } b h$$

• A: مساحت
• b: قاعده
• h: ارتفاع

اگر رابطه بالا را بر حسب ارتفاع (h) بازنویسی کنیم، به فرمول ارتفاع مثلث بر حسب قاعده و مساحت می‌رسیم:

$$h = \frac { ۲A } { b }$$

در مطلب «ارتفاع مثلث چیست و چگونه رسم می‌شود؟ — آموزش تصویری + حل تمرین»، تعریف، روش‌های محاسبه و نحوه رسم ارتفاع انواع مثلث را به طور کامل توضیح داده‌ایم. در ادامه، کلیات این مطلب را به طور خلاصه مرور می‌کنیم.

ارتفاع مثلث متساوی الاضلاع

مثلث متساوی‌الاضلاع، سه ضلع هم‌اندازه دارد. قاعده‌ها، زوایای داخلی و ارتفاع‌های این نوع مثلث با هم برابر هستند. به علاوه، تمام ارتفاع‌های مثلث متساوی‌الاضلاع درون این سه‌ضلعی قرار می‌گیرند.

تصویر زیر، اجزای مختلف این نوع مثلث را نمایش می‌دهد.

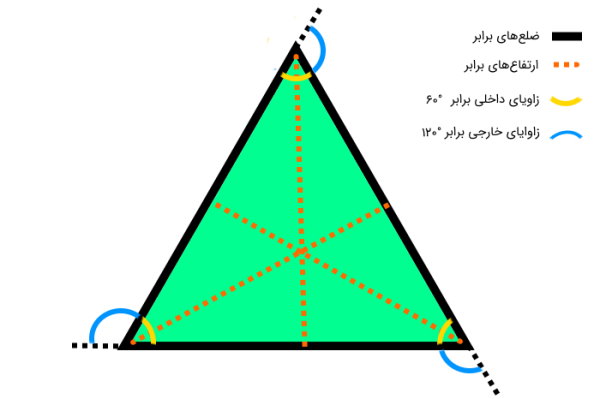
به دلیل برابر بودن تمام اندازه‌های مثلث متساوی‌الاضلاع، امکان نوشتن فرمول مساحت آن، بدون قاعده وجود دارد. این فرمول عبارت است از:

$$A = \frac { \sqrt { ۳ } } { ۳ } h^{۲ }$$

• A: مساحت مثلث متساوی الاضلاع
• h: اندازه ارتفاع مثلث متساوی الاضلاع

با نوشتن فرمول بالا بر حسب h، می‌توان ارتفاع را با استفاده از مساحت آن به دست آورد. روش‌های مختلفی برای محاسبه ارتفاع مثلث متساوی الاضلاع وجود دارد. به منظور آشنایی با این روش‌ها، مطالعه مطلب «مساحت مثلث متساوی الاضلاع — حل تمرین و مثال های متنوع» را به شما پیشنهاد می‌کنیم.

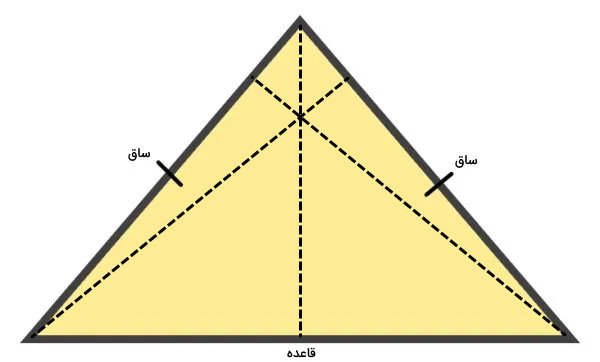
ارتفاع مثلث متساوی الساقین

مثلث متساوی‌الساقین، دو ضلع با اندازه‌های برابر دارد. اگر این مثلث، دارای یک زاویه بزرگ‌تر از ۹۰ درجه باشد، دو ارتفاع آن، بیرون از مثلث قرار می‌گیرند؛ در غیر اینصورت، هر سه ارتفاع مثلث، مانند تصویر زیر درون مثلث رسم می‌شوند. اندازه ارتفاع مثلث متساوی‌الساقین، با استفاده از رابطه کلی مساحت (ارتفاع ضربدر قاعده تقسیم بر دو) به دست می‌آید.

ارتفاع مثلث مختلف الاضلاع

مثلث مختلف‌الاضلاع، سه ضلع با اندازه‌های متفاوت دارد. ارتفاع این نوع مثلث، با استفاده از فرمول کلی معرفی شده در بخش‌های قبلی به دست می‌آید.

ارتفاع مثلث حاده

مثلث حاده، از سه زاویه داخلی با اندازه‌های کوچک‌تر از ۹۰ درجه (زاویه حاده) تشکیل می‌شود. در این مثلث، تمام ارتفاع‌ها داخل محیط قرار می‌گیرند.

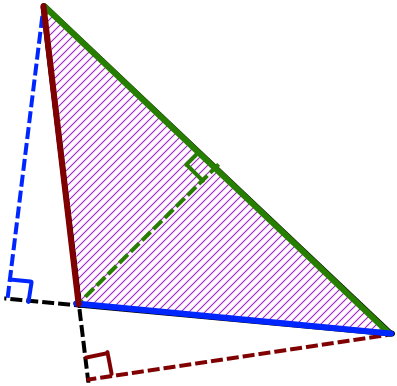
ارتفاع مثلث منفرجه

مثلث منفرجه، یک زاویه بزرگ‌تر از ۹۰ درجه و کوچک‌تر از ۱۸۰ درجه (زاویه منفرجه) دارد. در این مثلث، دو ارتفاع رسم شده از راس‌های حاده (کوچکتر از ۹۰ درجه)، بیرون از محیط مثلث قرار می‌گیرند.

ارتفاع مثلث قائم الزاویه

مثلث قائم‌الزاویه، یک زاویه داخلی قائمه (۹۰ درجه) دارد. به عبارت دیگر، دو ضلع این نوع مثلث بر هم عمود هستند. بنابراین، ساق‌ها (ضلع‌های تشکیل دهنده زاویه راست)، به عنوان دو ارتفاع مثلث قائم‌الزاویه در نظر گرفته می‌شود. فاصله عمودی بین راس قائمه تا ضلع روبه‌رویی آن (وتر)، ارتفاع سوم مثلث قائم‌الزاویه است که درون محیط آن قرار می‌گیرد.

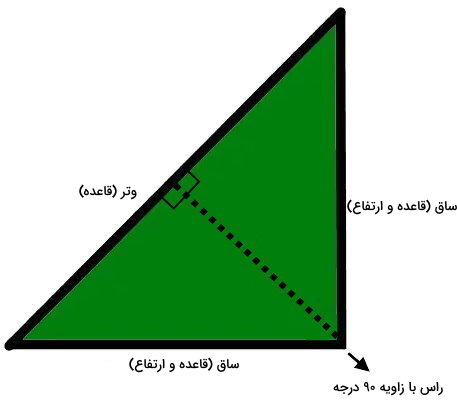
از آنجا که هر دو ساق مثلث قائم الزاویه به عنوان قاعده و ارتفاع آن محسوب می‌شوند، با داشتن اندازه این دو ضلع می‌توان مساحت را به دست آورد. در این حالت، مساحت مثلث قائم الزاویه، برابر با «نصفِ حاصل‌ضرب ساق‌ها» است:

۲ ÷ (ساق دوم × ساق اول) = مساحت مثلث قائم الزاویه

با نوشتن فرمول بالا بر حسب هر ساق، رابطه یکی از ارتفاع‌های مثلث قائم الزاویه به دست می‌آید. یکی دیگر از روش‌های به دست آوردن ارتفاع مثلث قائم الزاویه، استفاده از قضیه فیثاغورس است:

c^ { ۲ } = a^ { ۲ } + b^ {۲}

• c: وتر مثلث
• a: اندازه یکی از ساق‌ها برابر ۱۰
• b: اندازه ساق دیگر برابر ۱۰

روش های محاسبه ارتفاع مثلث

روش‌های مختلفی برای محاسبه ارتفاع مثلث‌ها وجود دارد. بر اساس اندازه‌های معلوم، ارتفاع یک سه‌ضلعی را می‌توان با استفاده از اندازه‌های زیر به دست آورد:

• مساحت و قاعده
• محیط و اندازه سه ضلع
• سینوس
  • دو ضلع و زاویه بین
  • دو زاویه و ضلع بین
• قضیه فیثاغورس

مثال ۱: محاسبه ارتفاع مثلث با قاعده و مساحت

مساحت یک مثلث برابر با ۳ سانتی‌متر مربع و اندازه یکی از ضلع‌های آن برابر با ۶ سانتی‌متر است. اندازه ارتفاع وارد بر این ضلع را حساب کنید.

ارتفاع مثلث، از رابطه زیر به دست می‌آید:

قاعده ÷ (مساحت × ۲) = ارتفاع مثلث

منظور از قاعده، ضلعی است که ارتفاع بر آن عمود می‌شود. اندازه‌های معلوم را درون رابطه بالا قرار می‌دهیم:

۶ ÷ (۳ × ۲) = ارتفاع مثلث

۶ ÷ (۶) = ارتفاع مثلث

۱ = ارتفاع مثلث

در نتیجه، ارتفاع نظیر ضلع ۶ سانتی‌متری مثلث برابر با ۱ سانتی‌متر است.

مثال ۲: محاسبه ارتفاع مثلث با سه ضلع

اندازه ضلع‌های یک مثلث برابر با ۶، ۸ و ۱۰ سانتی‌متر است. اندازه ارتفاع نظیر هر ضلع را به دست بیاورید.

برای به دست آوردن ارتفاع از روی اندازه ضلع‌ها، ابتدا با استفاده از فرمول هرون، مساحت مثلث را تعیین می‌کنیم. بر اساس این فرمول داریم:

$$A = \sqrt { s ( s - a ) ( s - b ) ( s - c ) }$$

• A: مساحت مثلث
• s: نصف محیط مثلث
• a: طول ضلع اول برابر با ۶
• b: طول ضلع دوم برابر با ۸
• c: طول ضلع سوم برابر با ۱۰

محیط مثلث، حاصل‌جمع تمام ضلع‌های آن است:

ضلع سوم + ضلع دوم + ضلع اول = محیط مثلث

۱۰ + ۸ + ۶ = محیط مثلث

۲۴ = محیط مثلث

بنابراین، نصف محیط مثلث به صورت زیر تعیین می‌شود:

$$s = \frac { ۲۴ } { ۲ }$$

$$s = ۱۲$$

اندازه‌های معلوم را درون فرمول هرون قرار می‌دهیم:

$$A = \sqrt { (۱۲) ( ۱۲ - ۶ ) ( ۱۲ - ۸ ) ( ۱۲ - ۱۰ ) }$$

$$A = \sqrt { (۱۲) ( ۶ ) ( ۴ ) ( ۲ ) }$$

$$A = \sqrt { ۵۷۶ }$$

$$A = ۲۴$$

اکنون که اندازه مساحت مثلث را داریم، می‌توانیم ارتفاع نظیر هر قاعده را محاسبه کنیم. به این منظور، اندازه ضلع و مساحت را درون فرمول زیر قرار می‌دهیم:

قاعده ÷ (مساحت × ۲) = ارتفاع مثلث

به این ترتیب داریم:

قاعده اول ÷ (مساحت × ۲) = ارتفاع اول

۶ ÷ (۲۴ × ۲) = ارتفاع اول

۸ = ارتفاع اول

قاعده دوم ÷ (مساحت × ۲) = ارتفاع دوم

۸ ÷ (۲۴ × ۲) = ارتفاع دوم

۶ = ارتفاع دوم

قاعده سوم ÷ (مساحت × ۲) = ارتفاع سوم

۱۰ ÷ (۲۴ × ۲) = ارتفاع سوم

۴/۸ = ارتفاع سوم

در نتیجه، ارتفاع نظیر قاعده‌های مثلث به ترتیب برابر با ۸، ۶ و ۴/۸ سانتی‌متر است. اگر به نتایج دقت کنید، متوجه خواهید شد که اندازه قاعده اول با ارتفاع دوم و قاعده دوم با ارتفاع اول برابر است. این ویژگی، وجود یک مثلث قائم الزاویه را نمایش می‌دهد.

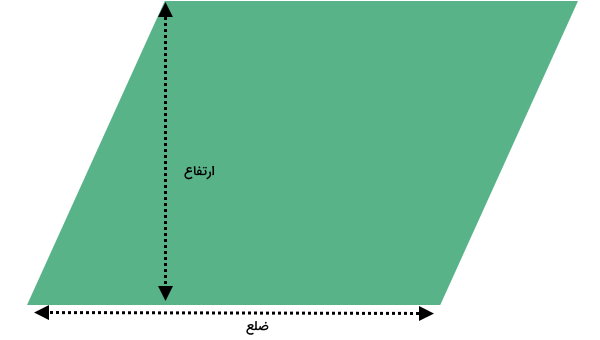
ارتفاع متوازی الاضلاع چیست ؟

ارتفاع متوازی‌الاضلاع، فاصله عمودی بین ضلع‌های روبه‌رویی آن است. هر متوازی‌الاضلاع، دو ارتفاع دارد. اندازه این دو ارتفاع، به منظور محاسبه مساحت متوازی‌الاضلاع مورد استفاده قرار می‌گیرد.

فرمول مساحت متوازی‌الاضلاع به صورت زیر نوشته می‌شود:

ارتفاع × قاعده = مساحت متوازی‌الاضلاع

به ضلع‌های متناظر ارتفاع، قاعده می‌گویند. بر اساس فرمول بالا، ارتفاع متوازی‌الاضلاع از رابطه زیر به دست می‌آید:

قاعده ÷ مساحت = ارتفاع متوازی‌الاضلاع

توجه داشته باشید که در رابطه بالا باید از اندازه یکی از ضلع‌های دو طرف ارتفاع (قاعده نظیر ارتفاع) استفاده کرد.

مثال ۳: محاسبه ارتفاع متوازی الاضلاع

مساحت یک متوازی‌الاضلاع برابر با ۶ سانتی‌متر مربع و اندازه دو ضلع مجاور آن برابر با ۳ و ۴ سانتی‌متر است. اندازه هر دو ارتفاع این متوازی‌الاضلع را به دست بیاورید.

برای حل این مسئله، ابتدا فرمول ارتفاع متوازی‌الاضلاع را می‌نویسیم:

قاعده ÷ مساحت = ارتفاع متوازی‌الاضلاع

اندازه مساحت و یکی از ضلع‌ها را دورن فرمول بالا قرار می‌دهیم:

۳ ÷ ۶ = ارتفاع متوازی‌الاضلاع

۲ = ارتفاع متوازی‌الاضلاع

بنابراین، ارتفاع نظیر ضلع (قاعده) ۳ سانتی‌متری برابر با ۲ سانتی‌متر است. ارتفاع نظیر ضلع دیگر نیز با جایگذاری اندازه آن در فرمول مساحت محاسبه می‌شود:

۴ ÷ ۶ = ارتفاع متوازی‌الاضلاع

۱٫۵ = ارتفاع متوازی‌الاضلاع

در نتیجه، ارتفاع نظیر ضلع (قاعده) ۴ سانتی‌متری برابر با ۱٫۵ سانتی‌متر است.

ارتفاع ذوزنقه

ذوزنقه، یک نوع چهارضلعی است که از دو ضلع موازی و دو ضلع غیر موازی تشکیل می‌شود. به ضلع‌های موازی ذوزنقه، قاعده‌ و به ضلع‌های غیر موازی آن، ساق می‌گویند. فاصله عمودی بین قاعده‌ها نیز با عنوان ارتفاع ذوزنقه شناخته می‌شوند.

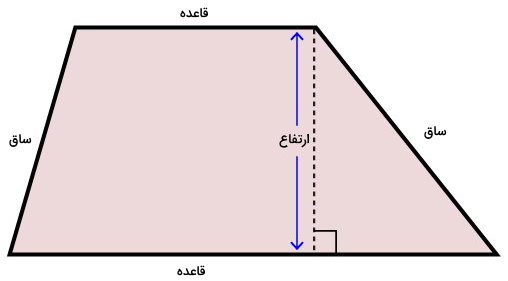
ارتفاع ذوزنقه، در محاسبه مساحت این شکل هندسی مورد استفاده قرار می‌گیرد. مساحت ذوزنقه از فرمول زیر به دست می‌آید:

ارتفاع × نصف مجموع قاعده‌ها = مساحت ذوزنقه

به این ترتیب، فرمول ارتفاع ذوزنقه، به صورت زیر نوشته می‌شود:

نصف مجموع قاعده‌ها ÷ مساحت = ارتفاع ذوزنقه

ذوزنقه‌ها، انواع مختلفی دارند. تصویر زیر، یکی از انواع ذوزنقه، با عنوان ذوزنقه قائم الزاویه را نمایش می‌دهد. در این ذوزنقه، یکی از ساق‌ها، با دو قاعده، زاویه راست می‌سازد. این ساق، ارتفاع ذوزنقه نیز هست.

مثال ۴: محاسبه ارتفاع ذوزنقه

مساحت ذوزنقه‌ای برابر با ۴۰ متر مربع است. اگر اندازه قاعده‌های این ذوزنقه برابر با ۷ و ۹ متر باشد، اندازه ارتفاع آن چقدر خواهد بود؟

به منظور تعیین ارتفاع ذوزنقه، ابتدا فرمول مساحت ذوزنقه را می‌نویسیم:

ارتفاع × نصف مجموع قاعده‌ها = مساحت ذوزنقه

سپس، فرمول بالا را بر حسب ارتفاع بازنویسی می‌کنیم؛

نصف مجموع قاعده‌ها ÷ مساحت = ارتفاع ذوزنقه

اندازه‌های معلوم را در فرمول قرار می‌دهیم:

[۲ ÷ (۹ + ۷)] ÷ ۴۰ = ارتفاع ذوزنقه

[۲ ÷ (۱۶)] ÷ ۴۰ = ارتفاع ذوزنقه

[۸] ÷ ۴۰ = ارتفاع ذوزنقه

۵ = ارتفاع ذوزنقه

در نتیجه، ارتفاع ذوزنقه برابر با ۵ متر است.

ارتفاع در چند ضلعی منتظم چیست ؟

چند ضلعی منتظم، چندضلعی با ضلع‌ها و زاویه‌های برابر است. در این شکل‌ها نیز مانند مثلث، متوازی‌الاضلاع و ذوزنقه، اندازه‌ای با عنوان ارتفاع تعریف می‌شود.

تعریف ارتفاع چند ضلعی منتظم با دیگر چندضلعی‌ها تفاوت دارد. در این شکل، به پاره‌خطی که از مرکز چندضلعی به مرکز ضلع‌ها عمود می‌شود، ارتفاع می‌گویند. ارتفاع، عمود منصف ضلع‌های چندضلعی منتظم است.

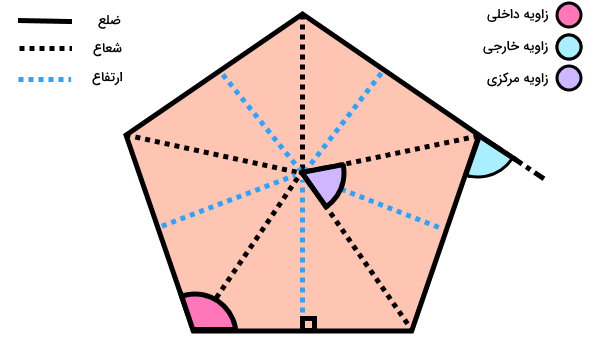
اندازه ارتفاع چند ضلعی منتظم با کمک روابط مثلثاتی به دست می‌‌آید:

$$a = \frac { s } { ۲ \tan { \frac { ۱۸۰ ^ { \circ } } { n } } }$$

• a: ارتفاع چندضلعی منتظم
• s: طول ضلع چندضلعی منتظم
• n: تعداد ضلع‌ها

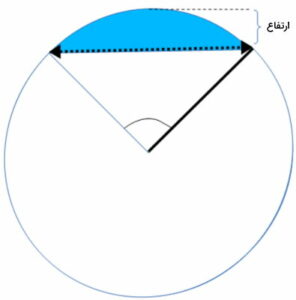
ارتفاع دایره چیست ؟

دایره، منحنی بسته‌ای است که تمام نقاط آن از یک نقطه ثابت (مرکز دایره)، به یک اندازه (شعاع) فاصله دارند. برای دایره‌ها، معمولا اندازه‌ای با عنوان ارتفاع تعریف نمی‌شود. با این وجود، در قطعه و کمان دایره، یک اندازه را به عنوان ارتفاع در نظر می‌گیرند.

ارتفاع در اشکال هندسی سه بعدی چیست ؟

ارتفاع، یکی از اجزا و اندازه‌های مهم در شکل‌های سه‌بعدی است. ارتفاع شکل‌های سه‌بعدی، در محاسبه حجم مورد استفاده قرار می‌گیرد. از مهم‌ترین شکل‌های سه‌بعدی می‌توان به مکعب، مکعب مستطیل، منشور، هرم، مخروط، استوانه و کره اشاره کرد. در ادامه، به بررسی ارتفاع در هر یک از این شکل‌ها می‌پردازیم.

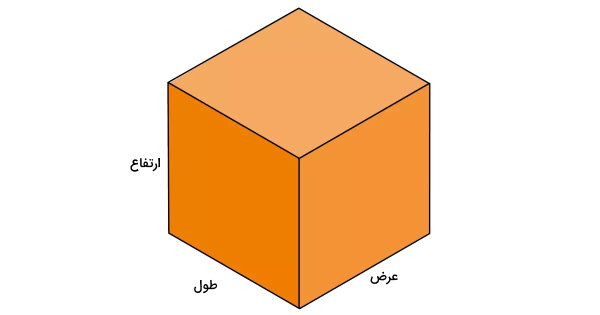
ارتفاع مکعب و مکعب مستطیل چیست ؟

مکعب، یک چندوجهی است که از شش وجه مربعی شکل تشکیل می‌شود. مکعب مستطیل به مکعب شباهت دارد. با این تفاوت که وجه‌های آن به شکل مستطیل هستند.

در هر دوی این شکل‌ها، به لبه‌ای که دو وجه بالایی و پایینی را به هم وصل می‌کند (فاصله عمودی بین وجه‌های بالایی و پایینی)، ارتفاع می‌گویند.

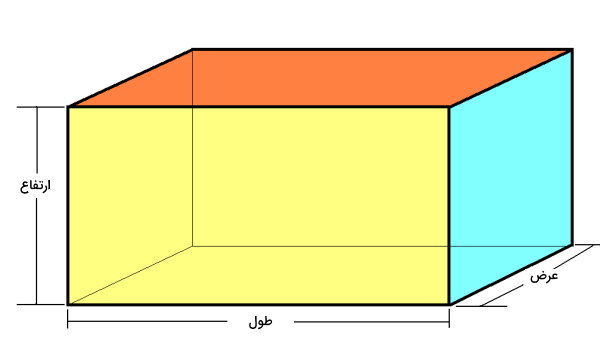
مکعب، یکی از حالت‌های خاص مکعب مستطیل محسوب می‌شود. در این شکل، هر سه اندازه طول، عرض و ارتفاع، با هم برابر هستند. به این ترتیب، اگر مساحت یکی از وجه‌های مکعب یا حجم مکعب را داشته باشیم، می‌توان ارتفاع آن را به دست بیاوریم.

مساحت وجه‌های مکعب از رابطه مساحت مربع به دست می‌آید:

خودش × یک ضلع = مساحت مربع = مساحت وجه مکعب

اندازه یک ضلع در فرمول بالا، همان ارتفاع مکعب است. بنابراین، داریم:

(مساحت وجه)∨ = ارتفاع مکعب

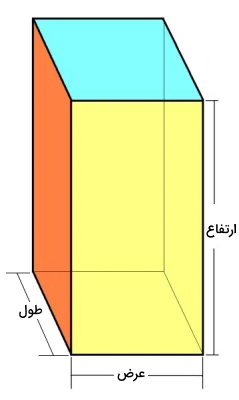
به منظور تعیین ارتفاع مکعب مستطیل، باید اندازه طول، عرض و حجم آن را داشته باشیم. فرمول حجم مکعب مستطیل عبارت است از:

ارتفاع × عرض × طول = حجم مکعب مستطیل

این فرمول را بر حسب ارتفاع بازنویسی می‌کنیم:

(عرض × طول) ÷ حجم = ارتفاع مکعب مستطیل

توجه داشته باشید که تعریف ارتفاع در مکعب مستطیل، به نحوه قرارگیری آن نیز بستگی دارد. به عنوان مثال، تصویر مکعب مستطیل در ابتدای بخش را در نظر بگیرید. اگر این تصویر را دوران دهیم، می‌توانیم عنوان اجزای آن را به صورت زیر تغییر دهیم.

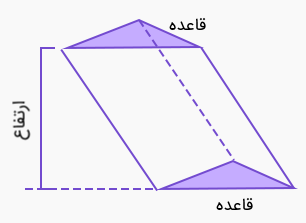
ارتفاع منشور چیست ؟

منشور، یکی دیگر از انواع چندوجهی‌ها است. این شکل، دو وجه هم‌شکل و هم‌اندازه دارد که توسط چند وجه مستطیلی به یکدیگر وصل می‌شوند. به دو وجه هم‌شکل و هم‌اندازه منشور، قاعده می‌گویند. قاعده منشور می‌تواند مثلثی، مربعی، مستطیلی و دیگر شکل‌های چندضلعی باشد. به عنوان مثال، تصویر زیر، یک منشور مثلثی را نمایش می‌دهد.

به فاصله عمودی بین دو قاعده، ارتفاع منشور می‌گویند. این تعریف، هم برای منشورهای قائم و هم برای منشورهای مایل مورد استفاده قرار می‌گیرد.

حجم منشور از رابطه زیر به دست می‌آید:

 مساحت قاعده × ارتفاع = حجم منشور

فرمول بالا را برحسب ارتفاع بازنویسی می‌کنیم:

مساحت قاعده ÷ حجم = ارتفاع منشور

مساحت قاعده به شکل آن بستگی دارد. به منظور آشنایی با مساحت شکل‌های هندسی، مطالعه مطلب «مساحت چیست؟ — به زبان ساده + حل مثال‌های متنوع» را به شما پیشنهاد می‌کنیم.

مثال ۵: محاسبه ارتفاع منشور مثلثی

یک منشور با قاعده مثلث متساوی‌الاضلاع را در نظر بگیرید. اگر اندازه ضلع قاعده برابر با ۲ سانتی‌متر و حجم منشور برابر با $$\sqrt{۳}$$۲ سانتی‌متر مکعب باشد، ارتفاع منشور و ارتفاع مثلث چقدر است؟

به منظور تعیین ارتفاع منشور در این مثال، ابتدا باید مساحت قاعده (مثلث متساوی‌الساقین) را به دست بیاوریم. فرمول مساحت مثلث متساوی الاضلاع با یک ضلع به صورت زیر نوشته می‌شود:

$$A = \frac { \sqrt { ۳ } } { ۴ } a ^ { ۲ }$$

• A: مساحت مثلث متساوی الاضلاع
• a: اندازه ضلع مثلث متساوی الاضلاع برابر با ۲ سانتی‌متر

$$A = \frac { \sqrt { ۳ } } { ۴ } \times ۲ ^ { ۲ }$$

$$A = \frac { \sqrt { ۳ } } { ۴ } \times ۴$$

$$A = \sqrt { ۳ }$$

بنابراین، مساحت قاعده منشور برابر با $$\sqrt{۳}$$ سانتی‌متر مربع است. بر اساس فرمول ارتفاع منشور داریم:

مساحت قاعده ÷ حجم = ارتفاع منشور

$$\sqrt{۳}$$ ÷ $$\sqrt{۳}$$۲ = ارتفاع منشور

۲ = ارتفاع منشور

به این ترتیب، ارتفاع منشور برابر با ۲ سانتی‌متر است. اکنون می‌خواهیم ارتفاع قاعده (ارتفاع مثلث متساوی الاضلاع) را محاسبه کنیم. برای این کار، فرمول کلی مساحت مثلث را مورد استفاده قرار می‌دهیم:

۲ ÷ (قاعده × ارتفاع) = مساحت مثلث

با توجه به اطلاعات سوال و اندازه‌های به دست آماده از مراحل قبلی داریم:

۲ ÷ (۲ × ارتفاع) = ۳∨

$$\sqrt{۳}$$۲ = ۲ × ارتفاع

۲ ÷ $$\sqrt{۳}$$۲ = ارتفاع

$$\sqrt{۳}$$ = ارتفاع

در نتیجه، ارتفاع مثلث متساوی‌الساقین در قاعده منشور برابر با $$\sqrt{۳}$$ است.

ارتفاع استوانه چیست ؟

استوانه، شکلی سه‌بعدی است که شباهت‌هایی به منشور دارد. این شکل، از دو قاعده دایره‌ای شکل و یک وجه جانبی منحنی تشکیل می‌شود. به فاصله عمودی بین دو قاعده دایره‌ای، ارتفاع استوانه می‌گویند.

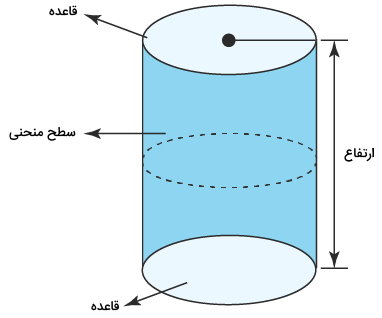
فرمول حجم استوانه، به صورت زیر نوشته می‌شود:

مساحت قاعده × ارتفاع = حجم استوانه

به عبارت دیگر:

مساحت دایره × ارتفاع = حجم استوانه

بنابراین، ارتفاع استوانه را می‌توان با استفاده از رابطه زیر محاسبه کرد:

مساحت دایره ÷ حجم = ارتفاع استوانه

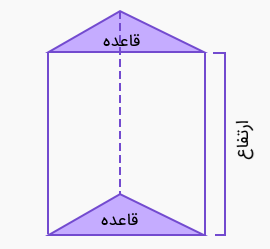
ارتفاع هرم چیست ؟

هرم، شکلی چند وجهی با یک قاعده و چند وجه جانبی است. وجه‌های جانبی این شکل در نقطه‌ای به نام راس به یکدیگر می‌رسند. ارتفاع، به عنوان یکی از اجزای اصلی هرم شناخته می‌شود. ارتفاع هرم، فاصله عمودی راس تا قاعده است.

تصویر زیر، اجزای یک هرم مربعی قائم را نمایش می‌دهد

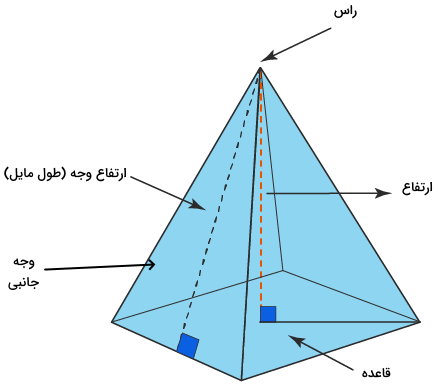
حجم هرم از رابطه زیر به دست می‌آید:

۳ ÷ (مساحت قاعده × ارتفاع) = حجم هرم

با بازنویسی رابطه بالا بر حسب ارتفاع، داریم:

مساحت قاعده ÷ (حجم × ۳) = ارتفاع هرم

مثال ۶: محاسبه ارتفاع هرم مربعی

قاعده یک هرم، مستطیلی به طول و عرض ۸ و ۵ متر است. اگر حجم این هرم برابر با ۸۰ متر مکعب باشد، ارتفاع آن چقدر خواهد بود؟

ارتفاع هرم، با استفاده از فرمول زیر محاسبه می‌شود:

مساحت قاعده ÷ (حجم × ۳) = ارتفاع هرم

مساحت قاعده، از فرمول مساحت مستطیل به دست می‌آید:

عرض × طول = مساحت مستطیل = مساحت قاعده

۵ × ۸ = مساحت قاعده

۴۰ = مساحت قاعده

مساحت قاعده برابر با ۴۰ متر مربع است. این اندازه را به همراه حجم در فرمول ارتفاع قرار می‌دهیم:

۴۰ ÷ (۸۰ × ۳) = ارتفاع هرم

۴۰ ÷ (۲۴۰) = ارتفاع هرم

۶ = ارتفاع هرم

در نتیجه، ارتفاع هرم برابر با ۶ متر است. روش‌های مختلفی برای محاسبه ارتفاع هر وجود دارد. برای آشنایی با این روش‌ها، مطالعه روابط و مثال‌های موجود در مطلب «حجم هرم و محاسبه آن — به زبان ساده» را به شما پیشنهاد می‌کنیم.

ارتفاع مخروط چیست ؟

مخروط، یکی از شکل‌های سه‌بعدی است که شباهت زیادی به هرم دارد. این شکل، از یک قاعده دایره‌ای شکل تشکیل می‌شود. وجه جانبی مخروط، مانند یک رویه منحنی شکل است. تصویر زیر، اجزای مختلف مخروط را نمایش می‌دهد.

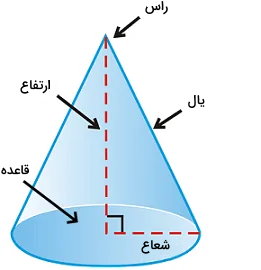
حجم مخروط نیز مشابه با حجم هرم، از رابطه زیر به دست می‌آید:

مساحت قاعده × ارتفاع = حجم مخروط

قاعده مخروط، یک دایره است. بنابراین داریم:

مساحت دایره × ارتفاع = حجم مخروط

در بخش‌های قبلی، با مفهوم ارتفاع در شکل‌های هندسی دوبعدی و سه‌بعدی آشنا شدیم.

سوالات متداول در رابطه با ارتفاع در اشکال هندسی

در این بخش، به برخی از سوالات پرتکرار در رابطه با ارتفاع در اشکال هندسی به طور مختصر پاسخ می‌دهیم.

ارتفاع یعنی چه ؟

به فاصله عمودی بین یک نقطه تا یک سطح مبنا، ارتفاع می‌گویند.

تعریف ارتفاع در شکل های هندسی چیست ؟

ارتفاع در شکل های هندسی، فاصله عمودی راس تا قاعده مقابل به آن راس است.

ارتفاع نظیر چیست ؟

ارتفاع نظیر یک قاعده، پاره‌خطی است که از راس روبه‌رویی آن قاعده، بر رویش عمود می‌شود.

آیا دایره ارتفاع دارد ؟

بله. قطر دایره را می‌توان به عنوان ارتفاع آن در نظر گرفت. البته در دایره، نیازی به تعریف اندازه‌ای با عنوان ارتفاع نیست.

مثلث قائم الزاویه چند ارتفاع دارد ؟

مثلث قائم الزاویه، مانند تمام مثلث‌ها، سه ارتفاع دارد. البته در این مثلث، ساق‌ها، قاعده و ارتفاع نظیر یکدیگرند.

ارتفاع نظیر راس مثلث چیست ؟

ارتفاع نظیر راس مثلث، ارتفاعی است که از آن راس رسم شده باشد.

به ضلعی که ارتفاع بر آن عمود شده است چه می گویند ؟

به ضلعی که ارتفاع بر آن عمود شده است، قاعده نظیر می‌گویند.