ارتفاع مثلث چیست و چگونه رسم می شود؟ — آموزش تصویری + حل تمرین

ارتفاع، پاره خطی است که از یک راس مثلث بر ضلع مقابل راس عمود میشود. به دلیل وجود سه راس و سه ضلع، هر مثلث دارای سه ارتفاع است. این سه ارتفاع، معمولا به منظور محاسبه مساحت مثلث مورد استفاده قرار میگیرند. از اینرو، آشنایی با خواص و روشهای محاسبه ارتفاعهای مثلث از اهمیت بالایی برخوردار است. در این آموزش از مجله فرادرس، به ارائه تعریف، فرمولهای محاسبه و خواص ارتفاع مثلث به همراه حل چندین مثال میپردازیم. سپس، روشهای رسم این جز مهم از مثلث توسط گونیا و پرگار را به صورت تصویری و گام به گام آموزش میدهیم.
مثلث چیست؟
در مطلب «مثلث چیست؟ — به زبان ساده (+ دانلود فیلم آموزش رایگان)» از مجله فرادرس با تعریف مثلث آشنا شدیم. مثلث، یکی از شکلهای چند ضلعی دو بعدی است. مثلثها، از شکلهای پایهای و اصلی در هندسه محسوب میشوند. تصویر زیر، نمونهای از یک مثلث متساوی الاضلاع را نمایش میدهد. تمام ضلعهای این نوع مثلث، هم اندازه هستند.
اجزای مثلث چه هستند؟
هر مثلث از سه جز اصلی شامل راسها، ضلعها و زوایای داخلی تشکیل میشود:
- راس: نقطه محل برخورد دو ضلع مثلث
- ضلع: پاره خط اتصال دهنده دو راس (المان تعیین کننده محیط مثلث)
- زاویه داخلی: زاویه میان دو ضلع مجاور در محل قرارگیری راس (مجموع زوایای داخلی مثلث برابر 180 درجه است.)
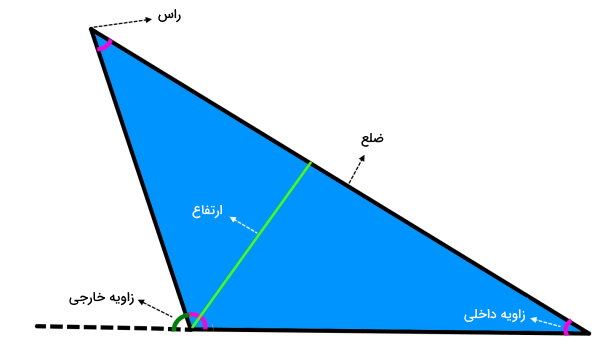
ضلع مثلث، با عنوانهایی مانند «یال» یا «قاعده» نیز شناخته میشود. عنوان قاعده، بیشتر در محاسبه مساحت مثلث به کار میرود. از اجزای فرعی مثلثها میتوان به زاویه خارجی و ارتفاع اشاره کرد:
- زاویه خارجی: زاویه بین یک ضلع با امتداد ضلع مجاور (مجموع زوایای خارجی مثلث برابر 360 درجه است.)
- ارتفاع: پاره خط عمود بر ضلع مثلث از راس مقابل آن (فاصله عمودی بین یک راس تا راستای ضلع مقابل)
قاعده و ارتفاع مثلث، اندازههایی هستند که معمولا به منظور محاسبه مساحت مثلث مورد استفاده قرار میگیرند. در صورت مشخص بودن این اندازهها، مساحت مثلث برابر «قاعده ضربدر ارتفاع تقسیم بر دو» خواهد بود.
ارتفاع مثلث چیست؟
«ارتفاع» (Height یا Altitude)، پاره خطی است که از راس مثلث رسم میشود و با ضلع مقابل خود یا امتداد آن ضلع، زاویه قائمه (90 درجه) میسازد. هر مثلث دارای سه ارتفاع است.
ارتفاعهای مثلث میتوانند داخلی یا خارجی باشند. داخلی یا خارجی بودن ارتفاع مثلث، به زاویه راسهای آن بستگی دارد.
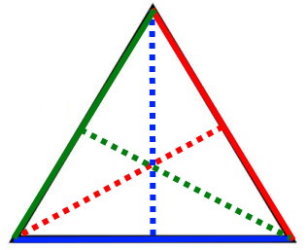
ارتفاع داخلی مثلث چیست؟
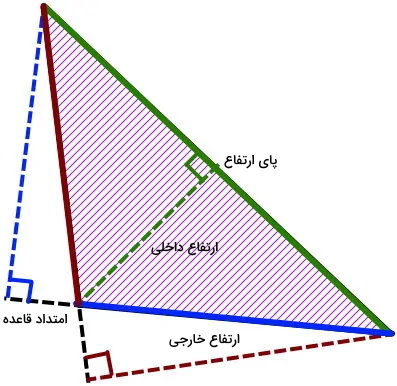
ارتفاع داخلی مثلث، ارتفاعی است که درون ضلعهای مثلث قرار میگیرد. به غیر از دو ارتفاع مثلث منفرجه، تمام ارتفاعهای انواع دیگر مثلثها، داخلی هستند. در تصویر قبل، خط چین سبز رنگ، یک ارتفاع داخلی را نمایش میدهد.
ارتفاع خارجی مثلث چیست؟
ارتفاع خارجی مثلث، ارتفاعی است که خارج از محیط مثلث قرار میگیرد. این پاره خط، بر امتداد ضلعهای مثلث عمود میشود. در تصویر قبل، خط چینهای آبی و قرمز، ارتفاعهای خارجی مثلث منفرجه بودند.
پای ارتفاع مثلث چیست؟
محل برخورد ارتفاع مثلث به قاعده نظیر یا امتداد قاعده نظیر، با عنوان پای ارتفاع یا «پای عمود» (Perpendicular Foot) شناخته میشود. در مثلثهای متساوی الاضلاع و متساوی الساقین، پای ارتفاع بر روی مرکز قاعده نظیر قرار میگیرد.
ارتفاع انواع مثلث ها
تمام مثلثها، دارای سه ارتفاع هستند. در مثلثهای مختلف، روشهای تشخیص و اندازهگیری این ارتفاعها با یکدیگر تفاوت دارند. در این بخش، نحوه تشخیص و فرمولهای محاسبه ارتفاع انواع مثلثها را ارائه میکنیم.
ارتفاع مثلث قائم الزاویه
مثلث قائم الزاویه، مثلثی است که یکی از راسهای آن دارای زاویه 90 درجه است. به ضلعهای مجاور زاویه قائمه، ساق و به ضلع مقابل زاویه قائمه، وتر میگویند. در مثلث قائم الزاویه، ساقها، ارتفاع و قاعده نظیر یکدیگر هستند. ارتفاع سوم این مثلث، از نوع داخلی است. این ارتفاع، بر وتر مثلث عمود میشود.
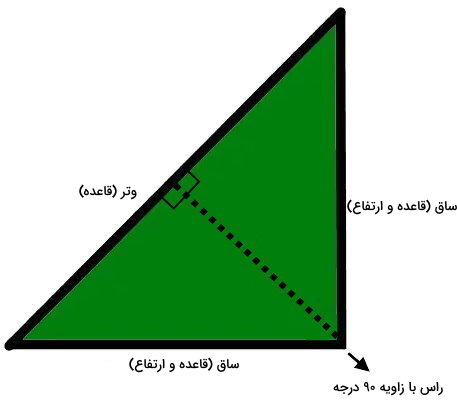
ارتفاع مثلث متساوی الاضلاع
مثلث متساوی الاضلاع، مثلثی با اندازه ضلعهای برابر است. هر سه ارتفاع این نوع مثلث، از نوع داخلی و با اندازههای برابر هستند. این ارتفاعها، قاعدههای نظیر خود را نصف میکنند. به عبارت دیگر، ارتفاع مثلث متساوی الاضلاع، عمود منصف ضلعهای آن است.
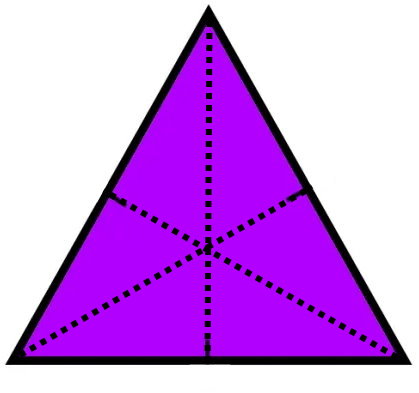
ارتفاع مثلث با زاویه بسته یا مثلث حاده
مثلث حاده یا مثلث با زاویه بسته، به مثلثی گفته میشود که اندازه تمام زوایای آن کمتر از 90 درجه است. در این مثلث، هر سه ارتفاع درون محدوده ضلعها قرار میگیرند (ارتفاعهای داخلی). تصویر زیر، ارتفاعهای یک مثلث متساوی الساقین با زاویه بسته را نمایش میدهد.
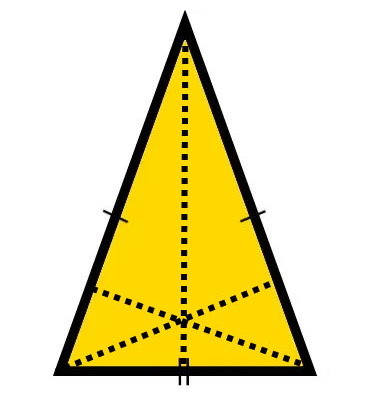
نکته: مثلثهای متساوی الساقین میتوانند قائم الزاویه یا منفرجه نیز باشند. به همین دلیل، هر سه ارتفاع این نوع مثلث، همیشه از نوع داخلی نیست.
ارتفاع مثلث متساوی الساقین
مثلث متساوی الساقین، مثلثی با دو ضلع و دو زاویه برابر است. نوع ارتفاع مثلث متساوی الساقین (داخلی یا خارجی بودن ارتفاع)، به اندازه زاویههای آن بستگی دارد. در هر حالت، ارتفاع رسم شده از راس با زاویه متفاوت (زاویه سوم)، عمود منصف قاعده نظیر و نیمساز آن زاویه است. به طور کلی، ضلعهای برابر در مثلث متساوی الساقین با عنوان «ساق»، ضلع سوم با عنوان «قاعده» و ارتفاع نظیر قاعده با عنوان «ارتفاع» شناخته میشوند. ساق، قاعده و ارتفاع، از اجزای اصلی معرف این نوع مثلث هستند.
ارتفاع مثلث با زاویه باز یا مثلث منفرجه
مثلث منفرجه یا مثلث با زاویه باز، مثلثی است که یک زاویه بزرگتر 90 درجه دارد. در این نوع مثلث، ارتفاع نظیر زاویه باز (ارتفاع نظیر بلندترین ضلع)، در داخل محدوده ضلعها و دو ارتفاع دیگر، در خارج از محدوده ضلعها قرار میگیرند. مثلثهای مختلف الاضلاع و متساوی الساقین میتوانند دارای زاویه باز باشند.
ارتفاع مثلث مختلف اضلاع
مثلث مختلف اضلاع، مثلثی با طول ضلعهای متفاوت است. این مثلث میتواند از نوع منفرجه، حاده یا قائمه باشد. به همین دلیل، مشخصات ارتفاعهای آن، به زوایای داخلی بستگی دارند. ارتفاعهای مثلث مختلف الاضلاع، معمولا با استفاده از فرمولهای کلی مساحت به دست میآیند.
ارتفاع مثلث چگونه رسم می شود ؟
ارتفاع مثلث، معمولا با استفاده از ابزارهایی مانند خطکش، گونیا و پرگار رسم میشود. در این بخش، نحوه رسم ارتفاعهای مثلث، توسط گونیا و پرگار را آموزش میدهیم.
رسم ارتفاع مثلث با گونیا
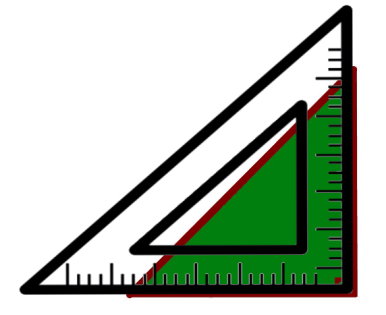
سریعترین روش برای رسم ارتفاع مثلث، استفاده از گونیا است. تصویر زیر، یک گونیا را نمایش میدهد.
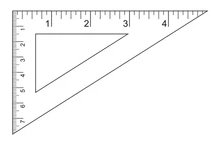
گونیا، ابزاری به شکل مثلث قائم الزاویه است. برای یادگیری نحوه رسم ارتفاعهای مثلث به کمک این ابزار، مثلث زیر را در نظر بگیرید.
اگر بخواهیم ارتفاع نظیر قاعده (ب پ) را رسم کنیم، گونیا را به شکل زیر بر روی مثلث قرار میهیم.
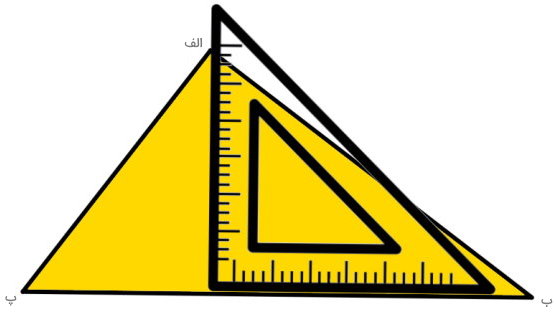
همانند تصویر بالا، یکی از ساقهای گونیا باید بر روی قاعده (ب پ) قرار گیرد و ساق دیگر، از روی راس (الف) عبور کند. این موارد در تصویر زیر نمایش داده شدهاند.
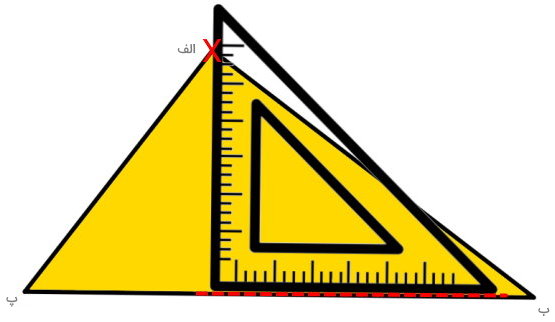
پس از تنظیم محل قرارگیری گونیا، یک پاره خط از راس (الف) در کنار ساق گونیا رسم میکنیم تا به پاره (ب پ) برخورد کند (پاره خط بنفش در تصویر زیر). عنوان محل برخورد ارتفاع با قاعده را با حرف (ت) نمایش میدهیم.
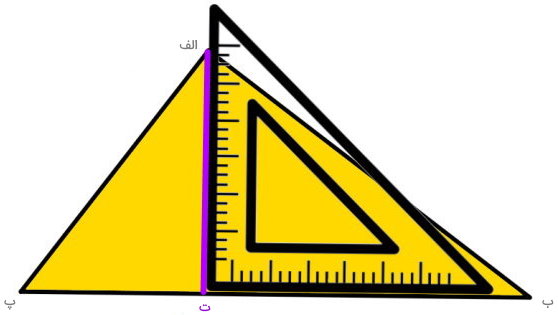
اکنون، گونیا را از روی مثلث بر میداریم. پاره خط (الف ت)، ارتفاع نظیر قاعده (ب پ) است.
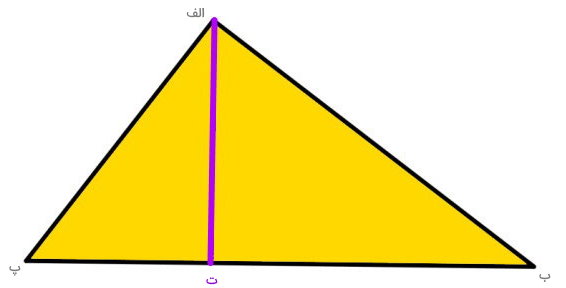
با تکرار فرآیند بالا برای قاعدههای (الف ب) و (الف پ)، میتوانیم ارتفاعهای نظیر این ضلعها را نیز رسم کنیم.
رسم ارتفاع مثلث قائم الزاویه
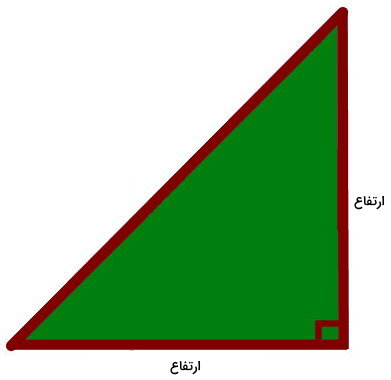
در مثلث قائم الزاویه، ضلعهای تشکیل دهنده زاویه 90 درجه (ساقها)، قاعده و ارتفاع نظیر یکدیگر هستند. اگر یکی از ضلعهای گونیا را مانند تصویر زیر بر روی یکی از ساقهای مثلث قرار دهیم، ضلع دوم گونیا نیز بر روی ساق دیگر مثلث منطبق میشود.
در مثلثهای قائم الزاویه، نیازی به رسم دو ارتفاع منطبق بر روی ساقها نیست. البته در صورت نیاز به رسم ساق سوم، باید از گونیا، پرگار یا روشهای دیگر استفاده کرد.
در مجموع، استفاده از گونیا برای رسم ارتفاع مثلثهای کوچکتر از ابعاد گونیا مناسب است.
رسم ارتفاع مثلث با پرگار و خط کش
یکی دیگر از روشهای رسم ارتفاع مثلث، استفاده از پرگار است. برای انجام این کار، علاوه بر پرگار، به یک خط کش نیاز دارید. مثلث مختلف اضلاع زیر را در نظر بگیرید. در این بخش، نحوه رسم ارتفاع نظیر قاعده AB برای این مثلث را به صورت گام به گام آموزش میدهیم.
مرحله اول: رسم دایره به مرکز راس مقابل قاعده
به منظور شروع رسم ارتفاع مثلث، ابتدا سوزن پرگار را بر روی راس (مقابل قاعده نظیر ارتفاع مورد نظر) قرار دهید. سپس، دهانه پرگار را به اندازهای باز کنید که در دو نقطه با قاعده نظیر و یا امتداد آن برخورد داشته باشد.
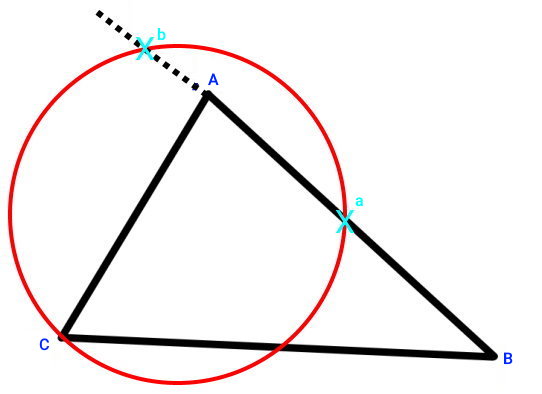
در تصویر بالا، دایره رسم شده از راس C، قاعده AB را در دو نقطه a و b قطع کرده است.
مرحله دوم: رسم دو دایره به مرکز نقاط برخورد
در مرحله بعدی، سوزن پرگار را بر روی نقطه a قرار دهید. دهانه پرگار را کمی بیشتر از نصف پاره خط ab باز کرده و یک دایره رسم کنید. بدون تغییر اندازه دهانه پرگار، رسم دایره را به مرکز نقطه b انجام دهید. نقطه برخورد این دو دایره را علامت بزنید.
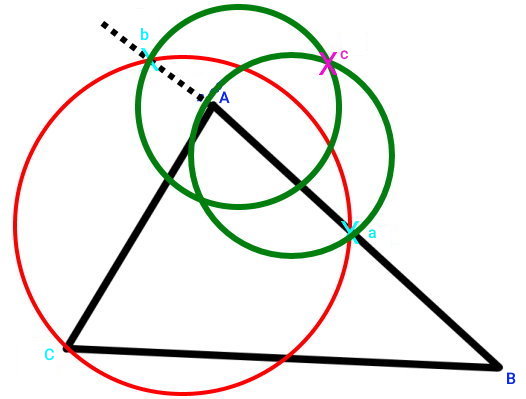
در تصویر بالا، دو دایره رسم شده از نقاط a و b، یکدیگر را در نقطه c قطع کردهاند.
مرحله سوم: رسم ارتفاع مثلث
در مرحله آخر، پاره خطی را توسط خط کش از راس C به نقطه c رسم کنید. این پاره خط، ضلع AB را در نقطه D قطع میکند. پاره خط CD، ارتفاع نظیر قاعده AB است. با اندازهگیری طول این ارتفاع میتوان مساحت مثلث را با استفاده فرمول ارتفاع ضربدر قاعده تقسیم بر دو به دست آورد.
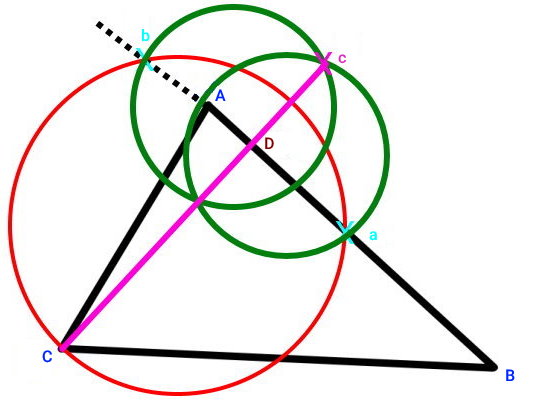
نکته: برای انجام مراحل بالا، نیازی به رسم کامل دایرهها نیست. به منظور جلوگیری از شلوغ شدن ترسیمات، رسم کمانهای دایره نیز کفایت میکند.
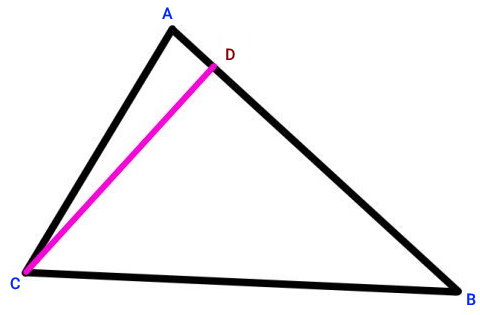
ارتفاع مثلث چگونه محاسبه می شود ؟
ارتفاع مثلث، معمولا با استفاده از فرمولهای مساحت محاسبه میشود. در بخش قبلی، نحوه استفاده از گونیا و پرگار برای رسم ارتفاع مثلث را آموزش دادیم. در این بخش، به معرفی فرمولهای محاسبه ارتفاع انواع مثلث بر اساس اندازهها اجزای مختلف آنها میپردازیم.
فرمول ارتفاع مثلث چیست؟
در حالت کلی، ارتفاع مثلث با استفاده از بازنویسی فرمولهای مساحت محاسبه میشود. فرمولهای ارتفاع مثلث بر اساس مساحت، عبارت هستند از:
- A: مساحت
- b: یکی از قاعدههای مثلث
- h: ارتفاع نظیر قاعده b
- ha: ارتفاع نظیر قاعده a
- hb: ارتفاع نظیر قاعده b
- hc: ارتفاع نظیر قاعده c
- a: طول ضلع اول
- b: طول ضلع دوم
- c: طول ضلع سوم
- s: نصف محیط مثلث
- A: زاویه بین ضلعهای b و c
- B: زاویه بین ضلعهای a و c
- C: زاویه بین ضلعهای a و b
به کمک فرمولهای بالا میتوان ارتفاع تمام انواع مثلثها را محاسبه کرد. البته در صورتی که مثلث مورد بررسی، یکی از انواع خاص مثلث (قائم الزاویه، متساوی الساقین یا متساوی الاضلاع) باشد، استفاده از فرمولهای مخصوص، گزینه مناسبتر و سادهتری خواهد بود.
مثال اول: محاسبه ارتفاع مثلث با مساحت
ارتفاعهای مثلثی با ضلعهای 3، 4 و 5 را به دست بیاورید.
به دلیل مشخص بودن اندازه هر سه ضلع مثلث، از فرمولهای زیر برای محاسبه ارتفاعهای مثلث استفاده میکنیم:
- ha: ارتفاع نظیر قاعده a
- hb: ارتفاع نظیر قاعده b
- hc: ارتفاع نظیر قاعده c
- a: طول ضلع اول برابر 3
- b: طول ضلع دوم برابر 4
- c: طول ضلع سوم برابر 5
- s: نصف محیط مثلث
پیش از شروع جایگذاری اندازهای بالا درون فرمول ارتفاع، نصف محیط را به دست میآوریم:
نصف محیط را به همراه اندازه ضلعها، درون فرمول ارتفاع قرار میدهیم:
از آنجایی که عبارت زیر رادیکال برابر 6 است و عبارت آن در فرمولهای دیگر نیز تکرار میشود، فرمول ارتفاع بعدی را به صورت زیر مینویسیم:
برای ارتفاع سوم نیز داریم:
به این ترتیب، ارتفاعهای مثلث برابر 4، 3 و 2/4 هستند.
فرمول ارتفاع مثلث قائم الزاویه
ساقهای مثلث قائم الزاویه، قاعده و ارتفاع نظیر یکدیگر هستند. بنابراین، برای محاسبه اندازه ساقهای این مثلث میتوان از فرمولهای محاسبه قاعده مثلث استفاده کرد. در صورت مشخص بودن اندازه هر سه ضلع مثلث قائم الزاویه، فرمول محاسبه ارتفاع نظیر وتر (ارتفاع سوم)، عبارت هستند از:
- hc: ارتفاع نظیر وتر
- a: اندازه یکی از ساقهای مثلث
- b: اندازه ساق دیگر مثلث
- c: اندازه وتر مثلث
با رسم ارتفاع نظیر وتر، مثلث قائم الزاویه به دو مثلث قائم الزاویه کوچکتر و متشابه تبدیل میشود.
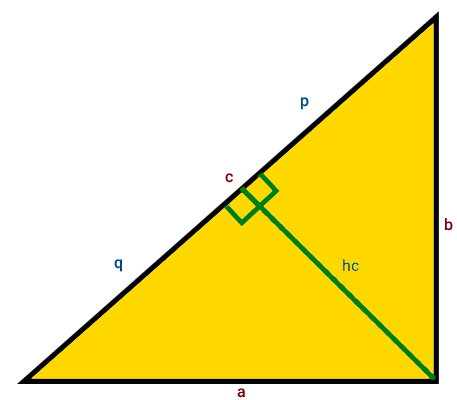
اگر ارتفاع مثلث قائم الزاویه، وتر را به دو پاره خط با اندازههای p و q تقسیم کند، میتوان ارتفاع نظیر وتر را از رابطه زیر به دست آورد:
- hc: ارتفاع نظیر وتر
- p: اندازه پای ارتفاع نظیر وتر تا یکی از راسها
- q: اندازه پای ارتفاع نظیر وتر تا راس دیگر
مثال دوم: محاسبه ارتفاع مثلث قائم الزاویه
ارتفاعهای مثلث قائم الزاویهای با اندازه ضلعهای 3، 4 و 5 را محاسبه کنید.
در مثال اول مقاله، هر سه ارتفاع مثلثی با اندازه ضلعهای 3، 4 و 5 را با استفاده از فرمولهای کلی ارتفاع به دست آوردیم. در این مثال، ارتفاعهای همان مثلث اما این بار با عنوان یک مثلث قائم الزاویه از ما خواسته شده است. به دلیل قائم الزاویه بودن مثلث، دو ساق با اندازههای 3 و 4، ارتفاعهای نظیر یکدیگر خواهند بود. ارتفاع نظیر وتر نیز توسط فرمول زیر محاسبه میشود:
- hc: ارتفاع نظیر وتر
- a: اندازه یکی از ساقها برابر 3
- b: اندازه ساق دیگر برابر 4
- c: اندازه وتر برابر 5
در نتیجه، ارتفاعهای مثلث برابر 4، 3 و 2/4 هستند.
فرمول ارتفاع مثلث متساوی الساقین
در مثلثهای متساوی الساقین، فرمول محاسبه دو ارتفاع نظیر ساقها، همان فرمولهای کلی معرفی شده در بخشهای قبلی است. البته در صورت رسم ارتفاع نظیر و نوشتن قضیه فیثاغورس برای مثلثهای تشکیل شده، میتوان فرمول محاسبه ارتفاع نظیر ساقهای مثلث متساوی الساقین را به صورت زیر نوشت:
- ha: ارتفاع نظیر ساقها
- a: اندازه ساق
- b: اندازه قاعده
ارتفاع نظیر قاعده مثلث متساوی الساقین نیز توسط فرمول اختصاصی زیر به دست میآید:
- hb: ارتفاع نظیر قاعده
- a: اندازه ساق
- b: اندازه قاعده
برای مثلثهای متساوی الساقین یک حالت خاص دیگر وجود دارد. اگر یک مثلث، علاوه بر دو ضلع برابر، دارای زاویه 90 درجه باشد (مثلث متساوی الساقین قائم الزاویه)، ارتفاع نظیر وتر آن توسط فرمول زیر تعیین میشود:
- hb: ارتفاع نظیر قاعده
- a: اندازه ساق
مثال سوم: محاسبه ارتفاع مثلث متساوی الساقین
سه ارتفاع مثلث زیر را به دست بیاورید.
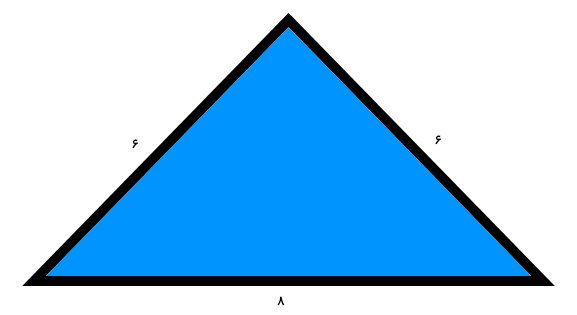
به دلیل برابر بودن اندازه دو ضلع، این مثلث از نوع متساوی الساقین است. بنابراین، برای شروع محاسبات، فرمول ارتفاع ساق مثلث متساوی را مینویسیم:
- ha: ارتفاع نظیر ساق
- a: اندازه ساق برابر 6
- b: اندازه قاعده برابر 8
ارتفاعهای نظیر ساقها در مثلثهای متساوی الساقین با هم برابر هستند. بنابراین، مقدار بالا، اندازه دو ارتفاع مثلث را نمایش میدهد. ارتفاع نظیر قاعده مثلث متساوی الساقین نیز به صورت زیر محاسبه میشود:
- hb: ارتفاع نظیر قاعده
- a: اندازه ساق برابر 6
- b: اندازه قاعده برابر 8
به این ترتیب، هر سه ارتفاع مثلث مشخص شدند.
فرمول ارتفاع مثلث متساوی الاضلاع
فرمول اصلی ارتفاع مثلث برابر است با:
مثال چهارم: محاسبه ارتفاع مثلث متساوی الاضلاع
ارتفاع مثلث متساوی الاضلاع به ضلع a را تعیین کنید.
به منظور تعیین ارتفاع مثلث متساوی الاضلاع، تصویر زیر را در نظر بگیرید. در این تصویر، یکی از ارتفاعهای مثلث رسم شده است.
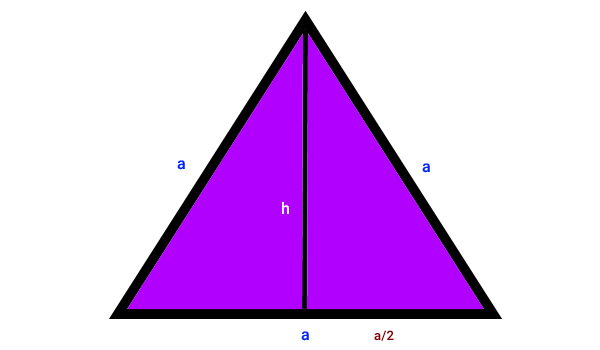
همانطور که مشاهده میکنید، پس از رسم ارتفاع، مثلث متساوی الاضلاع به دو مثلث قائم الزاویه تبدیل میشود. در مثلثهای متساوی الاضلاع، هر ارتفاع (h)، قاعده نظیر خود را به دو قسمت مساوی (a/2) تقسیم میکند. با توجه به این نکته، قضیه فیثاغورس را برای یکی از مثلثهای قائم الزاویه بالا مینویسیم:
- a: وتر مثلث قائم الزاویه
- h: یکی از ساقهای مثلث
- : ساق دیگر مثلث
رابطه بالا را بر حسب h حل میکنیم:
جواب به دست آمده، همان فرمول ارتفاع مثلثهای متساوی الاضلاع است. تفاوتی ندارد که روش حل این مثال چه باشد (قضیه هرون، روش سینوس یا فرمول کلی)، در هر حال، نتیجه نهایی، فرمول بالا خواهد بود.
جدول فرمول های ارتفاع انواع مثلث
فرمول مورد استفاده برای تعیین ارتفاع مثلث، به اندازههای معلوم و نوع مثلث بستگی دارد. بر این اساس، جدول زیر، خلاصهای از فرمولهای پرکاربرد ارتفاع انواع مثلثها را بر اساس اندازههای موجود نمایش میدهد.
| نوع مثلث | اندازههای معلوم | فرمول محاسبه ارتفاع مثلث |
| تمام مثلثها | مساحت (A) و قاعده نظیر (b) | |
| تمام مثلثها | نصف محیط (s) و اندازه هر سه ضلع (b ،a و c) | |
| تمام مثلثها | اندازه دو ضلع (a و b) و زاویه بین آنها (C) | |
| مثلث قائم الزاویه | اندازه ساقها (a و b) و وتر (c) | |
| مثلث متساوی الاضلاع | اندازه ضلع (a) | |
| مثلث متساوی الساقین | اندازه ساق (a) و قاعده (b) | |
| مثلث متساوی الساقین قائم الزاویه | اندازه ساق (a) |
برای آشنایی بیشتر با نحوه محاسبه ارتفاع مثلث با استفاده از فرمولهای بالا، مطالعه مطلب «محاسبه ارتفاع مثلث — تعریف، حل تمرین و مثال + جدول فرمولها» را به شما پیشنهاد میکنیم.
خواص ارتفاع مثلث چه هستند؟
ارتفاعهای مثلث، دارای خواص متعددی هستند که در این بخش به معرفی برخی از مهمترین آنها میپردازیم.
نقطه برخورد سه ارتفاع یک مثلث
ارتفاعهای مثلث یا امتداد آنها، همیشه از یک نقطه مشترک عبور میکنند. این نقطه با عنوان «نقطه برخورد سه ارتفاع یک مثلث» یا اصطلاحا (مرکز ارتفاعی) «Orthocenter» شناخته میشود. در اغلب موارد، حرف انگلیسی «H» برای نمایش محل برخورد ارتفاعها مورد استفاده قرار میگیرد.
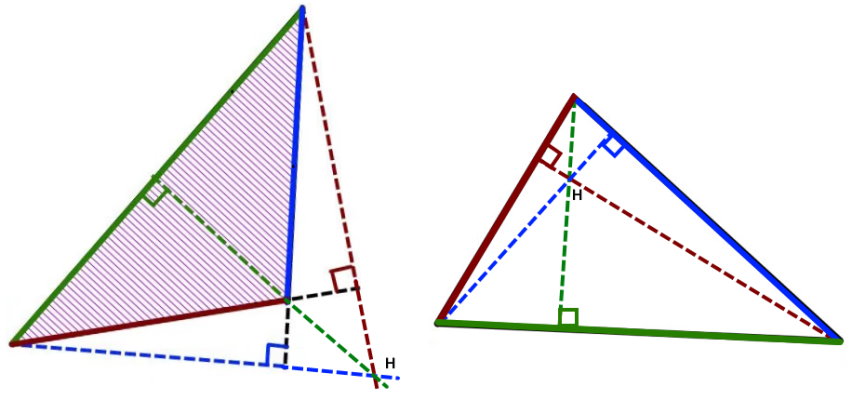
اگر مثلث از نوع حاده (زوایای کوچکتر از 90 درجه) باشد، نقطه مشترک ارتفاعها، درون مثلث قرار میگیرد. در صورت منفرجه بودن مثلث (وجود یک زاویه بزرگتر از 90 درجه)، محل برخورد ارتفاعها، در خارج از محدوده ضلعهای مثلث خواهد بود.
نسبت ارتفاعهای مثلث
حاصلضرب فاصله تقاطع تا راس در فاصله تقاطع تا پای ارتفاع در مثلث، همواره یک عدد ثابت است. برای درک این ویژگی، مثلث ABC را در نظر بگیرید. این مثلث از نوع حاده بوده و هر سه ارتفاع آن درون محدوده اضلاع قرار میگیرند.
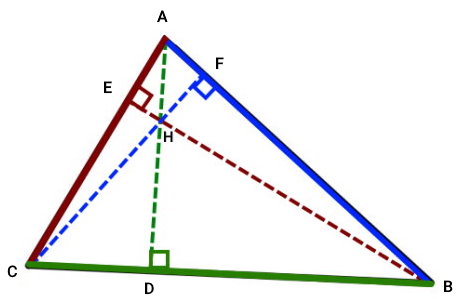
محل برخورد مثلثها با حرف H و پای ارتفاع مقابل راسهای B ،A و C به ترتیب با حرفهای E ،D و F نمایش داده شدهاند. بر توجه این نامگذاریها، رابطههای زیر بین ارتفاعهای مثلث برقرار هستند:
رابطههای بالا برای تمام مثلثها صادق است و قرار گرفتن نقطه تقاطع ارتفاعها در داخل یا خارج از ضلعهای مثلث، تغییری در آن ایجاد نمیکند.
ارتفاع در مثلث قائم الزاویه
در مثلثهای قائم الزاویه، رابطه بین ارتفاعهای مثلث عبارت است از:
- ha: ارتفاع نظیر قاعده a
- hb: ارتفاع نظیر قاعده b
- hc: ارتفاع نظیر قاعده c
رابطه بالا با عنوان «وارون قضیه فیثاغورس» شناخته میشود.
ارتفاع در مثلث متساوی الاضلاع
در مثلثهای متساوی الاضلاع، مجموع فاصله عمودی هر نقطه در داخل مثلث تا ضلعها، برابر ارتفاع است.
سوالات متداول در رابطه با ارتفاع مثلث
در این بخش، به برخی از سوالات متداول در زمینه ارتفاع مثلث پاسخ میدهیم.
ارتفاع نظیر مثلث چیست ؟
ارتفاع نظیر مثلث، پاره خطی است که از راس مقابل قاعده، به آن عمود میشود.
کاربرد ارتفاع نظیر مثلث چیست ؟
ارتفاع نظیر مثلث و قاعده، معمولا به منظور محاسبه مساحت مثلث مورد استفاده قرار میگیرند.
مثلث چند ارتفاع دارد؟
هر مثلث سه ارتفاع دارد.
ارتفاع مثلث را چگونه پیدا کنیم ؟
ارتفاع مثلث را میتوان به کمک ابزارهایی مانند پرگار، گونیا و خطکش پیدا کرد.
ارتفاع مثلث چگونه بدست می آید ؟
ارتفاع مثلث، با استفاده از فرمولهای مساحت مثلث به دست میآید.
تفاوت ارتفاع و میانه مثلث چیست؟
میانه، پاره خطی است که راس مثلث را به وسط ضلع رو به روی آن متصل میکند. در صورت ایجاد زاویه 90 درجه بین این پاره خط و ضلع مقابل آن، میانه و ارتفاع یکسان خواهند بود. اگر پاره خط رسم شده، فقط با ضلع مقابل خود، زاویه ۹۰ درجه بسازد و از وسط آن عبور نکند، به آن ارتفاع میگویند.
جمعبندی
در این مطلب از مجله فرادرس، ابتدا ارتفاعِ مثلث را تعریف کردیم. در ادامه، انواع ارتفاع و چگونگی رسم آنها را در انواع مثلثها توضیح دادیم.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت مثلث — انواع مثلث و تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مثلث چیست ؟ — به زبان ساده (+ دانلود فیلم آموزش رایگان)
- مساحت انواع مثلث چگونه بدست می آید ؟ — حل تمرین و مثال های متنوع
- محیط مثلث چگونه بدست می آید؟ + فیلم آموزش رایگان
- چگونه مساحت مثلث را حساب کنیم؟ + فیلم آموزشی و تمرین با جواب
- محاسبه آنلاین مساحت مثلث — معرفی بهترین سایتها + مثال
- فرمول محیط مثلث چیست ؟ انواع فرمول ها + حل مثال های متنوع
- فرمول مساحت مثلث چیست ؟ — تمام فرمول ها + حل تمرین
- قاعده مثلث چیست و چگونه بدست می آید ؟ + تعریف و مثال
- ارتفاع مثلث چیست و چگونه رسم می شود ؟ — آموزش تصویری + حل تمرین(همین مطلب)
- محاسبه ارتفاع مثلث — تعریف، حل تمرین و مثال + جدول فرمول ها
- محیط مثلث مختلف الاضلاع — به زبان ساده + حل مثال های متنوع
- چگونه مساحت مثلث مختلف الاضلاع را حساب کنیم؟ + حل تمرین و مثال
- چگونه مساحت مثلث با سه ضلع معلوم را حساب کنیم؟ + حل تمرین و مثال
- فرمول هرون — به زبان ساده
- مساحت مثلث با سینوس چگونه محاسبه می شود ؟ + حل تمرین و جدول فرمول ها
- مثلث قائم الزاویه چیست ؟ — تعریف، ویژگی ها و محاسبات | به زبان ساده
- محیط مثلث قائم الزاویه — به زبان ساده + حل مثال های متنوع
- مساحت مثلث قائم الزاویه — حل تمرین و مثال های متنوع
- مثلث متساوی الساقین چیست ؟ | تعریف، ویژگی ها و محاسبات — به زبان ساده
- محیط مثلث متساوی الساقین — به زبان ساده و با حل مثال
- مساحت مثلث متساوی الساقین — حل تمرین و مثال های متنوع
- محیط مثلث متساوی الاضلاع چگونه بدست می آید؟ + حل مثال و تمرین
- مساحت مثلث متساوی الاضلاع — حل تمرین و مثال های متنوع












