چگونه مساحت مثلث با سه ضلع معلوم را حساب کنیم؟ + حل تمرین و مثال

مساحت مثلث با سه ضلع، معمولا به روش فرمول هرون محاسبه میشود. در این آموزش، نحوه استفاده از فرمول هرون برای تعیین مساحت مثلث با سه ضلع مشخص را به همراه چند مثال توضیح میدهیم. در انتها نیز، فرمهای مختلف این فرمول را ارائه میکنیم.
مثلث چیست؟
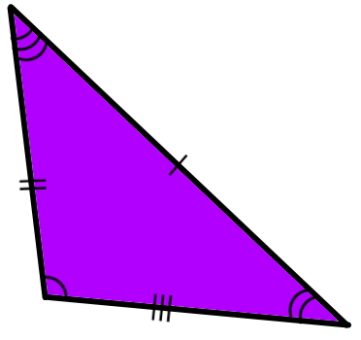
مثلث (به انگلیسی Triangle)، یکی از شکلهای هندسی اصلی است که از سه ضلع و سه راس تشکیل میشود. تصویر زیر، یک مثلث مختلف اضلاع را نمایش میدهد. در این نوع مثلث، اندازه هر سه ضلع و هر سه زاویه با یکدیگر تفاوت دارد.
مساحت مثلث چیست؟
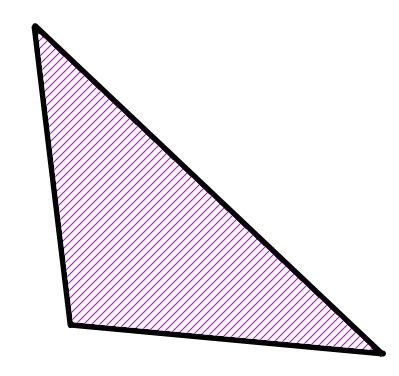
مساحت مثلث، سطح درون سه ضلع آن است. در تصویر زیر، ناحیه هاشور خورده، سطح داخل مثلث یا همان مساحت مثلث را نمایش میدهد.
روشهای مختلفی برای محاسبه سطح درون مثلث وجود دارد که از پرکاربردترین آنها میتوان به موارد زیر اشاره کرد:
- محاسبه مساحت مثلث با قاعده و ارتفاع (حاصلضرب قاعده ضربدر ارتفاع تقسیم بر دو)
- روش هرون یا فرمول محاسبه مساحت مثلث با سه ضلع
- روش مثلثاتی یا فرمول محاسبه مساحت مثلث با سینوس
مساحت مثلث با سه ضلع مختلف چگونه بدست می آید ؟
مساحت مثلث با سه ضلع با استفاده از فرمول هرون به دست میآید. این فرمول به صورت زیر نوشته میشود:
- A: مساحت
- s: نصف محیط مثلث
- a: طول ضلع اول
- b: طول ضلع دوم
- c: طول ضلع سوم
نصف محیط مثلث، از فرمول زیر به دست میآید:
فرمول هرون، روش اصلی محاسبه مساحت مثلث با سه ضلع مشخص است. البته این فرمول به شکلهای مختلفی نوشته میشود که در بخشهای بعدی به معرفی آنها خواهیم پرداخت.
مثال محاسبه مساحت مثلث با سه ضلع مساوی
مساحت مثلث متساوی الاضلاع زیر چقدر است؟
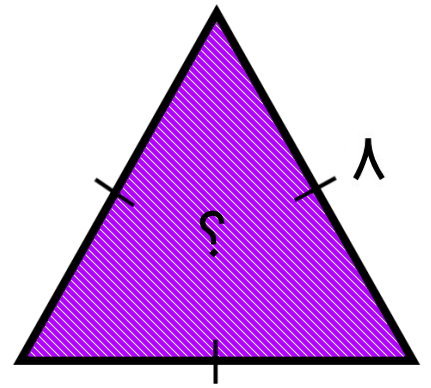
مثلث متساوی الاضلاع، مثلثی با اندازه ضلعهای برابر است. برای محاسبه مساحت این مثلث، فرمول هرون را مینویسیم:
- A: مساحت
- s: نصف محیط مثلث
- a: اندازه ضلع اول برابر 8
- b: اندازه ضلع دوم برابر 8
- c: اندازه ضلع سوم برابر 8
نصف محیط مثلث به صورت زیر محاسبه میشود:
عدد بالا را به همراه اندازه ضلعها درون فرمول هرون قرار میدهیم:
مساحت مثلث برابر 27/71 است. البته در این مثال، عدد بالا با استفاده رابطه مخصوص مساحت متساوی الاضلاع نیز به دست میآمد.
مثال محاسبه مساحت مثلث با 3 ضلع معلوم
مساحت مثلثی با اندازه ضلعهای 3، 6 و 7 سانتیمتر را محاسبه کنید.
برای شروع، اطلاعات مسئله را یادداشت میکنیم:
- a=3
- b=6
- c=7
سپس، فرمول هرون را مینویسیم:
اکنون، باید نصف محیط مثلث را نیز به دست بیاوریم:
عدد بالا را به همراه اندازههای ضلع درون فرمول هرون قرار میدهیم:
مساحت مثلث، تقریبا برابر 8/94 سانتیمتر مربع است.
مثال محاسبه ارتفاع سقف شیروانی
شخصی، سقف خانه چوبی خود را به صورت شیروانی ساخته است. اگر عرض این خانه برابر 8 متر و عرض هر طرف سقف برابر 5 متر باشد (تصویر زیر)، ارتفاع سقف شیروانی چقدر خواهد بود؟
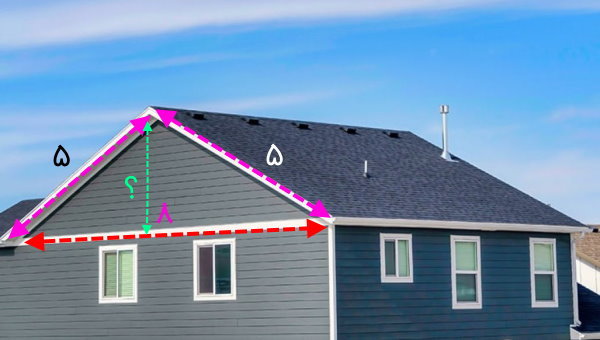
همان طور که در تصویر بالا مشاهده میکنید، نمای جانبی سقف شیروانی به شکل مثلث است. به دلیل مشخص بودن اندازه هر سه ضلع این مثلث، میتوانیم از فرمول هرون برای محاسبه مساحت آن و از فرمول کلی مساحت برای تعیین ارتفاع سقف شیروانی استفاده کنیم. در اولین مرحله، اطلاعات مسئله را مینویسیم:
- a: ضلع اول مثلث برابر 5 متر
- b: ضلع دوم مثلث برابر 5 متر
- c: ضلع سوم مثلث برابر 8 متر
به منظور استفاده از فرمول هرون، به نصف محیط مثلث بالا نیاز داریم. بنابراین، این مقدار را به صورت زیر محاسبه میکنیم:
عدد بالا را به همراه اندازه ضلعها درون فرمول هرون قرار میدهیم:
مساحت مقطع مثلثی شکل سقف شیروانی برابر 12 متر مربع است. اکنون، فرمول کلی مساحت مستطیل را مینویسیم:
۲ ÷ (قاعده ارتفاع) = مساحت مثلث
- A: مساحت مثلث برابر 12 متر مربع
- b: ضلع نظیر ارتفاع سقف شیروانی برابر 8 متر
- h: ارتفاع سقف شیروانی
مقادیر موجود را درون فرمول بالا قرار میدهیم و رابطه را بر حسب h حل میکنیم:
در نتیجه، ارتفاع بخش شیروانی سقف برابر 3 متر است.
مثال تعیین مساحت مثلث قائم الزاویه با وتر و یک ساق
مساحت مثلث قائم الزاویه با وتر 13 سانتیمتر و اندازه ساق 5 سانتیمتر را حساب کنید.
بر اساس قضیه فیثاغورس در مثلثهای قائم الزاویه، رابطه بین ساقها و وترهای این مثلث عبارت است از:
- c: وتر مثلث قائم الزاویه برابر 13 سانتیمتر
- a: یکی از ساقهای مثلث برابر 5 سانتیمتر
- b: ساق دیگر مثلث
اندازههای معلوم را درون فرمول بالا قرار میدهیم:
اندازه ساق دیگر مثلث برابر 12 سانتیمتر است. با داشتن اندازه تمام ضلعهای مثلث، فرمول هرون را مینویسیم:
از میان اطلاعات مورد نیاز در این فرمول، پارامتر s (نصف محیط) باقی مانده است. این پارامتر را به صورت زیر محاسبه میکنیم:
عدد بالا را به همراه اندازههای ضلعها درون رابطه هرون قرار میدهیم:
مساحت مثلث برابر 30 سانتیمتر مربع است. البته برای حل مساحت مثلثهای قائم الزاویه، فرمول سادهتری وجود دارد که در مطلب «فرمول مساحت مثلث — انواع روشهای محاسبه مساحت» به آن پرداختهایم.

شکل های مختلف فرمول مساحت مثلث با سه ضلع متفاوت
فرمول هرون، به شکلهای مختلفی نوشته میشود. پرکاربردترین فرم این فرمول را در بخش قبلی معرفی کردیم.
فرمهای دیگر فرمول هرون عبارت هستند از:
سوالات متداول محاسبه مساحت مثلث با سه ضلع
در این بخش، به برخی از سوالات متداول در زمینه محاسبه مساحت مثلث با سه ضلع پاسخ میدهیم.
از چه فرمولی برای محاسبه مساحت مثلث با سه ضلع استفاده میشود؟
به منظور محاسبه مساحت مثلث با سه ضلع، از «فرمول هرون» (Heron's formula) استفاده میشود.
اندازههای مورد نیاز برای محاسبه مساحت مثلث به روش هرون چه هستند؟
برای محاسبه مساحت مثلث با استفاده از روش هرون، باید اندازه تمام ضلعهای مثلث و نصف محیط آن مشخص باشد.
روش هرون برای محاسبه مساحت کدام مثلث کاربرد دارد؟
فرمول هرون برای محاسبه مساحت تمام مثلثها با اندازه ضلعهای مشخص (مثلث ض ض ض) کاربرد دارد.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت مثلث — انواع مثلث و تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مثلث چیست ؟ — به زبان ساده (+ دانلود فیلم آموزش رایگان)
- مساحت انواع مثلث چگونه بدست می آید ؟ — حل تمرین و مثال های متنوع
- محیط مثلث چگونه بدست می آید؟ + فیلم آموزش رایگان
- چگونه مساحت مثلث را حساب کنیم؟ + فیلم آموزشی و تمرین با جواب
- محاسبه آنلاین مساحت مثلث — معرفی بهترین سایتها + مثال
- فرمول محیط مثلث چیست ؟ انواع فرمول ها + حل مثال های متنوع
- فرمول مساحت مثلث چیست ؟ — تمام فرمول ها + حل تمرین
- قاعده مثلث چیست و چگونه بدست می آید ؟ + تعریف و مثال
- ارتفاع مثلث چیست و چگونه رسم می شود ؟ — آموزش تصویری + حل تمرین
- محاسبه ارتفاع مثلث — تعریف، حل تمرین و مثال + جدول فرمول ها
- محیط مثلث مختلف الاضلاع — به زبان ساده + حل مثال های متنوع
- چگونه مساحت مثلث مختلف الاضلاع را حساب کنیم؟ + حل تمرین و مثال
- چگونه مساحت مثلث با سه ضلع معلوم را حساب کنیم؟ + حل تمرین و مثال(همین مطلب)
- فرمول هرون — به زبان ساده
- مساحت مثلث با سینوس چگونه محاسبه می شود ؟ + حل تمرین و جدول فرمول ها
- مثلث قائم الزاویه چیست ؟ — تعریف، ویژگی ها و محاسبات | به زبان ساده
- محیط مثلث قائم الزاویه — به زبان ساده + حل مثال های متنوع
- مساحت مثلث قائم الزاویه — حل تمرین و مثال های متنوع
- مثلث متساوی الساقین چیست ؟ | تعریف، ویژگی ها و محاسبات — به زبان ساده
- محیط مثلث متساوی الساقین — به زبان ساده و با حل مثال
- مساحت مثلث متساوی الساقین — حل تمرین و مثال های متنوع
- محیط مثلث متساوی الاضلاع چگونه بدست می آید؟ + حل مثال و تمرین
- مساحت مثلث متساوی الاضلاع — حل تمرین و مثال های متنوع













مساحت مثلث با سه ضلع مساوی را غلط محاسبه کرده اید. چون 4*4*4=64 است نه 12
سلام و وقت بخیر؛
ممنون از دقت نظر شما. راهحل اصلاح شد.
از همراهی شما با مجله فرادرس سپاسگزاریم. موفق و سلامت باشید.