فرمول های ریاضی دهم در یک نگاه و با مثال
ریاضی دهم، در سال اول دوره متوسطه دوم با عنوان «ریاضی ۱» به دانشآموزان مقطع دهم در رشته ریاضی و فیزیک و رشته علوم تجربی آموزش داده میشود. دانش آموزان مقطع دهم در رشته ادبیات و علوم انسانی و رشته علوم و معارف اسلامی، مباحث ریاضی را در درسی با عنوان «ریاضی و آمار ۱» فرا میگیرند. ریاضی ۱ و ریاضی و آمار ۱، از دروس تخصصی در کنکور سراسری هستند. از اینرو، یادگیری و تسلط بر روی مطالب آنها، اهمیت بالایی برای متقاضیان ورود به دانشگاه دارد. در اغلب موارد، دانشآموزان و متقاضیان کنکور، به دنبال منبع جامعی هستند که تمام نکات و فرمولهای مهم ریاضی را به طور خلاصه و سریع به آنها ارائه دهد. در این مطلب از مجله فرادرس، قصد داریم مهمترین نکات و فرمول های ریاضی دهم را برای شما خلاصه کنیم تا در صورت نیاز به مرور کلی مباحث، بتوانید از این مطلب به عنوان یک منبع کمک آموزشی برای مرور و دوره استفاده کنید.
- یاد میگیرید انواع مجموعههای عددی و ویژگیهای هر کدام را تشخیص دهید.
- میآموزید فرمولهای دنباله حسابی و هندسی را در حل مسائل بهکار ببرید.
- یاد خواهید گرفت از نسبتهای مثلثاتی و کاربرد دایره مثلثاتی بهدرستی استفاده کنید.
- روش تبدیل ریشه و توان و استفاده از اتحادهای جبری را فرا میگیرید.
- حل گامبهگام معادلات و نامعادلات درجه دوم را خواهید آموخت.
- مفهوم تابع، دامنه، برد و روش رسم نمودار آن را یاد میگیرید.


در ادامه این مطلب از مجله فرادرس، فرمول های فصل اول کتاب ریاضی ۱ را معرفی میکنیم و به حل مثال برای هر یک از دروس این فصل میپردازیم. دانشآموزان رشته علوم انسانی، نگران نباشند. در یک فصل آخر این مطلب، به معرفی منابع یادگیری ریاضی و آمار ۱ خواهیم پرداخت.
۱. مجموعه، الگو و دنباله: فرمول های فصل اول ریاضی دهم
فصل اول کتاب ریاضی دهم، شامل چهار درس با عنوانهای «مجموعههای متناهی و نامتناهی»، «متمم یک مجموعه»، «الگو و دنباله» و «دنباله های حسابی و هندسی» است.
در ادامه، جدول مهمترین نکات و فرمول های فصل اول ریاضی دهم را آوردهایم.
| عنوان | توصیف |
| مجموعه اعداد طبیعی | |
| مجموعه اعداد حسابی | |
| مجموعه اعداد صحیح | |
| مجموعه اعداد گویا | |
| مجموعه اعداد گنگ | مجموعه اعدادی که نتوان آنها را به صورت نسبت دو عدد صحیح نمایش داد . |
| مجموعه اعداد حقیقی | |
| رابطه بین مجموعههای اعداد | |
| مجموعه متناهی | امکان نمایش تعداد عضوها با عدد حسابی |
| مجموعه نامتناهی | عدم امکان نمایش تعداد عضوها با عدد حسابی |
| مجموعه مرجع | شامل همه مجموعههای مورد بحث |
| متمم مجموعه A | |
| مجموعه مجزا | دو مجموعه با اشتراک تهی |
| تعداد عضوهای اجتماع و | |
| فرمول جمله ام دنباله حسابی | |
| فرمول جمله ام دنباله هندسی |
درس اول: مجموعههای متناهی و نامتناهی در ریاضی دهم
به مجموعههایی که تعداد اعضای آنها یک عدد حسابی باشد، مجموعه متناهی میگویند. در طرف مقابل، اگر تعداد اعضای یک مجموعه را نتوان با استفاده از یک عدد حسابی نمایش داد، آن مجموعه، به عنوان یک مجموعه نامتناهی در نظر گرفته میشود.

به عنوان مثال، مجموعه انسانهای روی کره زمین، یک مجموعه متناهی است؛ زیرا میتوان تعداد عضوهای این مجموعه (تعداد انسانها) با یک عدد حسابی (مانند ) نمایش داد. با این وجود، مجموعه مضربهای طبیعی عدد ، یک مجموعه نامتناهی است؛ چراکه مجموعه اعداد طبیعی، انتهایی ندارد و نمیتوان تعداد آن را با یک عدد حسابی مشخص نمایش داد.
- مجموعه اعداد طبیعی
- مجموعه شمارندههای طبیعی عدد
- بازه
- مجموعه مضربهای طبیعی عدد
متناهی یا نامتناهی بودن مجموعههای مورد سوال را به ترتیب مورد بررسی قرار میدهیم. مجموعه اعداد طبیعی، مجموعهای شامل تمام اعداد صحیح مثبت، از عدد به بعد است. این مجموعه به صورت زیر نمایش داده میشود:
به عبارت دیگر، مجموعه اعداد طبیعی تا مثبت بینهایت ادامه دارد و نمیتوان تعداد اعضای آن را به صورت یک عدد حسابی نمایش داد. در نتیجه، مجموعه اعداد طبیعی، نامتناهی است.
مجموعه مقسومعلیههای طبیعی یا شمارندههای طبیعی عدد ، به صورت زیر نوشته میشود:
این مجموعه دارای عضو است. از آنجایی که امکان نمایش تعداد عضوهای مجموعه بالا توسط یک عدد حسابی وجود دارد، آن را به عنوان یک مجموعه متناهی در نظر میگیریم.
مجموعه اعداد درون بازه ، بینهایت است. یعنی بینهایت عدد حقیقی را میتوانیم پیدا کنیم که در این بازه قرار بگیرند. بنابراین، امکان شمارش تعداد عضوهای بازه وجود ندارد. در نتیجه این مجموعه، یک مجموعه نامتناهی است.
مجموعه ، در حال نمایش های عضو مجموعه اعداد طبیعی () است که بین دو عدد و قرار دارند. هیچ عدد طبیعی بین و وجود ندارد. بنابراین میتوانیم عضوهای مجموعه را با عدد حسابی نمایش دهیم. در نتیجه، این مجموعه، یک مجموعه متناهی است. معمولا اگر در سوال، از شما مجموعهای شامل اعداد طبیعی، حسابی یا صحیح در یک بازه مشخص خواسته شود (به غیر از بازههای بینهایت)، با یک مجموعه متناهی طرف هستید.
مجموعه مضربهای عدد ، به صورت زیر نوشته میشود:
یا
به دلیل ادامه داشتن بازه بالایی مجموعه تا مثبت بینهایت، آن را به عنوان یک مجموعه نامتناهی در نظر میگیریم.
درس دوم: فرمول های متمم یک مجموعه در ریاضی دهم
به مجموعهای که تمام مجموعههای مورد نظر، زیرمجموعه آن باشند، مجموعه مرجع میگویند. این مجموعه را با نمایش میدهند. اگر مجموعه ، زیرمجموعه مجموعه مرجع باشد، مجموعه به عنوان متمم مجموعه در نظر گرفته میشود. این مجموعه را با علامت پرایم نمایش میدهند. بر این اساس، متمم مجموعه ، مجموعه خواهد بود. ، شامل عضوهایی از است که در نیستند.
به مجموعهای که فاقد عضو مشترک باشند، دو مجموعه جدا از هم یا مجزا میگویند. اشتراک دو مجموعه جدا از هم، مجموعه تهی است. به عبارت دیگر، اگر و ، دو مجموعه جدا از هم باشند، خواهیم داشت:
اگر بخواهیم تعداد عضوهای اجتماع دو مجموعه و را به دست بیاوریم، از رابطه زیر استفاده میکنیم:
در این رابطه داریم:
- : تعداد عضوهای مجموعه
- : تعداد عضوهای مجموعه
- : تعداد عضوهای اشتراک دو مجموعه و
- تعداد دانشآموزانی که فقط عضو گروه سرود هستند.
- تعداد دانشآموزانی که عضو هیچ یک از این دو گروه نیستند.
برای حل این مسئله، ابتدا مجموعههای موجود را تعریف و مشخص میکنیم:
- مجموعه دانشآموزان عضو گروه سرود:
- مجموعه دانشآموزان عضو گروه تئاتر:
- مجموعه کل دانشآموزان کلاس:
در مرحله بعد، اطلاعات صورت سوال را مینویسیم:
- تعداد دانشآموزان عضو گروه سرود:
- تعداد دانشآموزان عضو گروه تئاتر:
- تعداد دانشآموزان عضو هر دو گروه:
- تعداد کل دانش آموزان:
محاسبه تعداد دانش آموزانی که فقط عضو گروه سرود هستند، از رابطه زیر استفاده میکنیم:
این فرمول، به دنبال دانشآموزانی میگردد که عضو گروه سرود هستند () اما در گروه تئاتر عضویت ندارند (). مقادیر معلوم را درون رابطه قرار میدهیم:
بنابراین، دانشآموز، فقط عضو گروه سرود هستند. برای تعیین تعداد دانشآموزانی که عضو هیچ یک از این دو گروه نیستند، از فرمول زیر استفاده میکنیم:
این فرمول، تمام دانشآموزان کلاس را در نظر میگیرد (). سپس، دانشآموزانی که در گروه سرود یا در گروه تئاتر هستند () را از کل دانشآموزان کم میکند. به این ترتیب، دانشآموزانی باقی میمانند که در هیچ گروهی عضو نیستند. نکته مهم برای حل این سوال، استفاده از رابطه زیر به منظور تعیین اجتماع دو مجموعه است:
به این ترتیب، داریم:
در نتیجه، دانشآموز، در هیچ گروهی عضو نیستند.
درس سوم: فرمول های الگو و دنباله در ریاضی دهم
به مجموعه اعداد یا اشکالی که با یک نظم و ترتیب خاص در کنار یکدیگر قرار گرفتهاند، الگو میگویند. درس سوم از فصل اول کتاب ریاضی ۱، به معرفی فرمول الگو و دنباله میپردازد. بر اساس محتوای این درس، فرمول الگوی خطی به صورت زیر نوشته میشود:
- : جمله عمومی الگوی خطی
- و : اعداد حقیقی دلخواه و ثابت
- : شماره جمله در الگو

در الگوهای خطی، اختلاف دو جمله متوالی برابر با ضریب است. به الگویی که جمله عمومی آن به صورت نباشد، الگوی غیرخطی میگوییم. اگر جمله عمومی دنباله به صورت یک چندجملهای درجه دوم باشد، به آن دنباله درجه گفته میشود. پیدا کردن فرمول الگوها، روش مختص به خود را دارد که در مطلب «فرمول الگویابی | فرمول الگوی عددی — با مثال و به زبان ساده» از مجله فرادرس، آن را آموزش دادهایم.
اختلافهای به دست آمده را زیر دنباله مینویسیم:
اکنون، میزان تغییرات اختلاف بین هر دو عضو متوالی دنباله را به همین صورت زیر دنبالههای بالا مینویسیم:
فرم کلی دنباله درجه به صورت زیر نوشته میشود:
هدف ما، به دست آوردن ضرایب ثابت در فرمول بالا است. برای به دست آوردن ، اولین عدد در را برابر با قرار میدهیم:
برای به دست آوردن ، اولین عدد در را برابر با قرار میدهیم:
برای به دست آوردن ، اولین عدد در را برابر با قرار میدهیم:
این ضرایب را درون فرمول جمله عمومی جایگذاری میکنیم:
به این ترتیب، جمله عمومی دنباله درجه دوم به دست میآید. برای اطمینان از درستی این نتیجه، شماره عضو مورد نظر را در این رابطه قرار دهید و جواب را بررسی کنید.
درس چهارم: فرمول های دنباله های حسابی و هندسی در ریاضی دهم
از پشت هم قرار گرفتن اعداد، دنباله به وجود میآید. دنبالهها به دو دسته دنباله حسابی و دنباله هندسی تقسیم میشوند:
- دنباله حسابی: دنبالهای که در آن، هر جمله با اضافه شدن عددی ثابت (قدر نسبت) به جمله قبل خودش به دست میآید. مانند سالهای برگزاری المپیک (هر سال)
- دنباله هندسی: دنبالهای که در آن، هر جمله (به جز جمله اول)، از ضرب جمله قبل خودش در عددی ثابت و غیرصفر (قدر نسبت) به دست میآید.
جمله ام دنباله حسابی برابر است با:
- : جمله ام دنباله حسابی
- : جمله اول دنباله حسابی
- : شماره جمله مورد نظر
- : قدر نسبت دنباله
جمله ام دنباله هندسی برابر است با:
- : جمله ام دنباله هندسی
- : جمله اول دنباله هندسی
- : شماره جمله مورد نظر
- : قدر نسبت دنباله
در مبحث دنباله حسابی و هندسی، دو مفهوم دیگر با عنوان واسطه حسابی و هندسی وجود دارد که به صورت زیر تعریف میشوند:
- واسطه حسابی: اعدادی که با قرار دادن آنها در میان دو یا چند عدد، یک دنباله حسابی به وجود میآید.
- واسطه هندسی: اعدادی که با قرار دادن آنها در میان دو یا چند عدد، یک دنباله هندسی به وجود میآید.
- : جمله سوم دنباله برابر با
- : جمله هفتم دنباله برابر با
بنابراین میتوانیم جملات دنباله را به صورت زیر بنویسیم:
به دلیل ثابت بودن فاصله بین جملات متوالی (مانند )، برای تعیین قدر نسبت میتوانیم اختلاف دو جمله مشخص ( و ) را به دست بیاورم و عدد به دست آمده را بر اختلاف شماره آن دو جمله ( و ) تقسیم کنیم:
به این ترتیب، داریم:
در مطلبهای «فرمول های ریاضی هشتم در یک نگاه و با مثال» و «فرمول های ریاضی نهم در یک نگاه و با مثال»، مهمترین نکات و فرمولهای ریاضی دوره اول متوسطه را به صورت خلاصه ارائه کردیم. اگر تمایل دارید دانش پایه خود را قوی کنید و با آمادگی کامل به سراغ یادگیری ریاضی در سطوح بالاتر بروید، توصیه میکنیم نگاهی به این مطالب نیز داشته باشید. در ادامه این مطلب از مجله فرادرس، فرمول های فصل دوم کتاب ریاضی ۱ را معرفی میکنیم.

۲. مثلثات: فرمول های فصل دوم ریاضی دهم
فصل دوم کتاب ریاضی دهم، شامل درسهای با عنوانهای «نسبتهای مثلثاتی»، «دایره مثلثاتی» و «روابط بین نسبتهای مثلثاتی» است.
برخی از تعاریف و فرمول های مهم فصل دوم ریاضی دهم در جدول زیر خلاصه شدهاند.
| عنوان | توصیف |
| نسبتهای مثلثاتی | رابطه بین نسبت ضلعها مثلث قائمالزاویه و زاویههای آن |
| دایره مثلثاتی | دایرهای به شعاع واحد و مرکز منطبق بر مبدا مختصات |
| سینوس | نسبت ضلع مقابل به وتر |
| کسینوس | نسبت ضلع مجاور به وتر |
| تانژانت | نسبت ضلع مقابل به ضلع مجاور |
| کتانژانت | نسبت ضلع مجاور به ضلع مقابل |
| مقدار سینوس و کسینوس برای زاویه دلخواه | |
| شیب خط با زاویه نسبت به افق | |
| مساحت مثلث با سینوس | |
| رابطه فیثاغورس در مثلثات |
|
| رابطه تانژانت بر حسب کسینوس |
|
| رابطه کتانژانت بر حسب سینوس |
|
درس اول: فرمول های نسبت های مثلثاتی در ریاضی دهم
مثلثات، یکی از شاخههای پرکاربرد در علم ریاضی است که روابط بین زوایا و اضلاع مثلث را مورد مطالعه قرار میدهد. این علم، برای اندازهگیری فاصلهها در علوم مختلفی نظیر مهندسی، نقشهبرداری، فیزیک، نجوم و غیره به کاربرد میرود. در مثلثات، چهار تابع مهم با عنوانهای سینوس، کسینوس، تانژانت و کتانژانت وجود دارد که رابطه بین نسبت ضلعهای مثلث قامالزاویه و زاویههای آن را نمایش میدهند. این نسبتها با عنوان نسبتهای مثلثاتی شناخته شده و به صورت زیر نوشته میشوند:
- : سینوس زاویه θ
- O: ضلع مقابل زاویه θ
- H: وتر مثلث قائمالزاویه
وتر ÷ ضلع مجاور زاویه θ = کسینوس زاویه θ
- : کسینوس زاویه θ
- A: ضلع مجاور زاویه θ
- H: وتر مثلث قائمالزاویه
- : تانژانت زاویه θ
- O: ضلع مقابل زاویه θ
- A: ضلع مجاور زاویه θ
- : کتانژانت زاویه θ
- A: ضلع مجاور زاویه θ
- O: ضلع مقابل زاویه θ
یکی از کاربردهای مثلثات، محاسبه مساحت مثلث با سینوس است. فرمول مساحت مثلث با سینوس عبارت است از:
- : طول یکی از ضلعهای مثلث
- : طول یکی دیگر از ضلعهای مثلث
- : زاویه بین دو ضلع و
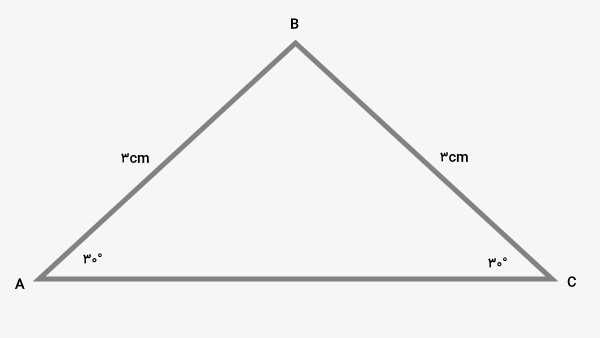
اندازه دو ضلع و دو زاویه مثلث مورد سوال را داریم. برای به دست آوردن مساحت مثلث با ضلع و زاویه، با اندازه زاویه بین دو ضلع معلوم را داشته باشیم. جمع زوایای داخلی مثلث، برابر با درجه است. بنابراین، داریم:
بر اساس فرمول مساحت مثلث با سینوس، داریم:
- : طول یکی از ضلعهای مثلث برابر با سانتیمتر
- : طول یکی دیگر از ضلعهای مثلث برابر با سانتیمتر
- : زاویه بین دو ضلع و برابر با درجه
مقادیر معلوم را درون فرمول قرار میدهیم:
بر اساس جدول سینوس کسینوس، مقدار برابر با است. بنابراین، داریم:
در نتیجه، مساحت مثلث برابر با سانتیمتر مربع است.
درس دوم: فرمول های دایره مثلثاتی در ریاضی دهم
دایره مثلثاتی، دایرهای به شعاع واحد است که مرکز آن بر روی مبدا مختصات قرار دارد. جهت مثبت در این دایره، خلاف عقربههای ساعت است. دایره مثلثاتی به منظور تعیین نسبتهای مثلثاتی و نمایش آنها مورد استفاده قرار میگیرد. این دایره به چهار ربع تقسیم میشود. علامت سینوس، کسینوس، تانژانت و کتانژانت، با توجه به ربع قرارگیری آنها تغییر میکند. خلاصهای از مشخصات ربع اول تا چهارم دایره مثلثاتی را در ادامه آوردهایم:
- ربع اول دایره مثلثاتی: زاویه بین تا درجه، مثبت بودن علامت همه نسبتهای مثلثاتی
- ربع دوم دایره مثلثاتی: زاویه بین تا درجه، مثبت بودن علامت سینوس و منفی بودن علامت کسینوس، تانژانت و کتانژانت
- ربع سوم دایره مثلثاتی: زاویه بین تا درجه، مثبت بودن علامت تانژانت و کتانژانت و منفی بودن علامت سینوس و کسینوس
- ربع چهارم دایره مثلثاتی: زاویه بین تا درجه، مثبت بودن علامت کسینوس و منفی بودن علامت سینوس، تانژانت و کتانژانت
علامت نسبتهای مثلثاتی را با «هستک» حفظ کنید:
- ه برای مثبت بودن همه
- س برای مثبت بودن سینوس
- ت برای مثبت بودن تانژانت و کتانژانت
- ک برای ثبت بودن کسینوس
اگر شیب یک خط با محور افقی برابر با باشد، مقدار شیب برابر با خواهد بود. به عبارت دیگر، شیب یک خط، با تانژانت زاویه آن خط نسبت به افق برابر است.
- : شیب خط
- : عرض از مبدا خط
میدانیم که تانژانت زاویه خط نسبت به افق (محور ها) برابر با شیب خط است. بنابراین:
عرض از مبدا، با قرار دادن شیب و نقطه معلوم در معادله خط به دست میآید:
در نتیجه، داریم:
درس سوم: فرمول های روابط نسبت های مثلثاتی در ریاضی دهم
برخی از مهمترین روابط بین نسبتهای مثلثاتی یا قوانین مثلثات عبارت هستند از:
این روابط با عنوان اتحادهای مثلثاتی نیز شناخته میشوند؛ زیرا به ازای هر دلخواه، این روابط برقرار هستند (البته ).

برای نمایش درستی رابطه ، سمت چپ رابطه را بسط میدهیم. به این منظور، ابتدا مخرج مشترک میگیریم:
بر اساس اتحادهای مثلثاتی و رابطه فیثاغورس در مثلثات، میدانیم:
از این رابطه برای ادامه اثبات استفاده میکنیم:
در صورت کسر، عبارت ، یک اتحاد مزدوج را تشکیل داده است. این اتحاد به صورت زیر تجزیه میشود:
این رابطه در کسر قرار میدهیم:
همانطور که مشاهده میکنید، عبارت در صورت کسر تکرار شده است. از این عبارت فاکتور میگیریم:
اکنون صورت و مخرج را باهم ساده میکنیم:
به این ترتیب، داریم:
چگونه فرمول های ریاضی دهم را به خوبی و کامل یاد بگیریم؟
یادگیری سریع فرمول های ریاضی دهم، کار دشواری نیست. اگر به اندازه کافی مثال و تمرین حل کنید. در ضمن، برای دستیابی به این هدف، ابتدا باید نکات و مفاهیم ریاضی دهم را به خوبی و کامل یاد بگیرید. ریاضی ۱، یکی از مواد آزمون ورود به دانشگاه، یا همان کنکور سراسری محسوب میشود. به همین دلیل، بسیاری از دانشآموزان، به دنبال یک روش سریع و قابل اطمینان برای یادگیری مفاهیم و فرمول های این درس هستند. در اغلب موارد، انتخاب یک منبع کمک آموزشی مناسب میتواند نیازهای دانشآموزان را برطرف کند. این منبع، باید به گونهای باشد که ضمن توضیح خوب درسنامههای کتاب، به حل مثالها و تمرینهای متنوع بپردازد. به این ترتیب، دانشآموزان دیگر دغدغه مواجهه با سوالات جدید در امتحانات یا کنکور را نخواهند داشت. فرادرس، یک فیلم آموزشی جامع و مفید را تهیه کرده است که میتواند شما را در یادگیری کامل نکات و فرمول های ریاضی دهم کمک کند. برای مشاهده این فیلم، بر روی لینک زیر کلیک کنید:
- فیلم آموزش ریاضی پایه دهم رشتههای تجربی و ریاضی فرادرس
- مجموعه فیلمهای آموزش دروس پایه دهم فرادرس
- مجموعه فیلمهای آموزش دروس دوره اول و دوم متوسطه فرادرس
۳. توان های گویا و عبارت های جبری: فرمول های فصل سوم ریاضی دهم
در فصل سوم کتاب ریاضی دهم، چهار درس عنوانهای «ریشه و توان»، «ریشه nام»، «توانهای گویا» و «عبارتهای جبری» آموزش داده میشود.
جدول زیر، خلاصهای از نکات و فرمول های مهم فصل سوم ریاضی دهم را نمایش میدهد.
| عنوان | توصیف |
| ریشه ام | |
| ریشه زوج عدد مثبت | دو ریشه قرینه |
| ریشه فرد عدد مثبت | یک ریشه مثبت |
| ریشه زوج عدد منفی | ریشه وجود ندارد |
| ریشه فرد عدد منفی | یک ریشه منفی |
| ضرب رادیکال با فرجه برابر | |
| تبدیل عدد با توان گویا به رادیکال | |
| ضرب دو عدد تواندار با توان گویا | |
| اتحاد مکعب |
|
| اتحاد چاق و لاغر مجموع |
|
| اتحاد چاق و لاغر تفاضل | |
| مزدوج | و |
درس اول: فرمول های ریشه و توان در ریاضی دهم
ریشه و توان، دو مفهوم مرتبط و دوسویه هستند. به عنوان مثال، اگر عدد را به توان برسانیم، به عدد میرسیم:
در طرف دیگر، اگر بخواهیم ریشه دوم عدد را به دست بیاوریم، آن را به زیر رادیکال با فرجه میبریم. به این ترتیب، به عدد میرسیم:
بنابراین:
یکی از نکات مهم فصل سوم ریاضی دهم، بحث نمایش تقریبی اعداد است. نمایش مقدار دقیق اعداد گنگ (مانند ) به صورت یک عدد اعشاری امکانپذیر نیست. به همین علت، این اعداد را به صورت رادیکالی یا تقریبی نمایش میدهیم.
- هر عدد مثبت دارای دو ریشه چهارم است که قرینهی یکدیگرند. عددهای منفی ریشه چهارم ندارند.
- هر عدد مثبت یا منفی دارای یک ریشه پنجم است. اگر عدد مثبت باشد، ریشه پنجم آن مثبت و اگر عدد منفی باشد ریشه پنجم آن منفی است.
عبارت اول، برای ریشههای زوج و عبارت دوم، برای ریشههای فرد صدق میکند. توجه داشته باشید که اگر یک عدد مثبت یا منفی را به توان عددی زوج برسانیم، علامت آن مثبت میشود اما اگر یک عدد مثبت یا منفی را به توان عددی فرد برسانیم، علامت آن تغییری نمیکند.
اکنون به جای ، نماد علمی یا معادل توانی آن را زیر رادیکال میبریم:
بر اساس قوانین رادیکال، عدد زیر رادیکال، به شکل زیر از آن خارج میشود:
میدانیم اگر عددی به توان منفی برسد، میتوانیم آن را بدون توان منفی معکوس کنیم:
یا
در نتیجه، دو عدد و ، برابر هستند.
درس دوم: فرمول های ریشه n ام در ریاضی دهم
ریشه ام یک عدد به صورت زیر تعریف میشود:
- :ریشه ام عدد
- : عددی بزرگتر از
فرمول ضرب دو عدد رادیکالی با فرجه برابر عبارت است از:
- : فرجه رادیکال
- و : دو عدد دلخواه
اگر فرجه رادیکال، زوج باشد، فرمول بالا برای و بزرگتر مساوی صفر (غیرمنفی) صدق میکند. در صورت فرد بودن فرجه رادیکال، و میتواند هر عدد مثبت یا منفی باشد. رابطه زیر، یکی دیگر از فرمول های مهم در درس ریشه و توان است:
در صورت زوج بودن ، علامت باید مثبت باشد. برای فرجههای زوج، جواب رادیکال به صورت نمایش داده میشود:
به عبارت دیگر، به دلیل تعریف قدر مطلق، خروجی رادیکال مثبت خواهد بود.

به این ترتیب، داریم:
میدانیم عدد به توان و ریشه هر عدد دیگر، برابر با همان میشود. بنابراین:
از طرفی، عدد همان است. از اینرو، به دلیل برابر بودن توان با فرجه رادیکال، پایه این عدد از رادیکال خارج میشود:
در نتیجه، داریم:
درس سوم: فرمول های توان های گویا در ریاضی دهم
منظور از توان گویا، توان کسری است. برای هر عدد طبیعی داریم:
اگر و و دو عدد طبیعی باشند، خواهیم داشت:
در صورت مثبت بودن هر سه متغیر ، رابطه زیر برقرار است:
این روابط نشان میدهند که در توانهای گویا، مخرج کسر به فرجه رادیکال و صورت کسر به توان عدد زیر رادیکال تبدیل میشود. برخی دیگر از قوانین اعداد تواندار با توان گویا عبارت هستند از:
به این ترتیب، داریم:
در ادامه، از فرمول زیر برای بیرون کشیدن عدد از زیر رادیکال استفاده میکنیم:
بر این اساس، داریم:
به همین ترتیب، خواهیم داشت:
در نتیجه:
درس چهارم: فرمول های عبارت های جبری در ریاضی دهم
عبارتهای جبری، عبارتهایی هستند که به منظور نمایش روابط و متغیرهای ریاضی مورد استفاده قرار میگیرند. اتحادهای ریاضی، از مهمترین و پرکاربردترین عبارتهای جبری به شمار میروند. کتاب ریاضی نهم، برخی از فرمولهای مهم اتحاد را به دانشآموزان معرفی میکند. این اتحادها عبارت هستند از:
در کتاب ریاضی ۱ دهم، فرمول های بیشتری از اتحادها به دانشآموزان معرفی میشوند. این فرمولها عبارت هستند از:
اتحادهای بالا به ترتیب با عنوان اتحاد مکعب، اتحاد چاق و لاغر مجموع و اتحاد چاق و لاغر تفاضل شناخته میشوند. اتحادها، به منظور سادهسازی عبارتهای جبری و حل معادلهها مورد استفاده قرار میگیرند. در انتهای این بخش، به حل یک مثال در این رابطه میپردازیم.
- ، مزدوج است.

یکی دیگر از مباحث فصل سوم ریاضی دهم، گویا کردن مخرج کسرها است. در صورت رادیکالی بودن مخرج یک کسر، با ضرب آن کسر در عددی کسری که صورت و مخرج آن برابر با همان عدد رادیکالی باشد، مخرج را گویا میکنیم. به عنوان مثال:
اگر مخرج کسر به صورت جمع یا تفریق یک عدد رادیکالی با یک عدد دیگر بود، آن را در عددی کسری با صورت و مخرج برابر با مزدوج مخرج ضرب میکنیم. به عنوان مثال:
بر این اساس، داریم:
۴. معادله ها و نامعادله ها: فرمول های فصل چهارم ریاضی دهم
فصل چهارم کتاب ریاضی دهم، به آموزش مباحث مربوط به معادلهها و نامعادلهها در قالب سه درس «معادله درجه دوم و روشهای مختلف حل آن»، «سهی» و «تعیین علامت» میپردازد.
در ادامه، برخی از نکات و فرمول های مهم فصل چهارم ریاضی دهم را آوردهایم.
| عنوان | توصیف |
| فرم کلی معادله درجه دوم | |
| فاکتورگیری | |
| اتحاد مزدوج | |
| اتحاد جمله مشترک | |
| ضرب صفر | |
| ریشهگیری | |
| فرمول محاسبه ریشههای معادله درجه دوم | |
| فرمول دلتا | |
| تعیین تعداد ریشه با دلتا |
دلتای مثبت: دو ریشه حقیقی دلتای صفر: یک ریشه حقیقی دلتای منفی: بدون ریشه حقیقی |
| مختصات راس سهمی |
|
| معادله محور تقارن سهمی |
|
| مختصات راس سهمی | |
| معادله خط تقارن سهمی | |
| خاصیت جمع در نامعادله | |
| خاصیت ضرب در نامعادله |
|
| نامعادله قدر مطلقی |
درس اول: فرمول های معادله درجه دوم و روش های مختلف حل آن در ریاضی دهم
معادله درجه دوم، معادلهای است که بزرگترین توان متغیر آن برابر با باشد. این معادله به شکل زیر نوشته میشود:
ضرایب ثابت در معادله بالا، اعداد حقیقی هستند. روشهای مختلفی برای حل معادله درجه دوم وجود دارد. یکی از این روشها، تجزیه به کمک فاکتورگیری یا اتحادهای جبری است. در حل معادله درجه به کمک فاکتورگیری، فرمی مشابه زیر به وجود میآید:
برای حل معادله درجه میتوان از اتحادهایی نظیر اتحاد مزدوج و اتحاد جمله مشترک نیز کمک گرفت. این اتحادها به صورت زیر نوشته میشوند:
حل سوالات مربوط به حل معادله درجه دو، معمولا با استفاده از یکی از روشهای بالا صورت میگیرد. در سادهترین حالت، امکان به دست آوردن جواب با ریشهگیری وجود دارد. فرم کلی این حالت به صورت زیر است:
روش مربع کامل، یکی دیگر از روشهای حل معادله درجه دوم است. این روش، با اضافه کردن یک جمله به دو طرف معادله و تبدیل آن به مربع کامل انجام میگیرد. به این ترتیب، جواب معادله توسط روش ریشهگیری به دست میآید. به عنوان مثال:
اگر امکان حل معادله درجه دوم با هیچ کدام از روشهای بالا وجود نداشت، از روش دلتا برای این کار استفاده میکنیم. حل معادله درجه دو به روش دلتا با استفاده از فرمول زیر انجام میگیرد:
در روش دلتا، سه حالت به وجود میآید:
- دلتای مثبت : دو ریشه حقیقی
- دلتای صفر : یک ریشه حقیقی (ریشه مضاعف)
- دلتای منفی : بدون ریشه حقیقی (دو ریشه مختلط با اعداد موهومی)
- : ریشه یا ریشههای معادله
- ضریب متغیر با توان دو برابر با
- : ضریب متغیر با توان یک برابر با
- : ثابت عددی برابر با
اکنون، این مقادیر را درون فرمول قرار میدهیم:
در نتیجه، ریشههای معادله مورد سوال برابر با و هستند.
درس دوم: فرمول های سهمی در ریاضی دهم
نمودار معادله درجه دوم با عنوان سهمی شناخته میشود. به پایینترین یا بالاترین نقطه این نمودار، راس سهمی میگویند. خط عمودی گذرنده از راس، با عنوان خط تقارن سهمی شناخته میشود.
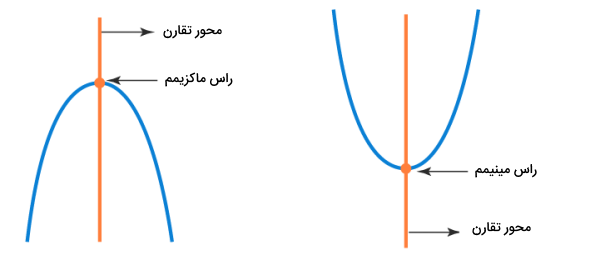
شکل سهمی معادله درجه دوم مانند ، بر اساس ضریب و به صورت زیر تعیین میشود:
- : راس سهمی در پایینترین نقطه قرار دارد.
- : راس سهمی در بالاترین نقطه قرار دارد.
اگر معادله سهمی به صورت باشد، مختصات راس آن برابر با بوده و معادله خط تقارن آن برابر با است.
نقطه بالا را درون معادله سهمی قرار میدهیم:
به این ترتیب، یکی از پارامترهای مجهول معادله به دست میآید. برای به دست آوردن پارامترهای دیگر، از دیگر اطلاعات مسئله استفاده میکنیم. بر اساس این اطلاعات، نمودار سهمی، محور را در نقاطی به طول و قطع کرده است. در این نقاط، مقدار برابر با است. به عبارت دیگر، نقاط زیر در معادله صدق میکنند:
این نقاط را درون معادله قرار میدهیم:
برای به دست آوردن و ، دو معادله به دست آمده را به صورت یک دستگاه معادله خطی مینویسیم:
روش حل دستگاه معادلههای خطی، در درس سوم از فصل ششم ریاضی نهم آموزش داده شده است. با استفاده از این روش، به نتیجه زیر میرسیم:
این مقادیر را درون رابطه کلی معادله سهمی قرار میدهیم:
درس سوم: فرمول های تعیین علامت در ریاضی دهم
بسیاری از مسائل ریاضی، مخصوصا مسائل دنیای واقعی، نیازمند یافتن علامت یک عبارت خاص هستند. به عنوان مثال، هدف شرکتهای تولیدی، رسیدن به سود است. به عبارت دیگر، معادله سود این شرکتها، باید مثبت باشد. بنابراین، کارشناسان باید مقدار متغیرهایی که باعث مثبت شدن سود میشود را پیدا کنند. به این فرآیند، تعیین علامت میگویند. به عنوان مثال، معادله زیر را در نظر بگیرید:
این معادله، به ازای ، برابر با است. اگر بزرگتر از باشد، مقدار ، مثبت و اگر کوچکتر از باشد، مقدار منفی میشود. در درس سوم فصل سوم ریاضی دهم، دانشآموزان با تعیین علامت و تهیه جدول تعیین علامت آشنا میشوند. در ادامه، یک نمونه جدول تعیین علامت را برای آوردهایم.
| + | + | + | + | ۰ | - | |
| - | ۰ | + | + | + | + | |
| - | ۰ | + | + | ۰ | - | |
همانطور که میبینید، ریشههای معادله در تعیین علامت مورد استفاده قرار میگیرند. معادله در ریشهها، علامتی ندارد و برابر با است. در عبارتهای کسری، اگر مقداری باعث صفر شدن مخرج شود، علامت در آن مقدار، «تعریف نشده» خواهد بود.

در ریاضی نهم، دانشآموزان مفهوم نامعادله را فرا میگیرند. در ریاضی دهم، خاصیت جمع و ضرب نامعادلهها به صورت زیر تعریف میشود:
خواص نامعادلههای قدر مطلقی به صورت زیر هستند:
با استفاده از اتحاد جمله مشترک میتوانیم معادله درجه دوم بالا را به صورت زیر تجزیه کنیم:
به این ترتیب، داریم:
اگر ضرب چند عبارت برابر با شود، قطعا یکی از آن عبارتها برابر با است. در ضرب بالا، که نمیتواند باشد. بنابراین، عبارتهای و را برابر با صفر قرار میدهیم:
با این کار، ریشههای معادله را به دست آوردیم. از عوامل ضرب و ریشههای معادله در تشکیل جدول تعیین علامت استفاده میکنیم. این جدول به صورت زیر خواهد بود.
علامت ، همواره مثبت است. بنابراین، در تمام خانههای ردیف مربوط به این عدد، علامت را مینویسیم. سپس، در محل ریشهها، عدد را قرار میدهیم.
| ۰ | ||||||
| ۰ | ||||||
| + | + | + | + | + | + | |
برای تعیین علامت عبارت اعداد کوچکتر و بزرگتر از ریشه را امتحان میکنیم و علامت به دست آمده را در جدول قرار میدهیم. به عنوان مثال، با فرض ، حاصل عبارت ، برابر با میشود. بنابراین، علامت این عبارت برای های بزرگتر از ، مثبت است. همین کار را برای های کوچکتر از ریشه و ردیف بعدی انجام میدهیم.
| + | + | + | + | ۰ | - | |
| + | ۰ | - | - | - | - | |
| + | + | + | + | + | + | |
برای تعیین علامت ردیف آخر، علامتهای هر ستون را در هم ضرب میکنیم. به عنوان مثال، در ستون اول در سمت چپ، دو علامت منفی و یک علامت مثبت داریم. حاصل ضرب منفی در منفی، مثبت میشود. حاصل ضرب مثبت در مثبت نیز مثبت خواهد بود. به این ترتیب، در انتهای ستون اول، علامت را مینویسیم. در نهایت، به جدول زیر میرسیم.
| + | + | + | + | ۰ | - | |
| + | ۰ | - | - | - | - | |
| + | + | + | + | + | + | |
| + | + | - | - | ۰ | + | |
۵. تابع: فرمول های فصل پنجم ریاضی دهم
فصل پنجم کتاب ریاضی دهم، شامل سه درس با عنوانهای «مفهوم تابع و بازنماییهای آن»، «دامنه و برد تابع» و «انواع تابع» است.
در ادامه، مهمترین نکات فصل پنجم ریاضی دهم را به طور خلاصه آوردهایم. این فصل، فرمول های زیادی ندارد.
| عنوان | توصیف |
| تابع | رابطه بین دو مجموعه که هر عضو ورودی، تنها به یک عضو خروجی وصل میشود. |
| دامنه | ورودیهای قابل قبول تابع |
| برد | خروجیهای تابع |
| تابع چندجملهای | تابعی با ساختار چندجملهایهای جبری |
| تابع همانی | تابعی با دامنه و برد یکسان |
| تابع ثابت | تابعی با خروجی ثابت |
| تابع قدرمطلق | تابعی با خروجی مثبت |
درس اول: مفهوم تابع و بازنمایی های آن در ریاضی دهم
تابع، رابطهای است که اعضای دو مجموعه را به یکدیگر وصل میکند. بر اساس تعریف کتاب ریاضی ۱، یک تابع از مجموعه A به مجموعه B، رابطهای بین این دو مجموعه است که در آن، به هر عضو از A، دقیقا یک عضو از B نسبت داده میشود. به عنوان مثال، در تصویر زیر، رابطههای راست و چپ، تابع هستند اما طبق تعریف، رابطه میانی، یک تابع نیست.

عضوهای متصل به هم در تابع، به صورت زوج مرتب نمایش داده میشوند. به عنوان مثال، تابع سمت راست در تصویر بالا را در نظر بگیرید. زوج مرتبهای این تابع عبارت هستند از:
ترتیب نوشتن عضوهای زوج مرتب، مهم است. به عضو اول زوج مرتب، مولفه اول و به عضو دوم، مولفه دوم میگویند. اگر زوج مرتبها از عدد تشکیل شوند، میتوان آنها را به صورت مختصات بر روی دستگاه مختصات مشخص کرد و نمودار تابع را کشید.
- اگر یک رابطه به صورت مجموعه زوجهای مرتب داده شده باشد، هنگامی این رابطه یک تابع است که هیچ دو زوج مرتب متمایزی در آن دارای مولفههای اول برابر نباشند.
تابع را معمولا با حرف f (ابتدای کلمه function) نمایش میدهند.
برای تشخیص تابع بودن یا نبود یک مجموعه، باید به تعریف تابع رجوع کنیم. بر اساس این تعریف، اگر یک رابطه به صورت مجموعه زوجهای مرتب داده شده باشد، هنگامی این رابطه یک تابع است که هیچ دو زوج مرتب متمایزی در آن، دارای مولفههای اول برابر نباشند. به این ترتیب، برای پاسخ به سوال، مولفههای اول زوجهای مرتب هر یک از مجموعهها را بررسی میکنیم.
در مجموعه ، دو زوج مرتب و ، دارای مولفه برابر هستند. بنابراین، این مجموعه، یک تابع نیست. در مجموعه و ، هیچ زوج مرتبی را نمیتوان پیدا کرد که مولفههای اول آنها با یکدیگر برابر باشد. از اینرو، هر یک از این مجموعهها، یک تابع را نمایش میدهند.
درس دوم: دامنه و برد توابع در ریاضی دهم
دامنه تابع، مجموعهای از تمامی مقادیر احتمالی و قابل قبول به عنوان ورودی یک تابع است. دامنه، مولفههای اول زوج مرتبهای تابع را تشکیل میدهد. برد تابع، مجموعهای از تمام خروجیهای یک تابع است که از جایگذاری ورودیها در آن تابع به دست میآید. برد، مولفه های دوم زوج مرتبهای را تشکیل میدهد.

به عنوان مثال، تابع زیر را در نظر بگیرید:
{(۱۳۹۳ ,مبینا) ,(۱۳۷۱ ,حسین) ,(۱۳۸۶ ,سارا) ,(۱۳۶۰ ,هاشم)} = f
در تابع f، دامنه و برد به صورت زیر تعریف میشوند:
{مبینا ,حسین ,سارا ,هاشم} = دامنه f
{۱۳۹۳ , ۱۳۷۱ , ۱۳۸۶ ,۱۳۶۰} = برد f
- اگر رابطه بین دامنه و برد یک تابع، به صورت یک معادله درجه یک مانند نمایش داده شود، آن تابع، یک تابع خطی خواهد بود.
- اگر نمودار یک رابطه داده شده باشد، هنگامی این نمودار تابع است که هر خط موازی محور عرضها، نمودار را حداکثر در یک نقطه قطع کند.
برد تابع با دامنهی چیست؟
برای به دست آوردن برد یک تابع، حدود دامنه را درون آن جایگذاری میکنیم. در اینجا، کران پایین دامنه، عدد است. علامت ، عدم حضور عدد (بلکه اعداد بزرگتر از آن) در دامنه را نمایش میدهد. اگر را درون تابع قرار دهیم، خواهیم داشت:
کران بالای دامنه، عدد است. علامت ، حضور عدد و اعداد کوچکتر از آن در دامنه را نمایش میدهد. اگر را درون تابع جایگذاری کنیم، به مقدار زیر میرسیم:
به این ترتیب، برد تابع برابر با است. توجه داشته باشید که برای تعیین برد، داشتن بازه دامنه و رابطه تابع کافی نیست. صعودی و نزولی بودن، نقاط عطف و غیره، بر روی مقادیر برد تاثیر میگذارند. در اینجا، یک مثال ساده را حل کردیم که به این موارد نیازی نداشت.
درس سوم: انواع تابع در ریاضی دهم
توابع ریاضی، انواع بسیار زیادی دارند که در کتاب ریاضی ۱ پایه دهم، به معرفی برخی از آنها پرداخته شده است. در ادامه، انواع تابع را بر اساس این کتاب تعریف میکنیم:
- توابعی را که نمایش جبری آنها، چندجملهایهای جبری از یک متغیر هستند، توابع چندجملهای مینامیم.
- اگر دامنه و برد یک تابع برابر باشند و هر عضو از دامنه تابع دقیقاً به همان عضو در برد نظیر شود، تابع همانی مینامند.
- نمودار تابع همانی، خط است. تابع همانی با نمایش داده میشود.
- به تابعی که برد آن تنها شامل یک عضو است، تابع ثابت میگویند.
- تابع ثابت را با نمایش میدهند.
- تابعی که هر مقدار در دامنه را به قدر مطلق آن در برد نظیر میکند، تابع قدر مطلق نام دارد.
- تابع قدر مطلق با یا نمایش داده میشود.
درس سوم فصل چهارم ریاضی دهم، به آموزش روشهای رسم تابع از جمله روش انتقال میپردازد. در این روش، فرض میکنیم نمودار تابعی مانند را داریم. بنابراین، برای رسم نمودار تابع ، نمودار را به اندازه واحد در امتداد محور جابجا میکنیم. اگر باشد، انتقال در جهت مثبت بوده و اگر باشد، انتقال در جهت منفی خواهد بود.
برای رسم نمودار ، میتوانیم نمودار را به اندازه واحد در امتداد محور انتقال دهیم. اگر باشد، انتقال در جهت منفی بوده و اگر باشد، انتقال در جهت مثبت خواهد بود.
- دامنه تابع برابر با و برد آن نیز برابر با است.
- دامنه تابع ، همه اعداد حقیقی و برد آن، است.
- دامنه تابع ثابت ، برابر با است.
- اگر ، آنگاه
گزاره شماره نادرست است. زیرا دامنه ، مجموعه اعداد حقیقی است. در واقع، هر عددی که در بازه باشد را میتوانیم به عنوان ورودی در این تابع قرار دهیم. به علاوه، در صورت قرار دادن عدد در رابطه تابع، به خروجی میرسیم. بنابراین، برد تابع برابر با است.
گزاره شماره ، نادرست است. هر عددی را میتوان به عنوان ورودی در تابع قرار داد. بنابراین، دامنه این تابع، مجموعه اعداد حقیقی است. برد این تابع نیز در تعریف میشود.
گزاره شماره ، درست است. دامنه توابع ثابت، همه اعداد حقیقی است. این دامنه به صورت نمایش داده میشود.
گزاره شماره ، نادرست است. زیرا:
۶. شمارش، بدون شمردن: فرمول های فصل ششم ریاضی دهم
در فصل ششم کتاب ریاضی دهم، مباحث دنیای آمار و احتمال در قالب سه درس با عنوانهای «شمارش»، «جایگشت» و «ترکیب» آموزش داده میشوند.
در ادامه، مهمترین فرمول های فصل ششم ریاضی دهم را آوردهایم.
| عنوان | توصیف |
| اصل جمع (روشهای انجام کار به چند روش) | |
| اصل ضرب (روشهای انجام کار در چند مرحله و چند روش) | |
| جایگشت | |
| فاکتوریل صفر | |
| ترکیب |
درس اول: فرمول های شمارش در ریاضی دهم
شمارش، فرآیندی است که طی آن، عضوهای یک مجموعه متناهی مشخص میشود. به عنوان مثال، اعداد ، و را در نظر بگیرد. به نظر شما، با استفاده از این سه عدد، چند عدد سه رقمی میتوان نوشت. علم شمارش، به ما کمک میکند تا به دقت به این سوال پاسخ دهیم. در شمارش، اصلهای مختلفی وجود دارد که مهمترین آنها عبارت هستند از:
- اصل جمع: اگر کاری را بتوان به دو روش انجام داد، به طوری که در روش اول، انتخاب و در روش دوم، انتخاب وجود داشته باشد، برای انجام کار مورد نظر، روش وجود دارد. تعمیم این اصل برای روش با انتخاب، به صورت نوشته میشود.
- اصل ضرب: اگر انجام یه کار، دومرحلهای باشد، به طوری که برای انجام مرحله اول، روش و برای مرحله دوم (هر کدام از این روش)، روش وجود داشته باشد، مجموع کل روشهای انجام کار برابر با روش خواهد بود. تعمیم این اصل برای مرحله با روش، به صورت نوشته میشود.

به عنوان یک نکته مهم به خاطر داشته باشید که فاکتوریل عدد صفر برابر با عدد یک است.
- چند نوع مختلف از این اتومبیل تولید میشود؟
- اگر یکی از رنگهای تولید شده مشکی باشد، چند نوع از این اتومبیل با رنگ مشکی تولید میشود؟
- چند نوع از این اتومبیل با رنگ مشکی و دنده اتوماتیک تولید میشود؟
برای تعیین تعداد انواع مدلهای ماشین، باید تعداد حالتهای مختلف را در هم ضرب کنیم:
با توجه به انواع مدلها ، انواع رنگها ، انواع حجمهای موتور و انواع دندهها ()، امکان تولید مدل مختلف از اتومبیل وجود دارد.
در محاسبه تعداد مدلهای ماشین با رنگ مشکی، عدد انواع رنگ () از محاسبات خارج میشود. به این ترتیب، داریم:
بنابراین، مدل از این ماشین، به رنگ مشکی هستند. به منظور محاسبه انواع مدلهای ماشین با رنگ مشکی و دنده اتوماتیک، اعداد مربوط به این ویژگیها را از محاسبه حذف میکنیم. با این کار، خواهیم داشت:
در نتیجه، مدل از این ماشین با رنگ مشکی و دنده اتوماتیک تولید میشوند.
درس دوم: فرمول های جایگشت در ریاضی دهم
جایگشت، روشهای ممکن برای انجام یک کار است. بر اساس تعریف کتاب ریاضی ۱ دهم، اگر چند شی متمایز داشته باشیم، به هر حالتِ چیدنِ این اشیا کنار هم، یک جایگشت میگوییم. به عنوان مثال، اگر اعداد ، و را داشته باشیم و بخواهیم با قرار دادن آنها کنار یکدیگر، یک عدد سهرقمی بدون رقمهای تکراری بسازیم، عدد ، یک جایگشت خواهد بود. اعداد ، ، ، و ، دیگر جایگشتهای این اعداد خواهند بود.
در مبحث جایگشت، یک علامت مهم وجود دارد. این علامت، فاکتوریل نام دارد. فاکتوریل را با علامت (شبیه به علامت تعجب) نمایش میدهند. قرار داشتن این علامت در کنار یک عدد طبیعی، به معنای ضرب متوالی آن عدد در اعداد طبیع کوچکتر است. به عنوان مثال:
در مثال جایگشت اعداد ، و برای نوشتن اعداد سهرقمی بدون رقمهای تکراری، سه عضو متمایز داشتیم. بنابراین، جایگشت مورد نظر برابر با سه فاکتوریل است:
بنابراین، شش حالت مختلف برای چینش اعداد ، و در کنار هم و نوشتن اعداد سهرقمی بدون رقمهای تکراری وجود دارد.
تعداد جایگشتهای تایی از شی متمایز، با نمایش داده شده و با استفاده از رابطه زیر محاسبه میشود:
به عنوان مثال، تعداد جایگشتهای دوتایی از سه عدد ، و برابر است با:
به عبارت دیگر، با سه عدد ، و میتوان شش عدد دو رقمی متمایز نوشت:
- : تعداد جایگشتهای تایی از شی متمایز
- : تعداد اشیا برابر با
- : تعداد اشیا متمایز انتخابی برای جایگشت برابر با
با قرار دادن مقادیر بالا در فرمول، خواهیم داشت:
درس سوم: فرمول های ترکیب در ریاضی دهم
ترکیب، نحوه چینش چند شی متمایز در کنار یکدیگر، بدون توجه به ترتیب آنها است. به عنوان مثال، در نوشتن اعداد سهرقمی بدون رقمهای تکراری با استفاده از ، و ، اعداد ، ، ، ، و ، شش انتخاب متفاوت در نظر گرفته میشدند. با این وجود، از آنجایی که هیچ تغییری در رقمهای این اعداد در حالتهای مختلف رخ نمیدهد، در مفهوم ترکیب، همه آنها با هم برابرند. یعنی، ترکیب اعداد سهرقمی بدون رقمهای تکراری با استفاده از ، و ، برابر با است.

ترکیب شی از شی متمایز با یا نمایش داده میشود. فرمول ترکیب عبارت است از:
بر اساس فرمول بالا، ترکیب اعداد سهرقمی بدون رقمهای تکراری با استفاده از ، و عبارت است از:
- : ترکیب شی متمایز از شی موجود
- : تعداد کل اشیا برابر با
- : تعداد اشیا انتخابی برابر با
در نتیجه، به روش مختلف میتوان یک جفت را از میان گروه انتخاب کرد.
مسیر یادگیری فرمول های ریاضی دهم از پایه

مباحث و فرمول های ریاضی دهم، در ادامه مباحث و فرمول های ریاضی نهم هستند. تسلط بر روی این مباحث و فرمولها، مسیر یادگیری ریاضی یازدهم و دوازدهم را هموار میکند. موفقیت در هر یک از این دروس در پایههای مختلف دوره متوسطه اول و دوم، به میزان تسلط شما بر روی مباحث سال قبل بستگی دارد. به عبارت دیگر، اگر شما بر روی مباحث ریاضی هفتم تسلط نداشته باشید، در یادگیری مباحث ریاضی هشتم به مشکل میخورید. این رابطه علت و معلولی میتواند تا پایه دوازدهم ادامه پیدا کند و حتی باعث گرفتن نتیجه نامناسب در کنکور شود. بنابراین، اگر میخواهید مسیر درست یادگیری فرمول های ریاضی دهم را بدانید، دانش پایه خود در رابطه با ریاضی نهم را ارزیابی کنید. در صورت مشاهده مشکل، مبانی مبحث مورد نظر را با مطالعه ریاضی هشتم و یا هفتم یاد بگیرید. با این کار، هیچ نقطهضعفی در یادگیری شما باقی نمیماند.
فرادرس، فیلمهای آموزشی متعددی را در زمینه مباحث ریاضی دوره متوسطه اول و دوم برای دانشآموزان پایههای هفتم تا دوازدهم تهیه کرده است که میتوانند شما را در یادگیری سریع درسهای ریاضی و تقویت دانش پایهتان کمک کنند. نقشه راه یادگیری ریاضی دبیرستان با فرادرس، در ادامه آورده شده است:
- فیلم آموزش ریاضی پایه هفتم فرادرس
- فیلم آموزش ریاضی پایه هشتم فرادرس
- فیلم آموزش ریاضی پایه نهم فرادرس
- فیلمهای آموزش ریاضی پایه دهم فرادرس
- فیلمهای آموزش ریاضی پایه یازدهم فرادرس
- فیلمهای آموزش ریاضی پایه دوازدهم فرادرس
- مجموعه فیلمهای آموزش دروس متوسطه دوم و کنکور فرادرس
فرمول های ریاضی و آمار ۱: مخصوص دانش آموزان انسانی
دوره متوسطه اول، دورهای است که دانشآموزان، علاوه بر دروس عمومی، دروس تخصصی رشته انتخابی خود را فرا میگیرند. ریاضی و آمار ۱، یکی از درسهای تخصصی دانشآموزان پایه دهم رشته انسانی است. بسیاری از مباحث این درس، به درسهای ریاضی ۱ رشتههای ریاضی و تجربی شباهت دارد. با این وجود، تمرکز دروس ریاضی انسانی، بیشتر بر روی مفاهیم آماری است.
در ادامه، سرفصلهای کتاب ریاضی و آمار ۱ پایه دهم انسانی را آوردهایم.
همانطور که مشاهده میکنید، سرفصلها و دروس ارائه شده در درس ریاضی و آمار ۱ برای دانشآموزان انسانی، شباهت زیادی به سرفصلهای ارائه شده در درس ریاضی ۱ برای دانشآموزان ریاضی و تجربی دارد. البته در اینجا، بر روی فرمولها و معادلات ریاضی، تمرکز نسبتا کمتری شده اما بر روی مباحث آماری، تمرکز نسبتا بیشتری شده است. با وجود این، فرادرس، یک فیلم آموزشی جامع و کاربردی را برای دانشآموزان انسانی تهیه کرده است که میتواند شما را در یادگیری بهتر و سریعتر نکات مهم و فرمول های ریاضی و آمار ۱ کمک کند که لینک آن در زیر آورده شده است.
- فصل اول: معادله درجه دوم
- درس ۱: معادله و مسائل توصیفی
- درس ۲: حل معادله درجه ۲ و کاربردها
- درس ۳: معادلههای شامل عبارتهای گوبا
- فصل دوم: تابع
- درس ۱: مفهوم تابع
- درس ۲: ضابطه جبری تابع
- درس ۳: نمودار تابع خطی
- درس ۴: نمودار تابع درجه ۲
- فصل سوم: کار با داده های آماری
- درس ۱: گردآوری دادهها
- درس ۲: معیارهای گرایش به مرکز
- درس ۳: معیارهای پراکندگی
- فصل چهارم: نمایش داده ها
- درس ۱: نمودارهای یکمتغیره
- درس ۲: نمودارهای چندمتغیره
۷. آمار و احتمال: فرمول های فصل هفتم ریاضی دهم
فصل هفتم کتاب ریاضی دهم، در ادامه فصل ششم، با ارائه درسهای «احتمال یا اندازهگیری شانس»، «مقدمهای بر علم آمار، جامعه و نمونه» و «متغیر و انواع آن»، به جنبههای بیشتری از مباحث آمار و احتمال میپردازد.
جدول زیر، فرمول های اصلی فصل هفتم ریاضی دهم را نمایش میدهد.
| عنوان | توصیف |
| احتمال رخ دادن پیشامد | |
| احتمال رخ دادن حداقل یکی از دو پیشامد یا | |
| احتمال رخ دادن حداقل یکی از دو پیشامد ناسازگار یا | |
| احتمال رخ دادن پیشامد بر اساس متمم | |
| انواع متغیر | متغیر کمی (پیوسته و ناپیوسته)، متغیر کیفی (ترتیبی و اسمی) |
درس اول: فرمول های احتمال یا اندازه گیری شانس در ریاضی دهم
پیشامدهایی وجود دارند که رخ دادن یا رخ ندادن آنها و چگونگی رخ دادنشان مشخص نیست. شانس رخ دادن این پیشامدها، با عنوان احتمال شناخته میشود. اگر از همه حالتهای ممکن در به وقوع پیوستن یک پیشامد مطلع باشیم، به آن پیشامد، پیشامد تصادفی میگوییم. عددی که پس از انداختن تاس ظاهر میشود، یکی از معروفترین مثالهای پیشامد تصادفی است. در این مثال، شش حالت ممکن (ظاهر شدن یکی از اعداد تا ) وجود دارد. به این حالتها، فضای نمونه گفته میشود.
مفهوم اجتماع، اشتراک و تفاضل مجموعهها، کاربرد گستردهای در بحث تعیین پیشامدها و فضای نمونه دارند:
- اجتماع دو پیشامد: پیشامد حاصل از اجتماع دو پیشامد، زمانی رخ میدهد که حداقل یکی از دو پیشامد رخ بدهد.
- در پیشامد ، یا رخ میدهد یا رخ میدهد.
- اشتراک دو پیشامد: پیشامد اشتراک دو پیشامد زمانی رخ میدهد که هر دو پیشامد با هم رخ بدهند.
- در پیشامد ، هم رخ میدهد و هم رخ میدهد.
- تفاضل دو پیشامد: پیشامد تفاضل دو پیشامد، زمانی رخ میدهد که یکی از پیشامدها رخ دهد اما پیشامد دیگر رخ ندهد.
- در پیشامد ، رخ میدهد اما رخ نمیدهد.
- متمم یک پیشامد: پیشامد متمم یک پیشامد زمانی رخ میدهد که آن پیشامد رخ ندهد.
- در پیشامد ، پیشامد رخ نمیدهد.

اگر اشتراک دو پیشامد تهی باشد، به آنها دو پیشامد ناسازگار میگوییم. محاسبه احتمال رخداد یک پیشامد یا اندازهگیری شانس، با استفاده از فرمول زیر انجام میگیرد:
- : شانس رخ دادن پیشامد و عددی بین تا
- : تعداد رخداد حالت مطلوب
- : تعداد تمام حالتهای ممکن در فضای نمونه
اکنون، با استفاده از مفهوم اجتماع، اشتراک و تفاضل پیشامد و فرمول بالا میتوان فرمول زیر را تعریف کرد:
اگر و ، دو پیشامد ناسازگار باشند، فرمول بالا به صورت زیر نوشته میشود:
رابطه بین احتمال رخ دادن یک پیشامد با احتمال رخ دادن متمم آن پیشامد نیز عبارت است از:
اعداد اول در این فضا عبارت هستند از:
اعداد مرکب در فضای نمونه، موارد زیر را شامل میشوند:
احتمال اینکه کارت بیرون کشیده شده، عدد اول را نمایش بدهد برابر است با:
در مرحله دوم، به دلیل کنار گذاشتن کارت خارج شده از کیسه، فضای نمونه به تغییر میکند. بنابراین، اکنون احتمال مرکب بودن عدد روی کارت انتخابی از کیسه، به صورت زیر محاسبه میشود:
اکنون میخواهیم احتمال اینکه این پیشامدها پشت سرهم اتفاق بیافتند را به دست بیاوریم. برای این کار، احتمالات بالا را در هم ضرب میکنیم:
در نتیجه، احتمال اینکه اولین کارت دارای عدد اول و دومین کارت، دارای عدد مرکب باشد، یا درصد است.
درس دوم: مقدمه ای بر علم آمار، جامعه و نمونه در ریاضی دهم
بر اساس تعریف کتاب ریاضی ۱ دهم، آمار، مجموعهای از اعداد، ارقام و اطلاعات است. مراحل علم آمار عبارت هستند از:
- جمعآوری اعداد و ارقام
- سازماندهی و نمایش
- تحلیل و تفسیر دادهها
- نتیجهگیری، قضاوت و پیشبینی پدیدهها و آزمایشهای تصادفی
تفاوت اصلی آمار و علم آمار این است که علم آمار، اعداد، ارقام و اطلاعات را مورد مطالعه قرار میدهد؛ در صورتی که آمار، همان اعداد، ارقام و اطلاعات مورد مطالعه توسط علم آمار محسوب میشود. در ادامه، تعریف مهم این درس را آوردهایم:
- جامعه یا جمعیت: مجموعه تمام افراد یا اشیایی که درباره یک یا چند ویژگی آنها تحقیق صورت میگیرد. هر یک از این افراد یا اشیا، به عنوان عضو جمعیت در نظر گرفته میشوند.
- اندازه یا حجم جامعه: تعداد اعضای جامعه
- نمونه: بخشی از جامعه که برای مطالعه انتخاب میشود. به هر یک از افراد یا اشیا نمونه، عضو نمونه میگویند.
- اندازه یا حجم نمونه: تعداد اعضای نمونه
به عنوان مثال، اگر بخواهیم کیفیت محصولات تولیدی یک کارخانه را مورد مطالعه قرار دهیم و برای این منظور، قطعه از کل قطعات تولید شده کارخانه ( قطعه) برداریم، اطلاعات مطالعات آماری ما به صورت زیر خواهد بود:
- جامعه: قطعات تولید شده در کارخانه
- اندازه جامعه: قطعه
- اندازه نمونه: قطعه
- ویژگی مورد بررسی: کیفیت قطعه
کدامیک از جملههای زیر درست و کدامیک نادرست هستند؟
- اندازه جامعه، کمتر از اندازه نمونه است.
- اعضای نمونه، همان اعضای جامعه هستند.
- نمونه، زیرمجموعهای از جامعه است.
نمونه، از اعضای جامعه انتخاب میشود. بنابراین، اندازه نمونه نمیتواند بیشتر از اندازه جامعه باشد. از اینرو، جمله شماره ، نادرست است.
اعضای نمونه، اعضای جامعه هستند اما لزوما تمام اعضای جامعه را تشکیل نمیدهند. به همین علت، اعضای نمونه، دقیقا همان اعضای جامعه نیستند. بنابراین، جمله شماره نیز نادرست است.
با توجه به تعریف جامعه و نمونه و توضیحات بالا، میتوانیم بگوییم که نمونه، زیرمجموعهای از جامعه محسوب میشود. بنابراین، جمله شماره ، درست است.
درس سوم: فرمول های متغیر و انواع آن در ریاضی دهم
متغیر، ویژگی اعضای جامعه آماری است که از عضوی به عضو دیگر تغییر میکند. عدد اختصاص یافته به ویژگی عضو، با عنوان مقدار متغیر شناخته میشود. به عنوان مثال، قد دانشآموزان، یک متغیر است. یکی از مقدارهای این متغیر میتواند عددی مانند سانتیمتر باشد. متغیرهای آماری به دو نوع متغیرهای کمی و کیفی تقسیم میشوند:
- متغیر کمی: قابل اندازهگیری است. مانند قد و وزن فرزندان یک خانواده
- متغیر کمی پیوسته: امکان اختیار کردن مقداری بین دو مقدار مجاز وجود دارد. مانند وزن که میتواند به عنوان مثال، کیلوگرم، کیلوگرم یا عددی بین این دو (مثلا کیلوگرم) باشد.
- متغیر کمی گسسته: امکان اختیار کردن مقداری بین دو مقدار مجاز وجود دارد. مانند تعداد فرزندان یک خانواده که میتواند به عنوان مثال، فرزند، فرزند و غیره بوده اما نمیتواند فرزند باشد.
- متغیر کیفی: قابل اندازهگیری نیست. مانند جنسیت و رنگ چشم فرزندان یک خانواده
- متغیر کیفی ترتیبی: ترتیب طبیعی در آن وجود دارد. مانند پایه تحصیلی دانشآموزان که از اول ابتدایی شروع میشود و به ترتیب تا دوازدهم ادامه مییابد.
- متغیر کیفی اسمی (غیرترتیبی): ترتیبی در آن وجود ندارد. مانند جنسیت دانشجویان یک کلاس که میتواند زن یا مرد باشد.

مطلب فرمول های ریاضی دهم برای دانشآموزان ریاضی و تجربی را با حل یک مثال به پایان میرسانیم. البته بخش بعدی این مطلب را به دانشآموزان انسانی اختصاص دادهایم.
- : شاخص توده بدنی
- : وزن به کیلوگرم برابر با کیلوگرم
- : قد به متر برابر با متر
شاخص توده بدنی شخص مورد سوال، برابر با است. این شاخص، یک متغیر کمی به شمار میرود؛ زیرا قابل اندازهگیری است و میتوان آن را به صورت یک عدد بیان کرد. از طرفی، شاخص توده بدنی، یک متغیر کمی پیوسته در نظر گرفته میشود؛ چراکه امکان اختیار کردن مقداری بین دو مقدار مجاز وجود دارد.
در مطلب «فرمولهای ریاضی نهم در یک نگاه و با مثال»، نکات مهم کتاب ریاضی نهم را برای دانشآموزان خلاصه کردیم که میتوانید مطلب مرتبط با آن را در مجله فرادرس مطالعه کنید.
آزمون فرمولهای ریاضی دهم
۱. تفاوت اصلی مجموعه متناهی و نامتناهی چیست؟
مجموعه متناهی فقط شامل اعداد طبیعی است، ولی مجموعه نامتناهی همه نوع عدد را دارد.
مجموعه متناهی همواره مجموعه مرجع است، اما مجموعه نامتناهی فقط زیرمجموعه است.
مجموعه متناهی تعداد عضو مشخص دارد، اما مجموعه نامتناهی بینهایت عضو دارد.
در مجموعه متناهی میتوان اعضا را نشمرد، اما در مجموعه نامتناهی شمارش ممکن نیست.
در تعریف، «مجموعه متناهی» دارای تعداد محدود و قابل تعیین از اعضا است، به این معنی که اعضای آن را میتوان به پایان رساند. اما «مجموعه نامتناهی» تعداد عضو بیپایان دارد، مانند مجموعه اعداد طبیعی.
۲. برای بهدستآوردن تعداد اعضای اجتماع دو مجموعه با اشتراک، از چه فرمولی استفاده میشود و این فرمول چه را نشان میدهد؟
تعداد اعضای اشتراک را بهتنهایی جمع میکنیم.
تعداد اعضای اجتماع همیشه برابر با بزرگترین مجموعه است.
فقط کافیست تعداد عناصر هر مجموعه را با هم جمع کنیم.
تعداد اجتماع برابر حاصل جمع اعضای هر دو مجموعه منهای اعضای اشتراک آنها است.
فرمول درست برای محاسبه تعداد اعضای اجتماع دو مجموعه شامل کسر اعضای مشترک است، یعنی باید تعداد اعضای مجموعه اول و دوم را جمع کنیم و اعضای اشتراک را کم کنیم. این روش، از شمارش تکراری اشتراک جلوگیری میکند. اگر فقط تعداد عناصر هر مجموعه را جمع کنیم یا فقط اشتراک را بشماریم یا تعداد اجتماع را به بزرگترین مجموعه نسبت دهیم، نتیجه غلط خواهد بود. زیرا اعضای مشترک دوبار شمرده میشوند یا کلا در نظر گرفته نمیشوند.
۳. برای محاسبه جمله nام یک دنباله خطی چه روشی کارآمد است؟
ضرب جمله اول در قدر نسبت r باعث یافتن جمله nام میشود.
محاسبه جمله nام با تقسیم مقدار n بر عدد ثابت الگو صورت میگیرد.
استفاده از رابطه tₙ = t₁ + (n-1) d برای تعیین جمله خواسته شده
جمله nام را با جمع کردن عدد ثابت d به جمله قبلی مییابیم.
برای به دست آوردن جمله nام دنباله خطی باید از رابطه «tₙ = t₁ + (n-1) d» استفاده کرد که جمله اول و تفاضل ثابت d را دخیل میکند. جمع عدد ثابت به جمله قبلی فقط روشی دستی است و فرمول دقیق نیست.
۴. دنباله ۳، ۶، ۱۲، ۲۴ را چگونه میتوان طبقهبندی کرد و چرا؟
این دنباله حسابی است زیرا جمع هر جمله با عدد ثابت ساخته میشود.
این دنباله هندسی است زیرا اختلاف بین جملات از یک قاعده پیروی میکند.
این دنباله هندسی است زیرا هر جمله حاصل ضرب جمله قبل در یک عدد ثابت است.
این دنباله حسابی است زیرا اختلاف هر دو جمله متوالی برابر است.
در دنباله «۶، ۱۲، ۲۴»، هر جمله با ضرب کردن جمله قبل در عدد ۲ به دست میآید، که مشخصه دنباله هندسی است. در این نوع دنبالهها هر جمله با ضرب عددی ثابت (قدر نسبت) ساخته میشود.
۵. در یک دنباله حسابی، اگر مقدار قدر نسبت (d) افزایش یابد، چگونه آرایش جملات این دنباله تغییر میکند و این تفاوت نسبت به دنباله هندسی در چیست؟
تغییر d در دنباله حسابی موجب غیرمنتظره شدن فاصله جملات میشود، اما در دنباله هندسی همه جملات برابر میشوند.
افزایش d در دنباله حسابی باعث افزایش یکنواخت اختلاف جملات میشود، ولی در دنباله هندسی رابطه ضربی است.
در هر دو نوع دنباله، افزایش d سبب کاهش تکراری جملات میشود.
با افزایش d در دنباله حسابی، تعیین جمله اول ناممکن میشود، در دنباله هندسی مقدار جملهها ثابت میماند.
در دنباله حسابی، افزایش قدر نسبت (d) سبب میشود فاصله بین جملات به صورت یکنواخت افزایش یابد، چون هر جمله با جمع عدد ثابتی به جمله بعدی میرسد. در مقابل، در دنباله هندسی رابطه جملات ضربی است و تغییر مقدار d هیچ اثری ندارد، چون آنجا به جای d، قدر نسبت (r) اهمیت دارد.
۶. اگر جمله اول و قدر نسبت یک دنباله هندسی را داشته باشیم، فرمول محاسبه جمله nام چیست؟
تقسیم جمله اول بر قدر نسبت به توان n
توزیع جمله اول میان قدر نسبت و جمع آنها
ضرب جمله اول در قدر نسبت به توان n منهای یک
جمع جمله اول با قدر نسبت ضربدر n
برای پیدا کردن جمله nام یک دنباله هندسی، جمله اول را در قدر نسبت به توان n منهای یک ضرب میکنیم. این روش با تعریف دنباله هندسی و فرمول استاندارد آن مطابقت دارد.
۷. از نظر تعریف، تفاوت نسبتهای مثلثاتی سینوس، کسینوس، تانژانت و کتانژانت چیست؟
سینوس و کسینوس با ضلع مقابل و مجاور در ارتباطاند، تانژانت و کتانژانت تقسیم دو نسبت قبلی هستند.
هر نسبت مثلثاتی بیانگر یک رابطه متفاوت میان اضلاع یک مثلث قائمالزاویه است.
سینوس فقط به وتر مربوط میشود اما کسینوس، تانژانت و کتانژانت به زاویه ارتباط دارند.
سینوس و تانژانت هردو نسبت به زاویه قائمه یکسان تعریف میشوند ولی کسینوس و کتانژانت متفاوتاند.
تعریف نسبتهای مثلثاتی بر اساس روابط بین ضلع مقابل، ضلع مجاور و وتر در مثلث قائمالزاویه است. سینوس نسبت ضلع مقابل به وتر و کسینوس نسبت ضلع مجاور به وتر را نشان میدهد. تانژانت حاصل تقسیم سینوس بر کسینوس است و کتانژانت معکوس تانژانت است. به همین دلیل، تعریف ریاضی هر کدام متفاوت بوده و همه بر اساس اضلاع و نسبتهای مختلف ساخته میشوند.
۸. کدام عبارت بیانگر رابطه فیثاغورس بین نسبتهای مثلثاتی است و کاربرد اصلی آن چیست؟
تفاضل مربعهای سینوس (sin) و کسینوس (cos) برابر صفر است و برای تشخیص زاویه قائمه استفاده میشود.
جمع مربعهای سینوس (sin) و کسینوس (cos) برابر یک است و برای بررسی طول ضلعهای مثلث استفاده میشود.
ضرب سینوس (sin) در کسینوس (cos) همیشه برابر یک است و برای محاسبه مساحت مثلث به کار میرود.
جمع تانژانت (tan) و کتانژانت (cot) برابر یک است و در تعیین نیمساز زاویه نقش دارد.
جمع مربعهای سینوس (sin) و کسینوس (cos) برابر یک است. این بدین معنا است که sin²θ + cos²θ = 1. این رابطه معروف به رابطه فیثاغورس مثلثاتی است و ارتباط بین ضلعهای مثلث قائمالزاویه و نسبتهای مثلثاتی زاویه را نشان میدهد. این فرمول برای تبدیل و سادهسازی عبارات مثلثاتی و بررسی ویژگیهای اضلاع و زوایای مثلث به کار میرود.
۹. در دایره مثلثاتی، علامت سینوس (sin) و کسینوس (cos) در ربعهای مختلف چگونه است؟
در ربع دوم هر دو منفی اند، در ربع چهارم فقط کسینوس مثبت است.
در ربع سوم هر دو مثبت اند، در ربع دوم فقط کسینوس مثبت است.
در ربع اول هر دو مثبت هستند، در ربع دوم فقط سینوس مثبت است.
در ربع اول سینوس منفی و کسینوس مثبت است، در ربع سوم هر دو منفی هستند.
علامت سینوس (sin) و کسینوس (cos) در دایره مثلثاتی به این صورت است که در ربع اول هر دو مقدار مثبت دارند و در ربع دوم فقط سینوس مثبت و کسینوس منفی است. بت، و در ربع چهارم فقط کسینوس مثبت است نه سینوس.
۱۰. در سادهسازی عبارتهای جبری که توان گویا و رادیکال دارند، رعایت کدام قانون ضروری است؟
ادغام مخرجهای گویا با جمع توانها
نوشتن همه عبارات به صورت رادیکال تنها
استفاده از ضرب و تقسیم توانها با پایه برابر
بیتوجهی به فرجه رادیکال هنگام ضرب
در سادهسازی عبارات جبری با توان گویا یا رادیکال، باید قانون ضرب و تقسیم توانها با پایه یکسان رعایت شود. با جمع یا تفریق توانها محاسبه انجام میگیرد.
۱۱. کدام روش باعث گویا شدن مخرج عبارتهای رادیکالی با استفاده از اتحاد مزدوج یا مکعب میشود؟
جایگزینی توان رادیکال با عدد صحیح مشابه
ضرب صورت و مخرج در مزدوج عبارت رادیکالی
تبدیل رادیکال به کسر اعشاری معادل
استفاده از مجموع جذرها برای سادهسازی مخرج
وقتی صورت و مخرج یک عبارت رادیکالی را در مزدوج عبارت رادیکالی ضرب کنیم، با استفاده از اتحاد مزدوج مخرج از حالت رادیکالی خارج میشود.
۱۲. فرم کلی معادله درجه دوم چیست و سه شیوه متداول برای حل آن کدامند؟
فرم کلی بوده و با روشهای هندسی، اشتراک و ضرب حل میشود.
فرم کلی به صورت و حل توسط نمودار، ترکیب و دامنه ممکن است.
فرم کلی به شکل است و حل با اتحادها، فاکتورگیری و فرمول دلتا انجام میشود.
فرم کلی ax + c = 0 است که با جداسازی، ترکیب و تجزیه حل میگردد.
عبارت «فرم کلی به شکل است و حل با اتحادها، فاکتورگیری و فرمول دلتا انجام میشود» دقیقا ساختار معادله درجه دوم را بیان کرده و سه روش اصلی حل آن را، یعنی استفاده از اتحاد، فاکتورگیری و فرمول دلتا، معرفی میکند.
۱۳. دلتا (Δ) در معادله درجه دوم چه تاثیری بر تعداد و نوع ریشههای معادله دارد؟
دلتا علامت محور تقارن سهمی را مشخص میکند.
دلتا فقط مقدار راس سهمی را نشان میدهد.
دلتا وجود یا عدم وجود ریشه حقیقی را تعیین میکند.
دلتا مقدار دامنه تابع درجه دوم را تعیین میکند.
عبارت «دلتا وجود یا عدم وجود ریشهٔ حقیقی را تعیین میکند» درست است، زیرا در معادله درجه دوم، مقدار دلتا مشخص میکند که آیا معادله ریشه حقیقی دارد یا خیر و چند ریشه دارد.
۱۴. کدام گزینه بهترین توضیح برای کاربرد جدول تعیین علامت در حل نامعادلههای ریاضی دهم است؟
جدول تعیین علامت نقاط بحرانی و بازههای مثبت و منفی عبارت جبری را مشخص میکند.
روش جدول تعیین علامت فقط برای دنبالههای هندسی استفاده میشود.
جدول تعیین علامت معمولا برای حل مسایل احتمال و آمار طراحی شده است.
با جدول تعیین علامت میتوان مقدار دقیق ریشههای معادله را به دست آورد.
نقش «جدول تعیین علامت» نمایش نقاط بحرانی یک عبارت جبری و بازههای مثبت یا منفی بودن آن است، تا بتوان با بررسی این جدول بازههایی که نامعادله برقرار است را تشخیص داد. گزینه «مشخص کردن نقاط بحرانی و بازههای مثبت و منفی» صحیح است.
۱۵. کدام عبارت تعریف دقیق تابع را به همراه شرط یکتایی خروجی بیان میکند؟
تابع رابطهای است که به هر ورودی فقط یک خروجی نسبت میدهد.
تابع رابطهای است که ممکن است به یک ورودی چند خروجی بدهد.
تابع مجموعهای از اعداد صحیح و کسری است.
تابع مجموعهای است که اعضا را بدون ترتیب مشخص قرار میدهد.
در تعریف تابع تاکید میشود که به هر ورودی دقیقا یک خروجی نسبت داده میشود و این ویژگی، شرط یکتایی خروجی است. عبارت «تابع رابطهای است که به هر ورودی فقط یک خروجی نسبت میدهد» این نکته را بهدرستی بیان میکند.
۱۶. برای یک تابع نمایشدادهشده با جدول زوج مرتب، چگونه میتوان دامنه و برد را تشخیص داد؟
دامنه و برد هر دو فقط شامل عددهای مثبت جدول هستند.
دامنه مجموعه اولین اعداد هر زوج مرتب و برد مجموعه دومین اعداد است.
دامنه، اعداد تکراری هر زوج مرتب و برد مجموعه اعداد بدون تکرار است.
دامنه برابر جمع اعداد زوج اول و برد برابر حاصلضرب اعداد دوم است.
در تابعی که با جدول زوج مرتب نمایش داده میشود، «دامنه» همان مجموعه اولین اعداد داخل هر زوج، یعنی ورودیهای تابع است و «برد» مجموعه دومین اعداد، یعنی خروجیهای تابع محسوب میشود.
۱۷. در اصول شمارش، چه تفاوتی میان اصل جمع و اصل ضرب وجود دارد و هریک در چه شرایطی به کار میرود؟
اصل ضرب در زمانی کاربرد دارد که بین دو عمل هیچ تداخلی نباشد و اصل جمع برای مواردی که اعمال مستقل هستند استفاده میشود.
اصل جمع فقط در شمارش اعضای مجموعههای متناهی استفاده میشود و اصل ضرب برای نامتناهی به کار میرود.
اصل ضرب برای شمارش آرایش اعضای مشابه و اصل جمع برای گزینش اعضای متفاوت به کار میرود.
اصل جمع هنگامی استفاده میشود که یک رویداد از بین چند حالت جداگانه انتخاب شود و اصل ضرب زمانی به کار میرود که چند عمل به صورت پشت سر هم و وابسته انجام شوند.
در مسائل شمارش، زمانی که باید تعداد حالتها را زمانی محاسبه کنیم که فقط یکی از چند حالت مستقل ممکن است رخ دهد، مانند انتخاب بین چند مسیر متفاوت، از اصل جمع بهره میبریم، مثل عبارت «یا». در مقابل، اصل ضرب هنگامی استفاده میشود که چند عمل به صورت متوالی و وابسته به هم انجام میشوند، یعنی باید هر عمل رخ دهد تا نتیجه نهایی حاصل شود. مانند انتخاب یک عضو از هر گروه مختلف پشت سر هم یا عبارت «و» بین اعمال.
۱۸. اگر هدف، تعیین تعداد حالت انتخاب r عضو از n عضو باشد، بدون آن که ترتیب اعضا اهمیت داشته باشد، کدام فرمول کاربرد دارد و این موضوع چه تفاوتی با حالت جایگشت دارد؟
از فرمول جایگشت P(n, r) استفاده میشود و انتخاب هر عضو مهم است.
از فرمول ضرب n در r استفاده میشود چون هر گزینش مستقل است.
از فرمول اجتماع دو مجموعه بهره گرفته میشود و ترتیب تاثیر ندارد.
از فرمول ترکیب C(n, r) استفاده میشود و ترتیب اهمیت ندارد.
در شرایطی که ترتیب اعضا مهم نباشد، باید از فرمول ترکیب "C(n, r)" برای شمارش حالتها استفاده کرد، چون این فرمول تعداد انتخابهای بدون ترتیب را میشمارد. در مقابل، زمانی که ترتیب مهم باشد، فرمول «جایگشت P(n, r)» باید به کار رود که تعداد چیدمان ممکن اعضا را محاسبه میکند. بنابراین، تفاوت اصلی در اهمیت یا عدم اهمیت ترتیب اعضای انتخابی است و ترکیب تعداد انتخابهای بدون ترتیب را تعیین میکند، در حالی که جایگشت مخصوص حالتهایی است که ترتیب اعضا لحاظ میشود.













سپاسگزارم از زحمات شما تونستم جمع کنم ریاضی رو🌹
فقط یک اشکالی که وجود داشت این بود که در «فرمول جمله
nام دنباله هندسی» a1 باید ضربدر r^n-1 بشه نه به اضافه.
با سلام خدمت شما؛
نکته بیان شده صحیح است و اصلاحات لازم در متن اعمال شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
خیلی خوب بود ممنون 💖
عالی🌹🌹