فرادرسفرمول الگویابی | فرمول الگوی عددی — با مثال و به زبان ساده
الگوها و دنباله‌های عددی، یکی از بخش‌های زیبای ریاضی است. به کمک فرمول الگویابی می‌توانیم رابطه بین عددهای یک دنباله را کشف کرده و مقدارهای بعدی را بشناسیم. الگوهای عدد، ساختار مشخصی دارند و نباید در اعدادی که در الگوی ریاضی وجود دارد، استثنا پیدا کرد. پس هر عددی از این الگو، طبق فرمول الگویابی محاسبه شده و به مقدارهای بعدی و قبلی وابسته است. در این متن از مجله فرادرس، به فرمول الگویابی با مثال و به زبان ساده توجه کردیم و توضیحاتی را برای پیدا کردن الگوی اعداد بیان خواهیم کرد.
در نوشتارهای دیگر از مجله فرادرس به موضوع الگویابی و الگوهای عددی اشاره شده است. بنابراین به عنوان متن مکمل می‌توانید به الگوها و دنباله های متداول عددی — به زبان ساده و الگوهای عددی سخت — به زبان ساده و با مثال مراجعه کنید. همچنین خواندن مطالب مجموعه ها در ریاضیات – مفاهیم پایه و اعداد طبیعی چیست و چه اعدادی هستند ؟ — به زبان ساده و با مثال نیز مفید است.
فرمول الگویابی
الگوها در همه جا، همراه ما هستند. الگویی که در برگ درختان، شکوفه‌ها، رنگ‌های بال پروانه‌ها، ساختمان‌ها و سرامیک آشپزخانه‌های آن‌ها طبق الگوهای ریاضی تعیین می‌شوند. البته همانطور که می‌دانید بعضی از این الگوها طبیعی هستند و بعضی هم الگوهای مصنوعی بوده که توسط بشر ساخته شده‌اند.
یافتن الگوها در چنین چیزهایی ممکن است به راحتی مشخص شود یا تبدیل به کاری سخت شده که به مهارت‌های ریاضی خاص نیاز داشته باشد. مثلا رابطه بین ضلع‌های مثلث با مساحت آن‌ها، الگویی است که توسط ریاضیدان‌های قدیم مشخص شده و با دانستن ارتفاع و قاعده مثلث، می‌توانیم مساحت هر مثلثی را تعیین کنیم.
موضوعی که در مورد الگویابی اعداد باید در نظر گرفت، وجود قاعده یا فرمول همیشگی و ثابت برای همه مقادیر آن‌ها است. بنابراین استثناء برای پیدا کردن مقدارهای الگو وجود ندارد. به دنباله زیر توجه کنید.
2, 4, 6, 8, 10, ...
مشخص است که این اعداد، دنباله اعداد زوج را مشخص کرده است. هر یک از این اعداد با عدد قبلی خود، ۲ واحد اختلاف دارد. از طرفی اولین شماره این دنباله (۱)، برابر با ۲ است. همچنین دومین شماره این دنباله (۲) برابر با ۴ است. از همین رابطه متوجه می‌شویم که هر شماره از این دنباله، از ضرب آن در عدد ۲ بوجود می‌آید. پس اگر شماره ۱۰ این دنباله را لازم داشته باشیم، کافی است از رابطه زیر کمک بگیریم.
۲ × ۱۰ = ۲۰
فرمول الگویابی را چگونه پیدا کنیم؟
الگوهای عددی را به چند شکل می‌توان فرمولبندی کرد. برای مثال رابطه‌ای که برای اعداد زوج گفتیم، برای پیدا کردن عدد شماره دهم، باید ۱۰ را در ۲ ضرب کنیم. پس در اینجا فرمول الگویابی به صورت ضربی است. بنابراین اگر شماره مربوط به عدد الگو را به صورت یک حرف انگلیسی مثل (a) نشان دهیم، فرمول الگویابی اعداد زوج به صورت زیر نوشته میشود.
۲a = 2 × a
توجه داریم که مقدارهایی را برای a در نظر می‌گیریم که از یک (۱) آغاز شده و یکی یکی افزایش می‌یابد و باید مقدارهای بعدی را به صورت 2, 3, 4, ... به کار ببریم. ولی برای پیدا کردن فرمول الگویابی اعداد فرد، باید هم از ضرب و هم از جمع استفاده کنیم. الگوی اعداد فرد را در زیر نوشته‌ایم.
1, 3, 5, 7, 9, ...
این‌بار برای پیدا کردن فرمول الگویابی این دنباله سعی می‌کنیم شماره‌ها یا مکان هر یک از آن‌ها را به مقدارشان ربط بدهیم. در مکان یکم (۱)، عدد ۱ قرار دارد. در مکان دوم (۲) عدد ۳ و در مکان سوم (۳) عدد پنج. اگر مکان هر عدد را از یک کم کنیم و در عدد ۲ ضرب کنیم، فرمول الگوی اعداد فرد را پیدا کرده‌ایم. یعنی اگر عدد مربوط به مکان ششم (۶) اعداد فرد را لازم داشته باشیم، از طریق زیر باید آن را بدست آوریم.
( 6 - ۱ ) × ۲ + ۱ = ۱۱
همانطور که می‌بینید عدد فرد بعد از ۹ که همان ۱۱ هست، محاسبه شد. این الگو را برای مکان ۱۰ هم تکرار می‌کنیم. باید نتیجه این محاسبه، یک عدد فرد باشد.
( 10 - 1 ) × ۲ + ۱ = ۱۹
پس اگر b را به عنوان شماره مکان اعداد در این الگو قرار دهیم، فرمول الگویابی اعداد فرد به صورت زیر نوشته میشود.
( b - 1 ) × 2 + 1
فرمول الگویابی براساس شکلی که برای اعداد رسم میشود، نیز ساخته و قابل محاسبه است. برای مثال الگوی اعداد زوج را به صورت شکل در زیر می‌بینید.
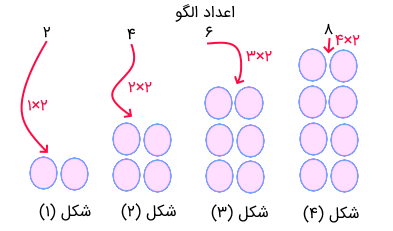
حتی ممکن است برعکس هم عمل کنیم و سعی کنیم که با توجه به الگوی شکل‌ها، ترتیب یا اعداد دنباله را مشخص کنیم. همانطور که در تصویر زیر می‌بینید، الگوی اعداد فرد، به کار رفته و ترتیب شکل‌ها با توجه به ترتیب اعداد فرد تعیین شده است.
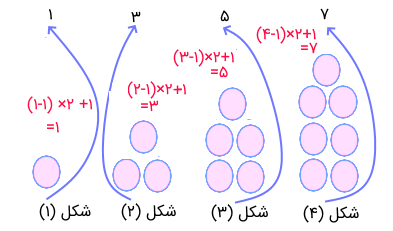
نکته: ممکن است این ترتیب افزایشی بوده یا کاهشی باشد. الگوهایی که برمبنای ضرب و جمع شکل گرفته باشند، فرمول الگویابی به صورت افزایشی دارند در حالیکه الگوهایی که به کمک تفریق و تقسیم ساخته می‌شوند، ممکن است مقدارهای آن‌ها کاهشی باشند.
الگوهای افزایشی
الگوهای اعداد زوج و فرد، نمونه‌ای از الگوهای افزایشی یا دنباله‌های صعودی بودند و دیدید که فرمول الگویابی در آن‌ها به کمک ضرب و جمع نوشته می‌شد. این بار می‌خواهیم به الگوی دیگری اشاره کنیم که آن هم از طریق جمع تشکیل شده و به الگو یا دنباله فیبوناچی مشهور است. الگوی عددی زیر همان دنباله فیبوناچی است که با مقدار ۱ شروع شده و هر مقدار از جمع دو عدد قبلی بدست می‌آید.
1, 1, 2, 3, 5, 8, 13, 21, ...
عدد اول در این دنباله، یک (۱) است و چون عددی قبل از آن وجود ندارد، برای پیدا کردن عدد دوم، یک و صفر (۱ و صفر به عنوان دو عدد قبلی) را با هم جمع می‌کنیم. حاصل برابر با ۱ است که به عنوان دومین عدد از دنباله بدست می‌آید. ولی برای عدد سوم، عددهای دوم و اول را با هم جمع می‌کنیم. حاصل برابر است با ۲. برای پیدا کردن عدد ششم، باید جمع عدد پنجم و چهارم را بدست بیاوریم که ۵ و ۳ هستند و جمع آن‌ها، برابر است با ۸. به این ترتیب یک دنباله افزایشی به شکل دنباله فیبوناچی حاصل میشود.
به نظر شما، عدد 9ام دنباله فیبوناچی چیست؟ با جمع کردن ۲۱ و ۱۳ به نتیجه می‌رسیم. پس ۹امین عدد در دنباله فیبوناچی ۳۴ خواهد بود. بد نیست برای تمرین عدد ۲۰ام دنباله فیبوناچی را هم مشخص کنید. این عدد برابر با ۶۷۶۵ خواهد بود.
یک مثال دیگر برای الگوهای افزایشی، الگوهای مثلثی و یا مربعی است. الگوی مثلثی اعداد به صورتی است که با تعداد نقاطی که در این الگو مشخص شده، می‌توان مثلث ساخت. به تصویر زیر و الگوی عددی بدست آمده نگاه کنید.
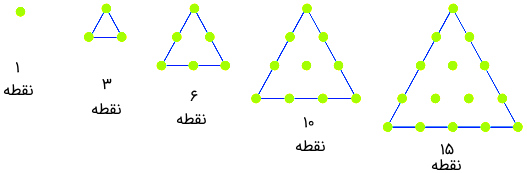
همانطور که می‌بینید، این دنباله به صورت ... ,15 ,10 ,6, 3, 1 نوشته میشود. قاعده الگویابی این اعداد به صورت زیر درخواهد آمد.
الگوی اعداد مثلث: ۲ / ( مکان عدد × ( مکان عدد + ۱) ) = عدد الگو
از طرفی الگوی مربعی اعداد نیز ... ,81 , 64, 49, 36, 25, 16, 9, 4, 1, 0 است. هر کدام از این اعداد، مربع کامل هستند و ریشه دوم صحیح دارند. تصویر زیر الگوی مربعی اعداد را نمایش داده است.
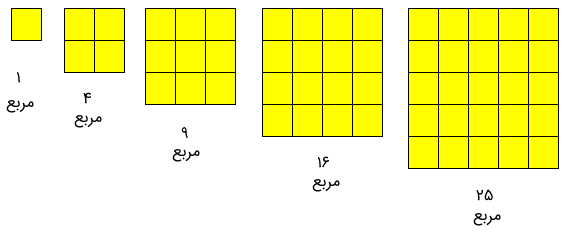
فرمول یا قاعده الگویابی اعداد مربعی هم به صورت زیر در می‌آید.
الگوی اعداد مربع: مکان عدد × مکان عدد = عدد الگو
همینطور الگوهایی شکل‌های چند ضلعی نیز داریم که پنج ضلعی و شش ضلعی آن معروف‌تر هستند. این الگوها را در ادامه می‌بینید.
الگوی پنج ضلعی به صورت ..., 35 ,22, 12, 5, 1 است که فرمول الگویابی آن به شکل زیر نوشته میشود.
الگوی پنج ضلعی: ۲ ÷ (۱ - (مکان عدد × ۳) × مکان عدد = عدد الگو
مثلا برای پیدا کردن عدد الگوی پنج ضلعی در مکان ۱۰ام به صورت زیر فرمول را می‌نویسیم.
۱۴۵ = ۲ ÷ ۲۹ × ۱۰ = ۲ ÷ (۱ - ( ۱۰ × ۳ ) × ۱۰ = عدد الگوی پنج ضلعی در مکان ۱۰ام
همچنین الگوی شش ضلعی نیز به صورت ... ,۶۶ ,۴۵ ,۲۸ ,۱۵ ,۶ ,۱ مشخص میشود که فرمول الگویابی آن هم به مانند زیر است.
الگوی شش ضلعی: ( ۱ - مکان عدد × ۲) × مکان عدد = عدد الگو
اگر قرار باشد عدد الگوی شش ضلعی را در مکان ۵ام بدست آوریم، به صورت زیر محاسبات را اجرا خواهیم کرد.
۴۵ = ( ۹ ) × ۵ = ( ۱ - ۵ × ۲) × ۵ = عدد الگوی شش ضلعی در مکان 5ام
الگوهای کاهشی
زمانی که یک الگو کاهشی یا دنباله نزولی را می‌بینیم، مشخص میشود که با افزایش مکان هر عدد در الگو، مقدار آن کمتر میشود. برای مثال پنجمین عدد در الگوی کاهشی از چهارمین عدد کوچکتر است. به همین ترتیب پنجمین عدد از ششمین عدد نیز بزرگتر خواهد بود. به الگوی کاهشی زیر توجه کنید.
30, ,25, 20, 15, 10, 5, 0
اولین عدد در این الگو، ۳۰ و دومین آن، ۲۵ است. پس الگو کاهشی است. البته این کاهش را در همه اعداد دنبال هم در الگو، می‌بینیم. جدول زیر برای مقایسه اختلاف اعداد این دنباله رسم شده است.
| مکان (شماره) | عدد در دنباله | فاصله با عدد بعدی |
| 1 | 30 | 5 |
| 2 | 25 | 5 |
| 3 | 20 | 5 |
| 4 | 15 | 5 |
| 5 | 10 | 5 |
| 6 | 5 | 5 |
| 7 | 0 | - |
پس باید فرمول الگویابی برای چنین دنباله‌ای را به صورت زیر بنویسیم.
۵ - عدد قبلی الگو = عدد الگو
نکته: همه اعداد این الگو، مضرب‌های پنج هستند. پس اگر بخواهیم الگوی عددی را برحسب مکان بنویسیم به شکل زیر خواهد بود.
(( ۱ - مکان) × ۵) - ۳۰ = عدد الگو
پس اگر بخواهیم مکان پنجم این الگو را بدست آوریم، کافی است از فرمول زیر استفاده کنیم.
10 = 20 - 30 = (( ۱ - ۵) × ۵) - ۳۰ = عدد الگو
به عنوان یک مثال دیگر از الگوهای کاهشی به دنباله زیر نگاهی می‌اندازیم.
100, 200, 400, 800
عدد اول این دنباله، ۸۰۰ ولی عدد دوم، ۴۰۰ است. پس باید این دنباله را کاهشی (نزولی) دانست. این بار به جای محاسبه تفاضل، نسبت هر عدد در دنباله را به عدد قبلی محاسبه می‌کنیم. جدول زیر برای این کار تهیه شده است.
| مکان (شماره) | عدد در دنباله | نسبت با عدد قبلی |
| 1 | 800 | - |
| 2 | 400 | ۸۰۰/۴۰۰ = ۰٫۵ |
| 3 | 200 | 400 / ۲۰۰ = ۰٫۵ |
| 4 | 100 | 100 / ۲۰۰ = 5 |
پس هر عدد در این دنباله، نصف (۰٫۵) عدد قبلی خود است. پس اگر بخواهیم در مکان پنجم، عدد دنباله را مشخص کنیم، باید ۱۰۰ را نصف کنیم. در نتیجه ۵۰، مقدار پنجم این دنباله است و همینطور ۲۵ هم عدد ششم این دنباله محسوب میشود. پس اعداد بعدی این دنباله به صورت زیر خواهند بود.
$$ 12٫5, 25, 50, 100, 200, 400, 800, . . . $$
نکته: در دنباله‌های کاهشی، بزرگترین مقدار همان اولین عدد الگو است و بقیه مقدارهای دنباله از آن کوچکتر هستند. چنین دنباله‌هایی را «کراندار از بالا» می‌گویند. در مقابل الگوهای عددی افزایشی، کمترین مقدار همان اولین عدد الگو بوده و کراندار از پایین هستند. به این ترتیب فرمول الگویابی آن‌ها به سرعت پیدا میشود، زیرا در اغلب موارد جمع و ضرب الگوهای افزایشی دارند و تقسیم یا تفریق الگوهای کاهشی را نشان می‌دهند.
آزمون سنجش یادگیری فرمول الگویابی
در این بخش از مجله فرادرس، سطح اطلاعات شما در مبحث فرمول الگویابی را با طرح سوال‌های چندگزینه‌ای می‌سنجیم. پس از جواب دادن به تمام سوال‌ها، نتیجه آزمون برای شما به نمایش درمی‌آید.
عدد بعدی در الگوی $$ ۳, \ ۱۰, \ ۱۷, \ ۲۴, \ ۳۱, \ ۳۸, \ . . . $$ چیست؟
۴۳
۴۴
۴۵
۴۶
در الگوی مورد سوال، هر عدد، از جمع عدد قبل از خود با عدد ۷ به دست می‌آید:
$$
\begin {aligned}& ۳ + ۷ = ۱۰ \\
& ۱۰ + ۷ = ۱۷ \\
& ۱۷ + ۷ = ۲۴ \\
& ۲۴ + ۷ = ۳۱ \\
& ۳۱ + ۷ = ۳۸ \\
\end {aligned}
$$
بنابراین، عدد بعدی، حاصل جمع عدد ۳۸ با عدد ۷ است:
$$ ۳۸ + ۷ = ۴۵ $$
به این ترتیب، گزینه صحیح، عدد ۴۵ را نمایش می‌دهد.
عدد بعدی در الگوی $$ ۷۱, \ ۶۲, \ ۵۳, \ ۴۴, \ . . . $$ چیست؟
۳۵
۳۶
۳۷
۳۸
در الگوی $$ ۷۱, \ ۶۲, \ ۵۳, \ ۴۴, \ . . . $$، اعداد بعد از عدد ۷۱، حاصل تفریق عدد قبلی خود با عدد ۹ هستند:
$$
\begin {aligned} & ۷۱- ۹ = ۶۲ \\
& ۶۲ - ۹ = ۵۳ \\
& ۵۳ - ۹ = ۴۴ \\
\end {aligned}
$$
بنابراین، عدد بعدی، عبارت است از:
$$ ۴۴ - ۹ = ۳۵ $$
عدد بعدی در الگوی $$ ۲, \ ۶, \ ۱۸, \ ۵۴, \ . . . $$ چیست؟
۱۰۸
۱۵۲
۱۶۲
۲۱۶
در الگوی $$ ۲, \ ۶, \ ۱۸, \ ۵۴, \ . . . $$، اعداد بعد از عدد ۲، از ضرب عدد قبلی در عدد ۳ به دست می‌آیند:
$$
\begin {aligned} & ۲ \times ۳ = ۶ \\
& ۶ \times ۳ = ۱۸ \\
& ۱۸ \times ۳ = ۵۴ \\
\end {aligned}
$$
از این‌رو، عدد بعدی الگو، حاصل‌ترین ضرب عدد ۵۴ در عدد ۳ است:
$$ ۵۴ \times ۳ = ۱۶۲ $$
کدامیک از گزینه‌های زیر، مقدار ؟ در الگوی $$ ۲, \ ۸, \ ۳۲, \ . . . , \ ۵۱۲, \ ۲۰۴۸ $$ را نمایش می‌دهد؟
۵۶
۶۴
۱۲۸
۲۵۶
با دقت بر روی رابطه بین اعداد الگوی مورد سوال می‌توان دریافت که اعداد این الگو از ضرب عدد قبلی خود در عدد ۴ به دست آمده‌اند. بنابراین:
$$
\begin {aligned} & ۲ \times ۴ = ۸ \\
& ۸ \times ۴ = ۳۲ \\
& ۳۲ \times ۴ = ۱۲۸ \\
& ۱۲۸ \times ۴ = ۵۱۲ \\
& ۵۱۲ \times ۴ = ۲۰۴۸ \\
\end {aligned}
$$
گزینه صحیح، عدد ۱۲۸ را نمایش می‌دهد.
عدد بعدی الگوی $$ ۱, \ ۳, \ ۷, \ ۱۵, \ ۳۱, \ . . . $$ چند است؟
۴۷
۴۸
۶۲
۶۳
فرمول الگوی مورد سوال، به صورت زیر است:
۱ + ۲ × عدد قبلی = عدد فعلی
به عبارت دیگر، اعداد بعد از اولین جمله (عدد ۱)، از ضرب عدد قبلی در عدد ۲ و جمع حاصل‌ضرب با عدد ۱ به دست می‌آیند:
$$
\begin {aligned} & ۱ \times ۲ + ۱ = ۳ \\
& ۳ \times ۲ + ۱ = ۷ \\
& ۷ \times ۲ + ۱ = ۱۵ \\
& ۱۵ \times ۲ + ۱ = ۳۱ \\
\end {aligned}
$$
بنابراین، عدد بعد از ۳۱ برابر است با:
$$ ۳۱ \times ۲ + ۱ = ۶۳ $$
عدد پنجم الگوی $$ ۲, \ ۶, \ ۱۲, \ ۲۰, \ . . . $$ چیست؟
۲۵
۲۸
۳۰
۳۲
برای پیدا کردن فرمول الگوی مورد سوال، ابتدا رابطه مستقیم بین اعداد آن را بررسی می‌کنیم. این رابطه به صورت زیر است:
۴ + عدد اول = عدد دوم
$$
۲ + ۴ = ۶
$$
۶ + عدد دوم = عدد سوم
$$
۶ + ۶ = ۱۲
$$
۸ + عدد سوم = عدد چهارم
$$
۱۲ + ۸ = ۲۰
$$
بنابراین، فرمول اعداد الگو را می‌توان به صورت زیر نوشت:
(۲ × جایگاه عدد) + عدد قبلی = عدد الگو
با استفاده از این فرمول، برای عدد پنجم الگو داریم:
(۲ × جایگاه عدد پنجم) + عدد چهارم = عدد پنجم
(۲ × ۵) + ۲۰ = عدد پنجم
۱۰ + ۲۰ = عدد پنجم
۳۰ = عدد پنجم
دهمین عدد مثلثی چیست؟
۳۰
۴۵
۵۵
۶۰
فرمول الگوی اعداد مثلثی به صورت زیر است:
۲ ÷ ( مکان عدد × ( مکان عدد + ۱) ) = عدد الگو
بنابراین، عدد دهم در این الگو برابر خواهد بود با:
۲ ÷ ( ۱۰ × ( ۱۰ + ۱) ) = عدد دهم الگوی اعداد مثلثی
۲ ÷ ( ۱۰ × ( ۱۱) ) = عدد دهم الگوی اعداد مثلثی
۲ ÷ ( ۱۱۰ ) = عدد دهم الگوی اعداد مثلثی
۵۵ = عدد دهم الگوی اعداد مثلثی
فرمول خطی الگوی عددی $$ ۳, \ ۱۰, \ ۱۷, \ ۲۴, \ . . . $$ بر اساس جایگاه هر عدد کدام گزینه است؟
$$ a _ n = n + 8 $$
$$ a _ n = 4 n + 2 $$
$$ a _ n = 6 n - 2 $$
$$ a _ n = 7 n - 4 $$
برای به دست آوردن فرمول الگوهای عددی بر اساس جایگاه هر عدد، ابتدا پارامترهای دخیل در الگو را می‌نویسیم. این پارامترها عبارت هستند از:
- $$ n $$: جایگاه عددم n ام
- $$ a _ n $$: مقدار عدد جایگاه n ام
- $$ d $$: اختلاف بین عدد n ام با عدد (n+1) ام
- $$ c $$: ثابت عددی
به منظور تعیین فرمول الگو، عدد اول آن را در نظر بگیرید. برای این عدد داریم:
- $$ n $$: جایگاه اول برابر با ۱
- $$ a _ n $$: مقدار عدد جایگاه اول برابر با ۳
- $$ d $$: اختلاف بین عدد جایگاه اول با عدد جایگاه دوم برابر با ۷=۳-۱۰ (در این سوال، فاصله $$ d $$ بین هر دو عدد متوالی یکسان است.)
- $$ c $$: ثابت عددی مجهول
فرم کلی الگوهای عددی خطی به صورت زیر نوشته میشود:
$$ a _ n = d n + c $$
پارامترهای مربوط به عدد اول الگو را درون این فرمول قرار می‌دهیم:
$$ a _ 1 = 7 \times 1 + c $$
$$ 3 = 7 \times 1 + c $$
$$ c = 3 - 7 $$
$$ c = - 4 $$
در نتیجه:
$$ a _ n = 7 n - 4 $$
خلاصه و جمع‌بندی
الگویابی اعداد و پیدا کردن مناسب‌ترین فرمول الگویابی برای یک دنباله عددی، علاوه بر اینکه یک سرگرمی ریاضی محسوب میشود ولی بسیاری از فرمول‌های ریاضی نیز بر این اساس ساخته شده است. بنابراین شناخت الگوها و دنباله‌های عدد و رابطه بین مقدارهای آن‌ها اهمیت زیادی دارد. در این مطلب از مجله فرادرس با توجه به چند الگوی معمول در ریاضی، فرمول الگویابی برای دنباله‌های عددی را بازگو کردیم و مشخص کردیم چگونه می‌توان در یک دنباله، مثلا عدد ۱۰ام را بدست آورد.
سلام خدمت شما میخواستن سوال بپرسم
رابطه ی این الگو چیه ۲۴،۳۱،۳۸
جمله عمومی:
۱۷+۷n
الگو ۲۴-۷۲-۱۲
سلام
دوعدد بعدی و لطف میکنین؟
این دنباله
…….4.9.22.69.278
سلام
لطفا رابطه‌ی الگوی زیر را بنوسید
۶ ۳ ۱
شکل (۳) شکل (۲) شکل (۱)
اصلا متوجه نشدم
سلام
خیلی از الگو ها رو ننوشته بودید 😕
سلام ببخشید کسی میتونه رابطه nام این الگو را به دست بیاره؟
3،10،29،66،……….
هرچند الگوهای زیادی به بچه‌ها میدن که ما پدر و مادرا هم توی حلشون مشکل داریم ولی توضیحاتتون عالی بود اینارو خوب یاد گرفتم😉🙏😍😍😍😍
الگوی شش ضلعی رو اشتباه نوشتید،حتی مثالی هم که نوشتید برای عدد پنجم ۶۶ که تو خود الگویی که گذاشتید۱۲۵ است
سلام و وقت بخیر؛
متن اصلاح شد. عدد ۴۵ درست است. الگوی شش ضلعی به صورت … ,66 ,45 ,28 ,15 ,6 ,1 نوشته میشود.
از همراهی شما با مجله فراردرس سپاسگزاریم.
سلام فرمول عداد حسا بی چیه
عددی بعدی چیست؟ فرمول چیه؟
،۲،۵،۱۳،۳۶
الگو ۴،۵،۷،۱۱،۱۹،۳۵
دو عدد بعدی
۶۷، ۱۳۱
۶۷-۱۳۱-۲۵۹
سلام
الگوی اعداد …و11و56و8888888 چی میشه؟ هرچی سعی میکنم براش الگویی پیدا نمیکنم.معلم دخترم بهشون سوال داده
جمع اعداد هر مولفه مولفه بعدیست
۸+۸+۸+۸+۸+۸+۸=۵۶
۵+۶=۱۱
۱+۱=۲
سلام
لطفا فرمول الگوی زیر را کمکم کنید
۹-۱۵-۸-۱۶-۷-۱۷
کلاس ششم
الگوی یک درمیان کم میشه و ۱۵ زیاد میشه
الگو ۴،۵،۷،۱۱،۱۹،۳۵
دو عدد بعدی
از +۶ شروع بعد _۷بعد+۸بعد_۹بعد+۱۰بعد __۱۱ یعنی از ۶شروع یک در میان مثبت ومنفی تا الی اخر
اعداد بعدی میشه ۶ ، ۱۸ ، ۵ که الگوی آن بصورت+۶ ،-۷ ،+۸ ،-۹ ،+۱۰ ،-۱۱ ، +۱۲ ، -۱۳
الگو تکرار یک درمیان اعداد هست .
رابطه ۹،۸،۷ کم کردن ۱
رابطه ۱۵،۱۶،۱۷ اضافه کردن ۱
9-15-8-16-7-17-6-18-5-19-4-20-3-21-2-22-1-23
در مورد الگوهای اعشاری هم اطلاعاتی بزارید
الگوی شش ضلعی رو نمیدونم اما عدد بعدی در دنباله 3-10-16-36-68 عدد 140 هست.
اعداد ضربدر 2 و یک در میون به ترتیب بعلاوه 4 و منهای 4 میشن
سلام
راهی هست برای اینا الگویی پیدا کرد؟
3,22,25,16,8,18,3,6,14,13,8,15,14,5,10,2,8,1,6
الگوی
۱،۰،۱،۱،۰،۱،۱،۱،۰،۱،۱،۱،۱،۰و الی آخر
چه نوع الگویی هست و جمله عمومی آن چیست؟
در حد کلاس هفتم
سلام من نمیتونم برای الگو ها به راحتی رابطه پیدا کنم باید چیکار کنم ممنون میشم پاسخ بدید/
سلام میشه فرمول این الگو رو بدید
۲-۵-۷
ممنون
سلام میشه فرمول الگوی زیر را بگویید لطفا
۲،۴،۸
سلام فرمول دنباله ۱۱ ۷ ۴ ۲ چی میشه؟
اعداد زوج
مکان عدد ×۲
سلام جناب دکتر
آموزش بسیار خوبی بود. سپاسگزارم. بنده در رشته برق قدرت با وجود فرمول نویسی های فراوان، از مقاله شما استفاده وافر کردم. لطفاً درصورت امکان جواب سوال زیر را بفرمایید:(سوء تفاهم نشود این سوال درس دخترم است که بنده و همسرم در مورد جواب آن اختلاف نظر داریم! ?)
الگوی زیر را ادامه دهید:(متن اصلی سوال درس ریاضی اول ابتدایی )
….………۷. ۸. ۸. ۷
دو به توان n
الگوی زیر را راهنمایی کنید,…,…1,2,5,14
رابطه را بگویی ممنون میشم
۱ – ( ۳ × عدد قبلی) = عدد بعدی
من دنبال رابطه الگو ی 2،6،12،20بودم اما هیچی در مورد این الگو ننوشته بودید. لطفا رسیدگی کنید یا حداقل سوال منو جواب بدید. ممنون.
سلام ،رابطه ی الگوی ۴,۹,۱۰ چی میشه؟
شماره شکل ضرب در یک واحد بزرگتر
۲ میشه شکل یک رابطه ش میشه ۱ضرب در ۲
۶ میشه شکل دو رابطه ش میشه ۲ ضرب در ۳
۱۲ میشه شکل سه رابطه ش میشه ۳ ضرب در ۴ و الی آخر
رابطه الگوی شما به شکل زیر است
شماره الگو ضربدر(شماره الگوی +۱)
مثال عدد پنجم الگو یعنی
۵ضربدر(۵+۱)
یعنی ۵ ضربدر ۶ که میشود۳۰
خواهش میکنم جواب بدید
سلام برای الگوی ۱،۳،۵،۷… فرمولبندی تون درسته ولی واسه ۵،۷،۹،۱۱… گفته هشتمین عدد چند میشه من اون فرمولبندی رو میرم ولی عدد ۱۵ در میاد با اینکه باید ۱۹ در بیاد میشه این رو توضیح بدید ممنون
عالی بود خانم دستان ممنون از شما🌷
در حالت اول که دنباله از عدد 1 شروع میشه فرمول ما 1-(i*2) است تا عدد i ام دنباله را بدست بیارید ، در حالت دوم که دنباله از عدد 5 شروع میشه ، عدد شروع کننده 4 واحد از عدد شروع کننده حالت اول ( 1 ) بیشتر است پس فقط کافیه فرمول حالت اول را با 4 جمع کنید یعنی 1-[(i*2)+4]
سلام.
دنباله‌ای که در متن بررسی شده، با دنباله‌ای که شما به آن اشاره کرده‌اید تفاوت دارد. اگر $$b$$ را شماره مکان عدد در نظر بگیریم، فرمول الگویابی اعداد شما به صورت $$2\times (b-1)+5$$ خواهد بود. اگر عدد $$b=8$$ را در این فرمول قرار دهید، به $$19$$ می‌رسید.
موفق باشید.
رابطه ی الگوی نا منظم چیه توی کلی بدید بلطفا
سلام.من یک الگو دارم به این شکل:1،۲،۲،۳،۳،۳،۴،۴،۴،۴
و به یک فرمول نیاز دارم
رابطه الگوی عددی ۸و ۵ و ۳ چگونه است؟
سلام
الگوی 4, 9, 10, ..
چی میشه
سلام و روز شما به خیر؛
با توجه به الگوریتمی که نوشته‌اید به آسانی می‌توان عدد بعدی و تعداد تکرار را با اضافه کردن یک واحد به عدد قبل به دست آورد. در حقیقت $$x_{i+1}=x_i+1$$ است که $$x_{i+1}$$ تعداد تکرار و مقدار عدد بعدی دنباله شما را مشخص می‌کند.
از همراهی شما با فرادرس خرسندیم.
چرا برای الگوی مربع و مستطیل و چند ضلعی ها هیچ‌نمونه ای تعریف نشده فقط فرمول دادید ممنون میشم براش مثال هم زنید
بسیارعالی
چرا برای الگوی شش ضلعی باهم جور در نمیان ؟ کدومش درسته ؟
عدد بعدی در الگوی زیر چیست؟؟۳و۱۰و۱۶و۳۶و۶۸و…..