یادگیری ترکیب و جایگشت به همراه مثال های عینی — به زبان ساده

معماها میتوانند به بسط شهود ما کمک کنند. برای مثال درک این که چگونه میتوانیم روی یک شبکه حرکت کنیم، میتواند کمک کند درکی شهودی از ترکیب و جایگشت به دست آوریم.
فرض کنید روی یک شبکه 6 × 4 قرار دارید و میخواهید از گوشه سمت پایین-چپ به گوشه راست –بالا بروید. چه تعداد مسیر میتوانید انتخاب کنید؟ اگر بازگشت به عقب مجاز نباشد، شما تنها میتوانید به سمت راست و بالا حرکت کنید.
چند ثانیه تأمل کنید و به دقت تعداد پاسخهای ممکن را بررسی نمایید.
تبدیل تصاویر به نوشته
زمانی که مسیرهای ممکن را بررسی میکنید و احتمالاً بدیدن منظور از انگشت خود کمک میگیرید ممکن است با خود زمزمه کنید: «بالا، راست، بالا، راست...»
بنابراین چرا همینها را نمینویسیم؟ با استفاده حروف u و r به ترتیب برای بالا و راست یکی از مسیرهای ممکن چنین خواهد بود:
r r r r r r r u u u u
یعنی همه مسیر را تا انتها به سمت راست بروید و سپس همه مسیر را به سمت بالا حرکت کنید. مسیر روی نمودار میتواند به صورت زیر باشد:
r r r r u u u u r r
اینک سؤال این است که با استفاده از تفسیر متنی خودمان «به چند روش میتوانیم حروف rrrrrrruuuu را بازآرایی کنیم؟»
البته ما قبلاً در نوشته دیگری به طور کامل در مورد جایگشت و ترکیب صحبت کردهایم.
درک ترکیب و جایگشت
چندین روش برای تفسیر ترکیب و جایگشت وجود دارد. زمانی که نخستین توضیح به ذهن میرسد، میتوان به عقب بازگشت و به روش متفاوتی فکر کرد. زمانی که قصد داریم درکی شهودی در مورد یک مسئله بیابیم، بهتر است از چندین مدل ذهنی برای مدلسازی آن استفاده کنیم. در این حالت بهرهگیری از یک بینش برای توسعه مدلهای دیگر راهگشا خواهد بود.
رویکرد اول: آغاز به روش مشابه
به جای این که 6 تا راست و 4 تا بالا داشته باشیم، تصور کنید که 10 تا راست داشته باشیم.
r r r r r r r r r r
بدیهی است که این وضعیت ممکن نیست، زیرا باید چهار مورد از آنها را به صورت u یعنی بالا تغییر دهیم. پس اینک باید پرسید به چند روش میتوان 4 جهت بالا را تغییر داد؟
اکنون 10 انتخاب برای سمت راست داریم که باید تغییر دهیم. وقتی یکی تغییر یابد 9 تغییر ممکن خواهد بود، و در مورد سوم 8 تا و در مورد تغییر چهارم که تغییر آخر نیز محسوب میشود، تنها 7 گزینه ممکن خواهد بود. بنابراین تعداد حالات ممکن برابر است با:
10 × 9 × 8 × 7 = 10!/6! = 5040
اما این پاسخ ما نیست چون باید موارد تکراری را حذف کنیم. در نهایت تبدیل #1 #2 #3 #4 (در همان ترتیب) معادل تبدیل #4 #3 #2 #1 است. بنابراین داریم:
4! = 4 × 3 × 2 × 1= 24
این تعداد روش برای بازآرایی جهتهای بالا انتخاب استفاده میشود و از این رو در نهایت داریم:
ما هم اینک آیتمهایی که باید تبدیل شوند را انتخاب کردیم (6!/10!) و آن را بر تعداد تکرارها (!6) تقسیم میکنیم.
رویکرد دوم: استفاده از فرمول ترکیب
در نیمههای توضیح فوق احتمالاً متوجه شدید که ما مشغول استفاده از فرمول ترکیب هستیم:
C(10,4)=210
وقتی بدانید که ترتیب اهمیتی ندارد، میتوانید از این میانبر استفاده کنید. با این حال برخی اوقات از همان ابتدا مطمئن نیستیم که به یک ترکیب نیاز داریم یا جایگشت. وقتی گفته میشود «فقط از (C(10,4 استفاده کنید» با این که گفته صحیحی است؛ اما به عنوان ابزار آموزشی چندان مفید محسوب نمیشود.
رویکرد سوم: آغاز متفاوت
این رویکرد نیز متفاوت است چون در آن به جای این که اجازه دهیم جاهای r و u با هم عوض شوند، حرکتهای رو به راست را به صورت r1 تا r6 و حرکتهای رو به بالا را به صورت u1 تا u4 نامگذاری میکنیم. بدین ترتیب باید پرسید چند روش برای چیدمان آیتمهای دهگانه وجود دارد؟
این سؤال سادهای است: !10 = 3628800 که عدد بزرگی است. ما برای گزینه اول 10 انتخاب داریم، برای گزینه دوم 9 انتخاب و همین طور تا آخر تا این که برای گزینه نهم دو انتخاب و برای گزینه دهم 1 انتخاب وجود دارد.
البته میدانیم که r1 r2 u1 u2 همان مسیر r2 u1 u2 r1 است. ما میتوانیم r ها و u ها را به صورت تصادفی در زیرگروههای خودشان بُر بزنیم و مسیر همچنان یکسان باقی بماند.
- به چند روش میتوان 10 آیتم را بُر زد؟ 10× = 3628800
- به چند روش میتوان 6 r را بُر زد؟ 6! = 720
- به چند روش میتوان 4 u را بُر زد؟ 4! = 24.
بنابراین کار خود را با تعداد احتمالها آغاز میکنیم و آنها را بر حالتهایی که میتوانیم r ها (720) و u ها (24) را بُر بزنیم تقسیم میکنیم:
10!/6!/4! = 10!/(6!.4!) = 210
بسیار جالب است چون میبینیم که مجموعه ضرب و تقسیمها با گروهبندی مجدد به روش متفاوتی صورت میگیرد.
فایده این بینش چیست؟
یکی از اهداف یادگیری ترکیب و جایگشت میتواند درک شیوه تبدیل باشد. آیا تا کنونی تصویر زیر را که ترکیبی از یک بانوی مسن و یک زن جوان است دیدهاید؟
آیا هر دو آنها را میبینید؟ آیا میتوانید بین هر دو سوئیچ کنید؟
بخشی از جذابیت معمای مسیر شبکهای به شیوه نگاه به آن با استفاده از استعارههای بصری و متنی است. هر چه ریاضیات بیشتری بلد باشید، مدلهای بیشتری در دسترس شما خواهد بود و میتوانید مسائل را به همدیگر تبدیل کنید.
البته این مسئله کارکرد عملی چندانی ندارد، بلکه بیشتر مشاهده این که فهرست مسیرها میتوانند با استفاده از حروف روی یک کاغذ نمایش یابند سرگرمکننده است.
در زبان ریاضیات مسائلی که به همدیگر تبدیل میشوند، ایزومورفیک (isomorphic) نامیده میشوند. از دید ریاضیاتی این مسائل میتوانند یکسان باشند؛ اما از منظر انسانی ممکن است یکی از مسائل آسانتر از دیگری باشد.
در مورد معمای شبکه ما از هر منظری که برایمان راحتتر است، برای حل مسئله کمک میگیریم:
بصریسازی شبکه: برای درک مسئله کلی و مشاهده مسیر منفرد
نوشتن مسیرها به صورت متنی: برای دیدن قالب کلی همه مسیرها و یک روش آسان برای شمارش آنها
این نکته اصلی این مقاله است: استفاده از یک مدل برای درک مسئله، و بهرهگیری از مدلی دیگر برای حل آن امری کاملاً رایج است. هر گاه فکر کنیم که هر مسئلهای تنها یک راهحل دارد، ریاضیات دشوار خواهد شد.
نسخههای مختلف و بسطها
اینک که مدلهای ذهنی خود را ساختهایم، میتوانیم با مسائل دشوارتر نیز مواجه شویم.
تصور کنید شبکه در واقع دارای 3 بُعد باشد، در این حالت ترسیم آن دشوارتر است؛ اما بازنمایی متنی همچنان جواب میدهد. فرض کنید یک مکعب داریم (ابعاد x، y و z) که هر ضلع آن 5 واحد طول دارد. چند مسیر از یک گوشه به گوشه دیگر وجود دارد.
در این مورد میتوانیم از رویکرد دوم کمک بگیریم که در آن همه احتمالهای مختلف فهرستبندی میشوند. فرض کنید هر حرکت را به طرز متفاوتی برچسبگذاری کنیم. ما 5 حرکت با برچسبهای متفاوت برای هر نوع داریم (x1-x5, y1-y5, z1-z5). میتوانیم اینها را به!15 روش بچینیم. این عدد بسیار بزرگی است و معادل 1.3 تریلیون است. اما نباید فراموش کنیم که باید تکرارها را در هر بعد حذف کنیم.
!5 روش برای بازآرایی حرکتهای یکسان در هر بعد وجود دارد و بنابراین آنها را تقسیم میکنیم:
15!/5!/5!/5! = 15!/(5! . 5! . 5!) = 756756
البته این تعداد مسیر نیز برای یک مکعب کوچک، عدد بزرگی محسوب میشود. شاید در ابتدا که با مثال اول این نوشته مواجه شدید در محاسبه پاسخ دچار دشواری بودید؛ اما اینک میتوانیم عددی به این بزرگی را محاسبه کنیم. ما با استفاده از همین رویکرد میتوانیم حتی ابعاد چهار، پنج یا حتی 10 گانه را نیز بی هیچ مشکلی حل کنیم.
تعریف کردن مسئله
در این بخش جنبه جالبی از این قضیه را بیان میکنیم. به جای تغییر دادن شیوه نگریستن به راهحل، چرا صورت مسئله را تغییر ندهیم؟ چه چیز دیگری میتواند نشان دهنده یک مسئله شبکهای باشد؟
- مجموعه درهای تله: فرض کنید مجموعهای از درهای تله داریم که به صورت 4 × 6 هستند، یعنی 6 ردیف چهارتایی که تنها یک راه خروج واقعی وجود دارد و بقیه درها رو به دهانه یک آتشفشان باز میشوند. احتمال این که یک نفر به صورت تصادفی از این مهلکه بگریزد چه مقدار است؟ از محاسبات قبلی میدانیم که 4×6 = 210 حالت وجود دارد. اگر شبکه 12×12 بود، پاسخ به صورت زیر خواهد بود. یعنی 2.7 میلیون مسیر با تنها 1 مسیر صحیح وجود خواهد داشت:
24!/12!12! = 2.7 m
- ترتیب عملیاتها: فرض کنید 10 مجموعه تمرین بدنسازی دارید که باید انجام دهید. 4 تمرین یکسان پا و 6 تمرین یکسان بازو. چه تعداد روال متفاوت میتوانید با استفاده از این تمرینها انتخاب کنید؟ این محاسبه دقیقاً معادل حرکت در مسیرهای روی شبکه است به جز این که نام محورها، به جای راست و بالا، پا و بازو هستند.
- حرکت تصادفی: فرض کنید میدانیم که شیئی حرکت تصادفی به سمت راست و بالا دارد. احتمال این که پس از 10 حرکت به نقطه مورد نظر ما برسد چه مقدار است؟ میدانیم که 2^10 = 1024 روش برای حرکت به سمت راست یا بالا وجود دارد. 210 حرکت نیز برای رسیدن به مقصد دقیق ما متصور است. از این رو میتوان انتظار داشت که شانس ما برابر با 210/ 1024 یعنی 20.5% باشد.
سخن پایانی
معماها روشی جالب برای یادگیری مدلهای ذهنی هستند و درک شما از مدلهایی که با آنها آشنا هستید را افزایش میدهند. با این که همه ما ممکن است با مفاهیم ترکیب و جایگشت آشنا باشیم؛ اما تا زمانی که به صورت بیپرده در مسائل مختلف با آنها مواجه نشدیم، نمیتوانیم آنها را به راحتی به کار ببریم.
اگر این نوشته مورد توجه شما واقع شده است، پیشنهاد میکنیم موارد زیر را نیز بررسی کنید:
- جایگشت و ترکیب — به زبان ساده
- مجموعه آموزشهای ریاضی
- آموزش ساختمان گسسته با رویکرد حل مسأله
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- آموزش تئوری احتمالات
==




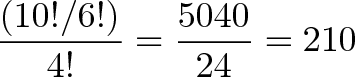













سپاس از توضیحات خوبتان
سلام
از مربع پايين سمت چپ تا مربع بالا سمت راست، مگر 9 خانه طي نميشود ؟
عالیی ممنونم واقعاا