مساحت مثلث با سینوس چگونه محاسبه می شود؟ + حل تمرین و جدول فرمول ها
مساحت مثلث با سینوس با استفاده از روابط مثلثاتی و قانون سینوسها محاسبه میشود. شناخته شدهترین رابطه تعیین مساحت مثلث با سینوس، ضرب اندازههای هر دو ضلع مثلث در سینوس زاویه بین آنها است. در این مقاله، فرمولهای محاسبه مساحت مثلث با سینوس در حالتهای مختلف (دو ضلع و زاویه بین، دو زاویه و ضلع بین، دو ضلع و زاویه غیر بین) را به همراه مثال آموزش میدهیم. در انتها نیز، جدولی را برای مرور این فرمولها ارائه میکنیم.
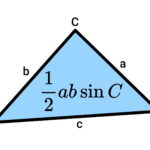
مثلث چیست؟
مثلث (به انگلیسی Triangle)، یکی از شناختهشدهترین و پرکاربردترین شکلهای هندسی چند ضلعی است که به عنوان مبنای علم مثلثات در نظر گرفته میشود. این چند ضلعی، سه ضلع و سه راس دارد.
مساحت مثلث چیست؟
مساحت مثلث، کمیتی است که اندازه سطح داخل ضلعهای مثلث را نمایش میدهد.
در تصویر زیر، میزان محدوده هاشور خورده، همان مساحت مثلث است.
روش های محاسبه مساحت مثلث چه هستند؟
به طور کلی، سه روش کلی برای تعیین مساحت تمام انواع مثلثها وجود دارد. این سه روش عبارت هستند از:
- محاسبه مساحت مثلث با قاعده و ارتفاع
- محاسبه مساحت مثلث با سه ضلع (روش هرون)
- محاسبه مساحت مثلث با سینوس (روش مثلثاتی)
مساحت مثلث با سینوس چگونه بدست می آید ؟
مساحت مثلث با سینوس توسط روابط مثلثاتی مخصوص به دست میآید.
تصویر زیر، ضلعها و زوایای یک مثلث را با حروه انگلیسی نمایش میدهد.
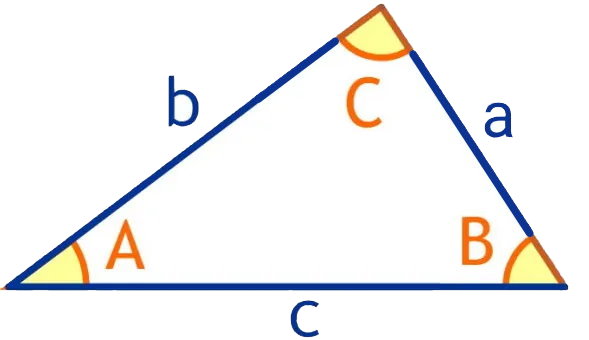
مثلث بالا از نظر مشخص بودن اندازه ضلعها و زوایا، به انواع زیر تقسیم میشود:
- مثلث ض ز ض: مثلث با دو ضلع و زاویه بین معلوم
- مثلث ز ض ز: مثلث با دو زاویه و ضلع بین معلوم
- مثلث ض ض ز: مثلث با دو ضلع و زاویه غیر بین معلوم
- مثلث ز ز ض: مثلث با دو زاویه و ضلع غیر بین معلوم
- مثلث ض ض ض: مثلث با سه ضلع معلوم (محاسبه مساحت این مثلث به روش هرون انجام میشود.)
- مثلث ز ز ز: مثلث با سه زاویه معلوم (محاسبه مساحت این مثلث غیر ممکن است.)
فرمول مساحت مثلث با سینوس چیست ؟
فرمول مساحت مثلث با سینوس به حالت مثلث بستگی دارد. مساحت مثلث با دو ضلع و زاویه بین توسط یکی از فرمولهای زیر محاسبه میشود:
- Area: مساحت
- a: طول ضلع BC
- b: طول ضلع AC
- c: طول ضلع AB
- A: زاویه راس A
- B: زاویه راس B
- C: زاویه راس C
فرمولهای محاسبه مساحت مثلث با دو زاویه و ضلع بین نیز عبارت هستند از:
نکته: در کسر فرمولهای بالا، امکان استفاده از زاویه سوم به جای جمع دو زاویه وجود دارد (مانند زوایه C به جای A+B). مقدار زاویه سوم از قانون جمع زوایای داخلی، به دست میآید.
فرمولهای مساحت مثلثهای ض ز ض و ز ض ز به عنوان فرمول مساحت مثلث با سینوس شناخته میشود. برای نوشتن این فرمولها، نیازی به تعیین پارامترهای اضافی یا نوشتن روابط دیگر نیست. با این وجود، شرایط برای مثلثهای دو ضلع و زاویه غیر بین یا دو زاویه و ضلع غیر بین کمی تفاوت دارد. در این مثلثها، ابتدا باید ضلعها و زوایای دیگر را با استفاده از قانون سینوسها به دست آورد. مطابق با این قانون داریم:
با داشتن دو ضلع و زاویه غیر بین یا دو زاویه و ضلع غیر بین، میتوان اندازههای دیگر را به کمک نسبتهای بالا تعیین کرد و مساحت مثلث را به دست آورد. در بخش بعدی، برای حالتهای مختلف، چند مثال ارائه و حل میکنیم.
مثال های محاسبه مساحت مثلث با سینوس
در این بخش، به حل سه مثال برای حالتهای مختلف محاسبه مساحت مثلث با سینوس (دو ضلع و زاویه بین، دو زاویه و ضلع بین و دو ضلع و زاویه غیر بین) میپردازیم.
مثال اول: مساحت مثلث با دو ضلع و زاویه بین
مثلثی با دو ضلع 10 سانتیمتر و 7 سانتیمتر را در نظر بگیرد. اگر زاویه بین این دو ضلع برابر 30 درجه باشد، مساحت مثلث چقدر خواهد بود؟
به دلیل مشخص بودن اندازه دو ضلع و زاویه بین، فرمول مساحت مثلث با سینوس برای حالت ض ز ض را مینویسیم:
- Area: مساحت
- a: اندازه یکی از ضلعها برابر 10 سانتیمتر
- b: اندازه ضلع دیگر برابر 7 سانتیمتر
- C: زاویه بین دو ضلع معلوم برابر 30 درجه
اندازههای معلوم را درون رابطه بالا قرار میدهیم:
سینوس زاویه 30 درجه برابر یک دوم است:
در نتیجه، مساحت مثلث برابر 17.5 سانتیمتر مربع است. برای آشنایی با مقادیر سینوس زوایای مهم و پرکاربرد، مطالعه مطلب «سینوس در ریاضی چیست و چگونه محاسبه میشود؟ — به زبان ساده و با مثال» را به شما پیشنهاد میکنیم.
مثال دوم: مساحت مثلث با دو زاویه و ضلع بین
مثلثی با دو زاویه 45 درجه را در نظر بگیرید. اگر طول ضلع بین این دو زاویه برابر 14 سانتیمتر باشد، مساحت مثلث چقدر خواهد بود؟
به دلیل مشخص بودن دو زاویه و ضلع بین آنها، از فرمول مساحت مثلث با سینوس برای حالت ز ض ز استفاده میکنیم:
- Area: مساحت
- c: اندازه ضلع بین دو زاویه معلوم برابر 14
- A: اندازه یکی از زوایای معلوم برابر 45 درجه
- B: اندازه دیگر زاویه معلوم برابر 45 درجه
اندازههای بالا را درون فرمول قرار میدهیم:
سینوس زاویه 45 درجه برابر و سینوس زاویه 90 درجه برابر 1 است:
در نتیجه، مساحت مثلث برابر 49 سانتیمتر مربع است. توجه داشته باشید که به دلیل وجود دو زاویه 45 درجه، زاویه سوم برابر 90 درجه خواهد بود. به عبارت دیگر، مثلث مورد سوال، از نوع قائم الزاویه بود. به علاوه، برابر بودن دو زاویه، متساوی الساقین بودن مثلث (برابر بودن اندازه ساقها) را نمایش میدهد. در صورت تمایل میتوانید با در نظر گرفتن این نکات و استفاده از قضیه فیثاغورس، مسئله حل کنید. در هر صورت، جواب مسئله یکسان خواهد بود.
مثال سوم: مساحت مثلث با دو ضلع و زاویه غیر بین
مساحت مثلث نمایش داده شده در تصویر زیر را به دست بیاورید. از اطلاعات زیر برای حل مسئله استفاده کنید:
- sin 31°≅0.51
- sin 57°≅0.83
- sin 92°≅1
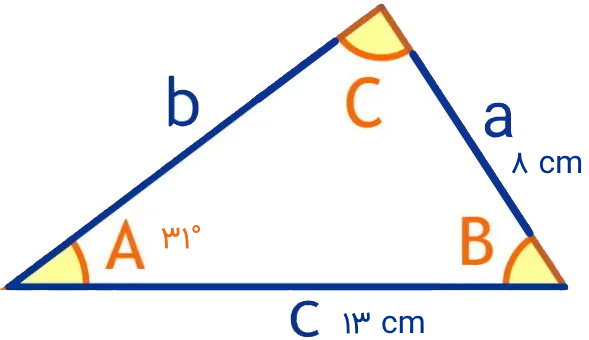
در حالت دو ضلع و زاویه بین، اولین مرحله، نوشتن قانون سینوسها و تعیین پارامترهای مجهول است:
بر اساس تصویر بالا، داریم:
- a=8
- c=13
- A=31°
این مقادیر را در تناسب بالا قرار میدهیم:
با توجه به اطلاعات مسئله و مقدار به دست آمده از محاسبات بالا، زاویه C برابر 57 درجه خواهد بود. این زاویه نیز مانند زاویه A، در بین ضلعهای a و c قرار ندارد. با این وجود، بر اساس قانون جمع زوایای داخلی، این زاویه به محاسبه زاویه B کمک میکند:
زاویه B برابر 92 درجه است. اکنون تمام زوایای مثلث معلوم هستند. در صورت تمایل میتوان ضلع b را نیز با استفاده از قانون سینوسها محاسبه کرد. البته برای محاسبه مساحت مثلث، داشتن ضلعهای a و c با زاویه بین آنها (B) کفایت میکند. به همین دلیل، فرمول مساحت مثلث برای این حالت (ض ز ض) را مینویسیم:
اندازههای موجود و به دست آمده را درون فرمول بالا قرار میدهیم:
مساحت مثلث برابر 52 سانتیمتر مربع است.
جدول فرمول های مساحت مثلث با سینوس
فرمهای مختلف نوشتن فرمول مساحت مثلث با سینوس بر اساس اندازهای مشخص در جدول زیر آورده شدهاند.
| حالت مثلث | اندازههای معلوم | فرمول مساحت مثلث با سینوس |
| ضزض | ضلع a، ضلع b و زاویه C در میان آنها |
|
| ضلع a، ضلع c و زاویه B در میان آنها |
| |
| ضلع b، ضلع c و زاویه A در میان آنها | ||
| زضز | زاویه A، زاویه B و ضلع c میان آنها |
|
| زاویه A، زاویه C و ضلع b میان آنها |
| |
| زاویه B، زاویه C و ضلع a میان آنها | ||
| ضضز | هر ترکیبی از اندازههای ضلع و زاویه | قانون سینوسها، اصل جمع زوایای داخلی و یکی از فرمولهای بالا |
| ززض |
سوالات متداول محاسبه مساحت با سینوس
در این بخش، به برخی از سوالات پرتکرار در زمینه تعیین مساحت مثلثها به کمک روابط مثلثاتی پاسخ میدهیم.
از چه فرمولی برای محاسبه مساحت مثلث با سینوس استفاده میشود؟
شناخته شدهترین فرمول برای محاسبه مساحت مثلث با روابط مثلثاتی، ضرب دو ضلع در سینوس زاویه بین آنها تقسیم بر دو است. قانون سینوسها نیز به طور گسترده برای حالتهای مختلف مورد استفاده قرار میگیرد.
اندازه های مورد نیاز برای محاسبه مساحت مثلث با سینوس چه هستند؟
به منظور محاسبه مساحت مثلث با سینوس، میتوان از اندازه دو ضلع و زاویه بین (ض ز ض)، دو زاویه و ضلع بین (ز ض ز)، دو ضلع و زاویه غیر بین (ض ض ز) و دو زاویه و ضلع غیر بین (ز ز ض) استفاده کرد.
روابط مثلثاتی برای محاسبه مساحت کدام مثلث کاربرد دارند؟
روابط مثلثاتی برای محاسبه تمام انواع مثلثها با اندازه حداقل یک ضلع و دو زاویه مشخص یا حداقل دو زاویه و یک ضلع مشخص کاربرد دارد.
آیا امکان محاسبه مساحت مثلث با سه زاویه معلوم وجود دارد؟
امکان استفاده از روابط مثلثاتی برای محاسبه مثلثی با سه زاویه معلوم (ز ز ز) وجود ندارد. معلوم بودن سه زاویه، فقط برای تعیین شکل کلی و نوع مثلث قابل استفاده است. برای تعیین مساحت، باید اندازه حداقل یک ضلع معلوم باشد.
آزمون مساحت مثلث با سینوس
۱. در کدام یک از حالتهای زیر میتوان بهطور مستقیم از فرمول مساحت مثلث بر پایه سینوس استفاده کرد؟
سه زاویه معلوم (ز ز ز)
سه ضلع معلوم (ض ض ض)
دو ضلع و زاویه بین (ض ز ض)
دو زاویه و ضلع غیر بین (ز ز ض)
وقتی دو ضلع و زاویه بین آنها معلوم باشند، یعنی حالت «دو ضلع و زاویه بین (ض ز ض)» وجود داشته باشد، میتوان مستقیما فرمول مساحت مثلث با سینوس را بهکار برد. در حالت «سه ضلع معلوم» و «سه زاویه معلوم»، ابتدا باید به کمک روشهای دیگر دادههای مناسب را بیابیم یا قادر به محاسبه مساحت نیستیم. حالت «دو زاویه و ضلع غیر بین» نیز نیاز به محاسبات تکمیلی دارد و استفاده مستقیم از فرمول سینوس ممکن نیست.
۲. در چه شرایطی استفاده مستقیم از فرمول سینوس برای محاسبه مساحت مثلث ممکن است؟
وقتی دو ضلع و زاویه بین آنها معلوم باشد، میتوان فرمول سینوس را مستقیما استفاده کرد.
زمانی که فقط سه زاویه معلوم باشد، بلافاصله فرمول سینوس قابل استفاده است.
اگر دو ضلع و زاویه غیر بین معلوم باشد، همیشه بدون محاسبه جدید میشود مساحت را یافت.
در صورتی که یک ضلع و دو زاویه غیر بین داشته باشیم، نیازی به قانون سینوسها نیست.
هنگامی که اطلاعات شامل دو ضلع و زاویه بین آنها باشد، فرمول سینوس مستقیما قابل اجراست، زیرا همه پارامترهای لازم را داریم؛ اما مثلا اگر زاویه دادهشده بین دو ضلع نباشد یا فقط زوایا معلوم باشد، ابتدا باید به کمک قانون سینوسها یا جمع زوایا، مقدار ضلع یا زاویه مورد نیاز را بهدست آورد تا بتوان از فرمول استفاده کرد.
۳. اگر دو ضلع و زاویه غیر بین یک مثلث داده شده باشد، برای محاسبه مساحت با استفاده از سینوس چه باید کرد؟
صرفا زاویه اصلی را سه برابر کنیم و حاصل را به کار ببریم.
مستقیم دو ضلع داده شده را در سینوس زاویه غیر بین ضرب کنیم.
برای همه حالتها فقط از روش قاعده و ارتفاع استفاده کنیم.
ابتدا با قانون سینوسها ضلع سوم یا زاویه بین را پیدا کرده و سپس فرمول مساحت را بکار ببریم.
برای مساحت مثلث با دو ضلع و زاویه غیر بین، کافی نیست که مستقیما دو ضلع دادهشده را در سینوس زاویه غیر بین ضرب کنیم؛ بلکه باید ابتدا با قانون سینوسها زاویه بین دو ضلع یا ضلع سوم را بهدست آورد و سپس فرمول استاندارد مساحت را استفاده کنیم.
۴. اگر در یک مثلث فقط دو زاویه و یک ضلع معلوم باشد، بهترین روش برای محاسبه مساحت کدام است و علت انتخاب آن چیست؟
محاسبه با تناسب اضلاع بدون نیاز به زاویه
استفاده از فرمول قاعده و ارتفاع چون نیاز به ضلع و ارتفاع دارد.
کاربرد فرمول سینوس چون با دو زاویه و یک ضلع نتیجه میدهد.
بهکارگیری فرمول هرون چون با سه ضلع سازگار است.
وقتی دو زاویه و یک ضلع از یک مثلث معلوم باشد، فرمول سینوس مناسبترین راه است زیرا میتوان با کمک قانون سینوسها سایر ضلع یا زاویه لازم را بهدست آورد و سپس مساحت را محاسبه کرد. در فرمول قاعده و ارتفاع باید ارتفاع را دانست که با این دادهها ممکن نیست. فرمول هرون هم نیاز به هر سه ضلع دارد که اینجا فراهم نیست. روش تناسب اضلاع نیز برای مساحت کاربرد دقیق ندارد. پس «کاربرد فرمول سینوس چون با دو زاویه و یک ضلع نتیجه میدهد» بهترین گزینه است.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت مثلث — انواع مثلث و تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مثلث چیست ؟ — به زبان ساده
- مساحت انواع مثلث چگونه بدست می آید ؟ — حل تمرین و مثال های متنوع
- محیط مثلث چگونه بدست می آید؟ + فیلم آموزش رایگان
- چگونه مساحت مثلث را حساب کنیم؟ + تمرین با جواب
- محاسبه آنلاین مساحت مثلث — معرفی بهترین سایتها + مثال
- فرمول محیط مثلث چیست ؟ انواع فرمول ها + حل مثال های متنوع
- فرمول مساحت مثلث چیست ؟ — تمام فرمول ها + حل تمرین
- قاعده مثلث چیست و چگونه بدست می آید ؟ + تعریف و مثال
- ارتفاع مثلث چیست و چگونه رسم می شود ؟ — آموزش تصویری + حل تمرین
- محاسبه ارتفاع مثلث — تعریف، حل تمرین و مثال + جدول فرمول ها
- محیط مثلث مختلف الاضلاع — به زبان ساده + حل مثال های متنوع
- چگونه مساحت مثلث مختلف الاضلاع را حساب کنیم؟ + حل تمرین و مثال
- چگونه مساحت مثلث با سه ضلع معلوم را حساب کنیم؟ + حل تمرین و مثال
- فرمول هرون — به زبان ساده
- مساحت مثلث با سینوس چگونه محاسبه می شود ؟ + حل تمرین و جدول فرمول ها(همین مطلب)
- مثلث قائم الزاویه چیست ؟ — تعریف، ویژگی ها و محاسبات | به زبان ساده
- محیط مثلث قائم الزاویه – به زبان ساده + حل مثال های متنوع
- مساحت مثلث قائم الزاویه — حل تمرین و مثال های متنوع
- مثلث متساوی الساقین چیست ؟ | تعریف، ویژگی ها و محاسبات — به زبان ساده
- محیط مثلث متساوی الساقین — به زبان ساده و با حل مثال
- مساحت مثلث متساوی الساقین — حل تمرین و مثال های متنوع
- محیط مثلث متساوی الاضلاع چگونه بدست می آید؟ + حل مثال و تمرین
- مساحت مثلث متساوی الاضلاع — حل تمرین و مثال های متنوع













سلام یه سوالی داشتم مگر مساحت مثلث همیشه قاعده ضرب در ارتفاع تقسیم بر ۲ نبوده، پس این فرمول قاعده ضرب در ارتفاع تقسیم بر ۲ ضرب در سینوس B چه فرقی با اون داره؟
و اینکه از کجا بفهمیم سینوس کدوم زاویه رو باید در فرمول قرار دهیم؟