رسم توابع چند جمله ای — به زبان ساده

در مطالب گذشته وبلاگ فرادرس مفاهیم مربوط به مشتق و تابع را توضیح دادیم. از این رو در این مطلب قصد داریم تا نحوه رسم توابع چند جمله ای را توضیح دهیم. البته پیشنهاد میشود به منظور درک بهتر، مطالب مفاهیم تابع و مشتق را مطالعه فرمایید.
توابع چند جملهای
شکل کلی یک تابع چند جملهای به صورت زیر است.
نمودار چنین توابعی به صورت زیر هستند.
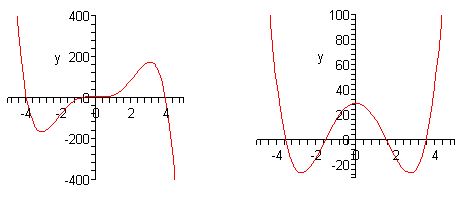
با توجه به دو نمودار فرضی ارائه شده در بالا توجه به دو نکته مهم در رسم توابع چند جملهای ضروری است.
- همانطور که از نمودارهای فوق نیز میتوان دید، نمودار توابع چند جملهای دارای ناپیوستگی، پرش یا تیزی نیستند.
- مشاهده میکنید که در دو نمودار فوق، در برخی از نقاط جهت نمودار از افزایشی به کاهشی یا بالعکس تغییر کرده است. برای یک چند جملهای از درجه n حداکثر میتوان n-1 مورد از این نقاط را یافت. بنابراین اگر ۵ مورد از تغییر روند افزایشی یا کاهشی در یک چند جملهای از درجه ۵ بیابید، تحلیل شما در مورد رسم نمودار اشتباه بوده چرا که در بیشترین حالت ۴ مورد از این تغییرات میتواند وجود داشته باشد.
با توجه به دو نکته فوق، در ابتدا باید نقاط تقاطعِ نمودار با محور xها را بیابید. بدین منظور کافی است تا معادلهای به صورت زیر را حل کنید.
توجه داشته باشید که اگر ریشه x=r به صورت مضاعف یافته شود، به معنای آن است که در این نقطه نمودار مماس به محور xها است. در حالت کلی با حل معادله فوق یکی از دو حالت زیر پیش خواهد آمد. در ابتدا فرض کنید معادله مذکور حل شده و ریشه x=r به اندازه k بار تکرار میشود. در این صورت:
- اگر k، عددی فرد باشد در این صورت نمودار در این نقطه به محور x مماس بوده و از آن عبور میکند.
- اگر k، عددی زوج باشد در این صورت نمودار در این نقطه به محور x مماس بوده و آن را قطع نمیکند.
برای نمونه در ادامه نمودار دو تابع و نشان داده شده است. با صفر قرار دادن آنها داریم:
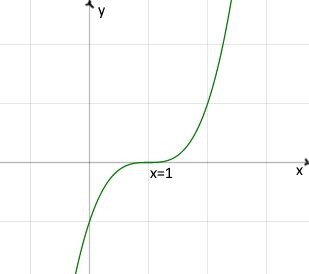
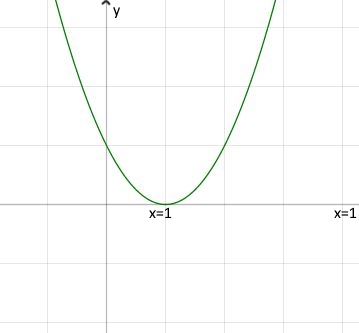
بنابراین ریشه x=1 در تابع ۳ بار و در تابع ۲ بار تکرار شده است. بنابراین نمودار آنها به صورت زیر خواهد بود.
مراحل رسم توابع چند جمله ای
به منظور رسم یک نمودار در حالت کلی مراحل زیر را به ترتیب انجام دهید:
- زوج یا فرد بودن تابع را مشخص کنید (البته در حالت کلی یک تابع میتواند نه زوج و نه فرد باشد).
- بررسی شکل تابع در بینهایت
- محل برخورد نمودار را با محورهای مختصات بیابید.
- مشتق اول تابع را یافته و نهایتا نقاط ماکزیمم و مینیمم تابع را بدست آورید.
- مشتق دوم تابع را یافته و با صفر قرار دادن آن، نقاط عطفِ تابع بدست خواهند آمد.
در ادامه مثالهایی ارائه شدهاند که مطالعه آنها را توصیه میکنیم.
مثال ۱
نمودار تابع را رسم کنید.
با توجه به شکل تابع میتوان دید، این رابطه نه زوج و نه فرد است. این تابع به ازای تمامی مقادیر اعداد حقیقی قابل تعریف است. از طرفی به ازای هیچ مقداری این تابع بینهایت نمیشود. بنابراین تابع مذکور دارای مجانبی افقی یا عمودی نخواهد بود. همچنین با میل دادن x به بینهایت داریم:
حد فوق نشان میدهد که در بینهایت، تابع دارای مجانبی مایل نیست. در مرحله بعد باید محل تقاطع تابع را با محور xها بدست آورد. بنابراین با صفر قرار دادن تابع، داریم:
با تجزیه تابع، ریشهها به صورت زیر بدست میآیند.
بنابراین تابع در ۳ نقطه محور xها را قطع میکند. با حل نامساوی زیر، بازههایی که در آنها تابع مثبت یا منفی است، بدست خواهد آمد.
در مرحله بعد، مشتق اول تابع به صورت زیر بدست میآید.
با صفر قرار دادن عبارت فوق، نقاط بحرانی به صورت زیر بدست میآیند.
زمانی که از نقطه عبور میکنیم، علامت مشتق از مثبت به منفی تغییر میکند. بنابراین این نقطه، ماکزیمم نسبی تابع است. با استدلالی مشابه میتوان دریافت که نقطه مینیمم نسبی تابع محسوب میشود. مقادیر ماکزیمم و مینیمم در این نقاط برابرند با:
$$\large \begin {align*} \require{cancel}<br /> { y \left ( { 1 – \frac { { \sqrt 3 } } { 3 } } \right) }<br /> & = { { \left( {1 – \frac { { \sqrt 3 } } { 3 } } \right)^3} }<br /> \\ & – {3{\left( {1 – \frac{{\sqrt 3 }}{3}} \right)^2} }<br /> \\ & + {2\left( {1 – \frac{{\sqrt 3 }}{3}} \right) }<br /> = {1 – 3 \cdot \frac{{\sqrt 3 }}{3} }<br /> \\ & + {3 \cdot {\left( {\frac{{\sqrt 3 }}{3}} \right)^2} }<br /> – {{\left( {\frac{{\sqrt 3 }}{3}} \right)^3} }<br /> \\ & – {3\left[ {1 – \frac{{2\sqrt 3 }}{3} }<br /> + {{{\left( {\frac{{\sqrt 3 }}{3}} \right)}^2}} \right] }<br /> + {2 – \frac{{2\sqrt 3 }}{3} }<br /> \\ & = {\cancel{1} – \sqrt 3 + \cancel{1} }<br /> – {\frac{{\sqrt 3 }}{9} – \cancel{3} }<br /> + {2\sqrt 3 – \cancel{1} + \cancel{2} }<br /> \\ & – {\frac{{2\sqrt 3 }}{3} }<br /> = {\frac{{9\sqrt 3 – \sqrt 3 – 6\sqrt 3 }}{9} }<br /> \\ & = {\frac{{2\sqrt 3 }}{9} \approx 0,38} \end {align*} $$
به همین صورت مقدار تابع در مینیمم برابر است با:
نهایتا مختصات ماکزیمم و مینیمم برابر هستند با:
در مرحله بعد مشتق دوم تابع به صورت زیر بدست میآید.
در مرحله بعد با صفر قرار دادن رابطه فوق داریم:
بنابراین در حالتی که باشد، خمیدگی تابع به سمت بالا و در حالتِ ، خمیدگی نمودار به سمت پایین است.
تحلیل علامت تابع و مشتقاتش در شکل زیر نشان داده شده است.
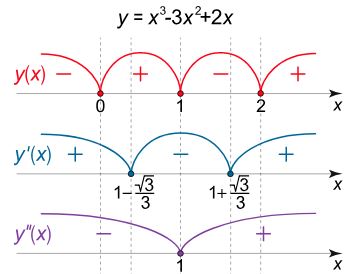
با توجه به چند جملهای بودن تابع، نقاط ماکزیمم، مینیمم و عطف، نمودار تابع به صورت زیر بدست میآید.
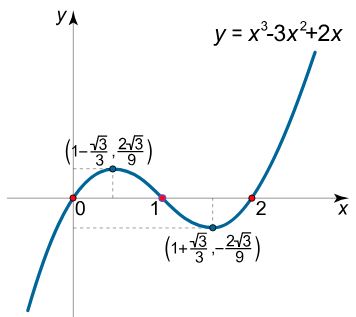
مثال ۲
نمودار تابع را ترسیم کنید.
این تابع به ازای تمامی مقادیر x قابل تعریف است، بنابراین دارای مجانب قائم نخواهد بود. همچنین به منظور بررسی رفتار تابع در بینهایت، باید حد زیر را بدست آورد.
بنابراین تابع در بینهایت دارای مجانبی مایل نیز نخواهد بود. در حقیقت شیب نمودار به بینهایت میل میکند. به منظور بدست آوردن تقاطع تابع با محورها داریم:
بنابراین تابع به ازای مقادیر x>1 مثبت بوده و به ازای مقادیر زیر منفی است.
مشتق تابع نیز برابر است با:
$$ \large \begin {align*} \require{cancel}<br /> {y ^ \prime \left( x \right) = {\left[ {{{\left( {x + 2} \right)}^2}\left( {x – 1} \right)} \right]^\prime } }<br /> & = {2\left( {x + 2} \right)\left( {x – 1} \right) + {\left( {x + 2} \right)^2} }<br /> \\ & = {\left( {x + 2} \right)\left( {2x – \cancel{2} + x + \cancel{2}} \right) }<br /> \\ & = {3x\left( {x + 2} \right) } \end {align*} $$
بنابراین نقاط اکسترمم برابرند با:
مقادیر تابع در نقاط فوق برابرند با:
مشتق دوم تابع نیز برابر است با:
بدیهی است که x=-1 مشتق دوم را صفر میکند. نهایتا علامت تابع و مشتقاتش به صورت زیر ارزیابی میشود.
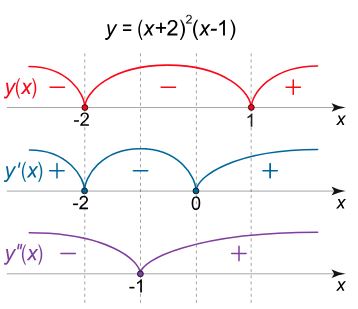
نهایتا شکل تابع به صورت زیر بدست میآید.
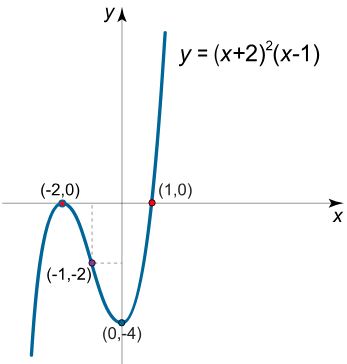
در این مطلب مراحل رسم تنها توابع چندجملهای توضیح داده شد. با این حال در مطالب آینده نحوه رسم دیگر توابع و همچنین مفاهیم مجانبها را با جزئیاتی بیشتر توضیح خواهیم داد.
در صورت علاقهمندی به مباحث مرتبط در زمینه ریاضی، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس دبیرستان و پیشدانشگاهی
- مجموعه آموزشهای ریاضی و فیزیک
- مفاهیم تابع – به زبان ساده
- مشتق - به زبان ساده
- ماکزیمم و مینیمم تابع - به زبان ساده
^^













عالی ممنون?
عالی ممنون