کاربرد فاکتورگیری در حل معادلات ریاضی – به زبان ساده

شاید تاکنون از خود پرسیده باشید که جبر به چه دردی می‌خورد؟ وقتی با متغیرهایی مانند x، y و z آشنا می‌شویم به نظر می‌رسد که قصد داریم عددی را مخفی کنیم:

5 = 3 + x

چه عددی می‌تواند در پس x مخفی شده باشد؟ در این مثال آن عدد 2 است.

به نظر می‌رسد که ما حتی در مواردی که اعداد را در اختیار نداریم نیز می‌توانیم از عملیات‌های حسابی استفاده کنیم. در ادامه ممکن است با این اعداد پنهان به روش‌های پیچیده‌ای مواجه شویم:

 x² + x = 6

بدیهی است که حل معادله فوق دشوارتر است. بنابراین می‌توانیم از اتحادهای مختلف یا فاکتورگیری استفاده کنیم. در این نوشته به مبحث فاکتورگیری و دلیل مفید بودن آن می‌پردازیم.

چندجمله‌ای‌ها

زمانی که یک چندجمله‌ای مانند  x² + x = 6 را می‌نویسیم. در سطح بالاتری با فاکتورگیری مواجه می‌شویم. در اینجا یک عدد مجهول x داریم که با خودش تعامل دارد (x * x = x²). سپس این عدد دوباره با خودش جمع شده است و نتیجه آن برابر با 6 است.

فیلم آموزش محاسبات عددی با متمتیکا Mathematica – مقدماتی در فرادرس

کلیک کنید

x² و 6 هر دو عدد محسوب می‌شوند؛ اما روش ایجاد آن‌ها متفاوت است:

• x² جزئی است که با خودش تعامل دارد
• x جزئی است که مستقل است
• 6 حالت مطلوبی است که می‌خواهیم کل سیستم به آن برسد.

بدین ترتیب می‌بینیم که پس از این که تعامل‌ها به پایان رسید باید به عدد 6 برسیم. چه عددی می‌تواند پشت x مخفی شده باشد تا این رابطه صحیح باشد؟

این سؤال تا حدودی پیچیده است. بنابراین برای حل کردن آن باید از روش پیچیده‌ای استفاده کنیم، یعنی آن را به سیستم متفاوتی تبدیل کنیم تا بتوانیم خطا را در عبارت اولیه دنبال کنیم.

سیستم اصلی ما به صورت x² + x و حالت مطلوب برابر با 6 است. یک سیستم جدید به صوت زیر است:

x² + x - 6

در این زمان ما همه تفاوت‌های بین سیستم اصلی و حالت مطلوب را بررسی می‌کنیم. کدام یک برای ما آسان‌تر است؟ زمانی که اختلافی نباشد:

x² + x - 6 = 0

و به همین دلیل است که همواره تلاش می‌کنیم چندجمله‌ای‌ها را برابر با صفر قرار دهیم. اگر یک سیستم و یک حالت مطلوب داشته باشیم، در این صورت می‌توانیم یک معادله جدید بنویسیم که تفاوت‌ها را پیگیری کند و تلاش کنیم تا آن را برابر با صفر قرار دهیم. توجه کنید که این وضعیت چیزی فراتر از عبارت «از هر دو طرف 6 را کم می‌کنیم» است و در واقع ما مشغول توصیف خطا هستیم.

اما واقعاً چگونه می‌توان خطا را صفر کرد؟ همچنان مشاهده می‌کنیم که اجزای x² ، x و 6 در عبارت ما جولان می‌دهند.

فاکتورگیری

فاکتورگیری کلید نجات است. اگر بخواهیم فاکتورگیری را به صورت شهودی تعریف کنیم باید بگوییم که فاکتورگیری به ما اجازه می‌دهد که یک سیستم پیچیده مانند x² + x - 6 را به صوت چند سیستم کوچک‌تر و مرتبط با هم درآوریم.

برای مثال فرض کنید یک کپه از میله‌های چوبی نامنظم داریم که آن‌ها را طوری روی هم می‌چینیم که شبیه یک کومه درآیند.

در مورد مثال خودمان ما دو میله داریم و می‌توانیم یک کومه دوبعدی به صورت زیر بسازیم:

/\

با برداشتن هر یک از این میله‌ها کل ساختار فرو می‌ریزد. بنابراین اگر بتوانیم سیستم خود را به صورت زیر بازنویسی بکنیم:

x² + x - 6 = 0

یعنی به صوت یک سری از ضرب‌ها در آید:

جزء A × جزء B = 0

در واقع توانسته‌ایم میله‌ها را به شکل کومه درآوریم. اگر جزء A یا جزء B صفر باشند، در این صورت ساختار فرو می‌ریزد و نتیجه کار صفر خواهد بود.

این توصیفی از طرز کار فاکتورگیری است. در فاکتورگیری، ما سیستم خطای خود را چنان بازآرایی می‌کنیم که به شکل یک کومه در آید، تا بتوانیم آن را خرد کنیم. بدین ترتیب می‌توانیم بدانیم که خطاهای ما چگونه از بین می‌رود و چگونه می‌توانیم سیستم خود را در وضعیت ایده‌آل قرار دهیم.

به خاطر داشته باشید که ما خطا را در سیستم خود تجزیه می‌کنیم و نه خود سیستم را.

به سوی فاکتورگیری

یادگیری روش فاکتورگیری از یک معادله فرایندی است که همان کومه را می‌سازد. در این مورد:

x² + x - 6 = (x + 3)(x - 2)

                = جزء A × جزء B

اگر x=-3 باشد در این صورت جزء A صفر می‌شود. اگر x=2 باشد جزء B فرو می‌ریزد. مقدار اولیه موجب از بین رفتن خطا می‌شود، یعنی سیستم اصلی ما شرایط مورد نظر ما را خواهد یافت:

وقتی x=-3 خطا از بین می‌رود و داریم:

(-3)² + -3 = 6

وقتی x=2 خطا از بین می‌رود و داریم:

2² + 2 = 6

جمع‌بندی

شاید برای شما سؤال باشد که در نهایت منظور از فاکتورگیری چیست. در کلاس‌های جبر، معادلات به طور مرسوم برابر با صفر قرار داده می‌شوند و ما دلیل این مسئله را نمی‌دانیم. اما آن چه در دنیای واقعی رخ می‌دهد به صورت زیر است:

• مدل خود را تعریف کنید: روش عملکرد سیستم خود را بنویسید (x² + x)
• حالت مطلوب را تعریف کنید: چه مقداری باید برابر 6 باشد؟
• خطا را تعریف کنید: خطا خود سیستم است یعنی خطا = واقعیت – مطلوب (6 - x² + x)
• از خطا فاکتور بگیرید: خطا را طوری بازنویسی کنید که اجزای در هم قفل شده باز شوند (x + 3)(x - 2)
• خطا را برابر با صفر قرار دهید: یکی از اجزا یا دیگری را برابر با صفر قرار دهید (x = -3,  یا x = 2)

زمانی که خطا =0 شود سیستم باید در حالت ایده‌آل باشد و بدین ترتیب معادله حل می‌شود. می‌بینیم که جبر در این مورد کاملاً راهگشا است.

• سیستم ما یک مسیر است. «حالت مطلوب» مقصد ماست. کدام مسیر ما را به مقصد می‌رساند؟
• سیستم ما میزان فروش محصولی خاص است. حالت مطلوب هدف درآمدی ما است. چه مقدار از فروش این میزان درآمد را تأمین می‌کند؟
• سیستم ما احتمال برد ما در بازی است. حالت مطلوب خروجی منصفانه 50-50 است. چه شرایطی این بازی منصفانه را تأمین می‌کند؟

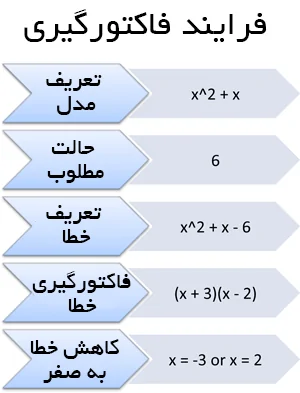
ایده مطابقت دادن یک سیستم با حالت مطلوبش تنها یکی از تفسیرهای ممکن برای مفید بودن فاکتورگیری است. در تصویر زیر می‌توانید فرایند فاکتورگیری را مشاهده کنید:

سخن پایانی

در این بخش برخی تأملات دیگر را ارائه کرده‌ایم:

ضرب را غالباً می‌توان به صورت عطف (AND) در نظر گرفت. یعنی جزء A باید وجود داشته باشد و جزء B نیز باید باشد. اگر هر کدام از شرط‌ها برقرار نباشند سیستم شکست می‌خورد.

• قضیه بنیادی جبر ثابت می‌کند که شما جزءهای زیادی را به عنوان بلندترین چندجمله‌ای دارید. اگر بزرگ‌ترین جمله شما به صورت x⁴ باشد در این صورت می‌توانید آن را به چهار جزء ضرب در هم تبدیل کنید. اگر یک سیستم x⁴ را به صورت حاصلضرب‌هایی بازنویسی کنید آیا نمی‌توان گفت که چهار جزء مستقل داریم که در هم ضرب شده‌اند؟ چون اگر سه جزء وجود داشتند هرگز نمی‌توانستیم سیستم x⁴ داشته باشیم و اگر 5 جزء بودند هم به سیستم x⁵ دست می‌یافتیم.
• فرمول درجه دوم را می‌توان به صورت سیستم متشکل از x² و x و یک ثابت تجزیه کرد. برای سیستم‌های پیچیده مانند x⁴ ، x³ و حتی  x⁵ نیز می‌توان اجزایشان را نوشت، اما تا حدودی پیچیده هستند.
• چنین سیستم‌هایی را می‌توان طوری طراحی کرد که غیرقابل فاکتورگیری (غیرقابل صفر شدن) شوند؛ اما چنین سیستم‌هایی را هم می‌توان با استفاده از اعداد موهومی حل کرد.

اگر این نوشته مورد توجه شما قرار گرفته است، پیشنهاد می‌کنیم موارد زیر را نیز ملاحظه کنید:

• مجموعه آموزش‌های ریاضیات
• چندجمله‌ای‌ها – به زبان ساده
• آموزش ریاضی پایه دانشگاهی
• تعریف های ابتدایی جبر – به زبان ساده
• آموزش حل معادلات جبری و ریشه یابی در متلب
• مجموعه آموزش های عمومی
• اتحاد و تجزیه در ریاضی — به زبان ساده

==