مقدار ویژه و بردار ویژه در علم داده — راهنمای تصویری

جبر خطی (Linear Algebra)، محاسبات برداری (Vectors) و ماتریسی (Matrix)، یکی از جنبههای ریاضی است که ذهن بشر را به ابعاد بزرگتر هدایت کرد. هندسه اقلیدسی برمبنای نقاط روی خط و حداکثر در یک صفحه دو بُعدی بنا شد ولی با گسترش مسئلههای پیش روی دانشمندان، تفکر و محاسبات روی ابعاد بزرگتر ضروری به نظر میرسید. بردارها و ماتریسها، ابزاری برای نشان دادن این ابعاد در جهان ریاضی هستند. ریاضیدانها سعی کردند مفاهیمی که در ریاضیات و هندسه تک بُعدی وجود داشت را به فضاهای جدید وارد کرده و تعمیمی بر روشهای حل مسائل گذشته ارائه کنند. مقدار ویژه و بردار ویژه (Eigen Value ،Eigen Vector) نیز از این قاعده مستثنی نیستند.
مقدار ویژه و بردار ویژه، از کاربردیترین مباحث جبر خطی است که در زمینههای مختلفی در علوم ریاضیات، فیزیک، مهندسی نظیر مکانیک، عمران، برق و… به کار میرود. برای مثال دینامیک سیالات محاسباتی، تئوری الاستیسیته، علم دادهها و یادگیری ماشین و سیستمهای کنترل از حوزههایی محسوب میشوند که مقدار ویژه و بردار ویژه در آنها بسیار به کار گرفته میشود.
برای آشنایی بیشتر با شیوه محاسبه مقدار ویژه و بردار ویژه یک ماتریس، به نوشتار بردار ویژه و مقدار ویژه — از صفر تا صد مراجعه کنید. همچنین خواندن کاربرد جبر خطی در علم دادهها و یادگیری ماشین — بخش دوم نیز خالی از لطف نیست.
مقدار ویژه و بردار ویژه در علم داده
هنگامی که پارامترهای «مدل پیشبینی» (Forecasting Model) را که براساس دادههای یک تصویر ، صدا یا متن، آموزش دیده است، برآورد میکنیم، میتوان مجموعهای از ویژگیها که اهمیت بیشتری در بیان پدیده تصادفی دارند را شناسایی کرده و مدل سادهتر و کاراتری ایجاد کرد. این عمل کاهش متغیرها یا کاهش بُعد نامیده میشود. به این ترتیب ابعاد یک مسئله پیچیده، کمتر شده و با استفاده از متغیرها و درنتیجه پارامترهای کمتری مدل ساخته و به کار گرفته میشود. از طرفی درک و تجسم دادهها با بیش از 3 بعد نیز دشوار است. در نتیجه، اغلب از یک تبدیل برای مقادیر ویژگیها استفاده میکنیم که باعث کاهش فضای متغیرها شود.
به این ترتیب میتوان گفت که مقدار ویژه و بردار ویژه امکان جمعبندی و خلاصهسازی را روی یک ماتریس بزرگ فراهم میکنند و میتوان عملیاتی که توسط این ماتریس بزرگ روی یک بردار صورت میگیرد را توسط مقادیر ویژه و بردار ویژه آن نیز به شکل سادهتر و کوتاهتر اجرا کرد. اغلب برای نمایش مختصات نقطهها یا ویژگیهای مشاهدات در علم داده از یک ماتریس استفاده میکنیم که سطرها بیانگر مشاهدات و ستونها نیز متغیرها یا ویژگیها را مشخص میکنند. بردار ویژه و مقدار ویژه، خصوصیات اصلی چنین ماتریسی را استخراج کرده و برای انجام محاسبات بعدی در اختیار قرار میدهند.
برای مثال تحلیل مولفههای اصلی (Principle Component Analysis) یا PCA از بردار و مقدار ویژه ماتریس پراکندگی (واریانس) استفاده کرده و به کمک تجزیه مقادیر تکین (SVD)، مولفههایی ایجاد میکند که میتوانند جایگزین ماتریس مشاهدات اصلی شود. به این ترتیب تعداد متغیرهای کمتری در مدلسازی به کار رفته و ساختار مدل، سادهتر خواهد شد. در عین حال میزان توصیفی از پراکندگی کل که توسط این مولفهها نشان داده میشود، تقریبا با پراکندگی کل براساس مشاهدات یکسان است. پس اطلاعاتی ناچیزی نادیده گرفته شد ولی در عوض سرعت و کارایی مدل افزایش یافته است.
قبل از اینکه در مورد مقدار ویژه و بردار ویژه بحث کنیم، الفبای محاسبات برمبنای ماتریس و بردارها را یادآوری میکنیم. به این منظور فهرستوار با بعضی از جنبههای محاسباتی ماتریسها و بردارها آشنا میشویم.
عملیات جبر خطی روی بردار و ماتریس
بردار ویژه، در حقیقت یک تبدیل خطی است. تصور کنید که یک نقطه که در صفحه مختصات دکارتی، توسط یک بردار نشان داده شده است، قرار است جابجا شده یا طول آن و شاید جهتش تغییر کند. تغییر دادن اندازه و حتی تغییر جهت یک بردار توسط جمع و ضرب یک ماتریس در آن بردار صورت میگیرد. بنابراین ابتدا به جمع و ضرب ماتریس و بردارها میپردازیم. برای مثال با ضرب یک ماتریس دوران میتوانید یک نقطه متقارن نسبت به محور افقی برای نقطه اولیه پیدا کنید.
جمع و ضرب ماتریسها
فرض کنید دو ماتریس به صورت زیر معرفی شدهاند. منظور از جمع این دو ماتریس، ماتریس جدیدی است که مولفههای نظیر به نظیر در آن با یکدیگر جمع شدهاند. واضح است برای جمع دو ماتریس باید ابعاد ماتریسها یکسان باشد. در مثال ما هر دو ماتریس هستند.
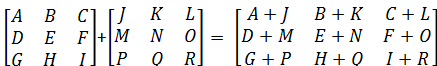
واضح است که تفاضل دو ماتریس نیز به همین ترتیب خواهد بود و کافی است که ماتریس اول را با قرینه ماتریس دوم جمع کنیم. پس باید ماتریس دوم را در مقدار ضرب کنیم. در ادامه نحوه ضرب یک ماتریس در یک مقدار (Scalar) را مشخص میکنیم. فرض کنید که یک عدد حقیقی (Scalar) باشد. ضرب این مقدار در ماتریس به صورت ضرب هر یک از درایههای آن در مقدار تعریف میشود. این کار در تصویر زیر نشان داده شده است.
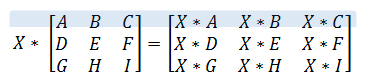
همچنین اگر قرار باشد دو ماتریس یا یک ماتریس در یک بردار ضرب شوند، باید به شکل خاصی منظم شده باشند. به این ترتیب اگر بخواهیم ضرب ماتریس را در بردار در نظر بگیریم، حتما باید تعداد ستونهای ماتریس با تعداد سطرهای بردار یکسان باشد تا عمل ضرب، امکانپذیر باشد. در ادامه تصویری مربوط به ضرب یک ماتریس را در یک بردار ستونی با سه سطر مشاهده میکنید. از آنجایی که بین ابعاد ماتریس و بردار رابطه گفته شده برقرار است، ضرب این دو، امکانپذیر است.
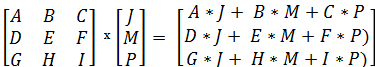
نکته: واضح است که براساس نظمی که بین تعداد ستون و سطر بردار باید برقرار باشد، عمل عکس، امکان پذیر نیست، یعنی نمیتوان بردار را در ماتریس مثال بالا ضرب کرد. برای ماتریسها نیز چنین وضعیتی باید برای تعداد سطرها و ستونهایشان برقرار باشد که در زیر به آن اشاره شده است.
ماتریس مربعی
اگر تعداد سطرها و ستونهای یک ماتریس یکسان و برابر با باشد، ماتریس را مربعی مینامند. اگر در یک ماتریس مربعی عناصر قطر اصلی برابر با یک و بقیه عناصر آن صفر باشند، آن را ماتریس یکه مینامیم. این ماتریس درست به مانند عدد ۱ در محاسبات ضرب عمل میکند و اگر در ماتریس یا برداری ضرب شود، تغییری در آن بوجود نمیآورد.
اثر ماتریس
یکی از خصوصیاتی جالب برای یک ماتریس مربعی، اثر یا Trace آن است. اگر عناصر روی قطر اصلی یک ماتریس را با یکدیگر جمع کنیم، اثر ماتریس را بدست آوردهایم. ماتریس مربعی را به صورت زیر در نظر بگیرید.
برای محاسبه اثر آن باید محاسبات را به شکل زیر انجام دهیم.
ماتریس منفرد
اگر بین ماتریس و بردار رابطه زیر برقرار باشد، ماتریس را منفرد (Singular) میگویند.
محاسبه مقدار ویژه و بردار ویژه
ماتریس مربعی که تعداد سطرهای (یا ستونهای) آن برابر با است، مقدار ویژه و بردار ویژه وجود دارد که مقدارهای ویژه به صورت با اندیسهای از ۱ تا نمایش داده میشوند. همچنین بردار ویژه چنین ماتریسی نیز با مشخص میشود. به این ترتیب بین ماتریس ، بردار و مقدار ویژه رابطه زیر برقرار است.
رابطه بین مقدار ویژه و بردار ویژه
این رابطه نشان میدهد که عمل یا تبدیلی که ماتریس روی بردار ویژهاش میگذارد، درست شبیه عملی است که مقدار ویژه روی آن بردار خواهد گذاشت. پس به نظر میرسد اختلاف این دو تبدیل باید برابر با صفر باشد.
این امر نشان میدهد که ماتریس باید یک ماتریس منفرد باشد.
چنین معادلهای با فرض معلوم بودن ماتریس ، تبدیل به یک دستگاه معادله و مجهول میشود که مجهولها، همان مقادیر ویژه هستند. اگر رابطه بالا را به کمک فاکتورگیری از بردار ویژه، سادهتر کنیم به رابطه زیر خواهیم رسید که به نظر یک دستگاه مجهولی میرسد.
رابطه ۱- معادله مشخصه
مشخص است که ماتریس به علت اینکه جمع ماتریسی مفهوم داشته باشد، اضافه شده است.
چنین معادلهای را ریاضیدان فرانسوی، «آگوستین کوشی» (Augustin Cauchy) «معادله مشخصه» (Characteristic Equation) و ریشههای آن را «ریشههای مشخصه» (Characteristic Root) نامید. بعدها در قرن بیستم، «هیلبرت» (David Hilbert) ریاضیدان آلمانی، اصطلاح «مقدار ویژه» (Eigenvalue) و «بردار ویژه» (Eigenvector) را از میان واژههای آلمانی انتخاب و به کار برد.
میتوان نشان داد که معادله مشخصه زمانی برای بردار غیر صفر دارای جواب است که دترمینان صفر باشد. پس باید رابطه زیر برای پیدا کردن ریشهها یا همان مقادیر ویژه برقرار باشد.
رابطه ۲
نکته: بین مقدارهای ویژه، رابطه خاصی برقرار است. اگر تا مقادیر ویژه ماتریس باشند، بین اثر این ماتریس و جمع مقادیر ویژه آن رابطه زیر برقرار است:
پس مجموع مقادیر ویژه با اثر ماتریس برابر است. بنابراین اگر برای یک ماتریس مربعی دو در دو به دنبال مقدار ویژه و بردار ویژه باشیم، کافی است که یکی از مقادیر ویژه را پیدا کرده و مسلما دومی از طریق تفاضل اثر ماتریس از مقدار ویژه اول، بدست خواهد آمد. همچنین برای پیدا کردن ریشههای رابطه ۲ برای یک ماتریس دو در دو کافی است معادله درجه ۲ زیر را حل کنیم.
که در آن اثر و نیز دترمینان ماتریس هستند. به این ترتیب نوشتن معادله ۲ و حل آن بسیار ساده خواهد شد. پس خواهیم داشت:
تفسیر و نمایش تبدیلها روی بردارها
براساس دو مثال سعی میکنیم نقش تبدیلات را روی بردارها و محورها نشان دهیم.
مثال ۱
تصویر زیر بردار را به صورت یک نقطه روی محور مختصات دکارتی، نشان میدهد. ماتریس نیز در اینجا نقش ماتریس انتقال یا همان را ایفا میکند. ستونهای این ماتریس نیز با دو مقدار و شکل گرفتهاند که در تصویر به صورت دو بردار دیده میشود.
فرض کنید ماتریس قرار است طول هر نقطه را دو برابر کرده و نقطه جدیدی ایجاد کند بدون آنکه عرض آن را تغییر دهد. با ضرب این ماتریس در بردار یا نقطهای با مختصات ، نقطه جدید حاصل میشود.
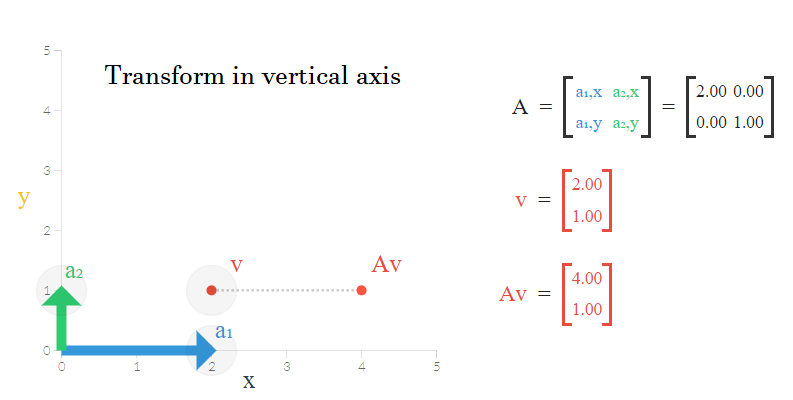
همانطور که گفته شد، از آنجایی که برای پیدا کردن مقدارهای ویژه، دترمینان ماتریس باید صفر باشد، مقادیر ویژه ماتریس برابر با و بدست خواهد آمد. واضح است که مجموع مقادیر ویژه با اثر ماتریس یکسان است.
حال برای پیدا کردن بردارهای ویژه متناظر با هر یک از مقادیر ویژه، باید معادله زیر را حل کنیم. ابتدا بردار ویژه برای را بدست میآوریم.
پس داریم:
که مترادف با برداری است که روی محور عمودی قرار دارد زیرا طول آن صفر است. این بردار را با نشان میدهیم. همین عمل را هم برای مقدار ویژه انجام میدهیم.
که این بردار نیز همان محور افقی را نشان میدهد زیرا مقدار عرض نقاط آن همگی صفر هستند. این بردار را با نشان میدهیم. مقدار ویژه و بردار ویژه در تصویر زیر قابل مشاهده هستند.
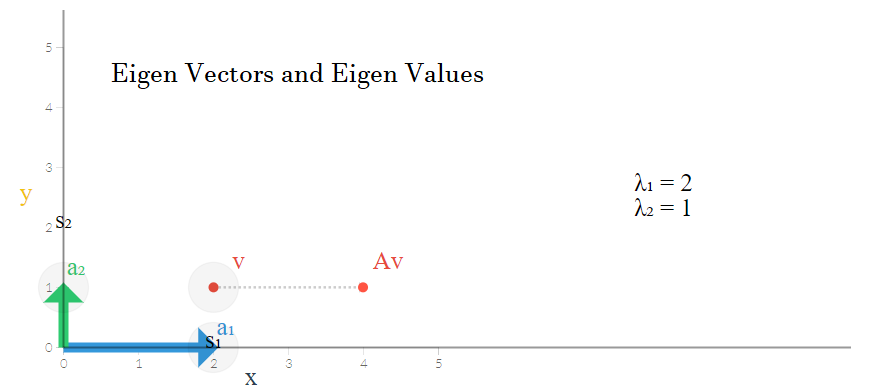
همانطور که مشخص شد، ماتریس تبدیل عجیبی انجام نداد و فقط مقادیر روی محور افقی را دو برابر کرد. بنابراین اینطور به نظر میرسد که محورهایی که بتوانند جهت تغییرات را نشان دهند، نسبت به محورهای مختصات تغییری نداشتهاند.
مثال ۲
این بار ترتیبی میدهیم که ماتریس یک تبدیل روی هر دو محور ایجاد کند. با توجه به فرضیات مثال ۱ تصویر زیر ترسیم شده است. بردار است و ماتریس تبدیل نیز به صورت زیر نوشته شده است.
واضح است که نتیجه یا حاصل ضرب ماتریس در بردار نیز به شکل زیر در خواهد آمد:
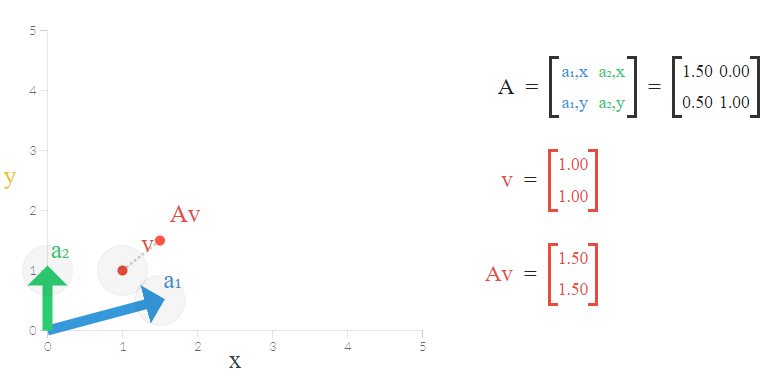
به نظر میرسد که تبدیل روی بردار باعث شده است که نقطه از مختصات به نقطه تبدیل شود. حال محاسبات مربوط به پیدا کردن مقادیر ویژه و بردار ویژه را اجرا میکنیم.
به منظور پیدا کردن مقدارهای ویژه، معادله مشخصه را ایجاد کرده و محاسبات را مطابق با مثال ۱ انجام میدهیم.
در اینجا مقدارهای ویژه بامقدارهای روی قطر اصلی ماتریس برابر هستند. پس شرطی که برای مقادیر ویژه و اثر ماتریس داشتیم، برآورده شده است.
با جایگذاری مقدار در رابطه ۱، بردار ویژه متناظر با به صورت در خواهد آمد.
از طرفی مقدار نیز نتیجه را نشان میدهد که همان محور عمودی است زیرا مقدار طول این نقاط (بردارها) همگی صفر است. پس محور و مطابق با آنچه در تصویر زیر قابل مشاهده است، ایجاد میشوند. بنابراین چنین محورهایی میتوانند یک فضای ویژه ایجاد کند.
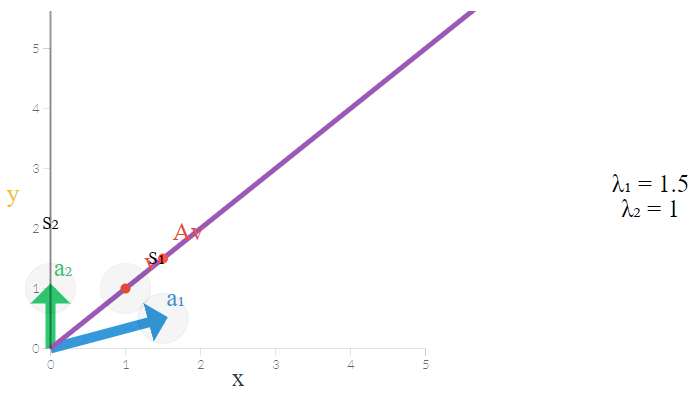
از آنجایی که رابطه ۱ برای بردارها و مقدارهای ویژهی ماتریس برقرار است، به نظر میرسد که باید نقطه و تبدیل یافته آن یعنی در یک راستا قرار گرفته باشند و این خط از مرکز مختصات نیز بگذرد.
نکته: واضح است که بردار اولیه که نقطه را نشان میداد در راستای بردار ویژه قرار گرفته است. یعنی میتوان یک خط راست بین نقطه صفر، نقطه تبدیل یافته یعنی و خود ایجاد کرد. این محور یا به کمک محور میتواند یک فضای ویژه ایجاد کند.
مثال ۳
این بار مثال میزنیم تا در آن فضای ویژه که توسط مقدار ویژه و بردار ویژه ساخته میشود، کاملا با مختصات دکارتی در هر بُعد متفاوت باشد. ماتریس تبدیل و بردار را به صورت زیر در نظر بگیرید.
تصویر زیر، این بردار و ماتریس تبدیل را به خوبی نمایش داده است.
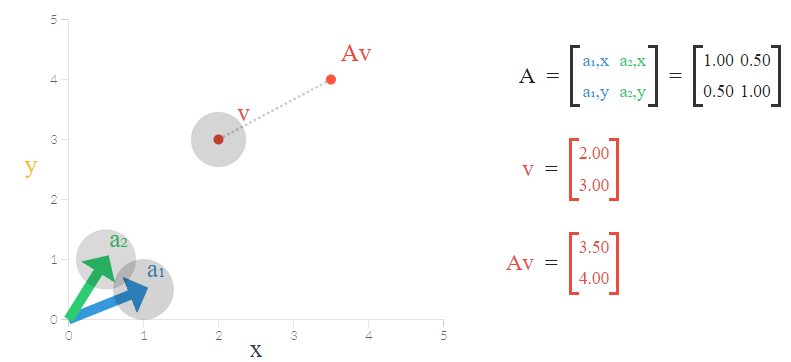
باز هم براساس رابطه ۱، معادله مشخصه را نوشته و مقادیر ویژه و بردار ویژه را محاسبه میکنیم.
البته مشخص است که برای حل معادله درجه ۲، از روش دلتا استفاده کردهایم. همانطور که دیده میشود مجموع مقادیر ویژه برابر است با ۳ که همان اثر ماتریس یا مجموع عناصر روی قطر اصلی ماتریس است. بنابراین فقط کافی بود که مقدار ویژه اول را پیدا میکردیم و به سادگی مقدار ویژه دوم بدست میآمد.
حال برای پیدا کردن بردارهای ویژه متناظر با هر یک از مقادیر ویژه، باید معادله زیر را حل کنیم. ابتدا بردار ویژه برای را بدست میآوریم.
پس داریم:
همچنین اگر باشد، آنگاه
که بردارها مترادف با محورهایی است که به ترتیب نیمساز ربع اول و دوم را ایجاد میکنند. پس با استفاده از این بردارها به عنوان محور مختصات، میتواند یک فضای ویژه ایجاد کرد که در تصویر زیر نشان داده شده است.
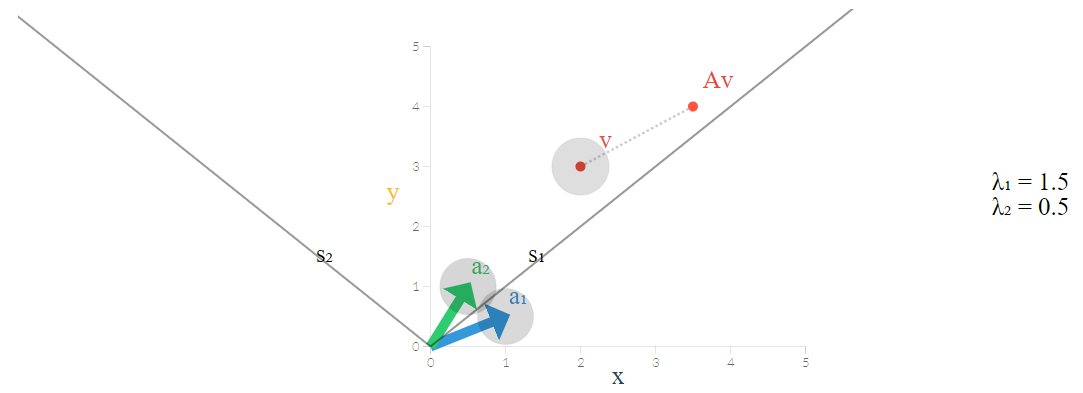
مختصات جدید یا فضای ویژه که توسط بردارهای ویژه تولید شده است، درست به مانند فضای مختصات دکارتی است با این تفاوت که ۴۵ درجه چرخش در جهت عکس عقربههای ساعت دارند.
نکته: اگر مقدار ویژه بزرگتر از ۱ باشد، تبدیل باعث دور شدن نقطه از مبدا مخصات خواهد شد و برعکس اگر مقدار ویژه کوچکتر از ۱ باشد، با هر بار اعمال تبدیل بر روی بردار، نقطه تبدیل یافته نسبت به نقطه اولیه به مرکز مختصات نزدیکتر میشود.
کاربردهای مقدار ویژه و بردار ویژه
فرض کنید طرف چپ رابطه ۱ که ارتباط بین بردار ویژه و همچنین ماتریس را نشان میداد دوباره و دوباره در ماتریس ضرب کنیم. آنچه حاصل میشود، است. فضای ویژه حاصل از بردارهای ویژه ماتریس ، نشان میدهند که آیا این دنباله از ضربها به سمت نقطه خواهند رفت یا از آن دور خواهند شد. به این ترتیب دنبالهای از تبدیلات یکسان را روی یک بردار اجرا کرده و میخواهیم تغییرات نقطه تبدیل یافته را دنبال کنیم. اگر این تغییرات به صفر برسد، به نظر میرسد که چنین سیستمی از تبدیلات دارای یک نقطه تعادل هستند که در آن دیگر تبدیل منجر به ایجاد نقطه جدیدی نخواهد شد.
به تصویر زیر دقت کنید. تبدیل نقطه یا بردار توسط ماتریس در هر بار ضرب ماتریس، دیده میشود. به نظر میرسد که تغییرات نقطههای تبدیل شده از یک مرحله به بعد ناچیز است.
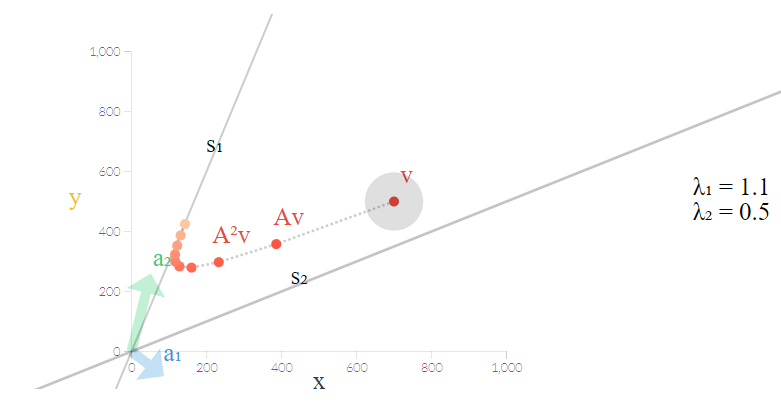
دنباله فیبوناچی
فرض کنید در آزمایشگاه بیولوژی، در حال کشت یا تکثیر یک تک سلولی هستید. یک تک سلولی بالغ (Adult) میتواند تکثیر پیدا کرده و یک تک سلول فرزند (Children) بوجود آورد. با رشد تک سلولی فرزند، او نیز تکثیر شده و تک سلولی دیگری تولید میکند. میخواهیم مشخص کنیم که در چه زمانی سیستم به تعادل میرسد و میزان جمعیت تک سلولیها (تعداد سلولهای بالغ و فرزند) در زمان چقدر خواهد بود.
نکته: البته اینجا فرض کردهایم که هر سلول بالغ در هر بار فقط یک فرزند تولید میکند، هر چند در واقعیت ممکن است چنین نباشد.
رابطه بین تعداد سلولهای بالغ و فرزندان در زمان با تعداد سلولهای بالغ در زمان به صورت زیر نوشته میشود.
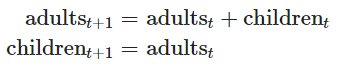
چنین دستگاهی را به صورت یک رابطه ماتریسی نیز میتوان نوشت. به معادله زیر توجه کنید.
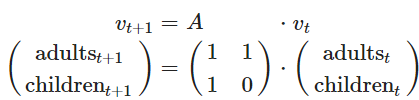
واضح است که ضرایب طرف راست معادلات بالا، همان مولفههای ماتریس هستند. مقدار ویژه برای چنین ماتریسی نیز برابر است با:
در نتیجه با هر بار اجرای تبدیل روی بردار، نقطه از مرکز مختصات دور خواهد شد. تصاویر زیر این موضوع را به خوبی نشان میدهند. محور افقی در این مختصات مربوط به تعداد فرزندان و محور عمودی نیز تک سلولیهای بالغ را شمارش میکند. دایرههای سیاه رنگ نیز فرزندان (Children) و دایرههای زرد رنگ نیز سلولهای بالغ (Adults) را در سمت چپ نشان میدهد. همانطور که مشاهده میشود برای توصیف رابطه بین فرزندان و والدین از مقدار ویژه و بردار ویژه استفاده شده است.
اولین تصویر برای زمانی است که فقط یک تک سلولی فرزند وجود دارد. این وضعیت را با بردار نشان دادهایم.
حال فرض کنید که این فرزند بالغ شده است و در گام بعدی فرزند آوری کرده است.چنین وضعیتی در تصویر زیر نشان داده شده است. واضح است که تعداد جمعیت در حالت قبلی (زمانی بالغ شدن تک سلولی در وضعیت ) افزایش نیافته است.
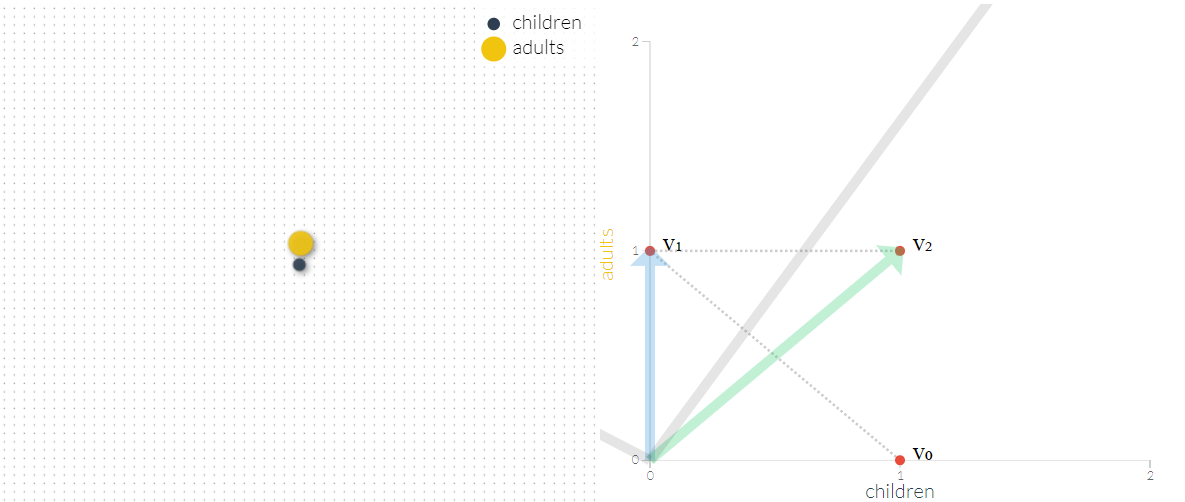
این گامها را ادامه میدهیم. تصاویر زیر این وضعیتها را برای دنباله جمعیتی تک سلولیها نشان میدهد.
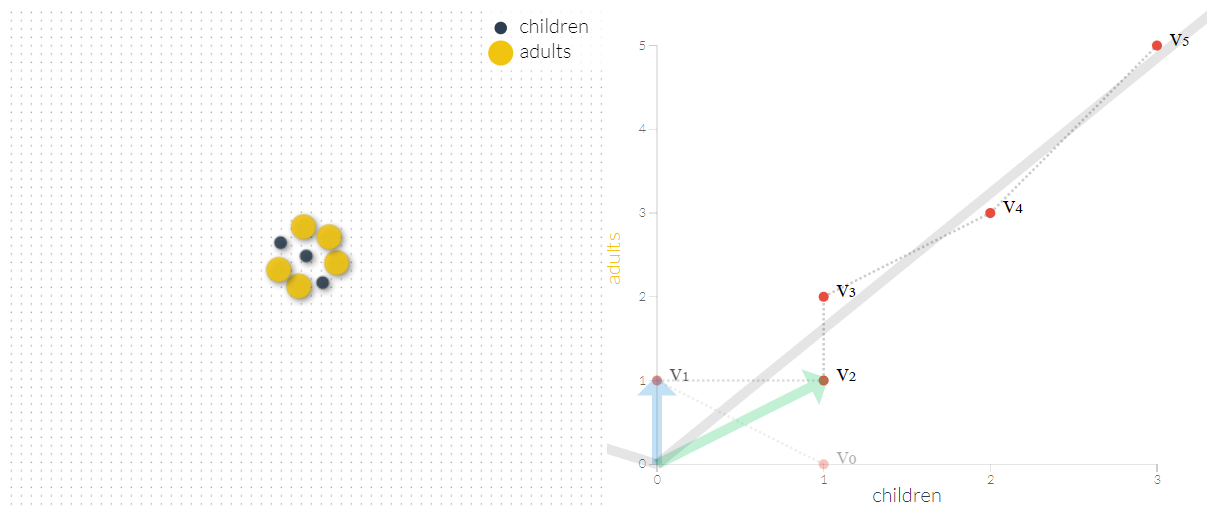
در گام هشتم تعداد جامعه تک سلولهای مطابق با تصویر زیر خواهد بود.
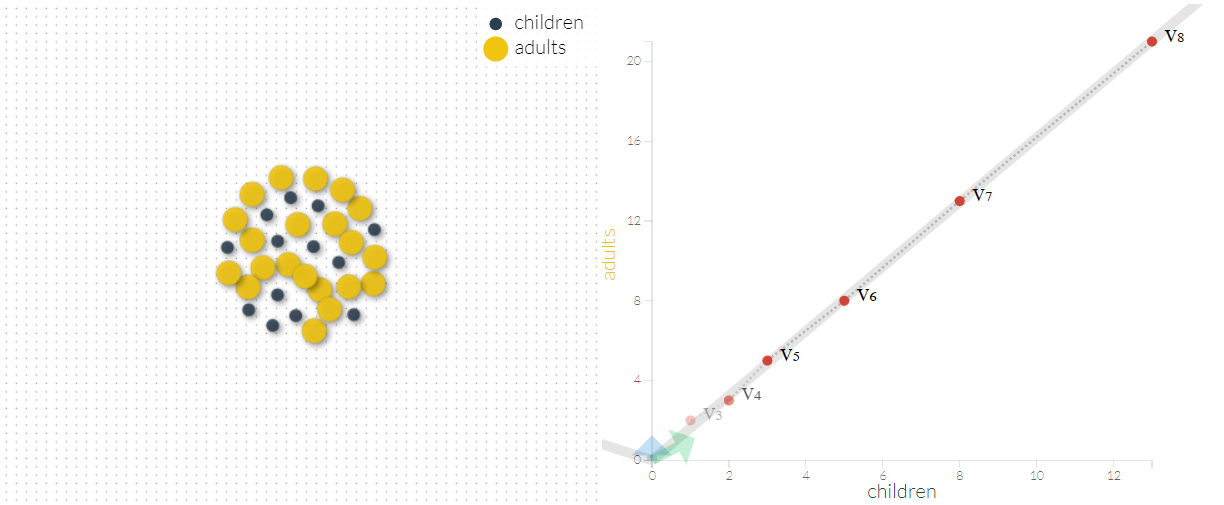
به نظر میرسد که این دنباله روی خط راست قرار خواهد گرفت به این معنی که نسبت هر مقدار جمعیت در گام با مقدار قبلی یعنی ثابت است. چنین دنبالهای را «دنباله فیبوناچی» (Fibonacci-sequence) میگویند که هر مقدار از جمع دو مقدار قبلی حاصل میشود. این مقادیر برای مثال ما به صورت زیر خواهد بود؛
به نظر میرسد که نسبت هر عدد با عدد قبلی همان عدد طلایی یعنی است. در این مسئله مشخص شد که محل تعادل، براساس مقدار ویژه و بردار ویژه ماتریس تبدیلات خواهد بود.
وضعیت پایدار جمعیتی
فرض کنید نقل و انتقالات شغلی فقط در بین دو شهر تهران و بابلسر رخ میدهد. در هر سال با احتمال یک نفر از ساکنین تهران به بابلسر نقل مکان میکند. شهر تهران و بابلسر را در فرمولها با اسامی و نشان میدهیم. در نتیجه به نظر میرسد که با احتمال فرد در تهران ساکن باقی میماند.
از طرف دیگر با احتمال ساکن بابلسر به تهران منتقل میشود. پس با احتمال همچنان ساکن بابلسر باقی خواهد ماند. اگر مولفه اول بردار جمعیت تهران و مولفه دوم نیز جمعیت بابلسر را نشان دهد، میتوان رابطه نقل و انتقالات را به صورت زیر نوشت.
ماتریسی مانند که مجموع هر ستون آن برابر با ۱ است در بحث «فرآیندهای تصادفی» (Stochastic Process) و فرآیند مارکوفی (Markov Process) به یک «ماتریس انتقال» (Transition Matrix) معروف است. چنین ماتریسی را گاهی ماتریس مارکوفی (Markov matrix) یا ماتریس احتمالی (Probability Matrix) مینامند. در این وضعیت، بزرگترین مقدار ویژه ماتریس انتقال است. پس سیستم میتواند به یک سیستم پایدار (Steady State) تبدیل شود. یعنی میتوان برداری مثل پیدا کرد که برای آن رابطه زیر برقرار باشد.
اگر این رابطه را به صورت احتمال در نظر بگیریم کاملا شبیه «امید ریاضی» (Mathematical Expectation) خواهد بود که بخصوص در بحث «مارتینگلها» (Martingales) به کار میرود. به این معنی که مقدار مورد انتظار برای این بردار در گام بعدی به صورت ترکیبی خطی از بردار قبلی نوشته میشود.
نکته: توجه داشته باشید تعادلی که در این رابطه بدست خواهد آمد، نه به جمعیت شهرها بستگی دارد و نه به احتمالات و .
به منظور نشان دادن این موضوع مقدار ویژه را برای ماتریس انتقال محاسبه میکنیم.
از آنجایی که بزرگترین مقدار ویژه برابر با ۱ است، شرط تعادل برقرار خواهد شد.
مقدار ویژه و بردار ویژه این وضعیتها در تصویر زیر مشاهده میشود. کاملا مشخص است که وضعیت پایدار یا تعادل روی یکی از محورهای حاصل از بردار ویژه رخ داده است.

خلاصه و نتیجهگیری
در این مطلب، با نحوه محاسبه مقدار ویژه و بردار ویژه آشنا شدیم و از جنبه تصویری نیز خصوصیات آنها را مورد بررسی قرار دادیم. در بسیاری از جنبههای علم داده، بخصوص در مدلسازی و استفاده از تکنیکهای کاهش بُعد، از مقدار ویژه و تجزیه مقادیر تکین (Singular Value Decomposition) یا SVD استفاده میشود. این تکنیکها در تحلیل تشخیصی فیشر، تحلیل مولفههای اصلی PCA و دیگر شیوههای آماری به کار گرفته میشوند.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس ریاضیات
- آموزش جبر خطی
- مجموعه آموزشهای داده کاوی و یادگیری ماشین
- مقدار ویژه تکراری — به زبان ساده
- دستگاه معادلات دیفرانسیل خطی — به زبان ساده
- تقلب نامه (Cheat Sheet) جبر خطی برای یادگیری ماشین — راهنمای سریع و کامل
^^













سلام تفاوت بردار ویژه وبردارpcaچیه