زنجیره و فرآیند مارکوف و مدل پنهان آن — به زبان ساده

همانطور که میدانید، فرآیندهای تصادفی، یکی از تئوریهای مدلسازی است که براساس آمار و احتمال شکل گرفته و برای تحلیل دادهها به کار میرود. در اکثر موارد فرآیندهای تصادفی برحسب زمان فهرستبندی یا «اندیسگذاری» (Index) شدهاند. «زنجیره مارکوف» (Markov Chain) یا «فرآیند مارکوف» (Markov Process)، مدلی برای نمایش دنبالهای از متغیرهای تصادفی است که در آن احتمال رویداد هر پیشامد فقط به پیشامد قبلی وابسته است. به این ترتیب احتمال رخداد پیشامدها در چنین مدلی فقط به زمان قبل وابسته بوده و بقیه پیشامدها در میزان احتمال دخالت نمیکنند. چنین وضعیتی را برای فرایند تصادفی گاهی خاصیت «عدم حافظه» (Memoryless) نیز مینامند. این مدل به افتخار ریاضیدان روسی «آندری مارکوف» (Andrey Markov) که در سالهای اولیه قرن بیستم در این زمینه دست به نوآوری زده بود، مدل مارکوف یا زنجیره مارکوف نامیده میشود.
از طرفی «مدل پنهان مارکوف» (Hidden Markov Model) یا به اختصار HMM یکی از مدلهای متداول برای دادههای موقتی یا مقطعی است. امروزه از این مدل برای بیان خصوصیات چنین دادههایی در علم داده استفاده میشود. به این منظور برای کسانی که میخواهند به عنوان متخصص در تحلیل دادهها (Data Scientist) فعالیت کنند، شناخت این مدل و خصوصیات آن ضروری است.

در این نوشتار به بررسی مدل مارکوف و مدل پنهان مارکوف پرداخته و با ذکر مثالهایی خصوصیات آنها را خواهیم شناخت. به منظور آشنایی با فرآیندهای تصادفی مارکوفی بهتر است مطلب فرایند تصادفی (Random Process) — مفاهیم اولیه و احتمال شرطی (Conditional Probability) — اصول و شیوه محاسبه را مطالعه کنید. همچنین خواندن نوشتار متغیر تصادفی، تابع احتمال و تابع توزیع احتمال نیز خالی از لطف نیست.
زنجیره و فرآیند مارکوف
قبل از اینکه به معرفی «زنجیره مارکوف» (Markov Chain) و «فرآیند مارکوف» (Markov Process) بپردازیم، باید اصطلاحاتی را در این زمینه معرفی کنیم. همانطور که گفته شد، در فرآیند مارکوف با دنبالهای از متغیرهای تصادفی سروکار داریم. بنابراین بهتر است ابتدا متغیر تصادفی، تکیهگاه و تابع احتمال و احتمال شرطی را تعریف کنیم.
متغیر تصادفی که به صورت $$X$$ نشان داده میشود، در حقیقت تابعی است از فضای پیشامد و مجموعهای از زیرمجموعههای اعداد حقیقی. این عبارت را به زبان ریاضیات به صورت زیر مینویسیم.
$$(\Omega,F,P) \xrightarrow {X} (R,B,P_x)$$
به این معنی که متغیر تصادفی $$X$$، اعضای فضای نمونه را به اعداد حقیقی، اعضای فضای پیشامد را به مجموعه بورل B از اعداد حقیقی و تابع احتمال مربوط به پیشامد را به احتمال متغیر تصادفی تبدیل میکند.
تکیهگاه متغیر تصادفی (Support)، مجموعه مقدارهایی است که متغیر تصادفی با احتمال مثبت اختیار میکند. معمولا برای نشان دادن تابع احتمال برای متغیر تصادفی $$X$$ کافی است، مقدار احتمال را برای تکیهگاه متغیر تصادفی مشخص کرده و برای بقیه نقاط در مجموعه اعداد حقیقی مقدار صفر را در نظر گرفت.
تابع احتمال، نیز بیانگر نحوه توزیع احتمال برای مقدارهای مختلف تکیهگاه متغیر تصادفی $$X$$ است. به بیان دیگر تابع احتمال را برای متغیر تصادفی گسسته میتوان مقدار احتمال برای پیشامد متناظر آن در نظر گرفت. در این حالت احتمال را به صورت $$p(x)=P(X=x)$$ نشان میدهند.
تابع احتمال توام، زمانی به کار میرود که لازم است مقدار احتمال را برای رخداد دو پیشامد همزمان بدست آورد. بنابراین اگر $$X$$ و $$Y$$ دو متغیر تصادفی باشند منظور از تابع احتمال توام، پیدا کردن احتمال رخداد پیشامدهای متناظر آنها به ازای همه مقادیر تکیهگاهشان است.
$$\large p(x,y)=P(X=x,Y=y)$$
تابع احتمال شرطی، زمانی به کار میرود که منظور پیدا کردن احتمال رخداد یکی از پیشامدها به شرط اطلاع از رخداد دیگری باشد. برای دو متغیر تصادفی $$X$$ و $$Y$$ احتمال شرطی در حالت گسسته به صورت زیر محاسبه میشود.
$$\large P(X=x\mid Y=y)=\dfrac{P(X=x,Y=y)}{P(Y=y)}$$
نکته: اگر متغیر تصادفی $$P(Y=y)=0$$ باشد، احتمال شرطی تعریف نخواهد شد.
اگر دو متغیر تصادفی $$X$$ و $$Y$$ مستقل باشند، رابطه زیر برحسب تابع احتمال شرطی یا تابع احتمال توام برقرار است.
$$ \large P(X=x\mid Y=y)=P(X=x), \;\;\;P(X=x,Y=y)=P(X=x)P(Y=y)$$
دنباله متغیرهای تصادفی نیز مجموعهای از متغیرهای تصادفی است که براساس اعداد طبیعی اندیسگذاری شدهاند. برای مثال $$X_t$$ بیانگر متغیر تصادفی در زمان یا وضعیت $$t$$ است. به این ترتیب دنباله متغیر تصادفی را به صورت $$\{X_t, t\in T\}$$ نشان میدهند. مجموعه $$T$$ که به آن مجموعه اندیس یا شاخص گفته میشود، ممکن است زمان یا مکان در نظر گرفته شود.
فرآیند تصادفی، یک دنباله از متغیرهای تصادفی را یک فرآیند تصادفی گویند اگر هر $$X(t)$$ به ازاء $$t$$ ثابت یک متغیر تصادفی باشد. اگر مجموعه $$t \in T$$ شامل مقادیر پیوسته باشد، دنباله یا فرآیند تصادفی را پیوسته میگویند. در صورتی که مقادیر مجموعه $$T$$ گسسته باشند، فرآیند را در دسته فرآیندهای گسسته قرار میدهند.
فضای حالت (State Space) مجموعه مقادیر ممکن برای فرآیند تصادفی $$\{X_t, t \in T\}$$ را گویند. میتوان به نوعی، فضای حالت را مرتبط با تکیهگاه متغیرهای تصادفی مربوط به فرآیند در نظر گرفت.
حال که با مفاهیم اولیه فرآیندهای تصادفی و متغیرهای تصادفی آشنا شدید، زنجیره مارکوف را معرفی کرده و خصوصیات آن را مورد بررسی قرار میدهیم.
زنجیره مارکوف و فرآیند مارکوف زمان-گسسته
دنبالهای از متغیرهای تصادفی $$X_1, X_2, \ldots$$ را که احتمال تغییر وضعیت از زمان $$t$$ به $$t+1$$ مستقل از وضعیتهای قبلی باشد را یک زنجیره مارکوف مینامند. این گزاره را به بیان متغیرهای تصادفی و تابع احتمال به صورت زیر نشان میدهیم.
$$\large \Pr(X_{t+1}=x\mid X_{1}=x_{1},X_{2}=x_{2},\ldots ,X_{n}=x_{t})=\Pr(X_{t+1}=x\mid X_{t}=x_{t})$$
نکته: واضح است که در محاسبه این احتمال شرطی باید $${\displaystyle \Pr(X_{1}=x_{1},\ldots ,X_{n}=x_{n})>0}$$ باشد در غیر اینصورت امکان محاسبه احتمال شرطی وجود ندارد. این احتمال به معنی طی کردن مسیر $${\displaystyle X_{1}=x_{1},\ldots ,X_{n}=x_{n})}$$) با احتمال مثبت در فرآیند تصادفی است. بنابراین در فرآیند تصادفی مارکوف، امکان رسیدن به نقطه $$X_t=x_t$$ از مسیر یاد شده وجود دارد.
بنابراین اگر یک فرآیند تصادفی که به صورت دنبالهای نامتناهی از متغیرهای تصادفی معرفی میشود، دارای خاصیت مارکوفی باشد، آن را فرآیند تصادفی مارکوف مینامند. اگر فضای حالت در این فرآیند متناهی بوده، فرآیند را متناهی و در غیر اینصورت نامتناهی مینامند. از آنجایی که ساختار یک فرآیند مارکوفی به خصوصیات زنجیره مارکوفی برمیگردد، در ادامه به بررسی بیشتر زنجیره مارکوف خواهیم پرداخت.
لازم به ذکر است که برای نمایش زنجیره مارکوفی معمولا از گراف جهتدار استفاده میشود. مقدار هر یک از یالهای این گراف، احتمال انتقال از یک راس به راس دیگر را نشان میدهد.
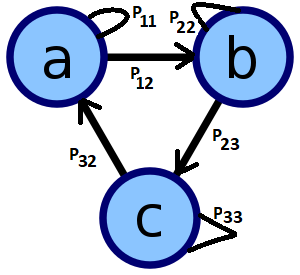
از آنجایی این گراف را میتوان به صورت یک ماتریس نمایش داد، ماتریس این زنجیره مارکوف نیز به صورت «ماتریس احتمال انتقال» (Transition Probability Matrix) قابل نمایش است. در این حالت عناصر ماتریس که به صورت $$p_{ij}$$ نوشته میشوند، احتمال انتقال از نقطه $$i$$ به $$j$$ را نشان میدهد. به این ترتیب ماتریس انتقال برای گراف بالا به ترتیب راسها (مقادیر مربوط به مجموعه فضای حالت) به صورت زیر قابل محاسبه است. واضح است که در اینجا فضای حالت دارای سه عنصر $$S=\{a,b,c\}$$ است.
$$ \large \begin{bmatrix}P_{11} &P_{12} & 0 \\ \large 0 & P_{22}& P_{23}\\\large P_{31}& 0&P_{33} \end{bmatrix}$$
البته در این ماتریس با توجه به اصول احتمال باید $$\sum_{j=1}^k p_{ij}=1$$ باشد. یعنی مجموع احتمالات هر سطر در ماتریس باید برابر با ۱ باشد.
بطور کلی در زنجیره مارکوف، احتمال اینکه از وضعیت $$i$$ به $$j$$ در گام $$n$$ام برسیم به صورت $$p^{(n)}_{ij}$$ نشان داده میشود. واضح است که به علت وجود خاصیت مارکوفی در زنجیره یا فرآیند مارکوفی داشته باشیم:
$$\large p_{ij}^{(n)}=\sum _{r\in S}p_{ir}^{(k)}p_{rj}^{(n-k)}, \forall k, 0<k < n$$
در حقیقت اگر بخواهیم احتمال گذر از یک نقطه و رسیدن به نقطهای دیگر از فضای حالت را در $$n$$ گام محاسبه کنیم باید ماتریس انتقال فرآیند را $$n$$ بار در خودش ضرب کنیم. برای مثال اگر قرار باشد احتمال اینکه در یک گام از نقطه $$i$$ به $$j$$ برسیم را محاسبه کنیم از احتمال شرطی زیر استفاده خواهیم کرد.
$$\large {\displaystyle p_{ij}=\Pr(X_{1}=j\mid X_{0}=i).\,}$$
انجام این کار در طی $$n$$ گام برای یک زنجیره مارکوف همگن-زمان، نیز به شکل زیر نوشته میشود.
$$\large {\displaystyle p^{(n)}_{ij}=\Pr(X_{k+n}=j\mid X_{k}=i).\,}$$
نکته: اگر رابطه زیر برای زنجیره مارکوف برقرار باشد آن را زنجیره مارکوف همگن-زمان (Time-Homogeneous Markov Chain) میگویند.
$$\large {\displaystyle \Pr(X_{t+1}=x|X_{t}=y)=\Pr(X_{t}=x|X_{t-1}=y)\,}$$
خصوصیات زنجیره مارکوف
در ادامه به بررسی بعضی از خصوصیات اصلی زنجیره مارکوف میپردازیم. البته بعضی از این خصوصیات وابسته به فرآیند تصادفی بودن این زنجیره است و بعضی نیز بطور انحصاری مربوط به زنجیره مارکوف هستند.
زنجیره مارکوف مرتبه $$k$$- با حافظه
همانطور که در ابتدای این متن اشاره شد، زنجیره مارکوف دارای خاصیت عدم حافظه است. اگر میزان حافظه زنجیره مارکوف به $$k$$ مرحله یا زمان قبل محدود شود، به آن زنجیره مارکوف با حافظه یا مرتبه $$k$$ گفته میشود. در این حالت رابطه زیر برقرار خواهد بود.
$$ \large {\displaystyle {\begin{aligned}{}&\Pr(X_{n}=x_{n}\mid X_{n-1}=x_{n-1},X_{n-2}=x_{n-2},\dots ,X_{1}=x_{1})\\=&\Pr(X_{n}=x_{n}\mid X_{n-1}=x_{n-1},X_{n-2}=x_{n-2},\dots ,X_{n-k}=x_{n-k}),\;\;{\text{ for }}n>k\end{aligned}}}$$
زنجیره مارکوف تقلیلناپذیر (Irreducible)
اگر رسیدن از هر نقطه به نقطه دیگر از فضای حالت با احتمال مثبت در زنجیره مارکوف میسر باشد، زنجیره را تقلیلناپذیر گویند. به بیان ریاضی میتوان تقلیلناپذیر بودن زنجیره مارکوف را به صورت زیر نشان داد.
$$\large {\displaystyle \Pr(X_{n_{ij}}=j\mid X_{0}=i)=p_{ij}^{(n_{ij})}>0.}$$
از این جهت نماد $$n_{ij}$$ را به کار بردهایم که نشان دهیم تعداد گامها ممکن است با توجه به نقطه آغاز و پایان میسر متفاوت و متغیر باشد. واضح است که $$n_{ij}$$ یک عدد طبیعی نامنفی است. ممکن است که این مقدار برابر با صفر باشد، که نشان دهنده احتمال درجا زدن برای زنجیره مارکوف است. به این ترتیب ممکن است در یک زنجیره مارکفی، با احتمال $$P_{11}$$ از نقطه یا وضعیت A به نقطه A درجا بزنیم.
زنجیره مارکوف تناوبی (Periodic)
اگر بتوان از وضعیت $$i$$ با گامهایی از مضرب $$k$$ مجدداً به نقطه $$i$$ رسید، زنجیره مارکوف را تناوبی گویند. در چنین حالتی مقدار تناوب زنجیره به شکل زیر محاسبه میشود.
$$\large k=\gcd\{n>0:\Pr(X_{n}=i\mid X_{0}=i)>0\}$$
توجه داشته باشید که در اینجا منظور از $$\gcd$$ همان بزرگترین مقسوم علیه مشترک است. گراف رسم شده در تصویر شماره ۱، یک زنجیره تناوبی با دوره تناوب ۱ است زیرا در گامهای $$\{1,3,4,5,6,\cdots,\}$$ میتوان از هر نقطه به همان نقطه رسید.
مدل پنهان مارکوف (Hidden Markov Model)
مدل پنهان مارکوف، درست به مانند یک فرآیند مارکوف است با این تفاوت که فضای حالت در این جا نامعلوم است. به این ترتیب نمیتوانیم تشخیص دهیم که وضعیت یا حالت با پیشامدها مطابقت دارد. ولی هر وضعیت با یک خروجی همراه است. به این ترتیب قرار است براساس خروجی حدس بزنیم که دنباله مقدارهای فرآیند (وضعیتها) چه بوده است. چنین مدلی بوسیله «لئونارد بام» ریاضیدان آمریکایی در سالهای حدود 1960 تحقیق و مورد بررسی قرار گرفت.
یکی از حوزههایی که در آن مدل پنهان مارکوف به کار گرفته شد، «تشخیص گفتار» (Speech Recognition) و دستخط بود که در سالهای ۱۹۷۰ ابداع و پیادهسازی شد. همچنین مدلهایی از نوع پنهان مارکف در سالهای اخیر در شاخههای مختلف بیوانفورماتیک نیز به کار گرفته شدهاند. برای روشنتر شدن نحوه عملکرد مدل پنهان مارکوف به یک مثال توجه کنید.
مثال
معمولا، با توجه به وضعیت آب و هوایی، لباسی که برای بیرون رفتن انتخاب میکنید، متفاوت است. به این ترتیب اگر از وضعیت هوا مطلع باشید، لباس مناسب را انتخاب خواهید کرد. در مدل پنهان مارکوف، خروجیها در طول زمان مشخص است و ما باید حدس بزنیم که چه توالی از متغیرها باعث ایجاد چنین خروجی شدهاند.
فرض کنید احتمال بارندگی در زمان $$t$$ به شرط آنکه در زمان $$t-1$$ بارندگی وجود داشته برابر با $$0.7$$ و برای هوای آفتابی در زمان $$t-1$$ برابر با $$0.3$$ باشد. به جدول زیر توجه کنید.
| $$P(Rain_t)$$ | $$Rain_{t-1}$$ |
| $$0.7$$ | بارانی (True) |
| $$0.3$$ | آفتابی (False) |
این وضعیت را هم در نظر بگیرید که در زمان صفر احتمال بارانی بودن $$P(Rain_0)=0.6$$ باشد. همچنین این را هم در نظر بگیرید که براساس شواهدی که در دو روز جمعآوری کردهایم توانستهایم متوجه بشویم که احتمال اینکه کسی چتر به همراه داشته باشد، به شرطی که هوا بارانی باشد برابر است با $$0.9$$ و احتمال داشتن چتر در زمانی که هوا بارانی نیست نیز برابر با $$0.2$$ است.
| $$Umbrella_t$$ | $$Rain_t$$ |
| $$P(Umbrella_t=True|Rain_t=True)=0.4$$ | بارانی (True) |
| $$P(Umbrella_t=True|Rain_t=False)=0.6$$ | آفتابی (False) |
از آنجایی که شما در خانه نشستهاید، هیچ اطلاعی از بارانی یا آفتابی بودن هوا ندارید. خوشبختانه هر روز دوست شما به خانهتان میآید و به شما سر میزند، با توجه به اینکه او در این دو روز چتر به همراه دارد یا خیر باید، تشخیص بدهید که هوای بیرون آفتابی یا بارانی است. به این ترتیب شما فقط از داشتن یا نداشتن چتر خبر دارید ولی باید وضعیت متغیر پنهان وضعیت آب و هوا (بارانی یا آفتابی بودن) را حدس بزنید.
براساس مدل احتمال شرطی احتمال توام دنبالهای از متغیرهای چتر و بارانی بودن را به صورت زیر بازنویسی میکنیم.
نکته: برای راحتی وضعیت باران را با R و چتر را با U نشان خواهیم داد.
$$\large P(R0,R_1,\cdots,R_t,U_0,U_1.\cdots,U_t)=\\ \large P(Rain_0)\prod_{i=1}^tP(R_i\mid R_{i-1})P(U_i\mid R_i)$$
مدلی را در نظر بگیرید که براساس دو روز بررسی وضعیت آب و هوایی و چتر ایجاد شده است. به این ترتیب احتمالات زیر را داریم.
$$\large P(R_t=T \mid R_{t-1}=T)=0.7$$
$$\large P(R_t=T \mid R_{t-1}=F)=0.3$$
$$\large P(R_t=F\mid R_{t-1}=T)=0.2$$
$$\large P(R_t=F\mid R_{t-1}=F)=0.8$$
$$\large P(R_0=T)=0.6,\;\;P(R_0=F)=0.4$$
از آنجایی که فرآیند دارای خاصیت مارکوفی است مشخص است که $$R_t$$ فقط به $$R_{t-1}$$ بستگی دارد. براساس شواهد جمعآوری شده از این سه روز نیز احتمالات زیر به دست آمده است.
$$\large P(U_t=F\mid R_t=F)=0.4$$
$$\large P(U_t=F\mid R_t=T)=0.3$$
$$\large P(U_t=T\mid R_t=T)=0.4$$
به کمک مدل پنهان مارکوف میتوانیم به سوالاتی نظیر سوال زیر پاسخ دهیم.
- براساس شواهدی که از همراه داشتن یا نداشتن چتر دراختیار داریم، احتمال اینکه دیروز بارانی و امروز آفتابی باشد چقدر است؟ در حقیقت میخواهیم بدانیم احتمال بارانی و آفتابی بودن (به عنوان وضعیتها نامعلوم و پنهان) را براساس وضعیت چتر بدست آوریم.
بر این اساس میخواهیم احتمال زیر را محاسبه کنیم.
$$\large P(R_t=F,R_{t-1}=T)=\\\large P(R_t=F,R_{t-1}=T , U_t=T , U_{t-1}=T)+P(R_t=F,R_{t-1}=T , U_t=T , U_{t-1}=F)+\\\large P(R_t=F,R_{t-1}=T , U_t=F , U_{t-1}=T)+\\\large P(R_t=F,R_{t-1}=T , U_t=F , U_{t-1}=F)$$
از آنجایی که محاسبات قدری طولانی است فقط قسمت اول را بدست خواهیم آورد. بقیه قسمتها نیز براساس احتمالات شرطی و قضیه بیز قابل محاسبه هستند.
$$\large P(R_t=F,R_{t-1}=T , U_t=T , U_{t-1}=T)=\\\large P( U_t=T , U_{t-1}=T\mid R_t=F,R_{t-1}=T)P(R_t=F,R_{t-1}=T)=\\ \large P( U_t=T \mid R_t=F)P( U_{t-1}=T \mid R_{t-1}=T)P(R_t=F\mid R_{t-1}=T)P(R_{t-1}=T)=\\ \large 0.6 \times 0.4 \times 0.2 \times 0.6 $$
خلاصه
مدل مارکوف و مدل پنهان مارکوف در زمینههای مختلف بخصوص در هوشمصنوعی به منظور تشخیص دستخط یا گفتار، تصدیق امضا و همچنین تعیین الگوهای صوتی در موسیقی به کار میروند. «نظریه صف» (Queuing Theory) و اقتصاد سنجی و تشخیص الگوهای مالی نیز از زمینههایی است که مدل مارکوف در آن بسیار به چشم میخورد. بنابراین حوزه استفاده از مدلهای پنهان مارکفی و فرآیندهای تصادفی مارکوفی بسیار وسیع است. در مطالب دیگر به بررسی شیوه پیادهسازی مدلهای مارکوفی در زبانهای برنامهنویسی مانند پایتون خواهیم پرداخت.
اگر مطلب بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- آموزش آمار و احتمال مهندسی
- مجموعه آموزشهای نرمافزارهای آماری
- احتمال شرطی (Conditional Probability) — اصول و شیوه محاسبه
- آزمایش تصادفی، پیشامد و تابع احتمال
- متغیر تصادفی و توزیع پواسن — به زبان ساده
^^











ببخشید ایراد مدل مارکوف در قبال الگوریتم های یادیگیری ماشین چیه؟
مثلا اگر در یک موضوعی بخواهیم بجای مدل مارکوف ازیکی از الگوریتم های یادگیری استفاده کنیم
و می شه بصورت ریاضی اثبات یا نشان داد
روابط ایراد نوشتاری داره و بدتر گیج شدم وقتی خوندمش!
با سلام؛
از ارائه بازخورد شما بسیار سپاسگزاریم. لطفا در صورت امکان، اشکالات را در همینجا بیان کنید تا در سریعترین زمان ممکن نسبت به رفع آنها اقدام شود.
با تشکر از همراهی شما با مجله فرادرس
منابع ذکر نشده
سلام، وقت شما بخیر؛
منابع مطالب مجله فرادرس در صورتیکه ترجمه یا تالیف از منبع دیگری باشند، در انتهای آنها و بعد از بخش معرفی مطالب و آموزشهای مرتبط ذکر شدهاند.
از اینکه با مجله فرادرس همراه هستید از شما بسیار سپاسگزاریم.
سلام. ببخشید اگه ما داده های سالانه برای یک متغیر رو داشته باشیم میتونیم با روش مارکوف پنهان وضعیت یک سال بعد اون متغیر رو پیش بینی کنیم؟
مثلا اگر آمار سالانه مصرف آب رو برای ۱۵ سال داشته باشیم میتونیم مصرف یک سال اینده رو پیش بینی کنیم؟
یا این روش برای داده های روزانه و هفتگی فقط کاربرد داره؟
واضح و ساده بود؛ در تحقیق دانشگاهی خودم تونستم ازش استفاده و کپی کنم. نگارش روان و بیان ساده از نقاط قوت مقاله بود/
با سلام عالی بود اما در مثال ارائه شده اعداد جداول با اعداد متن در تناقص هستند
سلام و درود،
جدولها با متن مطابقت داده شد. از تذکر شما بسیار سپاسگزارم.
تندرست و پیروز باشید.
اعداد این مقاله در رابطه با احتمالات به نظر درست نمیاد