تحلیل مولفه اساسی (PCA) – راهنمای عملی به همراه کد نویسی در پایتون و R

در این مطلب به بحث تحلیل مولفه اساسی (PCA) پرداخته شده است.

هنگامی که یک مجموعه داده دارای متغیرها یا ویژگی‌های زیادی باشند، برای تحلیل آن‌ها چه کار باید کرد؟ برخی از شرایط‌ احتمالی در ادامه فهرست شده‌اند.

1. بسیاری از متغیرها با یکدیگر همبستگی داشته باشند.
2. ممکن است تحلیل‌گر حوصله دسته بندی نداشته و یک مدل را روی کل مجموعه داده پیاده‌سازی کند. این کار موجب می‌شود دقت خروجی به شدت کاهش یابد.
3. ممکن است تحلیل‌گر در مورد این که چه کاری باید انجام دهد، سردرگم شود.
4. فرد ممکن است به استفاده از روش‌های راهبردی فکر کند تا با بهره‌گیری از آن‌ها بتواند متغیرهای مهم و تاثیرگذار بر تحلیل را بیاید.

گر چه چنین شرایطی ممکن است بسیار نگران کننده به نظر برسد؛ اما روش‌های آماری مانند تحلیل مولفه اساسی می‌تواند به تحلیل‌گر داده برای غلبه بر این شرایط کمک کند. در این نوشته، روش تحلیل مولفه اساسی به طور کامل و همراه با جزئیات به زبان ساده تشریح شده است. برای درک عملی این مفهوم، پیاده‌سازی روش تحلیل مولفه اساسی در زبان‌های برنامه‌نویسی پایتون و R نیز ارائه شده است. درک کامل این نوشتار نیازمند داشتن درک اولیه‌ای از مباحث آماری است.

تحلیل مولفه اساسی چیست؟

تحلیل مولفه اساسی به بیان ساده، روشی برای استخراج متغیرهای مهم (به شکل مولفه) از مجموعه بزرگی متغیرهای موجود در یک مجموعه داده است. تحلیل مولفه اساسی در واقع یک مجموعه با بُعد پایین از ویژگی‌ها را از یک مجموعه دارای بُعد بالا استخراج می‌کند تا به ثبت اطلاعات بیشتر با تعداد کمتری از متغیرها کمک کند.

بدین شکل، بصری‌سازی داده‌ها نیز معنادارتر می‌شود. تحلیل مولفه اساسی هنگامی که با داده‌های دارای سه یا تعداد بیشتری بُعد سر‌و‌کار داشته باشید، کاربردپذیرتر است. تحلیل مولفه اساسی همیشه روی ماتریس کوواریانس یا همبستگی اعمال می‌شود. این یعنی داده‌ها باید عددی و استاندارد شده باشند. برای درک بهتر این روش، در ادامه یک مثال بیان شده است:

فرض بر آن است که یک مجموعه داده با ابعادی که در زیر آمده است وجود دارد.

50 (p) ×300 (n)

در این مجموعه داده n تعداد کل نمونه‌ها و p تعداد پیش‌بین‌ها (متغیرهای پیش‌بینی) است. به دلیل آنکه تعداد ابعاد زیاد و برابر ۵۰ است می‌توان p(p-1)/2 نمودار پراکندگی برای آن رسم کرد، این یعنی بیش از ۱۰۰۰ نمودار برای انجام تحلیل روی روابط بین متغیرها وجود دارد و در نتیجه تحلیل آن‌ها کاری بسیار خسته‌کننده، دشوار و پیچیده خواهد بود.

در این شرایط، یک رویکرد صحیح می‌تواند آن باشد که یک زیر مجموعه از پیش‌بین‌ها که حاوی بیشترین اطلاعات درباره داده‌ها هستند، انتخاب شود. این امر موجب می‌شود نمودار پراکندگی داده‌ها در ابعاد پایین‌تری قابل ترسیم باشد. تصویر زیر نگاشت داده‌های دارای ابعاد بالا (۳ بُعد) را به داده‌های با ابعاد پایین‌تر (۲ بُعد) با استفاده از روش تحلیل مولفه اساسی نشان می‌دهد. لازم به ذکر است هر بُعد حاصل شده در فضای جدید، یک ترکیب خطی از p ویژگی اصلی است.

شکل ۱: کاهش ابعاد داده‌ها با استفاده از روش تحلیل مولفه اساسی

مولفه اساسی چیست؟

یک مولفه اساسی یک ترکیب خطی نرمال شده از پیش‌بین‌های اصلی موجود در مجموعه داده است. در شکل ۱، PC1 و PC2 مولفه‌های اساسی هستند. فرض می‌شود یک مجموعه از پیش‌بین‌ها به صورت X¹, X²...,X^p وجود دارد.

مولفه‌های اساسی این مجموعه از پیش‌بین‌ها را می‌توان بدین شکل نوشت:

Z¹ = Φ¹¹X¹ + Φ²¹X² + Φ³¹X³ + .... +Φ^p1X^p

که در آن:

• Z¹ اولین مولفه اساسی است.
• Φp¹ بردار بار شامل بردارهای بار (Φ¹, Φ²...) اولین مولفه اساسی است. بردارهای بار به مجموع مربعات مساوی با یک محدود شده‌اند. دلیل این امر آن است که داشتن مقادیر بار بزرگ ممکن است منجر به ایجاد واریانس بسیار بزرگ شود. این مقدار همچنین جهت مولفه اساسی (Z¹) را در جهتی که داده‌ها بیشترین تنوع را دارند، تعریف می‌کند. نتیجه این امر یک خط در فضای p ُبعدی است که نزدیک‌ترین مقدار به n نمونه را دارد. میزان نزدیکی به وسیله محاسبه میانگین مربعات فاصله‌های اقلیدسی اندازه‌گیری می‌شود.
• X¹..Xp پیش‌بین‌های نرمال شده هستند. میانگین پیش‌بین‌های نرمال شده برابر با صفر و انحراف معیار آن‌ها برابر با یک است.

بنابراین:

اولین مولفه اساسی، یک ترکیب خطی از پیش‌بین‌های اصلی است که بیشترین واریانس موجود در مجموعه داده‌ها را در بر می‌گیرد. این مولفه، جهت بیشترین تغییرات در داده‌ها را تعیین می‌کند. هرچه دامنه تغییرات موجود در اولین مولفه بالاتر باشد، اطلاعات موجود در این مولفه بیشتر است. هیچ مولفه دیگری نمی‌تواند بیش از مولفه اساسی اول دامنه تغییرات داشته باشد. نتیجه محاسبه اولین مولفه اساسی، خطی است که نزدیک‌ترین خط به داده‌ها محسوب می‌شود. در واقع این خط مجموع مربع فواصل را بین یک نقطه داده و خط، به کمینه مقدار می‌رساند.

مولفه اساسی دوم را نیز به روش مشابهی می‌توان به دست آورد:

دومین مولفه اساسی (Z²) نیز یک ترکیب خطی از پیش‌بین‌های اصلی است که واریانس باقی‌مانده در مجموعه داده را در خود حفظ می‌کند و با مقدار Z¹ ناهمبسته است. به عبارت دیگر، همبستگی بین مولفه اساسی اول و دوم صفر است. مولفه اساسی دوم را می‌توان به شکل زیر نمایش داد:

Z² = Φ¹²X¹ + Φ²²X² + Φ³²X³ + .... + Φp2Xp

اگر دو مولفه ناهمبسته باشند، جهت‌های آن‌ها باید متعامد (مانند شکل ۲) باشد. شکل ۲ براساس داده‌های شبیه‌سازی شده با دو ویژگی ترسیم شده است. جهت مولفه‌ها، چنان‌که انتظار می‌رود به صورت متعامد است و این یعنی مقدار همبستگی آن‌ها برابر با صفر است.

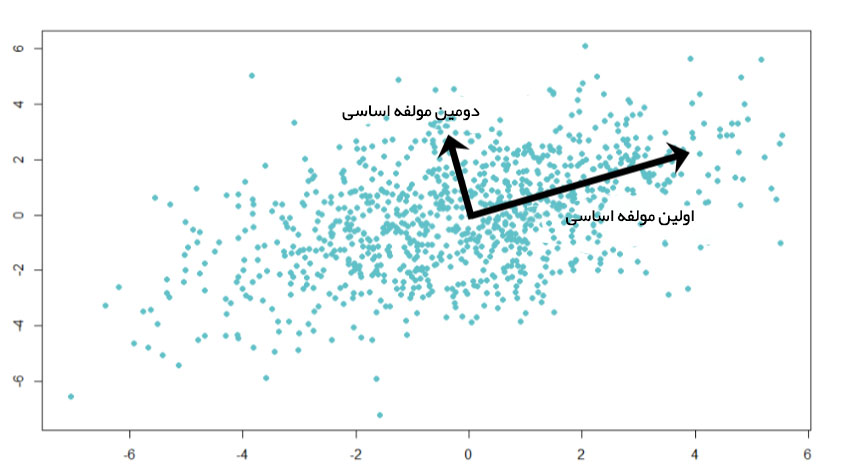
شکل ۲: همبستگی مولفه اساسی اول و دوم برابر با صفر و بنابراین بردارهای آن‌ها متعامد است.

کلیه مولفه‌های اساسی بعدی نیز از مفهومی مشابه آنچه بیان شد، پیروی می‌کنند. به عبارت دیگر، آن‌ها مقدار واریانس باقیمانده را بدون آنکه با مولفه‌های پیشین دارای همبستگی شوند، در خود حفظ می‌کنند. به‌طور کلی، در داده‌های دارای n × p بُعد، به میزان (min(n-1, p مولفه اساسی قابل ایجاد است.

جهت این مولفه‌ها به صورت نظارت نشده تعیین می‌شوند. یعنی، متغیر پاسخ (Y) برای تعیین جهت مولفه استفاده نمی‌شود. بنابراین، این رویکرد نظارت نشده است.

نکته: حداقل مربعات جزئي (PLS) یک جایگزین نظارت شده برای تحلیل مولفه اساسی (PCA) است. PLS برای تعیین مولفه اساسی، وزن بیشتری را به متغیرهایی که به شدت به متغیر پاسخ مرتبط هستند اختصاص می‌دهد.

چرا نرمال‌سازی متغیرها الزامی است؟

تحلیل مولفه اساسی روی نسخه نرمال شده پیش‌بین‌های اصلی قابل انجام است. این امر به آن دلیل است که پیش‌بین‌های اصلی ممکن است مقیاس‌های گوناگونی داشته باشند. به عنوان مثال می‌توان به یک مجموعه داده که شامل متغیرهایی با یکاهای گالون، کیلومتر، سال نوری و دیگر انواع واحدها است، اشاره کرد. واضح است که مقدار واریانس این متغیرها اعداد بزرگی خواهد بود. انجام PCA روی متغیرهای نرمال نشده منجر به بارهای فوق‌العاده بزرگی برای متغیرهای دارای واریانس بالا می‌شود و این امر به نوبه خود می‌تواند منجر به وابستگی مولفه اساسی به متغیرهای دارای واریانس بالا شود که بسیار نامطلوب است.

چنانکه در شکل ۳ می‌توان دید، PCA دو بار روی مجموعه داده اجرا گشته (با متغیرهای نرمال شده و نرمال نشده). مجموعه داده به‌کار برده شده در این مثال دارای ۴۰ ویژگی است. چنانکه مشهود است، اولین مولفه اساسی تحت سیطره متغیر MRP قرار گرفته است. دومین مولفه اساسی نیز تحت تسلط متغیر Item_Weight قرار گرفته است. این اتفاقات به دلیل بالا بودن واریانس متغیر است. هنگامی‌که متغیرها نرمال می‌شوند، بصری‌سازی آن‌ها در فضای دو بُعدی به شکل بهتری انجام‌پذیر است.

شکل ۳: تحلیل مولفه اساسی با نرمال‌سازی متغیرها و بدون نرمال‌سازی آن‌ها

پیاده‌سازی روش تحلیل مولفه اساسی در زبان‌های برنامه‌نویسی پایتون و R

برای هر مساله چند مولفه اساسی باید پیدا کرد؟ می‌توان پاسخ این سوال را با نگاهی عمیق‌تر به مفاهیم تئوریک داد؛ ولی بهتر است به صورت عملی و همراه با پیاده‌سازی، پاسخ آن را یافت تا قابل درک‌تر باشد.

در مثالی که در ادامه مورد بررسی قرار گرفته از مجموعه داده Big Mart Prediction Challenge III استفاده شده است. لازم به ذکر است، روش تحلیل مولفه اساسی را تنها می‌توان روی داده‌های عددی اعمال کرد. بنابراین، اگر داده‌ها دارای متغیرهای اسمی (دسته‌ای) باشند، باید ابتدا آن‌ها را به عدد تبدیل کرد. همچنین، داده‌ها پیش از اعمال این روش باید پاک‌سازی شده باشند. در گام اول و در قطعه کد زیر داده‌ها بارگذاری و پاک‌سازی می‌شوند:

#directory path

> path <- ".../Data/Big_Mart_Sales"

#set working directory

> setwd(path)

#load train and test file

> train <- read.csv("train_Big.csv")

> test <- read.csv("test_Big.csv")

#add a column

> test$Item_Outlet_Sales <- 1

#combine the data set

> combi <- rbind(train, test)

#impute missing values with median

> combi$Item_Weight[is.na(combi$Item_Weight)] <- median(combi$Item_Weight, na.rm = TRUE)

#impute 0 with median

> combi$Item_Visibility <- ifelse(combi$Item_Visibility == 0, median(combi$Item_Visibility), combi$Item_Visibility)

#find mode and impute

> table(combi$Outlet_Size, combi$Outlet_Type)

> levels(combi$Outlet_Size)[1] <- "Other"

تا اینجا، به چالش داده‌های از دست رفته (missing values) پرداخته شد. اکنون متغیرهای (پاسخ) وابسته و دیگر متغیرهای تعیین‌کننده (اگر وجود داشته باشد) باقیمانده‌اند که باید آن‌ها را حذف کرد. از همین‌رو، یک روش یادگیری نظارت نشده جهت حذف متغیرهای پاسخ مطابق کد زیر استفاده شده است.

#remove the dependent and identifier variables

> my_data <- subset(combi, select = -c(Item_Outlet_Sales, Item_Identifier, Outlet_Identifier))

اکنون باید متغیرهای موجود (پیش‌بین‌ها) در مجموعه داده را با کد زیر بررسی کرد:

#check available variables

> colnames(my_data)

به دلیل آنکه روش تحلیل مولفه اساسی فقط روی داده‌های عددی قابل اعمال است، در ابتدا و پیش از اعمال آن روی مجموعه داده، وجود یا عدم وجود متغیرهایی غیر عددی را باید بررسی کرد. برای این کار می‌توان از کد زیر استفاده کرد:

#check variable class

> str(my_data)

'data.frame': 14204 obs. of 9 variables:

$ Item_Weight : num 9.3 5.92 17.5 19.2 8.93 ...

$ Item_Fat_Content : Factor w/ 5 levels "LF","low fat",..: 3 5 3 5 3 5 5 3 5 5 ...

$ Item_Visibility : num 0.016 0.0193 0.0168 0.054 0.054 ...

$ Item_Type : Factor w/ 16 levels "Baking Goods",..: 5 15 11 7 10 1 14 14 6 6 ...

$ Item_MRP : num 249.8 48.3 141.6 182.1 53.9 ...

$ Outlet_Establishment_Year: int 1999 2009 1999 1998 1987 2009 1987 1985 2002 2007 ...

$ Outlet_Size : Factor w/ 4 levels "Other","High",..: 3 3 3 1 2 3 2 3 1 1 ...

$ Outlet_Location_Type : Factor w/ 3 levels "Tier 1","Tier 2",..: 1 3 1 3 3 3 3 3 2 2 ...

$ Outlet_Type : Factor w/ 4 levels "Grocery Store",..: 2 3 2 1 2 3 2 4 2 2 ...

متاسفانه 6 مورد از 9 متغیر موجود ذاتا اسمی (دسته‌ای) هستند. لذا باید آن‌ها را ابتدا به متغیرهای عددی تبدیل کرد. در ادامه از روش کدگذاری one hot برای تبدیل داده‌های اسمی (دسته‌ای) به عددی استفاده شده است.

#load library

> library(dummies)

#create a dummy data frame

> new_my_data <- dummy.data.frame(my_data, names = c("Item_Fat_Content","Item_Type",

"Outlet_Establishment_Year","Outlet_Size",

"Outlet_Location_Type","Outlet_Type"))

از کد زیر استفاده کرده و بررسی می‌کنیم که آیا پس از انجام اقدامات قبلی، کل مجموعه داده صرفاً دارای مقادیر عددی است یا نه:

#check the data set

> str(new_my_data)

نتیجه این قطعه کد نشان می‌دهد که در حال حاضر کل داده‌های موجود در مجموعه داده به صورت عددی هستند. بنابراین باید داده‌ها را با استفاده از قطعه کد زیر به دو دسته آزمون و آموزش (test و train) تقسیم کرد:

#divide the new data

> pca.train <- new_my_data[1:nrow(train),]

> pca.test <- new_my_data[-(1:nrow(train)),]

اکنون بستر لازم برای استفاده از روش تحلیل مولفه اساسی فراهم شده است. تابع پایه R یعنی ()prcomp برای اعمال PCA استفاده شده است. این تابع به‌طور پیش‌فرض، متغیرهایی که میانگین صفر دارند را در مرکز قرار می‌دهد. با استفاده از پارامتر scale = T، متغیرها نرمال می‌شوند تا انحراف معیار آن‌ها برابر با ۱ باشد.

#principal component analysis

> prin_comp <- prcomp(pca.train, scale. = T)

> names(prin_comp)

[1] "sdev" "rotation" "center" "scale" "x"

تابع ()prcomp پنج مقدار مفید را در خروجی ارائه می‌کند:

۱. مرکز (center) و مقیاس (scale)، میانگین و انحراف معیار متغیرهایی که برای نرمال‌سازی پیش از پیاده‌سازی PCA استفاده شده‌اند را نشان می‌دهد.

#outputs the mean of variables

prin_comp$center

#outputs the standard deviation of variables

prin_comp$scale

۲. مقدار دوران (rotation)، بار مولفه اساسی را فراهم می‌کند. هر ستون از ماتریس دوران شامل بردار بار مولفه اساسی است. این مهم‌ترین سنجه‌ای است که باید به آن توجه کرد.

> prin_comp$rotation

این کد ۴۴ مولفه اساسی بار را به عنوان خروجی ارائه می‌کند. باید توجه داشته باشید که این پاسخ قطعاً درست است. در یک مجموعه داده، بیشینه تعداد بارهای مولفه اساسی برابر با کمینه (n-1 و p) است. در ادامه چهار مولفه اساسی و پنج سطر اول آن‌ها قابل مشاهده است.

> prin_comp$rotation[1:5,1:4]

PC1 PC2 PC3 PC4

Item_Weight 0.0054429225 -0.001285666 0.011246194 0.011887106

Item_Fat_ContentLF -0.0021983314 0.003768557 -0.009790094 -0.016789483

Item_Fat_Contentlow fat -0.0019042710 0.001866905 -0.003066415 -0.018396143

Item_Fat_ContentLow Fat 0.0027936467 -0.002234328 0.028309811 0.056822747

Item_Fat_Contentreg 0.0002936319 0.001120931 0.009033254 -0.001026615

۳. برای محاسبه بردار امتیاز مولفه اساسی، نیاز به ضرب کردن بارها با داده‌ها نیست. ماتریکس x دارای بردارهای امتیاز مولفه اساسی در 44 × 8523 بُعد است.

> dim(prin_comp$x)

[1] 8523 44

نمودار مولفه‌های اساسی با استفاده از قطعه کد زیر ترسیم می‌شود.

> biplot(prin_comp, scale = 0)

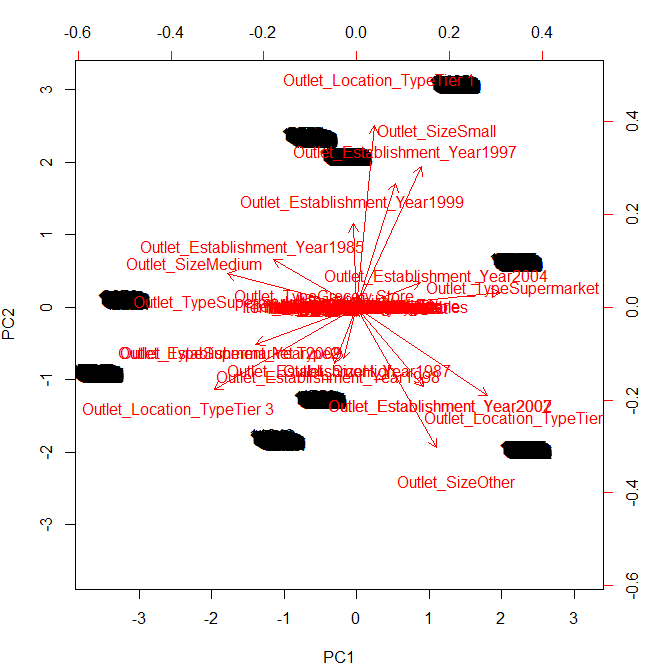
شکل ۴: رسم نمودار مولفه‌های اساسی در زبان برنامه‌نویسی R

پارامتر scale = 0 برای اطمینان از این امر است که بردارها برای نمایش بار مدرج شده‌اند. برای استنتاج از نمودار بالا، باید به نقاط پایانی نمودار (بالا، پایین، چپ و راست) توجه کرد.

از این نمودار می‌توان استنتاج کرد که مولفه اساسی مربوطه به مقدارهای Outlet_TypeSupermarket و Outlet_Establishment_Year 2007 است. به‌طور مشابه، می‌توان گفت که دومین مولفه مربوط به measure of Outlet_Location_TypeTier1 و Outlet_Sizeother است. برای تعیین مقادیر دقیق متغیرهای موجود در مولفه، باید ماتریکس دوران بالا را مجدداً بررسی کرد.

تابع ()prcomp امکان محاسبه انحراف معیار از هر مولفه اساسی را فراهم می‌کند. sdev به انحراف معیار مولفه‌های اساسی مربوط است.

#compute standard deviation of each principal component

> std_dev <- prin_comp$sdev

#compute variance

> pr_var <- std_dev^2

#check variance of first 10 components
> pr_var[1:10]
[1] 4.563615 3.217702 2.744726 2.541091 2.198152 2.015320 1.932076 1.256831
[9] 1.203791 1.168101

هدف پیدا کردن مولفه‌هایی است که بیشترین واریانس را نشان می‌دهند. این رویکرد به این دلیل است که در روش تحلیل مولفه اساسی هدف پیدا کردن مولفه‌هایی است که بیشترین اطلاعات را در بر دارند. برای محاسبه بخشی از واریانس که توسط هر مولفه ارائه می‌شود، در قطعه کرد زیر واریانس بر مجموع واریانس کل تقسیم شده است.

#proportion of variance explained

> prop_varex <- pr_var/sum(pr_var)

> prop_varex[1:20]

[1] 0.10371853 0.07312958 0.06238014 0.05775207 0.04995800 0.04580274

[7] 0.04391081 0.02856433 0.02735888 0.02654774 0.02559876 0.02556797

[13] 0.02549516 0.02508831 0.02493932 0.02490938 0.02468313 0.02446016

[19] 0.02390367 0.02371118

خروجی ارائه شده نشان می‌دهد که اولین مولفه ۱۰.۳٪ واریانس را در بر دارد. مولفه دوم ۷.۳٪ واریانس را در بر دارد. مولفه سوم ۶.۲٪ واریانس را در بر دارد و به همین ترتیب برای دیگر مولفه‌ها می‌توان استنتاج کرد. بنابراین باید تصمیم گرفت که چند مولفه باید برای مدل‌سازی انتخاب شوند.

برای پاسخ به این پرسش، از نمودار سنگ‌ریزه (scree plot) استفاده شده است. نمودار سنگ‌ریزه برای دسترسی داشتن به مولفه‌ها یا عامل‌هایی که بیشترین تنوع در داده‌ها را دارند استفاده می‌شود. این نمودار مقادیر را به صورت نزولی نمایش می‌دهد.

#scree plot

> plot(prop_varex, xlab = "Principal Component",

ylab = "Proportion of Variance Explained",

type = "b")

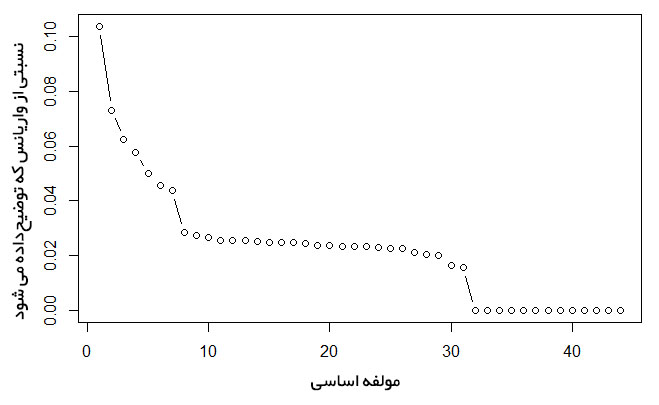
شکل 5: رسم نمودار سنگ‌ریزه در زبان برنامه‌نویسی R

نمودار بالا نشان می‌دهد که۳۰ مولفه حدود ۹۸.۴٪ از واریانس مجموعه داده‌ها را در بر دارند. به عبارت دیگر، با استفاده از روش مولفه اساسی، ۴۴ پیش‌بین به ۳۰ پیش‌بین (بدون از دست دادن واریانس) کاهش پیدا کرد. این قدرت روش تحلیل مولفه اساسی است. در ادامه برای کسب اطمینان و تایید نهایی، نمودار واریانس تجمعی ترسیم شده است. این نمودار یک تصویر روشن از تعداد مولفه‌ها ارائه می‌کند.

#cumulative scree plot

> plot(cumsum(prop_varex), xlab = "Principal Component",

ylab = "Cumulative Proportion of Variance Explained",

type = "b")

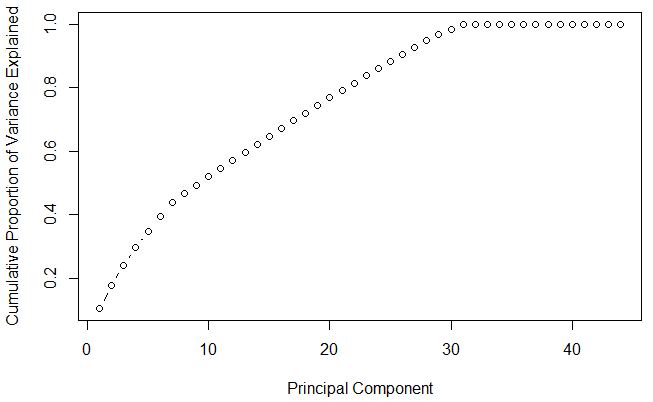
شکل 6: رسم نمودار سنگ‌ریزه در زبان برنامه‌نویسی R

این نمودار نشان می‌دهد که ۳۰ مولفه دارای واریانسی نزدیک به ۹۸٪ هستند. بنابراین، در این مساله تعداد ۳۰ مولفه (از مولفه اساسی اول تا سی‌ام) انتخاب می‌شوند و فاز مدل‌سازی آغاز می‌شود. این کار گام‌های پیاده‌سازی PCA روی مجموعه داده آموزش را کامل می‌سازد. برای مدل‌سازی از ۳۰ مولفه به عنوان ویژگی‌های موجود استفاده شده و فرآیند طبیعی مدل‌سازی انجام می‌شود.

مدل‌سازی پیش‌بین با مولفه‌های PCA

پس از محاسبه مولفه‌های اساسی در مجموعه داده، اکنون باید فرآیند پیش‌بینی روی داده‌های آزمون با استفاده از این مولفه‌ها بررسی شود. این فرآیند ساده است. همانطور که مولفه‌های PCA روی مجموعه داده آموزش تعیین شدند، گروه دیگری از مولفه‌ها روی مجموعه داده آزمون تبیین می‌شوند. در نهایت مدل آموزش ساخته می‌شود.

اما، چند نکته مهم که باید به آن‌ها توجه کرد:

1. نباید داده‌های آموزش و آزمون را برای تعیین مولفه‌های PCA روی کل مجموعه داده به طور یک‌باره، با یکدیگر ترکیب کنیم. زیرا، این کار موجب می‌شود کل فرضیه تعمیم باطل شود. دلیل این امر آن است که داده‌های آزمون به مجموعه داده آموزش «نشت» کرده‌اند. به عبارت دیگر، مجموعه داده آزمون «نادیده» باقی نمی‌ماند. این کار موجب از بین رفتن قابلیت تعمیم مدل می‌شود.
2. نباید PCA روی مجموعه داده‌های آزمون و آموزش به‌طور جداگانه اعمال شود. زیرا، بردارهای حاصل شده از مجموعه داده‌های آموزش و آزمون، جهت‌های مختلفی خواهند داشت (به دلیل داشتن واریانس نامساوی). به این ترتیب، با مقایسه داده‌ها روی محورهای گوناگون می‌توان نتیجه‌گیری کرد. بنابراین، بردارهای حاصل شده از مجموعه داده آزمون و آموزش باید محورهای مشابهی داشته باشند.

پس چه کاری باید انجام داد؟

باید دقیقا تبدیل‌هایی که روی مجموعه داده آموزش انجام شده، روی مجموعه داده‌های آزمون نیز انجام شود. این کار شامل center و scaling نیز می‌شود. قطعه کد لازم برای انجام این کار در زبان R در ادامه آورده شده است.

#add a training set with principal components

> train.data <- data.frame(Item_Outlet_Sales = train$Item_Outlet_Sales, prin_comp$x)

#we are interested in first 30 PCAs

> train.data <- train.data[,1:31]

#run a decision tree

> install.packages("rpart")

> library(rpart)

> rpart.model <- rpart(Item_Outlet_Sales ~ .,data = train.data, method = "anova")

> rpart.model

#transform test into PCA

> test.data <- predict(prin_comp, newdata = pca.test)

> test.data <- as.data.frame(test.data)

#select the first 30 components

> test.data <- test.data[,1:30]

#make prediction on test data

> rpart.prediction <- predict(rpart.model, test.data)

#For fun, finally check your score of leaderboard

> sample <- read.csv("SampleSubmission_TmnO39y.csv")

> final.sub <- data.frame(Item_Identifier = sample$Item_Identifier, Outlet_Identifier = sample$Outlet_Identifier, Item_Outlet_Sales = rpart.prediction)

> write.csv(final.sub, "pca.csv",row.names = F)

آنچه ارائه شد فرآیند ایجاد یک مدل کامل پس از استخراج PCA است. احتمالا پس از اعمال این روش متوجه خواهید شد که نتایج نهایی رضایت‌بخش نیست و استفاده از روش جنگل تصادفی گزینه‌ بهتری محسوب می‌شود!

کاربران پایتون

برای پیاده‌سازی PCA در پایتون، تنها کافی است PCA را از کتابخانه sklearn فراخوانی کرد. سایر توضیحات به صورتی است که برای زبان R گفته شد. البته، نتایج حاصل از پیاده‌سازی روش به هر دو زبان نیز مشابه خواهد بود.

مجموعه داده استفاده شده برای قطعه کد پایتون زیر، نسخه پاک‌سازی شده است که در آن مساله مقادیر از دست رفته حل شده و متغیرهای اسمی (دسته‌ای) به متغیرهای عددی تبدیل شده‌اند. فرآیند مدل‌سازی مشابه آنچه برای R گفته شد است.

import numpy as np

from sklearn.decomposition import PCA

import pandas as pd

import matplotlib.pyplot as plt

from sklearn.preprocessing import scale

%matplotlib inline

#Load data set

data = pd.read_csv('Big_Mart_PCA.csv')

#convert it to numpy arrays

X=data.values

#Scaling the values

X = scale(X)

pca = PCA(n_components=44)

pca.fit(X)

#The amount of variance that each PC explains

var= pca.explained_variance_ratio_

#Cumulative Variance explains

var1=np.cumsum(np.round(pca.explained_variance_ratio_, decimals=4)*100)

print var1

[ 10.37 17.68 23.92 29.7 34.7 39.28 43.67 46.53 49.27

51.92 54.48 57.04 59.59 62.1 64.59 67.08 69.55 72.

74.39 76.76 79.1 81.44 83.77 86.06 88.33 90.59 92.7

94.76 96.78 98.44 100.01 100.01 100.01 100.01 100.01 100.01

100.01 100.01 100.01 100.01 100.01 100.01 100.01 100.01]

plt.plot(var1)

#Looking at above plot I'm taking 30 variables

pca = PCA(n_components=30)

pca.fit(X)

X1=pca.fit_transform(X)

print X1

نکاتی که باید همواره درباره روش تحلیل مولفه اساسی به خاطر داشت:

1. روش تحلیل مولفه اساسی برای غلبه بر افزونگی متغیرهای موجود در مجموعه داده‌ها مناسب است.
2. این متغیرها ذاتا دارای ابعاد کمی هستند.
3. مولفه‌های این متغیرها حاصل ترکیب خطی نرمال شده متغیرهای پیش‌بین اصلی هستند.
4. هدف این مولفه‌ها حفظ بیشترین اطلاعات ممکن با واریانس‌های بالا است که پیش از این تشریح شد.
5. اولین مولفه اساسی بالاترین واریانس را داراست و پس از آن مولفه اساسی دوم دارای بیشترین مقدار واریانس است و این موضوع برای مولفه‌های اساسی سوم و دیگر مولفه‌های اساسی نیز صادق است.
6. مولفه‌ها باید ناهمبسته باشند (جهت‌های آن‌ها متعامد است).
7. نرمال‌سازی داده‌ها هنگامی‌که متغیرها دارای واحدهای (یکاهای) گوناگونی هستند، فوق‌العاده مهم است.
8. PCA روی مجموعه داده‌های دارای سه یا تعداد بیشتری بُعد بهترین عملکرد را دارد. زیرا، در ابعاد بالاتر، تفسیر ابْر داده‌ها (Cloud of Data) بسیار دشوار خواهد بود.
9. PCA روی مجموعه داده‌های دارای ویژگی‌های عددی قابل اعمال است.
10. PCA ابزاری است که به انجام بهترین بصری‌سازی از داده‌های دارای ابعاد بالا کمک می‌کند.

سخن پایانی

در این نوشته سعی ما بر آن بوده است که بدون اشاره به مفاهیم عمیق ریاضی، اصول مهم تحلیل مولفه اساسی که دانستن آن‌ها برای به‌کارگیری این روش الزامی است، تشریح شوند. ایده اساسی نهفته در پس این روش آن است که در مجموعه داده‌های با ابعاد بالا، مولفه‌هایی که بیشترین تغییرات داده‌‌ای را توضیح داده و بیشترین اطلاعات را درباره رابطه‌شان با متغیرهای پاسخ ارائه کند.

در نهایت پیاده‌سازی این روش در زبان‌های برنامه‌نویسی پایتون و R به منظور درک هرچه بهتر این روش ارائه شد.

• آموزش آمار و احتمال مهندسی
• شبکه‌های عصبی مصنوعی
• آمار، احتمالات و داده‌کاوی
• یادگیری ماشین و بازشناسی الگو
• مدل سازی، برازش و تخمین

==

^^