دستگاه معادلات دیفرانسیل خطی — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در آموزش‌های قبلی مجله فرادرس، با معادلات دیفرانسیل آشنا شدیم. همچنین، روش‌های حل معادلات دیفرانسیل مرتبه اول، معادلات دیفرانسیل مرتبه دوم و معادلات مرتبه بالاتر را معرفی کردیم. در این آموزش دستگاه متشکل از معادلات دیفرانسیل خطی مرتبه اول را معرفی و برخی از روش‌های حل آن را بیان می‌کنیم.

یک دستگاه خطی از معادلات دیفرانسیل با ضرایب ثابت را به‌صورت زیر نمایش می‌دهیم:

$${\frac{{d{x_i}}}{{dt}} = {x’_i} } = {\sum\limits_{j = 1}^n {{a_{ij}}{x_j}\left( t \right)} + {f_i}\left( t \right),\;\;}\kern-0.3pt {i = 1,2, \ldots ,n,}$$

که در آن، $$x_1(t)$$، $$x_2(t)$$، $$\ldots$$ و $$x_n(t)$$ توابعی نامشخص از متغیر $$t$$ هستند (متغیر $$t$$ اغلب زمان را نشان می‌دهد). ضرایب ثابت $$a_{ij}$$ ممکن است حقیقی یا مختلط باشند. توابع $$f_i(t)$$ که در حالت کلی می‌توانند مختلط باشند، توابعی از متغیر $$t$$ هستند.

فرض می‌کنیم همه این توابع در بازه $$\left[ {a,b} \right]$$ روی محور حقیقی $$t$$ پیوسته باشند.

نمادگذاری‌های زیر را در نظر بگیرید:

$${X\left( t \right) = \left[ {\begin{array}{*{20}{c}}<br /> {{x_1}\left( t \right)}\\<br /> {{x_2}\left( t \right)}\\<br /> \vdots \\<br /> {{x_n}\left( t \right)}<br /> \end{array}} \right],\;\;}\kern-0.3pt<br /> {X’\left( t \right) = \left[ {\begin{array}{*{20}{c}}<br /> {{x’_1}\left( t \right)}\\<br /> {{x’_2}\left( t \right)}\\<br /> \vdots \\<br /> {{x’_n}\left( t \right)}<br /> \end{array}} \right],\;\;}\kern-0.3pt<br /> {f\left( t \right) = \left[ {\begin{array}{*{20}{c}}<br /> {{f_1}\left( t \right)}\\<br /> {{f_2}\left( t \right)}\\<br /> \vdots \\<br /> {{f_n}\left( t \right)}<br /> \end{array}} \right],\;\;}\kern-0.3pt<br /> {A = \left[ {\begin{array}{*{20}{c}}<br /> {{a_{11}}}&{{a_{12}}}& \cdots &{{a_{1n}}}\\<br /> {{a_{21}}}&{{a_{22}}}& \cdots &{{a_{2n}}}\\<br /> \cdots & \cdots & \cdots & \cdots \\<br /> {{a_{n1}}}&{{a_{n2}}}& \cdots &{{a_{nn}}}<br /> \end{array}} \right],}$$

دستگاه معادلات دیفرانسیل را می‌توان به فرم ماتریسی زیر نوشت:

$$X’\left( t \right) = AX\left( t \right) + f\left( t \right).$$

اگر بردار $$f(t)$$ به‌صورت تحلیلی برابر با صفر باشد، آن‌گاه دستگاه معادلات را «همگن» (Homogeneous) می‌نامیم:

$$X’\left( t \right) = AX\left( t \right).$$

دستگاه معادلات همگن با ضرایب ثابت را می‌توان با روش‌های مختلفی حل کرد. روش‌های زیر، متداول‌ترین راه‌های حل دستگاه معادلات همگن هستند:

• روش حذف (کاهش $$n$$ معادله به یک معادله مرتبه $$n$$اُم).
• روش ترکیبات انتگرال‌پذیر
• روش مقدار ویژه و بردار ویژه
• روش ماتریس نمایی

در ادامه، دو روش حذف و ماتریس نمایی را توضیح می‌دهیم.

روش حذفی

با استفاده از روش حذفی می‌توان یک دستگاه $$n$$معادله‌ای را به یک معادله خطی مرتبه $$n$$اُم کاهش داد. این روش، برای سیستم‌های ساده، خصوصاً سیستم‌های مرتبه دوم مفید است.

دستگاه معادلات همگن با ضرایب ثابت زیر را در نظر بگیرید:

$$\left\{ \begin{array}{l} {x’_1} = {a_{11}}{x_1} + {a_{12}}{x_2}\\ {x’_2} = {a_{21}}{x_1} + {a_{22}}{x_2} \end{array} \right.,$$

که در آن، توابع $$x_1$$ و $$x_2$$، به متغیر $$t$$ وابسته هستند.

از معادله اول مشتق می‌گیریم و عبارت $${x’_2}$$ را از معادله دوم در آن جایگذاری می‌کنیم:

$${{x^{\prime\prime}_1} = {a_{11}}{x’_1} + {a_{12}}{x’_2},\;\;}\Rightarrow {{{x^{\prime\prime}_1} = {a_{11}}{x’_1} }+{ {a_{12}}\left( {{a_{21}}{x_1} + {a_{22}}{x_2}} \right),\;\;}}\\ \Rightarrow {{{x^{\prime\prime}_1} = {a_{11}}{x’_1} }+{ {a_{12}}{a_{21}}{x_1} + {a_{22}}{a_{12}}{x_2}.}}$$

اکنون مقدار $${a_{12}}{x_2}$$ را از معادله اول جایگذاری می‌کنیم. نتیجه، یک معادله دیفرانسیل خطی مرتبه دوم همگن به‌صورت زیر خواهد بود:

$${{{x^{\prime\prime}_1} = {a_{11}}{x’_1} + {a_{12}}{a_{21}}{x_1} }+{ {a_{22}}\left( {{x’_1} – {a_{11}}{x_1}} \right),\;\;}}\\ \Rightarrow {{{x^{\prime\prime}_1} = {a_{11}}{x’_1} + {a_{12}}{a_{21}}{x_1} }+{ {a_{22}}{x’_1} – {a_{11}}{a_{22}}{x_1},\;\;}}\\ \Rightarrow {{{x^{\prime\prime}_1} – \left( {{a_{11}} + {a_{22}}} \right){x’_1} }+{ \left( {{a_{11}}{a_{22}} – {a_{12}}{a_{21}}} \right){x_1} = 0.}}$$

حل معادله فوق ساده است. معادله مشخصه آن را می‌توان به‌صورت زیر نوشت:

$${{{\lambda ^2} – \left( {{a_{11}} + {a_{22}}} \right)\lambda }+{ \left( {{a_{11}}{a_{22}} – {a_{12}}{a_{21}}} \right) = 0.}}$$

در صورت حقیقی بودن ضرایب $${a_{ij}}$$، هر دو ریشه ممکن است حقیقی (مجزا یا تکراری) یا مختلط باشند. در حالت خاصی که دو ریشه $${a_{12}}$$ و $${a_{21}}$$ علامت یکسانی داشته باشند، مبیّن (یا دلتا) معادله مشخصه همواره مثبت است و در نتیجه ریشه‌ها حقیقی و متمایز خواهند بود.

بعد از آنکه تابع $${x_1}\left( t \right)$$ به‌دست آمد، تابع $$x_2(t)$$ را می‌توان از معادله اول پیدا کرد.

روش حذف، محدود به دستگاه معادلات خطی همگن نیست و می‌توان برای حل دستگاه‌های معادلات خطی ناهمگن یا دستگاه معادلات با ضرایب متغیر نیز از آن استفاده کرد.

مثال ۱

دستگاه معادلات دیفرانسیل زیر را حل کنید.

$${{x’_1} = 2{x_1} + 3{x_2},\;\;\;}\kern-0.3pt{{x’_2} = 4{x_1} – 2{x_2}.}$$

حل: ابتدا، از معادله اول مشتق می‌گیریم، سپس $${x’_2}$$‌ را از معادله دوم در آن جایگذاری می‌کنیم:

$${{x^{\prime\prime}_1} = 2{x’_1} + 3{x’_2},\;\;}\Rightarrow {{x^{\prime\prime}_1} = 2{x’_1} + 3\left( {4{x_1} – 2{x_2}} \right),\;\;}\\ \Rightarrow {{x^{\prime\prime}_1} = 2{x’_1} + 12{x_1} – 6{x_2}.}$$

مقدار $$3{x_2}$$ را از معادله اول در معادله فوق جایگذاری می‌کنیم:

$$3{x_2} = {x’_1} – 2{x_1}.$$

بنابراین، داریم:

$$\require{cancel}<br /> {{{x^{\prime\prime}_1} = 2{x’_1} + 12{x_1} }-{ 2\left( {{x’_1} – 2{x_1}} \right),\;\;}}\\<br /> \Rightarrow<br /> {{{x^{\prime\prime}_1} = \cancel{2{x’_1}} + 12{x_1} }-{ \cancel{2{x’_1}} + 4{x_1},\;\;}}\\<br /> \Rightarrow<br /> {{x^{\prime\prime}_1} – 16{x_1} = 0.}$$

ریشه‌های معادله مشخصه به‌صورت زیر محاسبه می‌شوند:

$${{\lambda ^2} – 16 = 0,\;\; }\Rightarrow{ {\lambda _{1,2}} = \pm 4.}$$

در نتیجه، حل معادله مرتبه دوم متغیر $$x_1$$ به‌صورت زیر خواهد بود:

$${{x_1}\left( t \right) }={ {C_1}{e^{4t}} + {C_2}{e^{ – 4t}},}$$

که در آن، $$C_1$$ و $$C_2$$ ضرایبی اختیاری هستند.

اکنون باید $${x’_1}$$ را محاسبه کنیم و با کمک آن، $$x_2$$ را به‌دست آوریم:

$${{x’_1}\left( t \right) = 4{C_1}{e^{4t}} – 4{C_2}{e^{ – 4t}},\;\;}\\ \Rightarrow {4{C_1}{e^{4t}} – 4{C_2}{e^{ – 4t}} }={ 2{C_1}{e^{4t}} + 2{C_2}{e^{ – 4t}} + 3{x_2},\;\;}\\ \Rightarrow {3{x_2} = 2{C_1}{e^{4t}} – 6{C_2}{e^{ – 4t}},\;\;}\\ \Rightarrow {{x_2} = \frac{2}{3}{C_1}{e^{4t}} – 2{C_2}{e^{ – 4t}}.}$$

برای آنکه ضرایب را به‌صورت بهتری بنویسیم (غیرکسری)، به‌جای $$C_1$$ از $$3C_1$$ استفاده می‌کنیم که البته تأثیری در پاسخ نخواهد داشت.

$$\left\{ \begin{array}{l} {x_1}\left( t \right) = 3{C_1}{e^{4t}} + {C_2}{e^{ – 4t}}\\ {x_2}\left( t \right) = 2{C_1}{e^{4t}} – 2{C_2}{e^{ – 4t}} \end{array} \right..$$

مثال ۲

دستگاه معادلات زیر را حل کنید.

$${x’ = 6x – y,\;\;}\kern-0.3pt{\;y’ = x + 4y.}$$

حل: دستگاه معادلات را به یک معادله مرتبه دوم از $$x(t)$$ تبدیل می‌کنیم. اگر از معادله اول مشتق بگیریم و $$y’$$ را از معادله دوم در آن جایگذاری کنیم، داریم:

$${x^{\prime\prime} = 6x’ – y’,\;\;}\Rightarrow {x^{\prime\prime} = 6x’ – \left( {x + 4y} \right),\;\;}\Rightarrow {x^{\prime\prime} = 6x’ – x – 4y.}$$

اکنون معادل $$y$$ را در معادله قرار می‌دهیم:

$${y = 6x – x’,\;\;}\Rightarrow {{x^{\prime\prime} = 6x’ – x }-{ 4\left( {6x – x’} \right),\;\;}}\\ \Rightarrow {{x^{\prime\prime} = 6x’ – x }-{ 24x + 4x’,\;\;}}\\ \Rightarrow {x^{\prime\prime} – 10x’ + 25x = 0.}$$

با حل معادله مشخصه داریم:

$${{\lambda ^2} – 10\lambda + 25 = 0,\;\;\;}\kern-0.3pt{D = 0,\;\;}\Rightarrow {{\lambda _1} = 5.}$$

همان‌طور که می‌بینیم ریشه $$\lambda = 5$$، دو بار تکرار شده است. در نتیجه، جواب عمومی تابع $$x(t)$$ را می‌توان به‌صورت زیر نوشت:

$$x\left( t \right) = \left( {{C_1} + {C_2}t} \right){e^{5t}},$$

که در آن، $$C_1$$ و $$C_2$$ ثوابت دلخواهی هستند.

با داشتن $$x(t)$$، مقدار $$x’\left( t \right)$$ را به‌دست آورده و آن را در معادله اول قرار می‌دهیم و $$y(t)$$ را محاسبه می‌کنیم:

$${{x’\left( t \right) }={ {C_2}{e^{5t}} }+{ \left( {5{C_1} + 5{C_2}t} \right){e^{5t}} }} = {\left( {5{C_1} + {C_2} + 5{C_2}t} \right){e^{5t}},\;\;}\\ \Rightarrow {\left( {5{C_1} + {C_2} + 5{C_2}t} \right){e^{5t}} }={ \left( {6{C_1} + 6{C_2}t} \right){e^{5t}} – y,\;\;}\\ \Rightarrow {y = \left( {{C_1} – {C_2} + {C_2}t} \right){e^{5t}}.}$$

بنابراین، حل عمومی دستگاه معادلات را می‌توان به‌صورت زیر نوشت:

$$\left\{ \begin{array}{l} {x\left( t \right) }={ \left( {{C_1} + {C_2}t} \right){e^{5t}}}\\ {y\left( t \right) }={ \left( {{C_1} – {C_2} + {C_2}t} \right){e^{5t}}} \end{array} \right..$$

مثال ۳

جواب عمومی دستگاه معادلات دیفرانسیل زیر را به‌دست آورید.

$${{x’_1} = 5{x_1} + 2{x_2},\;\;\;}\kern-0.3pt{{x’_2} = – 4{x_1} + {x_2}.}$$

حل: مشتق‌گیری از معادله اول، نتیجه زیر را خواهد داشت:

$${x^{\prime\prime}_1} = 5{x’_1} + 2{x’_2}.$$

با جایگذاری $${x’_2}$$ از معادله دوم، داریم:

$${{x^{\prime\prime}_1} = 5{x’_1} + 2\left( { – 4{x_1} + {x_2}} \right),\;\;}\Rightarrow {{x^{\prime\prime}_1} = 5{x’_1} – 8{x_1} + 2{x_2}.}$$

اکنون از معادله اول، $$2x_2$$ را برحسب $$x_1$$ می‌نویسیم:

$${{{x^{\prime\prime}_1} = 5{x’_1} – 8{x_1} }+{ {x’_1} – 5{x_1},\;\;}}\Rightarrow {{x^{\prime\prime}_1} – 6{x’_1} + 13{x_1} = 0.}$$

معادله بالا، یک معادله مرتبه دوم با ضرایب ثابت است که حل معادله مشخصه آن به‌صورت زیر است:

$${{\lambda ^2} – 6\lambda + 13 = 0,\;\;}\kern-0.3pt{D = 36 – 52 = – 16,\;\;}\Rightarrow {{\lambda _{1,2}} = \frac{{6 \pm \sqrt { – 16} }}{2} } = {\frac{{6 \pm 4i}}{2} }={ 3 \pm 2i.}$$

همان‌گونه که می‌بینیم، ریشه‌ها مختلط مزدوج هستند. بنابراین، جواب عمومی تابع $$x_1(t)$$ را می‌توان به‌صورت زیر نوشت:

$${{x_1}\left( t \right) }={ {e^{3t}}\left( {{C_1}\cos 2t + {C_2}\sin 2t} \right),}$$

که در آن، $$C_1$$ و $$C_2$$ ضرایبی دلخواه هستند.

اکنون تابع $$x_1(t)$$ را پیدا می‌کنیم. عبارت $${x’_1}$$ به‌صورت زیر است:

$${{x’_1}\left( t \right) }={ 3{e^{3t}}\left( {{C_1}\cos 2t + {C_2}\sin 2t} \right) } + {{e^{3t}}\left( { – 2{C_1}\sin 2t + 2{C_2}\cos 2t} \right) } \\= {{e^{3t}}\left[ {\left( {3{C_1} + 2{C_2}} \right)\cos 2t }\right.}+{\left.{ \left( {3{C_2} – 2{C_1}} \right)\sin 2t} \right].}$$

با جایگذاری $$x_1$$ و $${x’_1}$$ در معادله اول داریم:

$${{{e^{3t}}\left[ {\left( {3{C_1} + 2{C_2}} \right)\cos 2t }\right.}+{\left.{ \left( {3{C_2} – 2{C_1}} \right)\sin 2t} \right] } = {5{e^{3t}}\left( {{C_1}\cos 2t + {C_2}\sin 2t} \right) }+{ 2{x_2},\;\;}}$$

$$\Rightarrow {{2{x_2} }={ {e^{3t}}\left[ {\left( {2{C_2} – 2{C_1}} \right)\cos 2t }\right.}-{\left.{ \left( {2{C_2} + 2{C_1}} \right)\sin 2t} \right],\;\;}}$$

$$\Rightarrow {{{x_2} }={ {e^{3t}}\left[ {\left( {{C_2} – {C_1}} \right)\cos 2t }\right.}-{\left.{ \left( {{C_2} + {C_1}} \right)\sin 2t} \right].}}$$

در نهایت، جواب عمومی به‌صورت زیر خواهد بود:

$$\left\{ \begin{array}{l} {{x_1}\left( t \right) }={ {e^{3t}}\left[ {{C_1}\cos 2t + {C_2}\sin 2t} \right]}\\ {{x_2}\left( t \right) }={ {e^{3t}}\left[ {\left( {{C_2} – {C_1}} \right)\cos 2t }\right.}-{\left.{ \left( {{C_2} + {C_1}} \right)\sin 2t} \right]} \end{array} \right.$$

روش ماتریس نمایی

ماتریس مربعی $$A$$ را با ابعاد $$n \times n$$ در نظر بگیرید که درایه های آن ممکن است حقیقی یا مختلط باشند.

از آن‌جایی که ماتریس $$A$$ مربعی است، به توان رساندن برای آن تعریف می‌شود و قابل انجام است:‌

$${{A^0} = I,\;\;{A^1} = A,\;\;}\kern-0.3pt {{A^2} = A \cdot A,\;\;}\kern-0.3pt {{A^3} = {A^2} \cdot A,\; \ldots ,}\kern-0.3pt {{A^k} = \underbrace {A \cdot A \cdots A}_\text{k times},}$$

که در آن، $$I$$ یک ماتریس واحد یا همانی مرتبه $$n$$ است.

سری توانی بی‌نهایت ماتریسی را به‌صورت زیر تشکیل می‌دهیم:

$${I + \frac{t}{{1!}}A + \frac{{{t^2}}}{{2!}}{A^2} }+{ \frac{{{t^3}}}{{3!}}{A^3} + \cdots }+{ \frac{{{t^k}}}{{k!}}{A^k} + \cdots }$$

مجموع سری بی‌نهایت، ماتریس نمایی نامیده شده و با $${e^{tA}}$$ نشان داده می‌شود:

$${e^{tA}} = \sum\limits_{k = 0}^\infty {\frac{{{t^k}}}{{k!}}{A^k}} .$$

این سری کاملاً همگرا است.

در حالتی که ماتریس از یک عدد $$a$$ تشکیل شده باشد، یعنی اندازه آن $$1 \times 1$$ است. این فرمول را می‌توان به یک فرمول معین برای بسط به تابع نمایی $${e^{at}}$$ در قالب یک سری مک‌لوران تبدیل کرد:

$${{e^{at}} = 1 + at + \frac{{{a^2}{t^2}}}{{2!}} + \frac{{{a^3}{t^3}}}{{3!}} + \cdots } = {\sum\limits_{k = 0}^\infty {\frac{{{a^k}{t^k}}}{{k!}}} .}$$

مشخصات ماتریس نمایی به‌صورت زیر است:‌

• اگر $$A$$ یک ماتریس صفر باشد، آن‌گاه $${e^{tA}} = {e^0} = I$$ ($$I$$ ماتریس همانی است)
• اگر $$A = I$$، آن‌گاه $${e^{tI}} = {e^t}I$$
• اگر $$A$$ معکس داشته باشد، آن‌گاه $${e^A}{e^{ – A}} = I$$
• اگر $$m$$ و $$n$$ اعداد حقیقی یا مختلط دلخواهی باشند، آن‌گاه $${e^{mA}}{e^{nA}} = {e^{\left( {m + n} \right)A}}$$
• مشتق ماتریس نمایی به‌صورت $$\frac{d}{{dt}}\left( {{e^{tA}}} \right) = A{e^{tA}}$$ است.
• فرض کنید $$H$$ یک تبدیل خطی نامنفرد باشد. در این صورت اگر $$A = HM{H^{ – 1}}$$، آن‌گاه $${e^{tA}} = H{e^{tM}}{H^{ – 1}}$$.

از ماتریس نمایی می‌توان برای حل دستگاه معادلات دیفرانسیل استفاده کرد. یک دستگاه معادلات دیفرانسیل خطی همگن را در نظر بگیرید که به فرم ماتریسی زیر نوشته شده است:

$$\mathbf{X}’\left( t \right) = A\mathbf{X}\left( t \right)$$

جواب عمومی این دستگاه معادلات را می‌توان با کمک ماتریس نمایی به‌صورت زیر نوشت:

$$\mathbf{X}\left( t \right) = {e^{tA}}\mathbf{C}$$

که در آن، $$\mathbf{C} ={\left( {{C_1},{C_2}, \ldots ,{C_n}} \right)^T}$$، بردار دلخواهی به‌طول $$n$$ است. نماد «$${}^T$$»، ترانهاده ماتریس را نشان می‌دهد. در فرمول اخیر، نمی‌توانیم بردار $$\mathbf{C}$$ را قبل از ماتریس نمایی بنویسیم، زیرا در این صورت، ضرب $$\mathop {\mathbf{C}}\limits_{\left[ {n \times 1} \right]} \mathop {{e^{tA}}}\limits_{\left[ {n \times n} \right]}$$ تعریف نمی‌شود.

برای یک مسئله مقدار اولیه (مسئله کوشی)، درایه‌های $$\mathbf{C}$$ را با شرایط اولیه بیان کرد. در این حالت، حل دستگاه همگن را می‌توان به‌صورت زیر نوشت:

$${\mathbf{X}\left( t \right) = {e^{tA}}{\mathbf{X}_0}\;\;}$$

که در آن، $${{\mathbf{X}_0} = \mathbf{X}\left( {t = {t_0}} \right)}$$.

بنابراین، اگر ماتریس نمایی را محاسبه کنیم، می‌توانیم جواب دستگاه معادلات همگن را به‌دست آوریم. برای محاسبه آن می‌توانیم از سری بی‌نهایت استفاده کنیم که در تعریف ماتریس نمایی وجود دارد. هرچند، این روش مقدار ماتریس نمایی را به‌صورت تقریبی نتیجه خواهد داد. برای حل مسئله، می‌توان از یک روش جبری مبتنی بر آخرین ویژگی ماتریس نمایی استفاده کرد که در بالا ذکر کردیم.

الگوریتم حل دستگاه معادلات دیفرانسیل با استفاده از ماتریس نمایی

1. مقادیر ویژه $$\lambda _i$$ ماتریس $$A$$ را محاسبه کنید.
2. بردارهای ویژه مربوط به مقادیر ویژه را به‌دست آورید.
3. ماتریس تبدیل خطی نامنفرد $$H$$ را با یافتن بردار ویژه‌ها تشکیل دهید.
4. فرم نرمال جردن ($$J$$) ماتریس $$A$$ را با استفاده از فرمول $$J = {H^{ – 1}}AH$$ محاسبه کنید.
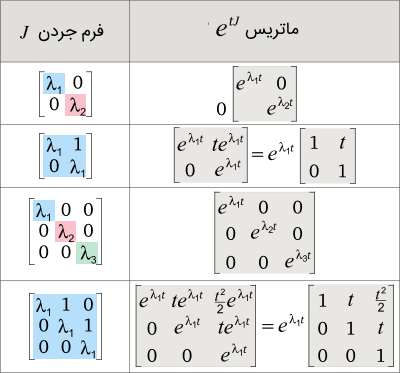
5. با داشتن فرم جردن $$J$$، می‌توانید ماتریس $${e^{tJ}}$$ را بنویسید. فرمول‌های متناظر با این تبدیل، از تعریف ماتریس نمایی به‌دست می‌آیند. ماتریس $${e^{tJ}}$$ برای چند فرم جردن ساده در جدول زیر آورده شده‌اند.

6. ماتریس نمایی $${e^{tA}}$$ را با فرمول زیر محاسبه کنید:

$${e^{tA}} = H{e^{tJ}}{H^{ – 1}}$$

7. جواب عمومی دستگاه را بنویسید:

$$\mathbf{X}\left( t \right) = {e^{tA}}\mathbf{C}$$

برای یک سیستم مرتبه دوم، جواب عمومی به‌صورت زیر خواهد بود:

$${\mathbf{X}\left( t \right) = \left[ {\begin{array}{*{20}{c}}<br /> x\\<br /> y<br /> \end{array}} \right] }={ {e^{tA}}\left[ {\begin{array}{*{20}{c}}<br /> {{C_1}}\\<br /> {{C_2}}<br /> \end{array}} \right],}$$

که در آن،‌ $${C_1}$$ و $${C_2}$$ ثوابت دلخواه هستند.

مثال ۴

جواب عمومی دستگاه معادلات زیر را به‌دست آورید.

$${\frac{{dx}}{{dt}} = 2x + 3y,\;\;}\kern-0.3pt{\frac{{dy}}{{dt}} = 3x + 2y.}$$

حل: برای محاسبه جواب این دستگاه معادلات، ابتدا مقادیر وبژه ماتریس $$A$$ را محاسبه می‌کنیم:

$${{\det \left( {A – \lambda I} \right) }={ \left| {\begin{array}{*{20}{c}}<br /> {2 – \lambda }&3\\<br /> 3&{2 – \lambda }<br /> \end{array}} \right| = 0,\;\;}}\\<br /> \Rightarrow<br /> {{\left( {2 – \lambda } \right)^2} – 9 = 0,\;\;}\Rightarrow<br /> {4 – 4\lambda + {\lambda ^2} – 9 = 0,\;\;}\\<br /> \Rightarrow<br /> {{\lambda ^2} – 4\lambda – 5 = 0,\;\;}\Rightarrow<br /> {{\lambda _1} = 5,\;{\lambda _2} = – 1.}$$

اکنون بردار ویژه‌های متناظر با هر مقدار ویژه را به‌دست می‌آوریم. برای $${\lambda _1} = 5$$، داریم:

$${\left[ {\begin{array}{*{20}{c}}<br /> {2 – 5}&3\\<br /> 3&{2 – 5}<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{V_{11}}}\\<br /> {{V_{21}}}<br /> \end{array}} \right] = \mathbf{0},\;\;}\Rightarrow<br /> {\left[ {\begin{array}{*{20}{c}}<br /> { – 3}&3\\<br /> 3&{ – 3}<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{V_{11}}}\\<br /> {{V_{21}}}<br /> \end{array}} \right] = \mathbf{0},\;\;}\\<br /> \Rightarrow<br /> {3{V_{11}} – 3{V_{21}} = 0,\;\;}\Rightarrow<br /> {{V_{11}} – {V_{21}} = 0.}$$

با تعریف $${V_{21}} = t$$، بردار ویژه $${\mathbf{V}_1} = {\left( {{V_{11}},{V_{21}}} \right)^T}$$ به‌دست می‌آید:

$${{V_{21}} = t,\;\; }\Rightarrow {{V_{11}} = {V_{21}} = t,\;\;}\Rightarrow<br /> {{\mathbf{V}_1} = \left[ {\begin{array}{*{20}{c}}<br /> {{V_{11}}}\\<br /> {{V_{21}}}<br /> \end{array}} \right] = \left[ {\begin{array}{*{20}{c}}<br /> t\\<br /> t<br /> \end{array}} \right] }={ t\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> 1<br /> \end{array}} \right] }<br /> \sim {\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> 1<br /> \end{array}} \right].}$$

به طریق مشابه، بردار ویژه $${\mathbf{V}_2} = {\left( {{V_{12}},{V_{22}}} \right)^T}$$ متناظر با مقدار ویژه $${\lambda _2} = -1$$ را محاسبه می‌کنیم:

$${\left[ {\begin{array}{*{20}{c}}<br /> {2 – \left( { – 1} \right)}&3\\<br /> 3&{2 – \left( { – 1} \right)}<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{V_{12}}}\\<br /> {{V_{22}}}<br /> \end{array}} \right] = 0,\;\;}\Rightarrow<br /> {\left[ {\begin{array}{*{20}{c}}<br /> 3&3\\<br /> 3&3<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{V_{12}}}\\<br /> {{V_{22}}}<br /> \end{array}} \right] = 0,\;\;}\\<br /> \Rightarrow<br /> {3{V_{12}} + 3{V_{22}} = 0,\;\;}\Rightarrow<br /> {{V_{12}} + {V_{22}} = 0.}$$

با در نظر گرفتن $${V_{22}} = t$$، داریم: $${V_{12}} = -{V_{22}}= -t$$. بنابراین:

$${{\mathbf{V}_2} = \left[ {\begin{array}{*{20}{c}}<br /> {{V_{12}}}\\<br /> {{V_{22}}}<br /> \end{array}} \right] = \left[ {\begin{array}{*{20}{c}}<br /> { – t}\\<br /> t<br /> \end{array}} \right] }<br /> = {t\left[ {\begin{array}{*{20}{c}}<br /> { – 1}\\<br /> 1<br /> \end{array}} \right] }<br /> \sim {\left[ {\begin{array}{*{20}{c}}<br /> { – 1}\\<br /> 1<br /> \end{array}} \right].}$$

اکنون که بردار ویژه‌های $${\mathbf{V}_1}$$ و $${\mathbf{V}_۲}$$ را به‌دست آورده‌ایم، می‌توانیم ماتریس $$H$$ را تشکیل دهیم:

$$H = \left[ {\begin{array}{*{20}{c}}<br /> 1&{ – 1}\\<br /> 1&1<br /> \end{array}} \right].$$

در ادامه، ماتریس معکوس $${H^{ – 1}}$$ را حساب می‌کنیم:

$${\Delta \left( H \right) = \left| {\begin{array}{*{20}{c}}<br /> 1&{ – 1}\\<br /> 1&1<br /> \end{array}} \right| }={ 1 + 1 }={ 2,}$$

$${{H^{ – 1}} }={ \frac{1}{{\Delta \left( H \right)}}{\left[ {\begin{array}{*{20}{c}}<br /> {{H_{11}}}&{{H_{12}}}\\<br /> {{H_{21}}}&{{H_{22}}}<br /> \end{array}} \right]^T} }<br /> = {\frac{1}{2}{\left[ {\begin{array}{*{20}{c}}<br /> 1&{ – 1}\\<br /> 1&1<br /> \end{array}} \right]^T} }<br /> = {\frac{1}{2}\left[ {\begin{array}{*{20}{c}}<br /> 1&1\\<br /> { – 1}&1<br /> \end{array}} \right].}$$

از آن‌جایی که در این مثال، مقادیر ویژه، ریشه‌های ساده معادله مشخصه هستند،‌ می‌توانیم فرم جردن را بنویسیم که یک ماتریس قطری خواهد بود:

$${J = \left[ {\begin{array}{*{20}{c}}<br /> {{\lambda _1}}&0\\<br /> 0&{{\lambda _2}}<br /> \end{array}} \right] }={ \left[ {\begin{array}{*{20}{c}}<br /> \color{blue}5&0\\<br /> 0&\color{red}{ – 1}<br /> \end{array}} \right].}$$

درستی فرم جردن بالا را می‌توانیم با استفاده از فرمول تبدیل ماتریس $$A$$ به فرم نرمال جردن $$J$$  تحقیق کنیم:

$${J = {H^{ – 1}}AH }<br /> = {\frac{1}{2}\left[ {\begin{array}{*{20}{c}}<br /> 1&1\\<br /> { – 1}&1<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> 2&3\\<br /> 3&2<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> 1&{ – 1}\\<br /> 1&1<br /> \end{array}} \right] }$$

$$={\frac{1}{2}\left[ {\begin{array}{*{20}{c}}<br /> 5&5\\<br /> 1&{ – 1}<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> 1&{ – 1}\\<br /> 1&1<br /> \end{array}} \right] }<br /> = {\frac{1}{2}\left[ {\begin{array}{*{20}{c}}<br /> {5 + 5}&{ – 5 + 5}\\<br /> {1 – 1}&{ – 1 – 1}<br /> \end{array}} \right] }$$

$$= {\frac{1}{2}\left[ {\begin{array}{*{20}{c}}<br /> {10}&0\\<br /> 0&{ – 2}<br /> \end{array}} \right] }<br /> = {\left[ {\begin{array}{*{20}{c}}<br /> 5&0\\<br /> 0&{ – 1}<br /> \end{array}} \right] = J.}$$

اکنون ماتریس $${e^{tJ}}$$ را تشکیل می‌دهیم (این ماتریس را نیز می‌توان ماتریس نمایی نامید):

$${e^{tJ}} = \left[ {\begin{array}{*{20}{c}}<br /> {{e^{5t}}}&0\\<br /> 0&{{e^{ – t}}}<br /> \end{array}} \right].$$

ماتریس نمایی $${e^{tA}}$$ به‌صورت زیر محاسبه می‌شود:

$${{e^{tA}} = H{e^{tJ}}{H^{ – 1}} }<br /> = {{\left[ {\begin{array}{*{20}{c}}<br /> 1&{ – 1}\\<br /> 1&1<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{e^{5t}}}&0\\<br /> 0&{{e^{ – t}}}<br /> \end{array}} \right] \cdot}\kern0pt{ \frac{1}{2}\left[ {\begin{array}{*{20}{c}}<br /> 1&1\\<br /> { – 1}&1<br /> \end{array}} \right] }}\\<br /> = {\frac{1}{2}\left[ {\begin{array}{*{20}{c}}<br /> {{e^{5t}}}&{ – {e^{ – t}}}\\<br /> {{e^{5t}}}&{{e^{ – t}}}<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> 1&1\\<br /> { – 1}&1<br /> \end{array}} \right] }\\<br /> = {\frac{1}{2}\left[ {\begin{array}{*{20}{c}}<br /> {{e^{5t}} + {e^{ – t}}}&{{e^{5t}} – {e^{ – t}}}\\<br /> {{e^{5t}} – {e^{ – t}}}&{{e^{5t}} + {e^{ – t}}}<br /> \end{array}} \right].}$$

در نتیجه، جواب عمومی دستگاه معادلات این مثال، به‌صورت زیر خواهد بود:

$${\mathbf{X}\left( t \right) = \left[ {\begin{array}{*{20}{c}}<br /> x\\<br /> y<br /> \end{array}} \right] }<br /> = {{e^{tA}}\left[ {\begin{array}{*{20}{c}}<br /> {{C_1}}\\<br /> {{C_2}}<br /> \end{array}} \right] }<br /> = {\frac{1}{2}\left[ {\begin{array}{*{20}{c}}<br /> {{e^{5t}} + {e^{ – t}}}&{{e^{5t}} – {e^{ – t}}}\\<br /> {{e^{5t}} – {e^{ – t}}}&{{e^{5t}} + {e^{ – t}}}<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{C_1}}\\<br /> {{C_2}}<br /> \end{array}} \right],}$$

که در آن، $$C_1$$ و $$C_2$$ اعداد دلخواهی هستند.

جواب فوق را می‌توان به فرم دیگری نیز نمایش داد:

$${\mathbf{X}\left( t \right) = \left[ {\begin{array}{*{20}{c}}<br /> x\\<br /> y<br /> \end{array}} \right] }<br /> = {\frac{1}{2}\cdot}\kern0pt{\left[ {\begin{array}{*{20}{c}}<br /> {{C_1}{e^{5t}} + {C_1}{e^{ – t}} \text{+} {C_2}{e^{5t}} – {C_2}{e^{ – t}}}\\<br /> {{C_1}{e^{5t}} – {C_1}{e^{ – t}} \text{+} {C_2}{e^{5t}} + {C_2}{e^{ – t}}}<br /> \end{array}} \right] }\\<br /> = {\frac{1}{2}\cdot}\kern0pt{\left[ {\begin{array}{*{20}{c}}<br /> {{e^{5t}}\left( {{C_1} + {C_2}} \right) + {e^{ – t}}\left( {{C_1} – {C_2}} \right)}\\<br /> {{e^{5t}}\left( {{C_1} + {C_2}} \right) – {e^{ – t}}\left( {{C_1} – {C_2}} \right)}<br /> \end{array}} \right] }\\<br /> = {\frac{1}{2}\left( {{C_1} + {C_2}} \right){e^{5t}}\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> 1<br /> \end{array}} \right] + \frac{1}{2}\left( {{C_1} + {C_2}} \right){e^{ – t}}\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> 1<br /> \end{array}} \right] }\\<br /> = {{B_1}{e^{5t}}\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> 1<br /> \end{array}} \right] + {B_2}{e^{ – t}}\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> 1<br /> \end{array}} \right],}$$

که در آن، $$B_1$$ و $$B_2$$ ثابت‌های دلخواه متناظر با $$C_1$$ و $$C_2$$ هستند.