مقدار ویژه تکراری – به زبان ساده

همان‌طور که در مطالب گذشته وبلاگ فرادرس نیز عنوان شد، یکی از روش‌های بدست آوردن پاسخ معادله دیفرانسیل، استفاده از مفهوم بردار و مقدار ویژه است. در این مطلب قصد داریم تا حالت خاصی از ماتریس ضرایبِ یک معادله دیفرانسیل، که در آن مقدار ویژه تکراری وجود دارد را مورد بررسی قرار دهیم.

مقدار ویژه تکراری

در ابتدا سیستمی از معادلات دیفرانسیل را به صورت زیر در نظر بگیرید.

$$\large \overrightarrow x ^ { \prime } = A \overrightarrow x$$

ابتدا به ساکن در نظر داشته باشید فرض بر این است که ماتریس $$A$$ از مرتبه دو است. حال فرض کنید سیستم فوق ریشه‌های تکراری داشته باشد. با توجه به مرتبه در نظر گرفته شده برای $$A$$، می‌توان گفت که این ماتریس دارای دو ریشه تکراریِ $$\lambda$$ است. از طرفی ما به دو معادله نیاز داریم. این در حالی است که دو ریشه تکراری تنها پاسخ زیر را به ما می‌دهد.

$$\large { \overrightarrow x _ 1 } = \overrightarrow \eta { { \bf { e } } ^ { \lambda t } }$$

بنابراین باید معادله دوم را نیز تعیین کنیم. در نتیجه به نظر می‌رسد هنگام حل یک معادله درجه دوم به مسئله‌ای مشابه خواهیم رسید. بدین منظور پاسخ دوم را به صورت زیر در نظر می‌گیریم.

$$\large \overrightarrow x = t \,{ { \bf{ e } } ^ { \lambda t } } \overrightarrow \eta$$

حال کافی است پاسخ در نظر گرفته شده را در معادله اولیه قرار دهید. با انجام این کار خواهیم داشت.

$$\large \begin {align*} A \overrightarrow \eta & = \lambda \overrightarrow \eta \hspace {0.25in } \Rightarrow \hspace {0.25in} \left ( { A - \lambda I } \right ) \overrightarrow \eta = \overrightarrow 0 \\ \overrightarrow \eta & = \overrightarrow 0\end {align*}$$

دقت داشته باشید که پاسخ در نظر گرفته شده به صورت بردار است، بنابراین از ترم سمت چپ با استفاده از قانون مشتق‌گیری ضربی، مشتق گرفته شده است. سمت چپ عبارت فوق از دو ترم تشکیل شده و یکی از آن‌ها در $$t$$ ضرب شده است. بنابراین به منظور برقراری عبارت فوق، عبارت ضرب شده در $$t$$ باید با $$A \overrightarrow \eta t { { \bf { e } } ^ { \lambda t } }$$ برابر باشد. از طرفی ضریب ترمِ $${ { \bf { e } } ^ { \lambda t } }$$ در سمت چپ نیز باید برابر با صفر باشد. در نتیجه نهایتا دو رابطه زیر بدست می‌آیند.

$$\large \begin {align*} A \overrightarrow \eta & = \lambda \overrightarrow \eta \hspace {0.25in} \Rightarrow \hspace {0.25in} \left ( { A - \lambda I } \right ) \overrightarrow \eta = \overrightarrow 0 \\ \overrightarrow \eta & = \overrightarrow 0 \end {align*}$$

رابطه اول مفهومی جدید را بیان نمی‌کند چرا که می‌گوید $$\lambda$$ مقدار ویژه و $$\overrightarrow \eta$$ بردار ویژه است. این در حالی است که عبارت دوم یک معادله محسوب می‌شود. با توجه به این‌که $$\overrightarrow \eta$$، یک بردار ویژه است، بنابراین مقدار آن نمی‌تواند صفر باشد؛ این در حالی است که معادله بالا می‌گوید این بردار باید برابر با صفر باشد. در نتیجه فرض انجام شده به منظور دست‌یابی به پاسخ دوم درست نیست. از این رو پاسخ دوم را به صورت زیر در نظر می‌گیریم (این حدس بر اساس تجربه به دست آمده است).

$$\large \overrightarrow x = t \, { { \bf { e } } ^ { \lambda t } } \overrightarrow \eta + { { \bf { e } } ^ { \lambda t } } \overrightarrow \rho$$

در رابطه فوق $$\overrightarrow \rho$$ برداری مجهول است که باید آن را بیابیم. دقیقا مشابه با حدس اول، پاسخ در نظر گرفته شده را در معادله قرار می‌دهیم.

$$\large \begin {align*} \overrightarrow \eta { { \bf { e } } ^ { \lambda t } } + \lambda \overrightarrow \eta t { { \bf { e } } ^ { \lambda t } } + \lambda \overrightarrow \rho { { \bf{ e } } ^ { \lambda t } } & = A \left ( { \overrightarrow \eta t { { \bf { e } } ^ { \lambda t } } + \overrightarrow \rho { { \bf { e } } ^ { \lambda t } } } \right ) \\ \left ( { \overrightarrow \eta + \lambda \overrightarrow \rho } \right ) { { \bf { e } } ^ { \lambda t } } + \lambda \overrightarrow \eta t { { \bf { e } } ^ { \lambda t } } & = A \overrightarrow \eta t { { \bf { e } } ^ { \lambda t } } + A \overrightarrow \rho { { \bf { e } } ^ { \lambda t } } \end{align*}$$

در این مرحله نیز با برابر قرار دادن ضرایب ترم‌های مشابه داریم:

$$\large \begin {align*} \lambda \overrightarrow \eta & = A \overrightarrow \eta & \Rightarrow \hspace {0.25in} \left ( { A - \lambda I } \right ) \overrightarrow \eta & = \overrightarrow 0 \\ \overrightarrow \eta + \lambda \overrightarrow \rho & = A \overrightarrow \rho & \Rightarrow \hspace {0.25in} \left ( { A - \lambda I } \right ) \overrightarrow \rho & = \overrightarrow \eta \end {align*}$$

همانند حدس اول، معادله اول مفهوم جدیدی را بیان نمی‌کند. معادله دوم نیز بیان می‌کند که $$\overrightarrow \rho$$، پاسخی از معادله است. در نتیجه به نظر می‌رسد حدس دوم صحیح است. بنابراین پاسخ دوم برابر است با:

$$\large { \overrightarrow x _ 2 } = t \, { { \bf { e } } ^ { \lambda t } } \overrightarrow \eta + { { \bf{ e } }^ { \lambda t } } \overrightarrow \rho$$

همچنین $$\overrightarrow \rho$$ با استفاده از معادله زیر بدست خواهد آمد.

$$\large \left ( { A - \lambda I } \right ) \overrightarrow \rho = \overrightarrow \eta$$

از طرفی این پاسخ و پاسخ اول از نظر خطی نسبت به هم مستقل خطی هستند. در نتیجه پاسخ عمومی برابر است با:

$$\large \overrightarrow x = { c _ 1 } \, { { \bf{ e } } ^ { \lambda t } } \overrightarrow \eta + {c_2}\left ( { t \, { { \bf { e } } ^ { \lambda t } } \overrightarrow \eta + { { \bf { e } } ^ { \lambda t } } \overrightarrow \rho } \right )$$

در ادامه مثال‌هایی ارائه شده که مطالعه آن‌ها را جهت درک بهتر این مبحث توصیه می‌کنیم.

مثال ۱

پاسخ معادله مقدار اولیه زیر را با استفاده از روش مقدار ویژه تکراری بیابید.

$$ \large \overrightarrow x ^ { \prime } = \left ( {\begin {array} {*{20}{c} } 7 & 1 \\ { - 4 } & 3 \end {array}} \right ) \overrightarrow x \hspace {0.25in} , \ \ \overrightarrow x \left ( 0 \right ) = \left ( { \begin {array}{*{20} { c } } 2 \\ { - 5 } \end{array}} \right ) $$

در ابتدا مقادیر ویژه ماتریس ضرایب را می‌یابیم. بدین منظور داریم:

$$ \large \begin{align*}\det \left( {A - \lambda I} \right) & = \left| {\begin {array} {*{ 20 } { c } } { 7 - \lambda }&1 \\ { - 4 } & { 3 - \lambda }\end{array}} \right|\\ & = {\lambda ^ 2 } - 10 \lambda + 25\\ & = {\left( {\lambda - 5} \right ) ^ 2 } \hspace {0.25in} \Rightarrow \hspace {0.25in}{\lambda _ { 1 , 2 } } = 5 \end {align*} $$

همان‌طور که می‌بینید این ماتریس دارای دو مقدار ویژه مشابه است. لذا این مسئله را باید با استفاده از روش ارائه شده در این مطلب حل کرد. از این رو در گام دوم بردار ویژه متناسب با این مقدار را بدست آورد.

$$ \large \left ( { \begin {array} {*{20} { c } } 2 & 1 \\ { - 4 } & { - 2 } \end {array}} \right ) \left ( { \begin{array}{*{20} { c} } { { \eta _1 } } \\ { { \eta _ 2 } } \end{array}} \right ) = \left( {\begin{array} {*{20}{c} } 0 \\0\end {array}} \right ) \hspace {0.25in} \Rightarrow \,\hspace {0.25in} 2 { \eta _1 } + {\eta _2} = 0 \hspace {0.25in} { \eta _ 2 } = - 2 { \eta _ 1 } $$

در نتیجه بردار‌های ویژه نیز برابرند با:

$$ \large \begin {align*} \overrightarrow \eta & = \left ( {\begin{array}{*{20}{c}}{ { \eta _ 1 } } \\ { - 2 { \eta _ 1 } } \end {array}} \right ) & \hspace{0.25in} { \eta _ 1 } & \ne 0\\ { { \overrightarrow \eta } ^ { \left ( 1 \right ) } } & = \left ( { \begin {array} {*{20} { c } } 1 \\ { - 2 } \end {array}} \right ) & \hspace {0.25in} { \eta _ 1 } & = 1 \end {align*} $$

در قدم بعدی بردار $$\overrightarrow { \rho }$$ را در بردار‌های ویژه ضرب کرده و به عبارت زیر می‌رسیم.

$$ \large \left ( { \begin{array}{*{20} { c } } 2 & 1 \\ { - 4 } & { - 2 } \end {array}} \right ) \left ( { \begin {array}{*{20} { c } } { { \rho _1}}\\{ {\rho _ 2 } } \end {array}} \right ) = \left ( { \begin {array} {*{20}{ c }‌} 1 \\ { - 2 } \end {array}} \right ) \hspace {0.25in} \Rightarrow \, \hspace {0.25in} 2 { \rho _ 1 } + { \rho _ 2 } = 1 \hspace {0.25in}{\rho _ 2 } = 1 - 2 { \rho _1 } $$

توجه داشته باشید که عبارت فوق تقریبا معادل با سیستمی است که به منظور بدست آوردن بردار‌های ویژه از آن استفاده کردیم. تنها تفاوت در سمت راست معادله است. از این رو محتمل‌ترین حالت برای $$\overrightarrow \rho$$ به صورت زیر است.

$$ \large \overrightarrow \rho = \left ( { \begin {array} {*{20} { c } } { { \rho _ 1 } } \\ { 1 - 2 { \rho _ 1 } } \end {array}} \right)\hspace {0.25in} \Rightarrow \hspace{0.25in}\overrightarrow \rho = \left ( {\begin{array} {*{20 } { c } } 0 \\ 1 \end{array}} \right) \hspace {0.25in}{\mbox {if } } { \rho _ 1 } = 0 $$

در این حالت بر خلاف سیستم بردار‌های ویژه، بردار ویژه را می‌توان به صورتی دلخواه تصور کرد. با توجه به مقدار $$\rho$$، پاسخ عمومی به صورت زیر در خواهد آمد.

$$ \large \overrightarrow x \left( t \right) = { c _1 } { { \bf { e } } ^ { 5 t } } \left( {\begin{array}{*{20} { c } } 1 \\ { - 2}\end {array}} \right ) + { c _ 2 } \left( { { { \bf { e } } ^ { 5 t } } t \left ( {\begin{array}{*{20} { c } } 1 \\ { - 2 } \end{array} } \right) + {{\bf { e } } ^ { 5 t } } \left ( {\begin{array}{*{20} { c } } 0 \\ 1 \end {array}} \right ) } \right ) $$

با اعمال شرایط اولیه، ثابت‌ها برابر می‌شوند با:

$$ \large \left ( { \begin {array} {*{20}{ c } } 2 \\ { - 5 } \end {array} } \right ) = \overrightarrow x \left( 0 \right) = { c _ 1 } \left ( {\begin {array} {*{20} { c } } 1 \\ { - 2 } \end {array}} \right ) + { c _ 2 } \left ( { \begin {array}{*{ 20 } { c } } 0 \\ 1 \end {array}} \right ) $$

$$ \left. { \begin {array} {*{20}{r} } { { c _ 1 } = 2 } \\ { - 2 { c _ 1 } + { c _ 2 } = - 5 } \end {array}} \right \} \hspace {0.25in} \Rightarrow \hspace {0.25in} {c _ 1 } = 2,\,\,\,{c_2} = - 1 $$

بنابراین پاسخ نهایی برابر است با:

$$ \large \begin {align*} \overrightarrow x \left ( t \right ) & = 2 { { \bf { e } } ^ { 5 t } } \left ( { \begin {array} {*{20} { c } } 1 \\{ - 2}\end {array}} \right ) - \left ( { t { { \bf { e } } ^ { 5 t } } \left ( { \begin {array} {*{20} { c } } 1 \\ { - 2 } \end{array}} \right ) + { { \bf { e } } ^ { 5 t } } \left ( { \begin {array} {*{20} { c } } 0 \\ 1 \end {array}} \right)} \right ) \\ & = { { \bf { e } } ^ { 5 t } } \left( {\begin{array}{*{20} { c } } 2 \\ { - 4 } \end {array} } \right ) - { { \bf { e } } ^ { 5 t } } t \left ( { \begin{array}{*{20} { c } } 1 \\ { - 2 } \end{array}} \right ) - { { \bf{e}}^{5t}}\left( {\begin{array}{*{20} { c } } 0 \\ 1 \end{array}} \right ) \\ & = {{\bf { e } } ^ { 5 t } } \left( {\begin{array}{*{20} { c } } 2 \\{ - 5 } \end{array}} \right) - { { \bf { e } } ^ { 5 t } } t \left ( { \begin {array} {*{20} { c } } 1 \\ { - 2}\end{array}} \right)\end{align*}$$

مثال ۲

پاسخ معادله مقدار اولیه زیر را بیابید.

$$ \large \overrightarrow x ^ { \prime } = \left ( { \begin {array} {*{20} { c } } { - 1 } & { \frac { 3 } { 2 } } \\ { - \frac { 1 } { 6 } } & { - 2 } \end {array}} \right ) \overrightarrow x \hspace {0.25in} \overrightarrow x \left ( 2 \right ) = \left ( { \begin {array} {*{20} { c } } 1 \\ 0 \end {array}} \right ) $$

فیلم آموزش ریاضی فیزیک ۱ + مفاهیم کلیدی در فرادرس

کلیک کنید

در اولین گام باید مقادیر ویژه ماتریس فوق را بیابیم. بنابراین داریم:

$$ \large \begin {align*} \det \left ( { A - \lambda I } \right ) & = \left| { \begin {array} {*{20} { c } } { - 1 - \lambda } & { \frac { 3 } { 2 } } \\ { - \frac { 1 } { 6 } } & { - 2 - \lambda } \end{array}} \right| \\ & = {\lambda ^2} + 3\lambda + \frac { 9 } { 4 } \\ & = { \left ( { \lambda + \frac { 3 } { 2 } } \right ) ^2 } \hspace {0.25in} \Rightarrow \hspace {0.25in} { \lambda _ { 1 , 2 } } = - \frac { 3 } { 2 } \end {align*} $$

در نتیجه بردار‌های ویژه نیز برابرند با:

$$ \large \left ( { \begin {array} {*{20} { c } } { \frac { 1 } { 2 } } & { \frac { 3 } { 2 } } \\ { - \frac { 1 } { 6 } } & { - \frac { 1 } { 2 } } \end {array}} \right ) \left( {\begin{array}{*{20} { c } } { { \eta _1 } } \\ { { \eta _ 2 } } \end{array}} \right) = \left( {\begin{array}{*{20}{ c } } 0 \\ 0 \end{array} } \right)\hspace {0.25in} \Rightarrow \,\hspace {0.25in}\frac { 1 } { 2 } { \eta _ 1 } + \frac { 3 } { 2 }{\eta _2} = 0\,\,\,\,\,\,\,\,\,{\eta _1} = - 3 { \eta _2 } $$

با بدست آمدن بردار‌های ویژه، بردار‌های $$\rho$$ نیز برابرند با:

$$ \large \left ( { \begin {array} {*{20} { c } } { \frac { 1 } { 2 } } & { \frac { 3 } { 2 } } \\ { - \frac { 1 } { 6 } } & { - \frac { 1 } { 2 } } \end{array}} \right ) \left ( { \begin{array} {*{20} { c } } { { \rho _1}}\\{ { \rho _ 2 } } \end {array} } \right ) = \left( {\begin{array} {*{20}{ c } } { - 3 } \\ 1 \end {array}} \right ) \hspace{0.25in} \Rightarrow \,\hspace {0.25in} \frac { 1 } { 2 } { \rho _ 1 } + \frac { 3 } { 2 } { \rho _ 2 } = - 3 \,\,\,\,\,\,\,\,\, { \rho _ 1 } = - 6 - 3 { \rho _2 } $$

$$ \large \overrightarrow \rho = \left( {\begin{array}{*{20}{ c } } { - 6 - 3{\rho _ 2 } } \\ { { \rho _2}}\end{array}} \right ) \hspace{0.25in} \Rightarrow \hspace{0.25in} \overrightarrow \rho = \left( { \begin{array}{*{ 20 } { c } } { - 6 } \\ 0 \end {array}} \right ) \hspace {0.25in} {\mbox{if } } { \rho _ 2 } = 0 $$

در نتیجه پاسخ عمومی معادله برابر است با:

$$ \large \overrightarrow x \left ( t \right ) = { c _ 1 } { { \bf { e } } ^ { - \frac { { 3 t } } { 2 } } } \left ( { \begin {array} {*{20}{c}}{ - 3 } \\1\end{array}} \right) + {c_2}\left( { t { { \bf { e } } ^ { - \frac { { 3 t } } {2 } } } \left( {\begin{array}{*{20} { c } } { - 3 } \\1\end{array}} \right) + { { \bf{e} } ^ { - \frac { { 3 t } } { 2 } } } \left( { \begin {array}{*{20}{ c } } { - 6 } \\ 0 \end {array}} \right ) } \right ) $$

با اعمال شرایط اولیه داریم:

$$ \large \left ( { \begin {array} {*{20} { c } } 1 \\ 0 \end {array}} \right ) = \overrightarrow x\left( 2 \right) = { c _ 1 } { {\bf{e}} ^ { - 3 } } \left ( { \begin {array} {*{20 } { c } } { - 3 } \\ 1 \end {array}} \right) + { c _ 2 } \left ( { 2 { { \bf { e } } ^ { - 3 } } \left ( { \begin{array}{*{20}{c}}{ - 3 } \\1\end{array}} \right) + { { \bf { e } } ^ { - 3 } } \left( { \begin{array}{*{20 } { c } } { - 6}\\0\end{array}} \right)} \right ) $$

نهایتا ثابت‌ها برابر با اعداد زیر بدست خواهند آمد.

$$ \large \left. {\begin{array}{*{20}{r}}{ - 3{{\bf{e}}^{ - 3 } } { c _ 1 } - 12 { { \bf { e } } ^ { - 3 } } { c _ 2 } = 1 } \\ { { { \bf { e } } ^ { - 3 } } { c _ 1 } + 2 { { \bf{e} } ^ { - 3 } } { c _ 2 } = 0 } \end{array}} \right\}\hspace {0.25in} \Rightarrow \hspace{0.25in}{c_1} = \frac { { { { \bf { e } } ^ 3 } } } { 3 } ,\,\,\,{ c _ 2 } = - \frac { { { { \bf { e } } ^ 3 } } } { 6 } $$

بنابراین پاسخ نهایی برابر است با:

$$ \large \begin{align*}\overrightarrow x\left( t \right) &= \frac { { { { \bf { e } } ^ 3 } } } { 3 } { { \bf { e } } ^ { - \frac { { 3 t } } { 2 } } } \left( {\begin{array}{*{20} { c } } { - 3}\\1\end{array}} \right ) - \frac{{{{\bf { e } } ^ 3 } } } { 6 } \left ( { t { { \bf { e } } ^ { - \frac { { 3 t } } { 2 } } } \left( {\begin{array}{*{20}{c}}{ - 3 } \\ 1 \end {array} } \right ) + { { \bf { e } } ^ { - \frac { { 3 t } } { 2 } } } \left ( {\begin {array} {*{20}{ c } } { - 6 } \\ 0 \end {array}} \right)} \right)\\ & = {{\bf{e}}^{ - \frac{{3t}}{2} + 3}}\left( {\begin{array} {*{20} { c } } 0 \\{\frac{1} { 3 } } \end{array}} \right) + t{{\bf{e}}^{ - \frac { { 3 t } } { 2 } + 3 } } \left( {\begin{array}{*{20} { c } } { \frac { 1 } { 2 } } \\ { - \frac{1}{6}}\end{array}} \right ) \end {align*} $$

مثال ۳

صفحه فازی سیستم زیر را ترسیم کنید.

$$ \large \overrightarrow x ^ { \prime } = \left ( { \begin {array} {*{20} { c } } { - 1 } & { \frac { 3 } { 2 } } \\ { - \frac { 1 } { 6 } } & { - 2 } \end {array} } \right ) \overrightarrow x$$

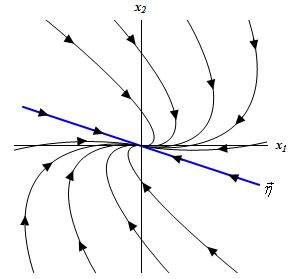
در ابتدا باید بگوییم که با توجه به منفی بودن مقادیر ویژه، خطوط فازی باید به سمت مرکز باشند. برای نمونه اجازه دهید تا مسیر عبور کرده از $$( 1 , 0 )$$ را بررسی کنیم. جهت بردار در این نقطه برابر است با:

$$ \large \left ( { \begin {array} {*{20} { c } } { - 1 } & { \frac { 3 } { 2 } } \\ { - \frac { 1 } { 6 } } & { - 2 } \end {array}} \right ) \left ( { \begin {array} {*{20}{ c } } 1 \\ 0 \end {array}} \right ) = \left ( { \begin{array} {*{20} { c } } { - 1 } \\ { - \frac { 1 } { 6 } } \end {array} } \right ) $$

همان‌طور که می‌بینید جهت بردار در این نقطه به سمت مرکز است. بنابراین می‌توان حدس زد صفحه فازی به صورت زیر باشد.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• معادلات دیفرانسیل - به زبان ساده
• بردار ویژه و مقدار ویژه - از صفر تا صد
• معادلات دیفرانسیل کامل — به زبان ساده

^^