ترمودینامیک آماری — مبانی و مفاهیم به زبان ساده

ترمودینامیک آماری نظریه‌ای است که از خواص مولکولی بمنظور پیش‌بینی رفتار مقادیر ماکروسکوپی ترکیبات بهره می‌گیرد. به عبارت دیگر، ترمودینامیک آماری ارتباطی بین خواص ماکروسکوپی موادِ در تعادل ترمودینامیکی با رفتار میکروسکوپی و حرکات داخل ماده ایجاد می‌کند. با وجود این‌که منشا ترمودینامیک آماری پیش از توسعه مکانیک کوانتوم است اما ترمودینامیک آماری مدرن فرض می‌کند مقادیر سطوح انر‌ژی کوانتیده در یک سیستم مشخص، معلوم هستند.

به کمک این داده‌های سطوح انرژی، کمیتی وابسته به دما موسوم به «تابع پارش» (Partition Function) یا «تابع تقسیم» را می‌توان محاسبه کرد. به کمک تابع پارش، تمامی خواص ترمودینامیکی یک سیستم، قابل محاسبه خواهد بود. از ترمودینامیک آماری همچنین در خصوص سرعت واکنش نیز استفاده شده که موسوم به نظریه حالت گذار است. در حقیقت، این امکان وجود دارد که بتوانیم سرعت هر واکنشی را پیش‌بینی کنیم. برای این کار، تنها باید معادلات مکانیک کوانتومی را حل کنیم که سطوح انرژی همراه با واکنش‌دهنده‌ها و حالت گذار واکنش را بدست دهد.

از طریق سطوح انرژی، تابع پارش، از تابع پارش، توابع ترمودینامیکی و از طریق این توابع، سرعت واکنش بدست خواهد آمد. اما در عمل، با مشکلاتی در خصوص پیش‌بینی سرعت مواجه هستیم. با وجود پیشرفت‌های علم کامپیوتر در محاسبات مکانیک کوانتوم، اما نتایج این محاسبات، دقت قابل قبولی ندارند تا به پیش‌بینی مناسبی دست پیدا کنیم.

با فهم دقیق مکانیک آماری، می‌توان ارتباط بین مکانیک آماری و ترمودینامیک کلاسیک را بررسی کرد. در این مطلب، ماده را به کمک مکانیک آماری با کمیات اساسی ترمودینامیکی همچون انرژی درونی، آنتروپی و انرژی آزاد گیبس مرتبط می‌کنیم.

آنسامبل بندادی

یک «آنسامبل» (Ensemble) به صورت مجموعه‌ای بزرگ از واحدهای مشابه یک سیستم تعریف می‌شود. به طور مثال، یک مول آب را می‌توان به کمک عدد آووگادرو به صورت یک آنسامبل در نظر گرفت. آنسامبل، مفهومی نظری را فراهم می‌کند که به کمک آن، خواص میکروسکوپی ماده را می‌توان به خواص ترمودینامیکی متناظر با سیستم طبق اصل زیر مرتبط کرد:

مقدار متوسط برای خاصیت یک آنسامبل، منطبق با مقدار متوسطِ زمانی خاصیت ماکروسکوپی متناظر با سیستم است.

اما این اصل به چه معناست. واحدهای مجزا از یک آنسامبلی را فرض کنید که بیانگر نمونه‌ای از فضای انرژی باشند. محتوای انرژی هر واحد در یک زمان اندازه‌گیری شده و انرژی‌های اندازه‌گیری شده بمنظور تعیین انرژی متوسط آنسامبل مورد استفاده قرار گرفته‌اند. برای مرتبط کردن مقادیر متوسط آنسامبل و خواص ترمودینامیکی،‌ تصویر زیر را در نظر می‌گیریم که کپی‌های مشابهی از سیستم را نشان می‌دهد. دما (T)، حجم (V) و تعداد ذرات در هر سیستم (N)، ثابت است. به آنسامبلی که در آن دما، حجم و تعداد ذرات ثابت باشد «آنسامبل بندادی» (Canonical Ensemble) یا آنسامبل کانونیک می‌گویند.

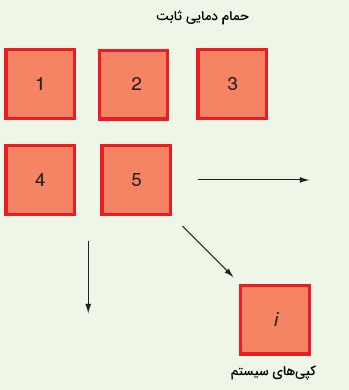
در آنسامبل بندادی، هر عضو آنسامبل در یک حمام دمایی یه گونه‌ای قرار داده شده است که انرژی کل آنسامبل، ثابت باشد. علاوه بر این، دیواره‌های تعیین کننده حجم، توانایی انتقال حرارت را برای تبادل انرژی با محیط دارند. انرژی کل سیستم را به صورت زیر در نظر می‌گیریم:

رابطه ۱:

$$\begin{equation}
E_{c}=\sum_{i} a_{(c) i} E_{i}
\end{equation}$$

در رابطه بالا، $$a_{(c) i}$$ «عدد اشغالی» (Occupation Number) متناظر با تعداد اعضای آنسامبل با انرژی $$E_i$$ هستند. وزن همراه با آرایش ویژه انرژی در میان $$N_c$$ عضو از آنسامبل، با رابطه زیر نشان داده می‌شود:

رابطه ۲:

$$\begin{equation}
W_{c}=\frac{N_{c} !}{\prod_{i} a_{(c) i} !}
\end{equation}$$

از این رابطه برای بدست آوردن احتمال پیدا کردن یک واحد آنسامبل در انرژی $$E_i$$ بهره می‌گیریم:

رابطه ۳:

$$\begin{equation}
p\left(E_{i}\right)=\frac{W_{i} e^{-\beta E_{i}}}{Q}
\end{equation}$$

در رابطه بالا، $$W_i$$ را می‌توان به عنوان تعداد حالت‌های موجود در انرژی مشخص $$E_i$$ در نظر گرفت. در این رابطه، $$Q$$ موسوم به تابع پارش بندادی است و به صورت زیر تعریف می‌شود:‌

رابطه ۴:

$$\begin{equation}
Q=\sum_{n} e^{-\beta E_{n}}
\end{equation}$$

در رابطه بالا، سیگما برای تمامی سطوح انرژی مورد استفاده قرار می‌گیرد. احتمال تعریف شده در رابطه ۳، وابسته به دو عامل است:

• $$W_i$$ که با افزایش انرژی، افزایش پیدا می‌کند.
• عبارت بولتزمن $$(e^{-\beta E_{i}} / Q)$$ که احتمال یک واحد آنسامبل با انرژی $$E_i$$ را توصیف می‌کند. این عبارت با انرژی به صورت نمایی کاهش می‌یابد.

رفتار کلی هر عبارت با انرژی را در تصویر زیر مشاهده می‌کنید. حاصلضرب این عبارات، به یک مقدار ماکزیمی می‌رسد که متناظر با انرژی متوسط آنسامبل است. این تصویر نشان می دهد که یک واحد مجزا از آنسامبل، انرژی خواهد داشت که برابر یا بسیار نزدیک به مقدار متوسط انرژی است و واحدی که انرژی بسیار دورتر از این مقدار داشته باشد، کمتر دیده می‌شود.

این مورد را به تجربه نیز دیده‌ایم، استخر آبی را در نظر بگیرید که به واحدهای ۱ لیتری تقسیم شده باشد. اگر دماسنج در گوشه‌ای از این استخر، دما را برابر با ۱۸ درجه سانتی‌گراد نشان دهد، شخصی که به درون آب شیرجه بزند، احتمال نمی‌دهد که در زیر آب، دما صفر درجه باشد زیرا دمایی که در یک بخش از آب اندازه‌گیری کردیم کافی است تا نشان دهد دما در هر بخش از استخر نیز همین مقدار را دارد. تصویر زیر، نمایشی آماری از این حالت را نشان می‌دهد.

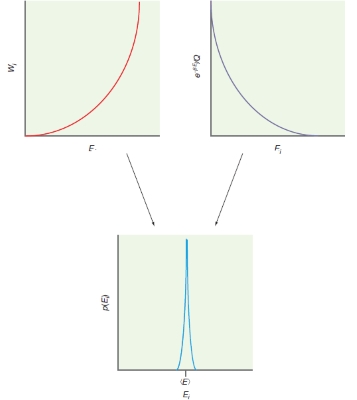
انرژی

برای شروع بحث در خصوص ترمودینامیک آماری باید مختصری در مورد آنسامبل بندادی صحبت می‌کردیم. با در نظر گرفتن انرژی متوسط یک واحد آنسامبل $$\langle \epsilon \rangle$$ که به طور ساده می‌توان آن‌را انرژی کل آنسامبل تقسیم بر تعداد واحدهای آنسامبل (N) تعریف کرد، رابطه زیر را خواهیم داشت:‌

رابطه ۵:

$$\begin{equation}
\langle\varepsilon\rangle=\frac{E}{N}=\frac{\sum_{n} \varepsilon_{n} a_{n}}{N}=\sum_{n} \varepsilon_{n} \frac{a_{n}}{N}
\end{equation}$$

در این رابطه، $$\varepsilon_{n}$$، انرژی سطح و $$a_n$$، عدد اشغالی برای سطح ذکر می‌شود. آنسامبل به گونه‌ای تقسیم (پارش) شده است که در هر واحد، یک اتم یا مولکول قرار داشته باشد. توزیع بولتزمن برای سری «سطوح انرژی ناتبهگن» (nondegenerate Energy Levels) برابر با رابطه زیر خواهد بود:

رابطه ۶:

$$\begin{equation}
\frac{a_{n}}{N}=\frac{e^{-\beta \varepsilon_{n}}}{q}
\end{equation}$$

در رابطه بالا q برابر با تابع پارش مولکولی و $$\beta = (kT) ^ {-1}$$ است. با جایگذاری رابطه ۶ در رابطه ۵، به رابطه زیر می‌رسیم:

رابطه ۷:‌

$$\begin{equation}
\langle\varepsilon\rangle=\sum_{n} \varepsilon_{n} \frac{a_{n}}{N}=\frac{1}{q} \sum_{n} \varepsilon_{n} e^{-\beta \varepsilon_{n}}
\end{equation}$$

به عنوان گام نهایی در تعریف $$\langle\varepsilon\rangle$$،‌ مشتق تابع پارش مولکولی را نسبت به $$\beta$$ در نظر می‌گیریم:

رابطه ۸:

$$\begin{equation}
\frac{-d q}{d \beta}=\sum_{n} \varepsilon_{n} e^{-\beta \varepsilon_{n}}
\end{equation}$$

به کمک رابطه ۸، رابطه ۷ را می‌توان بازنویسی کرد تا به روابط زیر برای محاسبه انرژی متوسط و انرژی کل آنسامبل دست پیدا کنیم:‌

روابط ۹ و ۱۰:

$$\begin{equation}
\begin{aligned}
\langle\varepsilon\rangle &=\frac{-1}{q}\left(\frac{d q}{d \beta}\right)=-\left(\frac{d \ln q}{d \beta}\right) \\
E=N\langle\varepsilon\rangle &=\frac{-N}{q}\left(\frac{d q}{d \beta}\right)=-N\left(\frac{d \ln q}{d \beta}\right)
\end{aligned}
\end{equation}$$

با توجه به تعریفی که پیش‌تر در خصوص $$\beta$$ ارائه شد در برخی موارد، روابط ۹ و ۱۰ را می‌توان به کمک مشتق نسبت به T (به جای $$\beta$$) بدست آورد.

رابطه ۱۱:

$$\begin{equation}
\frac{d \beta}{d T}=\frac{d}{d T}(k T)^{-1}=-\frac{1}{k T^{2}}
\end{equation}$$

به کمک رابطه ۱۱، روابط مربوط به انرژی متوسط و کل به صورت زیر بدست می‌آیند.

روابط ۱۲ و ۱۳:

$$\begin{equation}
\begin{aligned}
\langle\varepsilon\rangle &=k T^{2}\left(\frac{d \ln q}{d T}\right) \\
E &=N k T^{2}\left(\frac{d \ln q}{d T}\right)
\end{aligned}
\end{equation}$$

رابطه ۱۳ نشان می‌دهد که ‌E، با دما تغییر می‌کند. در مثال زیر، آنسامبلی متشکل از ذراتی با دو سطح انرژی را در نظر می‌گیریم که به «سیستم دو سطحی» (Two-level System) معروف است و به کمک آن، تغییر E با T را نشان می‌دهیم.

مثال برای انرژی کل سیستم دو سطحی

انرژی کل یک آنسامبل با N جزء را بدست آورید. این اجزا دارای دو سطح انرژی با فاصله $$h\nu$$ هستند.

برای بدست آوردن انرژی متوسط،‌ تابع پارش توصیف کننده این سیستم دو سطحی باید محاسبه شود. تابع پارش شامل مجموع دو عبارت به شکل زیر است:

$$\begin{equation}
q=1+e^{-\beta h \nu}
\end{equation}$$

مشتق تابع پارش نسبت به $$\beta$$ به صورت زیر خواهد بود.

$$\begin{equation}
\begin{aligned}
\frac{d q}{d \beta} &=\frac{d}{d \beta}\left(1+e^{-\beta h \nu}\right) \\
&=-h \nu e^{-\beta h \nu}
\end{aligned}
\end{equation}$$

به کمک رابطه بالا و رابطه ۱۰، انرژی کل را محاسبه خواهیم کرد.

$$\begin{equation}
\begin{aligned}
E &=\frac{-N}{q}\left(\frac{d q}{d \beta}\right)=\frac{-N}{\left(1+e^{-\beta h \nu}\right)}\left(-h \nu^{-\beta h \nu}\right) \\
&=\frac{N h \nu e^{-\beta h \nu}}{1+e^{-\beta h \nu}}=\frac{N h \nu}{e^{\beta h \nu}+1}
\end{aligned}
\end{equation}$$

انرژی و تابع پارش بندادی

رابطه ۱۳ به ما در محاسبه انرژی آنسامبل کمک کرد اما سوالی که پیش می‌آید این است که این انرژی به کدامیک از خواص ترمودینامیکی ارتباط دارد. به یاد دارید که آنسامبل بندادی را در نظر داریم که در آن، حجم، دما و تعداد ذرات ثابت باشند.

از آن‌جایی که حجم ثابت داریم، هیچ نوع کار PV نخواهیم داشت و طبق قانون اول ترمودینامیک، هر تغییری در انرژی درونی، توسط جریان حرارتی $$(q _ {Vol})$$ انجام می‌گیرد. بر اساس قانون اول ترمودینامیک، در حجم ثابت، تغییر حرارت، مرتبط با تغییر انرژی درونی سیستم طبق رابطه زیر خواهد بود.

رابطه ۱۴:

$$\begin{equation}
U-U_{o}=q_{V o l}
\end{equation}$$

انرژی که در رابطه بالا نشان داده شده، برابر با اختلاف انرژی درونی در دمایی محدود نسبت به صفر کلوین است. به طور معمول مقدار صفر را برای $$U_0$$ در نظر می‌گیرند. رابطه مهم دیگری که باید در نظر بگیریم، رابطه بین انرژی درونی و تابع پارش کانونیک است. برای آنسامبلی که اجزای آن با یکدیگر برهم‌کنشی نداشته باشند، تابع پارش کانویک به صوت زیر بدست می‌آید.

رابطه ۱۵:‌

$$\begin{equation}
Q=\frac{q^{N}}{N !}
\end{equation}$$

اگر از رابطه بالا، لگاریتم طبیعی بگیریم به رابطه زیر می‌رسیم:

رابطه ۱۶:

$$\begin{equation}
\ln Q=\ln \left(\frac{q^{N}}{N !}\right)=N \ln q-\ln N !
\end{equation}$$

در نهایت با مشتق‌گیری از رابطه بالا نسبت به $$\beta$$ و با توجه به مقدار ثابت $$\ln ( N ! )$$ در آنسامبل بندادی، رابطه زیر بدست می‌آید.

رابطه ۱۷:‌

$$\begin{equation}
\begin{aligned}
\frac{d \ln Q}{d \beta} &=\frac{d}{d \beta}(N \ln q)-\frac{d}{d \beta}(\ln N !) \\
&=N \frac{d \ln q}{d \beta}
\end{aligned}
\end{equation}$$

رابطه بالا مرتبط با انرژی کل است بنابراین، رابطه بین تابع پارش بندادی و انرژی درونی کل $$(U)$$ به صورت زیر خواهد بود:

رابطه ۱۸:

$$\begin{equation}
U=-\left(\frac{\partial \ln Q}{\partial \beta}\right)_{V}
\end{equation}$$

مثال برای محاسبه انرژی درونی

برای آنسامبلی شامل ۱ مول ذره در سیستمی با دو سطح انرژی $$(h \nu = 1.00 \times 10^{-20})$$، در چه دمایی انرژی درونی سیستم برابر با ۱ کیلوژول خواهد بود.

به کمک رابطه ۱۸ و استفاده از عدد آووگادرو $$(N = n N _ A)$$ خواهیم داشت:

$$\begin{equation}
U=-\left(\frac{\partial \ln Q}{\partial \beta}\right)_{V}=-n N_{A}\left(\frac{\partial \ln q}{\partial \beta}\right)_{V}
\end{equation}$$

به کمک رابطه بالا و توجه در نوع واحدها به رابطه زیر می‌رسیم:

$$\begin{equation}
\begin{aligned}
U=-n N_{A}\left(\frac{\partial}{\partial \beta} \ln q\right)_{V} &=-\frac{n N_{A}}{q}\left(\frac{\partial q}{\partial \beta}\right)_{V} \\
\frac{U}{n N_{A}}=& \frac{-1}{\left(1+e^{-\beta h \nu}\right)}\left(\frac{\partial}{\partial \beta}\left(1+e^{-\beta h \nu}\right)\right)_{V} \\
=& \frac{h \nu e^{-\beta h \nu}}{1+e^{-\beta h \nu}}=\frac{h \nu}{e^{\beta h \nu}+1}
\Rightarrow\frac{n N_{A} h \nu}{U}-1=e^{\beta h \nu} \\
& \ln \left(\frac{n N_{A} h \nu}{U}-1\right)=\beta h \nu=\frac{h \nu}{k T}
\end{aligned}
\end{equation}$$

با باز‌آرایی رابطه بالا و نوشتن آن بر حسب $$T$$، به دمای ۴۴۹ کلوین می‌رسیم.

$$\begin{equation}
\begin{aligned}
T=& \frac{h \nu}{k \ln \left(\frac{n N_{A} h \nu}{U}-1\right)} \\
=& \frac{1.00 \times 10^{-20} \mathrm{J}}{\left(1.38 \times 10^{-23} \mathrm{J} \mathrm{K}^{-1}\right) \ln \left(\frac{(1.00 \mathrm{mol})\left(6.022 \times 10^{23} \mathrm{mol}^{-1}\right)\left(1.00 \times 10^{-20} \mathrm{J}\right)}{\left(1.00 \times 10^{3} \mathrm{J}\right)}-1\right)} \\
=& 449 \mathrm{K}
\end{aligned}
\end{equation}$$

درجات آزادی انرژی مولکولی

رابطه زیر را در نظر بگیرید که رابطه بین تابع پارش مولکولی کل را به توابع پارش متناظر با درجه آزادی انرژی به صورت مجزا مرتبط می‌کند. در این رابطه، زیروندهای T و R و V و E به ترتیب به درجه آزادی انرژی انتقالی، دورانی، ارتعاشی و الکترونی اشاره دارند.

رابطه ۱۹:

$$\begin{equation}
q_{\text {Total}}=q_{T} q_{R} q_{V} q_{E}
\end{equation}$$

به این ترتیب می‌توان از رابطه ۱۸ و ۱۹ استفاده کرد تا به رابطه‌ای برای انرژی درونی برسیم.

رابطه۲۰:

$$\begin{equation}
\begin{aligned}
U &=-\left(\frac{\partial \ln Q}{\partial \beta}\right)_{V}=-N\left(\frac{\partial \ln q}{\partial \beta}\right)_{V} \\
&=-N\left(\frac{\partial \ln \left(q_{T} q_{R} q_{V} q_{E}\right)}{\partial \beta}\right)_{V} \\
&=-N\left(\frac{\partial}{\partial \beta}\left(\ln q_{T}+\ln q_{R}+\ln q_{V}+\ln q_{E}\right)\right)_{V} \\
&=-N\left[\left(\frac{\partial \ln q_{T}}{\partial \beta}\right)_{V}+\left(\frac{\partial \ln q_{R}}{\partial \beta}\right)_{V}+\left(\frac{\partial \ln q_{V}}{\partial \beta}\right)_{V}+\left(\frac{\partial \ln q_{E}}{\partial \beta}\right)_{V}\right] \\
&=U_{T}+U_{R}+U_{V}+U_{E}
\end{aligned}
\end{equation}$$

خط آخر رابطه بالا نتیجه بسیار مهمی را بیان می‌کند به این معنی که انرژی درونی کل برابر با مجموع موارد دخیل هر یک از درجات آزادی انرژی مولکولی است. علاوه بر این، این نتیجه، ارتباط بیبن خواص ماکروسکوپی آنسامبل (انرژی درونی) و جزئیات میکروسکوپی واحدها (سطوح انرژی مولکولی) را نشان می‌دهد. در ادامه متن، سهم هریک از حرکات به همراه روابط مربوطه به ‌آن‌ها به طور خلاصه آورده شده‌اند.

انتقال

سهم انرژی درونی سیستم از حرکت انتقالی را به صورت زیر نشان می‌دهیم:

رابطه ۲۱:

$$\begin{equation}
U_{T}=\frac{-N}{q_{T}}\left(\frac{\partial q_{T}}{\partial \beta}\right)_{V}
\end{equation}$$

در رابطه بالا، $$q_T$$ تابع پارش انتقالی است که شکل در سه بعد به صورت زیر تعریف می‌شود.

رابطه ۲۲:

$$\begin{equation}
q_{T}=\frac{V}{\Lambda^{3}} \\ \Lambda^{3}=\left(\frac{h^{2} \beta}{2 \pi m}\right)^{3 / 2}
\end{equation}$$

به کمک این تابع پارش، سهم انرژی درونی از انتقال به صورت زیر خواهد بود:

رابطه ۲۳:

$$\begin{aligned}
U_{T} &=\frac{-N}{q_{T}}\left(\frac{\partial q_{T}}{\partial \beta}\right)_{V}=\frac{-N \Lambda^{3}}{V}\left(\frac{\partial}{\partial \beta} \frac{V}{\Lambda^{3}}\right)_{V} \\
&=-N \Lambda^{3}\left(\frac{\partial}{\partial \beta} \frac{1}{\Lambda^{3}}\right)_{V} \\
&=-N \Lambda^{3}\left(\frac{\partial}{\partial \beta}\left(\frac{2 \pi m}{h^{2} \beta}\right)^{3 / 2}\right)_{V} \\
&=-N \Lambda^{3}\left(\frac{2 \pi m}{h^{2}}\right)^{3 / 2}\left(\frac{\partial}{\partial \beta} \beta^{-3 / 2}\right)_{V} \\
&=-N \Lambda^{3}\left(\frac{2 \pi m}{h^{2}}\right)^{3 / 2} \frac{-3}{2} \beta^{-5 / 2}
=\frac{3}{2} N \beta^{-1} \Rightarrow U_{T}=\frac{3}{2} N k T=\frac{3}{2} n R T \end{aligned}$$

دوران

به کمک فرضیات مربوط به یک روتور، تابع پارش برای مولکول دو‌اتمی در حد دمای بالا با رابطه زیر بدست می‌آید:‌

رابطه ۲۴:

$$\begin{equation}
q_{R}=\frac{1}{\sigma \beta h c B}
\end{equation}$$

به کمک این تابع پارش،  سهم انرژی درونی از حرکت دورانی به صورت زیر محاسبه خواهد شد:

رابطه ۲۵:

$$\begin{equation}
\begin{aligned}
U_{R}=\frac{-N}{q_{R}}\left(\frac{\partial q_{R}}{\partial \beta}\right)_{V} &=-N \sigma \beta h c B\left(\frac{\partial}{\partial \beta} \frac{1}{\sigma \beta h c B}\right)_{V} \\
&=-N \beta\left(\frac{\partial}{\partial \beta} \beta^{-1}\right)_{V} \\
&=-N \beta\left(-\beta^{-2}\right) \\
&=N \beta^{-1} \\
U_{R} &=N k T=n R T
\end{aligned}
\end{equation}$$

ارتعاش

به کمک مدل نوسانگر هارمونیک، رابطه مربوط به تابع پارش دورانی به صورت زیر خواهد بود:

رابطه ۲۶:

$$\begin{equation}
q_{V}=\left(1-e^{-\beta h c \bar{\nu}}\right)^{-1}
\end{equation}$$

عبارت $$\bar{\nu}$$ نشان‌دهنده فرکانس ارتعاش است. به کمک این تابع پارش، سهم ارتعاش از انرژی متوسط را به صورت زیر بدست می‌آوریم.

رابطه ۲۷:

$$\begin{equation}
\begin{aligned}
U_{V} &=\frac{-N}{q_{V}}\left(\frac{\partial q_{V}}{\partial \beta}\right)_{V}=-N\left(1-e^{-\beta h c \tilde{\nu}}\right)\left(\frac{\partial}{\partial \beta}\left(1-e^{-\beta h c \tilde{\nu}}\right)^{-1}\right)_{V} \\
&=-N\left(1-e^{-\beta h c \tilde{\nu}}\right)\left(-h c \tilde{\nu} e^{-\beta h c \tilde{\nu}}\right)\left(1-e^{-\beta h c \tilde{\nu}}\right)^{-2} \\
&=\frac{N h c \widetilde{\nu} e^{-\beta h c \bar{\nu}}}{\left(1-e^{-\beta h c \tilde{\nu}}\right)} \\
U_{V} &=\frac{N h c \widetilde{\nu}}{e^{\beta h c \tilde{\nu}}-1}
\end{aligned}
\end{equation}$$

در انتها، با باز کردن رابطه بالا و در نهایت ساده کردن آن خواهیم داشت:

رابطه ۲۸:

$$\begin{equation}
\begin{aligned}
U_{V}=\frac{N h c \tilde{\nu}}{e^{\beta h c \nu-1}} &=\frac{N h c \tilde{\nu}}{(1+\beta h c \tilde{\nu})-1} \\
&=\frac{N}{\beta} \\
U_{V} &=N k T=n R T
\end{aligned}
\end{equation}$$

الکترونی

در خصوص سطوح انرژی الکترونی، رابطه زیر برقرار است.

رابطه ۲۹:

$$U_E = 0$$

برای سیستمی که سطوح انرژی الکترونی، قابل قیاس با $$kT$$ هستند، رابطه بالا صدق نمی‌کند و باید تابع پارش کامل محاسبه شود.

جمع‌بندی

در نهایت، به کمک روابط گفته شده و اعمال آن برای سیستم دو اتمی، انرژی کل به صورت زیر بدست می‌آید:

رابطه۳۰:

$$\begin{equation}
\begin{aligned}
U_{\text {Total}} &=U_{T}+U_{R}+U_{V}+U_{E} \\
&=\frac{3}{2} N k T+N k T+\frac{N h c \tilde{\nu}}{e^{\beta h c \tilde{\nu}}-1}+0 \\
&=\frac{5}{2} N k T+\frac{N h c \tilde{\nu}}{e^{\beta h c \tilde{\nu}}-1}
\end{aligned}
\end{equation}$$

ظرفیت حرارتی

در بررسی ظرفیت حرارتی در ترمودینامیک آماری باید به تعریف ترمودینامیکی ظرفیت حرارتی در حجم ثابت اشاره کنیم:

رابطه ۳۱:

$$\begin{equation}
C_{V}=\left(\frac{\partial U}{\partial T}\right)_{V}=-k \beta^{2}\left(\frac{\partial U}{\partial \beta}\right)_{V}
\end{equation}$$

طرفیت حرارتی را نیز مانند انرژی درونی می‌توان به سهم‌های مختلف تقسیم کرد. ظرفیت حرارتی به کمک مشتق انرژی درونی نسبت به دما برای درجه آزادی انرژی مشخصی بدست می‌آید. شکل تابعی ظرفیت حرارتی قدری پیچیده است و نمودار آن‌را در تصویر زیر مشاهده می‌کنید.

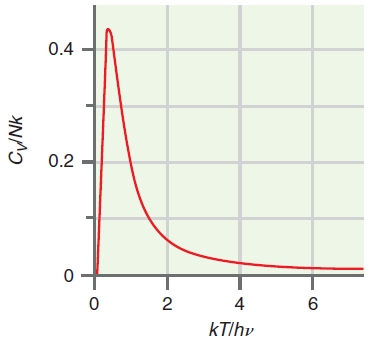
در پایین‌ترین دما، $$C_V$$ برابر با صفر است و بعد از افزایش دما، به یک مقدار ماکزیمم می‌رسد که بعد از این مقدار، افزایش دما سبب کاهش ظرفیت حرارتی خواهد شد.

ظرفیت حرارتی انتقالی

سهم حرکت انتقالی در انرژی متوسط مولکولی، برابر با رابطه زیر است:‌

رابطه ۳۲:

$$U _ T = \frac{3}{2}NkT$$

در نتیجه، رابطه مربوط به ظرفیت حرارتی را می‌توان با مشتق گرفتن از رابطه بالا بدست آورد.

رابطه ۳۳:

$$\begin{equation}
\left(C_{V}\right)_{T}=\left(\frac{\partial U_{T}}{\partial T}\right)_{V}=\frac{3}{2} N k
\end{equation}$$

ظرفیت حرارتی دورانی

با فرض کوچک بودن فواصل انرژی دورانی نسبت به $$kT$$، رابطه مربوط به سهم حرکت دورانی در انرژی را می‌توان برای تعیین سهم حرکت دورانی نسبت به $$C_V$$ محاسبه کرد. انرژی درونی وابسته به هندسه مولکولی است در نتیجه برای مولکول‌های چنداتمی خطی و غیرخطی به ترتیب خواهیم داشت:

روابط ۳۴ و ۳۵:

$$\begin{equation}
\begin{aligned}
U_{R} &=N k T \\
U_{R} &=\frac{3}{2} N k T
\end{aligned}
\end{equation}$$

در نتیجه، با مشتق‌گیری نسبت به دما به روابط زیر برای مولکول‌های خطی و غیرخطی می‌رسیم:

رابطه ۳۶:

$$\begin{equation}
\begin{array}{l}
\left(C_{V}\right)_{R}=N k \\
\left(C_{V}\right)_{R}=\frac{3}{2} N k
\end{array}
\end{equation}$$

ظرفیت حرارتی ارتعاشی

برای ظرفیت حرارتی ارتعاشی، اثبات رابطه به صورت زیر خواهد بود:

رابطه ۳۷:

$$\begin{equation}
\begin{aligned}
\left(C_{V}\right)_{V i b}=\left(\frac{\partial U_{V}}{\partial T}\right)_{V} &=-k \beta^{2}\left(\frac{\partial U_{V}}{\partial \beta}\right)_{V} \\
&=-N k \beta^{2} h c \widetilde{\nu}\left(\frac{\partial}{\partial \beta}\left(e^{\beta h c \bar{\nu}}-1\right)^{-1}\right)_{V} \\
&=-N k \beta^{2} h c \widetilde{\nu}\left(-h c \widetilde{\nu} e^{\beta h c \widetilde{\nu}}\left(e^{\beta h c \tilde{\nu}}-1\right)^{-2)} V\right.\\
\left(C_{V}\right)_{V i b} &=N k \beta^{2}(h c \widetilde{\nu})^{2} \frac{e^{\beta h c \tilde{\nu}}}{\left(e^{\beta h c \tilde{\nu}}-1\right)^{2}}
\end{aligned}
\end{equation}$$

آنتروپی در ترمودینامیک آماری

آنتروپی را به لحاظ مفهومی باید پیچیده‌ترین خاصیت ترمودینامیکی ماده به شمار آورد. در دروس پایه‌ای شیمی، آنتروپی یک واکنش را تمایل ذاتی سیستم برای افزایش بی‌نظمی ذکر می‌کنند. به کمک مکانیک و ترمودینامیک آماری خواهیم دید که تمامی یک سیستم ایزوله برای رسیدن به بیشترین آنتروپی، با آمار رابطه مستقیم دارد. یک سیستم با دستیابی به آرایش انرژی با بیشترین وزن به تعادل می‌رسد. به عبارت دیگر آرایش انرژی که در تعادل، شاهد آن هستیم متناظر با $$W _ {max}$$ است.

تمایل یک سیستم برای افزایش W و آنتروپی نشان از رابطه میان این دو کمیت دارد. «بولتزمن» (Boltzmann) این ارتباط را از طریق رابطه زیر نشان داد:‌

رابطه ۳۸:

$$\begin{equation}
S=k \ln W
\end{equation}$$

رابطه بالا به وضوح نشان می‌دهد که مقدار ماکزیمم $$W _ {max}$$ متناظر با مقدار ماکزیمم $$S$$ است. این رابطه در حقیقت، معادل با تعریف ترمودینامیکی آنتروپی است. برای نشان دادن این موضوع، انرژی ذرات یک آنسامبل را در نظر بگیرید. این انرژی برابر با مجموع حاصلضرب سطوح انرژی و اعداد اشغالی این سطوح است.

رابطه ۳۹:

$$\begin{equation}
E=\sum_{n} \varepsilon_{n} a_{n}
\end{equation}$$

دیفرانسیل کل E به صورت زیر محاسبه می‌شود:

رابطه ۴۰:

$$\begin{equation}
d E=\sum_{n} \varepsilon_{n} d a_{n}+\sum_{n} a_{n} d \varepsilon_{n}
\end{equation}$$

از آن‌جایی که حجم در آنسامبل بندادی ثابت است، سطوح انرژی نیز ثابت خواهند بود. بنابراین، عبارت دوم در رابطه بالا برابر با صفر خواهد بود. همچنین به دلیل ثابت بودن حجم و نداشتن کار PV، بر اساس قانون اول ترمودینامیک، تغییرات انرژی تنها به دلیل جریان گرمایی است.

رابطه ۴۱:

$$\begin{equation}
d E=d q_{r e v}=\sum_{n} \varepsilon_{n} d a_{n}
\end{equation}$$

تعریف ترمودینامیکی آنتروپی جایی که $$dq_ {rev}$$، گرمای تبادل شده بین سیستم و محیط باشد به صورت زیر تعریف می‌شود.

رابطه ۴۲:

$$\begin{equation}
d S=\frac{d q_{r e v}}{T}
\end{equation}$$

با مقایسه دو رابطه آخر در ترمودینامیک آماری به تعریف دیگر آنتروپی می‌رسیم:

رابطه ۴۳:

$$\begin{equation}
d S=\frac{1}{T} \sum_{n} \varepsilon_{n} d a_{n}=k \beta \sum_{n} \varepsilon_{n} d a_{n}
\end{equation}$$

با توجه به این‌که به $$\beta$$ نیاز پیدا می‌کنیم، معادله را بر حسب $$\beta$$ بازنویسی کردیم. با مشتق‌گیری از توزیع بولتزمن در نهایت رابطه زیر را خواهیم داشت:

رابطه ۴۴:

$$\begin{equation}
\begin{aligned}
\left(\frac{d \ln W}{d a_{n}}\right)+\alpha-\beta \varepsilon_{n} &=0 \\
\beta \varepsilon_{n} &=\left(\frac{d \ln W}{d a_{n}}\right)+\alpha
\end{aligned}
\end{equation}$$

در رابطه بالا، آلفا و بتا ثابت هستند. با بکارگیری رابطه ۴۴، تعریفی که از آنتروپی داشتیم به رابطه زیر ختم می‌شود:

رابطه ۴۵:

$$\begin{equation}
\begin{aligned}
d S &=k \beta \sum_{n} \varepsilon_{n} d a_{n}=k \sum_{n}\left(\frac{d \ln W}{d a_{n}}\right) d a_{n}+k \sum_{n} \alpha d a_{n} \\
&=k \sum_{n}\left(\frac{d \ln W}{d a_{n}}\right) d a_{n}+k \alpha \sum_{n} d a_{n} \\
&=k \sum_{n}\left(\frac{d \ln W}{d a_{n}}\right) d a_{n} \\
&=k(d \ln W)
\end{aligned}
\end{equation}$$

می‌توان فرض کرد رابطه‌ای بین تابع پارش و آنتروپی وجود دارد. این رابطه از طریق فرمول بولتزمن و به روش زیر بدست می‌آید:

رابطه ۴۶:

$$\begin{equation}
S=k \ln W=k \ln \left(\frac{N !}{\prod_{n} a_{n} !}\right)
\end{equation}$$

این رابطه را می‌توان به صورت زیر کاهش داد:

رابطه ۴۷:

$$\begin{equation}
\begin{aligned}
S &=k \ln \left(\frac{N !}{\prod_{n} a_{n} !}\right) \\
&=k \ln N !-k \ln \prod_{n} a_{n} ! \\
&=k \ln N !-k \sum_{n} \ln a_{n} ! \\
&=k(N \ln N-N)-k \sum_{n}\left(a_{n} \ln a_{n}-a_{n}\right) \\
&=k\left(N \ln N-\sum_{n} a_{n} \ln a_{n}\right)
\end{aligned}
\end{equation}$$

در مرحله آخر از تعریف N  به صورت $$(N = \sum_n a_n)$$ استفاده شد تا به رابطه زیر برسیم:

رابطه ۴۸:

$$\begin{equation}
\begin{aligned}
S &=k\left(N \ln N-\sum_{n} a_{n} \ln a_{n}\right) \\
&=k\left(\sum_{n} a_{n} \ln N-\sum_{n} a_{n} \ln a_{n}\right) \\
&=-k \sum_{n} a_{n} \ln \frac{a_{n}}{N} \\
&=-k \sum_{n} a_{n} \ln p_{n}
\end{aligned}
\end{equation}$$

به کمک قانون توزیع بولتزمن و بازنویسی عبارت مربوطه به احتمال در رابطه بالا، در نهایت رابطه مربوط به آنتروپی برای بررسی در ترمودینامیک آماری به صورت زیر بدست می‌آید:

رابطه ۴۹:

$$\begin{equation}
\begin{aligned}
S &=-k \sum_{n} a_{n} \ln p_{n} \\
&=-k \sum_{n} a_{n}\left(-\beta \varepsilon_{n}-\ln q\right) \\
&=k \beta \sum_{n} a_{n} \varepsilon_{n}+k \sum_{n} a_{n} \ln q \\
&=k \beta E+k N \ln q \\
&=\frac{E}{T}+k \ln q^{N} \\
S &=\frac{E}{T}+k \ln Q=\frac{U}{T}+k \ln Q
\end{aligned}
\end{equation}$$

در رابطه بالا، $$U$$ انرژی درونی سیستم و $$Q$$ تابع پارش بندادی است. انرژی درونی طبع رابطه زیر با تابع پارش کانونیک مرتبط است:

رابطه ۵۰:

$$\begin{equation}
U=-\left(\frac{\partial \ln Q}{\partial \beta}\right)_{V}=k T^{2}\left(\frac{\partial \ln Q}{\partial T}\right)_{V}
\end{equation}$$

به کمک رابطه بالا، به شکل دیگری از تعریف آنتروپی در ترمودینامیک آماری می‌رسیم:

رابطه ۵۱:

$$\begin{equation}
S=\left(\frac{\partial}{\partial T}(k T \ln Q)\right)_{V}
\end{equation}$$

آنتروپی پسماند

زمانیکه آنتروپی محاسبه شده به کمک روابط مکانیک و ترمودینامیک آماری را با نتایج آزمایش مقایسه می‌کنیم، این نتایج برای برخی از سیستم‌های اتمی و مولکولی با یکدیگر انطباق دارند. با این وجود، برای بسیاری از سیستم‌های مولکولی، این نتایج رفتار ایده‌آلی را نشان نمی‌دهند. از نمونه‌های چنین سیستم‌هایی می‌توان به مونواکسید کربن اشاره کرد که در آن، آنتروپی محاسبه شده در دما و فشار استاندارد برابر با $$197.9 \ J mol^ {-1} K ^{-1}$$ و مقدار آزمایشگاهی آن برابر با $$193 \ J mol^ {-1} K ^{-1}$$ است. در این نوع از سیستم‌ها، مقدار محاسبه شده آنتروپی، همواره بیشتر از مقدار آزمایشگاهی است.

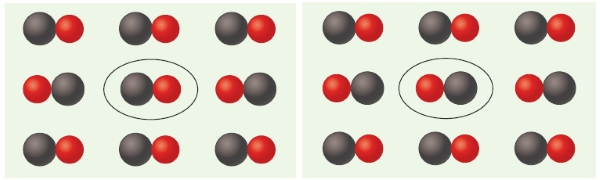
دلیل این اختلاف بین آنتروپی محاسبه شده و مقدار آزمایشگاهی، «آنتروپی پسماند» (Residual Entropy) یا آنتروپی همراه با جهت‌گیری مولکولی در بلور و دمای پایین است. به عنوان مثال در مونواکسید کربن، گشتاور دوقطبی ضعیف مولکول نشان می‌دهد که برهم‌کنش‌های دوقطبی-دوقطبی، نقش اساسی در تعیین جهت‌گیری مولکول $$CO$$ نسبت به مولکول‌های اطراف در بلور ندارند.

بنابراین، برای هر مولکول $$CO$$ می‌توان دو جهت‌گیری همچون تصویر زیر در نظر گرفت. با توجه به این‌که می‌توان فرض کرد که هر مولکول $$CO$$ دارای دو جهت‌گیری محتمل است، آنتروپی همراه با این جهت‌گیری‌ها برابر با رابطه زیر خواهد بود که در این رابطه، $$W$$ تعداد کل آرایش‌های مولکول $$CO$$ و برابر با $$2^ {N}$$ است که $$N$$ در اینجا تعداد مولکول‌های مونواکسید کربن است.

رابطه ۵۲:

$$\begin{equation}
S=k \ln W=k \ln 2^{N}=N k \ln 2=n R \ln 2
\end{equation}$$

در نهایت، توجه داشته باشید که مفهوم آنتروپی پسماند یا آنتروپی باقیمانده را می‌توان منشا قانون سوم ترمودینامیک دانست. قانون سوم بیان می‌کند که آنتروپی یک بلور خالص در دمای صفر کلوین برابر با صفر است.

سایر توابع ترمودینامیکی

مواردی که تا اینجا مطرح شد بیانگر همگرایی مباحث آماری و ترمودینامیکی در قالب ترمودینامیک آماری بودند. رابطه بین تابع پارش بندادی و سایر کمیات ترمودینامیکی را می‌توان با استفاده از روابط ترمودینامیکی مربوط به آنتالپی، انرژی هلمهولتز و انرژی آزاد گیبس بدست آورد که این روابط معروف به ترتیب در روابط ۵۳ تا ۵۵ آورده شده‌اند و در ادامه این مطلب به طور خلاصه به آن‌ها پرداخته می‌شود.

روابط ۵۳ تا ۵۵:

$$\begin{equation}
\begin{aligned}
H &=U+P V \\
A &=U-T S \\
G &=H-T S
\end{aligned}
\end{equation}$$

انرژی هلمهولتز در ترمودینامیک آماری

رابطه بین انرژی هلمهولتز و تابع پارش بندادی به صورت زیر خواهد بود که در نهایت می‌توان به کمک روابط فشار، به قانون گاز ایده‌آل رسید.

رابطه ۵۶:

$$\begin{equation}
\begin{aligned}
A &=U-T S \\
&=U-T\left(\frac{U}{T}+k \ln Q\right) \\
A &=-k T \ln Q
\end{aligned}
\end{equation}$$

آنتالپی در ترمودینامیک آماری

به کمک تعریف ترمودینامیکی آنتالپی (رابطه ۵۳)، این کمیت را در ترمودینامیک آماری می‌توان بر اساس تابع پارش کانونیک به شکل زیر بیان کرد.

رابطه۵۷:

$$\begin{equation}
\begin{aligned}
&\begin{aligned}
H &=U+P V \\
&=\left(\frac{-\partial}{\partial \beta} \ln Q\right)_{V}+V\left(\frac{-\partial A}{\partial V}\right)_{T}
\end{aligned}\\
&=\left(\frac{-\partial}{\partial \beta} \ln Q\right)_{V}+V\left(\frac{-\partial}{d V}(-k T \ln Q)\right)_{T}\\
&\begin{array}{l}
=k T^{2}\left(\frac{\partial}{\partial T} \ln Q\right)_{V}+V k T\left(\frac{\partial}{\partial V} \ln Q\right)_{T} \\
H=T\left[k T\left(\frac{\partial}{\partial T} \ln Q\right)_{V}+V k\left(\frac{\partial}{\partial V} \ln Q\right)_{T}\right] \end{array}
\end{aligned}
\end{equation}$$

انرژی گیبس در ترمودینامیک آماری

انرژی گیبس را شاید بتوان به عنوان مهم‌ترین تابع حالت در ترمودینامیک در نظر گرفت. به کمک این رابطه می‌توان انجام خود به خودی یک واکنش شیمیایی را پیش‌بینی کرد. در نهایت، در بررسی ترمودینامیک آماری برای انرژی گیبس، به رابطه زیر می‌رسیم:

رابطه ۵۸:

$$\begin{equation}
G=-N k T \ln \left(\frac{q}{N}\right)=-n R T \ln \left(\frac{q}{N}\right)
\end{equation}$$

تعادل شیمیایی در ترمودینامیک آماری

برای بررسی تعادل شیمیایی در ترمودینامیک آماری معادله شیمیایی کلی زیر را در نظر بگیرید:

رابطه ۵۹:

$$\begin{equation}
a \mathrm{J}+b \mathrm{K} \rightleftharpoons c \mathrm{L}+d \mathrm{M}
\end{equation}$$

انرژی گیبس برای این واکنش، مرتبط با انرژی گیبس برای ذرات دخیل در واکنش است که به صورت زیر نشان می‌دهند.

رابطه ۶۰:

$$\begin{equation}
\Delta G^{\circ}=c G_{L}^{\circ}+d G_{M}^{\circ}-a G_{J}^{\circ}-b G_{K}^{\circ}
\end{equation}$$

در این رابطه، زیروندها بیانگر حالت استاندارد ترمودینامیکی هستند. علاوه بر این، ثابت تعادل به صورت زیر محاسبه می‌شود:‌

رابطه ۶۱:

$$\begin{equation}
\Delta G^{\circ}=-R T \ln K
\end{equation}$$

در نهایت برای بررسی انرژی گیبس در ترمودینامیک آماری به رابطه زیر دست پیدا می‌کنیم:‌

رابطه۶۲:

$$\begin{equation}
\begin{aligned}
\Delta G^{\circ}=& c\left(-R T \ln \left(\frac{q_{L}^{\circ}}{N_{A}}\right)\right)+d\left(-R T \ln \left(\frac{q_{M}^{\circ}}{N_{A}}\right)\right)-a\left(-R T \ln \left(\frac{q_{J}^{\circ}}{N_{A}}\right)\right) \\
&-b\left(-R T \ln \left(\frac{q_{K}^{\circ}}{N_{A}}\right)\right) \\
=&-R T \ln \left(\frac{\left(\frac{q_{L}}{N_{A}}\right)^{c}\left(\frac{q_{M}}{N_{A}}\right)^{d}}{\left(\frac{q_{J}^{0}}{N_{A}}\right)^{a}\left(\frac{q_{K}^{\circ}}{N_{A}}\right)^{b}}\right)
\end{aligned}
\end{equation}$$

با مقایسه رابطه ۶۲ با تعریف ترمودینامیکی $$\Delta G^{\circ}$$، به رابطه زیر برای ثابت تعادل می‌رسیم:

رابطه ۶۲:

$$\begin{equation}
K_{P}=\frac{\left(\frac{q_{L}^{\circ}}{N_{A}}\right)^{c}\left(\frac{q_{M}^{\circ}}{N_{A}}\right)^{d}}{\left(\frac{q_{J}^{0}}{N_{A}}\right)^{a}\left(\frac{q_{K}^{\circ}}{N_{A}}\right)^{b}}
\end{equation}
$$

سوالات متداول در خصوص ترمودینامیک آماری

در انتهای بحث به طور خلاصه به برخی سوالات متداول در خصوص ترمودینامیک آماری می‌پردازیم.

ترمودینامیک آماری به چه معناست؟

به طور خلاصه، ترمودینامیک آماری بین خواص ماکروسکوپی موادِ در تعادل ترمودینامیکی با خواص میکروسکوپی ماده ارتباط ایجاد می‌کند.

آنسامبل کانونیک یا آنسامبل بندادی را تعریف کنید

به آنسامبلی که در آن، T، V و N ثابت باشند، آنسامبل کانونیک یا آنسامبل بندادی می‌گویند.

رابطه کلی تابع پارش بندادی را بنویسید

رابطه تابع پارش بندادی (Q) به صورت زیر نوشته می‌شود که در این متن، رابطه چهارم را شامل می‌شود:

$$\begin{equation}
Q=\sum_{n} e^{-\beta E_{n}}
\end{equation}$$

رابطه مربوط به انرژی کل آنسامبل در ترمودینامیک آماری را بنویسید

رابطه ۱۳ در این متن مربوط به انرژی کل آنسامبل است که به صورت زیر نوشته می‌شود:

$$\begin{equation}
E =N k T^{2}\left(\frac{d \ln q}{d T}\right)
\end{equation}$$

به کمک قانون بولتزمن رابطه ای برای آنتروپی در ترمودینامیک آماری بدست آورید

رابطه ۴۹ در این متن برای آنتروپی در ترمودینامیک آماری بکار می‌رود:‌

$$\begin{equation}
\begin{aligned}
S &=-k \sum_{n} a_{n} \ln p_{n} \\
&=-k \sum_{n} a_{n}\left(-\beta \varepsilon_{n}-\ln q\right) \\
&=k \beta \sum_{n} a_{n} \varepsilon_{n}+k \sum_{n} a_{n} \ln q \\
&=k \beta E+k N \ln q \\
&=\frac{E}{T}+k \ln q^{N} \\
S &=\frac{E}{T}+k \ln Q=\frac{U}{T}+k \ln Q
\end{aligned}
\end{equation}$$