آنتروپی چیست؟ – از صفر تا صد

پیش از این در بلاگ فرادرس در مورد اصول ترمودینامیک صحبت کردیم. اکنون قصد داریم تا در مورد نحوه محاسبه آنتروپی و هم‌چنین مسائلی بحث کنیم، که احتمالا در آزمون‌های مربوط به دروس ترمودینامیک و فیزیک، با آن‌ها مواجه خواهید شد. بدین منظور در ابتدا توضیح مختصری درباره قوانین ترمودینامیک خواهیم داد سپس در مورد خاصیت آنتروپی صحبت خواهیم کرد.

آنتروپی چیست؟

آنتروپی، اندازه گیری انرژی گرمایی یک سیستم در واحد دمایی است که برای انجام کار مفید غیر قابل دسترس است. از آنجایی که کار از حرکت مولکولی منظم به دست می‌آید، مقدار آنتروپی نیز معیاری برای بی نظمی مولکولی یا تصادفی بودن یک سیستم است. مفهوم آنتروپی بینش عمیقی را در مورد جهت تغییر خود به خودی برای بسیاری از پدیده‌های روزمره فراهم می‌کند. معرفی آن توسط فیزیکدان آلمانی رودولف کلازیوس در سال 1850 نقطه برجسته فیزیک قرن نوزدهم بود.

ایده آنتروپی یک راه ریاضی برای رمزگذاری این مفهوم شهودی ارائه می‌دهد که کدام فرآیندها غیرممکن هستند، حتی اگر اصل بقای انرژی را نقض نکنند. به عنوان مثال، یک قطعه یخ که روی یک اجاق گاز داغ قرار می‌گیرد، مطمئناً ذوب می‌شود، در حالی که اجاق گاز خنک‌تر می‌شود. چنین فرآیندی غیرقابل برگشت نامیده می‌شود زیرا هیچ تغییر جزئی باعث نمی‌شود که آب ذوب شده دوباره به یخ تبدیل شود در حالی که اجاق گاز داغ می‌شود. در مقابل، یک قطعه یخ که در یک حمام آب یخ قرار می‌گیرد، بسته به اینکه مقدار کمی گرما به سیستم اضافه شود یا از آن کم شود، یا کمی بیشتر آب می‌شود یا کمی بیشتر منجمد می‌شود. چنین فرآیندی برگشت پذیر است زیرا فقط مقدار بی نهایت کوچکی گرما برای تغییر جهت آن از انجماد تدریجی به ذوب تدریجی مورد نیاز است.

به طور مشابه، گاز فشرده محصور شده در یک سیلندر می‌تواند آزادانه در اتمسفر گسترش یابد (یک فرآیند غیرقابل برگشت)، یا می‌تواند با فشار دادن یک پیستون متحرک در برابر نیروی مورد نیاز برای محدود کردن گاز، کار مفیدی انجام دهد. فرآیند دوم برگشت پذیر است زیرا تنها افزایش جزئی در نیروی بازدارنده می‌تواند جهت فرآیند را از انبساط به تراکم معکوس کند. برای فرآیندهای برگشت‌پذیر، سیستم با محیط خود در تعادل است، در حالی که برای فرآیندهای برگشت‌ناپذیر اینطور نیست.

«کلازیوس» (Clausius) برای ارائه یک معیار کمی برای جهت تغییر خود به خودی، مفهوم آنتروپی را به عنوان روشی دقیق برای بیان قانون دوم ترمودینامیک معرفی کرد. کلازیوس قانون دوم را اینگونه بیان می‌کند که تغییر خود به خودی برای یک فرآیند برگشت ناپذیر در یک سیستم ایزوله (یعنی سیستمی که گرما را مبادله نمی‌کند یا بر روی محیط اطراف خود کار انجام نمی‌دهد) همیشه در جهت افزایش آنتروپی پیش می‌رود. به عنوان مثال، بلوک یخ و اجاق گاز دو بخش از یک سیستم جدا شده را تشکیل می‌دهند که با ذوب شدن یخ، آنتروپی کل افزایش می‌یابد.

طبق تعریف کلازیوس، اگر مقداری از گرما Q در یک مخزن حرارتی بزرگ در دمای T، بالای صفر مطلق شارش یابد، افزایش آنتروپی برابر با $$\Delta S=\frac{Q}{T}$$ است. این معادله به طور موثر یک تعریف جایگزین از دما ارائه می‌دهد که با تعریف معمول مطابقت دارد. به عنوان مثال فرض کنید که دو مخزن حرارتی $$R_1$$ و $$R_2$$ در دمای $$T_1$$ و $$T_2$$ (مانند اجاق گاز و بلوک یخ) وجود دارند. اگر مقدار گرمای Q از $$R_1$$ به $$R_2$$ جریان یابد، تغییر آنتروپی خالص برای دو مخزن برابر است با

$$\Delta S=Q(\frac{1}{T_2}-\frac{1}{T_1})$$

که اگر $$T_1>T_2$$ باشد، کمیت بالا یک مقدار مثبت است. بنابراین، مشاهده می‌شود که دلیل اینکه گرما هرگز به طور خود به خودی از محیط سرد به گرم جریان نمی‌یابد، معادل نیاز به تغییر آنتروپی مثبت خالص برای شارش خود به خودی گرما است. اگر $$T_1=T_2$$، مخازن در حالت تعادل هستند و شارش گرمایی وجود ندارد، در نتیجه $$\Delta S=0$$ خواهد بود.

شرط $$\Delta S\geq0$$ حداکثر بازده ممکن موتورهای حرارتی را تعیین می‌کند یعنی سیستم‌هایی مانند موتورهای بنزینی یا ماشین بخار که می‌توانند به صورت چرخه‌ای کار کنند. فرض کنید یک موتور حرارتی گرمای $$Q_1$$ را از $$R_1$$ جذب می‌کند و گرمای $$Q_2$$ را به $$R_2$$ برای هر چرخه کامل تخلیه می‌کند. با پایستگی انرژی، کار انجام شده در هر چرخه $$W=Q_1-Q_2$$ است و تغییر آنتروپی خالص برابر است با

$$\Delta S=\frac{Q_2}{T_2}-\frac{Q_1}{T_1}$$

برای بزرگ کردن W تا حد امکان، $$Q_2$$ باید تا حد امکان نسبت به $$Q_1$$ کوچک باشد. با این حال، $$Q_2$$ نمی‌تواند صفر باشد، زیرا این امر $$\Delta S$$ را منفی می‌کند و بنابراین قانون دوم را نقض می‌کند. در حقیقت کوچکترین مقدار ممکن $$Q_2$$ با شرط $$\Delta S=0$$ مطابقت دارد. بدین ترتیب داریم:

$$(\frac{Q_2}{Q_1})_{min}=\frac{T_2}{T_1}$$

معادله بالا به عنوان معادله اساسی است که کارایی تمام موتورهای حرارتی را محدود می‌کند. فرآیندی که برای آن $$\Delta S=0$$ است برگشت پذیر است زیرا یک تغییر بی نهایت کوچک برای اینکه موتور حرارتی به عنوان یخچال به سمت عقب کار کند کافی است.

همین استدلال می‌تواند تغییر آنتروپی را برای ماده‌‌ای که روی آن در موتور حرارتی کار انجام می‌شود، مانند گاز در سیلندر با پیستون متحرک را تعیین کند. اگر گاز مقدار گرمای $$dQ$$ را از یک مخزن حرارتی در دمای T جذب کند و به طور برگشت پذیر در برابر حداکثر فشار مهاری ممکن P منبسط شود، آن گاه حداکثر کار $$dW=P dV$$ را انجام می‌دهد که در آن $$dV$$ تغییر حجم است. انرژی داخلی گاز نیز ممکن است با انبساط به مقدار $$dU$$ تغییر کند. بدین ترتیب با استفاده از قانون پایستگی انرژی، $$dQ=dU+P dV$$. از آنجا که تغییر آنتروپی خالص برای سیستم به اضافه مخزن صفر است زمانی که حداکثر کار انجام می‌شود و آنتروپی مخزن به مقدار $$dS_{reservoir}=-\frac{dQ}{T}$$ کاهش می‌یابد، این مقدار باید به افزایش آنتروپی سیستم منجر شود و داریم:

$$d S_{s y s t e m}=\frac{d U+P d V}{T}=\frac{d Q}{T}$$

بدین ترتیب برای گازی که روی آن کار انجام می‌شود تغییرات آنتروپی صفر است و داریم:

$$d S_{\text {system }}+d S_{\text {reservoir }}=0$$

برای هر فرآیند واقعی به دلایل مختلف به عنوان مثال، اصطکاک کار انجام شده کمتر از مقدار حداکثر است و بنابراین مقدار واقعی گرمای $$dQ^{\prime}$$ جذب شده از مخزن حرارتی کمتر از حداکثر مقدار $$dQ$$ خواهد بود. به عنوان مثال، گاز می‌تواند آزادانه در خلاء منبسط شود و هیچ کاری انجام ندهد. بنابراین می توان بیان کرد که

$$d S_{\text {system }}=\frac{d U+P d V}{T} \geq \frac{d Q^{\prime}}{T}$$

اگر $$dQ=dQ^{\prime}$$ باشد، کار ماکزیمم روی سیستم انجام می‌شود و فرآیند برگشت پذیر است. این معادله سیستم را به عنوان یک متغیر حالت ترمودینامیکی تعریف می‌کند، به این معنی که مقدار آن کاملاً توسط وضعیت فعلی سیستم تعیین می‌شود نه اینکه چگونه سیستم به آن حالت رسیده است. آنتروپی یک خاصیت بسیط است که بزرگی آن به مقدار مواد موجود در سیستم بستگی دارد. در یکی از تفسیرهای آماری آنتروپی، مشخص شد که برای یک سیستم بسیار بزرگ در تعادل ترمودینامیکی، آنتروپی S متناسب با لگاریتم طبیعی کمیت $$\Omega$$ است که نشان‌دهنده حداکثر تعداد روش‌های میکروسکوپی است که در آن حالت ماکروسکوپی مربوط به S می‌تواند تحقق یابد، یعنی داریم $$S=k\ ln \Omega$$، که در آن k ثابت بولتزمن است که مربوط به انرژی مولکولی است. همه فرآیندهای خود به خودی غیر قابل برگشت هستند. از این رو گفته می‌شود که آنتروپی جهان در حال افزایش است، یعنی انرژی بیشتر و بیشتر برای تبدیل به کار در دسترس نیست و دقیقاً به همین دلیل، گفته می‌شود که جهان در حال فروپاشی است. در ادامه قوانین ترمودینامیک و روش های محاسبه تغییرات آنتروپی را بررسی می‌کنیم.

قانون اول ترمودینامیک

سیستمی را فرض کنید که مبادله حرارت با محیط اطراف انجام داده و کاری نیز روی آن صورت گرفته است. قانون اول ترمودینامیک بیان می‌کند که برای چنین سیستمی، افزایش انرژی، معادل با حاصل جمع حرارت اضافه شده به آن و کار صورت گرفته روی سیستم مفروض است.

بر مبنای آزمایشات صورت گرفته، دو خاصیت جدید را می‌توان برای یک سیستم ترمودینامیک، تحت عنوان انرژی درونی و دما تعریف کرد. رابطه میان این دو پارامتر، خاصیت جدیدی تحت عنوان آنتروپی را بوجود می‌آورد. در ادامه به‌طور مفصل در مورد این خاصیت صحبت خواهیم کرد.

قانون دوم ترمودینامیک

تصور کنید فنجانی قهوه ۸۰ درجه را در اتاقی با دمای ۲۵ درجه قرار داده‌اید. بدیهی است که هیچ‌گاه این فنجان قهوه گرم‌تر نخواهد شد و با گذشت زمان قطعا دمای آن افت خواهد کرد. حال فرآیندی عکس آن را در نظر بگیرید. تصور کنید با گذاشتن این فنجان در اتاق، دمای آن با گذشت زمان افزایش می‌یابد. این فرآیند قانون اول ترمودینامیک را نقض نمی‌کند،‌ اما واضح است که هیچ‌گاه اتفاق نخواهد افتاد. به‌راستی چرا هیچ‌گاه فنجان گرم‌تر نمی‌شود؟ چرا با گذشت زمان جوان‌تر نمی‌شویم؟ چرا مواد در بیرون از یخچال پس از مدتی فاسد می‌شوند.

برای اتفاق افتادن یک فرآیند، تنها صادق بودن قانون اول کافی نیست. قانون دوم ترمودینامیک بیان می‌کند که هر فرآیند تنها در یک جهت پیش می‌رود. به‌شکلی کمی‌تر، ‌قانون دوم ترمودینامیک بیان می‌کند که هر فرآیند در جهتی پیش می‌رود که خاصیتی تحت عنوان آنتروپی در سیستم افزایش یابد.

همچنین این قانون می‌گوید که برای هر سیستمی که در تعادل ترمودینامیکی خود است، این خاصیت را می‌توان برایش تعریف کرد. اگر این سیستم، فرآیندی برگشت‌پذیر را تجربه کند، تغییرات آنتروپی در آن برابر با مقدار زیر است.

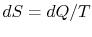
در این معادله T دمای مطلق سیستم و dQ مقدار حرارت جزئی منتقل شده است. آنتروپی سیستمی که عایق حرارتی شده، تحت هیچ شرایطی کاهش نخواهد یافت و تنها در حالتی ثابت می‌ماند که سیستم فرآیندی برگشت‌پذیر را تجربه کند.

ترکیب قوانین اول و دوم ترمودینامیک

قانون اول را می‌توان به شکل زیر بیان کرد:

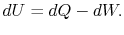
توجه داشته باشید که در این معادله، dU ،dQ و dW به ترتیب برابر با حرارت وارد شده به سیستم، تغییرات انرژی درونی و کار انجام شده توسط سیستم هستند. برای این فرآیند برگشت‌پذیر روابط زیر قابل بیان هستند.

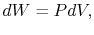
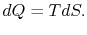
با جایگذاری این مقادیر در رابطه شماره ۱ داریم:

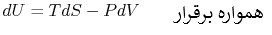
این معادله همواره برقرار است،‌ چراکه ارتباط میان خواص یک سیستم را بیان می‌کند؛ بنابراین این رابطه مستقل از مسیر فرآیند خواهد بود.

با تعریف خاصیت جدیدی تحت عنوان «آنتالپی» (Enthalpy)، این رابطه را می‌توان به شکل زیر نشان داد.

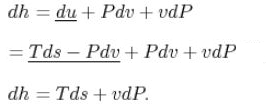
آنتالپی نیز همانند آنتروپی خاصیت ترمودینامیکی سیستم محسوب می‌شود.

محاسبه تغییرات آنتروپی

به‌منظور درک بهتر مفهوم آنتروپی، قصد داریم تا تغییرات این خاصیت را در چندین فرآیند مورد بررسی قرار دهیم.

محاسبه تغییرات آنتروپی در گازهای ایده‌آل

در بسیاری از کاربردها همچون هوافضا، دینامیک گاز و ... با فرآیندهایی روبرو هستیم که در آن‌ها از گاز ایده‌آل به عنوان سیال کاری استفاده شده است.

صورت مسئله: فرض کنید گازی ایده‌آل، فرآیندی را تجربه می‌کند که دمای آن از T₁ به T₂ و حجم آن از V₁ به V₂ تغییر کرده. تغییر آنتروپی گاز مدنظر چقدر است؟

برای یک گاز ایده‌آل، تغییرات انرژی درونی برابر است با:

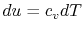
با جایگذاری این تغییر در معادله شماره 2، داریم:

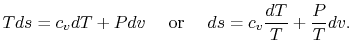
همان‌طور که از ترمودینامیک به یاد دارید برای یک گاز ایده‌آل، رابطه‌ای تحت عنوان «معادله حالت» (Equation of State) را می‌توان به شکل زیر نوشت:

PV=RT

با جایگذاری معادله حالت، در رابطه ۳ خواهیم داشت:

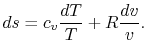
با انتگرال‌گیریِ معادله از ۱ تا ۲، تغییر آنتروپی به صورت زیر بدست می‌آید.

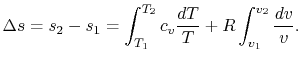
برای یک گاز کامل با ظرفیت‌های حرارتی ثابت، خواهیم داشت:

$$\begin{equation}\Delta s=s_{2}-s_{1}=c_{v} \ln \left(\frac{T_{2}}{T_{1}}\right)+R \ln \left(\frac{v_{2}}{v_{1}}\right)\end{equation}$$

برای بدون بعد کردن رابطه، از عبارت $$\begin{equation}R / c_{v}=(\gamma-1)\end{equation}$$ کمک می‌گیریم. بنابراین، تغییر آنتروپی یک گاز کامل به صورت زیر خواهد بود:

$$\begin{equation}\frac{\Delta s}{c_{v}}=\ln \left(\frac{T_{2}}{T_{1}}\right)+(\gamma-1) \ln \left(\frac{v_{2}}{v_{1}}\right)\end{equation}$$

این رابطه برای N مول گاز به صورت زیر محاسبه می‌شود:

$$\begin{equation}\frac{\Delta S}{C_{v}}=N\left[\ln \left(\frac{T_{2}}{T_{1}}\right)+(\gamma-1) \ln \left(\frac{V_{2}}{V_{1}}\right)\right]\end{equation}$$

رابطه بالا، تغییر آنتروپی را بر اساس دما و حجم بدست می‌دهد. می‌توان شکل دیگری از این رابطه را توسعه داد به گونه‌ای که تغییر آنتروپی را بر اساس فشار و حجم بیان کند تا بتوان درستی فرض‌های انجام شده را بررسی کرد. به همین منظور، رابطه گازهای ایده‌آل را به صورت زیر می‌نویسیم:

$$\begin{equation}\ln P+\ln v=\ln R+\ln T\end{equation}$$

با دیفرانسیل گرفتن از دو طرف رابطه بالا، به رابطه زیر می‌رسیم:

$$\begin{equation}\frac{d P}{P}+\frac{d v}{v}=\frac{d T}{T}\end{equation}$$

با استفاده از روابط بالا و همچنین رابطه‌های $$\begin{equation}c_{p}=c_{v}+R\ ; c_{p} / c_{v}=\gamma\end{equation}$$ به رابطه زیر می‌رسیم:

$$\begin{equation}d s=c_{v}\left[\frac{d P}{P}+\frac{d v}{v}\right]+R \frac{d v}{v}\end{equation}$$

یا

$$\begin{equation}\frac{d s}{c_{v}}=\frac{d P}{P}+\gamma \frac{d v}{v}\end{equation}$$

با محاسبه انتگرال خواهیم داشت:

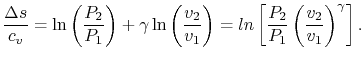
توجه داشته باشید که این معادله تغییر آنتروپی سیستمی را نشان می‌دهد که فرآیندی آدیاباتیک را تجربه کرده. با تعریف γ=c_p/c_v و استفاده از معادله حالت، افزایش آنتروپی را می‌توان بر حسب تغییرات فشار و حجم، به‌شکل زیر حساب کرد.

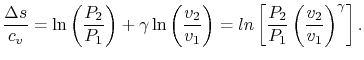
طبق این معادله، هرگاه در فرآیندی این تغییرات را معادل با صفر قرار دهیم، به عبارت زیر خواهیم رسید.

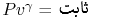
این رابطه نشان‌دهنده فرآیندی پلی‌تروپیک است که در مطلب سیکل‌های ترمودینامیکی در مورد آن بحث کردیم.

محاسبه تغییرات آنتروپی

در این قسمت قصد داریم تا تغییرات آنتروپی در فرآیندهای خاصی را مورد بررسی قرار دهیم.

۱. مبادله حرارت با یک منبع حرارتی

منبع حرارتی، بخشی از یک سیستم ترمودینامیکی محسوب می‌شود که تولید کننده یا مصرف کننده انرژی است. شکل زیر یک منبع حرارتی و انرژی‌های مبادله شده با محیط را نشان می‌دهد. توجه داشته باشید که دمای منبع مذکور، ثابت در نظر گرفته می‌شود. با فرض انتقال حرارتی برگشت‌پذیر با منبع، تغییرات آنتروپی را می‌توان به‌شکل زیر بیان کرد.

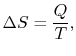
2. انتقال حرارت میان دو منبع حرارتی

به منظور محاسبه تغییرات آنتروپی دو منبع حرارتی که در حال مبادله انرژی با یکدیگر هستند، مجموع تغییرات آنتروپی هر دوی آن‌ها بایستی محاسبه شود. مطابق با شکل زیر، دو منبع حرارتی را با دمای T_H و T_L در نظر بگیرید. فرض کنید دمای T_H از T_L بیشتر باشد. بدیهی است که این اختلاف دما منجر به انتقال حرارتی از منبع بالا به پایین خواهد شد.

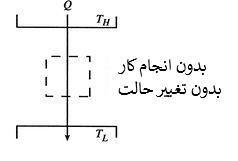
می‌توان تغییر آنتروپی کلی را برای چنین سیستمی به‌ شکل زیر محاسبه کرد.

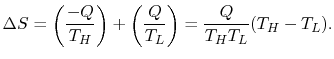
قانون دوم بیان می‌کند که برای یک سیستم این حاصل جمع بایستی بیشتر و یا مساوی صفر باشد. این معادله همان یک‌طرفه بودن فرآیندها را نشان می‌دهد.

۳. آیا می‌توان تنها با مبادله حرارت با یک منبع حرارتی کار تولید کرد؟

مطابق با شکل زیر تک‌ منبعی را فرض کنید که در حال مبادله حرارت با محیط است. فرض کنید کلِ حرارت مبادله شده با محیط اطراف، برابر با Q باشد.

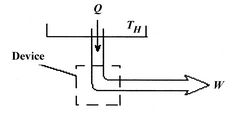
همان‌گونه که در بالا نیز بیان شد، تغییرات کل آنتروپی، برابر با حاصل جمع تغییرات آنتروپی تمامی سیستم‌ها است؛ بنابراین می‌توان این تغییر کلی را به شکل زیر محاسبه کرد.

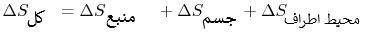
مقدار بدست آمده کمتر از صفر است؛ در نتیجه هیچ‌گاه چنین فرآیندی رخ نخواهد داد، چراکه قانون دوم ترمودینامیک را نقض کرده. این همان مفهومی است که تحت عنوان بیان کلوین-پلانک شناخته می‌شود.

۴. محاسبه تغییر آنتروپی دو جسم که به تعادل حرارتی می‌رسند

مطابق شکل زیر، دو جسم را تصور کنید که در دمای اولیه T_H و T_L قرار دارند. اگر این دو جسم در تماس با یکدیگر قرار گیرند، بدیهی است که پس از گذشت مدت زمانی به تعادل حرارتی می‌رسند؛ در این شرایط دمای آن‌ها با یکدیگر برابر خواهد شد.

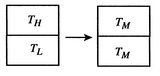
دمای تعادلِ دو جسم را برابر با T_M در نظر بگیرید. توجه داشته باشید که این فرآیند، بازگشت‌پذیر نیست؛ در حقیقت انتقال حرارت صورت گرفته از بینهایت فرآیند بازگشت‌پذیر، به نحوی تشکیل شده که در هر مرحله، دمای هر دو جسم به اندازه dT تغییر کرده. انرژی مبادله شده در هر‌یک از این مراحل را می‌توان برابر با dQ=CdT در نظر گرفت. در نتیجه تغییر آنتروپی جسم داغ، برابر است با:

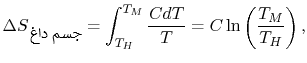
به همین شکل این تغییر برای جسم سرد را می‌توان به شکل زیر محاسبه کرد.

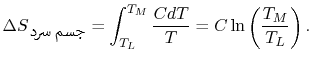
نهایتا تغییر آنتروپی کل سیستم، به صورت حاصل جمع این دو مقدار و با استفاده از رابطه زیر حساب می‌شود.

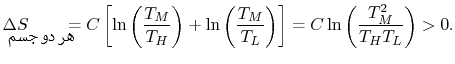
همان‌طور که معادله بالا نشان می‌دهد، تغییر آنتروپی این فرآیند، همواره بیشتر از صفر است؛ بنابراین فرآیند مذکور، برگشت‌پذیر خواهد بود. توجه داشته باشید هر فرآیندی که برگشت پذیر و آدیاباتیک باشد، آیزنتروپیک نامیده می‌شود. این مفهوم در ساخت کمپرسور‌ها و توربین‌ها کاربرد دارد. در حقیقت عددی تحت عنوان راندمان آیزنتروپیک به آن‌ها نسبت داده می‌شود که معیاری از ایده‌آل بودن آن‌ها است.

۳. تغییر آنتروپی در انبساط آزاد گاز ایده‌آل

فرض کنید مطابق با شکل زیر، گازی در یک محفظه عایق قرار گرفته که توسط شیری از یک محیط خلا جدا شده است.

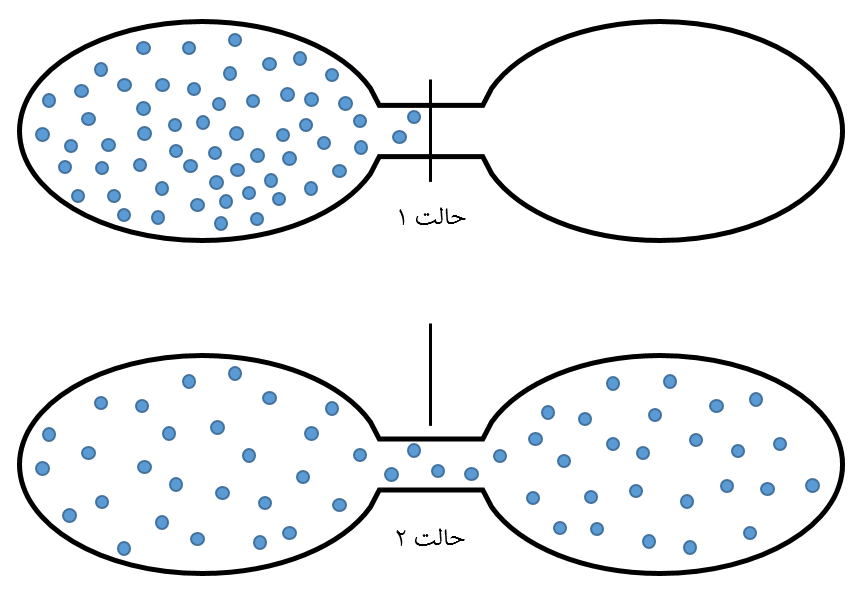
ناگهان شیر بازه شده و گاز در کل محفظه منبسط می‌شود. بدلیل عایق بودن سیستم، انتقال حرارتی رخ نمی‌دهد، در نتیجه دما و انرژی درونی سیستم ثابت می‌ماند (U و T = ثابت). حال می‌خواهیم تغییر آنتروپی این فرآیند را محاسبه کنیم. با استفاده از معادله شماره ۳، این تغییر به شکل زیر محاسبه خواهد شد.

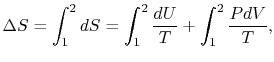
با عایق بودن سیستم، دما ثابت بوده، بنابراین انرژی درونی نیز تغییر نمی‌کند (ΔU=0). در نتیجه معادله بالا را می‌توان به صورت زیر بازنویسی کرد.

از طرفی به دلیل این‌که در سمت دیگر محفظه، گازی وجود ندارد، کاری نیز صورت نمی‌گیرد و تغییر آنتروپی اطراف برابر با صفر است (_اطرافΔS). حال می‌توان با جمع زدن این مقادیر، تغییرات کلی آنتروپی را به شکل زیر محاسبه کرد.

همان‌طور که محاسبه شد، آنتروپی کلی افزایش یافته؛ بنابراین فرآیند مفروض برگشت‌ناپذیر است.

آنتروپی منفی به چه معنا است؟

آنتروپی درجه بی نظمی است. آنتروپی منفی می‌تواند به معنای درجه نظم باشد. آنتروپی عالم در حال افزایش است و نرخ تغییرات آن بزرگتر از صفر است. آنتروپی منفی به معنای کاهش تغییرات آنتروپی یا بی نظمی است. در حقیقت، مثبت یا منفی در اینجا جهت پیشرفت روند را نشان می‌دهد.

اگرچه اغلب مثبت یا منفی بودن آنتروپی به عنوان مقایسه‌ای برای آنتروپی قبل و بعد از استفاده از انرژی استفاده می‌شود، به عنوان مثال قبل از استفاده از انرژی سیستم، آن را آنتروپی منفی می‌نامیم. پس از استفاده از انرژی سیستم آن را آنتروپی مثبت می‌نامیم. این کاربردی است که برای آنتروپی نسبی استفاده می‌شود و در آن برای یک گروه جرمی قبل و بعد از استفاده از انرژی آن، آنتروپی پایین را آنتروپی منفی می‌نامند و آنتروپی بالاتر آنتروپی مثبت نامیده می‌شود. در اینجا منفی به معنای نسبتاً منظم‌تر و مثبت به معنای نسبتاً بی نظم‌تر است.

در فضا و زمان و شرایط عادی، آنتروپی ترمودینامیکی همیشه در حال رشد و افزایش است. این در صورتی است که در شرایط خاصی که در سیاهچاله‌های مرکزی برقرار است، آنتروپی ترمودینامیکی همیشه در حال کاهش است. سیاهچاله‌های مرکزی آنتروپی منفی ایجاد نمی‌کنند، بلکه فقط آنتروپی مثبت را به آنتروپی منفی تبدیل می‌کنند.

این موضوع بدان معنا است که نسبت بین آنتروپی مثبت کل و آنتروپی منفی کل هرگز تغییر نمی‌کند. آنتروپی ترمودینامیکی شرایط نظم حالت انرژی (وضعیت حرکت آزاد) جرم را توصیف می‌کند و آنتروپی اطلاعات شرایط نظم وضعیت اطلاعات یعنی پیچیدگی ساختار و حالت حرکت جرم را توصیف می‌کند. بنابراین، آنتروپی ترمودینامیکی و آنتروپی اطلاعات شرایط نظم یک جرم را برای جنبه‌های مختلف حالات وجودی آن توصیف می‌کنند یعنی حالت انرژی یا حالت اطلاعات.

به عنوان مثال افزایش آنتروپی ترمودینامیکی فرآیندی است که طی آن ترتیب حالت انرژی جرم به ترتیب حالت اطلاعاتی همان سیستم تبدیل می‌شود و فرآیندی است که همواره در فضا و زمان معمولی رخ می‌دهد. در حالی که کاهش آنتروپی ترمودینامیکی فرآیندی است که در آن ترتیب وضعیت اطلاعات جرم به ترتیب حالت انرژی جرم تبدیل می‌شود که فقط در سیاهچاله‌های مرکزی اتفاق می‌افتد. تمام فرآیند تکامل ماده، این آنتروپی ترمودینامیکی منفی تبدیل شده توسط سیاهچاله‌های مرکزی را مصرف می‌کند.

شکلی از آنتروپی منفی که می‌توانیم برای بقا و تکامل از آن استفاده کنیم، شکل سیستماتیک آنتروپی ترمودینامیکی منفی تبدیل شده و تکامل‌ یافته طبیعت است. یک حالت انرژی درهم تنیده منظم و اطلاعات جرمی است که برای شکل گیری و تحویل، به ده‌ها یا صدها میلیارد سال فرآیند تکامل طبیعی نیاز دارد و بیشتر انرژی موجود در آن برای شکل گیری درجه نظم اطلاعات استفاده می‌شود که آن را ارزش مادی یا ارزش واقعی می‌نامیم.

این ارزش مادی ذاتاً در هر مکان و زمان محلی محدود است، اما با نگاه عمیق‌تر به آن به سطحی از انرژی می رسیم که می‌توانیم خود را به آینده بی‌پایان متصل کنیم. به دلیل محدودیت ارزش مادی در فضا و زمان محلی، همه فرآیندهای طبیعی در فضا و زمان محلی محدود است و در حقیقت همه فرآیندهای محلی دارای پایان هستند. تنها راهی که زندگی هوشمند می‌تواند به آینده بی پایان برسد، استفاده کامل از ارزش مادی داده شده برای طبیعت است تا به آن اجازه دهد در طبیعت با حداکثر بازه زمانی مشخص و در شرایط بهینه به سطح وضعیت اطلاعاتی دسترسی پیدا کنیم که ما را به یک فرآیند باز برای رسیدن به زندگی ابدی متصل کند.

آنتروپی سیاهچاله‌ها چگونه است؟

در فیزیک، ترمودینامیک سیاهچاله حوزه مطالعاتی است که به دنبال تطبیق قوانین ترمودینامیک با وجود افق رویداد سیاهچاله است. همان طور که مطالعه مکانیک آماری تابش جسم سیاه منجر به توسعه نظریه مکانیک کوانتومی شد، تلاش برای درک مکانیک آماری سیاهچاله‌ها تأثیر عمیقی بر درک گرانش کوانتومی داشته است و منجر به فرمول‌ بندی اصل هولوگرافیک می‌شود. قانون دوم ترمودینامیک مستلزم آنتروپی سیاهچاله ها است. اگر سیاهچاله‌ها فاقد آنتروپی باشند، می‌توان با پرتاب جرم به داخل سیاهچاله، قانون دوم را نقض کرد. افزایش آنتروپی سیاهچاله بیشتر از کاهش، آنتروپی حمل شده توسط جسم بلعیده شده را جبران می‌کند.

در سال 1972، یاکوب بکنشتاین حدس زد که سیاهچاله‌ها باید دارای آنتروپی باشند اما در همان سال، او هیچ نظریه‌ای را پیشنهاد نکرد. در سال 1973 بکنشتاین کمیت $${\displaystyle {\frac {\ln {2}}{8\pi }}\approx 0.276}$$ را به عنوان ثابت تناسب پیشنهاد کرد و بیان داشت که اگر ثابت دقیقاً این مقدار نباشد، باید بسیار نزدیک به آن باشد. سال بعد یعنی در سال 1974، استیون هاوکینگ نشان داد که سیاهچاله‌ها تابش‌های حرارتی هاوکینگ را که مربوط به دمای معین (دمای هاوکینگ) است، ساطع می‌کنند. هاوکینگ با استفاده از رابطه ترمودینامیکی بین انرژی، دما و آنتروپی توانست حدس بکنشتاین را تایید کند و ثابت تناسب با مقدار $$\frac{1}{4}$$ را اثبات کند.

$${\displaystyle S_{\text{BH}}={\frac {k_{\text{B}}A}{4\ell _{\text{P}}^{2}}},}$$

که در آن $$A$$ مساحت افق رویداد، $$k_B$$ ثابت بولتزمن و $${\displaystyle \ell _{\text {P}}={\sqrt {G\hbar /c^{3}}}}$$ طول پلانک است. این رابطه اغلب به عنوان فرمول بکنشتاین-هاوکینگ نامیده می‌شود. زیرنویس BH یا مخفف سیاه چاله یا Bekenstein-Hawking است. همان طور که از رابطه مشخص است آنتروپی سیاهچاله با مساحت افق رویداد آن یعنی A متناسب است. این واقعیت که آنتروپی سیاهچاله حداکثر آنتروپی است که می‌توان با حد بکنشتاین به دست آورد، مشاهده اصلی بود که به اصل هولوگرافی منتهی شد. این رابطه مساحتی، از طریق فرمول ریو تاکایاناگی به مناطق دلخواه تعمیم داده شد، که در نتیجه آنتروپی درهم تنیدگی یک نظریه میدان منسجم مرزی را به سطح خاصی در نظریه گرانشی دوگانه آن مرتبط می‌کند.

اگرچه محاسبات هاوکینگ شواهد ترمودینامیکی بیشتری برای آنتروپی سیاه‌چاله به دست داد، تا سال 1995 هیچ‌کس قادر به محاسبه کنترل‌شده آنتروپی سیاه‌چاله بر اساس مکانیک آماری که آنتروپی را با تعداد زیادی ریزحالت مرتبط می‌کند، نبود.

در واقع در اصطلاح قضایای «بدون مو» (no-hair)، نشان می‌دهند سیاه‌چاله‌ها می‌توانند تنها یک ریز حالت داشته باشند. وضعیت در سال 1995 زمانی که اندرو استرومینگر و کامران وفا آنتروپی بکنشتاین-هاوکینگ را برای یک سیاهچاله ابر متقارن در نظریه ریسمان، با استفاده از روش‌های مبتنی بر «صفحات دیریکله» (Dirichlet membrane) و دوگانگی ریسمان محاسبه کردند، تغییر کرد. محاسبات آن‌ها توسط بسیاری از محاسبات مشابه آنتروپی کلاس‌های بزرگ دیگر سیاهچاله‌های در انتهای عمر خود و نزدیک به انتها دنبال شد و نتیجه همیشه با فرمول بکنشتاین-هاوکینگ مطابقت داشت. با این حال برای سیاهچاله شوارتزشیلد، که به عنوان دورترین سیاهچاله تلقی می‌شود، رابطه بین میکرو و ماکرو حالت‌ها مشخص نشده است و تلاش‌ها برای ایجاد پاسخ مناسب در چارچوب نظریه ریسمان ادامه دارد.

در گرانش کوانتومی حلقه (LQG)، می‌توان یک تفسیر هندسی را با ریز حالت‌ها مرتبط کرد که هندسه‌های کوانتومی افق هستند. LQG توضیح هندسی محدود بودن آنتروپی و تناسب مساحت افق را ارائه می‌دهد. می‌توان از فرمول کوواریانس نظریه کوانتومی کامل (اسپیفوم) رابطه صحیح بین انرژی و مساحت (قانون اول)، «دمای اونروه» (Unruh temperature) و توزیعی که آنتروپی هاوکینگ را به وجود می‌آورد، استخراج کرد. این محاسبه از مفهوم افق دینامیکی استفاده می‌کند و برای سیاهچاله‌هایی که در پایان عمر خود نیز نیستند، استفاده می‌شود. به نظر می‌رسد که در مورد محاسبه آنتروپی بکنشتاین-هاوکینگ از نقطه نظر گرانش کوانتومی حلقه نیز بحث‌هایی وجود دارد.

قوانین مکانیک سیاهچاله‌ها

چهار قانون مکانیک سیاهچاله‌ها ویژگی‌های فیزیکی سیاهچاله‌ها هستند که اعتقاد بر این است که سیاهچاله‌ها آن‌ها را برآورده می‌کنند. این قوانین، مشابه قوانین ترمودینامیک، توسط جاکوب بکنشتاین، براندون کارتر و جیمز باردین کشف شد و ملاحظات بیشتر توسط استیون هاوکینگ ارائه شد. قوانین مکانیک سیاهچاله در واحدهای هندسی بیان می‌شوند.

قانون صفر

افق سیاهچاله دارای گرانش سطحی ثابت برای یک سیاهچاله ساکن است.

قانون اول

برای آشفتگی‌های سیاهچاله‌های ساکن، تغییر انرژی با تغییر مساحت، تکانه زاویه‌ای و بار الکتریکی مرتبط است.

$${\displaystyle dE={\frac {\kappa }{8\pi }}\,dA+\Omega \,dJ+\Phi \,dQ,}$$

که E انرژی، $${\displaystyle \kappa }$$ گرانش سطح، $$A$$ مساحت ناحیه افق، $$\Omega$$ سرعت زاویه‌ای، $$J$$ تکانه زاویه‌ای، $$\Phi$$ پتانسیل الکترواستاتیک و $$Q$$ بار الکتریکی است.

قانون دوم

مساحت ناحیه افق، با فرض شرایط انرژی ضعیف، تابعی غیر کاهشی از زمان است و داریم:

$${\displaystyle {\frac {dA}{dt}}\geq 0}$$

این قانون با کشف هاوکینگ مبنی بر تابش سیاهچاله‌ها جایگزین شد، که باعث می‌شود هم جرم سیاهچاله و هم مساحت افق آن در طول زمان کاهش یابند.

قانون سوم

امکان تشکیل سیاهچاله با گرانش سطحی در حال محو شدن وجود ندارد. یعنی نمی توان به $$\kappa =0$$ رسید.

آنتروپی بیگ بنگ چه قدر بوده است؟

پیکان ترمودینامیکی زمان نشان می‌دهد که آنتروپی همیشه بالا می‌رود و افزایش می‌یابد، بنابراین مقدار آن امروز بزرگتر از گذشته بوده است. با این حال، اگر به کیهان بسیار اولیه فکر کنیم، مطمئناً حالتی با آنتروپی بالا به نظر می‌رسد. تصور کنید دریایی از ذرات، از جمله ماده، پادماده، گلوئون، نوترینو و فوتون، که همگی با انرژی‌هایی میلیاردها برابر بیشتر از انرژی LHC امروزی می‌چرخند. تعداد زیادی از این ذرات شاید در حدود $$10^{90}$$ ذره همه در حجمی به کوچکی یک توپ فوتبال جمع شده بودند. درست در لحظه انفجار بزرگ، این منطقه کوچک با این ذرات بسیار پرانرژی در 13٫8 میلیارد سال قبل به کل جهان قابل مشاهده ما تبدیل شده است.

کاملاً واضح است که جهان امروزی بسیار سردتر، بزرگتر، با ساختار کامل‌تر و غیر یکنواخت است. اما در واقع می‌توانیم آنتروپی جهان را در هر دو زمان، در لحظه انفجار بزرگ و امروز، بر حسب ثابت بولتزمن یعنی $$k_B$$، کمی کنیم. در لحظه انفجار بزرگ، تقریباً تمام آنتروپی ناشی از تابش بود و کل آنتروپی جهان $$S=10^{88} k_B$$ بود. از سوی دیگر، اگر آنتروپی جهان را امروز محاسبه کنیم، تقریباً یک کوادریلیون برابر بزرگتر و برابر با $$S=10^{103} k_B$$ است. در حالی که هر دوی این اعداد بزرگ به نظر می‌رسند، عدد اول در مقایسه با دومی به طور قطع آنتروپی پایینی دارد.

هر چند وقتی در مورد این اعداد صحبت می‌کنیم یک نکته مهم را باید در نظر داشته باشیم. وقتی اصطلاحاتی مانند معیار بی نظمی را می‌شنوید، در واقع توصیف بسیار بسیار ضعیفی از آنتروپی است. در عوض، تصور کنید که هر سیستمی را که دوست دارید مانند ماده، تشعشع و هر چیزی دیگری را که احتمالاً مقداری انرژی در آن قرار دارد، خواه جنبشی، پتانسیل، انرژی میدان یا هر نوع دیگری باشد، در اختیار دارید. آنچه آنتروپی در واقع اندازه گیری می‌کند، تعداد ترکیبات احتمالی وضعیت سیستم شما است.

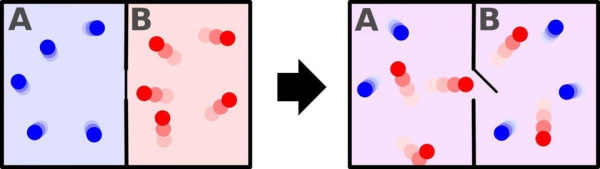
اگر سیستم شما مثلاً یک قسمت سرد و یک قسمت گرم دارد، می‌توانید آن را به روش‌های کمتری نسبت به حالتی که کل سیستم دمای یکسانی داشته باشد مرتب کنید، یعنی در حالت اول تعداد حالت‌های احتمالی سیستم کمتر است. در تصویر پایین سیستم سمت چپ، یک سیستم با آنتروپی پایین‌تر از سیستم سمت راست است. فوتون‌های موجود در پس‌زمینه مایکروویو کیهانی عملاً همان آنتروپی امروزی را دارند که در اولین تولد کیهان داشتند. به همین دلیل است که محققان باور دارند که جهان به صورت آدیاباتیک یعنی با یک آنتروپی ثابت منبسط می‌شود. در حالی که ممکن است به کهکشان‌ها، ستارگان، سیارات و غیره نگاه کنیم و از نظم یا بی نظمی آن‌ها شگفت زده شویم، آنتروپی آن‌ها ناچیز است. پس چه چیزی باعث افزایش بسیار زیاد آنتروپی شد؟

پاسخ سیاهچاله ها هستند. اگر به تمام ذراتی که در ایجاد یک سیاهچاله نقش دارند فکر کنید، عدد فوق العاده بزرگی است. هنگامی که در یک سیاهچاله سقوط می‌کنید، به ناچار به یک تکینگی می‌رسید و تعداد حالات به طور مستقیم با جرم ذرات سیاهچاله متناسب است، بنابراین هر چه سیاهچاله‌های بیشتری تشکیل دهید یا سیاهچاله‌های شما جرم بیشتری داشته باشند، آنتروپی بیشتری در جهان به دست می‌آورید. سیاهچاله بزرگ کهکشان راه شیری به تنهایی دارای آنتروپی $$S=10^{91} k_B$$ است که تقریباً 1000 بار بیشتر از آنتروپی کل جهان در زمان بیگ بنگ است. با توجه به تعداد کهکشان‌ها و جرم سیاهچاله‌ها به طور کلی، آنتروپی کل امروز به مقدار $$S=10^{103} k_B$$ رسیده است. این مقدار بزرگتر می‌شود زیرا در آینده‌ای دور، سیاه‌چاله‌های بیشتری شکل خواهند گرفت و سیاه‌چاله‌های بزرگی که امروزه وجود دارند، تا حدود $$10^{20}$$ سال آینده به رشد خود ادامه خواهند داد. اگر بخواهید کل کیهان را به یک سیاهچاله تبدیل کنید، به حداکثر آنتروپی تقریباً $$S=10^{123} k_B$$ یا ضریب 100 کوئینتیلیون بزرگتر از آنتروپی امروزی خواهیم رسید. وقتی این سیاهچاله‌ها در مقیاس‌های زمانی بزرگ‌تر تا حدود $$10^{100}$$ سال دیگر فروپاشی می‌کنند، آنتروپی تقریباً ثابت می‌ماند، زیرا تابش جسم سیاه (هاوکینگ) که توسط سیاه‌چاله‌های در حال فروپاشی تولید می‌شود، همان تعداد آرایش‌های حالت ممکن خود سیاهچاله موجود را خواهند داشت.

پس چرا کیهان اولیه آنتروپی کمی داشت؟ چون در آن زمان هیچ سیاهچاله‌ای وجود نداشت. آنتروپی $$S=10^{88} k_B$$ هنوز یک مقدار فوق‌العاده بزرگ است، اما این مقدار آنتروپی کل کیهان است که تقریباً به طور مشخص از تابش باقی‌مانده (و تا حدودی نوترینوها) از انفجار بزرگ کد گذاری می‌شود. از آنجا که موادی که وقتی به کیهان نگاه می‌کنیم، مانند ستاره‌ها، کهکشان‌ها و غیره که می‌بینیم، در مقایسه با پس‌زمینه باقی‌مانده آنتروپی ناچیزی دارند، به راحتی می‌توانیم خودمان را فریب دهیم که با شکل‌گیری ساختار، آنتروپی به‌طور قابل توجهی تغییر می‌کند، اما این صرفا یک تصادف، نه علت. اگر سیاهچاله ها وجود نداشتند، آنتروپی کیهان از 13٫8 میلیارد سال گذشته تا کنون تقریباً ثابت بود!

تفاوت آنتاپی و آنتروپی چیست؟

آنتالپی مقدار انرژی درونی موجود در یک ترکیب است در حالی که آنتروپی مقدار اختلال و بی نظمی ذاتی درون ترکیب است. آنتالپی برای عناصری مانند گاز هیدروژن و گاز اکسیژن صفر است اما آنتالپی برای آب غیر صفر است (بدون توجه به فاز). آنتروپی یا میزان بی نظمی، همیشه برای گازها بالاترین و برای جامدات کمترین است. این موضوع به این دلیل است که مولکول‌های گاز به طور گسترده‌ای پخش می‌شوند و بنابراین، بی نظم‌تر از جامدات و مایعات هستند. در نهایت باید گفت گاز هیدروژن آنتروپی بالاتری نسبت به آب مایع خواهد داشت. برای مطالعه بیشتر در مورد آنتالپی مطلب آنتالپی چیست؟ – از صفر تا صد (+ دانلود فیلم آموزش رایگان) را در مجله فرادرس مطالعه کنید.

معرفی فیلم‌های ترمودینامیک فرادرس

در ادامه برخی آموزش‌های ترمودینامیک فرادرس را که برای رشته‌های مختلف آماده شده است را معرفی می‌کنیم که با توجه به اینکه برخی منابع ترمودینامیک اصلی هنوز به زبان فارسی ترجمه نشده است، این فیلم‌های و دوره‌های ویدیویی در کنار یک منبع اصلی می‌تواند کمک شایانی به دانشجویان کند.

معرفی فیلم آموزش ترمودینامیک برای رشته فیزیک

ترمودینامیک یکی از دروس اصلی برای دانشجویان رشته فیزیک است و به همین دلیل در آموزش‌های فیزیک فرادرس دو آموزش ویدیویی ترمودینامیک 1 و ترمودینامیک 2 برای دانشجویان کارشناسی رشته فیزیک فراهم شده است. همچنین آموزش ویدیویی درس مکانیک آماری پیشرفته که یکی از دروس اصلی مقطع کارشناسی ارشد دانشجویان رشته فیزیک است نیز برای دانشجویان این رشته فراهم گردیده است. در نهایت به دلیل اینکه درس ترمودینامیک و مکانیک آماری یکی از دروس کنکور دکتری در رشته فیزیک است یک آموزش ویدیویی مختص حل مسائل و تست‌های مکانیک آماری پیشرفته کنکور دکتری نیز به هدف آماده سازی داوطلبان کنکور دکتری در رشته فیزیک آماده و در دسترس داوطلبان قرار گرفته است. این چهار آموزش ویدیویی فرادرس برای ترمودینامیک و مکانیک آماری را در ادامه به صورت مختصر معرفی می‌کنیم.

معرفی فیلم آموزش ترمودینامیک ۱

مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم آموزش ترمودینامیک ۱ کرده است. این مجموعه آموزشی از نه درس تشکیل شده و برای دانشجویان رشته فیزیک، مهندسی شیمی، پرتوپزشکی و مهندسی مکانیک مفید است. پیش‌نیاز این درس آموزش ریاضی عمومی ۱ و آشنایی با مفاهیم فیزیک است.

درس اول این مجموعه به توضیحات مقدماتی در مورد نیروگاه‌های ساده بخاری، پیل سوختی، سیکل‌های تبرید و موتور موشکی شیمیایی و درس دوم به معرفی مفاهیم و تعاریف اولیه مانند آحاد ترمودینامیکی، انرژی، قانون صفرم ترمودینامیک و مقیاس‌های دما می‌پردازد. درس سوم به خواص ماده خالص و رفتار گازهای ایده آل و غیرایده آل و درس چهارم به شناخت کار و گرما اختصاص دارد. در درس پنجم و ششم به ترتیب قانون اول ترمودینامیک و تحلیل قانون اول ترمودینامیک برای حجم کنترل را خواهید آموخت و در درس هفتم مفاهیم مربوط به قانون دوم ترمودینامیک بررسی می‌شود. درس هشتم این مجموعه به آموزش آنتروپی می‌پردازد و در نهایت درس نهم به تحلیل قانون دوم ترمودینامیک در حجم کنترل اختصاص دارد.

• برای دیدن فیلم آموزش ترمودینامیک ۱ +‌ اینجا کلیک کنید.

معرفی فیلم آموزش ترمودینامیک ۲

مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم آموزش ترمودینامیک ۲ کرده است. این مجموعه آموزشی از هشت درس تشکیل شده و برای دانشجویان رشته فیزیک، مهندسی نفت، مهندسی شیمی، مهندسی هوا فضا، مهندسی مکانیک، مهندسی پزشکی و زست شناسی یاخته مفید است. پیش‌نیاز این درس ترمودینامیک 1 است.

درس اول این مجموعه به معرفی سیکل‌های توانی گاز و درس دوم به معرفی سیکل‌های بخار و ترکیبی می‌پردازد. درس سوم به معرفی سیکل‌های تبرید و درس چهارم به شناخت روابط بین خواص ترمودینامیکی اختصاص دارد. در درس پنجم و ششم به ترتیب مخلوط‌های گازی و مخلوط‌های بخار-گاز و تهویه مطبوع را خواهید آموخت و در درس هفتم مفاهیم مربوط به سوخت و احتراق بررسی می‌شود. در نهایت و در درس هشتم این مجموعه جریان تراکم پذیر را خواهید آموخت.

• برای دیدن فیلم آموزش ترمودینامیک ۲ +‌ اینجا کلیک کنید.

معرفی فیلم آموزش مبانی مکانیک آماری پیشرفته ۱

مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم آموزش مبانی مکانیک آماری پیشرفته ۱ کرده است. این مجموعه آموزشی از هشت درس تشکیل شده و برای دانشجویان رشته فیزیک در مقطع کارشناسی ارشد مفید است. پیش‌نیاز این درس آشنایی با ترمودینامیک کلاسیک است.

درس اول این مجموعه به معرفی مبانی ترمودینامیک می‌پردازد و درس دوم نظریه آنسامبل را معرفی می‌کند. درس سوم به آنسامبل بندادی (کانونیک) و درس چهارم به آنسامبل کانونیک بزرگ اختصاص دارد. در درس پنجم و ششم به ترتیب آمار کوانتومی و تئوری گازهای ساده را خواهید آموخت و در درس هفتم مفاهیم مربوط به سیستم‌های ایده آل بوزون بررسی می‌شود. در نهایت در درس هشتم و آخر این مجموعه با سیستم‌های فرمیونی آشنا خواهید شد.

• برای دیدن فیلم آموزش آموزش مبانی مکانیک آماری پیشرفته ۱ +‌ اینجا کلیک کنید.

معرفی فیلم آموزش مکانیک آماری پیشرفته (مرور و حل تست کنکور دکتری)

مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم آموزش مکانیک آماری پیشرفته (مرور و حل تست کنکور دکتری) کرده است. این مجموعه آموزشی از یازده درس تشکیل شده و برای دانشجویان رشته فیزیک و داوطلبین کنکور دکتری فیزیک مفید است. پیش‌نیاز این درس آموزش ترمودینامیک ۱، آموزش ترمودینامیک ۲ و آموزش ترمودینامیک پیشرفته است.

درس اول و دوم این مجموعه در دو بخش آشنایی با آمار احتمالات را آموزش می‌دهد. درس سوم به برهمکنش بین سیستم‌های ماکروسکوپیک و درس چهارم به مکانیک آماری در حال تعادل کلاسیکی اختصاص دارد. درس پنجم و ششم در دو بخش به آموزش آنسامبل کانونیک در مکانیک آماری می‌پردازد و در درس هفتم آنسامبل گرندکانونیک در مکانیک آماری بررسی می‌شود. درس هشتم و نهم این مجموعه به آموزش مکانیک آماری سیستم‌های کوانتومی اختصاص دارد و در نهایت در درس دهم و یازدهم مدل آیزینگ و پدیده‌های بحرانی را خواهید آموخت.

• برای دیدن فیلم آموزش مکانیک آماری پیشرفته (مرور و حل تست کنکور دکتری) +‌ اینجا کلیک کنید.

فیلم‌های ترمودینامیک فرادرس برای رشته‌های دیگر

غیر از مجموعه‌های معرفی شده در بالا که به صورت اختصاصی برای رشته فیزیک دسته بندی شده است. فرادرس برای گروه‌ها و رشته‌های دیگر نیز آموزش درس ترمودینامیک را آماده کرده است. این آموزش‌ها را می‌توانید در مجموعه آموزش‌های شیمی و مهندسی بیابید. با این حال ما نیز این آموزش‌ها را به صورت فهرست وار در ادامه معرفی می‌کنیم.

• آموزش ترمودینامیک مهندسی شیمی
• آموزش ترمودینامیک ۲ (مرور و حل مساله)
• آموزش ترمودینامیک (حل سوالات کنکور ارشد و دکتری)
• آموزش ترمودینامیک پیشرفته

جمع بندی

در این مطلب در مورد آنتروپی صحبت کردیم و دلیل رخداد فرآیندهای خود به خودی را بررسی کردیم. همچنین قوانین ترمودینامیک را معرفی کردیم و آنتروپی منفی را نیز مورد بررسی قرار دادیم. در نهایت به بررسی آنتروپی سیاهچاله‌ها و آنتروپی بعد از بیگ بنگ پرداختیم.