آزمایش ژول تامسون — از صفر تا صد
در مباحث قبلی مجله فرادرس، به بیان اهمیت توابع حالت در انرژی درونی و آنتالپی پرداختیم و تغییرات آنتالپی را در شرایط مختلف برای گازهای ایدهآل، جامدات و مایعات بیان کردیم اما گازهای واقعی را مورد بررسی قرار ندادیم. در یک گاز کامل، $$( \frac {\partial H}{\partial P} ) _ P$$ و $$( \frac {\partial U}{\partial V} ) _ T$$، مقادیر کوچکی هستند اما تاثیر قابل توجهی بر روی خواص گازها به هنگام انبساط یا تراکم دارند. فناوریهای معمول در تبدیل گازها به مایع و همچنین عملکرد یخچالها بر این اساس بنا شده است که $$( \frac {\partial H}{\partial P} ) _ P$$ و $$( \frac {\partial U}{\partial V} ) _ T$$ برای گازهای حقیقی، عددی غیرصفر دارند. برای اینکه رابطه مناسبی برای محاسبه $$( \frac {\partial H}{\partial P} ) _ T$$ در یک گاز ایدهآل پیدا کنیم باید به بررسی اثر ژول تامسون در آزمایش ژول تامسون بپردازیم.
آزمایش ژول تامسون
اگر شیر یک کپسول فشرده نیتروژن $$(N_2)$$ را که در دمای ۲۹۸ کلوین قرار دارد، به طور کامل باز کنیم، اطراف شیر کپسول، برفک میزند. این امر نشان میدهد که دمای شیر به کمتر از نقطه انجماد $$H _ 2 O $$ رسیده است. این درحالیست که آزمایشی مشابه با هیدروژن $$(H_ 2 )$$، افزایش دما را به همراه خواهد داشت و حتی در مواقعی موجب انفجار میشود.
برای درک این فرآیندها باید به آزمایش ژول تامسون بپردازیم. آزمایش ژول تامسون را در تصویر زیر مشاهده میکنید. این آزمایش را میتوان نوع بهبود یافته آزمایش ژول دانست چراکه میتوانیم $$( \frac {\partial U} {\partial V} ) _ T$$ را با حساسیت بیشتری نسبت به آزمایش ژول اندازهگیری کنیم.
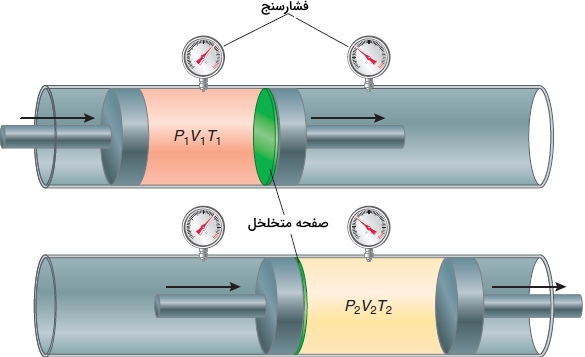
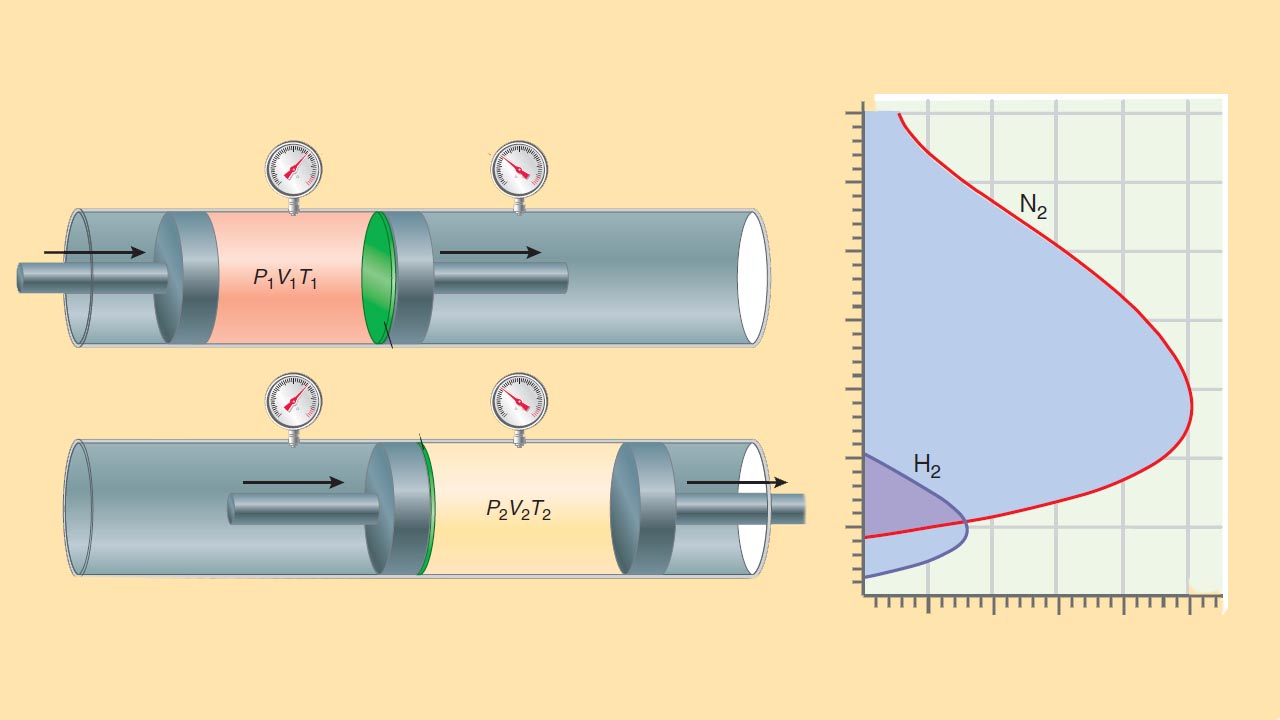
در آزمایش ژول تامسون گاز از داخل یک سیلندر پرفشار در طرف چپ به سیلندر کمفشار در راست جریان پیدا میکند. این جریان از طریق یک مسیر متخلخل در لولهای عایق ایجاد میشود. با حرکت پیستون در هر بخش، فشار ثابت میماند و این فرآیند تا زمان انتقال کامل گاز به طرف راست، ادامه پیدا میکند. اگر در فرآیند انبساط $$P_1 > P_2$$، از نیتروژن استفاده شود، در نهایت، $$T_ 2 < T_ 1$$ خواهد بود. به عبارت دیگر، همزمان با انبساط، گاز، سرد میشود. اما این اثر موسوم به اثر ژول تامسون از کجا نشأت میگیرد؟ مقدار گازی را با حجم اولیه $$V_1$$ در نظر بگیرید که در دستگاه از طرف چپ به راست حرکت میکند. کار انجام شده در این فرآیند انبساط، مجموع کار انجام شده در هر بخش به هنگام حرکت پیستون خواهد بود. رابطه کار انجام شده را به صورت زیر مینویسیم:
$$\begin{equation}w = w _ {l e f t} + w _ {r i g h t} = - \int _ {V_ {1}}^ {0} P _{l} d V -\int _{0} ^ {V_ { 2}} P _{2} d V = P _ {1} V _ {1} - P _ { 2} V _ {2 } \end {equation}$$
از آنجایی که لوله، عایق شده است، $$q = 0$$ خواهد بود. بنابراین خواهیم داشت:
$$\begin{equation} \Delta U = U _ {2} - U_ {1} = w = P_ {1} V _{1} - P_ {2} V _ {2} \end {equation}$$
این رابطه را میتوان به صورت زیر، بازآرایی کرد:
$$\begin {equation} U _ { 2} + P _{2} V _{ 2} = U_ {1}+ P_{1} V _{1} \\
\quad H _ {2} = H_ {1} \end {equation}$$
ضریب ژول تامسون
توجه داشته باشید که به هنگام انبساط، آنتالپی ثابت و فرآیند، «همآنتالپی» (Isenthalpic) است. برای آزمایشی که از نیتروژن بهره میگیرید، $$dT$$ و $$dP$$ هر دو منفی هستند و بنابراین، $$( \frac {\partial T} {\partial P} ) _ H $$ خواهد بود. نسبت تغییرات دمایی به فشار در آنتالپی ثابت را با نام ضریب ژول تامسون میشناسند که رابطه آن به صورت زیر است:
$$\begin {equation} \mu _{ J -T } = \lim _ {\Delta P \rightarrow 0} \left ( \frac { \Delta T } {\Delta P } \right ) _ {H}= \left (\frac {\partial T } {\partial P } \right) _ {H} \end {equation}$$
اگر ضریب ژول تامسون مثبت باشد، شرایط به گونهای است که بخش جاذب پتانسیل حاکم خواهد بود و اگر منفی باشد، بخش دافع پتانسیل حاکم است. به کمک مقادیر آزمایشگاهی ضریب ژول تامسون میتوان $$( \frac{\partial H}{\partial P} ) _ T $$ را محاسبه کرد. در یک فرآیند همآنتالپی خواهیم داشت:
$$\begin {equation} d H = C _ { P} d T + \left ( \frac {\partial H }{ \partial P } \right ) _ { T } d P = 0 \end {equation}
$$
با تقسیم رابطه بالا بر $$dP$$ داریم:
$$\begin {equation} \begin {aligned}
C _ {P} \left ( \frac { \partial T} {\partial P } \right ) _ {H} + \left ( \frac { \partial H } {\partial P } \right) _{ T} = 0\\
\left ( \frac { \partial H } { \partial P } \right ) _{ T} = - C _{P} \mu_ { J - T}
\end {aligned} \end {equation}$$
رابطه بالا بیان میکند که $$( \frac { \partial H } { \partial P } ) _{ T}$$ را میتوان به کمک اندازهگیری خواص وابسته به ماده $$C_P$$ و $$\mu _ { J - T }$$ اندازهگیری کرد. از آنجایی که ضریب ژول تامسون برای گازهای واقعی، مقداری غیرصفر دارد، در شرایطی که تغییرات فشار شدیدی داشته باشیم، نمیتوان از وابستگی فشاری آنتالپی در انبساط یا تراکم، چشمپوشی کرد. توجه داشته باشید که بسته به مقادیر فشار، دما و ضریب ژول تامسون، $$( \frac { \partial H } { \partial P } ) _{ T}$$ میتوانند مثبت یا منفی باشد.
اگر از یک آزمایش، مقدار ضریب ژول تامسون مشخص باشد، مقدار $$( \frac { \partial U } { \partial V } ) _{ T}$$ را میتوان محاسبه کرد که نحوه محاسبه را در مثال زیر بررسی خواهیم کرد. مقادیر ضریب ژول تامسون برای برخی از گازها در جدول زیر نشان داده شده است. توجه کنید که ضریب ژول تامسون تابعی از فشار و تغییرات فشار خواهد بود. در نتیجه، مقادیری که در این جدول فهرست شدهاند، تنها برای کاهش فشار کم در ۱ اتمسفر صدق میکنند.
| گاز | $$\begin {equation} \mu _ {J - T} (\mathrm {K} / \mathrm { M Pa } ) \end {equation}$$ |
| $$Ar$$ | $$3.66$$ |
| $$C _ 6 H _ {14}$$ | $$-0.39$$ |
| $$C H _ 4$$ | $$4.38$$ |
| $$CO _ 2$$ | $$10.9$$ |
| $$H _ 2$$ | $$-0.34$$ |
| $$H e$$ | $$-0.32$$ |
| $$N _ 2$$ | $$2.15$$ |
| $$N e$$ | $$-0.30$$ |
| $$N H _ 3$$ | $$28.2$$ |
| $$O _ 2$$ | $$2.69$$ |
مثال برای محاسبه تغییرات انرژی درونی نسبت به تغییرات حجم در دمای ثابت
به کمک معادله زیر، رابطهای برای محاسبه $$(\frac{\partial U}{\partial V})_T$$ بر اساس کمیات قابل اندازهگیری یک گاز بدست آورید:
$$\begin {equation} ( \partial H / \partial P )_ {T} = \left [(\partial U / \partial V) _ {T} + P \right] (\partial V / \partial P ) _ {T}+ V \end {equation}$$
برای حل، به صورت زیر عمل میکنیم:
$$\begin {equation} \begin {aligned}
\left (\frac {\partial H} {\partial P} \right)_ {T} & = \left [\left (\frac {\partial U} {\partial V } \right) _ {T} + P \right] \left( \frac{ \partial V } {\partial P }\right) _ {T} +V \\
\left (\frac {\partial U} {\partial V} \right) _{T} & =\frac {\left (\frac {\partial H} {\partial P }\right)_ {T} - V}{\left( \frac {\partial V} {\partial P} \right )_ {T}}- P \\
&= \frac {C_{P} \mu _ {J-T} + V} {\kappa V} - P
\end {aligned} \end {equation}$$
در رابطه بالا، $$\kappa$$ ضریب انبساط همدما است که در بحث اهمیت توابع حالت در انرژی درونی معرفی شد.
مثال برای اثبات صفر بودن ضریب ژول تامسون برای گاز ایدهآل
به کمک رابطه $$\begin {equation} (\partial H / \partial P) _ {T} = \left [(\partial U / \partial V) _ {T} + P \right] (\partial V / \partial P ) _{T} + V \end {equation}$$ نشان دهید ضریب ژول تامسون برای یک گاز ایدهآل برابر با صفر است.
$$\begin {equation} \begin {aligned}
\mu _ { J -T } &=- \frac {1} {C_ {P}} \left (\frac {\partial H }{ \partial P } \right )_ {T} = -\frac{1} {C _ {P}} \left [\left (\frac{ \partial U} {\partial V }\right ) _ {T} \left (\frac {\partial V}{\partial P} \right ) _ {T } + P \left (\frac {\partial V} {\partial P } \right ) _ { T } + V \right] \\
&= - \frac {1} {C_ {P}} \left [ 0+P \left (\frac {\partial V }{\partial P} \right )_ {T}+ V \right] \\
& = -\frac {1} { C_ {P} } \left [P \left ( \frac {\partial [n R T / P ] } {\partial P } \right ) _ { T } + V \right ] = -\frac{1} { C _ {P}} \left [- \frac {n R T} {P} + V \right]=0
\end {aligned} \end {equation}$$
در محاسبات بالا از رابطه $$(\frac{\partial U}{\partial V} )_ T = 0$$ در یک گاز ایدهآل کمک گرفتیم. این مثال نشان داد که برای یک گاز ایدهآل، مقدار ضریب ژول تامسون برابر با صفر است. میتوان نشان داد که برای یک گاز که از رابطه واندروالس پیروی میکند، ضریب ژول تامسون از رابطه زیر بدست میآید:
$$\begin {equation} \mu _ {J - T} = \frac{1} {C _ {P, m} } \left (\frac { 2 a} { R T} - b \right ) \end {equation}$$
مایع کردن یک گاز به کمک انبساط هم آنتالپی (ایزنتالپیک)
برای یک گاز کامل، ضریب ژول تامسون در نواحی مختلف فضای P_T، مقادیر مثبت یا منفی را اختیار میکند. اگر این ضریب، مثبت باشد، کاهش فشار موجب سرد شدن گاز خواهد شد و اگر منفی باشد، انبساط گاز، ایجاد گرما میکند. نمودار زیر، تغییرات این ضریب را با دما و فشار در گازهای نیتروژن و هیدروژن نشان میدهد.
در تصویر زیر، خط روی نمودار، متناظر با ضریب ژول تامسون صفر است. دمای متناسب با این ضریب را با نام «دمای وارونگی» (Inversion Temperature) میشناسند. داخل و در ناحیه هاشور خورده، این عدد مثبت و خارج از ناحیه هاشور خورده، منفی است. در شرایط دما و فشار خارج ناحیه هاشور خورده و جایی که $$\mu _ {J-T} < 0$$ باشد، گاز در اثر انبساط، افزایش دما پیدا میکند. بر روی مرز نمودار، در اثر انبساط، هیچ افزایش یا کاهش دما نخواهیم داشت و داخل نمودار و وقتی که $$\mu _ {J-T} > 0$$ باشد، در اثر انبساط، نمونه مورد نظر ما سرد خواهد شد.\
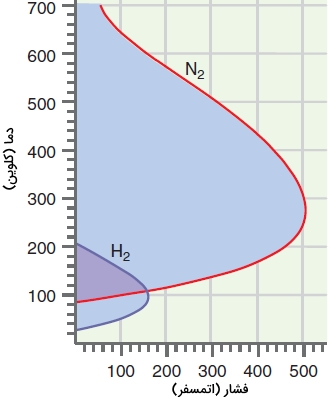
به عبارت دیگر اگر شرایط انبساط در محدوده داخل نمودار برقرار باشد، تغییرات دمایی به اندازهای خواهد بود که که در اثر کاهش فشار ناشی از انبساط، گاز به مایع تبدیل شود. توجه داشته باشید، رابطهای که در مثال قبل بیان کردیم پیشبینی میکند که دمای وارونگی برای یک گاز با پیروی از معادله واندروالس، مستقل از فشار است که این امر با آزمایشات همخوانی ندارد.
تصویر نمودار بالا مطابق با مشاهداتی است که بیان میکند در فشار بالا _ بین ۱۰۰ تا ۵۰۰ اتمسفر - انبساط نیتروژن و هیدروژن در دمای ۳۰۰ کلوین به ترتیب موجب سرد و گرم شدن گازها میشود. برای سرد کردن هیدروژن با انبساط، باید ابتدا آنرا تا دمای زیر 200 کلوین سرد کرد و فشار باید کمتر از 160 اتمسفر باشد.
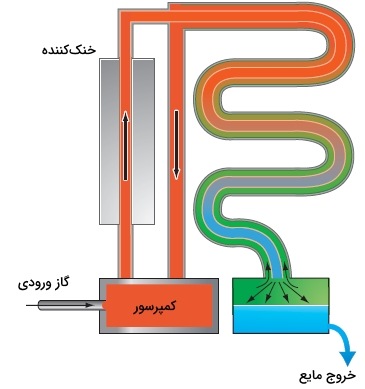
همانطور که در تصویر زیر نشان داده شده است، از اثر ژول تامسون برای مایع کردن گازی همچون نیتروژن میتوان استفاده کرد. گاز در فشار اتمسفری، ابتدا به فشاری بین 50 تا 200 اتمسفر میرسد و در اثر این اتفاق، افزایش دمای زیادی خواهیم داشت. در ادامه، این گاز سرد خواهد شد و با عبور از یک مبدل حرارتی، دمای آن به فاصله ۵۰ کلوین از نقطه جوش خواهد رسید. در خروجی مبدل حرارتی، در یک انبساط همآنتالپی، گاز از طریق یک نازل، به فشار نهایی ۱ اتمسفر میرسد. به دلیل $$\mu _ {J-T} > 0$$، سرد شدن و به دنبال آن مایع شدن صورت میگیرد.
گازی که تبخیر میشود، در خلاف جهت گاز قبلی، از مبدل حرارتی عبور خواهد کرد. این دو گاز از یکدیگر مجزا هستند اما به خوبی بین آنها انتقال حرارت صورت میگیرد. در اثر این اتفاق، گاز به خوبی «پیشسرد» (Precool) خواهد شد تا در یک مرحله انبساط، به مایع تبدیل شود.










نمودار اکسیژن نیست . هیدروژنه
با سلام؛
از نکتهسنجی شما سپاسگزاریم. متن اصلاح شد.
با تشکر