شکل موج سینوسی — به زبان ساده

در آموزش‌‌های قبلی مجله فرادرس درباره انواع شکل موج الکتریکی صحبت کردیم. در این آموزش قصد داریم درباره شکل موج سینوسی بحث کنیم. همانطور که در مباحث مربوط به مغناطیس دیدیم، هنگامی که جریان الکتریکی از یک سیم یا هادی عبور می‌کند، یک میدان مغناطیسی اطراف سیم ایجاد می‌شود. شدت این میدان مغناطیسی با مقدار جریان گذرنده از سیم، متناسب است.

فرض کنید یک میدان مغناطیسی ساکن داریم. اگر یک تک سیم رسانا را در این میدان مغناطیسی حرکت دهیم یا بچرخانیم، به دلیل حرکت هادی در خطوط شار مغناطیسی، یک «نیروی محرکه الکتریکی» (EMF) در هادی القا می‌شود.

فیلم آموزش مبانی مهندسی برق 1 – مرور و حل مساله در فرادرس

کلیک کنید

پس می‌توان استنباط کرد که یک رابطه بین الکتریسیته و مغناطیس وجود دارد. مایکل فارادی این رابطه را القای الکترومغناطیسی نامید. ماشین‌ها و ژنراتورهای الکتریکی از این اصل برای تولید موج سینوسی استفاده می‌کنند. از شکل موج سینوسی در خطوط برق شهری نیز استفاده می‌شود.

طبق اصل القای الکترومغناطیسی، هنگامی که یک سیم هادی تکی در میدان مغناطیسی دائمی حرکت و خطوط شار را قطع کند، یک نیروی محرکه الکتریکی (EMF) در آن القا می‌شود. شکل زیر نحوه تولید نیروی محرکه الکتریکی در یک هادی را نشان می‌دهد:

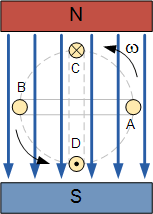
یک جفت سیم الکتریکی در نقاط A و B در نظر می‌گیریم. اگر این جفت سیم به موازات میدان الکتریکی حرکت کنند، هیچ خط شاری قطع نمی‌شود. در نتیجه، نیروی محرکه الکتریکی در هادی القا نمی‌شود. اما اگر هادی با زاویه ۹۰ درجه بچرخد و در نقاط C و D متوقف شود، ماکزیمم خطوط مغناطیسی قطع می‌شود. بنابراین در این حالت، بیشترین مقدار نیروی محرکه القایی در هادی القا خواهد شد.

همچنین، اگر یکی از هادی‌ها بین نقاط A و C واقع شود، نیروی محرکه القایی در هادی، عددی بین صفر و مقدار ماکزیمم خواهد داشت. پس مقدار emf القایی در هادی، به زاویه بین هادی و خطوط شار مغناطیسی و همچنین شدت میدان مغناطیسی وابسته است.

شکل موج سینوسی تولید شده در ژنراتور

یک ژنراتور AC از اصل القای الکترومغناطیسی فارادی استفاده می‌کند تا انرژی مکانیکی (چرخش) را به انرژی الکتریکی (شکل موج سینوسی) تبدیل کند. ژنراتور از یک جفت آهنربای دائم تشکیل شده است. این آهنربای دائم یک میدان مغناطیسی دائم بین قطب‌های مثبت و منفی خود دارد.

فیلم آموزش مبانی مهندسی برق 1 در فرادرس

کلیک کنید

داخل آهنربا، یک حلقه سیمی مستطیلی قرار گرفته است. این سیم به دور یک محور ثابت چرخانده می‌شود، به گونه‌ای که خطوط میدان مغناطیسی را در زوایای مختلف قطع کند. این مسئله در شکل زیر نشان داده شده است:

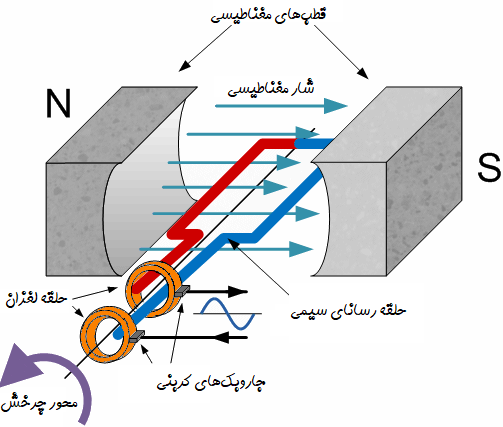
همچنان که سیم‌پیچ حول محور مرکزی خود در خلاف جهت عقربه‌های ساعت چرخش می‌کند، حلقه سیمی خطوط میدان مغناطیسیِ ایجاد شده توسط آهنربای دائمی را در زوایای مختلف قطع می‌کند. مقدار نیروی محرکه القایی حلقه در هر لحظه از زمان با زاویه بین حلقه و خطوط شار مغناطیسی، متناسب است.

با چرخش سیم‌پیچ، الکترون‌ها در حلقه جاری می‌شوند. هنگامی که حلقه سیمی با زاویه‌ای بیشتر از ۱۸۰ درجه بچرخد و خطوط میدان مغناطیسی را در خلاف جهت قطع کند، الکترونهای داخل حلقه سیمی، تغییر جهت می‌دهند. به این ترتیب، جریانی در خلاف جهت در سیم جاری می‌شود. جهت حرکت الکترون‌ها، قطبیت ولتاژ القا شده را تعیین می‌کند.

پس هنگامی که حلقه یا سیم‌پیچ به صورت فیزیکی یک چرخش کامل را انجام می‌دهد، یعنی به اندازه ۳۶۰ درجه می‌چرخد، شکل موج سینوسی، یک تناوب کامل را طی می‌کند. به این ترتیب با هر چرخش سیم‌پیچ، یک شکل موج سینوسی ایجاد می‌شود. جریان ایجاد شده در سیم‌پیچ که در حال چرخش در میدان مغناطیسی است، توسط حلقه‌های لغزان و جاروبک‌های کربنی به بیرون ژنراتور تحویل داده می‌شود. به این ترتیب، انرژی مکانیکی به انرژی الکتریکی تبدیل می‌شود. مقدار نیروی محرکه القایی ایجاد شده در سیم‌پیچ که خطوط میدان مغناطیسی را قطع می‌کند، به سه عامل زیر بستگی دارد:

1. سرعت: سرعتی که سیم‌پیچ داخل میدان مغناطیسی می‌چرخد.
2. شدت: شدت میدان مغناطیسی.
3. طول: طولی از سیم‌پیچ یا هادی که از میدان مغناطیسی عبور می‌کند.

همانطور که در مباحث مربوط به شکل موج الکتریکی گفتیم، فرکانس عبارت است از تعداد تناوب‌هایی که در یک ثانیه روی می‌دهد. فرکانس با واحد هرتز (Hz) اندازه‌گیری می‌شود.

با چرخش کامل سیم‌پیچ در میدان مغناطیسی که قطب شمال و جنوب مشخص دارد، یک تناوب کامل از سیگنال emf در هادی القا می‌شود. اگر سرعت چرخش سیم‌پیچ ثابت باشد، تعداد ثابتی تناوب در هر ثانیه تولید می‌شود. به این ترتیب یک فرکانس ثابت خواهیم داشت. با افزایش سرعت چرخش سیم‌پیچ، فرکانس نیز زیاد می‌شود. بنابراین، فرکانس به سرعت چرخش وابسته است. یعنی:

$$f \propto N \, \, \,(N=r.p.m)$$

همچنین، ژنراتور ساده با یک سیم‌پیچ که در شکل بالا نشان داده شد، فقط دو قطب دارد. یعنی فقط یک جفت قطب مثبت و منفی در این ژنراتور وجود دارد. فرض کنید دو قطب مغناطیسی دیگر به ژنراتور اضافه کنیم تا چهار قطب مغناطیسی (دو قطب شمال و دوقطب جنوب) داشته باشیم. هر چرخش سیم‌پیچ، منجر به تولید دو تناوب با همان سرعت چرخش قبلی می‌شود. بنابراین، فرکانس موج سینوسی تولید شده، با تعداد جفت قطب‌های مغناطیسی نیز متناسب است. یعنی:

$$f \propto P$$

که $$P$$ تعداد جفت قطب‌های ژنراتور است.

در نتیجه بر اساس این دو وابستگی می‌توان گفت که فرکانس خروجی یک ژنراتور AC عبارت است از:

$$f \propto N \, , \, f\propto P \to f = N \times P \, (cycles/min)$$

از آنجا که فرکانس با واحد هرتز اندازه‌گیری می‌شود، داریم:

$$Frequency , (f)= \frac{NP}{60} Hz$$

که در آن $$N$$، سرعت چرخش با واحد $$r.p.m$$ یا دور در دقیقه و $$P$$ تعداد جفت قطب‌های ژنراتور و عدد ۶۰ به دلیل تبدیل واحد در معادله ایجاد شده است.

ولتاژ لحظه‌ای

نیروی محرکه القا شده در سیم‌پیچ در هر لحظه از زمان به سرعتی بستگی دارد که سیم‌پیچ، خطوط شار مغناطیسی بین دو قطب را قطع می‌کند. سرعت چرخش سیم‌پیچ، خود به زاویه بین سیم‌پیچ و خطوط شار مغناطیسی نیز وابسته است. این زاویه را $$\theta$$ می‌نامیم. از آنجا که مقدار یا دامنه شکل موج AC دائما تغییر می‌کند، شکل موج در هر لحظه از زمان مقداری متفاوت از لحظه بعد خواهد داشت.

فیلم آموزش الکترونیک 1 – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

برای مثال، مقدار نیروی محرکه الکتریکیِ القا شده در سیم‌پیچ، در زمان یک میلی‌ثانیه با مقدار آن در زمان ۱.۲ میلی‌ثانیه متفاوت خواهد بود. این مقادیر را به نام «مقادیر لحظه‌ای» (Instantaneous Values) یا $$V_i$$ می‌شناسیم. مقدار لحظه‌ای شکل موج ولتاژ و فاز آن بسته به محل سیم‌پیچ نسبت به میدان مغناطیسی تغییر می‌کند. این مورد در شکل زیر نشان داده شده است:

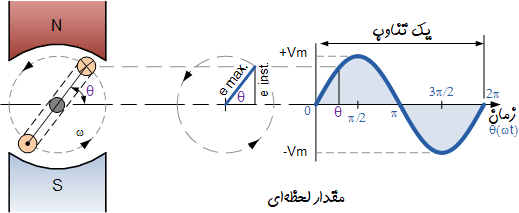
رابطه ولتاژ لحظه‌ای و ولتاژ ماکزیمم

مقادیر لحظه‌ای یک شکل موج سینوسی به صورت حاصلضرب مقدار ماکزیمم موج در سینوس زاویه نسبی سیم‌پیچ و میدان مغناطیسی با رابطه زیر داده می‌شود:

$$V_i = V_{max} \times sin \theta$$

که در آن $$V_{max}$$ مقدار ماکزیمم ولتاژ القا شده در سیم‌پیچ، $$V_i$$ مقدار لحظه‌ای ولتاژ و $$\theta = \omega t$$ زاویه چرخش سیم‌پیچ بر حسب زمان است.

اگر مقدار ماکزیمم یا قله شکل موج را بدانیم، با استفاده از رابطه بالا می‌توانیم مقادیر لحظه‌ای در زمان‌های مختلفِ شکل موج را محاسبه کنیم. با رسم این مقادیر روی کاغذ، شکل موج سینوسی حاصل می‌شود.

برای مثال، اگر مقادیر لحظه‌ای را در هر ۴۵ درجه با یک نقطه مشخص کنیم، برای یک تناوب کامل ۳۶۰ درجه، هشت نقطه خواهیم داشت. فرض کنید مقدار ماکزیمم ولتاژ ($$V_{max}$$) برابر ۱۰۰ ولت باشد. با رسم مقادیر لحظه‌ای در بازه‌های زمانی کوتاه‌تر، برای مثال در هر ۳۰ درجه (۱۲ نقطه) یا هر ۱۰ درجه (۳۶ نقطه) به یک شکل موج سینوسی دقیق‌تر خواهیم رسید.

ساخت شکل موج سینوسی

با تغییر زاویه سیم‌پیچ نسبت به میدان مغناطیسی، یک نقطه روی شکل موج سینوسی تشکیل می‌شود. حال اگر این زاویه برابر ۳۶۰ درجه شود، یعنی سیم‌پیچ یک دور کامل بچرخد، شکل موج سینوسی یک تناوب را کامل می‌کند. تصویر زیر، نحوه ساخت شکل موج سینوسی را نشان می‌دهد:

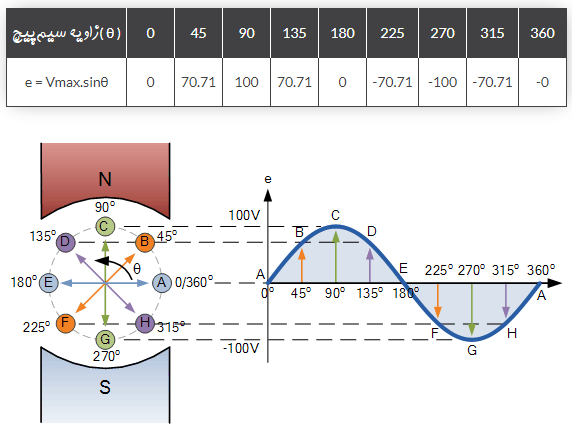
از روی شکل موج سینوسی مشاهده می‌شود که وقتی $$\theta$$ برابر اعداد $$0^ \circ$$ یا $$180 ^ \circ$$ یا $$360 ^ \circ$$ است، مقدار نیرو محرکه القایی صفر خواهد بود، زیرا سیم‌پیچ کمترین مقدار خطوط شار را قطع می‌کند. اما هنگامی که $$\theta$$ برابر $$90^\circ$$ یا $$270^\circ$$ درجه است، نیرو محرکه القایی، ماکزیمم مقدار خود را خواهد داشت، زیرا سیم‌پیچ، خطوط شار بیشتری را قطع می‌کند.

بنابراین یک شکل موج سینوسی در $$\theta = 90 ^ \circ$$ مقدار ماکزیمم مثبت خود را دارد. همچنین قله منفی آن نیز در $$270^\circ$$ رخ می‌دهد. نقاط $$B$$، $$D$$، $$F$$ و $$H$$ روی شکل موج سینوسی مقادیر مربوط به رابطه $$e= V_{max} \times sin \theta$$ هستند.

شکل موج تولید شده توسط ژنراتور با حلقه ساده را شکل موج سینوسی می‌گویند، زیرا شکل آن سینوسی و مانند تابع سینوس در ریاضیات مثلثاتی است ($$x(t)=A_{max} \times sin \theta$$).

هنگامی که با امواج سینوسی در حوزه زمان و مخصوصا جریان دارای شکل موج سینوسی کار می‌کنیم، واحد اندازه‌گیری استفاده شده در محور افقی می‌تواند زمان، درجه یا رادیان باشد. در مهندسی برق مرسوم است که از رادیان برای اندازه‌گیری زاویه در محور افقی به جای درجه استفاده شود. مثلا $$\omega = 100 rad/s$$ یا $$\omega = 500 rad/s$$.

سرعت زاویه‌ای یک شکل موج سینوسی

سرعت چرخش سیم‌پیچ به دور محور مرکزی، فرکانس شکل موج سینوسی را تعیین می‌کند. فرکانس شکل موج با $$f$$ با واحد هرتز یا چرخه در ثانیه داده می‌شود، فرکانس زاویه‌ای ($$\omega$$) شکل موج با واحد رادیان بر ثانیه مشخص می‌شود. سرعت زاویه‌ای یک شکل موج سینوسی به صورت زیر است:

$$\omega = 2 \pi f (rad/sec)$$

مثلا برای کشور ایران که فرکانس برق شهری برابر ۵۰ هرتز است، سرعت زاویه‌ای یا فرکانس زاویه‌ای برق شهری به صورت زیر خواهد بود:

$$\omega = 2 \pi f = 2 \pi . 50 =314.2 rad/s$$

در کشور آمریکا فرکانس استاندارد برق شهری، ۶۰ هرتز و فرکانس زاویه‌ای تقریبا برابر $$377 rad/s$$ است.

اکنون می‌دانیم که سرعت چرخش سیم‌پیچِ ژنراتور حول محور مرکزی خود، تعیین‌کننده فرکانس شکل موج سینوسی است. این سرعت را با نام سرعت زاویه‌ای ($$\omega$$) می‌شناسند.

اما می‌دانیم که زمان لازم برای کامل کردن یک چرخش برابر زمان تناوب ($$T$$) شکل موج سینوسی است. از آنجا که فرکانس با معکوس زمان تناوب متناسب است ($$f=1/T$$)، می‌توان در معادله بالا، فرکانس را با زمان تناوب جایگزین کرد. پس خواهیم داشت:

$$\omega  = \frac{2 \pi }{T} (rad/sec)$$

معادله اخیر بیان می‌کند که هرچه زمان تناوب در یک شکل موج سینوسی کوچکتر باشد، سرعت زاویه‌ای شکل موج بالاتر است. به همین ترتیب، هرچه فرکانس بالاتر باشد، سرعت زاویه‌ای نیز بالاتر خواهد بود.

مثالی از شکل موج سینوسی

یک شکل موج سینوسی به صورت $$V_m=169.8 sin (377t) (v)$$ را در نظر بگیرید. مقدار RMS ولتاژ، فرکانس شکل موج ولتاژ و مقدار لحظه‌ای ولتاژ ($$V_i$$) را بعد از گذشت ۶ میلی‌ثانیه محاسبه کنید.

حل: از روابط بالا می‌دانیم که عبارت کلی برای یک شکل موج سینوسی به صورت زیر است:

$$V_{(t)} = V_m sin (\omega t)$$

با مقایسه این عبارت با شکل موج سینوسی داده شده داریم:

$$V_m = 169.8 sin (377t)$$

پس در این شکل موج، مقدار ماکزیمم یا قله ولتاژ برابر 169.8 ولت است.

مقدار $$RMS$$ ولتاژ برای این شکل موج، به صورت زیر محاسبه می‌شود:

$$V_{(rms)} = 0.707 \times$$ مقدار ماکزیمم

$$V_{(rms)} = 0.707 \times 169.8 = 120 v$$

فرکانس زاویه‌ای ($$\omega$$) برابر با $$377 rad/s$$ داده می‌شود. یعنی $$2\pi f = 377$$ پس فرکانس شکل موج به صورت زیر محاسبه می‌شود:

$$Frequency, (f) = \frac{377}{2\pi} = 60 Hz$$

مقدار لحظه‌ای ولتاژ $$V_i$$ بعد از گذشت زمانی معادل 6 میلی‌ثانیه به صورت زیر خواهد بود:

$$V_{(i)} = V_(m) sin (\omega t)$$

$$V_{(i)} = 16907 sin (377 \times 0.006)$$

$$V_{(i)}= 169.8 sin (2.262 rad)$$

$$2.262$$ رادیان $$\times 57.3^ \circ = 129.6 ^ \circ$$

$$V_{(i)}= 169.8 sin (129.6^ \circ) = 169.8 \times 0.771$$

ولت$$=V_{(i)} = 130.8$$

ذکر این نکته ضروری است که سرعت زاویه‌ای در زمان $$t=6ms$$ بر حسب رادیان است.

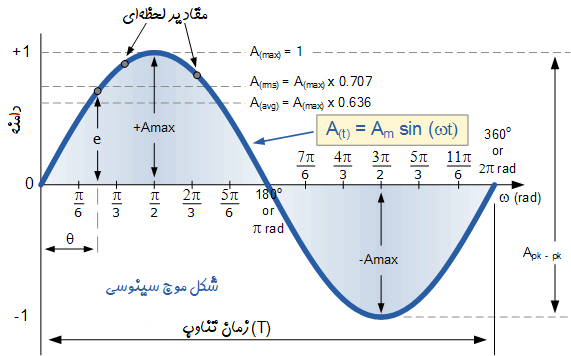
در شکل زیر یک موج سینوسی برای تحلیل و محاسبه مقادیر مختلف ولتاژ نشان داده شده است:

در مباحث بعدی مجله فرادرس درباره اختلاف فاز و رابطه بین دو موج سینوسی با فرکانس یکسان بحث خواهیم کرد.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، پیشنهاد می‌کنیم به آموزش های زیر مراجعه کنید:

• تقویت کننده های الکترونیکی — مجموعه مقالات جامع وبلاگ فرادرس
• مدارهای جریان مستقیم (DC) — مجموعه مقالات جامع وبلاگ فرادرس

^^