کدنویسی شبکه های عصبی مصنوعی چند لایه در پایتون — راهنمای کامل
بنابر «قضیه عمومی تقریب» (Universal Approximation Theorem)، در صورتی که تعداد مناسبی از لایهها (لایههای نهان) در «شبکه های عصبی مصنوعی» (Artificial Neural Networks) طراحی شود و «حاشیه خطای» (Error Margin) مطلوبی برای این دسته از الگوریتمهای حوزه «هوش مصنوعی» (Artificial Intelligence) و «یادگیری ماشین» (Machine Learning) تعریف شود، این مدلها قادر هستند تا هر نوع «تابعی» (Function) را تقریب بزنند، یاد بگیرند و نمایش دهند.
شبکه های عصبی مصنوعی چند لایه، معمولا با استفاده از مدلسازی یک نمایش پیچیده روی نمایشهای سادهتر از دادهها، رفتار توابع و مدلسازی یک «تابع واقعی» (True Function) مبتنی بر داده را یاد میگیرند. منظور از تابع واقعی، مدل تابعی است که میتواند دادههای مسئله را به بهترین شکل ممکن دستهبندی کند.
در هر کدام از «لایههای نهان» (Hidden Layers) تعبیه شده در مدلهای شبکه عصبی، ابتدا با استفاده از یک «تبدیل خطی» (Linear Transformation) از دادههای ورودی داده شده و در مرحله بعد، اعمال کردن یک «تابع غیرخطی» (Non-Linear Function)، شبکه عصبی قادر به یادگیری «فضای ویژگی» (Feature Space) جدید خواهد بود. حاصل این عملیات (خروجی این مراحل)، ورودی لایه بعدی را تشکیل خواهد داد. این فرایند تا زمانی که خروجیها به لایه آخر یا «لایه خروجی» (Output Layer) برسند، ادامه پیدا میکند.

بنابراین، یک شبکه عصبی را میتوان در قالب جریان اطلاعاتی از لایه ورودی به لایههای نهان و پس از آن به لایه خروجی تعریف کرد. برای یک «شبکه عصبی سه لایه» (Three-Layers Neural Network)، تابع واقعی که قرار است توسط شبکه یادگیری شود، به شکل زیر نمایش داده خواهد شد:
در این تابع، هر کدام از توابع تو در توی داخلی وظیفه خاصی بر عهده دارند:
- تابع : تابعی که در لایه نهان اول شبکه های عصبی مصنوعی یاد گرفته خواهد شد.
- تابع : تابعی که در لایه نهان دوم شبکه های عصبی مصنوعی یاد گرفته خواهد شد.
- تابع : تابعی که در لایه خروجی شبکه های عصبی مصنوعی یاد گرفته خواهد شد.
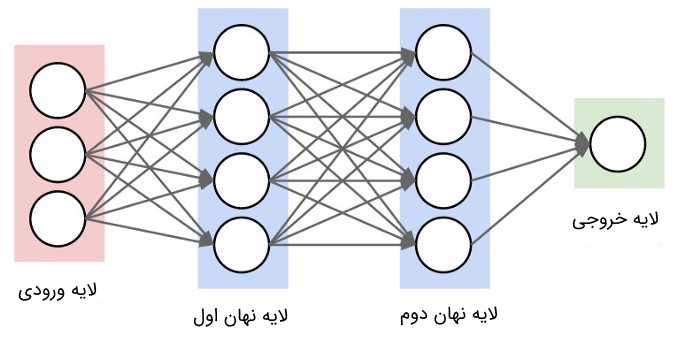
به عبارت دیگر، در هر کدام از لایههای شبکه های عصبی مصنوعی چند لایه، مدلهای نمایشی متفاوتی یاد گرفته میشود. البته نکته مهم در مورد یادگیری توابع بالا این است که هر چه قدر به سمت لایههای نهان انتهایی حرکت میکنیم، مدل نمایشی یادگیری شده در شبکه های عصبی مصنوعی، پیچیدهتر و پیشرفتهتر میشود. شکل زیر، نمونهای از یک شبکه عصبی سه لایه را نمایش میدهد (معمولا لایه اول، در محاسبه تعداد لایههای شبکه های عصبی مصنوعی لحاظ نمیشود).
به عنوان نمونه، کامپیوترها درکی از تصاویر دیجیتالی ندارند و به طور مستقیم، قادر به استنتاج در مورد مؤلفههای سازنده یک تصویر نیستند. از سوی دیگر، یک سیستم کامپیوتری بدون وجود یک مدل نرمافزاری (هوشمند)، قادر به انجام عملیات جهت استخراج اطلاعات بامعنی از تصاویر نیست. با این حال، شبکه های عصبی مصنوعی به راحتی قادر خواهند بود با استفاده از مدلسازی یک نمایش ساده از تصویر در لایههای نهان ابتدایی، «لبههای» (Edges) موجود در تصویر را شناسایی کنند.
شبکه های عصبی مصنوعی چند لایه، با داشتن خروجی متناظر با اولین لایه نهان، به راحتی میتوانند «گوشهها» (Corners) و «کانتورهای» (Contours) موجود در تصویر را تشخیص دهند. همچنین، این شبکههای عصبی، با داشتن خروجی متناظر با لایه نهان دوم، بخشهای خاصی از یک تصویر نظیر بینی یک انسان را شناسایی میکنند. در نهایت، و با در کنار هم قرار دادن تمامی مدلهای نمایشی تولید شده در لایههای نهان و تولید یک مدل نمایشی پیچیده، شبکه های عصبی مصنوعی قادر خواهند بود تا نوع اشیاء موجود در تصویر را نیز شناسایی کنند.
در تمامی مدلهای یادگیری ماشین (از جمله شبکه های عصبی مصنوعی چند لایه)، توابع واقعی (منظور از توابع واقعی در حوزه یادگیری ماشین، مدل خطی یا غیر خطی است که توسط این دسته از روشها یاد گرفته میشود و برای تصمیمگیری در مورد در دادههای ورودی، مورد استفاده قرار میگیرد) که قرار است توسط این روشها مدلسازی و یاد گرفته شوند، به ندرت خطی هستند. از آنجایی که مدل نمایشی، نقشی حیاتی در تضمین عملکرد بهینه مدلهای یادگیری ماشین خواهد داشت، با استفاده از شبکه های عصبی مصنوعی، سیستم قادر خواهد بود مدلهای نمایشی بسیار پیچیده و مبتنی بر دادههای ورودی را یاد بگیرد.
یکی از بخشهای مهم طراحی یک مدل یادگیری ماشین، «مهندسی ویژگیها» (Feature Engineering) یا مشخص کردن بهترین ویژگیهای ممکن برای تولید یک مدل نمایشی بهینه است. ویژگی مهم شبکه های عصبی مصنوعی این است که به «مهندسان هوش مصنوعی» (AI Engineers) و «دانشمندان داده» (Data Scientists) این امکان را میدهند که بدون صرف کردن وقت و هزینه زیاد روی بخش مهندسی ویژگیها، یک مدل نمایشی خوب از دادهها تولید و در کاربردهای مختلف مورد استفاده قرار دهند.
مطلب پیش رو از دو بخش اصلی تشکیل شده است:
- کدنویسی شبکه های عصبی مصنوعی چند لایه: در این بخش، نحوه تعریف توابع کمکی لازم برای پیادهسازی شبکه های عصبی مصنوعی چند لایه تشریح و کدهای پیادهسازی آنها در «زبان برنامهنویسی پایتون» (Python Programming Language) نمایش داده خواهد شد. همچنین، بنیان نظری بخشهای مختلف پیادهسازی شبکه های عصبی مصنوعی نیز شرح داده خواهد شد.
- کاربرد: در این بخش، از کدهای پیادهسازی شده در بخش قبل، برای توسعه یک سیستم «بازشناسی تصویر» (Image Recognition) استفاده میشود. از سیستم بازشناسی تصویر، برای سنجش عملکرد شبکه عصبی مصنوعی در تشخیص «گربه» (Cat) یا «غیر گربه» (No Cat) در تصاویر ورودی استفاده میشود.
1 Import packages
2import os as os
3
4import h5py
5import matplotlib.pyplot as plt
6import numpy as np
7import seaborn as snsکدنویسی شبکه های عصبی مصنوعی چند لایه
در این بخش، با بخشهای مختلف الگوریتم یادگیری در یک شبکه عصبی مصنوعی چند لایه آشنا خواهید شد.

انتشار رو به جلو (Forward Propagation)
ورودی ، اطلاعات ابتدایی لازم را در مورد دامنه مسئلهای که قرار است توسط شبکه های عصبی مصنوعی حل شود، در اختیار سیستم قرار میدهد. در مراحل بعد، ورودیها به واحدها یا «نودهای» (Nodes) موجود در هر کدام از لایهها انتشار پیدا میکنند و در نهایت، یک خروجی تولید میشود. برای مشخص کردن معماری شبکه های عصبی مصنوعی، لازم است تا «عمق» (Depth)، «پهنا» (Width) و «تابع فعالسازی» (Activation Function) که در هر لایه مورد استفاده قرار میگیرد، مشخص شوند.
منظور از عمق شبکه های عصبی مصنوعی، تعداد لایههای نهان آن است. منظور از پهنا، تعداد واحدها یا نودهای موجود در هر لایه نهان است. شایان توجه است که طراح معماری شبکه عصبی مصنوعی، هیچ کنترلی روی تعداد نرونهای لایه ورودی یا خروجی ندارد و دامنه مسأله چنین مشخصاتی را به سیستم دیکته میکند.
برای پیادهسازی شبکه های عصبی مصنوعی، توابع فعالسازی گوناگونی نظیر «واحد خطی اصلاح شده» (Rectified Linear Unit)، «تابع سیگموئید» (Sigmoid Function)، «تابع تانژانت هذلولوی یا هیپربولیک» (Hyperbolic Tangent) و سایر موارد معرفی شدهاند. تحقیقات انجام شده در مورد پیادهسازی شبکه های عصبی مصنوعی نشان داده است که شبکههای عمیقتر (شبکههای حاوی لایههای نهان بیشتر)، عملکرد به مراتب بهتری نسبت به شبکههای حاوی نودهای نهان بیشتر دارند.بنابراین، آموزش یک شبکه عصبی مصنوعی عمیقتر توصیه میشود.
ابتدا لازم است تا برخی از نمادهایی که در طول این مطلب با آنها برخورد میشود، تعریف شوند:
- ماتریس : ماتریس وزن لایه اُم.
- بردار : بردار بایاس لایه اُم.
- تابع : تابع تبدیل خطی ورودیهای داده شده برای لایه اُم.
- تابع : تابع فعالسازی که روی لایه اُم شبکه عصبی مصنوعی اعمال میشود.
- مقدار : خروجی حاصل پس از اعمال تابع فعالسازی روی لایه اُم شبکه عصبی مصنوعی.
- مقدار : مشتق «تابع هزینه» (Cost Function) نسبت به ().
- مقدار : مشتق «تابع هزینه» (Cost Function) نسبت به ().
- مقدار : مشتق «تابع هزینه» (Cost Function) نسبت به ().
- مقدار : مشتق «تابع هزینه» (Cost Function) نسبت به ().
- مقدار : تعداد واحدها یا نودهای لایه اُم.
- مقدار : تعداد نمونهها.
- مقدار : تعداد لایههای موجود در شبکه عصبی مصنوعی طراحی شده (بدون در نظر گرفتن لایه ورودی).
در مرحله بعد، «ابعاد» (Dimensions) یک شبکه عصبی چند لایه به «شکل عمومی» (General Form) نمایش داده خواهد شد تا عملیات ضرب ماتریسی در شبکه تسهیل شود. یکی از مهمترین چالشهای موجود در پیادهسازی شبکه های عصبی مصنوعی، محاسبه درست ابعاد آنها است.
- مقادیر (): تعداد نودهای موجود در لایه اُم شبکه x تعداد نودهای موجود در لایه اُم.
- مقادیر (): تعداد نودهای موجود در لایه اُم شبکه x عدد (1).
- مقادیر (): تعداد نودهای موجود در لایه اُم شبکه x تعداد نمونهها.
- مقادیر (): تعداد نودهای موجود در لایه اُم شبکه x تعداد نمونهها.
دو معادلهای که از طریق آنها قادر به پیادهسازی مرحله انتشار رو به جلو خواهیم بود عبارتند از:
محاسباتی که به وسیله این معادلات انجام میشوند، در تمامی لایههای شبکه های عصبی مصنوعی اتفاق میافتند.
مقداردهی اولیه پارامترها
در ابتدای کار، ماتریسهای وزن و بردارهای بایاس متناظر با هر کدام از لایهها، مقداردهی اولیه خواهند شد. شایان ذکر است که مقادیر پارامترهای مسئله نباید توسط مقادیر صفر مقداردهی اولیه شوند؛ زیرا، با انجام چنین کاری، «گرادیانها» (Gradients) محاسبه شده برای تمامی حالات برابر خواهد شد و در هر تکرار، خروجی یکسان خواهد شد. در نتیجه، الگوریتم شبکه عصبی مصنوعی، عملا چیزی یاد نخواهد گرفت. بنابراین، بسیار حیاتی است که پارامترهای شبکه های عصبی مصنوعی به وسیله مقادیر تصادفی بین 0 و 1 مقداردهی اولیه شوند.
همچنین توصیه میشود که مقادیر تصادفی ایجاد شده برای مقداردهی اولیه پارامترها، در یک مقدار عددی کوچک نظیر ۰٫۰۱ ضرب شوند؛ با چنین کاری، واحدهای فعالسازی شبکه فعال خواهند شد و در مناطقی قرار خواهند گرفت که مقادیر مشتقهای توابع فعالسازی در آنجا، نزدیک به صفر نیست.
1# Initialize parameters
2def initialize_parameters(layers_dims):
3 """
4 Initialize parameters dictionary.
5
6 Weight matrices will be initialized to random values from uniform normal
7 distribution.
8 bias vectors will be initialized to zeros.
9
10 Arguments
11 ---------
12 layers_dims : list or array-like
13 dimensions of each layer in the network.
14
15 Returns
16 -------
17 parameters : dict
18 weight matrix and the bias vector for each layer.
19 """
20 np.random.seed(1)
21 parameters = {}
22 L = len(layers_dims)
23
24 for l in range(1, L):
25 parameters["W" + str(l)] = np.random.randn(
26 layers_dims[l], layers_dims[l - 1]) * 0.01
27 parameters["b" + str(l)] = np.zeros((layers_dims[l], 1))
28
29 assert parameters["W" + str(l)].shape == (
30 layers_dims[l], layers_dims[l - 1])
31 assert parameters["b" + str(l)].shape == (layers_dims[l], 1)
32
33 return parametersتوابع فعالسازی در شبکه های عصبی مصنوعی چند لایه
یکی از چالشهایی که توسعه دهندگان در هنگام پیادهسازی شبکه های عصبی مصنوعی با آن دست و پنجه نرم میکنند، انتخاب تابع فعالسازی مناسب برای لایههای مختلف موجود در شبکه عصبی است. در این زمینه، راهکاری قطعی برای انتخاب بهترین تابع فعالسازی برای یک مسأله خاص وجود ندارد. انتخاب تابع فعالسازی مناسب، یک فرایند «آزمون و خطا» (Trial and Error) است که در آن، توسعه دهنده، مجموعهای از توابع متفاوت را امتحان و بهترین تابع را برای مسأله مورد نظر انتخاب میکند.
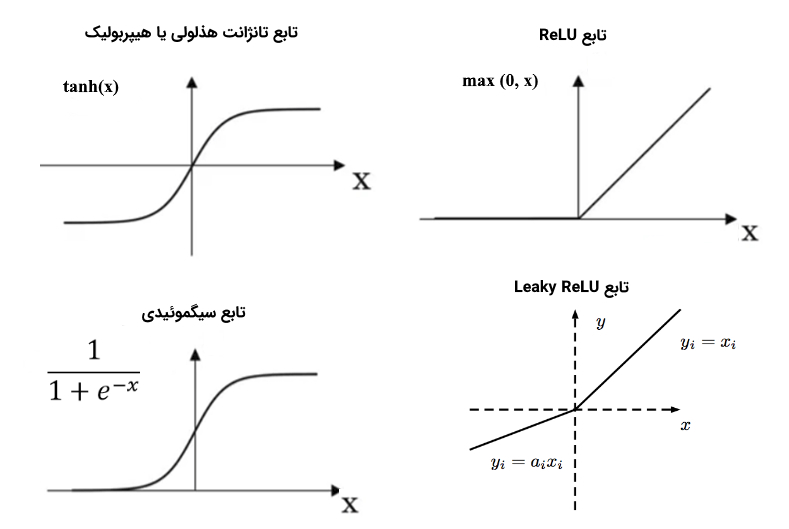
در این بخش، چهار تابع فعالسازی مهم و پر کاربرد در پیادهسازی شبکه های عصبی مصنوعی مورد بررسی قرار میگیرند:
- تابع سیگموئید: از آنجایی که برد مقادیر خروجی این تابع بین صفر و یک است، به شدت توصیه میود که از این تابع فعالسازی در لایه خروجی استفاده شود تا به راحتی بتوان خروجیها را در قالب مقادیر «احتمالی» (Probability) تفسیر کرد. یکی از معایب استفاده از تابع سیگموئیدی، به عنوان تابع فعالسازی در لایههای نهان، این است که مقادیر گرادیانها در بخش بزرگی از دامنه مسأله، بسیار نزدیک به صفر خواهند بود؛ در نتیجه، الگوریتم یادگیری بسیار کند و کار آن برای مدلسازی دادهها بسیار سخت خواهد شد.
- تابع تانژانت هذلولوی یا هیپربولیک: از آنجایی که «میانگین» (Mean) خروجی این تابع بسیار نزدیک به صفر است، نسبت به تابع سیگموئیدی برتری دارد. زیرا، مرکزیت خروجی واحدهای فعالسازی در اطراف صفر قرار میگیرد و این سبب میشود که برد مقادیر خروجی، بسیار کوچک و فرایند یادگیری، سریعتر انجام شود. یکی از معایب استفاده از تابع تانژانت هذلولوی یا هیپربولیک، به عنوان تابع فعالسازی در لایههای نهان (که با تابع سیگموئیدی در اشتراک است)، این است که مقادیر گرادیانها در بخش بزرگی از دامنه، بسیار نزدیک به صفر خواهند بود.
- تابع «واحد خطی اصلاح شده» (ReLU): مدلهای نزدیک به مدل خطی بسیار ساده هستند و بهینهسازی آنها نیز بسیار آسان است. از آنجایی که تابع ReLU، بسیاری از مشخصههای توابع خطی را به اشتراک میگذارد، در بسیاری از مسائل کارایی خوبی از خود نشان میدهد. تنها مشکل این توابع این است که مشتق آنها در تعریف نمیشود. راه حل این مشکل این است که در ، مشتق برابر صفر در نظر گرفته شود. با این حال، این بدین معنی است که برای تمامی مقادیر ، گرادیان برابر صفر خواهد شد و الگوریتم قادر به یادگیری نخواهد بود.
- تابع «واحد خطی اصلاح شده نشتی» (Leaky ReLU): این تابع، از طریق اختصاص مقدار (مقداری کوچک) به تمامی مقادیر ، بر مشکل «گرادیان صفر» (Zero Gradient) فائق آمده است.
در صورتی که مطمئن نیستید کدام تابع فعالسازی برای مسأله شما مناسب است، کار آموزش شبکه عصبی مصنوعی را تابع فعالسازی ReLU شروع کنید. در ادامه، هر کدام از توابع بالا در پایتون پیادهسازی و گراف متناظر با آنها رسم خواهد شد (از این طریق، دامنه و برد هر تابع به خوبی مشخص میشود).
1# Define activation functions that will be used in forward propagation
2def sigmoid(Z):
3 """
4 Computes the sigmoid of Z element-wise.
5
6 Arguments
7 ---------
8 Z : array
9 output of affine transformation.
10
11 Returns
12 -------
13 A : array
14 post activation output.
15 Z : array
16 output of affine transformation.
17 """
18 A = 1 / (1 + np.exp(-Z))
19
20 return A, Z
21
22
23def tanh(Z):
24 """
25 Computes the Hyperbolic Tagent of Z elemnet-wise.
26
27 Arguments
28 ---------
29 Z : array
30 output of affine transformation.
31
32 Returns
33 -------
34 A : array
35 post activation output.
36 Z : array
37 output of affine transformation.
38 """
39 A = np.tanh(Z)
40
41 return A, Z
42
43
44def relu(Z):
45 """
46 Computes the Rectified Linear Unit (ReLU) element-wise.
47
48 Arguments
49 ---------
50 Z : array
51 output of affine transformation.
52
53 Returns
54 -------
55 A : array
56 post activation output.
57 Z : array
58 output of affine transformation.
59 """
60 A = np.maximum(0, Z)
61
62 return A, Z
63
64
65def leaky_relu(Z):
66 """
67 Computes Leaky Rectified Linear Unit element-wise.
68
69 Arguments
70 ---------
71 Z : array
72 output of affine transformation.
73
74 Returns
75 -------
76 A : array
77 post activation output.
78 Z : array
79 output of affine transformation.
80 """
81 A = np.maximum(0.1 * Z, Z)
82
83 return A, Zنمایش گرافی توابع فعالسازی:
1# Plot the 4 activation functions
2z = np.linspace(-10, 10, 100)
3
4# Computes post-activation outputs
5A_sigmoid, z = sigmoid(z)
6A_tanh, z = tanh(z)
7A_relu, z = relu(z)
8A_leaky_relu, z = leaky_relu(z)
9
10# Plot sigmoid
11plt.figure(figsize=(12, 8))
12plt.subplot(2, 2, 1)
13plt.plot(z, A_sigmoid, label = "Function")
14plt.plot(z, A_sigmoid * (1 - A_sigmoid), label = "Derivative")
15plt.legend(loc = "upper left")
16plt.xlabel("z")
17plt.ylabel(r"$\frac{1}{1 + e^{-z}}$")
18plt.title("Sigmoid Function", fontsize = 16)
19# Plot tanh
20plt.subplot(2, 2, 2)
21plt.plot(z, A_tanh, 'b', label = "Function")
22plt.plot(z, 1 - np.square(A_tanh), 'r',label = "Derivative")
23plt.legend(loc = "upper left")
24plt.xlabel("z")
25plt.ylabel(r"$\frac{e^z - e^{-z}}{e^z + e^{-z}}$")
26plt.title("Hyperbolic Tangent Function", fontsize = 16)
27# plot relu
28plt.subplot(2, 2, 3)
29plt.plot(z, A_relu, 'g')
30plt.xlabel("z")
31plt.ylabel(r"$max\{0, z\}$")
32plt.title("ReLU Function", fontsize = 16)
33# plot leaky relu
34plt.subplot(2, 2, 4)
35plt.plot(z, A_leaky_relu, 'y')
36plt.xlabel("z")
37plt.ylabel(r"$max\{0.1z, z\}$")
38plt.title("Leaky ReLU Function", fontsize = 16)
39plt.tight_layout();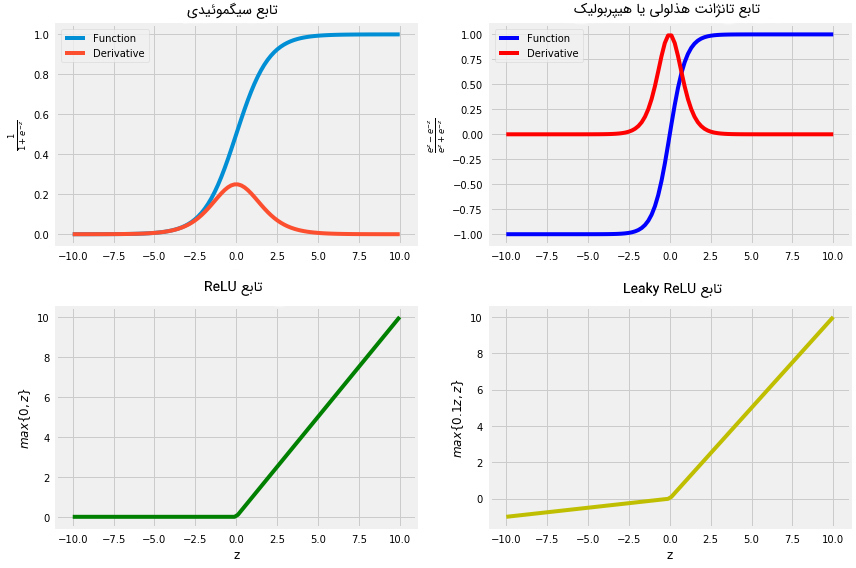
فرایند پیشخور (Feedforward) در شبکه های عصبی مصنوعی
هر واحد یا نود موجود در لایههای شبکه عصبی مصنوعی (به جز نودهای لایه ورودی)، با داشتن ورودیها از لایه قبلی (خروجی لایه قبلی، ورودی لایه بعدی خواهد بود)، تبدیل خطی ورودیها را محاسبه و تابع فعالسازی نظیر ReLU را، به صورت «عنصر به عنصر» (Element-Wise) بر روی عناصر آن اعمال میکند.
در طی این فرایند، تمامی متغیرهای محاسبه شده ذخیره میشوند تا در مرحله «پس انتشار» (BackPropagation) خطا مورد استفاده قرار بگیرند. شایان توجه است که ممکن است هر کدام از لایههای شبکه عصبی مصنوعی، توابع فعالسازی متفاوتی داشته باشند.
1# Define helper functions that will be used in L-model forward prop
2def linear_forward(A_prev, W, b):
3 """
4 Computes affine transformation of the input.
5
6 Arguments
7 ---------
8 A_prev : 2d-array
9 activations output from previous layer.
10 W : 2d-array
11 weight matrix, shape: size of current layer x size of previuos layer.
12 b : 2d-array
13 bias vector, shape: size of current layer x 1.
14
15 Returns
16 -------
17 Z : 2d-array
18 affine transformation output.
19 cache : tuple
20 stores A_prev, W, b to be used in backpropagation.
21 """
22 Z = np.dot(W, A_prev) + b
23 cache = (A_prev, W, b)
24
25 return Z, cache
26
27
28def linear_activation_forward(A_prev, W, b, activation_fn):
29 """
30 Computes post-activation output using non-linear activation function.
31
32 Arguments
33 ---------
34 A_prev : 2d-array
35 activations output from previous layer.
36 W : 2d-array
37 weight matrix, shape: size of current layer x size of previuos layer.
38 b : 2d-array
39 bias vector, shape: size of current layer x 1.
40 activation_fn : str
41 non-linear activation function to be used: "sigmoid", "tanh", "relu".
42
43 Returns
44 -------
45 A : 2d-array
46 output of the activation function.
47 cache : tuple
48 stores linear_cache and activation_cache. ((A_prev, W, b), Z) to be used in backpropagation.
49 """
50 assert activation_fn == "sigmoid" or activation_fn == "tanh" or \
51 activation_fn == "relu"
52
53 if activation_fn == "sigmoid":
54 Z, linear_cache = linear_forward(A_prev, W, b)
55 A, activation_cache = sigmoid(Z)
56
57 elif activation_fn == "tanh":
58 Z, linear_cache = linear_forward(A_prev, W, b)
59 A, activation_cache = tanh(Z)
60
61 elif activation_fn == "relu":
62 Z, linear_cache = linear_forward(A_prev, W, b)
63 A, activation_cache = relu(Z)
64
65 assert A.shape == (W.shape[0], A_prev.shape[1])
66
67 cache = (linear_cache, activation_cache)
68
69 return A, cache
70
71
72def L_model_forward(X, parameters, hidden_layers_activation_fn="relu"):
73 """
74 Computes the output layer through looping over all units in topological
75 order.
76
77 Arguments
78 ---------
79 X : 2d-array
80 input matrix of shape input_size x training_examples.
81 parameters : dict
82 contains all the weight matrices and bias vectors for all layers.
83 hidden_layers_activation_fn : str
84 activation function to be used on hidden layers: "tanh", "relu".
85
86 Returns
87 -------
88 AL : 2d-array
89 probability vector of shape 1 x training_examples.
90 caches : list
91 that contains L tuples where each layer has: A_prev, W, b, Z.
92 """
93 A = X
94 caches = []
95 L = len(parameters) // 2
96
97 for l in range(1, L):
98 A_prev = A
99 A, cache = linear_activation_forward(
100 A_prev, parameters["W" + str(l)], parameters["b" + str(l)],
101 activation_fn=hidden_layers_activation_fn)
102 caches.append(cache)
103
104 AL, cache = linear_activation_forward(
105 A, parameters["W" + str(L)], parameters["b" + str(L)],
106 activation_fn="sigmoid")
107 caches.append(cache)
108
109 assert AL.shape == (1, X.shape[1])
110
111 return AL, cachesتابع هزینه (Cost) در شبکه های عصبی مصنوعی
در این مطلب، از تابع هزینه باینری «آنتروپی متقابل» (Cross-Entropy) استفاده میشود. این روش، از «درستنمایی بر حسب لگاریتم» (Log-Likelihood) برای محاسبه خطا استفاده میکند. تابع هزینه به شکل زیر تعریف میشود:
تابع هزینه بالا، یک تابع محدب است؛ با این حال، شبکه عصبی معمولا در دام «کمینه محلی» (Local Minimum) قرار میگیرد و تضمینی برای رسیدن به پارامترهای «بهینه سراسری» (GLobal Optimum) وجود ندارد. در این مطلب، الگوریتم یادگیری شبکه عصبی، از روش «گرادیان کاهشی» (Gradient Descent) استفاده میکند.
1# Compute cross-entropy cost
2def compute_cost(AL, y):
3 """
4 Computes the binary Cross-Entropy cost.
5
6 Arguments
7 ---------
8 AL : 2d-array
9 probability vector of shape 1 x training_examples.
10 y : 2d-array
11 true "label" vector.
12
13 Returns
14 -------
15 cost : float
16 binary cross-entropy cost.
17 """
18 m = y.shape[1]
19 cost = - (1 / m) * np.sum(
20 np.multiply(y, np.log(AL)) + np.multiply(1 - y, np.log(1 - AL)))
21
22 return costالگوریتم یادگیری پس انتشار (BackPropagation) در شبکه های عصبی مصنوعی چند لایه
الگوریتم پس انتشار در شبکه عصبی مصنوعی به اطلاعات اجازه میدهد تا از تابع هزینه لایه خروجی به سمت لایههای پیشین شبکه عصبی انتشار پیدا کنند (پس انتشار اطلاعات) و از این طریق، گرادیانها محاسبه شوند. بنابراین، در الگوریتم پس انتشار، از نود پایانی در جهت معکوس «ترتیب توپولوژیکی» (Topological Order) شبکه عصبی، پیمایش انجام میشود تا مشتق مقدار خروجی نود پایانی، نسبت به هرکدام از نودهای لایه پیشین (و مشتق مقدار خروجی نود آخرین لایه نهان، نسبت به هرکدام از نودهای لایههای نهان پیشین و همینطور الی آخر) محاسبه شود.
چنین کاری به الگوریتم یادگیری شبکه عصبی اجازه میدهد تا مشخص کند که کدام نودها، مسئول تولید بیشترین خطا در عملکرد سیستم هستند و مقادیر پارامترها (به ویژه، پارامتر وزن) را بر این اساس تغییر دهد. روابط مشتقی که در ادامه آمده است، برای تولید توابع لازم جهت پیادهسازی الگوریتم پس انتشار مورد استفاده قرار میگیرند.
از آنجایی که همیشه یک بردار است، جمع ماتریسی در راستای سطرهای ماتریس انجام میشود (زیرا، هر ستون یک نمونه را نمایش میدهد).
1# Define derivative of activation functions w.r.t z that will be used in back-propagation
2def sigmoid_gradient(dA, Z):
3 """
4 Computes the gradient of sigmoid output w.r.t input Z.
5
6 Arguments
7 ---------
8 dA : 2d-array
9 post-activation gradient, of any shape.
10 Z : 2d-array
11 input used for the activation fn on this layer.
12
13 Returns
14 -------
15 dZ : 2d-array
16 gradient of the cost with respect to Z.
17 """
18 A, Z = sigmoid(Z)
19 dZ = dA * A * (1 - A)
20
21 return dZ
22
23
24def tanh_gradient(dA, Z):
25 """
26 Computes the gradient of hyperbolic tangent output w.r.t input Z.
27
28 Arguments
29 ---------
30 dA : 2d-array
31 post-activation gradient, of any shape.
32 Z : 2d-array
33 input used for the activation fn on this layer.
34
35 Returns
36 -------
37 dZ : 2d-array
38 gradient of the cost with respect to Z.
39 """
40 A, Z = tanh(Z)
41 dZ = dA * (1 - np.square(A))
42
43 return dZ
44
45
46def relu_gradient(dA, Z):
47 """
48 Computes the gradient of ReLU output w.r.t input Z.
49
50 Arguments
51 ---------
52 dA : 2d-array
53 post-activation gradient, of any shape.
54 Z : 2d-array
55 input used for the activation fn on this layer.
56
57 Returns
58 -------
59 dZ : 2d-array
60 gradient of the cost with respect to Z.
61 """
62 A, Z = relu(Z)
63 dZ = np.multiply(dA, np.int64(A > 0))
64
65 return dZ
66
67
68# define helper functions that will be used in L-model back-prop
69def linear_backword(dZ, cache):
70 """
71 Computes the gradient of the output w.r.t weight, bias, and post-activation
72 output of (l - 1) layers at layer l.
73
74 Arguments
75 ---------
76 dZ : 2d-array
77 gradient of the cost w.r.t. the linear output (of current layer l).
78 cache : tuple
79 values of (A_prev, W, b) coming from the forward propagation in the current layer.
80
81 Returns
82 -------
83 dA_prev : 2d-array
84 gradient of the cost w.r.t. the activation (of the previous layer l-1).
85 dW : 2d-array
86 gradient of the cost w.r.t. W (current layer l).
87 db : 2d-array
88 gradient of the cost w.r.t. b (current layer l).
89 """
90 A_prev, W, b = cache
91 m = A_prev.shape[1]
92
93 dW = (1 / m) * np.dot(dZ, A_prev.T)
94 db = (1 / m) * np.sum(dZ, axis=1, keepdims=True)
95 dA_prev = np.dot(W.T, dZ)
96
97 assert dA_prev.shape == A_prev.shape
98 assert dW.shape == W.shape
99 assert db.shape == b.shape
100
101 return dA_prev, dW, db
102
103
104def linear_activation_backward(dA, cache, activation_fn):
105 """
106 Arguments
107 ---------
108 dA : 2d-array
109 post-activation gradient for current layer l.
110 cache : tuple
111 values of (linear_cache, activation_cache).
112 activation : str
113 activation used in this layer: "sigmoid", "tanh", or "relu".
114
115 Returns
116 -------
117 dA_prev : 2d-array
118 gradient of the cost w.r.t. the activation (of the previous layer l-1), same shape as A_prev.
119 dW : 2d-array
120 gradient of the cost w.r.t. W (current layer l), same shape as W.
121 db : 2d-array
122 gradient of the cost w.r.t. b (current layer l), same shape as b.
123 """
124 linear_cache, activation_cache = cache
125
126 if activation_fn == "sigmoid":
127 dZ = sigmoid_gradient(dA, activation_cache)
128 dA_prev, dW, db = linear_backword(dZ, linear_cache)
129
130 elif activation_fn == "tanh":
131 dZ = tanh_gradient(dA, activation_cache)
132 dA_prev, dW, db = linear_backword(dZ, linear_cache)
133
134 elif activation_fn == "relu":
135 dZ = relu_gradient(dA, activation_cache)
136 dA_prev, dW, db = linear_backword(dZ, linear_cache)
137
138 return dA_prev, dW, db
139
140
141def L_model_backward(AL, y, caches, hidden_layers_activation_fn="relu"):
142 """
143 Computes the gradient of output layer w.r.t weights, biases, etc. starting
144 on the output layer in reverse topological order.
145
146 Arguments
147 ---------
148 AL : 2d-array
149 probability vector, output of the forward propagation (L_model_forward()).
150 y : 2d-array
151 true "label" vector (containing 0 if non-cat, 1 if cat).
152 caches : list
153 list of caches for all layers.
154 hidden_layers_activation_fn :
155 activation function used on hidden layers: "tanh", "relu".
156
157 Returns
158 -------
159 grads : dict
160 with the gradients.
161 """
162 y = y.reshape(AL.shape)
163 L = len(caches)
164 grads = {}
165
166 dAL = np.divide(AL - y, np.multiply(AL, 1 - AL))
167
168 grads["dA" + str(L - 1)], grads["dW" + str(L)], grads[
169 "db" + str(L)] = linear_activation_backward(
170 dAL, caches[L - 1], "sigmoid")
171
172 for l in range(L - 1, 0, -1):
173 current_cache = caches[l - 1]
174 grads["dA" + str(l - 1)], grads["dW" + str(l)], grads[
175 "db" + str(l)] = linear_activation_backward(
176 grads["dA" + str(l)], current_cache,
177 hidden_layers_activation_fn)
178
179 return grads
180
181
182# define the function to update both weight matrices and bias vectors
183def update_parameters(parameters, grads, learning_rate):
184 """
185 Update the parameters' values using gradient descent rule.
186
187 Arguments
188 ---------
189 parameters : dict
190 contains all the weight matrices and bias vectors for all layers.
191 grads : dict
192 stores all gradients (output of L_model_backward).
193
194 Returns
195 -------
196 parameters : dict
197 updated parameters.
198 """
199 L = len(parameters) // 2
200
201 for l in range(1, L + 1):
202 parameters["W" + str(l)] = parameters[
203 "W" + str(l)] - learning_rate * grads["dW" + str(l)]
204 parameters["b" + str(l)] = parameters[
205 "b" + str(l)] - learning_rate * grads["db" + str(l)]
206
207 return parametersکاربرد شبکه های عصبی مصنوعی در بازشناسی تصویر
مجموعه دادهای که برای این کاربرد مورد استفاده قرار گرفته است از 209 تصویر تشکیل شده است. دقت پیکسلی هر تصویر 64x64 است و در فضای رنگی RGB قرار دارد. هدف این کاربرد، پیادهسازی شبکه عصبی مصنوعی برای دستهبندی دستهبندی تصاویر در دو کلاس گربه و غیر گربه است.
بنابراین، .
- در ابتدا، تصاویر در سیستم بارگیری میشوند.
- سپس، ماتریس ورودی به گونهای تغییر شکل داده میشود که هر ستون، یک نمونه را نشان دهد. از آنجایی که ابعاد هر تصویر برابر با 64x64x3 است، بنابراین هر کدام از تصاویر، 12288 ویژگی خواهند داشت. بنابراین، اندازه ماتریس ورودی برابر با 12288x209 خواهد بود.
- دادهها «استانداردسازی» (Standardize) میشوند تا مقادیر گرادیانهای محاسبه شده از کنترل خارج نشوند. چنین کاری، سبب یکسان شدن «برد» (Range) مقادیر نودهای لایه نهان میشود. در این مطلب، برای استانداردسازی تصاویر، مقادیر تمامی پیکسلها بر عدد 255 تقسیم میشوند. با این حال، توصیه میشود که دادهها به گونهای استانداردسازی شوند که «میانگین» (Mean) آماری آنها برابر با صفر و «انحراف معیار» (Standard Deviation) آنها برابر با 1 باشد.
برای دانلود دادههای آموزشی و تست این کاربرد، به لینک [+] زیر مراجعه شود.
1# Import training dataset
2train_dataset = h5py.File("../data/train_catvnoncat.h5")
3X_train = np.array(train_dataset["train_set_x"])
4y_train = np.array(train_dataset["train_set_y"])
5
6test_dataset = h5py.File("../data/test_catvnoncat.h5")
7X_test = np.array(test_dataset["test_set_x"])
8y_test = np.array(test_dataset["test_set_y"])
9
10# print the shape of input data and label vector
11print(f"""Original dimensions:\n{20 * '-'}\nTraining: {X_train.shape}, {y_train.shape}
12Test: {X_test.shape}, {y_test.shape}""")
13
14# plot cat image
15plt.figure(figsize=(6, 6))
16plt.imshow(X_train[50])
17plt.axis("off");
18
19# Transform input data and label vector
20X_train = X_train.reshape(209, -1).T
21y_train = y_train.reshape(-1, 209)
22
23X_test = X_test.reshape(50, -1).T
24y_test = y_test.reshape(-1, 50)
25
26# standarize the data
27X_train = X_train / 255
28X_test = X_test / 255
29
30print(f"""\nNew dimensions:\n{15 * '-'}\nTraining: {X_train.shape}, {y_train.shape}
31Test: {X_test.shape}, {y_test.shape}""")خروجی:
Original dimensions: -------------------- Training: (209, 64, 64, 3), (209,) Test: (50, 64, 64, 3), (50,) New dimensions: --------------- Training: (12288, 209), (1, 209) Test: (12288, 50), (1, 50)

پس از این مرحله، مجموعه داده لازم برای «آموزش» (Training) و «تست» (Test) شبکه عصبی آماده خواهد شد. در ابتدا، تابع تولید «مدل چند لایه» (Multi-Layer Model) برای پیادهسازی الگوریتم یادگیری مبتنی بر روش گرادیان نمایش داده میشود. برای تولید این تابع، از تعداد تکرار (3000) و نرخ یادگیری (0٫۰۱) مشخص استفاده میشود.
1# Define the multi-layer model using all the helper functions we wrote before
2
3
4def L_layer_model(
5 X, y, layers_dims, learning_rate=0.01, num_iterations=3000,
6 print_cost=True, hidden_layers_activation_fn="relu"):
7 """
8 Implements multilayer neural network using gradient descent as the
9 learning algorithm.
10
11 Arguments
12 ---------
13 X : 2d-array
14 data, shape: number of examples x num_px * num_px * 3.
15 y : 2d-array
16 true "label" vector, shape: 1 x number of examples.
17 layers_dims : list
18 input size and size of each layer, length: number of layers + 1.
19 learning_rate : float
20 learning rate of the gradient descent update rule.
21 num_iterations : int
22 number of iterations of the optimization loop.
23 print_cost : bool
24 if True, it prints the cost every 100 steps.
25 hidden_layers_activation_fn : str
26 activation function to be used on hidden layers: "tanh", "relu".
27
28 Returns
29 -------
30 parameters : dict
31 parameters learnt by the model. They can then be used to predict test examples.
32 """
33 np.random.seed(1)
34
35 # initialize parameters
36 parameters = initialize_parameters(layers_dims)
37
38 # intialize cost list
39 cost_list = []
40
41 # iterate over num_iterations
42 for i in range(num_iterations):
43 # iterate over L-layers to get the final output and the cache
44 AL, caches = L_model_forward(
45 X, parameters, hidden_layers_activation_fn)
46
47 # compute cost to plot it
48 cost = compute_cost(AL, y)
49
50 # iterate over L-layers backward to get gradients
51 grads = L_model_backward(AL, y, caches, hidden_layers_activation_fn)
52
53 # update parameters
54 parameters = update_parameters(parameters, grads, learning_rate)
55
56 # append each 100th cost to the cost list
57 if (i + 1) % 100 == 0 and print_cost:
58 print(f"The cost after {i + 1} iterations is: {cost:.4f}")
59
60 if i % 100 == 0:
61 cost_list.append(cost)
62
63 # plot the cost curve
64 plt.figure(figsize=(10, 6))
65 plt.plot(cost_list)
66 plt.xlabel("Iterations (per hundreds)")
67 plt.ylabel("Loss")
68 plt.title(f"Loss curve for the learning rate = {learning_rate}")
69
70 return parameters
71
72
73def accuracy(X, parameters, y, activation_fn="relu"):
74 """
75 Computes the average accuracy rate.
76
77 Arguments
78 ---------
79 X : 2d-array
80 data, shape: number of examples x num_px * num_px * 3.
81 parameters : dict
82 learnt parameters.
83 y : 2d-array
84 true "label" vector, shape: 1 x number of examples.
85 activation_fn : str
86 activation function to be used on hidden layers: "tanh", "relu".
87
88 Returns
89 -------
90 accuracy : float
91 accuracy rate after applying parameters on the input data
92 """
93 probs, caches = L_model_forward(X, parameters, activation_fn)
94 labels = (probs >= 0.5) * 1
95 accuracy = np.mean(labels == y) * 100
96
97 return f"The accuracy rate is: {accuracy:.2f}%."در مرحله بعد، دو نسخه از شبکه عصبی پیادهسازی شده آموزش داده میشود؛ در نسخه اول، از تابع ReLU و در نسخه دوم، از تابع تانژانت هذلولوی یا هیپربولیک، به عنوان تابع فعالسازی لایههای نهان استفاده شده است. سپس، از دو مدل شبکه عصبی آموزش دیده، برای دستهبندی تصاویر تست و محاسبه نرخ دقت در مرحله تست استفاده میشود. با استفاده از نتایج دقت دو مدل آموزش دیده، بهترین تابع فعالسازی برای آموزش شبکه عصبی مشخص میشود.
1# Setting layers dims
2layers_dims = [X_train.shape[0], 5, 5, 1]
3
4# NN with tanh activation fn
5parameters_tanh = L_layer_model(
6 X_train, y_train, layers_dims, learning_rate=0.03, num_iterations=3000,
7 hidden_layers_activation_fn="tanh")
8
9# Print the accuracy
10accuracy(X_test, parameters_tanh, y_test, activation_fn="tanh")The cost after 100 iterations is: 0.6556 The cost after 500 iterations is: 0.6440 The cost after 1000 iterations is: 0.6439 The cost after 1500 iterations is: 0.6437 The cost after 2000 iterations is: 0.6124 The cost after 2500 iterations is: 0.3387 The cost after 3000 iterations is: 0.1040 'The accuracy rate is: 68.00%.'
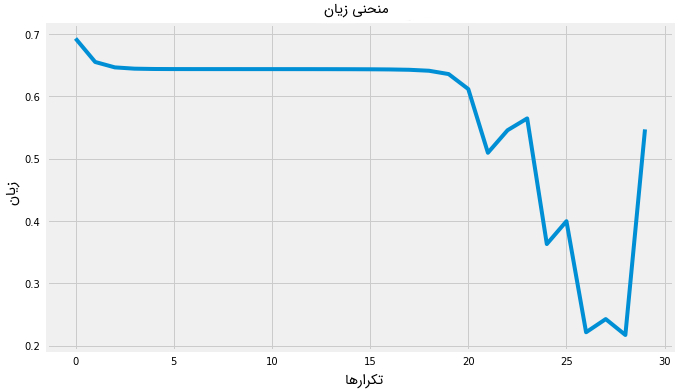
1# NN with relu activation fn
2parameters_relu = L_layer_model(
3 X_train, y_train, layers_dims, learning_rate=0.03, num_iterations=3000,
4 hidden_layers_activation_fn="relu")
5
6# Print the accuracy
7accuracy(X_test, parameters_relu, y_test, activation_fn="relu")1The cost after 100 iterations is: 0.6556
2The cost after 500 iterations is: 0.6440
3The cost after 1000 iterations is: 0.6440
4The cost after 1500 iterations is: 0.6439
5The cost after 2000 iterations is: 0.6432
6The cost after 2500 iterations is: 0.5262
7The cost after 3000 iterations is: 0.3641
8
9'The accuracy rate is: 42.00%.'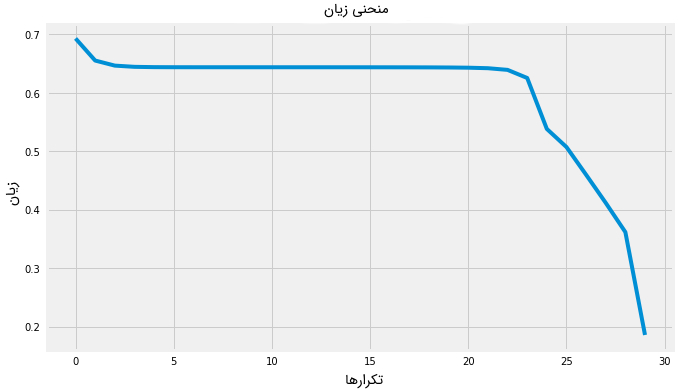
جمعبندی
هدف از این مطلب، ارائه مرحله به مرحله الگوریتم یادگیری در شبکه های عصبی مصنوعی و ویژگیهای مشخصه آن است. هدف اصلی پیادهسازی مدل یادگیری شبکه عصبی مصنوعی در این مطلب، ارائه یک مدل دقیق برای دستهبندی تصاویر نیست؛ بلکه، هدف آشنا کردن مخاطب با توابع لازم برای پیادهسازی شبکه های عصبی مصنوعی چند لایه است. با این حال، راهکارهای مختلفی برای افزایش دقت و عملکرد شبکه عصبی مصنوعی وجود دارد که در حیطه این مطلب نمیگنجد.
برخی از مهمترین نکات حاصل از این مطلب عبارتند از:
- حتی اگر شبکه های عصبی مصنوعی قادر به مدلسازی و نمایش هر نوع تابعی باشند، به دو دلیل مهم، ممکن است قادر به یادگیری بهینه آن نباشند:
- ممکن است الگوریتم بهینهسازی قادر به پیدا کردن بهترین مقادیر برای پارامترهای تابع نباشد؛ یعنی، در کمینه محلی قرار بگیرد.
- به دلیل «بیشبرازش» (Overfitting)، الگوریتم یادگیری ممکن است شکل تابعی متفاوت از شکل تابعی مورد نظر را پیدا کند.
- اگرچه شبکههای عصبی به ندرت به جواب بهینه سراسری همگرا میشوند و معمولا در کمینه سراسری قرار میگیرند، با این حال، هزینهها (محاسباتی) را به شدت کاهش میدهند و مدلهای بسیار پیچیده و با دقت بالا برای حل مسائل ارائه میدهند.
- شبکه عصبی استفاده شده در این مطلب، شبکه عصبی استاندارد «کاملا مصل» (Fully Connected) است. دو نوع شبکه عصبی متداول دیگر عبارتند از:
- «شبکههای عصبی پیچشی» (Convolutional Neural Network): در این نوع شبکه عصبی، نودهای شبکه کاملا به هم متصل نیستند و بیشتر برای کاربردهایی نظیر بازشناسی تصویر مورد استفاده قرار میگیرند.
- «شبکههای عصبی بازگشتی» (Recurrent Neural Network): در این نوع شبکه عصبی، وجود «ارتباطات بازخوردی» (Feedback Connection) در سیستم سبب میشود تا خروجی مدل، دوباره وارد همان مدل شود. از این دسته از روشها، بیشتر برای «مدلسازی ترتیبی» (Sequential Modelling) استفاده میشود.
- شبکههای عصبی استاندارد کاملا متصل، حافظهای از اتفاقات رخ داده در مراحل قبل ندارند. همچنین، هیچگونه اطلاعاتی در رابطه با خروجی ندارند.
- تعدادی از «اَبَرپارامترهای» شبکه عصبی را میتوان با استفاده از «اعتبارسنجی متقابل» (Cross-Validation) بهینهسازی کرد تا بهترین عملکرد ممکن توسط شبکه عصبی حاصل شود:
- نرخ یادگیری: اندازه گامهای به روز رسانی پارامترهای شبکه عصبی را مشخص میکند. مقدار کم برای نرخ یادگیری، سبب همگرایی آهسته و افزایش بار محاسباتی سیستم میشود. مقدار زیاد برای نرخ یادگیری، ممکن است سبب عدم همگرایی مدل به جواب (یا تقریب مناسبی از جواب) بهینه شود.
- تعداد لایههای نهان (عمق): تعداد بیشتر لایههای نهان، سبب عملکرد بهینه سیستم یادگیری میشود ولی هزینه محاسباتی را افزایش میدهد.
- تعداد نودهای در هر لایه (پهنا): تحقیقات نشان داده است که تعداد زیاد نودهای در لایههای مختلف، منجر به بهبود عملکرد سیستم نخواهد شد.
- تابع فعالسازی: انتخاب تابع فعالسازی مناسب برای یک کاربرد خاص، یک فرایند آزمون و خطا است و بستگی زیادی به نوع کاربرد دارد.
- تعداد تکرارهای الگوریتم یادگیری برای رسید به جواب.
- استانداردسازی دادهها: به توابع فعالسازی کمک میکند تا خروجیهای مشابهی (از لحاظ برد مقادیر) داشته باشند. همچنین، به سیستم در کنترل مقادیر گرادیانهای محاسبه شده کمک میکند.

اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دادهکاوی و یادگیری ماشین
- آموزش اصول و روشهای دادهکاوی (Data Mining)
- مجموعه آموزشهای هوش مصنوعی
- پرسپترون چند لایه در پایتون — راهنمای کاربردی
- پیشبینی قیمت بیت کوین با شبکه عصبی — راهنمای کاربردی
- نقشه دانش فناوریهای هوش مصنوعی و دسته بندی آنها — راهنمای جامع
^^













با تشکر بسیار عالی و مفید بود
با تشکر از زحمات شما نویسنده گرامی . مقاله بسیار عالی و کاملی بود. مدت ها بود به دنبال چنین مقاله کاملی بودم