کمیت چیست؟ + کمیت های اصلی فیزیک به زبان ساده
گستره اجسام و پدیدههای مطالعه شده در فیزیک بسیار زیاد است. به جرات میتوان گفت فیزیک علمی است که در آن کلِ جهان مطالعه میشود، از کوچکترین ذرات زیراتمی تا بزرگترین کهکشانها. اندازهگیری در فیزیک از اهمیت بالایی برخوردار است. در فیزیک به هر چیزی که بتوانیم اندازه بگیریم، کمیت فیزیکی گفته میشود. هر کمیت فیزیکی، اندازه و واحد یا یکا دارد. در این مطلب، در مورد کمیت فیزیکی و واحدهای اندازهگیری آنها در فیزیک صحبت میکنیم.
- تعریف دقیق کمیت فیزیکی و ویژگیهای اساسی آن را یاد خواهید گرفت.
- کاربرد واحدها و اهمیت استانداردسازی در اندازهگیری را میآموزید.
- دستهبندی کمیتهای اصلی و فرعی را خواهید آموخت.
- اصول سیستم «SI» و شیوه صحیح نمادگذاری واحدها را فرا میگیرید.
- میآموزید با کمک فرمول، واحد کمیتهای فرعی را محاسبه کنید.
- تفاوت و خصوصیات کمیتهای برداری و اسکالر را یاد میگیرید.

کمیت چیست ؟
در علم فیزیک، کمیت فیزیکی به هر ویژگی فیزیکی ماده یا جسم گفته میشود که بتوان آن را با استفاده از اندازهگیری کمی کرد. به بیان دیگر، کمیت فیزیکی را میتوان با استفاده از اعداد اندازه گرفت. کمیت فیزیکی میتواند توسط مقدار بیان شود. این مقدار، ضرب جبری مقداری عددی در واحدی مشخص است. جرم، طول، زمان، جریان الکتریکی، نیرو، سرعت و چگالی از معروفترین کمیتهای فیزیکی هستند. توجه به این نکته مهم است که تعداد کمیتهای فیزیکی بسیار بیشتر از چند مثال ذکر شده است.
گفتیم کمیت فیزیکی را میتوانیم به صورت حاصلضرب مقداری عددی در واحدی مشخص بیان کنیم. شاید از خود بپرسید منظور از واحد مشخص چیست. باید به این نکته توجه داشته باشید که هر کمیت فیزیکی توسط واحد اندازهگیری مشخصی بیان میشود. به عنوان مثال، کمیت فیزیکی جرم را میتوان به صورت «» نوشت. در این حالت، جرم جسم با استفاده از ترازو اندازه گرفته شد و مقدار عددی آن برابر ۳۲/۲ بهدست آمد. کیلوگرم نیز واحد اندازه گیری جرم است. به عبارت دیگر، ۳۲/۲ مقدار عددی و کیلوگرم واحد یا یکای کمیت است.
هر کمیت فیزیکی دو ویژگی مشخص دارد:
- مقدار عددی
- واحد
در مطالب بالا گفتیم کمیت فیزیکی به صورت حاصلضرب مقدار عددی در واحدی مشخص نوشته میشود. قبل از توضیح در مورد دستهبندی کمیتهای فیزیکی، واحد اندازهگیری را تعریف میکنیم. همچنین برای اینکه با روش یادگیری مفاهیم فیزیک بهتر آشنا شوید، پیشنهاد میکنیم پیش از پرداختن به سایر بخشها مطلب «بهترین روش مطالعه فیزیک چیست؟ – ۱۶ روش از مطالعه مفهومی تا حل مثال» را مطالعه کنید.
واحد اندازه گیری چیست ؟
از واحدها یا یکاها برای اندازهگیری کمیت فیزیکی استفاده میشود. در علم، واحدها مرجعی تثبیت شده هستند که به شما امکان میدهد مقدار یک کمیت را تعریف کنید. کمیت فیزیکی، مشخصه یا ویژگی از ماده است که آن را اندازه میگیریم، اما واحدها مرجع هستند و به ما این امکان را میدهند که مقدار اندازهگیری انجام شده را بدانیم. دو مثال زیر به ما نشان میدهند اندازهگیری کمیتهای فیزیکی چه معنایی دارد.
مثال ۱
طول شاخه درختی برابر ۲/۳ متر است. طول، کمیت فیزیکی شاخه و متر یکا یا واحدی است که به ما میگوید طول شاخه در مقایسه با مرجع چه مقدار خواهد بود. در این مثال، مرجع برابر یک متر و بنابراین طول شاخه برابر ۲/۳ طول یک متر است.
مثال ۲
برای درست کردن پنککیک برای صبحانه به ۲۰۰ گرم آرد نیاز داریم. جرم آرد مشخصهای است که آن را اندازه میگیریم. در حالیکه، گرم واحدی است که به عنوان مرجع از آن استفاده میکنیم.

به طور کلی، فرایند اندازهگیری فرایندی مقایسهای است. هرگاه کمیتی را اندازه میگیریم، آن را با مرجع استانداردی مقایسه میکنیم. بار دیگر به مثال شماره یک توجه کنید. در این مثال گفتیم طول شاخه درختی برابر ۲/۳ متر است. این بدان معنا است که طول این شاخه ۲/۳ برابر طول شاخهای به طول یک متر خواهد بود. به این استاندارد، واحد اندازهگیری گفته میشود. در اینجا، یک متر، واحد کمیت طول است. استانداردی که به طور دلخواه برای اندازهگیری هر کمیت فیزیکی انتخاب و در سطح بینالمللی پذیرفته شده باشد، واحد یا یکای کمیت نامیده میشود.
شاید از خود بپرسید اندازهگیری با واحدهای استاندارد چه مزیتی بر استفاده از مرجع دارد. برای پاسخ به این پرسش به مثال زیر توجه کنید.
مثال ۳
فرض کنید با استفاده از قطعه چوبی میخواهید صندلی برای اتاق خود بسازید. طول هر چهار پایه صندلی باید یکسان باشد. در غیر این صورت، صندلی تعادل نخواهد داشت. برای آنکه بتوانید طول پایهها را هر بار، برابر و یکسان اندازه بگیرید باید از الگوی مشخصی استفاده کنید. فرض کنید از مدادی به عنوان مرجع و برای اندازهگیری پایه اول استفاده میکنید. طول پایه صندلی برابر چهار مداد است. به آسانی میتوانید از مداد برای اندازهگیری سه پایه دیگر نیز استفاده کنید.
شاید دوستتان از شما بپرسد صندلی را چگونه ساختهاید. چگونه او را راهنمایی میکنید؟ به طور حتم به او میگویید طول هر پایه برابر چهار مداد است. دوست شما نیز ممکن است مداد داشته باشد، اما آیا طول مداد او با طول مداد شما برابر است؟ طول مداد، استاندارد نشده است. مدادهای دیگر ممکن است هماندازه، بلندتر یا کوتاهتر از مداد شما باشند. بنابراین، اگر دوست شما بخواهد صندلی هماندازه با صندلی شما بسازد، باید از مداد شما استفاده کند. اگر بخواهید تعداد زیادی صندلی با اندازه یکسان بسازید، چه کاری باید انجام دهید؟ باید از همان مداد اول استفاده کنید. همانطور که در این مثال میبینیم، نداشتن مرجع طول، کار ساخت وسایل مختلف را بسیار سخت میکند.
اگر از مرجعی ثابت برای ساختن صندلی استفاده کنید چه اتفاقی رخ میدهد؟ فرض کنید به جای مداد، از خطکش برای اندازهگیری هر پایه صندلی استفاده میکنید. در این حالت، طور هر پایه برابر ۴۵ سانتیمتر بهدست میآید. دوست شما نیز میتواند از خطکش خود برای ساخت صندلی استفاده کند و صندلی با اندازهای کاملا یکسان بسازد. واحدها به طور گسترده در صنعت و زندگی روزمره استفاده میشوند. زندگی مدرن بدون واحدها هیچ معنایی نداشت.
پرسش ۱: واحد استاندارد چیست؟
پاسخ: واحد استاندارد میتواند در همه جا به عنوان واحد پایه اندازهگیری استفاده شود.
پرسش ۲: واحد اندازهگیری در فیزیک چیست؟
پاسخ: هنگام اندازهگیری کمیتی فیزیک، آن را با استانداردی مقایسه میکنیم که ماهیت مشابه ماهیت کمیت داده شده دارد. به این استاندارد، واحد یا یکا میگوییم.
کمیت های اصلی و فرعی چیست ؟
تا اینجا میدانیم کمیت چیست و واحد اندازهگیری چگونه تعریف میشود. در این بخش، در مورد دستهبندی کمیتها صحبت میکنیم و در ادامه واحدهای اندازهگیری آنها را در دستگاههای مختلف اندازهگیری بیان میکنیم. کمیتها به دو گروه تقسیمبندی میشوند:
- کمیتهای اصلی
- کمیتهای فرعی
کمیت اصلی چیست؟
در مطالب بالا گفتیم کمیت فیزیکی به صورت حاصلضرب مقدار عددی در واحدی مشخص نوشته میشود. هنگام اندازهگیری کمیتهای فیزیک، آنها را با استانداردهایی مقایسه میکنیم که ماهیتی مشابه ماهیت کمیتهای داده شده دارند. به این استاندارد، واحد یا یکا میگوییم. کمیتهای زیادی را در فیزیک میتوانیم اندازه بگیریم. از میان کمیتهای اندازهگیری شده در فیزیک، هفت کمیت، کمیت اصلی هستند. کمیت اصلی، کمیت فیزیکی مستقلی است که برحسب کمیتهای فیزیکی دیگر نوشته نمیشود.
از این کمیتها به عنوان ستونی برای کمیتهای فرعی استفاده میکنند. کمیتهای اصلی عبارت هستند از:
- جرم: به مقدار ماده موجود در هر جسم، ماده گفته میشود. هرچه مقدار ماده موجود در جسمی بیشتر باشد، جرم آن نیز بیشتر خواهد بود. وزن، نیرویی است که بر جرم جسم وارد میشود. در بیشتر مواقع به اشتباه از جرم و وزن به جای یکدیگر استفاده میکنیم. به این نکته توجه داشته باشید که مقدار عددی جرم مثبت است.
- طول: طول کمیتی است که به ما درازای هر جسم را میگوید. این ویژگی به دو ویژگی مساحت و حجم مربوط میشود.
- زمان: این ویژگی مربوط به جریان اتفاقهای مختلف در زندگی است و همواره افزایش مییابد. زمان نیز همانند جرم نمیتواند منفی باشد. زمان در مورد جریان اتفاقهای مختلف در کیهان صحبت میکند.
- جریان الکتریکی: جریان الکتریکی کمیت فیزیکی است که میتواند مثبت یا منفی باشد.
- دما: این کمیت مقدار گرمای موجود در جسم را اندازه میگیرد. گرما به حرکت ذرات داخل جسم مربوط میشود.
- مول: مول کمیت فیزیکی ثابتی است که تعداد مولکولهای داخل ماده را اندازه میگیرد.
- شدت روشنایی: شدت روشنایی، مانند دما، کمیتی برای اندازهگیری انرژی است. شدت روشنایی، مقدار انرژی الکترومغناطیسی ساطع شده از یک جسم را به صورت نور در واحد زمان اندازهگیری میکند.
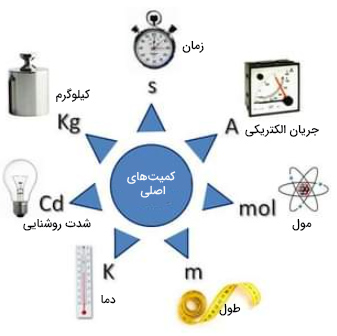
میدانیم هر یک از این کمیتها توسط واحدی مشخص بیان میشوند. برای بیان واحدهای اندازهگیری باید از سیستمی به نام سیستم یکاها استفاده کنیم. سیستم واحدها یا سیستم یکاها، مجموعهای از واحدها هستند که در آنها واحدهای مشخصی به عنوان واحدهای بنیادی یا اصلی انتخاب و واحدهای دیگر از واحدهای اصلی مشتق میشوند. به این سیستم، سیستم واحدهای مطلق نیز میگوییم. در بیشتر سیستمها، جرم، طول و زمان به عنوان کمیتهای اصلی در نظر گرفته میشوند. به واحدهای اندازهگیری کمیتهای اصلی، واحدهای اصلی میگوییم.
رایجترین دستگاهها برای واحدهای اندازهگیری عبارت هستند از:
- سیستم CGS: واحد اندازهگیری طول، جرم و زمان در دستگاه CGS به ترتیب برابر با سانتیمتر، گرم و ثانیه است.
- سیستم MKS یا دستگاه SI: واحد اندازهگیری طول، جرم و زمان در دستگاه CGS به ترتیب برابر با متر، کیلوگرم و ثانیه است.
- سیستم FPS: واحد اندازهگیری طول، جرم و زمان در دستگاه CGS به ترتیب برابر با فوت، پوند و ثانیه است.
سیستم SI
در سال ۱۹۶۰ میلادی، یازدهمین کنفرانس عمومی وزنها و مقیاسها، سیستم بینالمللی یکاها (International System of Units | SI) را معرفی کرد.
کمیتهای اصلی به همراه واحد اندازهگیری آنها در سیستم SI در جدول زیر آمده است.
| کمیت اصلی | واحد SI | نماد |
| طول | متر | m |
| جرم | کیلوگرم | kg |
| زمان | ثانیه | s |
| دما | کلوین | K |
| بار الکتریکی | آمپر | A |
| شدت روشنایی | کندلا (شمع) | cd |
| مقدار ماده | مول | mol |
علاوه بر واحدهای اصلی نوشته شده در جدول بالا، دو واحد مکمل دیگر نیز وجود دارند. واحد SI برای زاویه صفحهای برابر «رادیان» (Radian | rad) و برای زاویه فضایی برابر «استرادیان» (Streradian | sr) است.
| کمیت اصلی | واحد SI | نماد |
| زاویه مسطحه | رادیان | rad |
| زاویه فضایی | استرادیان | sr |
نوشتن واحدهای SI و نماد آنها
به هنگام نوشتن واحدهای SI و نماد هر واحد باید به نکتههای زیر توجه کنیم:
- تمام واحدها و نماد آنها باید با حروف کوچک نوشته شوند. به عنوان مثال، سانتیمتر به صورت cm، متر به صورت m مترمکعب به صورت نوشته میشوند.
- برخی واحدها از نام دانشمندان گرفته شدهاند. برای نوشتن نماد این واحدها از حروف بزرگ انگلیسی استفاده میشود. به عنوان مثال، نیوتن، واحد نیرو، به شکل N یا کلوین، واحد دما، به شکل K نوشته میشوند.
- پس از نماد نباید نقطه قرار بگیرد.
- همانطور که در بخش بعد خواهیم دید، واحدهای فرعی از واحدهای اصلی بهدست میآیند. واحدهای فرعی گاهی برابر حاصلضرب واحدهای اصلی یا گاهی برابر تقسیم آنها بر یکدیگر هستند. واحد اندازهگیری قرار گرفته در مخرج کسر باید با توان منفی نوشته شود. به عنوان مثال، واحد سرعت باید به جای به صورت نوشته شود.
- واحدهای اندازهگیری یا نماد آنها نباید به صورت جمع نوشته شوند. به عنوان مثال، ۵ نیوتن باید به صورت نوشته شود. نوشتن اشتباه است.
- بین عدد و واحد باید فاصله وجود داشته باشد.
مزیتهای سیستم SI چیست؟
مزیتهای استفاده از سیستم SI عبارت هستند از:
- بیان واحدها ساده است.
- در این سیستم برای هر کمیت فیزیک از یک واحد استفاده میشود.
- واحدهای بسیاری از کمیتهای فیزیکی از طریق روابط ساده و ابتدایی به یکدیگر مربوط میشوند. به عنوان مثال، یک آمپر برابر یک ولت تقسیم بر یک اهم است.
- از آنجا که این سیستم، سیستمی متری است، بین واحدهای کمیت یکسان، رابطهای اعشاری وجود دارد. بنابراین، هر کمیت کوچک یا بزرگ را میتوان برحسب توان ۱۰ بیان کرد. به عنوان مثال، یک کیلوگرم، برابر ۱۰۰۰ گرم یا گرم است.
- کمیتهای فیزیکی را میتوان برحسب پیشوندهای مناسب بیان کرد.
- ژول واحد اندازهگیری تمام شکلهای انرژی و واحد اندازهگیری کار است. از اینرو، این واحد اندازهگیری پلی بین واحدهای الکتریکی و مکانیکی خواهد بود. در نتیجه، سیستم SI سیستمی عقلانی است، زیرا برای یک کمیت فیزیکی از یک واحد استفاده میکند.
- سیستم SI،چارچوبی منطقی و بههمپیوسته را برای تمام اندازهگیریهای انجام شده در علم، فناوری و تجارت تشکیل میدهد.
- تمام واحدهای فرعی میتوانند از تقسیم و ضرب واحدهای مکمل و اصلی بهدست بیایند. برای انجام این کار، هیچ عامل عددی دیگری، همانند سیستم واحدهای دیگر، معرفی نمیشود. در نتیجه، سیستم SI سیستم یکپارچهای است که به صورت جهانی استفاده میشود.

یکی از مزیتهای استفاده از سیستم SI برای نوشتن واحد کمیتهای مختلف استفاده از پیشوندهای مناسب است. برخی از این پیشوندها در جدول زیر نوشته شدهاند.
| پیشوند | خلاصه | ضرب نمایی | معنی |
| گیگا | G | ۱۰۰۰۰۰۰۰۰۰ | |
| مگا | M | ۱۰۰۰۰۰۰ | |
| کیلو | k | ۱۰۰۰ | |
| هکتا | h | ۱۰۰ | |
| دکا | da | ۱۰ | |
| متر | m | ۱ | ۱ |
| دسی | d | ||
| سنتی | c | ||
| میلی | m | ||
| میکرو | |||
| نانو | n | ||
| پیکو | p |
کمیت فرعی چیست ؟
کمیتهای فرعی، مانند حجم، مساحت یا سرعت، به دو یا بیشتر از دو کمیت اصلی وابسته هستند. برای آشنایی بیشتر با کمیتهای اصلی و چگونگی ارتباط آنها با کمیتهای فرعی، به چند مثال زیر توجه کنید.
مثال اول کمیت فرعی
سرعت چه کمیتی است؟
پاسخ
کمیتهای اصلی عبارت هستند از:
- جرم
- طول
- مول
- زمان
- شدت روشنایی
- دما
- بار الکتریکی
سرعت به صورت تقسیم جابجایی جسم بر مدت زمان لازم برای انجام جابجایی تعریف میشود:
در رابطه بالا، سرعت از تقسیم دو کمیت اصلی بر یکدیگر بهدست آمده است. بنابراین، سرعت کمیتی فرعی است که با استفاده از کمیتهای اصلی طول و زمان بهدست آمده است. شاید از خود بپرسید واحد اندازهگیری سرعت چیست. در حالت کلی، برای آنکه بتوانیم واحد اندازهگیری کمیتهای فرعی را بهدست آوریم، گامهای زیر را طی میکنیم:
- فرمول کمیت فیزیکی موردنظر را مینویسیم.
- واحدهای همه کمیتها در سیستمی واحد را به شکل بنیادی یا استاندارد آنها جایگزین میکنیم.
- پس از سادهسازی، واحد کمیت موردنظر بهدست میآید.
فرمول سرعت در رابطه بالا نوشته شده است. واحدهای اندازهگیری جابجایی و زمان را در رابطه بالا قرار میدهیم. ماهیت جابجایی و طول یکسان و واحد هر کدام، متر و واحد زمان در سیستم SI برابر ثانیه است.
$$SI unit \of velocity = \frac { SI unit \of displacement} { SI unit \of time} \ SI unit \of velocity = \frac { m} { s} $$
در نتیجه، واحد سرعت برابر متر بر ثانیه یا است.
مثال دوم کمیت فرعی
شتاب چه کمیتی است؟ واحد اندازهگیری آن چیست؟
پاسخ
به تغییرات سرعت برحسب زمان، شتاب میگوییم. شتاب به صورت فرمولی به شکل زیر نوشته میشود:
در رابطه بالا، شتاب از تقسیم یک کمیت فرعی بر یک کمیت اصلی بهدست میآید. همانطور که در مثال قبل دیدیم، سرعت کمیتی فرعی است. شتاب نیز همانند سرعت به عنوان کمیت فرعی در نظر گرفته میشود. برای بهدست آوردن واحد شتاب، همانند مثال قبل عمل میکنیم:
$$SI unit \of acceleration = \frac { SI unit \of velocity} { SI unit \of time} \ SI unit \of acceleration= \frac { \frac { m} { s} } { s} \ SI unit \of acceleration = \frac { m} { s^ 2} $$
در نتیجه، واحد شتاب برابر متر بر مجذور ثانیه یا است.
مثال سوم کمیت فرعی
نیرو چه کمیتی است؟ واحد اندازهگیری آن چیست؟
پاسخ
همانطور که در بخشهای بعدی خواهیم دید نیرو کمیتی فرعی و برداری است. کمیتهای برداری اندازه و جهت دارند. نیرو به صورت حاصلضرب جرم جسم در شتاب حرکت آن تعریف میشود:
در رابطه بالا، جرم، کمیت اصلی و شتاب کمیت فرعی است که واحد آن را در مثال دو بهدست آوردیم. واحد اندازهگیری شتاب برابر متر بر مجذور ثانیه و واحد اندازهگیری جرم برابر کیلوگرم است.
$$SI unit \of force = ({ SI unit \of mass)} \times ( { SI unit \of acceleration}) \ SI unit \of force= kg \times \frac {m}{ s^2} \ SI unit \of force= \frac {kg. m}{ s^2} $$
میدانیم واحد نیرو در سیستم SI برابر نیوتن است، بنابراین یک نیوتن برابر خواهد بود.
مثال چهارم کمیت فرعی
ضریب اصطکاک جنبشی چه کمیتی است؟ واحد اندازهگیری آن چیست؟
پاسخ
نیروی اصطکاک جنبشی به صورت حاصلضرب ضریبی به نام ضریب اصطکاک جنبشی در نیروی عمودی سطح تعریف میشود. نیروی عمودی سطح نیرویی است که از طرف سطحی که جسم روی آن قرار دارد به سمت بالا و عمود بر سطح بر جسم وارد میشود.
برای آنکه بتوانیم واحد ضریب اصطکاک جنبشی را بهدست آوریم، رابطه بالا را برحسب آن مرتب میکنیم:
و نیرو و کمیت فرعی هستند که واحد آنها را در مثال قبل بهدست آوردیم. از آنجا که واحد اندازهگیری نیرو در سیستم SI نیوتن و برای تمام نیروها یکسان است، ضریب اصطکاک جنبشی کمیتی بدون واحد و فرعی خواهد بود.
در مطالب بالا در مورد واحدهای کمیتهای فیزیکی صحبت کردیم و چند مثال در مورد چگونگی بهدست آوردن واحدهای کمیتهای فرعی، مانند سرعت، حل کردیم. در ادامه، در مورد تحلیل دیمانسیون یا ابعادی کمیتهای فیزیکی صحبت میکنیم.
دیمانسیون کمیت های فیزیکی
دیمانسیون هر کمیت فیزیکی، وابستگی کمیتهای فرعی را به کمیتهای اصلی با استفاده از حاصلضرب نمادها نشان میدهد. توان نمادهای استفاده شده ممکن است صفر، مثبت یا منفی باشد. در مطالب بالا واحدهای کمیتهای اصلی و نماد هر واحد را نشان دادیم. جدول زیر، کمیتهای اصلی و نمادهای استفاده شده برای هر کمیت در دیمانسیون را نشان میدهد. به عنوان مثال، اندازهگیری طول، دیمانسیون L یا و اندازهگیری جرم، دیمانسیون M یا دارند.
| کمیت اصلی | نماد استفاده شده در دیمانسیون یا بعد |
| طول | L |
| جرم | M |
| زمان | T |
| جریان الکتریکی | I |
| دمای ترمودینامیکی | |
| مقدار ماده | N |
| شدت روشنایی | J |
فیزیکدانها اغلب برای نشان دادن دیمانسیون کمیتهای فیزیکی از براکت استفاده میکنند. به عنوان مثال، اگر r شعاع استوانه و h ارتفاع آن باشد، دیمانسیون شعاع و ارتفاع به صورت زیر نوشته میشوند:
دو رابطه بالا به ما نشان میدهند که دیمانسیون شعاع و ارتفاع طول یا L هستند. به طور مشابه، دیمانسیون مساحت و حجم استوانه به صورت زیر نوشته میشوند:
زیرا واحد اندازهگیری مساحت و حجم به ترتیب مترمربع و مترمکعب هستند. آیا میدانید دیمانسیون چگالی چیست؟ چگالی با استفاده از رابطه زیر بهدست میآید:
در نتیجه، دیمانسیون چگالی برابر دیمانسیون جرم تقسیم بر دیمانسیون حجم و برابر است.
پس از پاسخ به پرسش کمیت چیست، در مورد کمیتهای اصلی و فرعی و تفاوت آنها با یکدیگر صحبت کردیم. هر کمیت اصلی یا فرعی ممکن است بردار باشد یا عدد (اسکالر). در ادامه، در مورد کمیتهای برداری و اسکالر صحبت میکنیم و ویژگیهای مهم کمیتهای برداری را توضیح میدهیم.
کمیت های برداری و اسکالر چیست ؟
تا اینجا میدانیم کمیت چیست. در بخشهای قبل در مورد کمیتهای اصلی و فرعی در فیزیک صحبت کردیم. در این بخش، در مورد کمیتهای نردهای و برداری صحبت میکنیم. کمیت نردهای یا اسکالر کمیتی است که تنها اندازه دارد، اما کمیت برداری علاوه بر اندازه، جهت نیز دارد. شاید از خود بپرسید منظور از اندازه چیست.
اندازه، بزرگی یا مقدار کمیتهای برداری یا نردهای را نشان میدهد. آیا میدانیم منظور از جهت در کمیتهای برداری چیست؟ جهت در کمیتهای برداری به معنای اشاره بردار به جهتهای جغرافیایی است. به عنوان مثال، جهت کمیت برداری ممکن است به سمت شمال، جنوب، شرق یا غرب باشد.
پرسش: آیا مسافت کمیتی برداری است یا کمیتی نردهای؟
پاسخ: مسافت، کمیتی نردهای یا اسکالر است. هنگامی که در حرکت روی خط راست در مورد مسافت طی شده توسط اجسام مختلف صحبت میکنیم، در مورد جهت حرکت آنها هیچ اطلاعی نداریم. بلکه، تنها میدانیم جسم به اندازه متر حرکت کرده است.
اگر بگوییم جسمی به اندازه ۳ متر به سمت راست حرکت کرده است، در مورد مسافت طی شدهای صحبت میکنیم که جهت نیز دارد و آن را جابجایی مینامیم. بنابراین، جابجایی کمیتی برداری است. در جابجایی اجسام، نهتنها اندازه، بلکه جهت حرکت نیز مهم است.
پرسش: آیا تندی کمیتی برداری است یا کمیتی نردهای؟
پاسخ: هنگامی که میگوییم اتوبوسی با تندی ۶۰ کیلومتر بر ساعت حرکت میکند، آیا در مورد کمیتی برداری صحبت میکنیم یا کمیتی اسکالر؟ از آنجا که در مورد جهت حرکت اتوبوس هیچ صحبتی نکردهایم، تندی کمیتی نردهای خواهد بود. تندی برابر نسبت مسافت طی شده بر مدت زمان لازم برای طی کردن آن مسافت است. از آنجا که مسافت نیز کمیتی نردهای است، تندی نیز به عنوان کمیتی نردهای در فیزیک تعریف میشود.
اگر بگوییم اتومبیلی با سرعت ۶۰ کیلومتر بر ساعت به سمت شرق حرکت کند، در مورد کمیت برداری صحبت میکنیم، زیرا در این حالت اندازه و جهت حرکت را با یکدیگر داریم. بنابراین، سرعت کمیتی برداری است.

پرسش: آیا نیرو کمیتی برداری است یا کمیتی نردهای؟
پاسخ: فرض کنیم جسمی روی میز قرار دارد و فردی نیرویی برابر ۵۰ نیوتن بر آن وارد میکند. جسم پس از اعمال نیرو از طرف فرد به اندازه ۵۰ متر به سمت راست جابجا میشود. در واقع جسم به اندازه ۵۰ متر در راستای اعمال نیرو جابجا شده است. بنابراین، نتیجه میگیریم نیروی ۵۰ نیوتنی به سمت راست بر جسم وارد شده است. از اینرو، نیرو کمیتی برداری است و اندازه و جهت دارد. نیرو در هر جهتی میتواند بر جسم وارد شود.
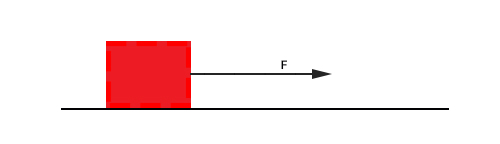
پرسش: آیا جرم کمیتی برداری است یا کمیتی نردهای؟
پاسخ: برای پاسخ به این پرسش از خود بپرسید آیا میتوان برای جرم جهت در نظر گرفت. آیا عبارت «جسمی به جرم ۶ کیلوگرم در جهت شمال» صحیح است؟ خیر، نمیتوانیم برای جرم، جهت در نظر بگیریم. بنابراین، جرم کمیتی اسکالر است و تنها اندازه یا بزرگی دارد.
پرسش: آیا دما کمیتی برداری است یا کمیتی نردهای؟
پاسخ: برای پاسخ به این پرسش از خود بپرسید آیا میتوان برای دما جهت در نظر گرفت. آیا عبارت «جسمی با دما ۱۰۰ درجه سلسیوس در جهت شرق» صحیح است؟ خیر، نمیتوانیم برای دما، جهت در نظر بگیریم. بنابراین، دما کمیتی نردهای است و تنها اندازه یا بزرگی دارد.

پرسش: آیا شتاب، کمیتی برداری است یا کمیتی نردهای؟
پاسخ: به نرخ تغییرات سرعت برحسب زمان، شتاب گفته میشود. در مطالب بالا فهمیدیم که سرعت کمیتی برداری است، بنابراین شتاب را نیز میتوانیم به عنوان کمیتی برداری در نظر بگیریم. اتومبیل هنگام شروع حرکت میتواند در یکی از جهتهای جغرافیایی شتاب بگیرد و سرعت خود را افزایش دهد.
پرسش: آیا حجم، کمیتی برداری است یا کمیتی نردهای؟
پاسخ: برای پاسخ به این پرسش از خود بپرسید آیا میتوان برای حجم جهت در نظر گرفت. آیا عبارت «جسمی با حجم یک متر مکعب در جهت جنوب» صحیح است؟ خیر، نمیتوانیم برای حجم، جهت در نظر بگیریم. بنابراین، حجم کمیتی نردهای است و تنها اندازه یا بزرگی دارد.
تا اینجا میدانیم چگونه کمیتهای برداری و اسکالر را تشخیص دهیم. اگر برای کمیتی تنها بتوانیم اندازه تعیین کنیم، آن کمیت کمیتی نردهای است. در مقابل، اگر بتوانیم علاوه بر اندازه، جهت نیز به کمیتی نسبت دهیم، آن کمیت، کمیتی برداری خواهد بود. راههای مختلفی برای توصیف کمیتی برداری وجود دارند. به عنوان مثال، ممکن است بگوییم نیرویی برابر ۳۰ نیوتن با زاویه ۳۰ درجه نسبت به افق بر جسمی وارد میشود. در حالت دیگر، بردار را میتوانیم به صورت تصویری نمایش دهیم.
بردارها را میتوان براساس مولفههای آنها نیز نوشت. برای نوشتن بردارها براساس مولفههای یکه، باید ابتدا بردار را در مختصات دو یا سهبعدی رسم کنیم. سپس آن را در جهتهای در دو بعد یا در سه بعد تجزیه کرد. در ادامه، در مورد تجزیه بردار صحبت میکنیم.
نکته: کمیتهای نردهای را میتوان با یکدیگر جمع، از یکدیگر کم، با یکدیگر ضرب و بر یکدیگر تقسیم کرد. در واقع تمام کارهایی که در حالت معمولی با اعداد انجام میدهیم، با کمیتهای نردهای نیز میتوان انجام داد.
نکته: کمیتهای برداری را نیز میتوان با یکدیگر جمع یا از یکدیگر کم کرد. دو بردار را میتوان با هم ضرب کرد، اما ضرب آنها همانند ضرب دو کمیت نردهای در یکدیگر نیست. بردارها به دو صورت با یکدیگر ضرب میشوند:
- ضرب داخلی: حاصل این ضرب، عدد است.
- ضرب خارجی: حاصل این ضرب کمیتی برداری است.
در ادامه، در مورد جمع و ضرب بردارها توضیح میدهیم.
جمع کمیت های برداری
در مطالب بالا گفتیم، کمیتهای برداری اندازه و جهت دارند. بنابراین، بردار را میتوان توسط پیکانی با جهت مشخص نمایش دهیم. طول پیکان، بزرگی یا اندازه بردار و جهت پیکان، جهت بردار را نشان میدهد. هرچه، اندازه برداری بزرگتر باشد، طول پیکان نیز بزرگتر خواهد بود. به عنوان مثال، به پیکان نشان داده شده در زیر توجه کنید. جهت این پیکان به سمت چپ است. 
جمع بردارها یا برایند بردارها در فیزیک از اهمیت ویژهای برخوردار است. به عنوان مثال، اگر نیروهایی در جهتهای مختلف بر جسمی وارد شوند، برای آنکه بدانیم جسم در اثر وارد شدن این نیروها در چه راستایی حرکت خواهد کرد، باید برایند نیروهای وارد شده بر آن را بهدست آوریم. بهترین راه برای جمع بردارها با یکدیگر استفاده از روش تصویری است. قبل از توضیح این روش باید بدانیم که بردارها ممکن است در دو حالت نسبت به یکدیگر قرار داشته باشند:
- بردارها در یک راستا اما در جهتهای یکسان یا مخالف با یکدیگر باشند.
- بردارها همراستا نباشند.
جمع بردارهای هم راستا
جهت بردارهای همراستا ممکن است یکسان یا مخالف باشد. ابتدا، بردارهای همجهت را در نظر میگیریم. توجه به این نکته مهم است که مقدار بردار میتواند منفی یا مثبت باشد. مثبت یا منفی بودن بردار به جهت انتخابی مثبت در حل مسائل فیزیکی بستگی دارد. در حالت کلی، جهتهای بالا (شمال) و راست (شرق) را مثبت در نظر میگیریم. اگر برداری خلاف این جهتهای قراردادی مثبت باشد، منفی در نظر گرفته میشود.
جمع برداری برای بردارهای همجهت
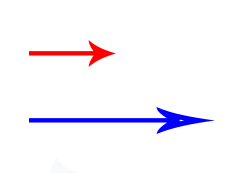
در نخستین حالت فرض میکنیم دو بردارِ همراستا در جهت یکسانی قرار دارند. هنگامی که جهت بردارها یکسان باشد، آنها را به صورت جبری با یکدیگر جمع میکنیم. حاصلِ جمع، برداری همراستا و همجهت با بردارهای اولیه با طولی برابر حاصل جمع طولهای هر یک از بردارهای اولیه است. به تصویر نشان داده شده در زیر توجه کنید. طول بردارهای قرمز و آبی به ترتیب برابر ۴ و ۹ سانتیمتر است. این دو بردار، همراستا و همجهت هستند. بنابراین، به راحتی میتوانیم آنها را با یکدیگر جمع کنیم. حاصل جمع این دو بردار، برداری به سمت راست به طول ۱۳ سانتیمتر است.
در حالت دوم، ممکن است دو بردار همراستا، اما در دو جهت مخالف قرار داشته باشند. نخستین کاری که در این حالت باید انجام دهیم آن است که جهتی را به صورت قراردادی به عنوان جهت مثبت انتخاب کنیم. از آنجا که دو بردار در راستای افقی قرار دارند، جهت راست را به عنوان جهت مثبت انتخاب میکنیم. بردار قرمزرنگ در جهت مثبت قرار دارد، بنابراین اندازه آن برابر است. در مقابل، جهت بردار آبیرنگ به سمت چپ و اندازه آن منفی و برابر خواهد بود.
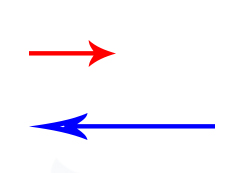
برایند این دو بردار برابر است با:
بنابراین، بردار حاصل، برداری به طول ۵ سانتیمتر و در جهت چپ (منفی) است. توجه به این نکته مهم است که بردار آبیرنگ برداری بزرگتر و در جهت منفی قرار دارد. بنابراین، قبل از جمع دو بردار با یکدیگر انتظار داریم که جهت بردار برایند در راستای بردار آبیرنگ باشد. اگر تعداد بردارهای همراستا سه یا بیشتر از سه باشد، باز هم راهحل مشابهی را برای بهدست آوردن برایند آنها طی میکنیم.
مثال ۱
برایند سه بردار نشان داده شده در تصویر زیر را بهدست آورید.
| رنگ بردار | طول بردار |
| قرمز | ۴ سانتیمتر |
| آبی | ۹ سانتیمتر |
| بنفش | ۶ سانتیمتر |
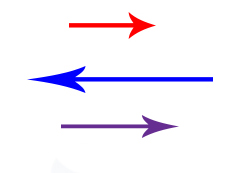
پاسخ
تا اینجا جمع برداری دو بردار هم راستا را بررسی کردیم. در این مثال جمع سه بردار را با یکدیگر بررسی میکنیم. همانطور که در تصویر بالا دیده میشود سه بردار در جهت یکسانی قرار نگرفتهاند، بنابراین نخستین کاری که در این حالت باید انجام دهیم آن است که جهتی را به صورت قررادادی به عنوان جهت مثبت انتخاب کنیم. از آنجا که سه بردار در راستای افقی قرار دارند، جهت راست را به عنوان جهت مثبت انتخاب میکنیم. بنابراین:
- بردار قرمزرنگ در جهت مثبت قرار دارد، بنابراین اندازه آن برابر است.
- جهت بردار آبیرنگ به سمت چپ و اندازه آن منفی و برابر خواهد بود.
- بردار بنفشرنگ در جهت مثبت قرار دارد، بنابراین اندازه آن برابر است.
در نتیجه، برایند این سه بردار برابر است با:
بنابراین، بردار حاصل، برداری به طول یک سانتیمتر و در جهت راست (مثبت) است. توجه به این نکته مهم است که دو بردار قرمز و بنفش به ترتیب با طولهای ۴ و ۶ سانتیمتر در جهت مثبت قرار دارند. بنابراین، قبل از جمع سه بردار با یکدیگر انتظار داریم که جهت بردار برایند در راستای دو بردار قرمز و بنفش باشد.
مثال ۲
جهت و طول شش بردار همراستا در جدول زیر نوشته شده است. برایند بردارها را بهدست آورید.
| نام بردار | طول بردار | جهت بردار |
| A | ۴ سانتیمتر | راست |
| B | ۹ سانتیمتر | چپ |
| C | ۶ سانتیمتر | راست |
| D | ۱۰ سانتیمتر | راست |
| E | یک سانتیمتر | چپ |
| F | ۸ سانتیمتر | چپ |
پاسخ
در این مثال جمع شش بردار را با یکدیگر بررسی میکنیم. همانطور که در جدول بالا دیده میشود شش بردار در جهت یکسانی قرار نگرفتهاند، بنابراین نخستین کاری که در این حالت باید انجام دهیم آن است که جهتی را به صورت قراردادی به عنوان جهت مثبت انتخاب کنیم. از آنجا که شش بردار در راستای افقی قرار دارند، جهت راست را به عنوان جهت مثبت انتخاب میکنیم. بنابراین، بردارهای A و C و D مثبت و بردارهای B و E و F منفی هستند. در نتیجه، برایند بردارها برابر است با:
مثال ۳
جهت و طول سه بردار همراستا در جدول زیر نوشته شده است. برایند بردارها را بهدست آورید.
| نام بردار | طول بردار | جهت بردار |
| A | ۴ سانتیمتر | بالا |
| B | ۹ سانتیمتر | پایین |
| C | ۶ سانتیمتر | پایین |
پاسخ
در این مثال جمع سه بردار را با یکدیگر بررسی میکنیم. همانطور که در جدول بالا دیده میشود سه بردار در جهت یکسانی قرار نگرفتهاند، بنابراین نخستین کاری که در این حالت باید انجام دهیم آن است که جهتی را به صورت قراردادی به عنوان جهت مثبت انتخاب کنیم. از آنجا که سه بردار در راستای عمودی قرار دارند، جهت بالا را به عنوان جهت مثبت انتخاب میکنیم. بنابراین، بردار A مثبت و بردارهای B و C منفی هستند. در نتیجه، برایند بردارها برابر است با:
جمع بردارهای غیر هم راستا
در حالت کلی، بردارها در راستاهای مختلفی قرار دارند. به عنوان مثال، نیروهای وارد شده بر جسم میتوانند در راستاهای متفاوتی قرار داشته باشند. چند روش برای بهدست آوردن برایند بردارهای غیرهمراستا وجود دارند که در ادامه هر یک از آنها را با حل مثال بررسی میکنیم.
روش ۱
در مطالب بالا گفتیم که بردار توسط پیکان نشان داده میشود، بنابراین هر برداری نقطه آغاز و نقطه پایان دارد.
از آنجا که بردارها اندازه و جهت دارند، آنها را با پیکان نشان میدهیم و طول پیکان بیانگر طول بردار است. در روش اول، برایند بردارها را به صورت تصویری و با رسم دقیق آنها روی کاغذ بهدست میآوریم. هنگام رسم بردارها روی کاغذ باید طول بردارها و زاویه آنها نسبت به یکدیگر را با دقت بالایی رسم کنیم. فرض کنید جمع دو بردار A و B نشان داده در تصویر زیر را میخواهیم به صورت تصویری بهدست آوریم.
برای جمع این دو بردار کافی است که یکی از بردارها را در مکان خود ثابت نگه داریم و نقطه آغاز بردار دوم را روی نقطه انتهای بردار اول قرار دهیم. به عنوان مثال، برای دو بردار نشان داده شده در تصویر بالا، بردار A را در مکان خود ثابت نگه میداریم و ابتدای بردار B را روی نقطه انتهایی بردار A قرار میدهیم. توجه به این نکته مهم است که ترتیب اتصال بردارها به یکدیگر مهم نیست. به بیان دیگر برابر است.
برای بهدست آوردن بردار برایند دو بردار A و B نقطه آغاز بردار A را به نقطه انتهایی بردار B به صورت نشان داده شده در تصویر زیر وصل میکنیم.
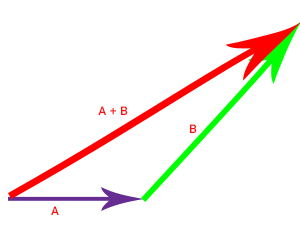
پرسش: بردار برایند را با رسم شکل بهدست آورید.
پاسخ: به تفریق دو بردار نیز گفته میشود که با رسم برداری بسیار ساده بهدست میآید. قبل از حل این پرسش به این نکته توجه داشته باشید که اگر علامت منفی در برداری ضرب شود، جهت آن بردار برعکس خواهد شد. به عنوان مثال، اگر جهت برداری به سمت راست باشد، پس از ضرب کردن آن در منفی یک، جهت بردار به سمت چپ میشود. در این پرسش، بردار در منفی ضرب شده است، بنابراین جهت آن به صورت نشان داده شده در تصویر زیر تغییر میکند.
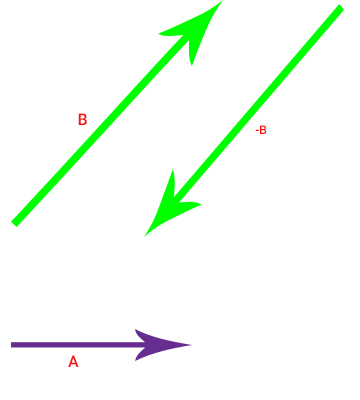
همانطور که در تصویر بالا دیده میشود، بردار B به اندازه ۱۸۰ درجه چرخیده، اما طول آن هیچ تغییری نکرده است. در ادامه، همانند جمع دو بردار عمل میکنیم. در واقع با بهدست آوردن بردار ، عبارت را میتوان به صورت نوشت. برای جمع این دو بردار، ابتدای بردار را به انتهای بردار وصل میکنیم.
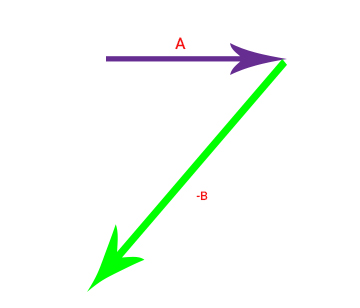
برای بهدست آوردن بردار برایند بردارهای و ، نقطه آغاز بردار A را به نقطه انتهایی بردار به صورت نشان داده شده در تصویر زیر وصل میکنیم.
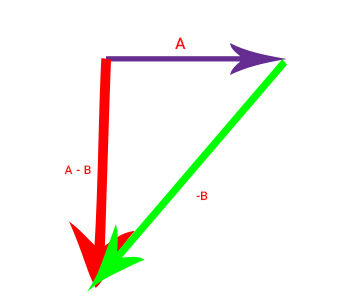
اگر تعداد بردارها بیشتر از دو باشند، برایند آنها را چگونه بهدست میآوریم؟ اگر تعداد بردارهای داده شده سه یا بیشتر از سه بردار باشند، برای جمع آنها به صورت زیر عمل میکنیم:
- یکی از بردارها را به عنوان اولین بردار و بردار ثابت در نظر میگیریم.
- ابتدای دومین بردار را به انتهای اولین بردار متصل میکنیم.
- ابتدای سومین بردار را به انتهای دومین بردار متصل میکنیم.
- این کار را تا آخرین بردار انجام میدهیم.
- پس از اتصال تمام بردارها به یکدیگر، برای بهدست آوردن بردار برایند ابتدای نخستین بردار را به انتهای آخرین بردار متصل میکنیم.
تصویر زیر را در نظر بگیرید. در این تصویر چگونگی بهدست آوردن برایند چهار بردار نشان داده شده است. همانطور که مشاهده میکنید بردار A به عنوان اولین بردار در نظر گرفته شده است. در ادامه، نقطه ابتدای بردار B به نقطه انتهای بردار A وصل و این کار تا آخرین بردار، یعنی بردار D، تکرار میشود.
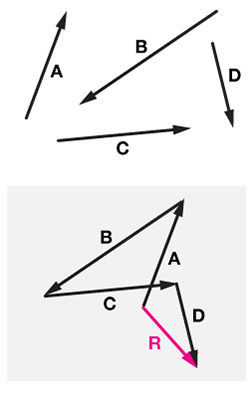
هنگام بهدست آوردن بردار حاصل، به نکتههای زیر دقت داشته باشید:
- طول بردار حاصل را تنها در صورتی میتوانید به طور دقیق با خطکش اندازه بگیرید که طول تمام بردارها و زاویه بین آنها را به طور دقیق رسم کرده باشید. همچنین، برای بهدست آوردن جهت دقیق بردار برایند میتوانید زاویه آن را با خط افقی و عمودی با استفاده از نقاله اندازه بگیرید.
- اگر طول و زاویه بین بردارها را به طور دقیق رسم نکرده باشید، برای بهدست آوردن اندازه بردار برایند باید از مثلثات استفاده کنید. برای بهدست آوردن برایند سه و بیشتر از سه بردار با یکدیگر بهتر است ابتدا دو بردار را انتخاب و برایند آنها را بهدست آورید. سپس، بردار برایند دو بردار انتخاب شده را با بردار سوم جمع و این کار را تا آخرین بردار ادامه دهید.
- طول و جهت دو مشخصه اصلی در کمیتهای برداری هستند. بنابراین، باید بتوانیم طول و جهت بردار برایند را با دقت بالایی بهدست آوریم.
روش ۲
در این روش، بردارها را براساس مولفهها آنها مینویسیم و سپس مولفه به مولفه با یکدیگر جمع یا تفریق میکنیم. برای آنکه بتوانیم برداری را برحسب مولفههای آن در جهتهای مختلف بنویسیم باید تصویر بردار را در راستای محورهای مختصات بهدست آوریم یا به بیان دیگر، بردار را به مولفههای آن تجزیه کنیم.
تجزیه بردار در دو بعد
بردارها، یکبعدی، دوبعدی یا سهبعدی هستند. تجزیه بردارهای یکبعدی بسیار راحت است. بردارهای یکبعدی یا در راستای افقی قرار دارند یا در راستای عمودی. راستای افقی را و راستای عمودی را مینامیم. اگر بردار A به طول ۴ سانتیمتر در راستای مثبت محور قرار داشته باشد، این بردار به صورت مولفهای به صورت زیر نوشته میشود:
به احتمال زیاد از خود پرسیدهاید چیست. برداری با اندازه واحد در راستای محور است که به آن بردار یکه در راستای محور نیز گفته میشود. به همین ترتیب، بردار واحد یا یکه در راستای محور y را به شکل مینویسیم. بردار A، برابر چهار بردار یکه است. اگر بردار B به طول ۵ سانتیمتر در راستای منفی محور y قرار داشته باشد، این بردار به صورت مولفهای به صورت زیر نوشته میشود:
تا اینجا فهمیدیم بردارها در فضای یکبعدی چگونه برحسب مولفههایشان نوشته میشوند، در ادامه، تجزیه بردار را در فضای دوبعدی بررسی میکنیم. برای تجزیه کمیت برداری در فضای دوبعدی به دو پارامتر نیاز داریم:
- طول بردار
- زاویه بردار با محور افقی یا محور عمودی
برداری به طول ۳ را در نظر بگیرید که با محور زاویه ۳۰ درجه میسازد. برای تجزیه این بردار، ابتدا نقطه آغاز بردار را روی مبدأ مختصات و تقاطع محورهای و قرار میدهیم.
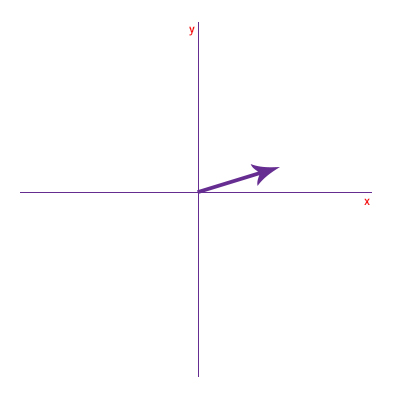
سپس از انتهای بردار دو خط موازی محورهای و رسم میکنیم.
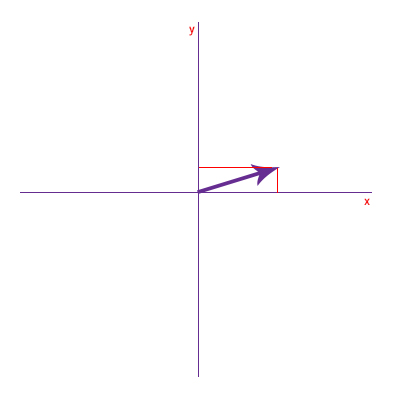
محل تقاطع خطهای موازی رسم شده را با محورهای و مشخص و دو بردار از مبدأ مختصات، به محل تقاطع رسم میکنیم به گونهای که مبدأ مختصات، نقطه ابتدای هر بردار و محل تقاطع، نقطه انتهای هر یک از این دو بردار باشد. بردارهای رسم شده روی محورهای و را به ترتیب ۱ و ۲ مینامیم.

مولفه بردار مادر یعنی بردار شماره یک برابر است با:
به طور مشابه، مولفه بردار مادر یعنی بردار شماره دو برابر است با:
در نتیجه، بردار r برحسب مولفههایش به صورت زیر نوشته میشود:
مثال ۱
بردار A با طول ۴ واحد در تصویر زیر نشان داده شده است. این بردار را برحسب مولفههایش در راستای محورهای و بنویسید. زاویه این بردار با راستای مثبت محور برابر ۱۳۵ درجه است.

پاسخ
برای تجزیه این بردار به مولفههای سازندهاش در راستای دو محور، ابتدا زاویه آن را با جهت منفی محور افقی بهدست میآوریم. از آنجا که زاویه این بردار با جهت مثبت محور برابر ۱۳۵ درجه است، زاویه آن با جهت منفی محور برابر است با:
سپس از انتهای بردار دو خط موازی محورهای و رسم میکنیم.
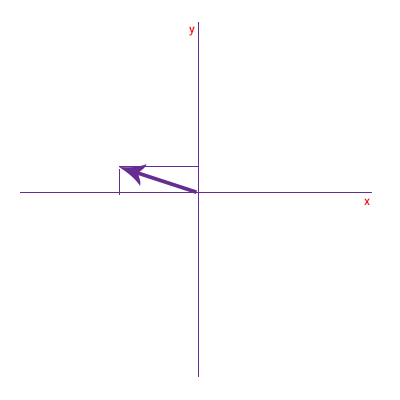
در ادامه، محل تقاطع خطهای موازی رسم شده را با محورهای و مشخص و دو بردار از مبدأ مختصات به محل تقاطع رسم میکنیم به گونهای که مبدأ مختصات، نقطه ابتدای هر بردار و محل تقاطع، نقطه انتهای هر یک از این دو بردار باشد. بردارهای رسم شده روی محورهای و را به ترتیب و مینامیم. به این نکته توجه داشته باشید که در جهت منفی محور قرار دارد. مولفه برابر است با:
به طور مشابه، مولفه برابر است با:
در نتیجه، بردار A برحسب مولفههایش به صورت زیر نوشته میشود:
مثال ۲
بردار B با طول ۲ واحد در تصویر زیر نشان داده شده است. این بردار را برحسب مولفههایش در راستای محورهای و بنویسید. زاویه این بردار با راستای مثبت محور برابر ۴۰ درجه است.
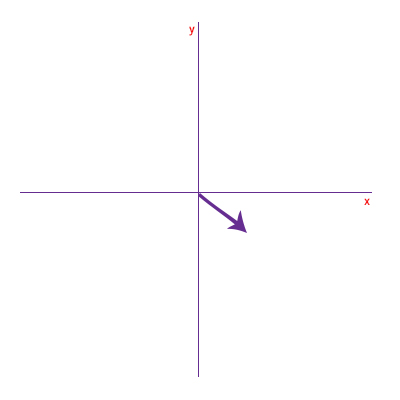
پاسخ
زاویه این بردار با جهت مثبت محور برابر ۴۰ درجه است. از انتهای بردار دو خط موازی محورهای و رسم میکنیم. در ادامه، محل تقاطع خطهای موازی رسم شده را با محورهای و مشخص و دو بردار از مبدأ مختصات به محل تقاطع رسم میکنیم به گونهای که مبدأ مختصات، نقطه ابتدای هر بردار و محل تقاطع، نقطه انتهای هر یک از این دو بردار باشد. بردارهای رسم شده روی محورهای و را به ترتیب و مینامیم. به این نکته توجه داشته باشید که در جهت منفی محور قرار دارد. مولفه برابر است با:
به طور مشابه، مولفه برابر است با:
در نتیجه، بردار A برحسب مولفههایش به صورت زیر نوشته میشود:
مثال ۳
بردار C با طول ۲ واحد در تصویر زیر نشان داده شده است. این بردار را برحسب مولفههایش در راستای محورهای و بنویسید. زاویه این بردار با راستای منفی محور برابر ۴۰ درجه است.
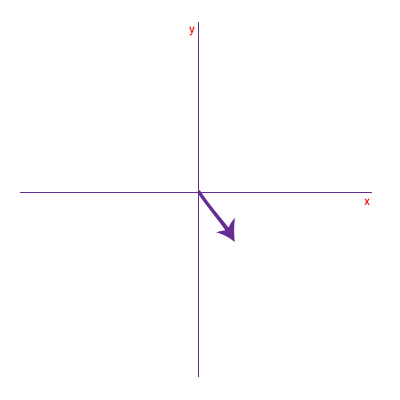
پاسخ
در این مثال، زاویه بردار C با جهت منفی محور داده شده و برابر ۴۰ درجه است. برای تجزیه این بردار به مولفههای سازندهاش در راستای دو محور، همانند دو مثال قبل عمل میکنیم. از انتهای بردار C دو خط، موازی محورهای و رسم میکنیم. در ادامه، محل تقاطع خطهای موازی رسم شده را با محورهای و مشخص و دو بردار از مبدأ مختصات به محل تقاطع رسم میکنیم به گونهای که مبدأ مختصات، نقطه ابتدای هر بردار و محل تقاطع، نقطه انتهای هر یک از این دو بردار باشد.
بردارهای رسم شده روی محورهای و را به ترتیب و مینامیم. به این نکته توجه داشته باشید که در جهت منفی محور قرار دارد. مولفه برابر است با:
به طور مشابه، مولفه برابر است با:
در نتیجه، بردار C برحسب مولفههایش به صورت زیر نوشته میشود:
تا اینجا میدانیم بردارها را چگونه در دو بعد تجزیه کنیم. در ادامه و با استفاده از تجزیه بردارها در دو بعد، برایند آنها را بهدست میآوریم. این قسمت را با حل مثالی ساده توضیح میدهیم.
مثال ۴
دو بردار A (بنفشرنگ) و B (قرمزرنگ) با طول دو واحد به ترتیب با جهت مثبت و منفی محور زاویه ۴۵ و ۳۰ درجه ساختهاند. اندازه و جهت برایند این دو بردار را بهدست آورید.
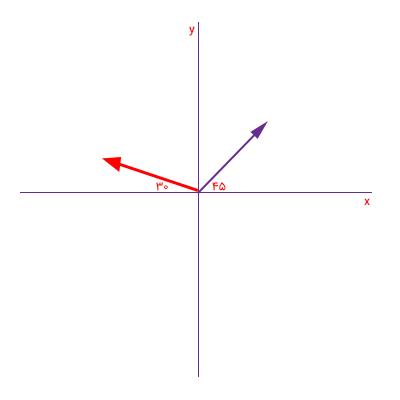
پاسخ
بردار A برحسب مولفههایش به صورت زیر نوشته میشود:
بردار B برحسب مولفههایش به صورت زیر نوشته میشود:
بردارهای A و B را به مولفههایشان تجزیه کردیم. برای بهدست آوردن بردار برایند، تنها کافی است که مولفههای متناظر رو دو به دو با یکدیگر جمع کنیم.
مولفههای و بردار برایند را بهدست آوردیم. برای بهدست آوردن جهت آن، زاویه آن با جهت مثبت محور را بهدست میآوریم. برای انجام این کار از رابطه زیر استفاده میکنیم:
مولفههای و بردار R را در رابطه بالا قرار میدهیم:
$$\tan \theta = \frac {\sqrt {2} + \sqrt {3} } { \sqrt {2} - 1} \ $$
مثال ۵
سه بردار A و B و C با طول دو واحد در تصویر زیر نشان داده شدهاند:
- بردار A با جهت مثبت محور زاویه ۴۵ درجه میسازد.
- بردار B با جهت منفی محور زاویه ۳۰ درجه میسازد.
- بردار C با جهت مثبت محور زاویه ۶۰ درجه میسازد.
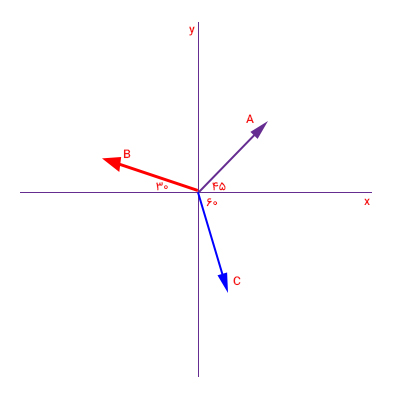
پاسخ
بردار A برحسب مولفههایش به صورت زیر نوشته میشود:
بردار B برحسب مولفههایش به صورت زیر نوشته میشود:
بردار C برحسب مولفههایش به صورت زیر نوشته میشود:
بردارهای A و B و C را به مولفههایشان تجزیه کردیم. برای بهدست آوردن بردار برایند، تنها کافی است که مولفههای متناظر رو با یکدیگر جمع کنیم.
مولفههای و بردار برایند را بهدست آوردیم. برای بهدست آوردن جهت آن، زاویه آن با جهت مثبت محور را بهدست میآوریم. برای انجام این کار از رابطه زیر استفاده میکنیم:
مولفههای و بردار R را در رابطه بالا قرار میدهیم:
$$\tan \theta = \frac {\sqrt {2} - \sqrt {3} + 1} { \sqrt {2} + 1 + \sqrt { 3 }} \ $$
مثال ۶
جسمی به جرم یک کیلوگرم توسط دو طناب به صورت نشان داده شده در تصویر زیر از سقف آویزان شده است. نیروی کشش در طنابهای شماره یک و دو را بهدست آورید.
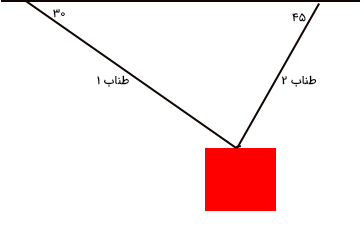
پاسخ
در مثالهای بالا با تجزیه کمیتهای برداری آشنا شدیم و برایند آنها را با استفاده از تجزیه بردارها بهدست آوردیم. در این مثال، از تجزیه بردار برای بهدست آوردن نیروهای وارد شده بر جسم استفاده میکنیم. در این مثال، جسمی توسط طناب از سقف آویزان شده است. آیا جسم حرکت میکند؟ خیر. بنابراین، جسم در حالت سکون یا تعادل قرار دارد. بر طبق قوانین حرکت نیوتن، برایند نیروهای وارد بر جسمی ساکن یا جسمی که با سرعت ثابت حرکت میکند، برابر صفر است.
نیروهای وارد شده بر جسم بردارهای دوبعدی هستند. برای آنکه نیروی برایند برابر صفر شود، باید مولفههای و این نیرو هر دو همزمان برابر صفر شوند. ابتدا نیروی برایند را بهدست میآوریم. سه نیرو بر جسم یک کیلوگرمی وارد میشوند:
- نیروی : این نیرو از طرف طناب یک بر جسم وارد میشود.
- نیروی : این نیرو از طرف طناب دو بر جسم وارد میشود.
- نیروی : این نیرو به سمت پایین بر جسم وارد میشود.
برای تجزیه هر یک از این نیروها، ابتدا باید محور مختصات دوبعدی را رسم کنیم و زاویه هر نیرو را با محورهای مختصات بهدست آوریم. برای این کار مبدأ مختصات را در مکان جسم در نظر میگیریم و محورهای و را از آنجا رسم میکنیم.
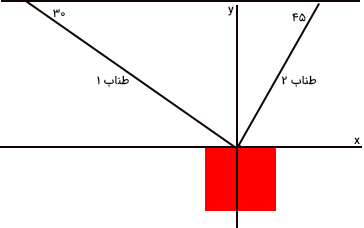
زاویه نیروهای کششی و با محورهای مختصات چیست؟ برای یافتن زاویه نیروهای کششی از طرف هر طناب با محورهای مختصات، تنها کافی است زاویه طنابها را با محورهای و بهدست آوریم. طناب یک با جهت منفی محور زاویه ۳۰ درجه و طناب دو با جهت منفی محور زاویه ۴۵ درجه میسازند.
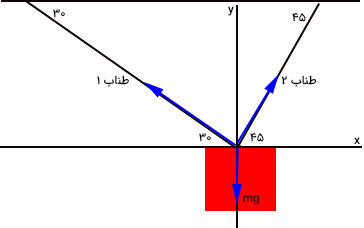
نیروی برحسب مولفههایش به صورت زیر نوشته میشود:
نیروی برحسب مولفههایش به صورت زیر نوشته میشود:
نیروی کششی برایند برابر است با:
برای آنکه نیروی برایند برابر صفر شود، هر یک از مولفههای نیروی برایند باید برابر صفر باشند. به این نکته توجه داشته باشید که مولفه باید برابر نیروی شود.
طرفین رابطههای بالا را در دو ضرب میکنیم:
با حل دو معادله و دو مجهول بالا، نیروی وارد شده از طرف طنابهای یک و دو را بهدست میآوریم:
تجزیه بردار در سه بعد
در بخش قبل با تجزیه کمیتهای برداری در فضای دو بعدی آشنا شدیم. در این بخش، تجزیه بردارها را در فضا سهبعدی بررسی میکنیم. همانطور که گفتیم فضای دوبعدی از دو محور و تشکیل شده است. در فضای سهبعدی، محور به گونهای رسم میشود که بر محورهای و عمود باشد.
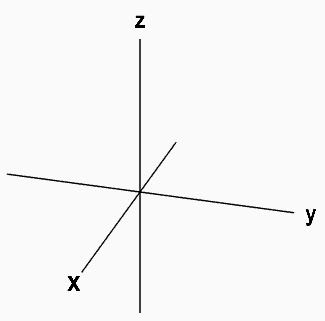
بردار دلخواهی به نام A را به صورت نشان داده شده در تصویر زیر از مبدأ مختصات رسم میکنیم.
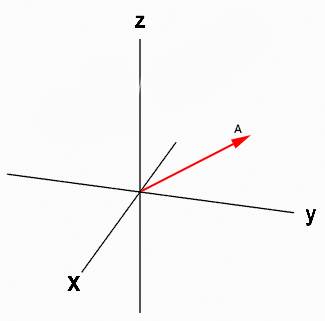
فرض کنید زاویه بردار A با جهت و مثبت محور برابر است. برای تجزیه بردار A در امتداد سه محور مختصات به ترتیب زیر عمل میکنیم:
- تصویر بردار A را روی صفحه بهدست میآوریم. برای انجام این کار، از نقطه انتهایی بردار A خطی موازی محور رسم میکنیم. محل تقاطع خط موازی را با صفحه بهدست میآوریم. در ادامه، مبدأ مختصات را به این نقطه وصل میکنیم.
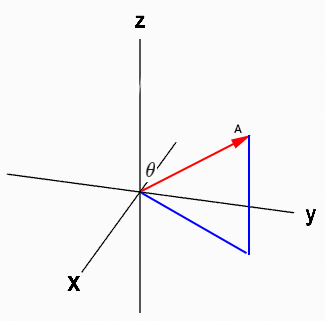
- تصویر بردار A روی صفحه را مینامیم. این بردار برحسب زاویه به صورت زیر نوشته میشود:
- برای بهدست آوردن مولفههای A در امتداد محورهای و ابتدا فرض میکنیم زاویه با جهت مثبت محور برابر است.

- در ادامه، از انتهای دو خط موازی محورهای و رسم میکنیم و محل تقاطع خطهای موازی را با این دو محور بهدست میآوریم.
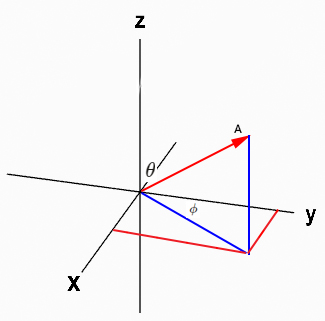
- محل تقاطع خطهای موازی با محورهای و را به ترتیب و مینامیم.
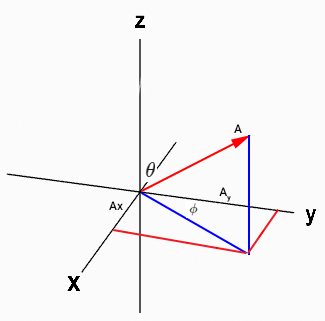
- از آنجا که زاویه با جهت مثبت محور برابر است، و به صورت زیر نوشته میشوند:
در قسمتهای قبل گفتیم برابر است. بنابراین، رابطههای بالا به صورت زیر نوشته میشوند:
- تا اینجا، مولفههای بردار A در امتداد دو محور و را بهدست آوردیم. مولفه بردار A در امتداد محور است با:
شاید از خود بپرسید مولفه یکه در راستای محور چه نام دارد. بردار یکه در امتداد محور را با نشان میدهیم. بنابراین، بردار A برحسب بردارهای یکه به صورت زیر نوشته میشود:
ضرب کمیت های برداری
ضرب بردارها به دو نوع تقسیم میشود:
- ضرب داخلی
- ضرب خارجی
ضرب داخلی کمیت های برداری
به ضرب داخلی بردارها، ضرب اسکالر نیز گفته میشود. نتیجه ضرب داخلی بردارها، مقدار نردهای یا اسکالر است. ضرب داخلی دو بردار برابر حاصلضرب طول هر بردار در کسینوس زاویه بین آنها است. نتیجه ضرب داخلی دو بردار در صفحه گذرنده از آنها قرار میگیرد. عدد بهدست آمده پس از ضرب داخلی بردارها ممکن است منفی یا مثبت باشد. به تصویر زیر دقت کنید. زاویه بین بردارهای و برابر است. تصویر روی برابر است.
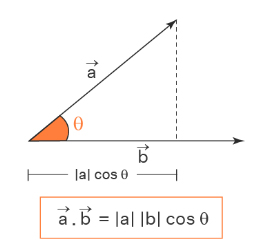
در رابطه نشان داده شده در تصویر بالا، و به ترتیب اندازه بردارهای a و b هستند. در تعریف ضرب داخلی، جهت زاویه بین دو بردار مهم نیست. به بیان دیگر، زاویه بین دو بردار را میتوان نسبت به هر یک از دو بردار اندازه گرفت، زیرا:
اگر بین ۹۰ تا ۱۸۰ درجه باشد، ضرب داخلی دو بردار مقداری منفی و اگر بین صفر تا ۹۰ درجه باشد، ضرب داخلی دو بردار مقداری مثبت خواهد بود. در حالت خاص، اگر دو بردار فرضی A و B موازی و در جهت یکسانی قرار داشته باشند، ضرب داخلی آنها برابر و اگر این دو بردار، موازی و در دو جهت مخالف باشند، ضرب داخلی آنها برابر است.
پرسش: اگر دو بردار A و B بر یکدیگر عمود باشند، حاصل ضرب داخلی آنها چه مقدار است؟
پاسخ: همانطور که در مطالب بالا اشاره شد، ضرب داخلی دو بردار با استفاده از رابطه زیر بهدست میآید:
در رابطه فوق، زاویه بین دو بردار و برابر ۹۰ درجه است. از آنجا که ، ضرب داخلی دو بردار عمود بر هم برابر صفر خواهد بود.
ضرب خارجی کمیت های برداری
به ضرب خارجی بردارها، ضرب برداری نیز گفته میشود. به بیان دیگر، ضرب خارجی عملیات دودویی روی دو بردار در فضای سهبعدی است. نتیجه این ضرب، برداری عمود بر هر یک از دو بردار خواهد بود. ضرب برداری دو بردار دلخواه مانند بردارهای a و b، به صورت زیر نوشته میشود:
نتیجه این ضرب برداری عمود بر بردارهای a و b است. برای بهدست آوردن جهت بردار حاصل از قانون دست راست استفاده میکنیم. توجه به این نکته مهم است که نتیجه بر صفحه گذرنده از بردارهای a و b عمود است.
فرمول ضرب خارجی دو بردار
اگر زاویه بین دو بردار A و B باشد، ضرب خارجی این دو بردار با استفاده از رابطه زیر بهدست میآید:
در رابطه بالا:
- و اندازه دو بردار داده شده هستند.
- زاویه بین دو بردار است.
- بردار واحدی عمود بر صفحه ساخته شده توسط دو بردار A و B است. جهت بردار نیز با استفاده از قانون دست راست تعیین میشود.
از آنجا که سینوس دو زاویه صفر و ۱۸۰ درجه برابر صفر است، ضرب خارجی دو بردار موازی و همجهت یا دو بردار موازی و در دو جهت مخالف با یکدیگر نیز برابر صفر خواهد بود. بنابراین، ضرب خارجی بردار دلخواهی مانند a در خودش برابر صفر است. همچنین، اگر دو بردار بر یکدیگر عمود باشند، ضرب خارجی آنها برابر است با:
در مطالب بالا گفتیم بردارها را میتوان برحسب بردارهای یکه در راستای هر محور نوشت. اگر بردار A برداری در فضای دوبعدی باشد، آن را میتوان به صورت نوشت. همچنین، اگر بردار A برداری در فضای سهبعدی باشد، آن را به صورت مینویسیم. دو بردار A و B را به صورت زیر در نظر بگیرید:
بردارهای یکه و و دو به دو بر یکدیگر عمود هستند. در نتیجه، ضرب خارجی هر بردار یکه با بردار یکه دیگر به صورت زیر نوشته میشود:
به این نکته توجه داشته باشید که با با یکدیگر برابر نیستند، بلکه:
همچنین، در مطالب بالا اشاره کردیم که ضرب خارجی برداری دلخواه با خودش برابر صفر میشود، بنابراین حاصلضرب هر بردار یکه در خودش، برابر صفر خواهد شد:
با توجه به اطلاعات بالا، حاصلضرب خارجی دو بردار A و B را برحسب بردارهای یکه بهدست میآوریم:
با توجه به ضرب خارجی بردارهای یکه در یکدیگر، ضرب خارجی دو بردار A و B به صورت زیر نوشته میشود:
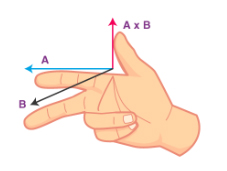
قانون دست راست
در مطالب بالا گفتیم که جهت بردار حاصل از ضرب خارجی دو بردار دلخواه A و B را با استفاده از قانون دست راست میتوان بهدست آورد. در این قانون، دست راست خود را به گونهای قرار میدهیم که انگشت اشاره در جهت بردار اول و انگشت میانی در جهت بردار دوم قرار بگیرند. سپس، انگشت شصت دست راست جهت بردار حاصل یا جهت بردار یکه را نشان میدهد. با استفاده از قانون دست راست به آسانی میتوانیم نشان دهیم که ضرب خارجی دو بردار، جابجاپذیر نیست.
مثال ضرب خارجی دو بردار
ضرب خارجی دو بردار زیر را بهدست آورید:
یکی از راههای ساده برای بهدست آوردن ضرب خارجی دو بردار، نوشتن آنها به شکل ماتریسی به صورت زیر است:
دترمینان ماتریس فوق را بهدست میآوریم:
تا اینجا میدانیم کمیت چیست و به چند دسته تقسیم میشود. کمیتها در حالت کلی به دو دسته کمیتهای اصلی و فرعی تقسیم میشوند. در بخش پایانی، برای داشتن درک بهتری از کمیتها به چند پرسش در مورد آنها پاسخ میدهیم.
حل پرسش های مطرح شده در مورد کمیت
در این بخش به چند پرسش در مورد کمیت پاسخ میدهیم.
پرسش ۱
کدامیک از کمیتهای زیر کمیت فیزیکی اصلی است؟
- طول
- زمان
- سرعت
- جرم
پاسخ
برای پاسخ به این پرسش، هر گزینه را جداگانه بررسی میکنیم:
- طول: همانطور که در مطالب بالا اشاره شد طول یکی از هفت کمیت اصلی و واحد اندازهگیری آن در سیستم SI متر است.
- زمان: زمان نیز همانند طول یکی از واحدهای اصلی و واحد اندازهگیری آن در سیستم SI ثانیه است.
- سرعت: سرعت به صورت نسبت جابجایی بر زمان لازم برای انجام جابجایی تعریف میشود. بنابراین، این کمیت، کمیتی فرعی و واحد آن متر بر ثانیه است.
- جرم: جرم نیز مانند طول و زمان، یکی از کمیتهای اصلی و واحد اندازهگیری آن در سیستم SI کیلوگرم است.
پرسش ۲
دیمانسیون کمیتی فیزیکی به صورت داده شده است. کدامیک از گزینههای زیر صحیح است؟
- اگر a=1 و b=0 و c=-1 باشند، کمیت موردنظر سرعت است.
- اگر a=1 و b=1 و c=-2 باشند، کمیت موردنظر شتاب است.
- اگر a=0 و b=-1 و c=-2 باشند، کمیت موردنظر نیرو است.
- اگر a=1 و b=-1 و c=-۲ باشند، کمیت موردنظر فشار است.
پاسخ
برای پاسخ به این پرسش، دیمانسیون کمیتهای سرعت، شتاب، نیرو و فشار را بهدست میآوریم و آن را به شکل مینویسیم.
دیمانسیون سرعت
سرعت با استفاده از رابطه زیر بهدست میآید:
دیمانسیون برابر و دیمانسیون t برابر است. در نتیجه، دیمانسیون سرعت برابر خواهد بود. از اینرو، برای آنکه کمیت فیزیکی در این پرسش سرعت باشد، مقدارهای a و b و c باید به ترتیب برابر صفر، ۱ و ۱- باشند. در نتیجه گزینه یک اشتباه است.
دیمانسیون شتاب
شتاب با استفاده از رابطه زیر بهدست میآید:
دیمانسیون برابر و دیمانسیون t برابر است. در نتیجه، دیمانسیون شتاب برابر خواهد بود. از اینرو، برای آنکه کمیت فیزیکی در این پرسش سرعت باشد، مقدارهای a و b و c باید به ترتیب برابر صفر، ۱ و ۲- باشند. در نتیجه گزینه دو نیز اشتباه است.
دیمانسیون نیرو
نیرو با استفاده از رابطه زیر بهدست میآید:
دیمانسیون برابر و دیمانسیون a برابر است. در نتیجه، دیمانسیون نیرو برابر خواهد بود. از اینرو، برای آنکه کمیت فیزیکی در این پرسش سرعت باشد، مقدارهای a و b و c باید به ترتیب برابر ۱، ۱ و ۲- باشند. در نتیجه گزینه ۳ نیز اشتباه است.
دیمانسیون فشار
فشار با استفاده از رابطه زیر بهدست میآید:
دیمانسیون برابر و دیمانسیون A برابر است. در نتیجه، دیمانسیون فشار برابر خواهد بود. از اینرو، برای آنکه کمیت فیزیکی در این پرسش سرعت باشد، مقدارهای a و b و c باید به ترتیب برابر ۱، ۱- و ۲- باشند. در نتیجه گزینه ۴ صحیح است.
پرسش ۳
کمیت فیزیکی P به صورت زیر نوشته میشود:
اگر خطاهای نسبی در اندازهگیری a و b و c و d به ترتیب برابر ۲، یک، ۳ و ۵ درصد باشند، خطای نسبی P برابر است با:
- ۸٪
- ۲۵٪
- ۱۲٪
- ۳۲٪
پاسخ
کمیت فیزیکی p به صورت زیر نوشته میشود:
از طرفین رابطه بالا لگاریتم میگیریم:
در ادامه، از طرفین رابطه بالا مشتق میگیریم:
یا
از آنجا که درصد خطاهای نسبی در اندازهگیری a و b و c و d به ترتیب برابر ۲، یک، ۳ و ۵ درصد هستند:
بنابراین، خطای نسبی p برابر است با:
در نتیجه، گزینه ۴ صحیح است.
جمعبندی
در این مطلب، ابتدا با تعریف کمیت در فیزیک آشنا میشویم. سپس کمیتهای اصلی و فرعی و در ادامه، کمیتهای نردهای و برداری را تعریف و در مورد جمع و ضرب بردارها به طور مفصل توضیح میدهیم. طول، جرم، زمان، دما، جریان الکتریکی، شدت روشنایی و مقدار ماده هفت کمیت اصلی هستند و کمیتهای فرعی دیگر با استفاده از این کمیتها ساخته میشوند.
| کمیت اصلی | واحد SI | نماد |
| طول | متر | m |
| جرم | کیلوگرم | kg |
| زمان | ثانیه | s |
| دما | کلوین | K |
| جریان الکتریکی | آمپر | A |
| شدت روشنایی | کندلا (شمع) | cd |
| مقدار ماده | مول | mol |
آزمون کمیت فیزیکی
۱. یک کمیت فیزیکی را چگونه و با چه اجزایی معرفی میکنند و علت اهمیت هر یک از این اجزا چیست؟
به کمک یک مقدار عددی و واحد استاندارد، تا مقایسه و کاربرد کمیت امکانپذیر باشد.
تنها با عدد بدون اشاره به واحد، چون واحدها قابل حدس هستند.
با چند واحد مختلف به صورت همزمان، چون دقت را بالا میبرد.
صرفا با اسم و توضیح، چون واحد و عدد اهمیتی ندارد.
کمیت فیزیکی باید با یک مقدار عددی و یک واحد استاندارد معرفی شود، زیرا فقط در این صورت معنا، قابلیت مقایسه و کاربرد علمی خواهد داشت. معرفی صرفا با اسم یا توضیح بدون عدد و واحد کافی نیست و نوشتن تنها عدد بدون یکا باعث ابهام و بیمعنایی علمی میشود. استفاده از چند واحد مختلف بهطور همزمان اشتباه است چون منجر به سردرگمی و فقدان هماهنگی میگردد. بنابراین «مقدار عددی و واحد استاندارد» برای هر کمیت فیزیکی ضروریاند.
۲. اگر برای بیان یک کمیت فیزیکی عدد داده شود اما هیچ واحد (یکا) برای آن نوشته نشود، چه نتیجهای در اندازهگیری و مقایسه حاصل میشود؟
امکان مقایسه دقیق با دیگر مقدارهای مشابه وجود نخواهد داشت.
مقدار کمیت همیشه بزرگتر از مقدار واقعی به نظر میرسد.
میتوان کمیت را فقط با کمیتهای برداری مقایسه کرد.
فقط مقدارهای کمیت اصلی تحت تاثیر قرار میگیرند.
بیان عددیِ یک کمیت فیزیکی بدون استفاده از واحد (یکا) باعث میشود منظور کمیت کاملا مشخص نباشد و امکان مقایسه یا کاربرد کمی دقیق از بین برود. مقایسه معنیدار نیازمند وجود واحد مرجع است. این مشکل مستقل از برداری یا اصلی بودن کمیت است و صرفا به نبود واحد برمیگردد، پس «عدم مقایسه دقیق با دیگر مقدارهای مشابه» پاسخ درست است. سایر گزینهها مانند «بزرگتر به نظر رسیدن»، «مقایسه فقط با کمیت برداری» یا «تاثیر فقط بر کمیتهای اصلی» صحیح نیستند، زیرا واحد برای همه کمیتها و تمام کاربردها ضروری است.
۳. واحد اندازهگیری چه ویژگی اساسی دارد و چرا داشتن مرجع استاندارد در اندازهگیری اهمیت دارد؟
واحد اندازهگیری باید ثابت و همگانی باشد تا مقایسه دقیق ممکن شود.
واحد اندازهگیری باید براساس مقدار تقریبی واقع شود تا خطا کم شود.
واحد اندازهگیری باید تنها برای هر کشور منحصر باشد تا آسانتر شود.
واحد اندازهگیری باید قابل تقسیم باشد تا همه بتوانند آن را انجام دهند.
«واحد اندازهگیری باید ثابت و همگانی باشد تا مقایسه دقیق ممکن شود» درست است، زیرا اگر همه افراد یا کشورها از مرجع مشخص و یکسان برای سنجش کمیتها (مانند متر یا کیلوگرم) استفاده کنند، اختلاف و ابهام از بین میرود و در فعالیتهای علمی و روزمره، نتیجهگیری درست و همکاری ممکن میشود. عبارت «قابل تقسیم بودن واحد» ویژگی اساسی نیست و تقسیمپذیری تضمین هماهنگی نمیکند. واحد مبتنی بر مقدار تقریبی به خطای بیشتر میانجامد، نه کمتر. استفاده از واحد منحصر به کشورها موجب سردرگمی و مشکل در ارتباط بینالمللی میشود.
۴. استفاده از واحدهای استاندارد متفاوت برای یک کمیت فیزیکی توسط کشورها چه اثری در فعالیتهای علمی یا صنعتی دارد؟
دقت اندازهگیری افزایش مییابد و تبادل علمی سریعتر میشود.
تنها در علوم نظری مشکلآفرین است و بر کاربرد عملی اثری ندارد.
همکاری یا مقایسه دادهها دشوار بوده و خطاهای صنعتی ایجاد میشود.
مانع استفاده از دستگاههای پیشرفته داخلی میشود ولی بر تجارت تاثیر ندارد.
زمانی که چند کشور برای یک کمیت فیزیکی از واحدهای استاندارد متفاوت استفاده کنند، همکاری و مقایسه دادههای علمی دچار مشکل میشود و خطاهای جدی در فعالیتهای صنعتی مثل تولید یا طراحی میتواند رخ دهد. متن به اهمیت استانداردسازی واحدها برای ایجاد دقت، همدلی و توسعه صنعتی اشاره میکند. عبارات «دقت اندازهگیری افزایش مییابد و تبادل علمی سریعتر میشود» و «تنها در علوم نظری مشکلآفرین است و بر کاربرد عملی اثری ندارد» با محتوای متن همخوانی ندارند، زیرا نبود استاندارد نهتنها کمبود دقت بلکه مانع کاربرد صحیح نتایج میشود. همچنین، این مشکل صرفا مربوط به دستگاههای داخلی نیست، بلکه مستقیما بر تجارت و همکاری علمی بینالمللی نیز تاثیرگذار است.
۵. کدام ویژگی واحدهای SI باعث برتری آنها نسبت به دیگر سیستمهای اندازهگیری شده است؟
همه کمیتها یک واحد ثابت دارند و هماهنگی بینالمللی سادهتر است.
محاسبات فقط با اعداد طبیعی انجام میشود.
تمام کمیتهای اصلی فقط با جرم و طول تعریف میشوند.
نمادهای واحدها به زبان یونانی نوشته میشوند.
برتری واحدهای SI در این است که برای هر کمیت اصلی یک واحد ثابت و جهانی در نظر گرفته شده و این هماهنگی بینالمللی، ارتباط، دقت و کاربرد آن را آسان میکند. استفاده از اعداد طبیعی یا یونانی بودن نمادها در SI مطرح نیست. همچنین کمیتهای اصلی فقط با جرم و طول تعریف نمیشوند و سایر کمیتهای اصلی مانند زمان، دما و جریان الکتریکی نیز دارای واحد مستقل هستند.
۶. سه نمونه از کمیتهای اصلی فیزیکی را انتخاب کنید و بیان کنید چرا اصلی خوانده میشوند؟
جریان الکتریکی، حجم و مساحت چون در سنجش بهکار میروند.
فشار، انرژی و توان چون اجزای اساسی هر آزمایشاند.
جرم، طول و زمان چون بدون وابستگی به کمیتهای دیگر تعریف میشوند.
چگالی، سرعت و دما چون در هر مسئله فیزیکی حضور دارند.
«جرم»، «طول» و «زمان» جزو کمیتهای اصلی هستند زیرا به طور مستقل تعریف میشوند و برحسب سایر کمیتها بیان نمیشوند. برعکس، فشار، انرژی، توان، چگالی، سرعت، حجم و مساحت همگی با استفاده از کمیتهای اصلی قابل تعریفاند.
۷. یک کمیت فرعی چگونه از کمیتهای اصلی ساخته میشود؟ همچنین یک نمونه کمیت فرعی را ذکر کنید.
کمیت فرعی با ضرب یا تقسیم چند کمیت اصلی بدست میآید، مثل سرعت.
کمیت فرعی بدون نیاز به کمیت اصلی تعریف میشود، مثل زمان.
کمیت فرعی تنها بهصورت عددی بیان میشود و واحد ندارد، مانند طول طی شده.
کمیت فرعی فقط از یک کمیت اصلی تشکیل میشود، مانند جرم.
کمیت فرعی از ترکیب کمیتهای اصلی از طریق ضرب یا تقسیم آنها ساخته میشود؛ برای مثال «سرعت» با تقسیم «طول» بر «زمان» بدست میآید. گزینههایی مانند «جرم» یا «زمان» کمیتهای اصلی هستند و به کمیت دیگری وابسته نیستند. جمله «فقط عددی و بدون واحد» غلط است چون هر کمیت فرعی هم عدد و هم واحد دارد.
۸. دانشآموز برای نوشتن کمیت سرعت طبق سیستم SI باید چه روشی را رعایت کند؟
به کار بردن حرف s، عدد و واحد m/s بدون فاصله
نوشتن نام کامل speed، عدد و واحد m/s
نوشتن حرف v، عدد و واحد m/s بدون فاصله
استفاده از حرف v، عدد، فاصله و واحد m/s
برای نوشتن کمیت سرعت در سیستم SI باید از نماد v، مقدار عددی، سپس یک فاصله و بعد واحد m/s استفاده شود. این روش مطابق اصول نگارش SI است و قراردادن فاصله میان عدد و واحد اجباری است. نگارش نام کامل speed یا انتخاب حرف s نادرست است، زیرا حرف v نماد استاندارد سرعت میباشد و speed نام انگلیسی است و باید نماد به کار رود. همچنین قرار ندادن فاصله میان عدد و واحد مطابق استاندارد SI نیست.
۹. در نگارش صحیح نمادها و واحدهای SI کدام مورد درست است؟
پس از واحد نقطه قرار داده میشود.
بین عدد و واحد، فاصله گذاشته میشود.
نماد واحدها همیشه با حروف بزرگ نوشته میشود.
یکای هر کمیت با خط تیره جدا میشود.
قرار دادن فاصله میان عدد و واحد در نگارش SI الزام است، مانند «۱۵ kg»، که باعث خوانایی و استاندارد بودن بیان مقدار میشود. نوشتن نماد واحدها با حروف بزرگ فقط برای اسامی خاص (مانند K برای کلوین) معتبر است و همیشه اینگونه نیست. واحد نباید با نقطه یا خط تیره از مقدار جدا شود، چرا که این کار خلاف قواعد SI است.
۱۰. در سیستم SI استفاده از پیشوندهایی مانند مگا (Mega) و میلی (Milli) چه تاثیری بر مقدار عددی کمیت دارند و چرا وجود این پیشوندها اهمیت دارد؟
پیشوند مگا عدد کمیت را هزار برابر و پیشوند میلی عدد را ده برابر میکند و باعث راحتی تبدیل میشود.
پیشوند مگا و میلی فقط برای کمیتهای طول کاربرد دارند و نقش آنها تغییر نوع کمیت است.
پیشوند مگا عدد را نصف و پیشوند میلی عدد را دو برابر میکند و باعث استاندارد شدن واحدها میشود.
پیشوند مگا مقدار را یک میلیون برابر و پیشوند میلی مقدار را یک هزارم میکند و سبب بیان ساده کمیتهای بزرگ یا کوچک میشود.
استفاده از پیشوند مگا مقدار عددی یک کمیت را یک میلیون برابر و پیشوند میلی آن را یک هزارم میکند؛ این ویژگی باعث میشود بتوانیم کمیتهای بسیار بزرگ یا بسیار کوچک را به صورت سادهتر، خواناتر و منظمتر بیان کنیم. پیشوندها موجب میشوند واحدهای SI در گسترههای بزرگ و کوچک قابل استفاده باشند. عبارتهایی مانند «فقط برای کمیتهای طول» یا «نصف کردن عدد» نادرست هستند، چون پیشوندها به همه کمیتهای SI قابل اضافه شدناند و نقش آنها ضرب یا تقسیم مقدار عددی بر پایه ثابت است نه تغییر نوع کمیت.
۱۱. واحد یک کمیت فرعی مثل شتاب را بر چه اساسی میتوان به دست آورد؟
تعیین واحد با توجه به مقدار عددی شتاب
استفاده مستقیم از واحد جرم برای شتاب
انتخاب دلخواه واحد برای هر کمیت فرعی
قرار دادن واحدهای کمیتهای اصلی در فرمول شتاب و سادهسازی آن
برای به دست آوردن واحد یک کمیت فرعی مانند شتاب، باید واحد تمام کمیتهای اصلی مورد استفاده در فرمول آن، مانند متر و ثانیه، را جایگذاری و سپس واحد حاصل را ساده کنیم. مثلا واحد شتاب برابر با متر بر مجذور ثانیه است. استفاده از واحد جرم به تنهایی یا تعیین واحد بر اساس مقدار عددی یا انتخاب دلخواه، صحیح نیست و باعث ناسازگاری واحد در اندازهگیری خواهد شد.
۱۲. هدف اصلی از بهکارگیری تحلیل ابعادی (دیمانسیون) بین کمیتها کدام مورد است؟
شناسایی ابعاد کمیتهای اصلی و بررسی رابطه بین آنها
مقایسه مقدار دقیق کمیت ها میان دستگاه های مختلف
یافتن مقدار عددی کمیتها در مسائل عددی
مشخص کردن نوع واحد اندازهگیری مناسب برای هر کمیت
تحلیل ابعادی با بررسی نمادها و ابعاد کمیتهای اصلی، امکان شناسایی نوع بعد هر کمیت و نحوه ترکیب یا ارتباط آنها در روابط فیزیکی را فراهم میکند. به این ترتیب، میتوان رابطه درست بین کمیتهای اصلی و فرعی را بررسی و صحت معادلهها را از جنبه ساختاری سنجید. کاربرد تحلیل ابعادی «شناسایی ابعاد کمیتهای اصلی و بررسی رابطه بین آنها» است، نه محاسبه عددی مقدار کمیت، یافتن نوع واحد مناسب یا مقایسه عددی دقیق میان دستگاهها؛ چون این موارد اصولا به تحلیل ابعادی ارتباطی ندارند یا موضوع دیگری را پوشش میدهند.
۱۳. کمیت برداری و نردهای (اسکالر) چه تفاوتی با هم دارند و یکی از ویژگیهای هر نوع را بیان کنید.
کمیت برداری مقدار و جهت دارد، اما اسکالر فقط مقدار دارد و بدون جهت است.
کمیت برداری با یکاهای مختلف بیان میشود، اما اسکالر فقط با یکای استاندارد اندازهگیری میشود.
کمیت برداری همیشه کوچکتر از اسکالر است و مقدار آن متغیر میماند.
کمیت برداری فقط عددی است، اما اسکالر با حرف و نماد نوشته میشود.
در کمیت برداری هم اندازه وجود دارد هم جهت، مانند نیرو و جابجایی که جهتمند هستند. اما کمیت اسکالر یا نردهای فقط مقدار عددی دارد و جهت مشخصی ندارد، مانند جرم و مسافت. عبارت «کمیت برداری مقدار و جهت دارد، اما اسکالر فقط مقدار دارد و بدون جهت است» صحیح است و سایر جملات یا درباره تفاوت بین این دو اشتباه هستند یا اساس علمی ندارند.
۱۴. در فیزیک، هنگام حل یک مسئله، چه زمانی باید به جای جمع عددی معمولی، جمع برداری انجام داد؟
زمانی که کمیتها دارای اندازه و جهت هستند و جهتیابی مهم است.
هنگامی که فقط مقدار عددی مورد نظر باشد و ارتباط مکانی یا جهتی لحاظ نشود.
اگر کمیتها همواره به صورت مثبت بیان شوند و منفی شدن آنها بیمعنی باشد.
وقتی که کمیتها فقط اندازه دارند و جهت اهمیت ندارد.
هنگامی باید از جمع برداری استفاده کرد که کمیتها، مانند نیرو (force)، سرعت (velocity) یا جابجایی (displacement)، هم اندازه و هم جهت داشته باشند. در این حالت جهت هر کمیت اهمیت دارد و نتیجه جمع وابسته به جهت آنهاست. در مقابل، برای کمیتهایی مانند جرم یا زمان که تنها اندازه دارند و جهت بیمعنی است، جمع فقط عددی انجام میشود. بنابراین عبارت «زمانی که کمیتها دارای اندازه و جهت هستند و جهتیابی مهم است» شرایط درست برای الزام جمع برداری را بیان میکند. سایر گزینهها مربوط به کمیتهای نردهای (اسکالر) هستند که جمع آنها صرفا عددی انجام میشود و جهت تاثیری ندارد.
۱۵. برای تجزیه یک بردار به مولفههای x و y و کاربرد آن در حل مسائل، کدام عبارت درست است؟
نیاز به تجزیه بردار زمانی ایجاد میشود که بخواهیم جمع بردارها را فقط به روش عددی انجام دهیم.
برای تجزیه بردار به مولفهها نیازی به زاویه بردار با محور x نیست و کافی است طول مشخص باشد.
تجزیه بردار فقط در سیستم سهبعدی امکانپذیر است و در دو بعد کاربردی ندارد.
هر بردار را میتوان با ترسیم یک مثلث مستطیل به مولفههای مختصاتی تقسیم کرد تا محاسبات دقیقتر شوند.
عبارت «هر بردار را میتوان با ترسیم یک مثلث مستطیل به مولفههای مختصاتی تقسیم کرد تا محاسبات دقیقتر شوند» صحیح است، زیرا تجزیه بردار به مولفههای x و y بر اساس زاویه نسبت به محورها انجام میشود و در حل بسیاری از مسائل فیزیکی دقت را افزایش میدهد. گزینه «تجزیه بردار فقط در سیستم سهبعدی امکانپذیر است و در دو بعد کاربردی ندارد» نادرست است زیرا در دوبعد نیز کاربرد فراوان دارد. گفته «تجزیه بدون زاویه ممکن است و فقط طول بردار کافی است» اشتباه است، زیرا برای تعیین مولفهها باید زاویه مشخص باشد. همچنین نیاز به تجزیه بردار محدود به انجام جمع عددی نیست و برای تحلیل گرافیکی هم کاربرد دارد، پس این عبارت نیز پاسخ مناسبی نیست.
۱۶. از نظر مفهومی و نتیجه، تفاوت اصلی بین ضرب داخلی (dot product) و ضرب خارجی (cross product) چیست؟
در ضرب داخلی دو بردار حتما باید هماندازه باشند، اما ضرب خارجی چنین شرطی ندارد.
ضرب داخلی فقط برای بردارهای موازی ممکن است، اما ضرب خارجی همیشه ممکن است.
ضرب داخلی اندازه اسکالر میدهد و جهت ندارد، ولی ضرب خارجی برداری است و جهت دارد.
ضرب داخلی فقط با اعداد حقیقی تعریف میشود، ولی ضرب خارجی اعداد مختلط نیاز دارد.
در ضرب داخلی (dot product) حاصل یک عدد اسکالر است و این مقدار فقط به طولها و زاویه بین بردارها بستگی دارد، جهتگیری ندارد. اما ضرب خارجی (cross product) نتیجهای برداری با جهت مشخص بر اساس قانون دست راست دارد. عبارت «ضرب داخلی اندازه اسکالر میدهد و جهت ندارد، ولی ضرب خارجی برداری است و جهت دارد» درست است. سایر گزارهها صحیح نیستند: ضرب داخلی و ضرب خارجی هر دو برای هر دو بردار تعریف میشوند و فقط نیازمند تعریف زاویهاند، نه برابری طول یا موازی بودن؛ همچنین انجام ضرب داخلی یا خارجی ارتباطی به اعداد مختلط ندارد.
۱۷. کدام گزینه مثالهایی از کمیتهای اصلی فیزیکی است که مستقل از سایر کمیتها تعریف میشوند؟
جرم، طول، زمان، دما، جریان الکتریکی، شدت روشنایی، مقدار ماده
حجم، چگالی، سرعت، مساحت
توان، بار الکتریکی، شتاب، زاویه
نیرو، کار، فشار، انرژی
«جرم، طول، زمان، دما، جریان الکتریکی، شدت روشنایی، مقدار ماده» نمونههایی از کمیتهای اصلی هستند که هرکدام بدون نیاز به تعریف بر اساس کمیتهای دیگر بیان میشوند و اساس واحدهای اندازهگیری را تشکیل میدهند. در مقابل، هرکدام از گزینههای دیگر شامل کمیتهایی هستند که همگی وابسته به یک یا چند کمیت اصلی بوده و برحسب آنها تعریف یا محاسبه میشوند؛ مانند چگالی یا سرعت که رابطه مستقیمی با جرم، طول و زمان دارند، یا انرژی و فشار که ترکیبی از کمیتهای اصلی محسوب میشوند.
۱۸. در جدول دیمانسیون، حجم و سرعت هر کدام به چه صورت برحسب ابعاد اصلی فیزیکی نمایش داده میشوند؟
حجم: L²، سرعت: L T
حجم: M T⁻²، سرعت: L² T⁻¹
حجم: M³، سرعت: M L⁻¹
حجم: L³، سرعت: L T⁻¹
در جدول دیمانسیون کمیتها، بعد حجم به صورت "L³" (توان سوم طول) بیان میشود چون حجم حاصل ضرب سه طول است. بعد سرعت به صورت "L T⁻¹" است چرا که سرعت برابر با نسبت طول به زمان است و بنابراین باید بعد طول تقسیم بر زمان نوشته شود. سایر گزینهها با ساختار بعدی این کمیتها مطابقت ندارند؛ مثلا "M T⁻²" مربوط به شتاب نیست و "L²" و "L T" هیچکدام بعد درست حجم یا سرعت نیستند. همچنین عبارت "M³" برای جرم مکعبی بوده اما حجم با طول بیان میشود، نه جرم.













خدا خیرتو بده. خسته نباشید
ایا همون طور که کمیت فیزیکی داریم کمیت شیمیایی نیز داریم؟چیست؟
قطعا کمیت هرچیز قابل اندازه گیری رو گوییم
قطعا تو شیمی خیلی مباحث قابل اندازه گیری هست که واحد داره