مشتق توابع کسری — به زبان ساده

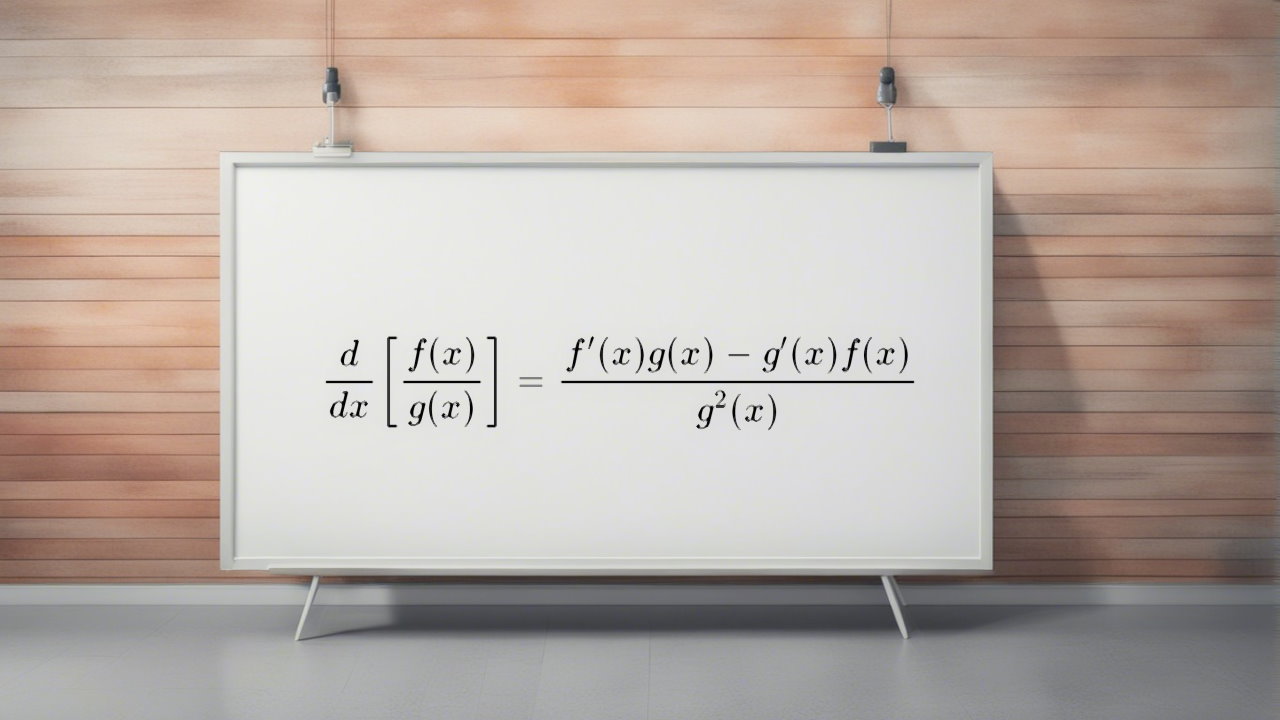
در آموزش‌های قبلی مجله فرادس، با مفاهیم مشتق و روش‌های مشتق‌گیری آشنا شدیم. همچنین، مباحثی مانند مشتق لگاریتم و تابع نمایی، مشتق ضمنی، مشتق جزئی، مشتق زنجیره‌ای، مشتق توابع معکوس،‌ و مشتق جهتی را توضیح دادیم. در این آموزش، با مشتق توابع کسری آشنا می‌شویم.

مشتق توابع کسری و قاعده خارج قسمت

مشتق توابع کسری یا گویا را می‌توان با استفاده از «قاعده خارج قسمت» (Quotient Rule) به دست آورد. تابع کسری $$ { h ( x ) = \frac { f ( x ) } { g ( x ) } } $$ را در نظر بگیرید. مشتق این تابع برابر است با:

$$ \large { h' ( x ) = \frac { g ( x ) \cdot f' ( x ) - f ( x ) \cdot g' ( x ) } { \left ( g ( x ) \right ) ^ 2 } } $$

اثبات: از تعریف پایه مشتق استفاده می‌کنیم:

$$ \large \displaystyle \dfrac { d h ( x ) } { d x } = \lim _ { \Delta x \rightarrow 0 } { \frac { h ( x + \Delta x ) - h ( x ) } { \Delta x } } . $$

از آنجا که $$ \frac { f ( x ) } { g ( x ) } = h ( x ) $$ است، می‌توان نوشت:

$$ \large \displaystyle \dfrac { d h ( x ) } { d x } = \lim _ { \Delta x \rightarrow 0 } { \dfrac { \frac { f ( x + \Delta x ) } { g ( x + \Delta x ) } - \frac { f ( x ) } { g ( x ) } } { \Delta x } } . $$

عبارت بالا را به صورت زیر ساده می‌کنیم:

$$ \large \begin {aligned} \frac { d h ( x ) } { d x } & = \lim _ { \Delta x \rightarrow 0 } { \frac { f ( x + \Delta x ) g ( x ) -f ( x ) g ( x + \Delta x ) } { \Delta x g ( x ) g ( x + \Delta x ) } } \\\\ & = \lim _ { \Delta x \rightarrow 0 } { \frac { 1 } { g ( x ) g ( x + \Delta x ) } } \lim _ { \Delta x \rightarrow 0 } { \frac { f ( x + \Delta x ) g ( x ) - f ( x ) g ( x + \Delta x ) } { \Delta x } } \\\\ & = \frac { 1 } { \big ( g ( x ) \big ) ^ 2 } \lim _ { \Delta x \rightarrow 0 } { \frac { f ( x + \Delta x ) g ( x ) -f ( x ) g ( x + \Delta x ) } { \Delta x } } . \end {aligned} $$

با اضافه و کم کردن $$ f (x) g ( x ) $$ در صورت کسر، داریم:

$$ \large \displaystyle \frac { d h ( x ) } { d x } = \frac { 1 } { { \big ( g ( x ) \big ) } ^ { 2 } } \lim _ { \Delta x \rightarrow 0 } { \frac { f ( x + \Delta x ) g ( x ) - f ( x ) g ( x ) + f ( x ) g ( x ) - f ( x ) g ( x + \Delta x ) } { \Delta x } } $$

با اعمال چند تغییر کوچک در عبارت بالا، خواهیم داشت:

$$ \large \begin {aligned} \frac { d h ( x ) } { d x } & = \frac { 1 } { { g ( x ) } ^ { 2 } } \lim _ { \Delta x \rightarrow 0 } { \left ( g ( x ) \bigg ( \frac { f ( x + \Delta x ) - f ( x ) } { \Delta x } \bigg ) - f ( x ) \bigg ( \frac { g ( x + \Delta x ) - g ( x ) } { \Delta x } \bigg ) \right ) } \\\\ & = \dfrac { \displaystyle \left ( g ( x ) \bigg ( \lim _ { \Delta x\rightarrow 0 } { \frac { f ( x + \Delta x ) - f ( x ) } { \Delta x } } \bigg ) - f ( x ) \bigg ( \lim _ { \Delta x \rightarrow 0 } { \frac { g ( x + \Delta x ) -g ( x ) } { \Delta x } } \bigg ) \right) } { { g ( x ) } ^ { 2 } } . \end {aligned} $$

در نهایت، فرمول مورد نظر به دست می‌آید:

$$ \large \displaystyle \boxed { \dfrac { d h ( x ) } { d x } = \dfrac { f' ( x ) g ( x ) - g' ( x ) f ( x ) } { { \big ( g ( x ) \big ) } ^ { 2 } } } . \ _ \square $$

مثال‌های مشتق توابع کسری

در این بخش، مثال‌های متنوعی را از مشتق توابع کسری بررسی می‌کنیم.

مثال ۱ مشتق توابع کسری

حاصل $$ \frac { d } { d x } \left ( \frac { 3 x ^ 3 - x - 2 } { 2 x } \right ) $$ را به دست آورید.

حل:‌ با توجه به فرمول بالا، توابع $$ 3x^3-x-2=f(x)$$ و $$ 2x=g(x) $$ را داریم. با جایگذاری این توابع در فرمول، خواهیم داشت:

$$ \large \begin {aligned} \frac { d } { d x } h ( x ) & = \frac { ( 2 x ) ( 9 x ^ 2 - 1 ) - ( 3 x ^ 3 - x - 2 ) ( 2 ) } { ( 2 x ) ^ 2 } \\ & = \frac { 1 8 x ^ 3 - 2 x - 6 x ^ 3 + 2 x + 4 } { 4 x ^ 2 } \\ & = \frac { 3 x ^ 3 + 1 } { x ^ 2 } . \ _ \square \end {aligned} $$

وقتی عبارات صورت و مخرج یک عبارت کسری پیچیده باشند، مشتق‌گیری از آن کسر کاملاً پیچیده و گیج‌کننده خواهد بود. در چنین مواردی، می‌توانیم صورت را به عنوان یک عبارت و مخرج را به عنوان یک عبارت فرض کرده و مشتقات آن‌ها را جداگانه بیابیم. پس از آن، مشتقات ترکیبی کسر را با استفاده از فرمول فوق برای مشتق توابع کسری می‌نویسیم و مستقیماً جایگزین می‌کنیم تا هیچ‌گونه سردرگمی ایجاد نشود و احتمال اشتباه کاهش یابد. در ادامه، چند مثال را برای این مورد بیان می‌کنیم.

مثال ۲ مشتق توابع کسری

اگر $$y = \frac { a - x } { a + x }$$ باشد ($$ x \neq - a  $$)، عبارت $$ \frac{dy}{dx} $$ را به دست آورید.

حل: توابع $$ u ( x ) = a - x \implies u' ( x ) = - 1 $$ و $$ v ( x ) = a + x \implies v' ( x ) = 1 $$ را در نظر بگیرید، به گونه‌ای که $$ y = \frac { u ( x ) } { v ( x ) } $$. بنابراین، خواهیم داشت:

$$ \large \begin {aligned} \dfrac { d y } { d x } & = \dfrac { v ( x ) u' ( x ) - v' ( x ) u ( x ) } { \big ( v ( x ) \big ) ^ 2 } \\\\ & = \dfrac { ( a + x ) ( - 1 ) - ( a - x ) ( 1 ) } { ( a + x ) ^ 2 } \\\\ & = \dfrac { - 2 a } { a ^ 2 + 2 a x + x ^ 2 } . \ _ \square \end {aligned} $$

مثال ۳ مشتق توابع کسری

اگر $$ y = \frac { p x ^ 2 + q x + r } { a x + b } $$ را داشته باشیم ($$ | a | + | b | \neq 0$$)، آنگاه $$ \frac { d y } { d x } $$ را بیابید.

حل: تابع را به صورت $$ y = \frac{u(x)}{v(x)} $$ می‌نویسیم که در آن، $$ u ( x ) = p x ^ 2 + q x + r \implies u' ( x ) = 2 p x + q $$ و $$ v ( x ) = a x + b \implies v' ( x ) = a $$ است. بنابراین، حاصل مشتق $$ y = \frac { u ( x ) } { v ( x ) } $$ به شکل زیر محاسبه می‌شود:

$$ \large \begin {aligned} \dfrac { d y } { d x } & = \dfrac { d }{ d x } \left ( \dfrac { u ( x ) } { v ( x ) } \right ) \\\\ & = \dfrac{ v ( x ) u' ( x ) - v' ( x ) u ( x ) } { \big ( v ( x ) \big ) ^ 2 } \\\\ & = \dfrac { ( a x + b ) ( 2 p x + q ) - ( a ) ( p x ^ 2 + q x + r ) } { ( a x + b ) ^ 2 } \\\\ & = \dfrac { a p x ^ 2 + 2 b p x + b q - a r } { a ^ 2 x ^ 2 + 2 a b x + b ^ 2 } . \ _ \square \end {aligned} $$

مثال ۴ مشتق توابع کسری

اگر $$ y = \frac { 1 } { a x ^ 2 + b x + c } $$ باشد ($$ |a| + |b| + |c| \neq 0 $$)، آنگاه حاصل $$ \frac{dy}{dx} $$ را بیابید.

حل: تابع را به صورت $$ y = \frac{u(x)}{v(x)} $$ می‌نویسیم که در آن، $$ u(x) = 1 \implies u'(x) = 0 $$ و $$ v(x) = ax^2 + bx + c \implies v'(x) = 2ax + b $$ است. بنابراین، حاصل مشتق تابع کسری $$ y = \frac { u ( x ) } { v ( x ) } $$ به شکل زیر محاسبه می‌شود:

$$ \large \begin {aligned} \dfrac { d y } { d x } & = \dfrac { d } { d x } \left ( \dfrac { u ( x ) } { v ( x ) } \right ) \\\\ & = \dfrac { v ( x ) u' ( x ) - v' ( x ) u ( x ) } { \big ( v ( x ) \big ) ^ 2 } \\\\ & = \dfrac { ( a x ^ 2 + b x + c ) ( 0 ) - ( 2 a x + b ) ( 1 ) }{ ( a x ^ 2 + b x + c ) ^ 2 } \\\\ & = \dfrac { - ( 2 a x + b ) }{ ( a x ^ 2 + b x + c ) ^ 2 } .\ _ \square \end {aligned} $$

مثال ۵ مشتق توابع کسری

اگر $$ y = \frac{ax + b}{cx + d} $$ باشد ($$|c| + |d| \neq 0$$)، آنگاه حاصل $$ \frac{dy}{dx} $$ را بیابید.

حل: تابع را به صورت $$ y = \frac{u(x)}{v(x)} $$ می‌نویسیم که در آن، $$ u(x) = ax + b \implies u'(x) = a $$ و $$ v(x) = cx + d \implies v'(x) = c $$ است. بنابراین، مشتق $$ y = \frac { u ( x ) } { v ( x ) } $$ به شکل زیر محاسبه می‌شود:

$$ \large \begin {aligned} \dfrac { d y } { d x } & = \dfrac { d } { d x } \left ( \dfrac { u ( x ) } { v ( x ) } \right ) \\\\ & = \dfrac { v ( x ) u' ( x ) - v' ( x ) u ( x ) } { \big ( v ( x ) \big ) ^ 2 } \\\\ & = \dfrac { ( c x + d ) ( a ) - ( c ) ( a x + b ) } { ( c x + d ) ^ 2 } \\\\ & = \dfrac { a d - b c } { ( c x + d ) ^ 2 } . \ _ \square \end {aligned} $$

مثال ۶ مشتق توابع کسری

اگر $$ y = \frac { 1 - x \sqrt { x } } { 1 + x \sqrt { x } } $$ باشد، آنگاه حاصل $$ \frac{dy}{dx} $$ را بیابید.

حل: تابع را به صورت $$ y = \frac{u(x)}{v(x)} $$ می‌نویسیم که در آن، $$ u ( x ) = 1 - x \sqrt { x } \implies u' ( x ) = 0 - \sqrt { x } - \frac { x } { 2 \sqrt { x } } = - \frac { 3 \sqrt { x } } { 2 } $$ و $$ v ( x ) = 1 + x \sqrt { x } \implies v' ( x ) = 0 + \sqrt { x } + \frac { x } { 2 \sqrt { x } } = \frac { 3 \sqrt { x } } { 2 } $$ است. بنابراین، خواهیم داشت:

$$ \large \begin {aligned} y & = \dfrac { u ( x ) } { v ( x ) } \\\\ \Rightarrow \dfrac { d y } { d x } & = \dfrac { v ( x ) u' ( x ) - v' ( x ) u ( x ) } { \big ( v ( x ) \big ) ^ 2 } \\\\ & = \dfrac { ( 1 + x \sqrt { x } ) \left ( - \dfrac { 3 \sqrt { x } } { 2 } \right ) - \left ( \dfrac { 3 \sqrt { x } } { 2 } \right ) ( 1 - x \sqrt { x } ) } { ( 1 + x \sqrt { x } ) ^ 2 } \\\\ & = \dfrac { - 3 \sqrt { x } - 3 x ^ 2 - ( 3 \sqrt { x } - 3 x ^ 2 ) } { 2 ( 1 + x \sqrt { x } ) ^ 2 } \\\\ & = \dfrac { - 6 \sqrt { x } } { 2 ( 1 + x \sqrt { x } ) ^ 2 } \\\\ & = - \dfrac { 3 \sqrt { x } } { ( 1 + x \sqrt { x } ) ^ 2 } . \ _ \square \end {aligned} $$

مثال ۷ مشتق توابع کسری

مشتق تابع $$ f ( x ) = \frac { x ^ 2 + 1 } { x } $$ را محاسبه کنید.

حل: از آنجا که $$ (x^2+1)' = 2x $$ و $$ (x)' = 1 $$، داریم:

$$ \large \begin {aligned} f' ( x ) & = \frac { x ( 2 x ) -( 1 ) \big ( x ^ 2 + 1 \big ) } { x ^ 2 } \\ & = \frac { 2 x ^ 2 - x ^ 2 - 1 } { x ^ 2 } \\ & = \frac { x ^ 2 - 1 } { x ^ 2 } . \ _ \square \end {aligned} $$

مثال ۸ مشتق توابع کسری

مشتق تابع $$ f ( x ) = \frac { e ^ x } {x ^ 2 } $$ را محاسبه کنید.

حل: از آنجا که $$ (e^x)'=e^x $$ و $$ \big(x^2\big)'=2x $$، خواهیم داشت:

$$ \large \begin {aligned} f' ( x ) & = \frac { \big ( x ^ 2 \big ) ( e ^ x ) - ( 2 x ) ( e ^ x ) } { x ^ 4 } \\ & = \frac { x ^ 2 e ^ x - 2 x e ^ x } { x ^ 4 } \\ & = \frac { x e ^ x - 2 e ^ x } { x ^ 3 } . \ _ \square \end {aligned} $$

مثال ۹ مشتق توابع کسری

اگر $$ \displaystyle f ( x ) = \frac { \sin x } { x ^ 3 } $$ باشد، مقدار $$ f' (x)$$ را به دست آورید.

حل: از آنجا که $$(\sin x)'=\cos x$$ و $$\left(x^3\right)'=3x^2$$، می‌توان نوشت:

$$ \large \begin {aligned} f' ( x ) & = \frac { \left ( x ^ 3 \right ) \left ( \cos x \right ) - \left ( \sin x \right ) \left ( 3 x ^ 2 \right ) } { x ^ 6 } \\ & = \frac { x ^ 2 \left ( x \cos x - 3 \sin x \right ) } { x ^ 6 } \\ & = \frac { x \cos x - 3 \sin x } { x ^ 4 } . \ _ \square \end {aligned} $$

مثال ۱۰ مشتق توابع کسری

مشتق تابع زیر را به دست آورید:

$$ \large f ( x ) = \frac { e ^ { \cos x } + \tan x } { e ^ { 3 x } } . $$

حل: با توجه به $$(e^{\cos x} + \tan x)'=-\sin x e^{\cos x} + \sec ^2 x$$ و $$ \big(e^{3x}\big)' = 3e^{3x} $$، خواهیم داشت:

$$ \large \begin {aligned} f' ( x ) & = \frac { \big ( e ^ { 3 x } \big ) ( - \sin x e ^ { \cos x } + \sec ^ 2 x ) - \big ( 3 e ^ { 3 x } \big ) ( e ^ { \cos x } + \tan x ) } { ( e ^ { 3 x } ) ^ 2 } \\ & = \frac { ( - \sin x e ^ { \cos x } + \sec ^ 2 x ) - 3 ( e ^ { \cos x } + \tan x ) } { e ^ { 3 x } } \\ & = \frac { - \sin x e ^ { \cos x } + \sec ^ 2 x - 3 e ^ { \cos x } - 3 \tan x }{ e ^ { 3 x } } . \ _ \square \end {aligned} $$

مثال ۱۱ مشتق توابع کسری

مشتق تابع کسری زیر را به دست آورید:

$$ \large f (x) = - \frac { x ^ 2 + 1 } { ( x ^ 2 - 1 ) ^ 2 } $$

حل: مشتق این تابع به صورت زیر به دست می‌آید:

$$ \large \begin {align*}
\frac { d } { d x } \left ( - \frac { x ^ 2 + 1 } { ( x ^ 2 - 1 ) ^ 2 } \right ) & = - \frac { d } { d x } \left ( \frac { x ^ 2 + 1 } { ( x ^ 2 - 1 ) ^ 2 } \right ) \\
& = - \left ( \frac { ( x ^ 2 - 1 ) ^ 2 ( x ^ 2 + 1 )' - ( x ^ 2 + 1 ) \left ( ( x ^ 2 - 1 ) ^ 2 \right )' } { \left ( ( x ^ 2 - 1 ) ^ 2 \right ) ^ 2 } \right ) \\
& = - \frac { ( x ^ 2 - 1 ) ^ 2 ( 2 x ) - ( x ^ 2 + 1 ) \left ( 2 ( x ^ 2 - 1 ) ( x ^ 2 - 1 )' \right ) } { ( x ^ 2 - 1 ) ^ 4 } \\
& = - \frac { 2 x ( x ^ 2 - 1 ) ^ 2 - ( x ^ 2 + 1 ) ( 2 ( x ^ 2 - 1 ) 2 x ) } { ( x ^ 2 - 1 ) ^ 4 } \\
& = - \frac { 2 x ( x ^ 2 - 1 ) ^ 2 - 4 x ( x ^ 2 + 1 ) ( x ^ 2 - 1 ) } { ( x ^ 2 - 1 ) ^ 4 } \\
& = - \frac { 2 x ( x ^ 2 - 1 ) \left ( ( x ^ 2 - 1 ) - 2 ( x ^ 2 + 1 ) \right ) } { ( x ^ 2 - 1 ) ^ 4 } \\
& = - \frac { 2 x ( x ^ 2 - 1 ) \left ( x ^ 2 - 1 - 2 x ^ 2 - 2 \right ) } { ( x ^ 2 - 1 ) ^ 4 } \\
& = - \frac { 2 x ( x ^ 2 - 1 ) ( - x ^ 2 - 3 ) } { ( x ^ 2 - 1 ) ^ 4 } \\
& = - \frac { 2 x ( - x ^ 2 - 3 ) } { ( x ^ 2 - 1 ) ^ 3 } \\
& = - \frac { - 2 x ( x ^ 2 + 3 ) } { ( x ^ 2 - 1 ) ^ 3 } \\
& = - ( - 2 ) \frac { x ( x ^ 2 + 3 ) } { ( x ^ 2 - 1 ) ^ 3 } \\
& = 2 \frac { x ( x ^ 2 + 3 ) } { ( x ^ 2 - 1 ) ^ 3 } .
\end {align*} $$

مثال ۱۲ مشتق توابع کسری

مشتق تابع تانژانت را محاسبه کنید.

حل: با توجه به اینکه تانژانت برابر با نسبت سینوس به کسینوس است، می‌توان مشتق آن را به صورت زیر محاسبه کرد:

$$ \large \begin {aligned}
\frac { d } { d x } \tan ( x ) & = \frac { d } { d x } \left ( \frac { \sin ( x ) } { \cos ( x ) } \right ) \\
& = \frac { ( \cos ( x ) ) ( \cos ( x ) ) - ( \sin ( x ) ) ( - \sin ( x ) ) } { \cos ^ { 2 } ( x ) } \\
& = \frac { \cos ^ { 2 } ( x ) + \sin ^ { 2 } (x ) } { \cos ^ { 2 } ( x ) } \\
& = \frac { 1 } { \cos ^ { 2 } ( x ) } \\
& = \sec ^ { 2 } ( x )
\end {aligned} $$

مثال ۱۳ مشتق توابع کسری

مشتق تابع کتانژانت را محاسبه کنید.

حل: با توجه به اینکه کتانژانت برابر با نسبت کسینوس به سینوس است، می‌توان مشتق آن را به صورت زیر محاسبه کرد:

$$ \large \begin {aligned}
\frac { d } { d x } \cot ( x ) & = \frac { d } { d x} \left ( \frac { \cos ( x ) } { \sin ( x ) } \right ) \\
& = \frac { ( \sin ( x ) ) ( - \sin ( x ) ) - ( \cos ( x ) ) ( \cos ( x ) ) } { \sin ^ { 2 } ( x ) } \\
& = - \frac { \sin ^ { 2 } ( x ) + \cos ^ { 2 } ( x ) } { \sin ^ { 2 } ( x ) } \\
& = - \frac { 1 } { \sin ^ { 2 } ( x ) } \\
& = - \csc ^ { 2 } ( x )
\end {aligned} $$

مثال ۱۴ مشتق توابع کسری

مشتق تابع سکانت را محاسبه کنید.

حل: با توجه به اینکه سکانت عکس کسینوس است، می‌توان مشتق آن را به صورت زیر محاسبه کرد:

$$ \large \begin {aligned}
\frac { d } { d x } \sec ( x ) & = \frac { d } { d x } \frac { 1 } { \cos ( x ) } \\
& = \frac { \cos ( x ) ( 0 ) - ( - \sin ( x ) ) } { \cos ^ { 2 }( x ) } \\
& = \frac { \sin ( x ) } { \cos ^ { 2 } ( x ) } \\
& = \frac { 1 } { \cos ( x ) } \frac { \sin ( x ) } { \cos ( x ) } \\
& = \sec ( x ) \tan ( x )
\end {aligned} $$

مثال ۱۵ مشتق توابع کسری

مشتق تابع کسکانت را محاسبه کنید.

حل: با توجه به اینکه کسکانت عکس سینوس است، می‌توان مشتق آن را به صورت زیر محاسبه کرد:

$$ \large \begin {aligned}
\frac { d } { d x } \csc ( x ) & = \frac { d } { d x } \frac { 1 } { \sin ( x ) } \\
& = \frac { \sin ( x ) ( 0 ) - \cos ( x ) } { \sin ^ { 2 } ( x ) } \\
& = - \frac { \cos ( x ) } { \sin ^ { 2 } ( x ) } \\
& = - \frac { 1 } { \sin ( x ) } \frac { \cos ( x ) } { \sin ( x ) } \\
& = - \csc ( x ) \cot ( x )
\end {aligned} $$

مثال ۱۶ مشتق توابع کسری

مشتق تابع زیر را محاسبه کنید:

$$ \large y = \frac { { { e ^ x } – { e ^ { – x } } } } { { { e ^ x } + { e ^ { – x } } } } $$

حل: با استفاده از قاعده زنجیره‌ای و قاعده خارج قسمت، خواهیم داشت:

$$ \large \require {cancel} \begin {align*} y ^ \prime & = \left ( { \frac { { { e ^ x } – { e ^ { – x } } } } { { { e ^ x } + { e ^ { – x } } } } } \right ) ^ \prime = { \frac { { \left ( { { e ^ x } + { e ^ { – x } } } \right ) \left ( { { e ^ x } + { e ^ { – x } } } \right ) – \left ( { { e ^ x } – { e ^ { – x } } } \right ) \left ( { { e ^ x } – { e ^ { – x } } } \right ) } }{ {{ { \left ( { { e ^ x } + { e ^ { – x } } } \right ) } ^ 2 } } } } = { \frac { { { { \left ( { { e ^ x } + { e ^ { – x } } } \right ) } ^ 2 } – { { \left ( { { e ^ x } – { e ^ { – x } } } \right ) } ^ 2 } } } { { { { \left ( { { e ^ x } + { e ^ { – x } } } \right ) } ^ 2 } } } } \\ & = { \frac { { \cancel { e ^ { 2 x } } + 2 + \cancel { e ^ { – 2 x } } – \cancel { e ^ { – 2 x } } + 2 – \cancel { e ^ { – 2 x } } } } { { { { \left ( { { e ^ x } + { e ^ { – x } } } \right ) } ^ 2 } } } } = { \frac { 4 } { { { { \left ( { { e ^ x } + { e ^ { – x } } } \right ) } ^ 2 } } } . } \end {align*} $$

مثال ۱۷ مشتق توابع کسری

مشتق تابع $$ y = \frac { { { x ^ 2 } } } { { { 2 ^ x } } } $$ را به دست آورید.

حل: با استفاده از قاعده خارج قسمت برای مشتق توابع کسری می‌توان نوشت:

$$ \large \begin {align*}
\require {cancel} y’ \left ( x \right ) & = { \left ( { \frac { { { x ^ 2 } } } { { { 2 ^ x } } } } \right ) ^ \prime } = { \frac { { { { \left ( { { x ^ 2 } } \right ) } ^ \prime } \cdot { 2 ^ x } – { x ^ 2 } \cdot { { \left ( { { 2 ^ x } } \right ) } ^ \prime } } } { { { { \left ( { { 2 ^ x } } \right ) } ^ 2 } } } } = { \frac { { 2 x \cdot { 2 ^ x } – { x ^ 2 } \cdot { 2 ^ x } \ln 2 } } { { { { \left ( { { 2 ^ x } } \right ) } ^ 2 } } } } \\ & = { \frac { { x \cancel { 2 ^ x } \left ( { 2 – x \ln 2 } \right ) } } { { { { \left ( { { 2 ^ x } } \right ) } ^ { \cancel { 2 } } } } } } = { \frac { { x \left ( { 2 – x \ln 2 } \right ) } } {{ { 2 ^ x } } } . \; \; }
\end {align*} $$

مثال ۱۸ مشتق توابع کسری

مشتق تابع $$ y = { \large \frac { { 1 + \cos x } } { { \sin x } } \normalsize } $$ را محاسبه کنید.

حل: با استفاده از قاعده خارج قسمت می‌توان نوشت:

$$ \large \begin {align*}
\require {cancel} y’ \left ( x \right ) & = { \left ( { \frac { { 1 + \cos x } } { { \sin x } } } \right ) ^ \prime } = { \frac { { \left ( { – \sin x } \right ) \sin x – \left ( { 1 + \cos x } \right ) \cos x } } { { { { \sin } ^ 2 } x } } } \\ & = { \frac { { – { { \sin } ^ 2 } x – \cos x – { { \cos } ^ 2 } x } } { { { { \sin } ^ 2 } x } } } = { \frac { { – \left ( { { { \sin } ^ 2 } x + { { \cos } ^ 2 } x } \right ) – \cos x } } { { { { \sin } ^ 2 } x } } } \\ &= { \frac { { – 1 – \cos x } } { { { { \sin } ^ 2 } x } } = \frac { { – 1 – \cos x } } { { 1 – { { \cos } ^ 2 } x } } } = { \frac { { – \cancel { \left ( { 1 + \cos x } \right ) } } } { { \left ( { 1 – \cos x } \right ) \cancel { \left ( { 1 + \cos x } \right ) } } } } \\ & = { \frac { { – 1 } } { { 1 – \cos x } } = \frac { 1 } { { \cos x – 1 } } . } \end {align*} $$

توجه کنید که دامنه عبارت نهایی مشتق متفاوت از دامنه تابع اصلی است. این امر به دلیل حذف ریشه در هنگام ساده کردن عبارت $${\left( {1 + \cos x} \right)} $$ از صورت و مخرج است. در حقیقت، دامنه تابع اصلی و مشتق آن کل مجموعه اعداد حقیقی است، به جز $$x = \pi n,\;n \in \mathbb{Z}$$.

مثال ۱۹ مشتق توابع کسری

مشتق تابع $$ y = {\large\frac{{\sqrt x – 1}}{{\sqrt x + 1}}\normalsize} $$ را محاسبه کنید.

حل: با استفاده از قاعده خارج قسمت، خواهیم داشت:

$$ \large \begin {align*}
\require {cancel} y’ \left ( x \right ) & = { { \left ( { \frac { { \sqrt x – 1 } } { { \sqrt x + 1 } } } \right ) ^ \prime } } = { \frac { { \large \frac { 1 } { { 2 \sqrt x } } \normalsize \left ( { \sqrt x + 1 } \right ) – \left ( { \sqrt x – 1 } \right ) \large \frac { 1 } { { 2 \sqrt x } } \normalsize } } { { { { \left ( { \sqrt x + 1 } \right ) } ^ 2 } } } } \\ & = { \frac { { \large \frac { 1 } { { 2 \sqrt x } } \normalsize \left ( { \cancel { \color {blue}{ \sqrt x } } + \color {red} { 1 } – \cancel { \color {blue} { \sqrt x } } + \color {red} { 1 } } \right ) } } { { { { \left ( { \sqrt x + 1 } \right ) } ^ 2 } } } } = { \frac { { \large \frac { 1 } { { 2 \sqrt x } } \normalsize \cdot \color {red} { 2 } } } { { { { \left ( { \sqrt x + 1 } \right ) } ^ 2 } } } } = { \frac { 1 } { { \sqrt x { { \left ( { \sqrt x + 1 } \right ) } ^ 2 } } } . } \end {align*} $$

مثال ۲۰ مشتق توابع کسری

مشتق تابع $$ f \left ( x \right ) = { \large \frac { { u \left ( x \right ) v \left ( x \right ) } } { { w \left ( x \right ) } } \normalsize } $$ ا محاسبه کنید.

حل: ابتدا با استفاده از قاعده خارج قسمت از تابع مشتق می‌گیریم:

$$ \large { f’ \left ( x \right ) = { \left ( { \frac { { u v } } { w } } \right ) ^ \prime } } = { \frac { { { { \left ( { u v } \right ) } ^ \prime } \cdot w – u v \cdot w’ } } { { { w ^ 2 } } } . } $$

در ادامه، با استفاده از قاعده زنجیره‌ای، خواهیم داشت:

$$ \large \begin {align*}
f’ \left ( x \right ) & = { \frac { { { { \left ( { u v } \right ) } ^ \prime } \cdot w – u v \cdot w’ } } { { { w ^ 2 } } } } = { \frac { { \left ( { u’ v + u v’ } \right ) w – u v w’ } } { { { w ^ 2 } } } } \\ & = { \frac { { u’ v w + u v’ w – u v w’ } } { { { w ^ 2 } } } . } \end {align*} $$

مثال ۲۱ مشتق توابع کسری

مشتق تابع $$ y = \frac { { { { \log } _ 2 } \left ( { { x ^ 2 } } \right ) } } { { { x ^ 2 } } } $$ را به دست آورید.

حل: با استفاده از قاعده خارج قسمت، داریم:

$$ \large { y’ \left ( x \right ) = { \left ( { \frac { { { { \log } _2 } \left ( { { x ^ 2 } } \right ) } } { { { x ^ 2 } } } } \right ) ^ \prime } } = { \frac { { \frac { { 2 { x ^ 3 } } } {{ { x ^ 2 } \ln 2 } } – 2 x { { \log } _ 2 } \left ( { { x ^ 2 } } \right ) } }{ { { x ^ 4 } } } } = { \frac { { 2 \left [ { 1 – { { \log } _ 2 } \left ( { { x ^ 2 } } \right ) \ln 2 } \right ] } } { { { x ^ 3 } \ln 2 } } } $$

که در آن، $$x \ne 0 $$ است.

مثال ۲۲ مشتق توابع کسری

مشتق تابع زیر را محاسبه کنید:

$$ \large y = \frac { { { { \sin } ^ 2 } x } } { { 1 + \cot x } } + \frac { { { { \cos } ^ 2 } x } } { { 1 + \tan x } } $$

حل: ابتدا تابع را برحسب جملات سینوس و کسینوس ساده می‌کنیم:

$$ \large \begin {align*}
y & = \frac { { { { \sin } ^ 2 } x } } { { 1 + \cot x } } + \frac { { { { \cos } ^ 2 } x } } { { 1 + \tan x } } = { \frac { { { { \sin } ^ 2 } x } } { { 1 + \frac { { \cos x } } { { \sin x } } } } + \frac { { { { \cos } ^ 2 } x } } { { 1 + \frac { { \sin x } } { { \cos x } } } } } \\ & = { \frac { { { { \sin } ^ 2 } x } } { { \frac { { \sin x + \cos x } } { { \sin x } } } } + \frac { { { { \cos } ^ 2 } x } } { { \frac { { \cos x + \sin x } } { { \cos x } } } } } = { \frac { { { { \sin } ^ 3 } x } } { { \sin x + \cos x } } + \frac { { { { \cos } ^ 3 } x } }{ { \sin x + \cos x } } } \\ & = { \frac { { { { \sin } ^ 3 } x + { { \cos } ^ 3 } x } } { { \sin x + \cos x } } . }
\end {align*} $$

از اتحاد چاق و لاغر برای صورت کسر استفاده می‌کنیم:

$$ \large { { a ^ 3 } + { b ^ 3 } } = { \left ( { a + b } \right ) \left ( { { a ^ 2 } – a b + { b ^ 2 } } \right ) } $$

بنابراین، تابع به فرم زیر در می‌آید:

$$ \large y = { \sin ^ 2 } x – \sin x \cos x + { \cos ^ 2 } x . $$

اکنون از قاعده زنجیره‌ای و ضرب استفاده می‌کنیم و از تابع مشتق می‌گیریم:

$$ \large \begin {align*} \require {cancel}
y ^ \prime & = \left ( { { { \sin } ^ 2 } x } \right ) ^ \prime - { \left ( { \sin x \cos x } \right ) ^ \prime } + { \left ( { { { \cos } ^ 2 } x } \right ) ^ \prime } \\ &= { 2 \sin \cos x } - { \left ( { \sin x } \right ) ^ \prime \cos x } - { \sin x\left ( { \cos x } \right ) ^ \prime } + { 2 \cos x \left ( { – \sin x } \right ) } \\ & = { \cancel { 2 \sin x \cos x } } - { { \cos ^ 2 } x } + { { \sin ^ 2 } x } - { \cancel { 2 \sin x \cos x } } \\ & = { – \left ( { { { \cos } ^ 2 } x – { { \sin } ^ 2 } x } \right ) } = { – \cos 2 x . }
\end {align*} $$

مثال ۲۳ مشتق توابع کسری

مشتق مرتبه $$n$$اُم تابع $$ \large y = \large { \frac { 1 } { { 1 – 5 x } } } \normalsize $$ را به دست آورید.

حل: ابتدا مشتق اول تابع را با استفاده از قاعده توان و زنجیره‌ای می‌نویسیم:

$$ \large \begin {align*}
y ^ \prime & = \left ( { \frac { 1 } { { 1 – 5 x } } } \right ) ^ \prime = { \left ( { { { \left ( { 1 – 5 x } \right ) } ^ { – 1 } } } \right ) ^ \prime } = { – 1 \cdot { \left ( { 1 – 5 x } \right ) ^ { – 2 } } \cdot \left ( { 1 – 5 x } \right ) ^ \prime } \\ & = { – 1 \cdot { \left ( { 1 – 5 x } \right ) ^ { – 2 } } \cdot \left ( { – 5 } \right ) } = { 1 \cdot { \left ( { 1 – 5 x } \right ) ^ { – 2 } } \cdot 5 } = { \frac { { 1 \cdot 5 } }{ { { { \left ( { 1 – 5 x } \right ) } ^ 2 } } } ; }
\end {align*} $$

مشتق دوم و سوم و چهارم نیز به صورت زیر هستند:

$$ \large \begin {align*}
y ^ { \prime \prime } & = \left ( { 1 \cdot { { \left ( { 1 – 5 x } \right ) } ^ { – 2 } } \cdot 5 } \right ) ^ \prime = { 1 \cdot \left ( { – 2 } \right ) \cdot { \left ( { 1 – 5 x } \right ) ^ { – 3 } } \cdot 5 \cdot \left ( { – 5 } \right ) } \\ & = { 2 ! \cdot { \left ( { 1 – 5 x } \right ) ^ { – 3 } } \cdot { 5 ^ 2 } } = { \frac { { 2 ! \, { 5 ^ 2 } } } { { { { \left ( { 1 – 5 x } \right ) } ^ 3 } } } ; }
\end {align*} $$

$$ \large \begin {align*}
y ^ { \prime \prime \prime } & = \left ( { 2 ! \cdot { { \left ( { 1 – 5 x } \right ) } ^ { – 3 } } \cdot { 5 ^ 2 } } \right ) ^ \prime = { 2 ! \cdot \left ( { – 3 } \right ) \cdot { \left ( { 1 – 5 x } \right ) ^ { – 4 } } \cdot { 5 ^ 2 } \cdot \left ( { – 5 } \right ) } \\ & = { 3 ! \cdot { \left ( { 1 – 5 x } \right ) ^ { – 4 } } \cdot { 5 ^ 3 } } = { \frac { { 3 ! \, { 5 ^ 3 } } }{ { { { \left ( { 1 – 5 x } \right ) } ^ 4 } } } ; }
\end {align*} $$

$$ \large \begin {align*}
{ y ^ { \left ( 4 \right ) } } & = \left ( { 3 ! \cdot { { \left ( { 1 – 5 x } \right ) } ^ { – 4 } } \cdot { 5 ^ 3 } } \right ) ^ \prime = { 3 ! \cdot \left ( { – 4 } \right ) \cdot { \left ( { 1 – 5 x } \right ) ^ { – 5 } } \cdot { 5 ^ 3 } \cdot \left ( { – 5 } \right ) } \\ & = { 4 ! \cdot { \left ( { 1 – 5 x } \right ) ^ { – 5 } } \cdot { 5 ^ 4 } } = { \frac { { 4 ! \, { 5 ^ 4 } } } { { { { \left ( { 1 – 5 x } \right ) } ^ 5 } } } . }
\end {align*} $$

بنابراین، مشتق مرتبه $$n$$اُم تابع برابر خواهد بود با:

$$ \large { y ^ { \left ( n \right ) } } = \frac { { n ! \, { 5 ^ n } } } { { { { \left ( { 1 – 5 x } \right ) } ^ { n + 1 } } } } . $$

مثال ۲۴ مشتق توابع کسری

مشتق تابع کسری زیر را بیابید:

$$ \large { y \left ( x \right ) } = { \frac { { { { \left ( { x + 1 } \right ) } ^ 2 } } } { { { { \left ( { x + 2 } \right ) } ^ 3 }{ { \left ( { x + 3 } \right ) } ^ 4 } } } , \; \; } \kern-0.3pt { x \gt – 1 } $$

حل: اگر از قاعده خارج قسمت مشتق توابع کسری استفاده کنیم، محاسبات بسیار طولانی خواهند بود. بنابراین، از دو طرف تابع لگاریتم می‌گیریم:

$$ \large \begin {align*}
\ln y & = \ln \frac { { { { \left ( { x + 1 } \right ) } ^ 2 } } }{ { { { \left ( { x + 2 } \right ) } ^ 3 } { { \left ( { x + 3 } \right ) } ^ 4 } } } , \; \; \\ &\Rightarrow { \ln y = \ln { \left ( { x + 1 } \right ) ^ 2 } } - { \ln { \left ( { x + 2 } \right ) ^ 3 } } - { \ln { \left ( { x + 3 } \right ) ^ 4 } , \; \; } \\ & \Rightarrow { \ln y = 2 \ln \left ( { x + 1 } \right ) } - { 3 \ln \left ( { x + 2 } \right ) } - { 4 \ln \left ( { x + 3 } \right ) . } \end {align*} $$

اکنون از دو طرف عبارت بالا مشتق می‌گیریم و مشتق تابع اصلی را به دست می‌آوریم:

$$ \large \begin {align*}
{ \frac { { y’ } } { y } } & = { \frac { 2 } { { x + 1 } } } - { \frac { 3 } { { x + 2 } } } - { \frac { 4 } { { x + 3 } } , \; \; } \Rightarrow { y’ = y \cdot } \kern0pt { \left ( { \frac { 2 } { { x + 1 } } – \frac { 3 } { { x + 2 } } – \frac { 4 } { { x + 3 } } } \right ) , \; \; } \\ & \Rightarrow { y’ = \frac { {{ { \left ( { x + 1 } \right ) } ^ 2 } } } { { { { \left ( { x + 2 } \right ) } ^ 3 } { { \left ( { x + 3 } \right ) } ^ 4 } } } \cdot } \kern0pt { \left ( { \frac { 2 } { { x + 1 } } – \frac { 3 } { { x + 2 } } – \frac { 4 } { { x + 3 } } } \right ) . } \end {align*} $$