فرمول مساحت مثلث چیست؟ – تمام فرمول ها + حل تمرین
فرمول مساحت هر مثلثی برابر است با نصف حاصلضرب قاعده در ارتفاع آن. البته فرمولهای دیگری نظیر فرمول هرون، فرمول مثلثاتی (فرمول سینوس) و فرمول برداری نیز برای محاسبه مساحت مثلث مورد استفاده قرار میگیرند. در این آموزش از مجله فرادرس، به معرفی فرمولهای پرکاربرد مساحت مثلث همراه با حل چند مثال میپردازیم. همچنین در آخرین بخش از این مطلب، فرمول کلی مساحت مثلث را اثبات میکنیم.
- با انواع فرمولهای مساحت مثلث آشنا میشوید.
- یاد میگیرید که چگونه مساحت مثلث قائمالزاویه را محاسبه کنید.
- روش پیدا کردن مساحت مثلث را با داشتن سه ضلع و توسط فرمول هرون یاد میگیرید.
- میآموزید که روش سینوس چگونه مساحت مثلث را به دست میدهد.
- با مثلث و اجزای آن مانند قاعده و ارتفاع آشنا میشوید.
- فرمول مساحت مثلث با سه راس را خواهید شناخت.


فرمول مساحت مثلث چیست؟
شناخته شدهترین و پرکاربردترین فرمول برای محاسبه مساحت مثلث برابر است با قاعده ضرب در ارتفاع تقسیم بر دو. در واقع فرم ریاضی فرمول مساحت مثلثی با قاعده b و ارتفاع h به صورت زیر نوشته میشود:
- A: حرف اول کلمه انگلیسی «Area» به معنای «مساحت»
- h: حرف اول کلمه انگلیسی «height» به معنای «ارتفاع»
- b: حرف اول کلمه انگلیسی «base» به معنای «قاعده»
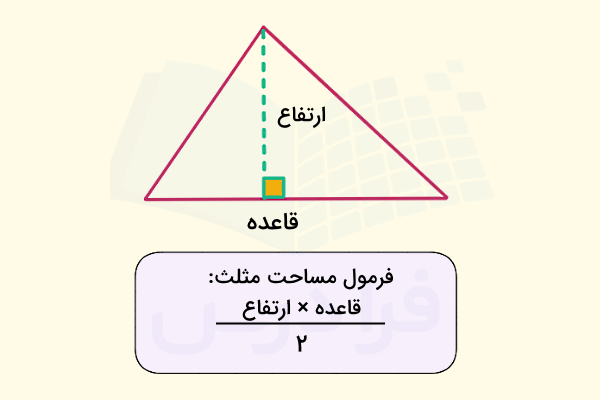
همانطور که مشاهده میکنید، برای بهدست آوردن مساحت مثلث ابتدا باید قاعده و ارتفاع آن را تعیین کرد. به همین دلیل، آشنایی با این مفاهیم از اهمیت بالایی برخوردار است و در بخشهای بعد به آن خواهیم پرداخت.
جدول فرمول های مساحت مثلث
جدول زیر پرکاربردترین فرمولهای محاسبه مثلث را بر اساس دادههای مسئله و نوع مثلث نمایش میدهد. در بخشهای بعدی، با ارائه مثال هر کدام را بیشتر توضیح میدهیم:
| نوع مثلث | فرمول مساحت مثلث |
| تمام مثلثها با قاعده b و ارتفاع h | |
| متساوی الاضلاع | فرمول با ضلع a: |
| فرمول با ارتفاع h: | |
| متساوی الساقین قائم الزاویه | فرمول با ساق a: |
| فرمول با وتر c: | |
| قائم الزاویه با ضلع a و وتر c | |
| تمام مثلثها با داشتن سه ضلع | |
| تمام مثلثها با داشتن دو ضلع و زاویه بین | |
| تمام مثلثها | |
| مختصات دو بعدی سه راس | |
| مختصات سه بعدی سه راس |
مساحت مثلث چیست؟
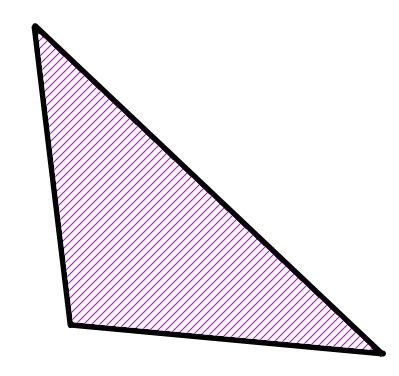
مساحت (به انگلیسی Area)، اندازه سطح قرار گرفته در داخل ضلعهای یک شکل بسته هندسی است. سطح درون ضلعهای مثلث، با عنوان مساحت مثلث شناخته میشود. در تصویر زیر، ناحیه هاشور خورده، مساحت مثلث را نمایش میدهد.
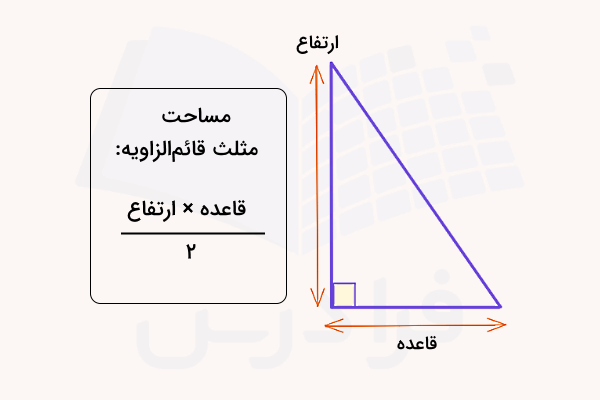
قاعده و ارتفاع مثلث چه هستند؟
در مطالب قبل از سری مطالب مجله فرادرس در مورد مثلث صحبت کردیم. مثلث، یکی از شکلهای چند ضلعی و بسته دو بعدی است که از سه ضلع و سه راس تشکیل میشود. تصویر زیر، نمونهای از یک مثلث مختلف اضلاع را نمایش میدهد.
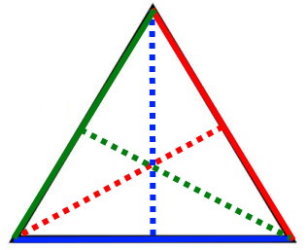
در مطلب «قاعده چیست؟ | قاعده در اشکال هندسی به زبان ساده» از مجله فرادرس قاعده را در حالت کلی تعریف کردیم. در مثلث، به ضلع مورد استفاده برای محاسبه مساحت مثلث، قاعده مثلث میگویند. هر مثلث دارای سه قاعده است. به فاصله عمودی بین راس تا قاعده مثلث، ارتفاع مثلث گفته میشود. هر مثلث دارای سه قاعده و سه ارتفاع است. تصویر زیر، قاعدهها و ارتفاعهای نظیر در یک مثلث متساوی الاضلاع را نمایش میدهد.
مثال
مساحت مثلثی به قاعده ۷ و ارتفاع ۶ چقدر است؟
پاسخ
به دلیل مشخص بودن قاعده و ارتفاع، فرمول مساحت مثلث با قاعده و ارتفاع را مینویسیم:
- A: مساحت
- h: ارتفاع مثلث و برابر ۶
- b: قاعده مثلث و برابر ۷
اندازههای داده شده را در فرمول بالا قرار میدهیم:
مساحت مثلث برابر ۲۱ است.
فرمول مساحت مثلث متساوی الاضلاع
مثلث متساوی الاضلاع، مثلثی با طول ضلعهای برابر است. یکسان بودن اندازه ضلعها، امکان محاسبه مساحت این مثلث را با یک فرمول اختصاصی فراهم میکند.
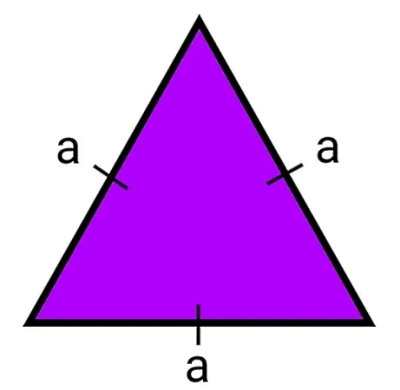
رابطه معرفی شده در بخش قبلی، به عنوان یک رابطه کلی بین قاعده، ارتفاع و مساحت مثلث شناخته میشود. فرمول مساحت مثلث متساوی الاضلاع به ضلع a برابر است با:
- A: مساحت
- a: طول یکی از ضلعهای مثلث متساوی الاضلاع
در صورت مشخص بودن ارتفاع این مثلث، فرمول بالا را میتوان به صورت زیر بازنویسی کرد:
- A: مساحت
- h: طول یکی از ارتفاعهای مثلث متساوی الاضلاع
مثال
اندازه یکی از ضلعهای یک مثلث متساوی الاضلاع، برابر ۱۰ است. مساحت این مثلث و ارتفاع آن را محاسبه کنید.

پاسخ
به دلیل برابر بودن طول تمام ضلعها، میتوانیم از فرمول مساحت مثلث متساوی الاضلاع استفاده کنیم:
- A: مساحت
- a: اندازه ضلع مثلث برابر ۱۰
مساحت مثلث برابر است. برای به دست آوردن ارتفاع مثلث، فرمول کلی مساحت مثلث را مینویسیم:
- A: مساحت برابر
- b: قاعده مثلث برابر طول یکی از ضلعهای آن (۱۰)
- h: ارتفاع مثلث
اطلاعات مسئله و مساحت به دست آمده را درون فرمول کلی قرار میدهیم:
ارتفاع مثلث برابر است.
فرمول مساحت مثلث قائم الزاویه با وتر
مثلث قائم الزاویه، مثلثی با یک راس ۹۰ درجه است. به ضلعهای متصل به راس ۹۰ درجه، ساقهای مثلث و ضلع رو به روی این راس، وتر مثلث گفته میشود. ساقهای مثلث قائم الزاویه، قاعده و ارتفاع نظیر یکدیگر هستند.
مطابق با قضیه فیثاغورس، رابطه زیر بین ساقها و وتر مثلث قائم الزاویه برقرار است:
- c: وتر مثلث قائم الزاویه
- a: یکی از ساقهای مثلث
- b: ساق دیگر مثلث
در صورتی که اندازه یکی از ساقها و وتر مثلث قائم الزاویه مشخص باشد، اندازه ساق دیگر از رابطه فیثاغورس به دست میآید. از آنجایی که دو ساق، قاعده و ارتفاع نظیر یکدیگر هستند، مساحت مثلث با استفاده از فرمول کلی محاسبه میشود. البته با جانمایی قضیه فیثاغورس در فرمول کلی، به فرمول مساحت مثلث قائم الزاویه با وتر میرسیم:
- A: مساحت
- a: یکی از ساقهای مثلث قائم الزاویه
- c: وتر مثلث قائم الزاویه
مثال
مساحت یک مثلث قائم الزاویه با وتر ۵ و اندازه ساق ۴ را حساب کنید. طول ساق دیگر مثلث چقدر است؟
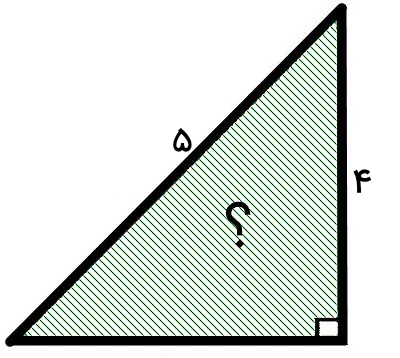
پاسخ
به دلیل داشتن اندازه ساق و وتر، امکان استفاده از فرمول مخصوص مساحت مثلث قائم الزاویه وجود دارد. این فرمول به صورت زیر نوشته میشود:
- A: مساحت
- a: یکی از ساقهای مثلث برابر ۴
- c: وتر مثلث برابر ۵
اندازههای مشخص را درون فرمول قرار میدهیم:
مساحت مثلث برابر ۶ است. به منظور محاسبه اندازه ساق دیگر، از فرمول کلی مساحت مثلث استفاده میکنیم:
- A: مساحت برابر ۶
- b: قاعده مثلث برابر اندازه یکی از ساقها (۴)
- h: اندازه ساق دیگر
مقادیر را درون فرمول قرار میدهیم:
ساق دیگر این مثلث برابر ۳ است. البته در دنیای مثلثهای قائم الزاویه و قضیه فیثاغورس، ترکیب اعداد ۳، ۴ و ۵ بسیار شناخته شده و قابل تشخیص هستند.
فرمول مساحت مثلث متساوی الساقین قائم الزاویه
مثلث متساوی الساقین، مثلثی با دو ضلع هم اندازه است. دو ضلع هم اندازه این مثلث با عنوان ساق شناخته میشوند. اگر زاویه بین ساقهای مثلث متساوی الساقین برابر ۹۰ درجه باشد، یکی از انواع خاص مثلث با عنوان «مثلث متساوی الساقین قائم الزاویه» به وجود میآید.
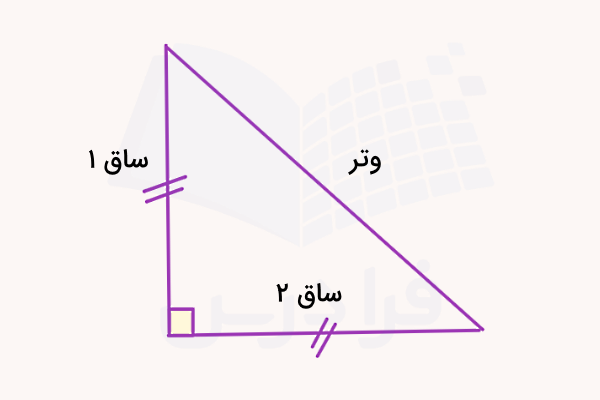
فرمول مساحت مثلث متساوی الساقین قائم الزاویه با ضلع a برابر است با:
به کمک قضیه فیثاغورس، فرمول مساحت مثلث متساوی الساقین قائم الزاویه با وتر c به صورت زیر نوشته میشود:
در این حالت خاص نیز مانند مثلث متساوی الاضلاع، داشتن یکی از اندازهها برای محاسبه مساحت کفایت میکند.
مثال ۱
اندازه هر دو ساق یک مثلث قائم الزاویه برابر ۹ است. مساحت این مثلث را محاسبه کنید.
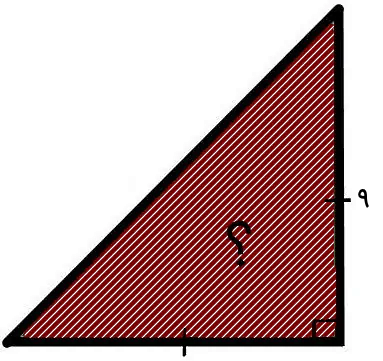
پاسخ
در صورت برابر بودن اندازه ساقهای یک مثلث قائم الزاویه، رابطه مخصوص محاسبه مساحت آن به صورت زیر خواهد بود:
- A: مساحت
- a: اندازه ساق برابر ۹
مثال ۲
مساحت مثلث قائم الزاویه زیر چند است؟
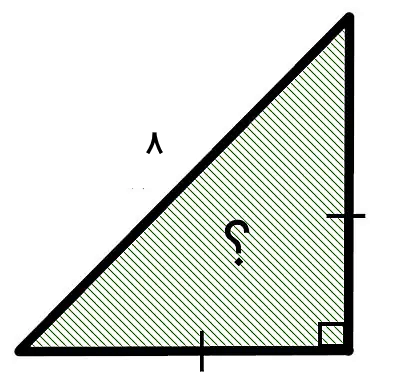
پاسخ
به دلیل برابر بودن اندازه ساقهای مثلث قائم الزاویه بالا، امکان محاسبه مساحت آن به صورت مستقیم و توسط اندازه وتر وجود دارد. فرمول مساحت مثلث متساوی الساقین قائم الزاویه با وتر برابر است با:
فرمول مساحت مثلث با سه ضلع یا فرمول هرون
فرمول هرون یک رابطه ریاضی است که به منظور محاسبه مساحت مثلثی با طول ضلعهای مشخص مورد استفاده قرار میگیرد.
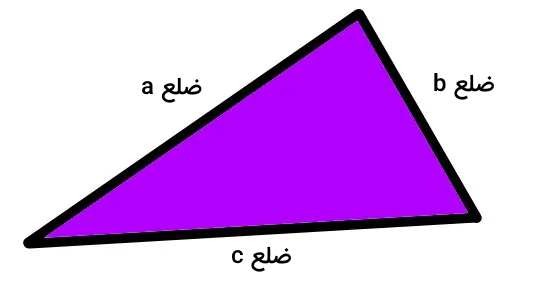
اگر اندازه هر ضلع مثلث معلوم باشد، فرمول مساحت مثلث به روش هرون به صورت زیر نوشته میشود:
- A: مساحت
- s: نصف محیط مثلث
- a: طول ضلع اول
- b: طول ضلع دوم
- c: طول ضلع سوم
نصف محیط مثلث از رابطه زیر به دست میآید:
نکته: برای مثلثهای متساوی الاضلاع، نیازی به نوشتن فرمول هرون به شکل بالا نیست. برای این مثلثها، همان رابطه خاص معرفی شده در بخشهای قبلی کفایت میکند.
مثال
مساحت مثلث مختلف الاضلاع با اندازه ضلعهای ۴، ۵ و ۶ را حساب کنید:
پاسخ
به دلیل معلوم بودن اندازه ضلعها، محاسبه مساحت مثلث را با استفاده از فرمول هرون انجام میدهیم:
- A: مساحت
- s: نصف محیط مثلث
- a: طول ضلع اول برابر ۴
- b: طول ضلع دوم برابر ۵
- c: طول ضلع سوم برابر ۶
پیش از جایگذاری اندازههای مشخص، نصف محیط مثلث را با فرمول زیر تعیین میکنیم:
اکنون، اندازه ضلعها و نصف محیط را درون فرمول هرون قرار میدهیم:
مساحت مثلث حدود ۹٫۹ است.
فرمول مساحت مثلث با سینوس
روابط و فرمولهای مثلثاتی، قانون سینوس ها و مقادیر سینوس زوایا از ابزارهای دیگری هستند که در محاسبه مساحت مثلث مورد استفاده قرار میگیرند. در صورت مشخص بودن دو ضلع و زاویه بین (مثلث ض ز ض)، دو زاویه و ضلع بین (مثلث ز ض ز)، دو ضلع و زاویه غیر بین (مثلث ض ض ز) و دو زاویه و ضلع غیر بین (مثلث ز ز ض)، میتوان از فرمول مساحت مثلث با سینوس استفاده کرد.
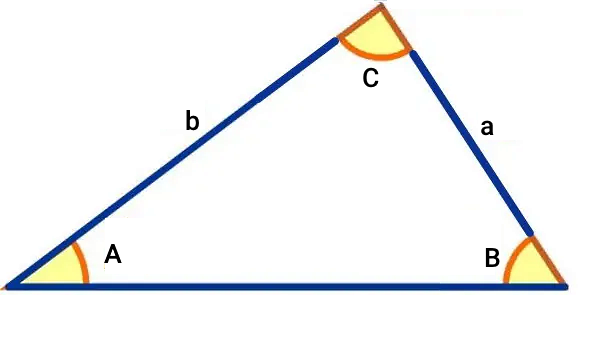
فرمول مساحت مثلث با دو ضلع و سینوس زاویه بین
اگر اندازه دو ضلع (مانند a و b) و زاویه بین این دو ضلع (A) مشخص باشد، مساحت مثلث از فرمول زیر به دست میآید:
- Area: مساحت
- a: طول ضلع CB
- b: طول ضلع AC
- C: زاویه راس C
فرمول مساحت مثلث با یک ضلع و سینوس زوایا
در صورت مشخص بودن اندازه دو زاویه (مانند A و B) و ضلع بین این دو زاویه (c)، مساحت مثلث از فرمول زیر محاسبه میشود:
- Area: مساحت
- c: طول ضلع AB
- A: زاویه راس A
- B:زاویه راس B
- C: زاویه راس C (زاویه سوم از قانون جمع زوایای داخلی)
فرمول مساحت مثلث با دو ضلع و زاویه غیر بین یا دو زاویه و ضلع غیر بین
در صورتی که دو ضلع و زاویه غیر بین یا دو زاویه و ضلع غیر بین مشخص باشد، محاسبه اندازههای نامشخص توسط قانون سینوسها صورت میگیرد:
- a: طول ضلع BC
- A: زاویه راس A
- b: طول ضلع AC
- B: زاویه راس B
- c: طول ضلع AB
- C: زاویه راس C
در مرحله بعدی، مساحت مثلث با استفاده از فرمول هرون یا یکی از دو فرمول قبلی تعیین میشود.
مثال
مساحت مثلث زیر چقدر را تعیین کنید:
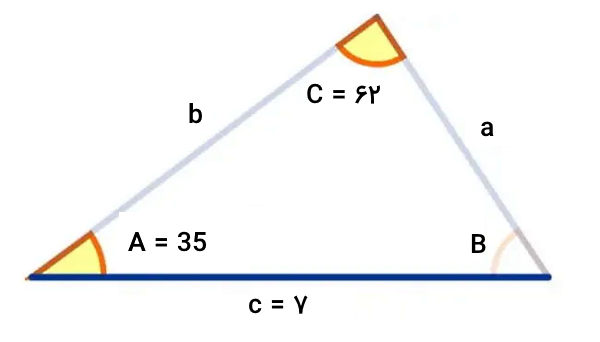
پاسخ
در مثلث بالا، اندازه دو زاویه و ضلع غیر بین مشخص است. به همین دلیل، ابتدا باید با استفاده از قانون سینوسها، اندازههای دیگر را به دست آورد. قانون سینوسها را برای مثلث بالا مینویسیم:
- a: طول ضلع BC
- A: زاویه راس A برابر ۳۵ درجه
- b: طول ضلع AC
- B: زاویه راس B
- c: طول ضلع AB برابر ۷
- C: زاویه راس C برابر ۶۲ درجه
بر اساس قانون جمع زوایای داخلی، زاویه B برابر (°B=۱۸۰°-۳۵°-۶۲°=۸۳) است. مقادیر مشخص را درون نسبتهای بالا قرار میدهیم:
با توجه به سینوس زاویه ۳۵ درجه برابر ۰٫۵۷، سینوس زاویه ۶۲ درجه برابر ۰٫۸۸ و سینوس زاویه ۸۳ درجه برابر ۰٫۹۹ است:
با حل نسبتهای بالا، طول ضلع BC برابر ۴٫۵۵ و طول ضلع AC برابر ۷٫۸۷ به دست میآید. با داشتن اندازه تمام ضلعها و زوایا میتوان از فرمول هرون یا فرمولهای سینوس برای محاسبه مساحت استفاده کرد. در صورت استفاده از دو ضلع مانند a و c و زاویه بین آنها (B)، فرمول محاسبه مساحت مثلث به صورت زیر نوشته میشود:
اگر میخواستیم مسئله را با دو زاویه مانند A و C و ضلع بین آنها (b) حل کنیم، میتوانستیم رابطه زیر را بنویسیم:
مساحتهای به دست آمده با استفاده از هر دو فرمول با هم برابر هستند. در نتیجه، انتخاب مناسبترین فرمول بر عهده شما خواهد بود.
فرمول مساحت مثلث با سه راس
فرمول مساحت مثلث با داشتن سه نقطه توسط مفاهیم مرتبط با دستگاه مختصات، بردارها، ماتریسها و دترمینان نوشته میشود.
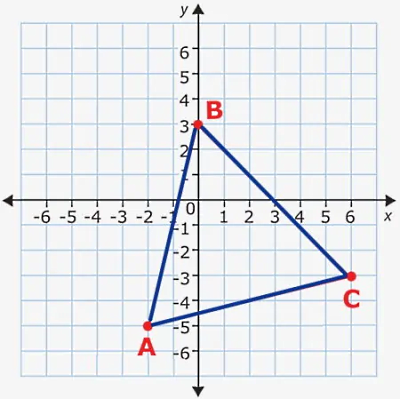
برای راسهای بالا، فرمول مساحت مثلث با سه راس عبارت است از:
- α: مساحت
- xA: مختصات راس A بر روی محور x
- yA: مختصات راس A بر روی محور y
- xB: مختصات راس B بر روی محور x
- yB: مختصات راس B بر روی محور y
- xC: مختصات راس C بر روی محور x
- yC: مختصات راس C بر روی محور y
شکل سادهتر فرمول محاسبه مساحت مثلث بر اساس مختصات راسها (بدون نیاز به آشنایی با مفهوم دترمینان)، به صورت زیر نوشته میشود:
مثال
تصویر زیر ، سه راس مثلث در دستگاه مختصات دو بعدی را نمایش میدهد. مساحت مثلث ABC چقدر است؟
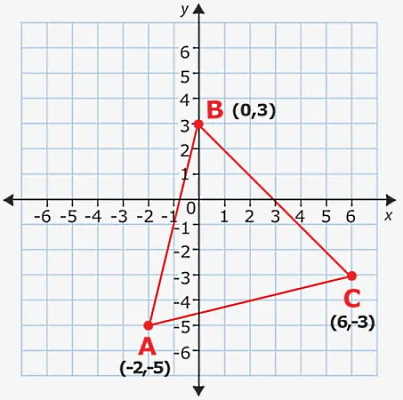
پاسخ
برای حل این مسئله، از فرمول مساحت مثلث با سه راس استفاده میکنیم. مطابق با این فرمول، داریم:
مطابق با اطلاعات مسئله داریم:
- xA=-۲
- yA=-۵
- xB=۰
- yB=۳
- xC=۶
- yC=-۳
اطلاعات مسئله را درون فرمول قرار میهیم:
مساحت مثلث ABC برابر ۳۰ است.
فرمول مساحت مثلث در فضای سه بعدی
در دستگاه مختصات سه بعدی، ضلعهای مثلث به عنوان بردار در نظر گرفته میشوند. با دانستن مختصات سه راس مثلث، نوشتن بردارهای معرف ضلعهای مثلث و ضرب خارجی بردارها، مساحت مثلث در فضای سه بعدی به دست میآید.
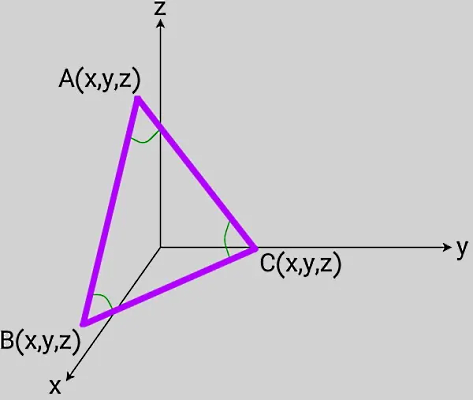
اگر بردارهای معرف ضلعهای b و c را در نظر بگیریم، فرمول محاسبه اندازه سطح مثلث به روش برداری به صورت زیر خواهد بود:
- Area: مساحت
- : بردار رسم شده از راس A به راس B
- : بردار رسم شده از راس A به راس C
اثبات فرمول مساحت مثلث
اثبات فرمول کلی مساحت مثلث، با استفاده از قضیه فیثاغورس در مثلثهای قائم الزاویه و رابطه مساحت مستطیل انجام میگیرد. برای اثبات فرمول مساحت مثلث، ابتدا یک مستطیل مشابه تصویر زیر را در نظر بگیرید.
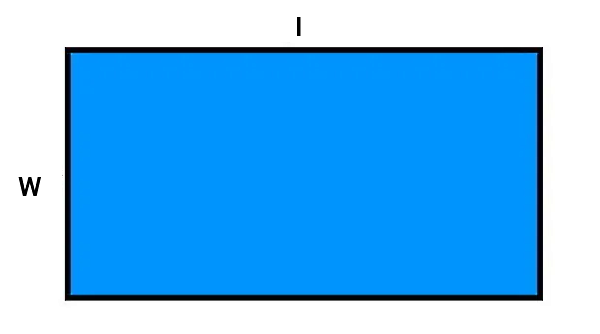
مطابق با فرمول مساحت مستطیل، داریم:
- A: مساحت
- l: طول
- w: عرض
اگر قطر مستطیل را رسم کنیم، مستطیل به دو مثلث قائم الزاویه با ابعاد برابر تبدیل میشود.
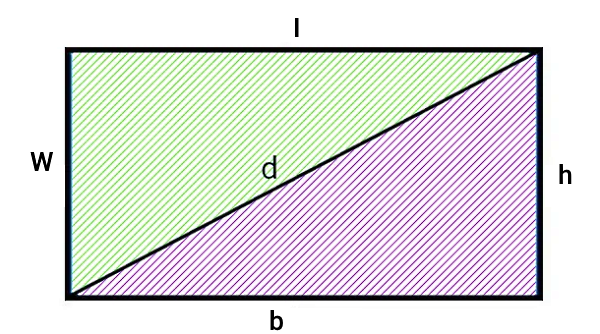
عرض مستطیل بالا برابر ارتفاع (h) و طول آن برابر قاعده (b) مثلث است. به این ترتیب، میتوان فرمول قبلی را به شکل زیر بازنویسی کرد:
از آنجایی که مستطیل بالا، از دو مثلث قائم الزاویه تشکیل میشود، مساحت یکی از مثلثهای قائم الزاویه برابر فرمول زیر خواهد بود:
به این ترتیب، اثبات میشود که مساحت مثلث قائم الزاویه برابر حاصل ضرب ساقها تقسیم بر دو است. در مرحله بعد، مثلث مختلف الاضلاع زیر را در نظر بگیرید.
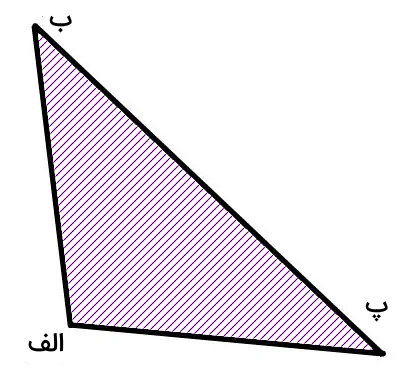
برای شروع اثبات فرمول مساحت، از راس (الف)، ارتفاع نظیر ضلع (ب پ) را رسم میکنیم. ارتفاع (الف ت)، مثلث (الف ب پ) را به دو مثلث قائم الزاویه (الف ب ت) و (الف ت پ) تقسیم میکند.
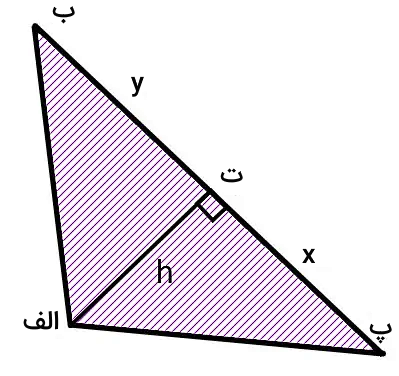
با توجه به تصویر بالا، داریم:
مساحت (الف ت پ) + مساحت (الف ب ت) = مساحت (الف ب پ)
مساحت مثلث قائم الزاویه (الف ب ت) برابر است با:
مساحت مثلث قائم الزاویه (الف ت پ) نیز به صورت زیر محاسبه میشود:
اکنون، مساحت این دو مثلث را باهم جمع میکنیم:
از h در رابطه بالا فکتور میگیریم:
حاصل y+x، همان طول قاعده b است. بنابراین، داریم:
در نتیجه، فرمول مساحت مثلث مختلف الاضلاع (الف ب پ)، برابر فرمول کلی قاعده ضربدر ارتفاع تقسیم بر دو است.
آزمون فرمول های مساحت مثلث
۱. کدام یک فرمول اصلی محاسبه مساحت مثلث بر اساس قاعده (b) و ارتفاع (h) است؟
فرمول درست برای محاسبه مساحت مثلث زمانی که قاعده (b) و ارتفاع (h) معلوم باشد، است. این فرمول بیان میکند باید حاصلضرب قاعده در ارتفاع را تقسیم بر ۲ کرد.
۲. کدام ویژگیها باعث میشود برای محاسبه مساحت مثلث متساوی الاضلاع به جای فرمول عمومی از فرمول مخصوص آن استفاده کنیم و تفاوت اصلی این فرمول با فرمول عمومی چیست؟
تمام ضلعهای مثلث متساوی الاضلاع برابر هستند و فرمول مخصوص فقط بر پایه ضلع نوشته میشود.
این فرمول زمانی استفاده میشود که فقط ارتفاع معلوم باشد و نیازی به دانستن ضلعها نیست.
در مثلث متساوی الاضلاع همیشه یک زاویه قائمه وجود دارد و همین دلیل نیاز به فرمول مجزا است.
فرمول مخصوص فقط زمانی کاربرد دارد که مختصات رئوس دقیق باشند و عمومیت ندارد.
فرمول مخصوص مساحت برای «تمام ضلعهای برابر» مثلث متساوی الاضلاع کاربرد دارد و فقط به طول یک ضلع نیاز دارد، بنابراین سادهتر و سریعتر از فرمول عمومی (بر پایه قاعده و ارتفاع) است. استفاده از فرمول خاص زمانی توجیه دارد که ویژگی همضلع بودن برقرار باشد؛ در حالی که فرمول عمومی برای هر مثلثی حتی با اضلاع یا ارتفاعهای متفاوت نیز کاربرد دارد.
۳. برای محاسبه مساحت مثلثی که تنها اندازه سه ضلع آن a و b و c معلوم است، کدام روش سریعتر و مستقیمتر به جواب میرسد و چرا؟
استفاده از فرمول هرون که فقط به اضلاع نیاز دارد.
استفاده از فرمول قاعده و ارتفاع بدون داشتن ارتفاع
یافتن مختصات رئوس و استفاده از فرمول مختصاتی
محاسبه زاویه بین دو ضلع و استفاده از سینوس
پاسخ «استفاده از فرمول هرون که فقط به اضلاع نیاز دارد» صحیح است چون فمرول هرون دقیقا برای حالتی طراحی شده که تنها سه ضلع داده شده باشد و هیچ اطلاعاتی از زاویه یا ارتفاع وجود نداشته باشد. در این روش با محاسبه نصف محیط (s) و جایگذاری فقط مقادیر عددی a، b و c، فرایند محاسبه به آسانی و سرعت انجام میشود.
۴. انتخاب بهترین فرمول برای محاسبه مساحت مثلث چگونه به نوع دادههای موجود مانند داشتن قاعده و ارتفاع، سه ضلع، دو ضلع و زاویه یا مختصات رئوس بستگی دارد؟
اگر دو ضلع و زاویه بین آنها داده شده باشد، فرمول مثلثاتی با سینوس سادهترین روش خواهد بود.
هر زمان هر سه ضلع داشته باشیم باید از فرمول هرون استفاده کنیم.
با داشتن مختصات دقیق سه راس همیشه باید فرمول قاعده ضربدر ارتفاع را به کار ببریم.
در صورت داشتن وتر و یک ساق در مثلث قائمالزاویه، از فرمول اختصاصی برداری بهره میگیریم.
هنگامی که دو ضلع و زاویه بین آنها موجود باشد، فرمول مثلثاتی با سینوس امکان محاسبه سریع و مستقیم مساحت را فراهم میکند. برخلاف این حالت، با داشتن سه ضلع باید فرمول هرون و با مختصات سه راس فرمول مختصاتی ویژه را به کار برد. همچنین اگر وتر و یک ساق در مثلث قائمالزاویه داده شود، فرمول مخصوص همین حالت با استفاده از فیثاغورس لازم است، نه روش برداری.
۵. در حل مساحت مثلث قائمالزاویه با داشتن وتر و یکی از ساقها، کدام فرمول رویکرد سریعتر و مناسبتری را ارائه میدهد؟
فرمول هرون با استفاده از سه ضلع
فرمول کلی مساحت با قاعده و ارتفاع
فرمول مثلثاتی با استفاده از سینوس
فرمول اختصاصی براساس وتر و ساق
وقتی اندازه وتر و یکی از ساقهای مثلث قائمالزاویه معلوم باشد، «فرمول اختصاصی براساس وتر و ساق» مستقیم با جایگذاری همین دو مقدار، مساحت را به سرعت محاسبه میکند. برخلاف استفاده از «فرمول کلی با قاعده و ارتفاع» یا «فرمول هرون» که نیازمند محاسبه مقدار سوم (مثلا ارتفاع یا سومین ضلع) هستند، و «فرمول مثلثاتی» که اغلب به دانستن زاویه نیاز دارد، فرمول ویژه وتر و ساق به دلیل سادگی و عدم نیاز به محاسبه سایر دادهها، راهکار بهینه برای چنین شرایطی است.
۶. وقتی مختصات سه راس یک مثلث را داشته باشیم، چگونه میتوان مساحت آن را در دستگاه دکارتی محاسبه کرد؟
بدستآوردن محیط و تقسیم آن بر مساحت مستطیل
استفاده از مجموع طول اضلاع و تقسیم بر دو
محاسبه مثلث به کمک رابطه فیثاغورس برای هر ضلع
با جایگذاری مختصات رئوس در فرمول عددی مخصوص مساحت مختصاتی
زمانیکه مختصات هر سه راس مثلث در دستگاه دکارتی موجود باشد، کافی است این مقادیر را در یک فرمول خاص که وابسته به تفاوتهای ضرب مختصات x و y رئوس است، وارد کنیم. این روش مساحت را به صورت مستقیم و بدون نیاز به استفاده از محیط یا روابط فیثاغورس به دست میدهد. روشهایی چون تقسیم مجموع اضلاع بر دو یا استفاده از محیط مخصوص حالت هرون است و همیشه کارساز نیستند. همچنین نسبت دادن مساحت به مستطیل، فقط در هنگام توضیح اثبات فرمول کلی مساحت کارایی دارد و برای مختصات دکارتی کاربرد ندارد. پس دقیقا این فرمول مختصاتی است که برای محاسبه صحیح بهکار میرود.
۷. برای استفاده از فرمول مساحت مثلث بر اساس روابط مثلثاتی، کدام حالت داده اولیه کفایت میکند و روند کلی استفاده از آن چگونه است؟
سه زاویه دلخواه بدون دانستن هیچ ضلعی کافی خواهد بود.
دو ضلع و زاویه بین آنها برای قرار دادن در فرمول سینوس کافی است.
یک ضلع و زاویه مقابل آن بدون اطلاعات دیگر کافی است.
دانستن مساحت و یک ضلع میتواند جایگزین همه دادهها باشد.
داشتن مقدار دو ضلع مثلث و زاویه بین آن دو، به شما امکان میدهد با فرمول مثلثاتی مساحت را به طور مستقیم محاسبه کنید. این حالت رایجترین شرایط کاربردی است. اگر فقط سه زاویه یا یک ضلع و زاویه مقابل آن را داشته باشید، ابتدا باید ابعاد دیگر را با قوانین سینوس یا کسینوس پیدا کنید و به اطلاعات بیشتر نیاز دارید.
۸. سه راس مثلثی در فضای سه بعدی داده شدهاند: A(1,2,3)، B(4,0,5) و C(2,1,7). مساحت این مثلث را با استفاده از فرمول ضرب خارجی بردارها چگونه میتوان به دست آورد؟
ابتدا دو بردار AB و AC را میسازیم، ضرب خارجی آنها را میگیریم، قدرمطلق را حساب و تقسیم بر دو میکنیم.
مختصات هر راس را جمع کرده و مجموع را بر سه تقسیم میکنیم.
ابتدا فاصله هر دو راس را محاسبه و با فرمول هرون مساحت را به دست میآوریم.
فقط طول بردار AB را با طول بردار AC ضرب و سپس تقسیم بر دو میکنیم.
در روش برداری، ابتدا دو بردار از یک راس به دو راس دیگر (مثلا AB و AC) ساخته میشود. سپس ضرب خارجی این دو بردار گرفته میشود تا برداری به دست آید که قدرمطلق آن اندازه مساحت متوازیالاضلاع تشکیلشده با این بردارها را میدهد. برای محاسبه مساحت مثلث، این مقدار بر دو تقسیم میشود.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت مثلث — انواع مثلث و تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- مثلث چیست ؟ — به زبان ساده
- مساحت انواع مثلث چگونه بدست می آید ؟ — حل تمرین و مثال های متنوع
- محیط مثلث چگونه بدست می آید؟ + فیلم آموزش رایگان
- چگونه مساحت مثلث را حساب کنیم؟ + تمرین با جواب
- محاسبه آنلاین مساحت مثلث — معرفی بهترین سایتها + مثال
- فرمول محیط مثلث چیست ؟ انواع فرمول ها + حل مثال های متنوع
- فرمول مساحت مثلث چیست ؟ — تمام فرمول ها + حل تمرین(همین مطلب)
- قاعده مثلث چیست و چگونه بدست می آید ؟ + تعریف و مثال
- ارتفاع مثلث چیست و چگونه رسم می شود ؟ — آموزش تصویری + حل تمرین
- محاسبه ارتفاع مثلث — تعریف، حل تمرین و مثال + جدول فرمول ها
- محیط مثلث مختلف الاضلاع — به زبان ساده + حل مثال های متنوع
- چگونه مساحت مثلث مختلف الاضلاع را حساب کنیم؟ + حل تمرین و مثال
- چگونه مساحت مثلث با سه ضلع معلوم را حساب کنیم؟ + حل تمرین و مثال
- فرمول هرون — به زبان ساده
- مساحت مثلث با سینوس چگونه محاسبه می شود ؟ + حل تمرین و جدول فرمول ها
- مثلث قائم الزاویه چیست ؟ — تعریف، ویژگی ها و محاسبات | به زبان ساده
- محیط مثلث قائم الزاویه – به زبان ساده + حل مثال های متنوع
- مساحت مثلث قائم الزاویه — حل تمرین و مثال های متنوع
- مثلث متساوی الساقین چیست ؟ | تعریف، ویژگی ها و محاسبات — به زبان ساده
- محیط مثلث متساوی الساقین — به زبان ساده و با حل مثال
- مساحت مثلث متساوی الساقین — حل تمرین و مثال های متنوع
- محیط مثلث متساوی الاضلاع چگونه بدست می آید؟ + حل مثال و تمرین
- مساحت مثلث متساوی الاضلاع — حل تمرین و مثال های متنوع













کاش اثبات فرمول مساحت مثلث با داشتن سه راس در مختصات دو بعدی و سه بعدی رو می گذاشتید…
خوب بود ممنون