شتاب متوسط چیست؟ – فرمول و محاسبه + حل مسئله
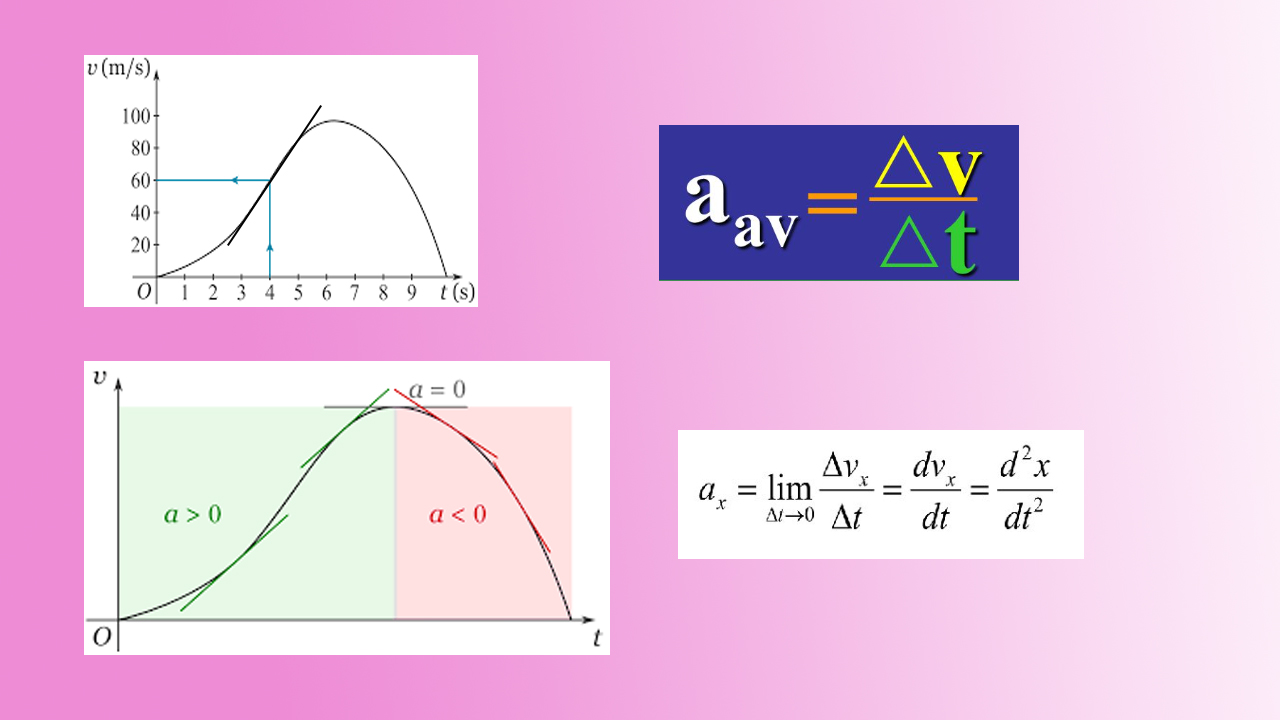
اجسام متحرک مختلف در اطراف ما یا با سرعت ثابت حرکت میکنند یا با سرعت متغیر. به عنوان مثال، به هنگام رانندگی، هنگامی که پای خود را روی گاز یا ترمز فشار میدهید، سرعت حرکت اتومبیل را افزایش یا کاهش میدهید. به تغییرات سرعت حرکت جسم، شتاب گفته میشود. توجه به این نکته مهم است که شتاب نه تنها از تغییر اندازه سرعت، بلکه از تغییر جهت سرعت نیز به وجود میآید. شتاب متوسط به صورت تغییر سرعت حرکت جسم در بازه زمانی مشخصی، تعریف میشود. علاوه بر شتاب متوسط، شتاب لحظهای را نیز به صورت تغییر سرعت در هر لحظه از زمان، تعریف میکنیم. در این مطلب، در مورد این دو شتاب و تفاوتهای آنها با یکدیگر، صحبت میکنیم.
شتاب متوسط چیست ؟
شتاب متوسط به صورت تغییر سرعت حرکت جسم در بازه زمانی بین تا ، تعریف میشود. اگر جسمی در زمان با سرعت و در زمان با سرعت حرکت کند، شتاب متوسط آن بین تا برابر است با:
نقطههای یک و دو را میتوان نقطههای آغاز و پایان حرکت نیز در نظر گرفت. تعریف این نقطهها به مسئله داده شده بستگی دارد.
مثال اول
اتومبیلی از حال سکون شروع به حرکت میکند و سرعت آن، ۶/۲ ثانیه پس از شروع حرکت به ۹۵ کیلومتر بر ساعت میرسد. مقدار شتاب متوسط را برحسب واحدهای استاندارد بهدست آورید.
پاسخ: یکای شتاب در سیستم SI (واحد استاندارد) برابر متر بر مجذور ثانیه است. سرعت حرکت اتومبیل در این مسئله برحسب کیلومتر بر ساعت داده شده است. بنابراین، در ابتدا باید سرعت را برحسب متر بر ثانیه بهدست آوریم. برای این کار لازم است ساعت و کیلومتر را به ترتیب برحسب ثانیه و متر بنویسیم. یک ساعت برابر ۳۶۰۰ ثانیه و یک کیلومتر برابر ۱۰۰۰ متر است.
پس از بهدست آوردن مقدار سرعت بر حسب متر بر ثانیه، آن را در فرمول شتاب متوسط قرار میدهیم:
توجه به این نکته مهم است که اگر جسم از حال سکون شروع به حرکت کند، زمان و سرعت اولیه آن را برابر صفر در نظر میگیریم.
مثال دوم
اتومبیلی با سرعت ثابت در حال حرکت است و در مدت زمان ۵/۰ ثانیه، ۱۱۰ متر جابجا میشود. اگر راننده ناگهان ترمز کند و پس از ۴/۰ ثانیه اتومبیل را متوقف کند، شتاب حرکت را بهدست آورید.

پاسخ: در مثال اول، اتومبیل از حال سکون شروع به حرکت کرد، اما در این مثال، اتومبیل ابتدا با سرعت مشخصی در حال حرکت است و سپس متوقف میشود. بنابراین، سرعت نهایی برابر صفر خواهد بود. برای محاسبه شتاب متوسط، ابتدا باید سرعت اولیه اتومبیل را بهدست آوریم. بر طبق صورت مسئله، اتومبیل در مدت زمان ۵/۰ ثانیه، ۱۱۰ متر جابجا میشود. برای بهدست آوردن سرعت اولیه، از رابطه زیر استفاده میکنیم:
اکنون، با داشتن سرعتهای اولیه و نهایی، میتوانیم شتاب متوسط اتومبیل را محاسبه کنیم. به این نکته توجه داشته باشید که سرعت اتومبیل در مدت زمان ۵/۰ ثانیه ثابت است و پس از آن کاهش مییابد، بنابراین، شتاب حرکت را در مدت زمان ۴/۰ ثانیه باید حساب کنیم. به بیان دیگر، حرکت اتومبیل در این مسئله به دو بخش تقسیم میشود:
- ۵/۰ ثانیه اول: در این مدت اتومبیل با سرعت ثابت حرکت و در انتهای این بازه زمانی، راننده ناگهان ترمز میکند. بنابراین، سرعت اتومبیل کاهش مییابد.
- ۴/۰ ثانیه تا توقف کامل: پس از ترمز، ۴/۰ ثانیه طول میکشد تا سرعت اتومبیل به صفر برسد. در این بازه زمانی، اتومبیل با شتاب ثابت و منفی به حرکت خود ادامه میدهد. مقدار شتاب متوسط و ثابت آن برابر است با:
مثال سوم
رانندهای در مدت زمان ۲/۵ ثانیه، سرعت اتومبیل را از ۲۵ متر بر ثانیه به ۱۵ متر بر ثانیه کاهش میدهد. شتاب متوسط اتومبیل را بهدست آورید.
پاسخ: تغییرات سرعت اتومبیل برابر است با:
تغییرات سرعت، منفی است، زیرا سرعت اتومبیل کاهش یافته است. آیا شتاب متوسط، منفی میشود؟ بله.
نکته: در این مثال، اگر فرض کنیم اتومبیل به سمت راست حرکت میکند، جهت شتاب متوسط و تغییرات سرعت به سمت چپ است.
مثال چهارم
اتومبیلی با سرعت ثابت ۸۰ مایل بر ساعت به مدت ۱۰ ثانیه در اتوبان، به سمت راست، حرکت میکند. شتاب متوسط آن را بهدست آورید.
پاسخ: شتاب متوسط را به صورت تغییرات سرعت در مدت زمان داده شده، تعریف کردیم. از آنجا که اندازه سرعت اتومبیل و جهت آن در مدت زمان داده شده در مسئله (۱۰ ثانیه) ثابت هستند، مقدار شتاب متوسط، با توجه به تعریف آن، برابر صفر است.
نکته: مقدار شتاب متوسط در حرکت با سرعت ثابت، برابر صفر است.
مثال پنجم
سرعت برخاستن هواپیمایی از سطح زمین برابر ۳۰۰ کیلومتر بر ساعت است. اگر هواپیما از حالت سکون شروع به حرکت کرده باشد و در مدت زمان ۴۵ ثانیه به سرعت موردنظر رسیده باشد، مقدار شتاب متوسط آن را برحسب متر بر مجذور ثانیه بهدست آورید.

پاسخ: هواپیما در ابتدا ساکن است، بنابراین سرعت اولیه آن برابر صفر خواهد بود. سرعت برخاستن هواپیما از سطح زمین، برابر ۳۰۰ کیلومتر بر ساعت است. برای بهدست آوردن شتاب متوسط برحسب ، ابتدا باید یکای سرعت را از کیلومتر بر ساعت به متر بر ثانیه تبدیل کنیم:
در ادامه، شتاب متوسط را به صورت زیر بهدست میآوریم:
مثال ششم
اتومبیلی از مکان با سرعت شروع به حرکت میکند. پس از ۲ ثانیه، مکان آن برابر و سرعت آن برابر میشود:
- جابجایی اتومبیل را بهدست آورید.
- سرعت متوسط اتومبیل چه مقدار است؟
- شتاب متوسط اتومبیل چه مقدار است؟
پاسخ
قسمت ۱: جابجایی جسم به صورت زیر تعریف میشود:
قسمت ۲: سرعت متوسط اتومبیل را به صورت زیر بهدست میآوریم:
قسمت ۳: شتاب متوسط را به صورت زیر بهدست میآوریم:
سرعت منفی در این مثال نشان میدهد که اتومبیل در راستای منفی محور x حرکت میکند، اما جهت شتاب آن در راستای مثبت محور x است. از آنجا که حاصلضرب شتاب در سرعت، منفی است، حرکت کندشونده خواهد بود.
نکته ۱: اگر حاصلضرب سرعت در شتاب منفی باشد، نوع حرکت کندشونده خواهد بود.
نکته ۲: اگر حاصلضرب سرعت در شتاب مثبت باشد، نوع حرکت تندشونده خواهد بود.
اتومبیلی با سرعت ۵۰ کیلومتر بر ساعت در حال حرکت است. اگر اتومبیل در مدت زمان ۳۲ ثانیه با شتاب ۰/۵ متر بر مجذور ثانیه حرکت کند، سرعت حرکت آن در انتهای بازه زمانی ۳۲ ثانیه چه مقدار است؟
20.9 متر بر ثانیه
۲۹/۹ متر بر ثانیه
۲۸/۹ متر بر ثانیه
۱۹/۹ متر بر ثانیه
سرعت اولیه، شتاب و بازه زمانی شتاب گرفتن اتومبیل داده شدهاند. برای بهدست آوردن سرعت نهایی اتومبیل، از فرمول شتاب متوسط استفاده میکنیم:
مدت زمان مورد نیاز برای تغییر سرعت حرکت اتومبیلی از ۵۰ کیلومتر بر ساعت به ۱۰۰ کیلومتر بر ساعت با نرخ برابر است با:
۱۴ ثانیه
۱۰ ثانیه
۸ ثانیه
۲۰ ثانیه
در این مسئله، باید بازه زمانی که در آن شتاب متوسط رخ می دهد را بهدست آوریم. فرض میکنیم اتومبیل رو خط راست حرکت میکند. تعریف شتاب متوسط در امتداد خط راست برابر است با:
تا اینجا میدانیم شتاب متوسط چیست و با استفاده از چه فرمولی محاسبه میشود. توجه به این نکته مهم است که شتاب متوسط میتواند از روی نمودار سرعت-زمان یا فرمول دیگری نیز محاسبه شود. در ادامه، در مورد روشهای مختلف بهدست آوردن شتاب متوسط، توضیح میدهیم.
روش های محاسبه شتاب متوسط
در بخش قبل، فرمول کلی محاسبه شتاب متوسط را همراه با چند مثال، توضیح دادیم. در ادامه، در مورد محاسبه شتاب متوسط از روی نمودار سرعت-زمان و متوسط گرفتن سرعتهای مختلف جسم در زمانهای متفاوت، صحبت میکنیم.
محاسبه شتاب متوسط با استفاده از نمودار سرعت-زمان
شتاب متوسط با استفاده از رابطه زیر بهدست میآید:
رابطه سرعت متوسط بسیار شبیه رابطه بالا است، با این تفاوت که به جای از استفاده میشود.
اگر نمودار سرعت برحسب زمان جسمی را داشته باشیم، شتاب متوسط در بازه زمانی خواسته شده، برابر شیب نمودار در آن بازه زمانی است. نمودار سرعت-زمان حرکت جسمی در تصویر زیر داده شده است.
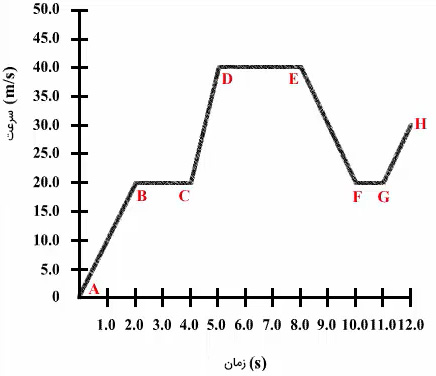
شتاب متوسط را در هر یک از بازههای زمانی داده شده بهدست میآوریم.
مقدار شتاب در بازه زمانی A تا B: نقطه A را شروع حرکت و زمان آن را برابر صفر در نظر میگیریم. سرعت حرکت جسم پس از ۲/۰ ثانیه، به ۲۰/۰ متر بر ثانیه میرسد. مقدار شتاب متوسط در بازه زمانی A تا B برابر است با:
مقدار شتاب در بازه زمانی B تا C: نمودار حرکت بر حسب زمان در بازه زمانی B تا C خط افقی موازی محور زمان است. همانطور که در تصویر مشاهده میکنید، سرعت اولیه و نهایی جسم در بازه BC یکسان و برابر ۲۰/۰ متر بر ثانیه است. بنابراین، جسم در این بازه زمانی با سرعت ثابت حرکت میکند. مقدار شتاب در حرکت با سرعت ثابت، برابر صفر خواهد بود.
مقدار شتاب در بازه زمانی C تا D: نقطه C در بازه CD نقطه آغاز و نقطه D، نقطه پایان است. سرعت در نقطه C و D به ترتیب برابر ۲۰/۰ و ۴۰/۰ متر بر ثانیه هستند.
مقدار شتاب در بازه زمانی D تا E: نمودار حرکت برحسب زمان در بازه زمانی D تا E، خط افقی موازی محور زمان است. همانطور که در تصویر مشاهده میکنید، سرعت اولیه و نهایی جسم در بازه DE، یکسان و برابر ۴۰/۰ متر بر ثانیه است. بنابراین، جسم در این بازه زمانی با سرعت ثابت حرکت میکند. مقدار شتاب متوسط در حرکت با سرعت ثابت، برابر صفر خواهد بود.
مقدار شتاب در بازه زمانی E تا F: نقطه E در بازه EF، نقطه آغاز و نقطه F، نقطه پایان است. سرعت در نقطه E و F به ترتیب برابر ۴۰/۰ و ۲۰/۰ متر بر ثانیه هستند. با قرار دادن مقدار سرعتِ این دو نقطه در فرمول شتاب متوسط، مقدار آن را بهدست میآوریم:
مقدار شتاب در بازه زمانی F تا G: نمودار سرعت-زمان در بازه زمانی F تا G، خط افقی موازی محور زمان است. همانطور که در تصویر مشاهده میکنید، سرعت اولیه و نهایی جسم در بازه GF، یکسان و برابر ۲۰/۰ متر بر ثانیه است. بنابراین، جسم در این بازه زمانی با سرعت ثابت حرکت میکند. مقدار شتاب متوسط در حرکت با سرعت ثابت، برابر صفر است.
مقدار شتاب در بازه زمانی G تا H: نقطه G در بازه GH، نقطه آغاز و نقطه H، نقطه پایان است. سرعت در نقطه G و H به ترتیب برابر ۳۰/۰ و ۲۰/۰ متر بر ثانیه هستند. با قرار دادن مقدار سرعتِ این دو نقطه در فرمول شتاب متوسط، مقدار آن را بهدست میآوریم:
پرسش: با توجه به نمودار سرعت-زمان نشان داده شده در تصویر بالا، مقدار شتاب متوسط را در کل مسیر حرکت بهدست آورید.
پاسخ: جسم از نقطه A، شروع به حرکت میکند و پس از ۱۲/۰ ثانیه به نقطه H، نقطه پایانی حرکت میرسد. برای بهدست آوردن مقدار شتاب در این بازه زمانی، باید مقدارهای سرعت در این دو نقطه را داشته باشیم. با توجه به نمودار سرعت-زمان، مقدار سرعت در نقطههای A و H، به ترتیب برابر صفر و ۳۰/۰ متر بر ثانیه است.
توصیف نمودار سرعت-زمان
درک مفهوم نمودار سرعت-زمان یکی از راههای ضروری برای توصیف حرکت جسم است. نمودار سرعت-زمان حرکت اتومبیلی در مدت زمان ۱۵ ثانیه، در تصویر زیر نشان داده شده است.
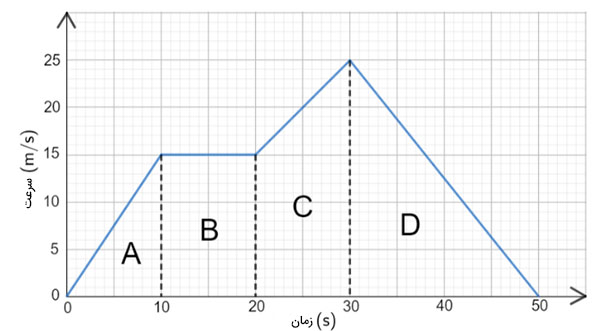
گام اول: نمودار را ابتدا به قسمتهای مختلف تقسیم و برای انجام این کار، به شیب نمودار سرعت-زمان دقت میکنیم. هر قسمت از نمودار که شیب تغییر کند، آن قسمت را به عنوان بخشی جداگانه در نظر میگیریم. نمودار بالا به چهار قسمت A و B و C و D تقسیم شده است.
گام دوم: هر قسمت را جداگانه بررسی میکنیم.
- بخش A: در این قسمت، سرعت اتومبیل از صفر به ۱۵ متر بر ثانیه در مدت زمان ۱۰ ثانیه افزایش یافته است. از آنجا که نمودار در این قسمت خطی با شیب ثابت است، اتومبیل با شیب ثابت و مثبت حرکت میکند.
- بخش B: در قسمت B، خط افقی و موازی محور زمان است و سرعت اتومبیل در این قسمت تغییر نمیکند. بنابراین، اتومبیل در این قسمت با سرعت ثابت و شیب صفر به حرکت خود ادامه میدهد.
- بخش C: در این قست، سرعت اتومبیل در مدت ۱۰ ثانیه از ۱۵ متر بر ثانیه به ۲۵ متر بر ثانیه افزایش مییابد. بنابراین، حرکت اتومبیل در این قسمت شتابدار و مقدار شتاب مثبت و ثابت است.
- قسمت D: در قسمت D، سرعت اتومبیل از ۲۵ متر بر ثانیه در مدت زمان ۲۰ ثانیه به صفر کاهش مییابد. در نتیجه، حرکت اتومبیل در این قسمت کندشونده و مقدار شتاب آن ثابت و منفی خواهد بود.
مثال اول
خط افقی در نمودار سرعت-زمان، چه چیزی را نشان میدهد؟
- مسافت ثابت
- سرعت ثابت
- شتاب ثابت
پاسخ
هنگامی که نمودار سرعت-زمان جسمی، خطی افقی و موازی محورِ زمان باشد، جسم با سرعت ثابت حرکت میکند و شتاب حرکت آن برابر صفر خواهد بود. بنابراین، پاسخ صحیح، گزینه ۲ است.
مثال دوم
با توجه به نمودار سرعت-زمان نشان داده شده در تصویر زیر، حرکت جسم چگونه است؟
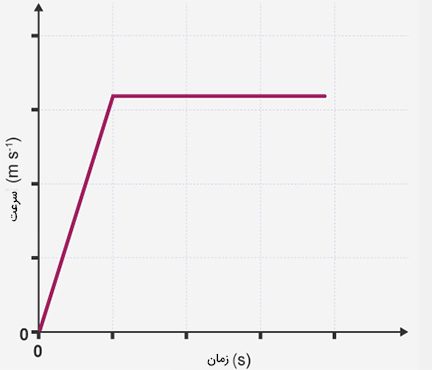
- ابتدا، جسم با سرعت ثابت حرکت میکند، سپس حرکت آن کند میشود.
- جسم ابتدا با شتاب تند شونده و در ادامه، با شتاب کندشونده به حرکت خود ادامه میدهد.
- جسم ابتدا با شتاب حرکت میکند، سپس حرکت خود را با سرعت ثابت ادامه میدهد.
پاسخ
نمودار سرعت-زمان از دو قسمت تشکیل شده است. در قسمت اول، خطی با شیب مثبت و در قسمت دوم، خطی با شیب صفر داریم. گفتیم شیب نمودار سرعت-زمان در بازه زمانی معین برابر شتاب متوسط است. بنابراین، جسم ابتدا با شتاب ثابت و مثبت حرکت میکند. سپس، به حرکت خود با شتاب صفر و سرعت ثابت ادامه میدهد. از اینرو، پاسخ صحیح، گزینه ۳ است.
نکته: شیب نمودار سرعت-زمان در بازه زمانی مشخص، برابر شتاب متوسط در آن بازه زمانی است.
مثال سوم
به نمودار سرعت-زمان نشان داده شده در تصویر زیر دقت کنید. قسمتی از نمودار که زیر محور زمان است، چه چیزی را نشان میدهد؟

- جسم به سمت پایین حرکت میکند.
- جسم در جهت مخالفِ حرکت اولیه، حرکت میکند.
- جسم به سمت بالا حرکت میکند.
پاسخ
هنگامی که نمودار سرعت-زمان زیر محور افقی باشد، جسم در جهتی مخالف جهت اولیه حرکت، حرکت میکند.
کدام یک از گزینههای زیر، بهترین توصیف برای نمودار سرعت-زمان نشان داده شده در تصویر است؟
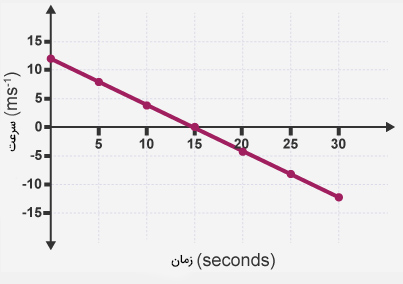
ابتدا، جسم از سطحی با شیب مشخص پایین میآید، سپس از سطحی با شیب مشابه، بالا میورد.
جسم از سطحی با شیب زیاد، پایین میآید.
جسمی از سطحی با شیب مشخص بالا میرود. سپس، به نقطه اولیه شروع حرکت، بازمیگردد.
حرکت جسم تا ثانیه ۱۵/۰ کند و در زمان ۱۵/۰ ثانیه متوقف میشود (سرعت حرکت آن برابر صفر میشود). سپس در جهت مخالف، شروع به حرکت میکند. از میان گزینههای داده شده، گزینه ۳، بهترین توصیف را ارائه می دهد. هنگامی که جسمی از سطحی با شیب مشخص بالا میرود، پس از مدت زمان مشخصی به طور کامل متوقف میشود و به دلیل نیروی جاذبه، از سطح پایین میآید.
مثال چهارم
نمودار سرعت-زمان قطار P که بین دو ایستگاه با فاصله ۱/۵ کیلومتر حرکت میکند، در تصویر زیر نشان داده شده است. قطار از ایستگاه اول با شتاب ثابت از حالت سکون شروع به حرکت میکند و سرعت آن پس از ۳۰۰ متر به ۳۰ متر بر ثانیه میرسد. سپس، قطار با سرعت ۳۰ متر بر ثانیه به مدت T ثانیه به حرکت خود ادامه میدهد. در پایان، سرعت قطار با شتاب ۱/۲۵ متر بر مجذور ثانیه کاهش مییابد و پس از رسیدن به ایستگاه، به طور کامل متوقف میشود.
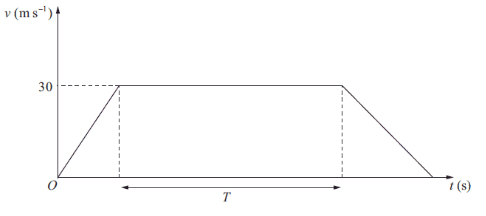
- قطار P مسافت ۳۰۰ متر را با چه شتابی طی میکند؟
- مقدار T را بهدست آورید.
قطار دیگری به نام Q، همانند قطار P، مسیر یکسانی را در مدت زمان مشابهی طی میکند. قطار Q پس از ترک ایستگاه اول با شتاب ثابتی حرکت میکند و سرعت آن از صفر به متر بر ثانیه میرسد. این قطار، بلافاصله پس از رسیدن به سرعت ، با شتاب ثابت و کندشوندهای به حرکت خود تا رسیدن به ایستگاه دوم و توقف کامل، ادامه میدهد.
۳. نمودار سرعت-زمان حرکت قطار Q را رسم کنید.
۴. مقدار را بهدست آورید.
پاسخ
به نمودار سرعت-زمان دقت کنید. نمودار سرعت-زمان قطار P به چند قسمت تقسیم میشود؟ سه قسمت:
- قسمت اول: مسافت طی شده در این قسمت برابر ۳۰۰ متر است و با شتاب ثابت و مثبت حرکت میکند.
- قسمت دوم: در این قسمت، به مدت T ثانیه با سرعت ثابت ۳۰ متر بر ثانیه حرکت میکند.
- قسمت سوم: قطار P ترمز میکند و با شتاب ثابت و کندشوندهای برابر ۱/۲۵ متر بر مجذور ثانیه، متوقف میشود.
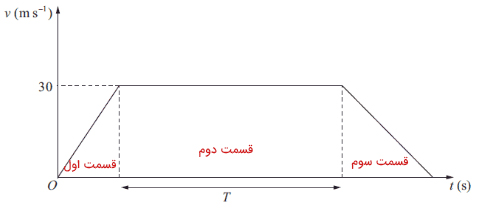
قسمت ۱: در این قسمت، شتاب حرکت را بهدست میآوریم. توجه به این نکته مهم است که مساحت زیر نمودار سرعت-زمان برابر جابجایی جسم است. از آنجا که قطار P در قسمت اول حرکت ۳۰۰ متر جابجا شده است، مساحت زیر نمودار این قسمت& برابر ۳۰۰ خواهد بود. برای بهدست آوردن شتاب متوسط قطار P، از رابطه استفاده میکنیم، زیرا سرعتهای اولیه، نهایی و جابجایی را داریم.
قسمت ۲: در این قسمت، زمان T را بهدست میآوریم. برای محاسبه این زمان، ابتدا مسافت طی شده توسط قطار P را در قسمت سوم حرکت، محاسبه میکنیم. از آنجا که مسافت کل طی شده توسط قطار برابر 1/5 کیلومتر است، با دانستن مسافتهای دو قسمت اول و سوم، به راحتی مسافت طی شده توسط قطار در قسمت دوم، بهدست میآید. در قسمت سوم، سرعت اولیه، نهایی و شتاب حرکت قطار را داریم، بنابراین برابر است با:
شاید این سوال برایتان به وجود آمده باشد چرا شتاب در رابطه بالا، علامت منفی دارد. زیرا حرکت قطار در قسمت سوم، کندشونده و علامت آن منفی خواهد بود. در ادامه، مسافت طی شده توسط قطار را در قسمت دوم بهدست میآوریم.
فاصله دو ایستگاه از یکدیگر = ۱/۵ کیلومتر
قطار P در قسمت دوم حرکت، مسافت ۸۴۰ متر را با سرعت ثابت طی میکند. اگر جسمی با سرعت ثابت حرکت کند، مسافت طی شده توسط آن برابر است با:
برابر ۸۴۰ متر و سرعت حرکت برابر ۳۰ متر بر ثانیه است، بنابراین زمان T برابر است با:
در قسمت دوم این مثال، قطار دیگری به نام Q، همانند قطار P، مسیر یکسانی را در مدت زمان مشابهی طی میکند. حرکت این قطار از دو قسمت تشکیل شده است:
- پس از ترک ایستگاه اول، سرعت آن با شتاب ثابتی از صفر به میرسد.
- بلافاصله، ترمز میکند و پس از مدت زمان t، در ایستگاه دوم متوقف میشود. در این قسمت، سرعت قطار با شتاب ثابت و کندهشوندهای از به صفر میرسد.
ابتدا، نمودار سرعت-زمان قطار Q را رسم میکنیم. برای رسم این نمودار باید به این نکته توجه داشته باشیم که مساحت زیر نمودار سرعت-زمانِ قطار Q باید برابر قطار P باشد. نمودار سرعت-زمان قطار Q از دو خط با شیبهای منفی و مثبت تشکیل شده است که در نقطه ، به یکدیگر میرسند. سرعت باید بیشتر از ۳۰ متر بر ثانیه باشد، در این صورت مساحت زیر نمودار سرعت-زمان دو قطار با یکدیگر برابر خواهند بود.
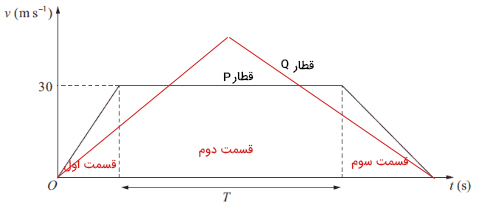
مساحت زیر نمودار قطار P برابر مساحت زیر نمودار قطار Q است. گفتیم زمانی که طول میکشد تا قطارهای P و Q از ایستگاه اول به ایستگاه دوم حرکت کنند، با یکدیگر برابر هستند. با توجه به اطلاعات داده شده برای قطار P، کل زمانی که طول میکشد تا از ایستگاه اول به دوم برسد را محاسبه میکنیم. در قسمت قبل زمان T برای قسمت دوم حرکت را برابر ۲۸ ثانیه بهدست آوردیم.
زمان برای قطار P در قسمت اول حرکت: قطار P در این قسمت مسافت ۳۰۰ متر را در مدت زمان ، طی میکند. با داشتن سرعتهای اولیه، نهایی و شتاب حرکت، زمان را به صورت زیر محاسبه میکنیم:
زمان برای قطار P در قسمت دوم حرکت: قطار P در این قسمت مسافت ۳۶۰ متر را در مدت زمان ، طی میکند. با داشتن سرعتهای اولیه، نهایی و شتاب حرکت، زمان را به صورت زیر محاسبه میکنیم:
بنابراین، زمان کل حرکت قطار P و Q برابر خواهد بود. مساحت زیر نمودار v-t برای قطار Q، برابر مساحت مثلت رسم شده است:
در اینجا، قاعده مثلث برابر زمان کل حرکت قطار Q و ارتفاع، برابر سرعت است.
محاسبه شتاب متوسط در فاصله زمانی مشخص با استفاده از رابطه مکان برحسب زمان
فرض کنید ذرهای در یک بعد حرکت میکند و مکان آن برحسب زمان، به صورت زیر داده شده است:
شتاب متوسط حرکت این ذره را در بازه یک تا دو ثانیه بهدست میآوریم. قبل از بهدست آوردن شتاب متوسط این ذره، به دو نکته زیر توجه کنید.
نکته ۱: سرعت متوسط حرکت به صورت تغییرات مکان نسبت به زمان، تعریف میشود.
اگر بسیار کوچک و به صفر نزدیک شود، سرعت در هر لحظه از زمان را میتوان به صورت زیر بهدست آورد:
بنابراین، مشتق مکان نسبت به زمان، برابر سرعت جسم در هر لحظه از زمان است.
نکته ۲: شتاب متوسط حرکت را به صورت تغییرات سرعت نسبت به زمان، تعریف کردیم:
اگر بسیار کوچک و به صفر نزدیک شود، شتاب را در هر لحظه از زمان میتوان به صورت زیر بهدست آورد:
بنابراین، مشتق سرعت نسبت به زمان برابر شتاب جسم در هر لحظه از زمان است.
برای بهدست آوردن رابطه سرعت بر حسب زمانِ حرکت جسم، از S(t) بر حسب زمان مشتق میگیریم.
شتاب متوسط بین یک تا دو ثانیه را به دو روش بهدست میآوریم.
روش اول: شتاب متوسط بین دو زمان یک تا دو ثانیه، با استفاده از رابطه زیر بهدست میآید:
سرعت در زمان یک ثانیه برابر است با:
سرعت در زمان دو ثانیه برابر است با:
سرعت متوسط برابر است.
روش دوم: در نکته ۲ گفتیم، مشتق سرعت نسبت به زمان، شتاب حرکت را در هر لحظه از زمان میدهد. بنابراین، برای بهدست آوردن رابطه شتاب نسبت به زمان، مشتق سرعت نسبت به زمان را بهدست میآوریم:
با داشتن رابطه شتاب نسبت به زمان، شتاب متوسط در بازه زمانی تا به صورت زیر بهدست میآید:
اگر و باشند، شتاب متوسط برابر است با:
محاسبه شتاب متوسط جسم در بازه های زمانی مختلف
هنگامی که جسم در بازههای زمانی مختلف مانند تا با سرعتهای تا حرکت کند، شتاب متوسط آن برابر است با:
اکنون میدانیم شتاب متوسط چیست و چگونه بهدست میآید. نکته مهم در مورد شتاب متوسط آن است که مقدار آن را در بازه زمانی تا محاسبه میکنیم. شاید از خود پرسیده باشید، چگونه مقدار شتاب را در هر لحظه از زمان بهدست میآوریم. برای پاسخ به این پرسش باید با مفهومی به نام شتاب لحظهای، آشنا شویم. در ادامه، در مورد شتاب لحظهای و تفاوت آن با شتاب متوسط صحبت میکنیم.
شتاب لحظه ای چیست ؟
سرعت لحظهای به صورت شیب خط مماس بر نمودار مکان-زمان در هر لحظه از زمان، تعریف میشود. به نمودار مکان بر حسب زمان جسمی دلخواه در تصویر زیر، دقت کنید. سرعت لحظهای در نقطه آبیرنگ برابر شیب خط مماس بر این نقطه است.
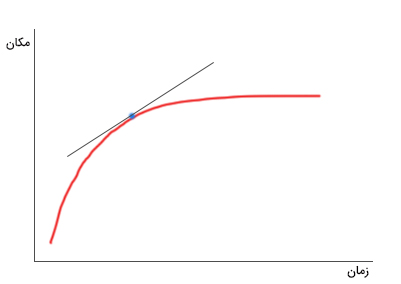
از نمودار مکان-زمان برای بهدست آوردن سرعت متوسط و لحظهای استفاده میشود. در مقابل، از نمودار سرعت-زمان، شتاب متوسط و لحظهای را بهدست میآوریم. نمودار سرعت-زمان جسمی در تصویر زیر نشان داده شده است. نقطه دلخواهی به نام A را روی نمودار در نظر میگیریم و خطی مماس بر آن رسم میکنیم. شیب خط مماس برابر شتاب لحظهای در زمان دلخواه t است.
نکته ۱: شیب خط مماس بر هر نقطه دلخواهی روی نمودار سرعت-زمان در زمان t، برابر شتاب لحظهای در آن زمان است.
سوالی که ممکن است مطرح شود آن است که شتاب متوسط را چگونه میتوان با استفاده از نمودار سرعت-زمان بهدست آورد. در مطالب بالا گفتیم اگر نمودار سرعت-زمان، خطی راست با شیب ثابت باشد، شیب خط برابر شتاب متوسط خواهد بود. به بیان دیگر، اگر نمودار سرعت-زمان خطی با شیب ثابت باشد، جسم با شتاب ثابت حرکت میکند. در حرکت با شتاب ثابت، اندازه شتابهای متوسط و لحظهای با یکدیگر برابر هستند. در ادامه، در مورد نمودارهای غیرخطی سرعت-زمان صحبت میکنیم. نمودار غیرخطی دلخواهی را به شکل نشان داده شده در تصویر زیر در نظر بگیرید. دو نقطه A و B روی نمودار در نظر میگیریم و آنها را توسط خط به یکدیگر وصل میکنیم.
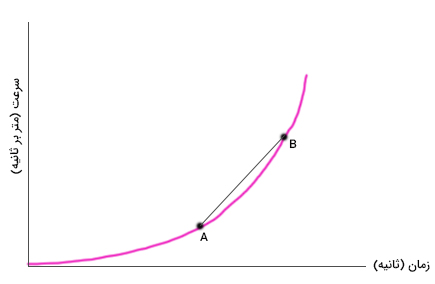
محاسبه شیب خط AB بسیار راحت است. تنها کافی است از نقطههای A و B خطی موازی محورهای افقی و عمودی رسم کنیم و مختصات سرعت و زمان آنها را بهدست آوریم. اگر سرعت و زمان در نقطه A برابر و و در نقطه B برابر و باشند، شیب خط AB برابر است با:
شیب خط AB همان شتاب متوسط در بازه زمانی تا است و با نشان داده میشود:
هنگامی که بازه زمانی بسیار کوچک شود و نقطههای A و B به یکدیگر نزدیک شوند ()، شتاب حرکت جسم را میتوانیم در هر لحظه بهدست آوریم.
رابطه بالا همان تعریف مشتق است. به بیان دیگر، اگر رابطه سرعت برحسب زمان را داشته باشیم، برای بهدست آوردن شتاب لحظهای در هر لحظه از زمان کافی است، مشتق سرعت نسبت به زمان را بهدست آوریم.
مثال اول
نمودار سرعت-زمانِ جسمی دلخواه به صورت زیر رسم شده است.

حرکت جسم را چگونه توصیف میکنید. جسم از حالت سکون شروع به حرکت میکند و پس از مدت زمان مشخصی، سرعت آن به مقدار بیشینه میرسد. در ادامه، سرعت جسم کاهش مییابد و صفر میشود. دو حالت برای حرکت جسم میتوان تصور کرد:
- فرض میکنیم جسم تنها میتواند روی خط راست، به شرق یا غرب حرکت کند. جسم از حالت سکون شروع به حرکت میکند و پس از آنکه سرعت آن به مقدار بیشینه V رسید، تغییر جهت میدهد و با کم کردن سرعت حرکت، به مسیر خود تا توقف کامل ادامه میدهد.
- جسم از حالت سکون شروع به حرکت میکند و پس از رسیدن سرعت آن به بیشینه، سرعت خود را تا توقف کامل، کاهش میدهد. به عنوان مثال، اتومبیلی را در نظر بگیرید که شروع به حرکت و پس از رسیدن سرعت آن به مقدار ، به دلیل ترافیک، ترمز میکند و به طور کامل متوقف میشود.
در ادامه، نقطههای A و B و C و D را روی نمودار در نظر میگیریم و علامت شتاب را در هر یک از آنها بهدست میآوریم. به یاد داشته باشید که شتاب در هر لحظه برابر شیب خط مماس بر نمودار سرعت-زمان در آن لحظه است. اگر شیب خط مماس در نقطه موردنظر مثبت باشد، علامت شتاب مثبت و اگر شیب خط مماس، منفی باشد، علامت شتاب منفی خواهد بود. توجه به این نکته نیز مهم است که هرچه زاویه خط مماس نسبت به محور افقی (زمان) بزرگتر باشد، شیب خط بزرگتر (شتاب بزرگتر) و هرچه اندازه زاویه کوچکتر باشد، شیب خط و در نتیجه اندازه شتاب، کوچکتر است.
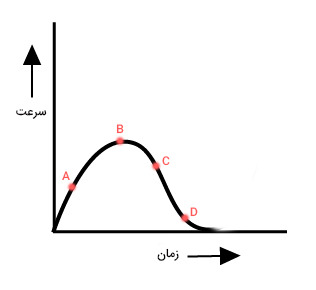
- نقطه A: خط مماسی را در این نقطه رسم میکنیم. از آنجا که زاویه خط مماس در نقطه A با محور افقی، کوچکتر از ۹۰ درجه است، شیب خط و بنابراین، علامت شتاب، مثبت خواهد بود. شاید از خود بپرسید شتابِ مثبت چه تاثیری بر حرکت جسم میگذارد. هنگامی که شتاب جسمی مثبت باشد، سرعت حرکت در حال افزایش است.
- نقطه B: خط مماسی را در این نقطه رسم میکنیم. از آنجا که خط مماس در نقطه B با محور افق یا محور زمان، موازی است، شیب خط و بنابراین، اندازه شتاب، برابر صفر خواهد بود. در دو حالت ممکن است شتاب حرکت جسمی برابر صفر شود:
- جسم با سرعت ثابت حرکت کند.
- جسم ابتدا با سرعت افزایشی حرکت کند، سپس سرعت خود را کاهش دهد.
- نقطه C: خط مماسی را در این نقطه رسم میکنیم. از آنجا که زاویه خط مماس در نقطه C با محور افقی، بزرگتر از ۹۰ درجه است، شیب خط و بنابراین، علامت شتاب، منفی خواهد بود. هنگامی که شتاب جسمی منفی باشد، سرعت حرکت در حال کاهش است.
- نقطه D: خط مماسی را در این نقطه رسم میکنیم. همانند نقطه C، شیب خط و بنابراین، علامت شتاب، منفی است.
از بین چهار نقطه نشان داده شده روی نمودار، کدام یک بزرگترین شتاب را دارد؟ خط مماس بر هم یک از نقطههای A و B و C و D، در تصویر زیر نشان داده شده است. شیب نقطه B برابر صفر است. بنابراین، به سه نقطه دیگر توجه میکنیم. خط مماس بر نقطه A، زاویه بزرگتری با محور افقی ساخته است. در نتیجه، جسم در نقطه A با شتاب بزرگتری نسبت به نقطههای دیگر حرکت میکند.
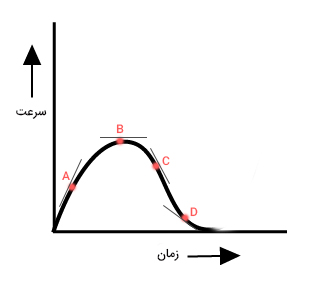
علامت شتاب در نقطههای C و D، منفی است. سوالی که ممکن است مطرح شود آن است که اندازه شتاب در کدام نقطه بزرگتر است. به بیان دیگر، کاهش سرعت در کدام نقطه سریعتر است. به خطهای مماس رسم شده در نقطههای C و D دقت کنید. شیب خط مماس در نقطه C بزرگتر از شیب خط مماس در نقطه D است، بنابراین شتاب در نقطه C بزرگتر از شتاب در نقطه D خواهد بود.
مثال محاسبه شتاب لحظهای
ذرهای با شتاب متغیر، حرکت میکند. اگر سرعت آن بر حسب زمان به صورت نوشته شود، مطلوب است:
- تابع شتاب برحسب زمان را بهدست آورید.
- سرعت لحظهای را در زمانهای یک، دو، سه و پنج ثانیه محاسبه کنید.
- شتاب لحظهای را در زمانهای یک، دو، سه و پنج ثانیه، بهدست آورید.
- جوابهای قسمت ۳ را براساس جهتهای بردارهای شتاب و سرعت بررسی کنید.
- نمودار سرعت و شتاب را برحسب زمان رسم کنید.
پاسخ: برای بهدست آوردن تابع شتاب برحسب زمان، از تابع سرعت برحسب زمان مشتق میگیریم. سپس، مقدار شتاب و سرعت لحظهای را در زمانهای خواسته شده با استفاده از تابع آنها برحسب زمان، بهدست میآوریم.
قسمت ۱: شتاب لحظهای برابر مشتق سرعت نسبت به زمان است:
قسمت ۲: برای بهدست آوردن سرعت لحظهای، زمان داده شده را در تابع سرعت برحسب زمان قرار میدهیم.
قسمت 3: برای بهدست آوردن شتاب لحظهای، زمان داده شده را در تابع شتاب برحسب زمان قرار میدهیم.
قسمت ۴: با توجه به قسمتهای ۲ و ۳، سرعت و شتاب در زمان یک ثانیه، مثبت هستند، بنابراین جهت هر دو یکسان و حرکت ذره تندشونده است. در زمان ۲ ثانیه، سرعت برابر ۲۰ متر بر ثانیه و شتاب برابر صفر است. در این زمان، ذره به سرعت بیشینه خود میرسد. بیشینه سرعت زمانی اتفاق میافتد که شیب نمودار سرعت-زمان برابر صفر شود. صفر شدن شیب نمودار سرعت-زمان، بیانگر شتابِ صفر است.
در زمان سه ثانیه، سرعت برابر ۱۵ متر بر ثانیه و شتاب منفی است. در این زمان، سرعت ذره کاهش یافته و بردار شتاب منفی است. به بیان دیگر، حرکت ذره آهسته میشود.
در زمان پنج ثانیه، سرعت برابر ۲۵- متر بر ثانیه و شتاب برابر ۳۰- متر بر مجذور ثانیه است. سرعت ذره بین زمانهای ۳ تا ۵ ثانیه کاهش مییابد و به صفر میرسد و پس از آن منفی میشود. این بدان معنا است که جهت حرکت ذره برعکس شده و در جهت مخالف سرعت آن افزایش مییابد.
قسمت ۵:
برای رسم نمودار سرعت زمان، گامهای زیر را طی میکنیم.
گام اول
ابتدا، تابع را برابر صفر قرار میدهیم و ریشههای آن را بهدست میآوریم.
مقدار سرعت در زمانهای صفر و ۴ ثانیه برابر صفر است.
گام دوم
بیشینه یا کمینه تابع را بهدست میآوریم. برای انجام این کار، مشتق سرعت برحسب زمان را حساب میکنیم و برابر صفر قرار میدهیم.
مشتق سرعت (شتاب) در زمان ۲ ثانیه برابر صفر است. برای بهدست آوردن کمینه یا بیشینه بودن سرعت در زمان دو ثانیه، مشتق بهدست آمده را تعیین علامت میکنیم.
| منفی | مثبت |
با توجه به تعیین علامت تابع ، مقدار سرعت در زمان دو ثانیه، بیشینه و مقدار آن برابر ۲۰ متر بر ثانیه است. نمودار سرعت برحسب زمان بین صفر تا ۵ ثانیه به صورت نشان داده شده در تصویر زیر است.
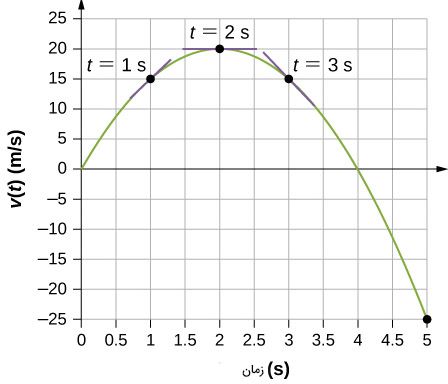
تابع شتاب برحسب زمان به شکل است. نمودار شتاب خطی مستقیم با شیب ۱۰- است و مقدار آن در زمان ۲ ثانیه برابر صفر است.
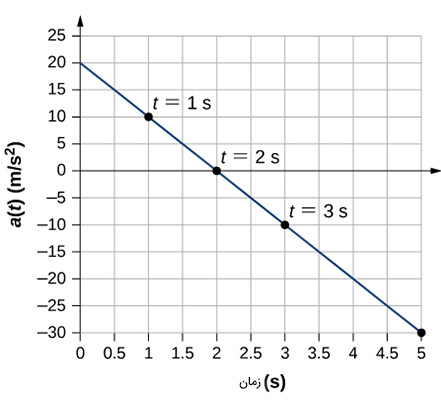
رسم نمودارهای سرعت و شتاب برحسب زمان، کمک زیادی به درک بهتر حرکت ذره میکند. به دو نمودار رسم شده در بالا توجه کنید. در این مثال، هنگامی که شتاب برابر صفر میشود، مقدار سرعت به بیشینه مقدار خود میرسد. همچنین، هنگامی که شتاب مثبت و همجهت با سرعت است، اندازه سرعت افزایش مییابد.
تفاوت شتاب لحظه ای و شتاب متوسط چیست ؟
تاکنون با تعریف شتاب متوسط و لحظهای آشنا شدیم. در این بخش، در مورد تفاوت آنها با یکدیگر صحبت میکنیم. شتاب متوسط در بازه زمانی مشخصی بین تا بهدست میآید. بنابراین، مقدار شتاب متوسط را در لحظهای مشخص نداریم، بلکه متوسط شتاب را در بازههای زمانی متفاوت داریم. در مقابل، شتاب لحظهای، مقدار شتاب را در هر لحظه از زمان میدهد. اگر بازه زمانی بسیار کوچک باشد، مقدار شتاب متوسط و لحظهای، به یکدیگر بسیار نزدیک هستند.
شتاب متوسط چه کمیتی است ؟
شتاب برابر تغییرات سرعت نسبت به زمان است. سرعت کمیتی برداری است، یعنی هم اندازه دارد و هم جهت. بنابراین، نهتنها تغییر اندازه سرعت، بلکه تغییر جهت آن نیز ممکن است سبب ایجاد شتاب شود. از اینرو، شتاب متوسط نیز همانند سرعت کمیتی برداری است. به عنوان مثال، دوندهای با سرعت ۱۰ کیلومتر بر ساعت به سمت شرق میدود، سپس توقف میکند و به دویدن به سمت غرب با همان سرعت ادامه میدهد. در اینجا، دونده با سرعت یکسانی میدود، اما جهت سرعت او تغییر کرده است. در نتیجه، شتاب در دو حالت ایجاد میشود:
- تغییر اندازه سرعت (کاهش یا افزایش).
- تغییر جهت سرعت
حالت دوم را در ادامه توضیح میدهیم.
شتاب متوسط یا لحظهای، برداری در راستای تغییرات سرعت () است. به یاد داشته باشید گرچه شتاب در راستای تغییرات سرعت قرار دارد، ممکن است در راستای حرکت نباشد. هنگامی که حرکت جسمی آهسته میشود، شتاب حرکت آن در جهت مخالف حرکت است.
مثال اول
اسب مسابقهای پس از خارج شدن از جایگاه مخصوص، سرعت خود را در مدت ۱/۸۰ ثانیه از صفر به ۱۵/۰ متر بر ثانیه افزایش میدهد. شتاب متوسط را به دست آورید.

پاسخ: در ابتدا، سیستم مختصاتی را برای این مثال در نظر میگیریم. به این نکته توجه داشته باشید که جهت شرق را مثبت و غرب را منفی در نظر گرفتهایم. از آنجا که اسب به سمت غرب حرکت میکند سرعت آن منفی خواهد بود.
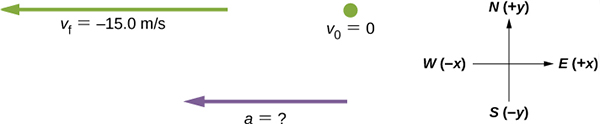
شتاب متوسط با استفاده از رابطه زیر بهدست میآید:
اسب در ابتدا ساکن است، بنابراین سرعت اولیه آن برابر صفر خواهد بود. ۱/۸ ثانیه پس از شروع حرکت، سرعت آن به ۱۵ متر بر ثانیه میرسد. از آنجا که اسب به سمت غرب میدود و جهت مثبت، به سمت شرق انتخاب شده است، برابر خواهد بود. همچنین، برابر ۱/۸ ثانیه است.
علامت منفی شتاب نشاندهنده جهت شتاب به سمت غرب است. شتابِ ۸/۳۳ متر بر مجذور ثانیه به سمت غرب نشان میدهد که اسب سرعت خود را در هر ثانیه به اندازه ۸/۳۳ متر بر ثانیه، به سمت غرب افزایش میدهد. عدد بهدست آمده برای شتاب همان شتاب متوسط است، زیرا حرکت اسب در مسابقات اسبدوانی، حرکت ساده و یکنواختی نیست. از اینرو، بهدست آوردن شتاب متوسط، منطقیتر و راحتتر از شتاب لحظهای است.
شتاب متوسط در حرکت دایره ای
تا اینجا، در مورد حرکت روی خط راست صحبت کردیم و شتاب متوسط و لحظهای را برای آن بهدست آوردیم. در ادامه، حرکت ذره یا جسمی دلخواه روی دایره را در نظر میگیریم و ابتدا، حرکت دایرهای و در ادامه شتاب متوسط در حرکت دایرهای را توضیح میدهیم.
در حرکت یکبعدی، اگر ذرهای با سرعت ثابت حرکت کند، شتاب آن برابر صفر خواهد بود. اما در حرکت دو و سهبعدی، قضیه کمی متفاوت است. اگر ذرهای با سرعت ثابت در امتداد مسیر منحنی، مانند دایره، حرکت کند، شتاب آن مخالف صفر خواهد بود. چرا؟ به این نکته توجه داشته باشید که سرعت، بردار است، یعنی هم جهت دارد و هم اندازه. شتاب، نهتنها از تغییرات اندازه سرعت، بلکه از تغییر جهت آن نیز ایجاد میشود. در حرکت دایرهای، ممکن است اندازه سرعت تغییر نکند، اما به دلیل تغییر جهت آن، شتاب ایجاد میشود.
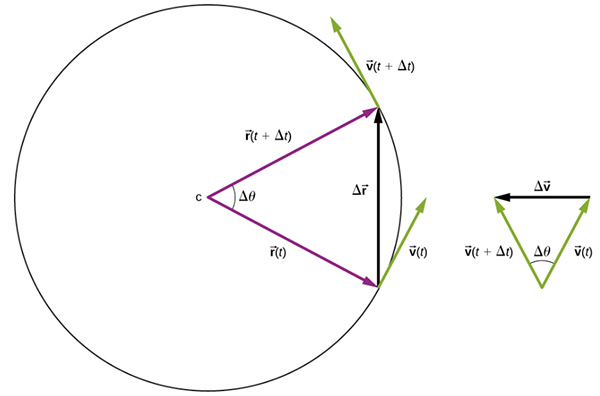
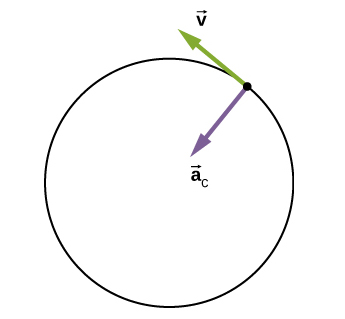
به تصویر نشان داده شده در بالا توجه کنید. ذرهای روی دایره، در زمان t در مکان قرار دارد. این ذره در جهت عقربههای ساعت، حرکت و مکان آن از به تغییر میکند. بردار سرعت بر مسیر حرکت ذره مماس و اندازه آن ثابت است، اما جهت آن تغییر میکند. از آنجا که بردار سرعت بر بردار مکان، عمود است، مثلثهای شکل گرفته توسط بردارهای مکان و و بردارهای سرعت و ، مشابه هستند. همچنین، از آنجا که و ، دو مثلث متساویالساقین هستند. بنابراین، رابطه زیر را میتوان بهدست آورد:
بزرگی شتاب در حرکت دایرهای به صورت زیر بهدست میآید:
شاید از خود بپرسید، جهت بردار شتاب در حرکت دایرهای چگونه است. به این نکته توجه داشته باشید که با نزدیک شدن و به سمت صفر، بردار بر عمود میشود. از آنجا که بر دایره مماس است، جهت شتاب به سمت مرکز دایره خواهد بود. بنابراین، شتاب ذرهای که با سرعت ثابت روی دایره حرکت میکند برابر است با:
جهت بردار شتاب به سمت مرکز دایره است. این شتاب، شتاب شعاعی است و به آن شتاب مرکزگرا گفته میشود.
شتاب مرکزگرا یا شعاعی میتواند مقادیر گستردهای داشته باشد. مقدار آن به سرعت و شعاع انحنای مسیر حرکت، بستگی دارد. جدول زیر برخی از مقدارهای این شتاب را نشان میدهد.
| جسم | شتاب مرکزگرا برحسب متر بر مجذور ثانیه یا g |
| چرخش زمین به دور خورشید | |
| چرخش ماه به دور زمین | |
| ترن هوایی | |
| چرخش الکترون به دور پروتون در مدل اتمی بوهر |
معادلات حرکت برای حرکت دایره ای یکنواخت
ذرهای را در نظر بگیرید که روی دایرهای با شعاع معین در جهت عقربههای ساعت، حرکت میکند. موقعیت ذره توسط بردار توصیف میشود. اگر زاویه نسبت به محور xها برابر باشد، مکان ذره را میتوان به صورت زیر نوشت:
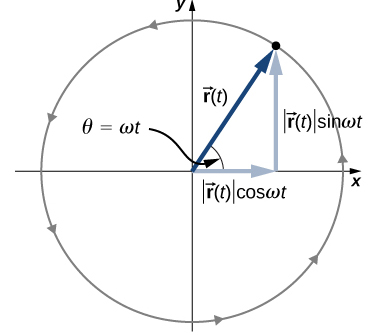
فرکانس زاویهای است. زمانی که ذره یک دور کامل یا رادیان میچرخد برابر است با:
سرعت و شتاب حرکت ذره نیز به ترتیب از مشتق اول مکان نسبت به زمان و مشتق دوم مکان نسبت به زمان (مشتق سرعت نسبت به زمان)، بهدست میآیند.
حرکت دایره ای غیریکنواخت
همیشه سرعت حرکت ذره روی دایره، ثابت نیست. ذره میتواند روی دایره حرکت کند و سرعت خود را افزایش یا کاهش دهد. در این صورت، شتاب مولفهای در راستای حرکت یا مسیر ذره نیز خواهد داشت.
در حرکت دایرهای یکنواخت، ذره با سرعت ثابت روی دایرهای با شعاع ثابت، حرکت میکند. اگر بزرگی سرعت ذره تغییر کند، شتاب مولفهای در جهت مماس بر دایره دارد:
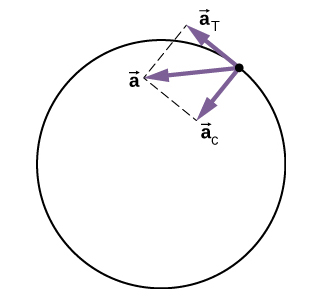
شتاب مماسی، مماس بر دایره و شتاب مرکزگرا، در راستای شعاع دایره و به سمت مرکز دایره است. بنابراین، شتاب حرکت ذره در حرکت دایرهای غیریکنواخت برابر است با:
به این نکته توجه داشته باشید که شتابهای مرکزگرا و مماسی بر یکدیگر عمود هستند.
مثال شتاب متوسط در حرکت دایره ای
برای درک بهتر چگونگی محاسبه شتاب در حرکت دایرهای، به مثالهای زیر توجه کنید.
مثال اول
ذرهای روی دایرهای به شعاع ۲/۰ متر حرکت میکند. سرعت ذره در فاصله زمانی بین ۱/۵ تا ۴/۰ ثانیه به صورت زیر با زمان تغییر میکند:
شتاب کل ذره را در زمان ۲/۰ ثانیه بهدست آورید.
پاسخ: در این مثال، شعاع دایره و سرعت حرکت ذره داده شدهاند. بنابراین، به راحتی میتوانیم شتاب مرکزگرا را بهدست آوریم. جهت شتاب مرکزگرا در راستای شعاع دایره و به سمت مرکز آن است.
شتاب مماسی از مشتق تابع سرعت داده شده نسبت به زمان بهدست میآید.
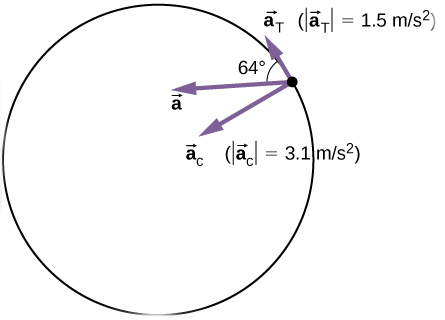
با داشتن شتابهای مرکزگرا و مماسی، شتاب کل را بهدست میآوریم:
زاویه نیز برابر است با:
مثال دوم
ذرهای روی دایرهای به شعاع r حرکت میکند. اگر این ذره یک دور کامل روی دایره حرکت کند، شتاب متوسط آن برابر است با:
- برداری ثابت با مقدار
- اندازه شتاب متوسط ذره برابر و بر صفحه دایره عمود است.
- برابر بردار شتاب لحظهای در آغاز حرکت است.
- بردار صفر
پاسخ: هنگامی که ذره یک دور کامل روی دایره حرکت میکند، جابجایی و در نتیجه، سرعت متوسط آن برابر صفر است. از اینرو، بردار شتاب متوسط نیز برابر صفر خواهد بود. پاسخ صحیح، گزینه ۴ است.
حل مسئله در شتاب متوسط
تا اینجا، با شتاب متوسط و تفاوت آن با شتاب لحظهای، نحوه بهدست آوردن شتاب متوسط و شتاب متوسط در حرکت دایرهای آشنا شدیم. در ادامه، برای درک بهتر این مطلب، چند مسئله حل خواهیم کرد.
مسئله ۱
سرعت اتومبیلی نسبت به زمان برابر است.
- شتاب متوسط اتومبیل را در بازه زمانی ۲ تا ۵ ثانیه بهدست آورید.
- شتاب لحظهای را در ثانیههای ۲ و ۵، محاسبه کنید.
پاسخ
در مطالب بالا، در مورد شتاب متوسط و لحظهای و تفاوت آنها با یکدیگر صحبت کردیم. در این مسئله، تابع زمانی سرعت داده شده است. برای بهدست آوردن شتاب متوسط در بازه زمانی داده شده، ابتدا مقدار سرعت را در ابتدا و انتهای بازه بهدست میآوریم:
شتاب متوسط در بازه زمانی ۲ تا ۵ ثانیه، با استفاده از رابطه زیر بهدست میآید:
با قرار دادن سرعتهای بهدست آمده در رابطه شتاب، مقدار آن را بهدست میآوریم:
برای بهدست آوردن شتاب لحظهای از سرعت نسبت به زمان مشتق میگیریم:
میدانیم مشتق سرعت نسبت به زمان برابر شتاب لحظهای است. مشتق، برابر ۱۰- و مستقل از زمان بهدست آمد. بنابراین، شتاب حرکت جسم ثابت و در ثانیههای ۲ و ۵ ، برابر ۱۰- متر بر مجذور ثانیه است.
اکنون فرض کنید، تابع داده شده برای سرعت بر حسب زمان به صورت باشد، شتاب متوسط و لحظهای را در ثانیههای دوم و پنجم حرکت بهدست آورید. برای بهدست آوردن شتاب متوسط در بازه زمانی داده شده، ابتدا مقدار سرعت را در ابتدا و انتهای بازه بهدست میآوریم:
شتاب متوسط در بازه زمانی ۲ تا ۵ ثانیه، با استفاده از رابطه زیر بهدست میآید:
در ادامه، از سرعت نسبت به زمان مشتق میگیریم:
در اینجا، مشتق سرعت یا شتاب لحظهای به زمان وابسته است، بنابراین مقدار شتاب در لحظههای ۲ و ۵ ثانیه با یکدیگر متفاوت خواهند بود. از اینرو، جسم با شتاب متغیر حرکت میکند.
مسئله ۲
اتومبیلی در امتداد جادهای افقی و مستقیم، مسیر ۲۱۴۵ متری بین دو چراغ راهنمایی و رانندگی را در مدت زمان ۱۲۰ ثانیه طی میکند. این اتومبیل از حالت سکون با شتاب ثابت شروع به حرکت میکند و پس از مدت زمان ۳۰ ثانیه، سرعت آن به ۳۰ متر بر ثانیه میرسد. سپس، در مدت T ثانیه با همین سرعت حرکت میکند. اتومبیل، نزدیکِ چراغ دوم با شتاب ثابتی ترمز میکند و به هنگام قرمز شدن چراغ، به طور کامل متوقف میشود.
- نمودار سرعت-زمان حرکت اتومبیل را رسم کنید.
- زمان T را بهدست آورید.
پاسخ
داشتن درک درستی از مسئله به هنگام حل مسائل حرکتشناسی، بسیار مهم است. در این مسئله، حرکت اتومبیلی بین دو چراغ راهنمایی و رانندگی به فاصله ۲۱۴۵ متر، توصیف شده است. در قسمت یک، نمودار سرعت-زمان را رسم میکنیم.
قسمت ۱: برای رسم نمودار سرعت-زمان، گامهای زیر را طی میکنیم:
- گام اول: کلِ زمان حرکت اتومبیل برابر ۱۲۰ ثانیه است. بنابراین، نمودار سرعت-زمان را برای ۱۲۰ ثانیه رسم میکنیم.
- گام دوم: اتومبیل از حالت سکون، با شتاب شروع به حرکت میکند و در مدت ۳۰ ثانیه، سرعت آن به ۲۲ متر بر ثانیه میرسد. مدت زمان مرحله اول حرکت برابر ۳۰ ثانیه است. در این زمان، شتاب حرکت، ثابت است. بنابراین، نمودار سرعت-زمان خطی با شیب مثبت و ثابت خواهد بود.
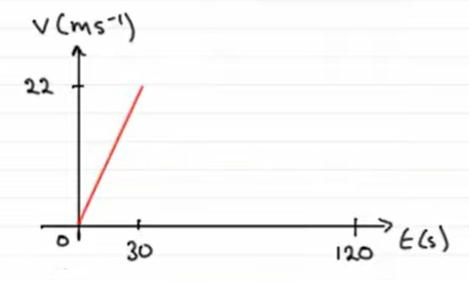
- گام سوم: پس از آنکه سرعت اتومبیل به ۲۲ متر بر ثانیه رسید، به مدت T ثانیه با همین سرعت حرکت میکند. بنابراین، در مرحله دوم حرکت، اتومبیل با سرعت ثابت و شتاب صفر به حرکت خود ادامه میدهد. در نتیجه، نمودار سرعت-زمان خطی افقی و موازی محور زمان است.
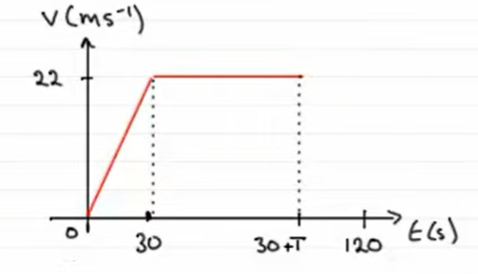
- گام چهارم: پس از T ثانیه، اتومبیل ترمز میکند و سرعت آن با شتاب ثابتی کاهش مییابد و به صفر میرسد. در این مرحله، شتاب منفی و حرکت کندشونده است. بنابراین، نمودار سرعت-زمان خطی یا شتاب ثابت و منفی خواهد بود.
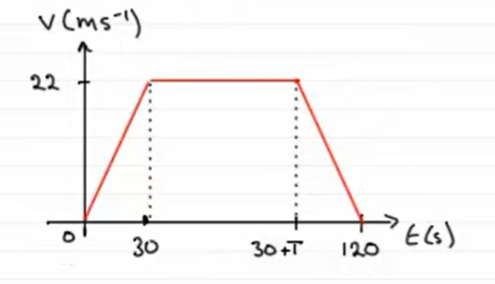
قسمت ۲: در این قسمت، زمان T را بهدست میآوریم. مسافت کلِ طی شده توسط اتومبیل، ۲۱۴۵ متر و برابر مساحت زیر نمودار سرعت-زمان (ذوزنقه) است:
مسئله ۳
اتومبیل مسئله دو را در نظر بگیرید. فرض کنید موتورسیکلتی ۱۰ ثانیه پس از آن، چراغ اول راهنمایی و رانندگی را ترک کند. موتورسیکلت از حالت سکون و با شتاب ثابت شروع به حرکت میکند و در فاصله ۹۹۰ متری از چراغ اول از اتومبیل سبقت میگیرد. سرعت اتومبیل به هنگام سبقت موتورسیکلت از آن برابر ۲۲ متر بر ثانیه است.
- موتورسیکلت چند ثانیه پس از آغاز حرکت از اتومبیل سبقت میگیرد؟
- شتاب حرکت موتور را بهدست آورید.
پاسخ
مسئله ۳ در ادامه مسئله ۲ داده شده است، بنابراین برای حل آن میتوانیم از مسئله دو کمک بگیریم.
قسمت ۱: موتورسیکلت، ده ثانیه پس از اتومبیل، شروع به حرکت میکند و در فاصله ۹۹۰ متری از چراغ اول به اتومبیل میرسد و از آن سبقت میگیرد. بر طبق صورت مسئله، موتور با شتاب ثابت شروع به حرکت میکند و t ثانیه بعد به اتومبیل میرسد. بنابراین، نمودار سرعت-زمان آن، خطی با شیب ثابت و مثبت است. توجه به این نکته مهم است که نمودارهای سرعت-زمان موتورسیکلت و اتومبیل را در یک دستگاه مختصات رسم میکنیم.
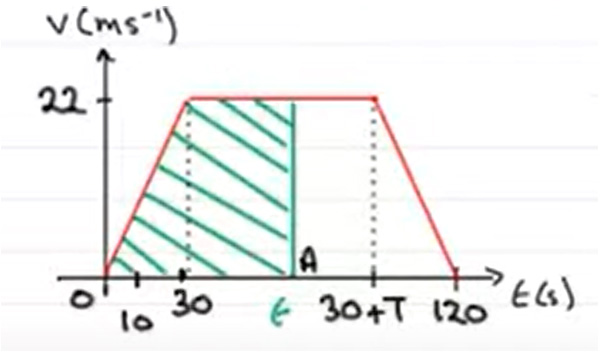
حل این قسمت، همانند قسمت دوم مسئله ۲ خواهد بود. مسافت کلِ طی شده توسط موتورسیکلت برابر ۹۹۰ متر و برابر مساحت زیر نمودار سرعت-زمان (ذوزنقه) است:
زمان t نشان داده شده در نمودار سرعت-زمان را برابر ۶۰ ثانیه بهدست آوردیم. نکتهای که باید به آن توجه شود آن است که این زمان، نسبت به لحظه حرکت اتومبیل، محاسبه شده است. اما ما باید مدت زمان حرکت موتورسیکلت را بهدست آوریم. از آنجا که موتورسیکلت، ۱۰ ثانیه پس از اتومبیل، شروع به حرکت کرده، مدت زمان حرکت آن برابر ۵۰ ثانیه است.
قسمت ۲: در قسمت قبل دیدیم که موتورسیکلت، ۵۰ ثانیه پس از شروع حرکت با شتاب ثابت به اتومبیل رسید و از آن سبقت گرفت. در این قسمت میخواهیم شتاب حرکت آن را بهدست آوریم.
نکته: در این قسمت میتوانیم از معادله suvat استفاده کنیم که در آن:
- s مسافت طی شده است. در اینجا، مسافت طی شده توسط اتومبیل برابر ۹۹۰ متر است.
- u سرعت اولیه حرکت است. از آنجا که موتور از حالت سکون شروع به حرکت کرده، سرعت اولیه آن برابر صفر است.
- v سرعت نهایی است که مقدار آن را نمیدانیم.
- a شتاب حرکت است و باید آن را بهدست آوریم.
- t مدت زمان حرکت و برابر ۵۰ ثانیه است.
از میان معادلههای حرکت بر خط راست، از معادله استفاده میکنیم. با قرار دادن مقدارهای داده شده در این رابطه، مقدار شتاب ۰/۷۹۲ متر بر مجذور ثانیه بهدست میآید.
اگر جسمی با شتاب غیرصفر حرکت کند، آیا سرعت آن میتواند ثابت باشد؟
بله
خیر
در حرکت یکبعدی، مقدار شتابِ حرکت با سرعت ثابت، برابر صفر خواهد بود.
در کدامیک از گزینههای زیر، سرعت صفر ولی شتاب مخالف صفر است.
در پرتاب توپ به سمت بالا، سرعت در ارتفاع اوج صفر، ولی شتاب مخالف صفر است.
حرکت اتومبیل در اتوبان
بازی بسکتبال
جمعبندی
در این مطلب، در مورد شتاب متوسط و روشهای محاسبه آن صحبت کردیم:
- شتاب متوسط برابر تغییرات سرعت در بازه زمانی مشخصی است. با داشتن سرعتهای اولیه و نهایی و قرار دادن آنها در فرمول شتاب متوسط، مقدار آن را بهدست میآوریم.
- از نمودار سرعت-زمان برای بهدست آوردن شتاب متوسط استفاده میکنیم.
در ادامه، تفاوت شتاب متوسط با شتاب لحظهای و مفهوم شتاب متوسط در حرکت دایرهای را توضیح دادیم.












