شتاب لحظه ای چیست؟ – تعریف و فرمول + حل تمرین
به طور حتم عبارتهایی مانند «دونده شماره یک، سریعتر از دونده شماره ۲ میدود» را در زندگی روزمره شنیدهاید. عبارت علمیتر برای واژههایی مانند سریعتر و آهستهتر در فیزیک، سرعت زیاد یا کم و حرکت با شتاب ثابت یا متغیر است. سرعت، به صورت تغییرات مکان جسم در بازه زمانی مشخصی تعریف میشود و یکای اندازهگیری آن برابر متر بر ثانیه است. با دانستن سرعت جسمی بر حسب متر بر ثانیه، میدانیم که جسم در هر ثانیه، چند متر حرکت میکند. باید بدانیم که سرعت حرکت اجسام همیشه ثابت نیست و ممکن است با گذر زمان اندازه آن کم یا زیاد شود. به تغییرات سرعت برحسب زمان، شتاب گفته میشود و همانند سرعت، دو نوع شتاب، به نامهای شتاب لحظه ای و شتاب متوسط داریم. در این مطلب، ابتدا شتاب لحظه ای را تعریف میکنیم و سپس فرمول محاسبه آن را بهدست میآوریم. در ادامه، تفاوت شتاب لحظه ای و متوسط را توضیح میدهیم و مثالهایی برای درک بهتر شتاب لحظهای حل خواهیم کرد.
شتاب لحظه ای چیست ؟
سرعت جسم در فیزیک به صورت مقدار جابجایی در مدت زمان مشخصی تعریف میشود و واحد اندازهگیری آن برابر متر بر ثانیه است. به بیان دیگر، با دانستن سرعت حرکت جسم، میدانیم در هر ثانیه چند متر حرکت میکند. دو نوع سرعت داریم:
- سرعت متوسط: به جابجایی جسم در مدت زمان مشخصی، سرعت متوسط گفته میشود و با استفاده از رابطه زیر بهدست میآید:
- سرعت لحظهای: سرعت لحظهای، سرعت حرکت جسم را در هر لحظه از زمان به ما میدهد. برای بهدست آوردن سرعت لحظهای، زمان را به زمان نزدیک میکنیم. بنابراین، بازه زمانی به سمت صفر میل میکند:
نکته: با توجه به رابطه بالا، سرعت لحظهای از مشتق مکان برحسب زمان بهدست میآید.

به این نکته توجه داشته باشید که سرعت حرکت اجسام، همیشه ثابت نیست و گاهی افزایش یا کاهش مییابد. به تغییرات سرعت برحسب زمان، شتاب گفته میشود. هنگام شروع رانندگی، سرعت از صفر به مقدار معینی میرسد. در این حالت، اتومبیل با شتاب مثبت شروع به حرکت میکند. به هنگام توقف، سرعت از مقدار مشخصی به صفر میرسد. بنابراین، اتومبیل با شتاب منفی، متوقف میشود. هنگامی که تغییرات سرعت مثبت باشد، شتاب حرکت مثبت و هنگامی که تغییرات سرعت منفی باشد، شتاب حرکت منفی خواهد بود. دو نوع شتاب داریم:
- شتاب متوسط: به تغییرات سرعت جسم در مدت زمانی مشخص، شتاب متوسط گفته میشود و با استفاده از رابطه زیر بهدست میآید:
- شتاب لحظهای: شتاب لحظهای، شتاب حرکت جسم را در هر لحظه از زمان به ما میدهد. برای بهدست آوردن شتاب لحظه ای، زمان را به زمان نزدیک میکنیم. بنابراین، بازه زمانی به سمت صفر میل میکند:
برای آنکه بدانیم از رابطه بالا چگونه برای محاسبه شتاب لحظه ای استفاده کنیم، در ادامه مثالهای سادهای را در این زمینه حل میکنیم.
مثال اول محاسبه شتاب لحظه ای
ذرهای با سرعت در مسیر مستقیمی حرکت میکند. شتاب حرکت ذره را در زمان سه ثانیه بهدست آورید.
پاسخ
سرعت ذره یک ثانیه پس از شروع حرکت برابر ۲ متر بر ثانیه، دو ثانیه پس از شروع حرکت برابر ۸ متر بر ثانیه و ۳ ثانیه پس از شروع حرکت برابر ۱۸ متر بر ثانیه خواهد بود. در نخستین گام باید بازه زمانی را به گونهای انتخاب کنیم که زمان در آن باشد.
برای سادگی زمان را برابر سه ثانیه و زمان را اندکی بزرگتر از سه ثانیه انتخاب و با نزدیک کردن به سه ثانیه، بازه را کوچکتر میکنیم.
در ابتدا، مقدار را برابر 3/1 ثانیه انتخاب میکنیم:
شتاب متوسط در بازه زمانی برابر است با:
مقدار سرعت در زمان برابر است با:
همچنین، مقدار سرعت در زمان برابر است با:
با داشتن مقدارهای سرعتهای اولیه و نهایی، شتاب متوسط را به صورت زیر بهدست میآوریم:
بنابراین، هنگامی که بازه زمانی بین ۳ ثانیه و ۳/۱ ثانیه است، مقدار شتاب متوسط برابر ۱۲/۲ متر بر مجذور ثانیه بهدست میآید.
در ادامه، بازه زمانی را با نزدیک کردن به ، کوچکتر میکنیم. برای انجام این کار، زمان را برابر ۳/۰۱ ثانیه قرار میدهیم.
از آنجا که زمان تغییر نکرده است، سرعت همچنان برابر ۱۸ متر بر ثانیه خواهد بود. سرعت در زمان برابر است با:
با داشتن مقدارهای سرعتهای اولیه و نهایی، شتاب متوسط را به صورت زیر بهدست میآوریم:
در آخرین گام، را با انتخاب زمان برابر ۳/۰۰۱ ثانیه باز هم کوچکتر میکنیم:
اندازه باز هم تغییر نکرده است. سرعت برابر است با:
شتاب متوسط برابر است با:
بنابراین، با کوچکتر شدن بازه ، شتاب متوسط به مقدار نزدیکتر میشود. هرچه بازه زمانی را کوچکتر کنیم، به شتابِ ۱۲ متر بر مجذور ثانیه نزدیکتر میشویم. از اینرو، اینگونه به نظر میرسد که شتاب لحظه ای در زمان سه ثانیه، برابر ۱۲ متر بر مجذور ثانیه خواهد بود.
در ادامه، با استفاده از رابطه سرعت برحسب زمان، رابطه شتاب متوسط را در بازه زمانی بهدست میآوریم، سپس با قرار دادن برابر صفر، شتاب لحظه ای را در زمان سه ثانیه محاسبه میکنیم.
بازه زمانی را بین زمانهای و انتخاب میکنیم:
بار دیگر را برابر t یا بسیار نزدیک به آن قرار میدهیم. را به گونهای انتخاب میکنیم که به بسیار نزدیک باشد:
بنابراین، مرزهای بازه زمانی برابر و هستند. سرعت جسم در زمان برابر است با:
همچنین، سرعت در زمان برابر است با:
شتاب متوسط در بازه زمانی برابر است با:
اگر بازههای زمانی انتخاب شده در بالا را در رابطه بهدست آمده برای شتاب متوسط قرار دهیم، به نتیجه یکسانی میرسیم:
اگر بازه زمانی به سمت صفر میل کند، داریم:
بنابراین، شتاب لحظه ای جسم در هر لحظه از زمان با رابطه داده میشود. به طور خاص، مقدار شتاب لحظه ای در زمان سه ثانیه، برابر ۱۲ متر بر مجذور ثانیه است.
نکته: شتاب لحظه ای برابر مشتق سرعت نسبت به زمان است.
فی
مثال دوم محاسبه شتاب لحظه ای
ذرهای روی خط مستقیم با سرعت حرکت میکند. شتاب لحظه ای ذره در زمان ۴۵/۰ ثانیه، چه مقدار است؟
پاسخ
برای حل این مثال از دو روش استفاده میکنیم:
- روش حد
- روش مشتق
روش حد
شتاب لحظه ای ذره با استفاده از رابطه زیر بهدست میآید:
با استفاده از روش حد، رابطه شتاب لحظه ای برحسب زمان را بهدست آوردیم. بنابراین، شتاب لحظه ای در زمان ۴۵ ثانیه برابر است با:
روش مشتق
شتاب لحظه ای در هر لحظه از زمان برابر مشتق سرعت نسبت به زمان است:
شتاب در زمان ۴۵ ثانیه برابر است با:
مثال سوم محاسبه شتاب لحظه ای
شتاب ذرهای با استفاده از رابطه زیر داده شده است:
مقدار شتاب لحظه ای را در زمان ۳ ثانیه بهدست آورید.
پاسخ
در این مثال، رابطه شتاب برحسب زمان داده شده است. بنابراین، شتاب لحظه ای در زمان ۳ ثانیه برابر است با:
مثال چهارم محاسبه شتاب لحظه ای
الکترونی در امتداد محور x با شتاب a حرکت میکند. مکان الکترون برحسب زمان به صورت زیر داده شده است:
مقدار a را در زمان یک ثانیه بهدست آورید.
پاسخ
در این مثال، رابطه مکان برحسب زمان داده شده است. سرعت، برابر مشتق اول مکان نسبت به زمان و شتاب نیز برابر مشتق سرعت برحسب زمان یا مشتق دوم مکان برحسب زمان است. در این مثال، برای بهدست آوردن رابطه شتاب برحسب زمان، از رابطه داده شده برای مکان، دو بار نسبت به زمان مشتق میگیریم:
با قرار دادن زمان یک ثانیه در رابطه بالا، شتاب لحظه ای را بهدست میآوریم:
مثال پنجم محاسبه شتاب لحظه ای
رابطه مکان برحسب زمان ذرهای به صورت زیر داده شده است:
در رابطه بالا برحسب متر و برحسب ثانیه است.
- در چه زمانی سرعت ذره برابر صفر است؟
- شتاب ذره در چه زمانی برابر صفر است؟
- شتاب لحظه ای حرکت ذره در چه زمانی منفی و در چه زمانی مثبت است؟
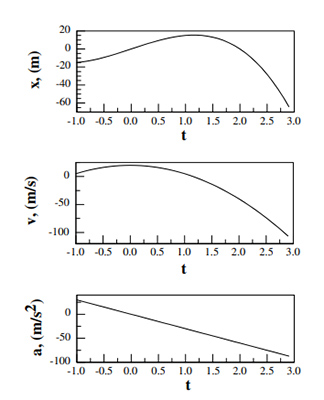
- نمودارهای و و را برحسب زمان رسم کنید.
پاسخ
سرعت از مشتق اول مکان نسبت به زمان بهدست میآید:
در قسمت اول باید زمانی را بهدست آوریم که سرعت ذره برابر صفر میشود. به همین دلیل، رابطه بهدست آمده برای سرعت را برابر صفر قرار میدهیم:
معادله فوق را برای حل میکنیم:
معادله بالا دو جواب برای زمان صفر شدن سرعت میدهد. از آنجا که زمان منفی در فیزیک معنایی ندارد، جواب قابلقبول برابر ۱/۱۵ ثانیه است.
قسمت ۲: در این قسمت، ابتدا شتاب حرکت را بهدست میآوریم:
برای آنکه بدانیم در چه زمانی شتاب حرکت برابر صفر است، را برابر صفر قرار میدهیم:
بنابراین، مقدار شتاب تنها در زمان صفر (ابتدای حرکت)، برابر صفر است.
قسمت ۳: برای آنکه بدانیم،شتاب ذره در چه لحظاتی منفی و در چه لحظاتی مثبت است، باید را تعیین علامت کنیم:
در فیزیک، زمان منفی معنایی ندارد، بنابراین شتاب حرکت ذره همواره منفی است.
قسمت ۴: نمودارهای و و در تصویر زیر نشان داده شدهاند.
مثال ششم محاسبه شتاب لحظه ای
حرکت نقطه روی صفحه در بازی ویدیویی «آرکِید» (Arcade) با استفاده از رابطه زیر انجام میشود:
در رابطه بالا، بر حسب سانتیمتر و برحسب ثانیه است. توجه به این نکته مهم است که مکان نسبت به لبه چپ صفحه اندازه گرفته میشود. هنگامی که نقطه به لبههای صفحه میرسد ( یا ) زمان را برابر صفر قرار میدهیم و نقطه دوباره شروع به حرکت میکند.
- نقطه در چه زمانی پس از شروع حرکت، به طور آنی ساکن میشود؟
- ساکن شدن نقطه در چه مکانی رخ میدهد؟
- شتاب حرکت را در قسمت یک بهدست آورید.
- نقطه، قبل از ساکن شدن در چه جهتی حرکت میکند؟
- نقطه برای نخستین بار در چه زمانی پس از شروع حرکت به لبه صفحه میرسد؟

پاسخ
در ابتدا، سرعت لحظهای نقطه را بهدست میآوریم:
توجه به این نکته مهم است که یکای سرعت در اینجا، سانتیمتر بر ثانیه است.
قسمت ۱: در این قسمت باید زمانی را بهدست آوریم که ذره به صورت آنی ساکن میشود. ساکن شدن به معنای صفر شدن سرعت آن است. از اینرو، سرعت نقطه را برابر صفر قرار میدهیم:
از آنجا که تنها زمانهای مثبت در فیزیک پذیرفته میشوند، سرعت نقطه دو ثانیه پس از شروع حرکت برابر صفر میشود.
قسمت ۲: در این قسمت باید مکانی را پیدا کنیم که در آنجا سرعت لحظهای نقطه برابر صفر است. در قسمت قبل دیدیم دو ثانیه پس از شروع حرکت، سرعت لحظهای نقطه برابر صفر میشود، مکان نقطه در این لحظه برابر است با:
آیا نقطه به لبه صفحه رسیده است؟ خیر، زیرا طول صفحه برابر ۱۵/۰ سانتیمتر است.
قسمت ۳: برای آنکه شتاب لحظه ای را در همه زمانها بهدست آوریم، باید از سرعت برحسب زمان مشتق بگیریم:
در قسمت قبل گفتیم در زمان دو ثانیه، نقطه به طور آنی ساکن و سرعت آن صفر میشود. شتاب لحظه ای در این زمان برابر است با:
قسمت ۴: در قسمت ۳ دیدیم در لحظه صفر شدن سرعت، شتاب لحظه ای منفی است. شتاب منفی به معنای کاهش سرعت نسبت به زمان است. سرعت در زمان دو ثانیه صفر و شتاب منفی است. بنابراین، سرعت در زمان دو ثانیه باید از مثبت به منفی برود. از اینرو، درست قبل از این زمان، سرعت مثبت بوده است.
قسمت ۵: در قسمتهای قبل دیدیم نقطه از لبه سمت چپ صفحه شروع به حرکت میکند و دو ثانیه پس از شروع حرکت و در فاصله ۱۲ متری از لبه صفحه، سرعت آن صفر میشود. از آنجا که شتاب حرکت منفی است، نقطه تغییر جهت میدهد و در جهت معکوس شروع به حرکت میکند. در نتیجه، نقطه هیچگاه به لبه سمت راست نمیرسد. سوالی که ممکن است مطرح شود آن است که نقطه چند ثانیه پس از شروع حرکت، به مکان اولیه خود (لبه راست) میرسد. برای بهدست آوردن این زمان، مکان نقطه را برابر صفر قرار میدهیم:
زمان صفر زمانی است که ذره شروع به حرکت میکند.
بنابراین، نقطه در زمان صفر از لبه چپ صفحه شروع به حرکت میکند و دو ثانیه بعد سرعت آن صفر و شتاب آن، منفی میشود. در نتیجه، جهت حرکت معکوس خواهد شد و نقطه بار دیگر به لبه چپ صفحه برمیگردد و ۳/۴۶ ثانیه پس از آغاز حرکت به آن میرسد. توجه به این نکته مهم است که نقطه هیچگاه به لبه راست صفحه نمیرسد.
مثال هفتم محاسبه شتاب لحظه ای
تابع مکان برحسب زمان جسمی به صورت زیر داده شده است:
شتاب لحظه ای را در زمان ۳/۳ ثانیه بهدست آورید.
پاسخ
تابع مکان برحسب زمان به صورت زیر داده شده است:
سرعت لحظهای برابر مشتق مکان نسبت به زمان است:
با گرفتن مشتق سرعت نسبت به زمان، شتاب لحظه ای را بهدست میآوریم:
با داشتن شتاب لحظه ای برحسب زمان، به راحتی مقدار آن را در زمان ۳/۳ ثانیه بهدست میآوریم:
اگر تابع مکان جسمی متناسب با مربع زمان باشد، شتاب لحظهای آن:
افزایش مییابد.
کاهش مییابد.
صفر است.
ثابت است.
مکان جسم متناسب با مربع زمان است، بنابراین آن را میتوان به صورت زیر نوشت:
در رابطه بالا، A ثابت و زمان است. شتاب لحظهای از مشتق دوم مکان نسبت به زمان بهدست میآید:
در نتیجه، شتاب لحظهای جسم ثابت و مستقل از زمان است.
نکته ۱: اگر جسمی بر روی خط مستقیم یکبعدی با شتاب ثابت حرکت کند، معادلات حرکت آن عبارت هستند از:
نکته ۲: اگر جسمی را از ارتفاع مشخصی رها کنیم، با شتاب ثابتی برابر شتاب جاذبه زمین (۹.۸ متر بر مجذور ثانیه) شروع به حرکت میکند.
الکترونی با سرعت اولیه وارد ناحیهای به طور ۱/۰ سانتیمتر میشود و در آنجا به دلیل نیروی الکتریکی، شتاب میگیرد. اگر الکترون با سرعت از این ناحیه خارج شود، اندازه شتاب حرکت آن کدام گزینه است؟ (الکترون با شتاب ثابت حرکت میکند)
در اینجا فرض میشود که الکترون با شتاب ثابت حرکت میکند. بنابراین، از معادلات نوشته شده در نکته ۱ استفاده میکنیم. سرعت اولیه، سرعت نهایی و مسافت طی شده توسط الکترون داده شده است. از اینرو، برای بهدست آوردن شتاب حرکت از معادله استفاده میکنیم:
یکای شتاب متوسط و لحظهای برابر متر بر مجذور ثانیه است. شتاب لحظه ای ممکن است مثبت یا منفی باشد. شاید از خود بپرسید شتاب مثبت یا منفی چیست یا در حالت کلی، چگونه علامت شتاب را تعیین میکنیم.
تفاوت شتاب متوسط و لحظه ای چیست ؟
به تغییرات سرعت نسبت به زمان شتاب گفته میشود. اگر این تغییرات در بازه زمانی مشخصی محاسبه شود، شتاب متوسط و اگر در هر لحظه از زمان محاسبه شود، شتاب لحظهای را خواهیم داشت.
سوالات متداول در مورد شتاب لحظه ای
در ادامه به دو سوال متداول در مورد شتاب لحظه ای پاسخ میدهیم.
شتاب لحظه ای چه نوع کمیتی است ؟
شتاب لحظه ای کمیتی برداری و دارای اندازه و جهت است.
تعیین علامت شتاب لحظه ای
برای تعیین علامت شتاب، ابتدا باید به چند سوال پاسخ دهیم:
- حرکت جسم در چه بعدی انجام میشود؟
- جهتهای مثبت و منفی به کدام سمت هستند؟
در این قسمت، فرض میکنیم که جسم روی خط راست و تنها به سمت چپ یا راست میتواند حرکت کند. سمت راست را به صورت قراردادی، جهت مثبت انتخاب میکنیم. در ادامه، برای تعیین علامت شتاب لحظه ای، حالتهای مختلف حرکت ذرهای را در نظر میگیریم. در تمام حالتها، حرکت به سمت راست محور افقی، مثبت، و حرکت به سمت چپ محور افقی، منفی است.
حالت اول
سرعت اولیه ذرهای در راستای مثبت محور افقی (محور x) برابر یک متر بر ثانیه و شتاب حرکت آن برابر دو متر بر مجذور ثانیه است. علامت شتاب لحظه ای، مثبت است. بنابراین، سرعت ذره با گذر زمان، افزایش خواهد یافت. حرکت ذره را یک ثانیه بعد، توصیف کنید.
هنگامی که میگوییم شتاب حرکت ذرهای برابر دو متر بر مجذور ثانیه است، یعنی هر ثانیه، دو متر بر ثانیه به سرعت ذره، اضافه میشود. در اینجا، سرعت اولیه ذره برابر یک متر بر ثانیه است. یک ثانیه بعد، سرعت ذره برابر سه متر بر ثانیه خواهد بود. یعنی، ذره یک ثانیه بعد، با سرعت بیشتری حرکت میکند. سرعت ذره یک ثانیه بعد چه مقدار است؟ ۵ متر بر ثانیه. با گذشت زمان، سرعت ذره بیشتر و بیشتر خواهد شد. به عنوان مثال، هنگامی که سنگی را از ارتفاع مشخصی رها میکنیم، در ثانیههای اول، با سرعت زیادی حرکت نمیکند، اما هنگام رسیدن به زمین، سرعت آن بسیار زیاد میشود.

حالت دوم
سرعت اولیه ذره در این حالت نیز برابر یک متر بر ثانیه، اما شتاب لحظه ای آن برابر است. ذره با سرعت مثبت به سمت راست حرکت میکند، زیرا به صورت قراردادی، حرکت به سمت راست روی محور افقی را مثبت در نظر میگیریم. از آنجا که شتاب حرکتِ ذره منفی است، از سرعت آن کاسته و یا به عبارتی حرکت ذره با گذشت زمان، آهسته میشود. به این نکته توجه داشته باشد که اگر علامت سرعت و شتاب، مخالف یکدیگر باشد، آنها در حال جنگ با یکدیگر و از بین بردن اثر هم هستند.
شتاب لحظه ای بدان معنا است که در هر ثانیه از سرعت ذره ، کم میشود. ذره، ابتدا با سرعت یک متر بر ثانیه حرکت میکند. سرعت آن نیم ثانیه پس از شروع حرکت، برابر صفر و یک ثانیه پس از شروع حرکت برابر است. در ابتدای حرکت بردار سرعت به سمت راست و اندازه آن برابر یک است. پس از یک ثانیه، بردار سرعت به سمت چپ و اندازه آن برابر یک متر بر ثانیه خواهد بود. به بیان دیگر، در مدت زمان یک ثانیه، ذره ابتدا متوقف میشود، سپس با سرعت یک متر بر ثانیه در جهت مخالف (به سمت چپ) شروع به حرکت میکند.

حالت سوم
ذرهای با سرعت اولیه یک متر بر ثانیه به سمت چپ حرکت میکند. بنابراین، سرعت اولیه آن برابر است. اگر شتاب حرکت ذره برابر دو متر بر مجذور ثانیه باشد، سرعت و جهت حرکت آن یک ثانیه پس از شروع حرکت چگونه است؟
علامتهای سرعت اولیه و شتاب، مخالف یکدیگر است، بنابراین، سرعت و شتاب با یکدیگر در رقابت و مبارزه هستند. ذره به سمت چپ حرکت میکند، اما جهت شتاب به سمت راست است. در هر ثانیه، دو متر بر ثانیه به سرعت ذره اضافه میشود. بنابراین، سرعت ذره یک ثانیه پس از شروع حرکت برابر است. در واقع، جهت حرکت ذره پس از گذشت یک ثانیه، تغییر میکند.

حالت چهارم
ذره با سرعت اولیه یک متر بر ثانیه به سمت چپ حرکت میکند. بنابراین، سرعت اولیه آن برابر است. اگر شتاب حرکت ذره برابر باشد، سرعت و جهت حرکت آن یک ثانیه پس از شروع حرکت چگونه است؟ در این حالت، علامتهای سرعت و شتاب با یکدیگر یکسان (منفی) هستند. بنابراین، اثر یکدیگر را تقویت میکنند. پس از یک ثانیه، سرعت ذره برابر میشود.
نکته: اگر علامت و جهت بردارهای شتاب و سرعت با یکدیگر یکسان باشند، اندازه سرعت با گذشت زمان در همان جهت اولیه افزایش مییابد.
شتاب لحظه ای در نمودار سرعت بر حسب زمان
شتاب لحظه ای را به صورت تغییرات سرعت برحسب زمان در هر لحظه از زمان، تعریف کردیم. به عبارت دیگر، مشتق سرعت برحسب زمان برابر شتاب لحظه ای است.
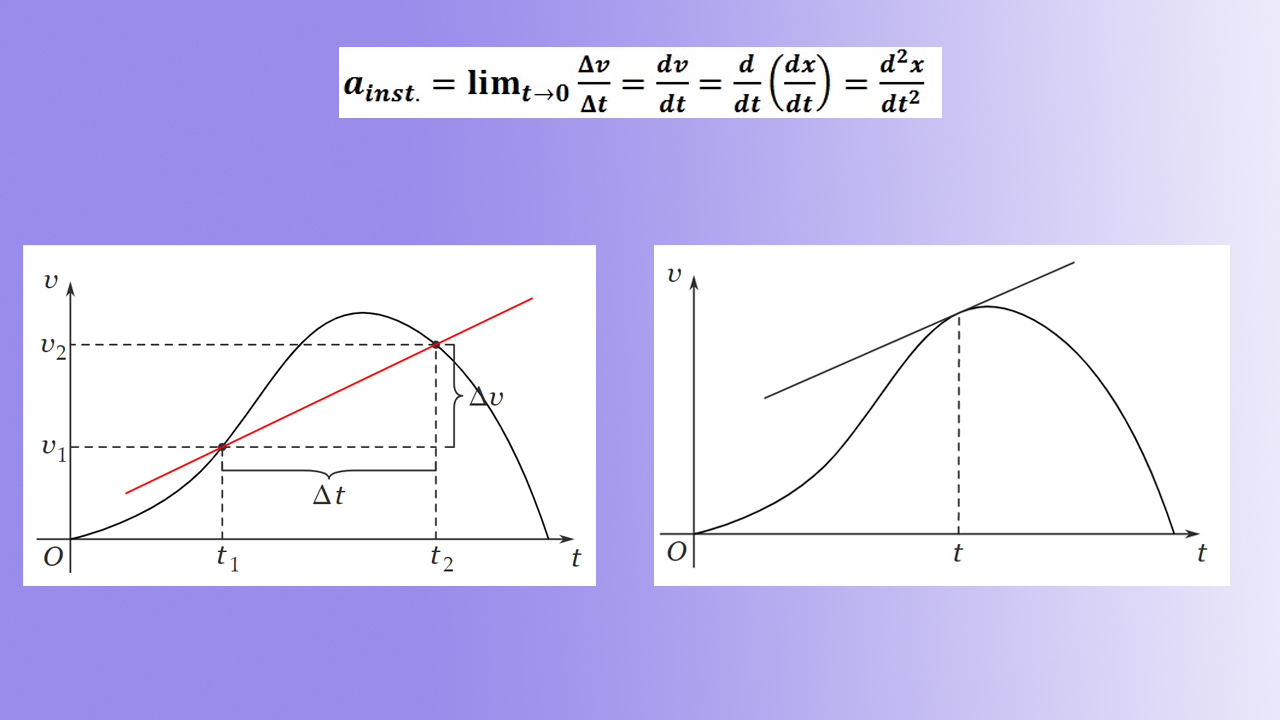
در تصویر نشان داده شده در ادامه، شتاب لحظه ای در زمان برابر شیب خط مماس بر نمودار سرعت-زمان در زمان است.
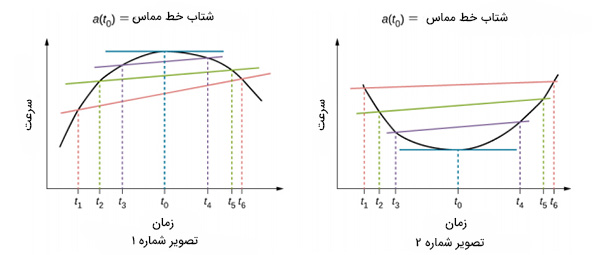
در مطالب بالا گفتیم که هنگامی که بازه زمانی به سمت صفر میل میکند، شتاب متوسط به شتاب لحظه ای نزدیک میشود. همانطور که در تصویر شماره یک دیده میشود، هنگامی که سرعت به بیشینه مقدار خود میرسد، شیب آن برابر صفر است. در این زمان، مقدار شتاب نیز برابر صفر خواهد بود. در تصویر شماره دو نیز شرایط مشابهی برای سرعت کمینه برقرار است. شیب خط مماس بر نمودار سرعت-زمان در نقاطی که سرعت کمینه یا بیشینه است، برابر صفر خواهد بود. بنابراین، مقدار شتاب لحظه ای در این نقاط برابر صفر است.
نکته: مقدار شتاب لحظه ای در نمودار سرعت-زمان در نقاط بیشینه و کمینه سرعت، برابر صفر است.
نمودار سرعت-زمان حرکت ذرهای به صورت زیر است:
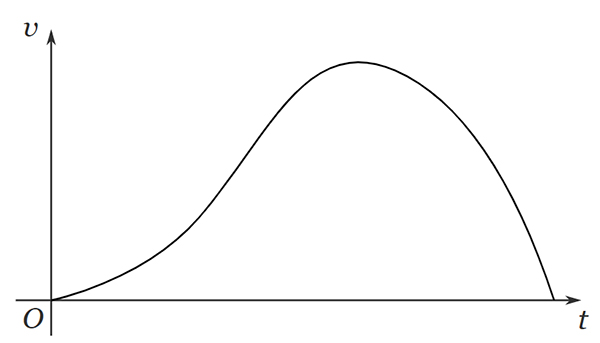
اگر بخواهیم شتاب ذرهای را در بازه زمانی بهدست آوریم، بازه زمانی را از تا در نظر میگیریم. برای بهدست آوردن شتاب لحظه ای، مقدار را بسیار کوچک و نزدیک به صفر انتخاب میکنیم. از این موضوع میتوانیم برای بهدست آوردن شتاب لحظه ای در نمودار سرعت برحسب زمان، استفاده کنیم. در ابتدا، خطی از نقطه به نقطه رسم میکنیم.
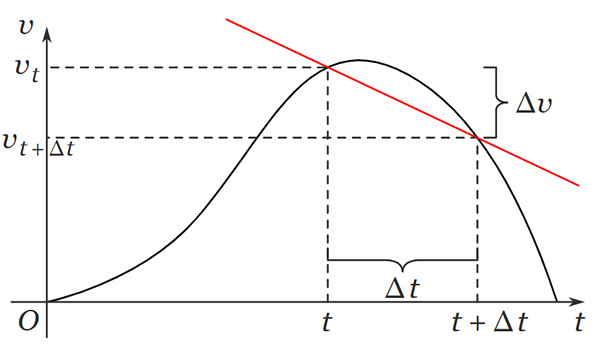
شیب خط رسم شده برابر شتاب متوسط در بازه زمانی خواهد بود، زیرا ، شتاب متوسط و شیب خط رسم شده را نشان میدهد. از اینرو، شتاب لحظه ای در زمان برابر شیب خط رسم شده به هنگام نزدیک شده به صفر است. با کوچکتر شدن مقدار ، خط گذرنده از دو نقطه و به خط مماس بر نمودار در نقطه نزدیک میشود. در نتیجه، شتاب لحظه ای در لحظه برابر با شیب خط مماس بر نمودار سرعت-زمان در نقطه است.
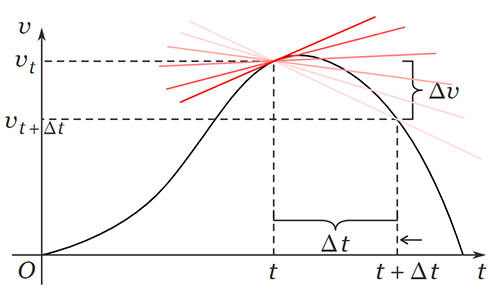
نکته: شتاب لحظه ای در زمان برابر شیب خط مماس بر نمودار سرعت برحسب زمان در نقطه است. اگر شیب خط مماس را با نشان دهیم، داریم:
تعیین علامت شتاب لحظه ای با استفاده از نمودار سرعت-زمان
تعیین علامت شتاب لحظه ای از روی نمودار سرعت-زمان، بسیار ساده است. نمودار سرعت-زمانی را به شکل نشان داده شده در تصویر زیر در نظر بگیرید. علامت شتاب لحظه ای را در زمان بهدست میآوریم.

با توجه به مطالب بالا میدانیم که شتاب در زمان برابر با شیب خط مماس بر نمودار سرعت-زمان در نقطه است. بنابراین، ابتدا خط مماس بر نمودار را در نقطه رسم میکنیم. همانطور که در تصویر زیر دیده میشود، زاویه خط مماس با جهت مثبت محور زمان برابر است.
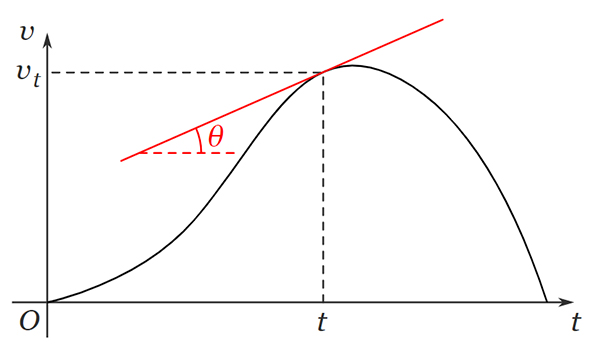
برای آنکه بدانیم شتاب لحظه ای در زمان ، مثبت، منفی یا صفر است، باید به علامت زاویه توجه کنیم.
- اگر زاویه مثبت باشد، شیب خط مماس نیز مثبت خواهد بود. بنابراین، شتاب لحظه ای در زمان مثبت است.
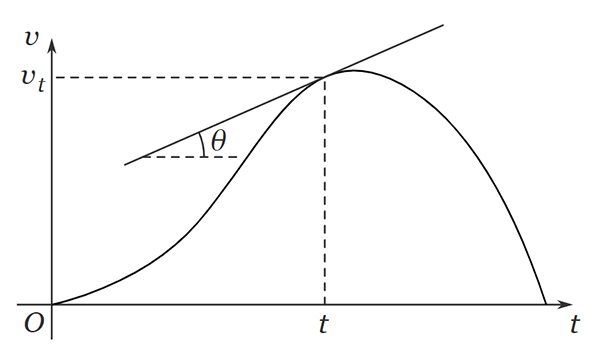
- اگر زاویه منفی باشد، شیب خط مماس نیز منفی خواهد بود. بنابراین، شتاب لحظه ای در زمان منفی است.
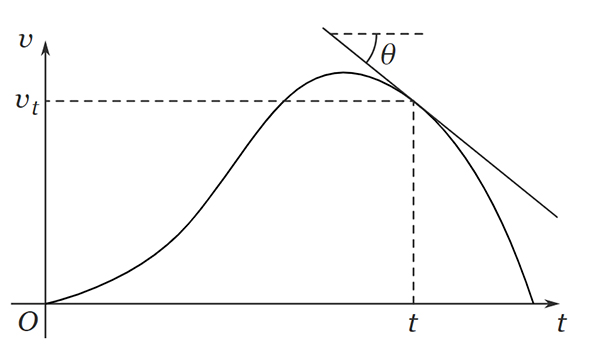
- اگر زاویه برابر صفر باشد، شیب خط مماس نیز صفر خواهد بود. بنابراین، شتاب لحظه ای در زمان برابر صفر است.
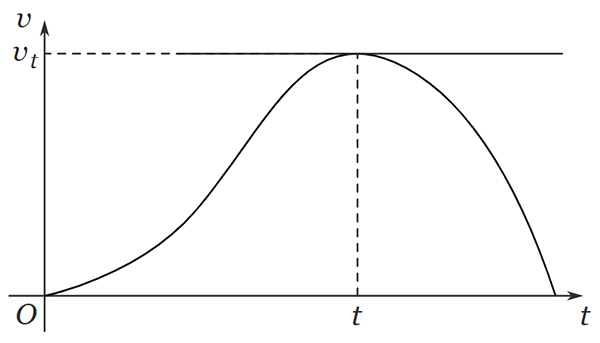
در نتیجه، علامت شتاب در زمان برابر علامت زاویه خط مماس بر نمودار سرعت-زمان در نقطه ، نسبت به جهت مثبت محور زمان است.
حل مثال های کاربردی محاسبه شتاب با استفاده از نمودار سرعت-زمان
در ادامه برای درک بهتر چگونگی محاسبه شتاب لحظه ای با استفاده از نمودار سرعت-زمان، چند مثال کاربردی را حل میکنیم.
مثال اول
نمودار سرعت-زمان حرکت جسمی در تصویر زیر نشان داده شده است. شتاب لحظه ای جسم را در زمان یک ثانیه بهدست آورید.
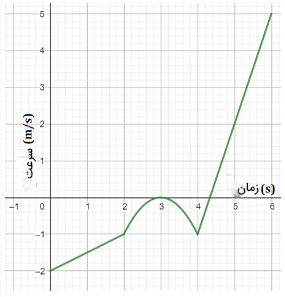
پاسخ
برای بهدست آوردن شتاب لحظه ای از روی نمودار سرعت-زمان در زمان ، ابتدا خطی مماس بر نمودار، در نقطه رسم میکنیم. نمودار سرعت-زمان در زمان یک ثانیه، خط راستی با شیب معین است. بنابراین، خط مماس بر نمودار در این زمان، به صورت نشان داده شده در تصویر زیر خواهد بود.
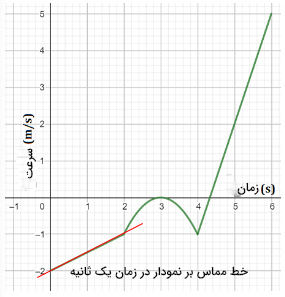
در ادامه، شیب خط مماس را بهدست میآوریم. برای انجام این کار، دو نقطه روی خط مماس انتخاب میکنیم و در رابطه زیر قرار میدهیم:
از آنجا که هیچ محدودیتی برای انتخاب دو نقطه نداریم، به دلخواه دو نقطه و را انتخاب میکنیم و در رابطه بالا قرار میدهیم:
شتاب لحظه ای در زمان یک ثانیه برابر شیب خط مماس بر نمودار در این زمان است. بنابراین، شتاب لحظه ای در برابر ۰/۵ متر بر مجذور ثانیه خواهد بود.
نکته: از آنجا که زاویه خط مماس بر نمودار سرعت زمان در زمان یک ثانیه، مثبت است، علامت شتاب لحظه ای نیز در این زمان، مثبت خواهد بود.
مثال دوم
نمودار سرعت-زمان حرکت ذرهای در تصویر زیر نشان داده شده است. شتاب لحظه ای جسم را در زمان سه ثانیه بهدست آورید.
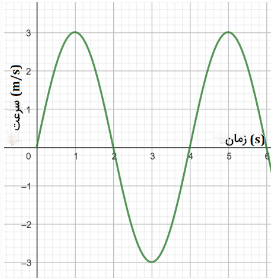
پاسخ
برای بهدست آوردن شتاب لحظه ای از روی نمودار سرعت-زمان در زمان ، ابتدا خطی مماس بر نمودار در این نقطه رسم میکنیم. نمودار سرعت-زمان در زمان سه ثانیه، کمینه است. بنابراین، خط مماس بر نمودار در این زمان، به صورت خطی افقی و موازی محور زمان، خواهد بود.
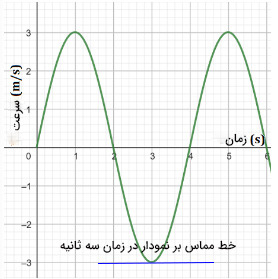
در ادامه، شیب خط مماس را بهدست میآوریم. برای انجام این کار، دو نقطه دلخواه روی خط مماس انتخاب میکنیم و در رابطه زیر قرار میدهیم:
از آنجا که هیچ محدودیتی در انتخاب دو نقطه نداریم، به دلخواه دو نقطه و را انتخاب میکنیم و در رابطه بالا قرار میدهیم:
بنابراین، شتاب لحظه ای در زمان سه ثانیه برابر صفر است. به این نکته توجه داشته باشید که مقدار سرعت در زمان سه ثانیه، کمینه است، بنابراین بدون انجام محاسبات بالا میتوانستیم نتیجه بگیریم که مقدار شتاب لحظه ای در این زمان برابر صفر خواهد بود.
مثال سوم
نمودار سرعت-زمانِ ذرهای در تصویر زیر نشان داده شده است. شتاب لحظه ای را در زمانهای زیر بهدست آورید:
- در زمان
- در زمان
- در زمان
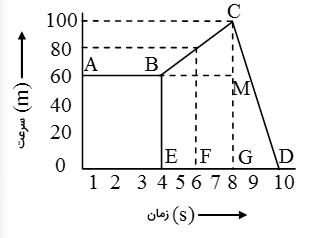
پاسخ
قبل از پاسخ به این مثال، به نکتههای زیر توجه داشته باشید:
- شتاب لحظه ای در هر لحظه از زمان برابر شیب خط مماس بر نمودار سرعت-زمان در آن زمان است.
- اگر زاویه خط مماس بر نمودار سرعت-زمان با جهت مثبت محور سرعت-زمان، مثبت باشد، شتاب لحظه ای نیز مثبت خواهد بود.
- اگر زاویه خط مماس بر نمودار سرعت-زمان با جهت مثبت محور سرعت-زمان، منفی باشد، شتاب لحظه ای نیز منفی خواهد بود.
- شتاب لحظه ای در نقطههای کمینه و بیشینه سرعت، برابر صفر است.
- اگر نمودار سرعت-زمان خط مستقیمی با شیب ثابت باشد، شتاب لحظه ای همان شیب خط و برابر شتاب متوسط است.
- اگر نمودار سرعت-زمان خط مستقیمی با شیب صفر باشد، شتاب لحظه ای و متوسط برابر صفر خواهند بود.
قسمت ۱: شتاب لحظه ای در زمان سه ثانیه به صورت زیر داده میشود:
صفر = شیب خط = شتاب لحظه ای
قسمت ۲: شتاب لحظه ای در زمان ۶ ثانیه برابر شیب خط است:
قسمت 3: شتاب لحظه ای در زمان ۶ ثانیه برابر شیب خط است:
مثال چهارم
نمودار سرعت-زمان ذرهای به صورت نشان داده شده در تصویر زیر است. مقدار شتاب لحظه ای ذره را در زمان بهدست آورید.
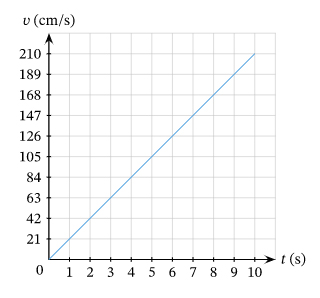
پاسخ
قبل از حل این مثال به دو نکته توجه داشته باشید:
- اگر نمودار سرعت-زمان خط راست باشد، شتابهای متوسط و لحظهای با یکدیگر برابر هستند و جسم با شتاب ثابت حرکت میکند. به عنوان مثال، اگر نمودار سرعت-زمان جسمی در پنج ثانیه اول حرکت خطی با شیب دو و در پنج ثانیه دوم حرکت، خطی با شیب صفر باشد، جسم در پنج ثانیه اول حرکت، با شتاب ثابت دو و در پنج ثانیه دوم حرکت، با شتاب صفر حرکت میکند.
- گرچه در بیشتر مسئلههای فیزیک، نمودار سرعت-زمان خطی است، اما گاهی اوقات نمودار سرعت برحسب زمانی منحنی با شیب متغیر خواهد بود. در این حالت، شتابهای متوسط و لحظهای با یکدیگر برابر نیستند و شتاب حرکت جسم با زمان تغییر خواهد کرد.
نمودار سرعت-زمان در مثال چهارم، خطی با شیب ثابت و مشخص است. بنابراین، شتاب لحظه ای در هر لحظه از زمان برابر شیب خط است. برای بهدست آوردن شیب خط، دو نقطه روی آن انتخاب میکنیم و در رابطه زیر قرار میدهیم:
نقطه ۱:
نقطه ۲:
شیب خط گذرنده از این دو نقطه برابر است با:
بنابراین، شتاب لحظه ای در زمان سه ثانیه برابر ۲۱ سانتیمتر بر مجذور ثانیه است.
پرسش ۱: شتاب لحظهای در زمان نه ثانیه چه مقدار است؟
پاسخ: از آنجا که نمودار سرعت-زمان در ده ثانیه اول حرکت، خطی با شیب ثابت ۲۱ است، شتاب لحظه ای در ده ثانیه اول حرکت ثابت و برابر ۲۱ سانتیمتر بر مجذور ثانیه خواهد بود.
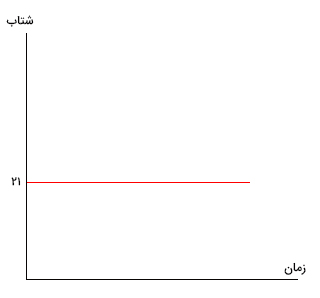
پرسش ۲: نمودار شتاب برحسب زمان را برای مثال چهارم رسم کنید.
پاسخ: گفتیم، جسم در ده ثانیه اول حرکت با شتاب ثابت ۲۱ سانتیمتر بر مجذور ثانیه حرکت میکند. بنابراین، نمودار شتاب برحسب زمان، خطی افقی است که محور عمودی (شتاب) را در نقطه ۲۱ قطع میکند.
مثال پنجم
ذرهای روی خط مستقیم با سرعت متغیر حرکت میکند. اگر نمودار سرعت-زمان این ذره به صورت زیر باشد، شتاب لحظه ای آن را در زمانهای دو، ده و سی ثانیه بهدست آورید.
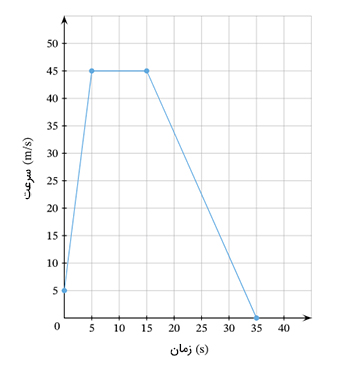
پاسخ
نمودار سرعت-زمان در این مثال به سه بخش تقسیم میشود:
- بخش اول: در این قسمت، نمودار سرعت بر حسب زمان، خطی با شیب ثابت و مثبت است. ذره با سرعت اولیه پنج متر بر ثانیه شروع به حرکت با شتاب ثابت میکند و ۵ ثانیه پس از شروع حرکت، سرعت آن به مقدار ۴۵ متر بر ثانیه میرسد. همانند مثالهای قبل میتوانیم شیب خط و در نتیجه، شتاب لحظه ای را بهدست آوریم. اما، از آنجا که شتابهای لحظهای و متوسط در حرکت با شتاب ثابت با یکدیگر برابر هستند، برای محاسبه شتاب لحظه ای، از رابطه شتاب متوسط به صورت زیر استفاده میکنیم:
مقدارهای سرعت اولیه در زمان صفر و سرعت نهایی در زمان پنج ثانیه را با استفاده از نمودار سرعت-زمان بهدست میآوریم و آنها را در رابطه بالا قرار میدهیم:
- بخش دوم: هنگامی که سرعت ذره به ۴۵ متر بر ثانیه رسید، به مدت ده ثانیه با همین سرعت، به حرکت خود ادامه میدهد. بنابراین، نمودار سرعت-زمان در بخش دوم حرکت، خطی افقی با شیب صفر است. در نتیجه، مقدار شتاب لحظه ای ذره برابر صفر خواهد بود.
- بخش سوم: در بخش سوم حرکت، نمودار سرعت زمان خطی با شیب ثابت و منفی است، بنابراین، سرعت ذره از مقدار ۴۵ متر بر ثانیه با شتاب منفی و ثابت کاهش مییابد و ذره پس از ۲۰ ثانیه به طور کامل متوقف میشود. همانند بخش اول، برای بهدست آوردن شتاب لحظه ای از فرمول استفاده میکنیم:
نمودار سرعت-زمان حرکت جسمی روی خط راست، در تصویر زیر نشان داده شده است. چه زمانی شتاب حرکت ذره برابر صفر است؟
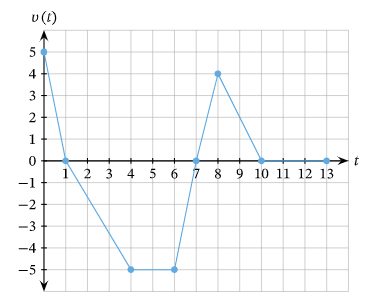
از زمان ۴ تا ۶ ثانیه و از زمان ۱۰ تا ۱۳ ثانیه
از زمان ۴ تا ۶ ثانیه
از زمان یک تا ۷ ثانیه
از زمان ۱۰ تا ۱۳ ثانیه
نمودار سرعت-زمان جسم از شش بخش تشکیل شده است:
- بخش اول: در این بخش نمودار سرعت-زمان، خطی با شیب ثابت و منفی است. جسم با سرعت ۵ متر بر ثانیه و با شتاب منفی شروع به حرکت میکند و سرعت آن پس از یک ثانیه به صفر میرسد.
- بخش دوم: در این بخش، نیز همانند بخش اول، نمودار سرعت-زمان، خطی با شیب ثابت و منفی است و سرعت جسم با شتاب منفی و ثابت در مدت ۳ ثانیه از صفر به ۵- متر بر ثانیه میرسد.
- بخش سوم: جسم در زمان ۴ تا ۶ ثانیه با سرعت ثابت ۵- متر بر ثانیه به حرکت خود ادامه میدهد. در این قسمت، نمودار سرعت-زمان خطی افقی با شیب صفر است، بنابراین شتاب حرکت جسم برابر صفر خواهد بود.
- بخش چهارم: در این قسمت، نمودار سرعت-زمان، خطی ثابت با شیب مثبت است. بنابراین، در این قسمت سرعت جسم با شتاب مثبت از ۵- متر بر ثانیه به ۴ متر بر ثانیه میرسد.
- بخش پنجم: پس از آنکه سرعت جسم به ۴ متر بر ثانیه رسید، یا شتاب منفی به حرکت خود ادامه میدهد و پس از ۲ ثانیه، به طور کامل متوقف میشود.
- بخش ششم: نمودار سرعت-زمان خطی افقی با شیب ثابت و صفر است. بنابراین، شتاب حرکت ذره نیز صفر خواهد بود.
با توجه به توضیحات بالا، شتاب لحظهای ذره در بازه زمانی ۲ تا ۴ ثانیه و ۱۰ تا ۱۳ ثانیه برابر صفر است.
نمودار سرعت زمان جسمی به صورت زیر داده شده است. شتاب لحظهای آن را در زمان ۳/۵ ثانیه بهدست آورید.
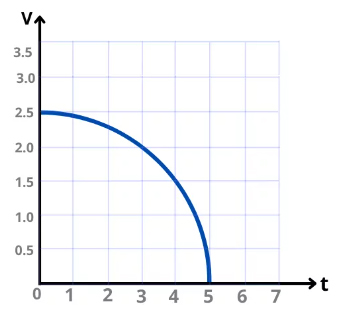
برای حل این پرسش، گامهای زیر را طی میکنیم:
گام اول
زمان ۳/۵ ثانیه را روی نمودار زمان مشخص میکنیم و خطی موازی محور سرعت از آن عبور میدهیم. محل تقاطع خط با نمودار سرعت-زمان را علامت میزنیم:
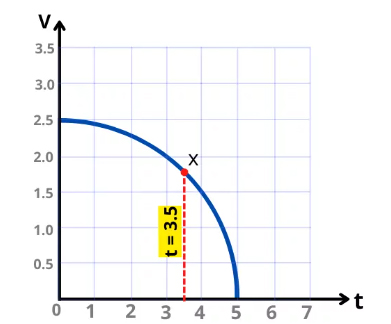
گام دوم
خطی مماس بر نقطه مشخص شده روی نمودار رسم میکنیم:
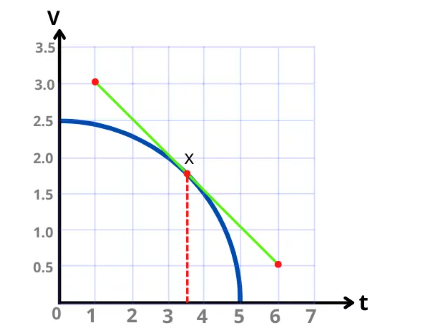
گام سوم
شیب خط مماس را بهدست میآوریم. شتاب لحظهای در زمان ۳/۵ ثانیه به صورت زیر بهدست میآید:
از نمودار بالا داریم:
مقداهای بالا را در رابطه شتاب لحظهای قرار میدهیم:
شتاب لحظه ای در حرکت دو و سه بعدی
تاکنون در مورد شتاب لحظهای در حرکت یکبعدی صحبت کردیم. شتاب کمیتی برداری و واحد آن متر بر مجذور ثانیه است.
- بردار شتاب در دستگاه مختصات سهبعدی به صورت زیر نوشته میشود:
- بردار شتاب در دستگاه مختصات دوبعدی به صورت زیر نوشته میشود:
اندازه شتاب در دو و سه بعد به صورت زیر نوشته میشود:
مثال شتاب لحظه ای در دو بعد
شهابسنگی در فضا با سرعت حرکت میکند. اگر سرعت شهابسنگ بر حسب زمان به صورت باشد، مطلوب است:
- شتاب متوسط شهابسنگ بین زمانهای ۲ تا ۴ ثانیه
- شتاب لحظهای شهابسنگ در زمان ۶ ثانیه

پاسخ
قسمت ۱: دادههای مساله عبارت هستند از:
برای بهدست آوردن شتاب متوسط از رابطه زیر استفاده میکنیم:
زمانهای و را میدانیم. برای محاسبه شتاب متوسط تنها کافی است مقدارهای سرعت را در این دو زمان بهدست آوریم و در رابطه شتاب متوسط قرار دهیم. سرعت در زمان برابر است با:
سرعت در زمان برابر است با:
با جایگزینی و در رابطه مربوط به شتاب متوسط داریم:
قسمت ۲: در این قسمت، شتاب لحظه ای شهابسنگ را در زمان ۶ ثانیه بهدست میآوریم.
از سرعت برحسب زمان مشتق میگیریم:
با قرار دادن زمان ۶ ثانیه در رابطه بالا، شتاب لحظه ای را بهدست میآوریم:
جمعبندی
در این مطلب، ابتدا شتاب لحظه ای را تعریف کردیم و تفاوت آن با شتاب متوسط را توضیح دادیم. در ادامه، با حل چند مثال کاربردی شتاب لحظه ای را با استفاده از نمودار سرعت برحسب زمان بهدست آوردیم. در پایان، در مورد شتاب لحظه ای در دو و سه بعد صحبت کردیم.












