توزیع های آماری در علم داده — راهنمای کاربردی
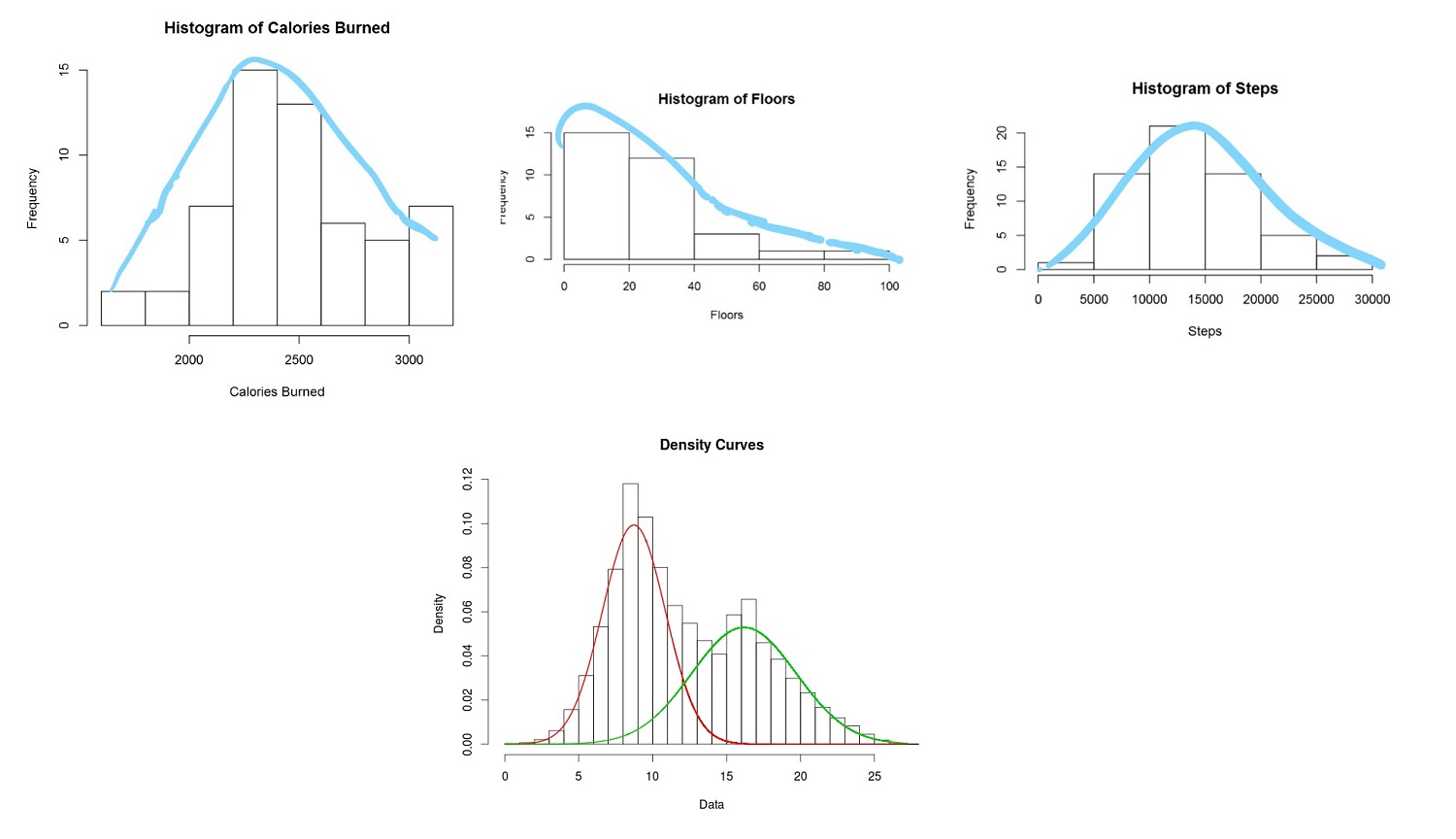
این نوشتار قسمت دوم از مطالب دنبالهدار در مورد نقش آمار در حوزه علم داده است که به موضوع و مبحث توزیع های آماری و تابع توزیع احتمال میپردازد. البته برای نمایش تابع توزیع احتمال از نمودارهایی نیز کمک خواهیم گرفت.
برای آشنایی با انواع توزیعهای احتمالی مطلب توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس را بخوانید. همچنین به منظور آشنایی با نحوه ترسیم نمودار تابع توزیع احتمال به نوشتار توزیع های آماری و رسم نمودار تابع احتمال — با کدهای R مراجعه کنید. قسمتهای مختلف این دنباله مقالات مطابق با فهرست زیر هستند.
- قسمت اول: شاخصهای آمار توصیفی در علم داده --- راهنمای کاربردی
- قسمت دوم: توزیع های آماری مهم در علم داده --- راهنمای کاربردی
- قسمت سوم، معیارهای مکانی و گشتاورها در علم داده --- راهنمای کاربردی
- قسمت چهارم: وابستگی- کوواریانس و ضریب همبستگی --- راهنمای کاربردی
- قسمت پنجم: احتمال شرطی، قضیه بیز (Bayes's Theorem) --- راهنمای کاربردی
توزیع های آماری و علم داده
تابع توزیع احتمال (Probability Distribution Function)، بیان میکند که میزان رخداد پیشامدها چه میزان است. در ادامه به معرفی تابع توزیع احتمال برای متغیرهای پیوسته و گسسته خواهیم پرداخت.
تابع چگالی احتمال (Probability Density Function)
اگر به نمودارهای چگالی احتمال نگاه کنیم، به نظر میرسد که مقدار احتمال در هر نقطه را نشان میدهند. البته اگر متغیر تصادفی از نوع گسسته باشد این موضوع کاملا صحیح است. ولی برای متغیرهایی که از نوع پیوسته هستند تابع چگالی یا جرم احتمال، فقط میزان تمرکز احتمال را در یک نقطه نشان میدهد زیرا در حالت پیوسته نمیتوان برای یک نقطه میزان احتمال را محاسبه کرد. در حقیقت مقدار احتمال به علت پیوسته بودن تابع احتمال در هر نقطه برابر با صفر است.
سطح زیر منحنی تابع چگالی همیشه برابر با 1 است. همچنین اگر بخواهید مقدار احتمال را تا نقطه x محاسبه کنید باید سطح زیر منحنی تابع چگالی را تا نقطه x بدست آورید. این مقدار همان انتگرال تابع چگالی تا نقطه x خواهد بود.
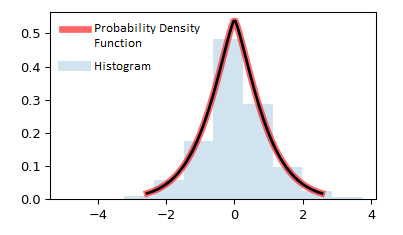
یکی از مهمترین توزیعهای آماری، توزیع زنگی شکل (Bell-shaped) یا توزیع نرمال است. این توزیع براساس میانگین و واریانس معرفی میشود. در تصویر زیر مقدار احتمال را در هر ناحیه از این منحنی مشاهده میکنید.
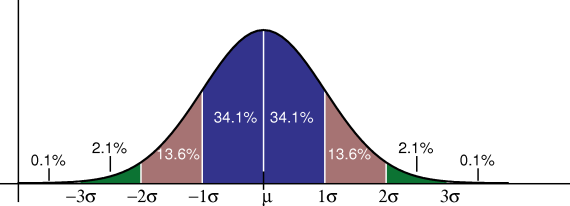
همانطور که در نمودار مشخص است، بین میانگین و یک انحراف استاندارد ($$\sigma$$) فاصله از میانگین حدود 68.2٪ دادهها قرار دارند. به این معنی که اگر عددی تصادفی از توزیع نرمال انتخاب کنید، با احتمال 68 درصد بین یک انحراف استاندارد از میانگین بیشتر یا کمتر قرار دارد.
این امر نشان میدهد که تمرکز دادهها (حدود ۶۸ درصد) حول میانگین با یک انحراف استاندارد فاصله قرار گرفته است. البته اگر فاصله از میانگین را بیشتر در نظر بگیرید، احتمال نیز بیشتر میشود. ولی از طرفی تمرکز نیز از میانگین کمتر میشود. برای مثال حدود 99.8 درصد دادهها با فاصله سه انحراف استاندارد از میانگین قرار گرفتهاند. پس این دادهها نسبت به میانگین دورتر هستند.
تابع جرم احتمال (Probability Mass Function)
زمانی که متغیر تصادفی یا دادهها از نوع گسسته باشند، «تابع جرم احتمال» یا PMF، به کار میرود. این تابع میزان احتمال را در هر نقطه یا هر مقدار مشخص میکند. برای مثال نمودار زیر با توجه به مقدارهای گسسته، میزان احتمال رخداد هر یک از مقادیر را نشان میدهد.
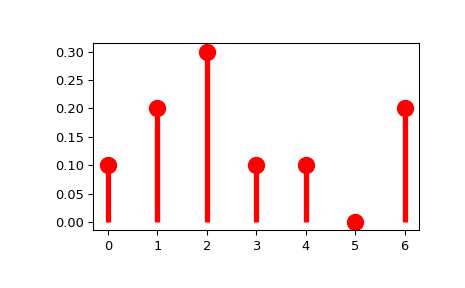
همانطور که میبینید این نمودار شبیه یک بافتنگار فراوانی (هیستوگرام) است. برای مثال میزان احتمال رخداد برای مقدار ۲ در این نمودار برابر با 30٪ است، در حالیکه احتمال برای مقدار ۵ تقریبا برابر با صفر محاسبه میشود.
توزیع احتمال دادههای پیوسته (Continuous Data Distributions)
با توجه به تفاوتی که بین تابع چگالی احتمال (PDF) و تابع جرم احتمال (PMF) وجود دارد، برای دادههای پیوسته باید از تابع چگالی احتمال استفاده شود. در ادامه به معرفی بعضی از این توزیعهای احتمال خواهیم پرداخت.
توزیع یکنواخت یا مستطیلی (Uniform / Rectangular Distribution)
دادههایی که دارای چگالی احتمال یکسانی برای همه مقادیر باشند، دارای توزیع یکنواخت یا مستطیلی هستند. باید توجه داشت که مجموعه مقادیری که دادهها در آن تغییر میکنند در این حالت محدود است. در شکل زیر توزیع یکنواخت برای دادههای در محدود ۰ تا ۱ ترسیم شده است این مقدارها در محور افقی ظاهر شدهاند. فراوانی نسبی یا همان تابع چگالی احتمال نیز توسط یک نمودار بافتنگار فراوانی (هیستوگرام) ترسیم شده. البته خط قرمز ترسیم شده مقدار تابع احتمال را براساس تابع چگالی احتمال یکنواخت نشان داده است. اگر محدوده مقادیر در فاصله ۰ تا ۱ باشد، تابع چگالی احتمال را یکنواخت استاندارد مینامند.
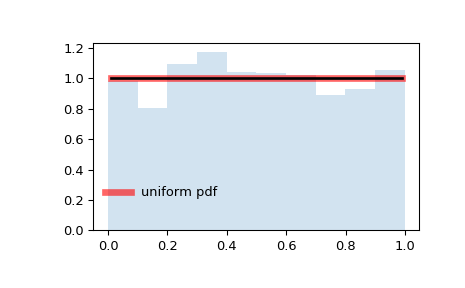
مشخص است که ممکن است مقدار تابع چگالی احتمال تجربی (محاسبه شده از روی مشاهدات) گاهی بیشتر یا کمتر از ۱ باشد، ولی محاسبه مقدار تابع چگالی طبق فرمول تابع چگالی احتمال یکنواخت استاندارد، همیشه مقداری برابر با ۱ خواهد داشت.
توزیع نرمال یا گوسی (Normal / Gaussian Distribution)
در ابتدای متن، توزیع نرمال معرفی شد. معمولا پدیدههای طبیعی میتوانند دادههایی با توزیع نرمال تولید کنند. ولی یکی از خصوصیات جالب برای نمونههای بزرگ و ارتباط توزیع میانگینشان با توزیع نرمال، قضیه حد مرکزی است که امکان استفاده از توزیع نرمال را برای بیشتر دادههای تصادفی میدهد.
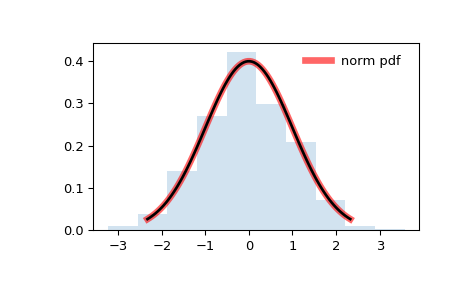
در نمودار بالا میانگین توزیع نرمال برابر با صفر ($$\mu=0$$) و انحراف استاندارد نیز ۱ ($$\sigma=1$$) در نظر گرفته شده است.
توزیع نمایی (Exponential Probability Distribution)
یکی دیگر از توزیعهای کاربردی در علم داده، توزیع نمایی است. شیب کاهشی این توزیع به صورت نمایی است. به این معنی که با افزایش مقدارها، تابع چگالی احتمال آنها به صورت نمایی منفی، کاهش مییابد. این طور به نظر میرسد که احتمال رخداد پیشامدهای نزدیک صفر بیشتر از احتمال رخداد پیشامدهایی است که از صفر دورتر هستند.
برای مثال میتوان به مثال پول خرج شده توسط مشتریان در یک فروشگاه اشاره کرد. مشتریانی که خرید روزانه کمی دارند (حدود ۰ البته نسبت به بقیه مشتریان) بیشتر از کسانی هستند که هزینه زیاد میکنند. زیرا مشتریهایی محلی (که البته تعدادشان هم زیاد است) خریدهای روزانه را انجام میدهند که به این ترتیب مبلغ پرداختی زیادی ندارد. ولی از طرفی بعضی از مشتریان (که البته تعدادشان کم است) هزینه زیادی میکنند و ممکن است خرید یک ماهه را در یک روز انجام دهند. به همین دلیل فراوانی کسانی که خرید کم انجام میدهند زیاد و کسانی که خرید پر هزینه دارند، کم است. تغییرات این فراوانی به صورت نمایی منفی است.
از طرف دیگر، چون مقادیر این توزیع، مثبت هستند، میتوان از آن برای توصیف دادههای مربوط به طول عمر استفاده کرد. برای مثال توان باطری در طول زمان از نمونه پدیدههای است که توسط توزیع نمایی قابل توصیف است. همچنین از این توزیع برای زمان انتظار رسیدن به یک رخداد استفاده میشود.
توزیعهای گسسته (Discrete Data Distributions)
معمولا در علم داده از توزیعهای گسسته به طور گستردهای استفاده میشود. توزیع دو جملهای و توزیع پواسن از این گروه هستند. در ادامه به بررسی این دو توزیع که البته در علم داده، پرکاربرد نیز هستند، میپردازیم.
توزیع دو جملهای (Binomial Distribution)
اگر یک آزمایش برنولی با شانس موفقیت ثابت را $$N$$ بار تکرار کنیم، تعداد موفقیتها دارای توزیع دو جملهای است. مشخص است که نتایج یک آزمایش برنولی به صورت دو وضعیتی (۱ موفقیت و ۰ شکست) است و در این حالت در توزیع دو جملهای، مجموع مقدارهای ۱ محاسبه میشود.
نکته: یکی از شرطهای مهم در توزیع دو جملهای مستقل بودن آزمایشهای برنولی و ثابت بودن احتمال موفقیت است.
در تصویر زیر با توجه به ۴ بار تکرار آزمایش برنولی، تابع جرم احتمال توزیع دو جملهای ترسیم شده است.
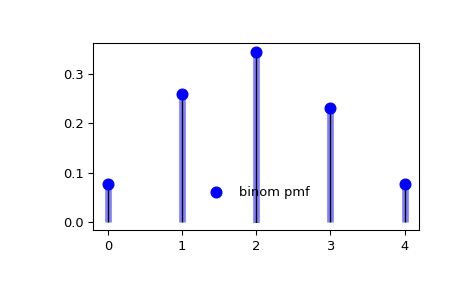
توزیع پواسن (Poisson Distribution)
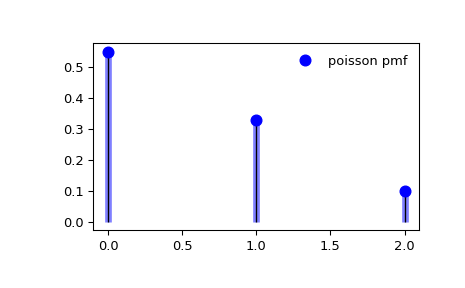
احتمال رخداد تعدادی از پیشامدها در یک بازه زمانی یا مکانی توسط توزیع پواسن محاسبه میشود. معمولا چنین پیشامدهایی دارای یک نرخ یا متوسط رخداد در بازه زمانی هستند. از طرفی احتمال رخداد آنها، مستقل از زمانی است که رخداد قبلی اتفاق افتاده است.
یکی از مثالهای معروف برای دادههایی با این توزیع، مربوط به تعداد تماسهایی است که با یک مرکز تلفن برقرار میشود. به این ترتیب اگر بدانیم در هر ساعت بطور متوسط k تماس برقرار میشود، میتوانیم احتمال آنکه در یک ساعت هیچ تماسی صورت نگیرد را محاسبه کنیم.
در مطلب فرآیند پواسن و توزیع آن — مفاهیم و کاربردها و توزیع پواسون و حل مسائل مرتبط با کدهای R — از صفر تا صد به طور مفصل به بررسی پدیدههای تصادفی از این دست پرداختهایم.
اگر مطلب بالا برای شما مفید بوده است، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- مجموعه آموزش های SPSS
- مجموعه آموزش های Minitab
- مفاهیم آماری – شاخصهای توصیفی
- توزیع فراوانی – به زبان ساده
- مفاهیم آماری – آمار و جامعه آماری – به زبان ساده
- توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس
^^










