متغیر تصادفی و توزیع برنولی — به زبان ساده

یکی از مفاهیم اولیه در تئوری احتمال، مفهوم آزمایش تصادفی است. آزمایشی که قابل تکرار است و در شرایط یکسان نتایج متفاوت ولی قابل پیشبینی دارد، را «آزمایش تصادفی» (Random Experiment) میگویند. به این ترتیب قبل از انجام آزمایش تصادفی، میتوانیم حدس بزنیم چه نتیجهای ظاهر خواهد شد ولی فقط پس از انجام آزمایش تصادفی است که از نتیجه با خبر میشویم. گفتنی است با توجه به شیوه این نوع آزمایش و مقدارهای «نتیجه» (Outcome)، متغیرهای و آزمایشهای تصادفی را طبقهبندی میکنند. این نوع آزمایش با متغیر تصادفی و توزیع برنولی در ارتباط است.
برای آشنایی با متغیر تصادفی و شیوه محاسبه امید-ریاضی و واریانس آن میتوانید به مطلب متغیر های تصادفی – میانگین، واریانس و انحراف معیار – به زبان ساده مراجعه کنید. همچنین خواندن نوشتارهای متغیر تصادفی و توزیع دو جملهای — به زبان ساده و متغیر تصادفی، تابع احتمال و تابع توزیع احتمال نیز خالی از لطف نیست.
آزمایش برنولی
آزمایش تصادفی که فقط دو مقدار داشته باشد و نتایج آن از قبل قابل پیشبینی باشد، یک «آزمایش برنولی» (Bernoulli Trials) است. معمولا نتایج آزمایش برنولی را با «موفقیت» (Success) یا «شکست» (Failure) مشخص میکنند.
برای مثال پرتاب یک سکه به منظور مشاهده شیر، یک آزمایش برنولی است. زیرا اگر موفقیت را مشاهده شیر و شکست را مشاهده خط در نظر بگیریم، نتایج این آزمایش تصادفی، فقط دو مقدار موفقیت یا شکست را خواهد داشت.
یکی از شرایط مهم آزمایش برنولی، ثابت بودن احتمال موفقیت یا شکست است. به این معنی که با تکرار این آزمایش در شرایط یکسان، احتمال موفقیت تغییر نمیکند. باید توجه داشت که این تکرارها باید مستقل از یکدیگر باشند.
نام برنولی برای این نوع آزمایش براساس نام ریاضیدان سوئیسی «جاکوب برنولی» (Jacob Bernoulli) که در این زمینه تحقیقات زیادی داشته، انتخاب شده است.
تابع احتمال متغیر تصادفی برنولی
اگر $$X$$ یک متغیر تصادفی باشد که مقدار ۱ را با احتمال $$p$$ و مقدار ۰ را با احتمال $$1-p$$ بگیرد، آنگاه $$X$$ را یک متغیر تصادفی با «توزیع برنولی» (Bernoulli Distribution) مینامند. $$p$$ پارامتر توزیع برنولی نامیده میشود که مقداری بین صفر و یک است.
به منظور نمایش توزیع برنولی برای متغیر تصادفی X از شکل $$X\sim B(1,p)$$ استفاده میکنیم و میخوانیم «متغیر تصادفی X دارای توزیع برنولی با پارامتر p است.»
نکته: اگر مقدار p برابر با یک یا صفر باشد، متغیر تصادفی، «تباهیده» (Degenerate) یا با مقدار ثابت خواهد بود و نتیجه آزمایش برنولی یا همیشه موفقیت یا همیشه شکست است.
«تابع احتمال» (Probability Function) برای چنین متغیر تصادفی به صورت زیر خواهد بود:
$$\large P(X=x) = \begin{cases} p \;\;\;\;\;\;\; ,x=1 \\ 1-p \;\; ,x=0 \\ \end{cases} $$
به طوری که $$p+(1-p)=1$$ است یعنی مجموع احتمال موفقیت و شکست برابر با ۱ است. رابطه زیر، شکل دیگری برای تابع احتمال این متغیر تصادفی محسوب میشود که اغلب برای انجام محاسبات از آن استفاده میکنیم.
$$\large P(X=x) = p^x(1-p)^{1-x} \;\;\;\; ,x=0,1$$
همچنین اگر احتمال شکست را به جای $$1-p$$ با $$q$$ نشان دهیم، فرم تابع احتمال به شکل زیر درخواهد آمد:
$$\large P(X=x) = p^xq^{1-x} \;\;\;\; ,x=0,1$$
گاهی تابع احتمال را «تابع جرم احتمال» (Probability Mass Function) نیز میگویند.
در تصویر زیر، نمودار توزیع احتمال متغیر تصادفی برنولی با پارامتر p=0.7 ترسیم شده است.
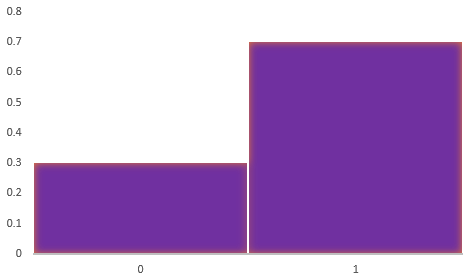
در این نمودار مقدارهای متغیر تصادفی در محور افقی و احتمال برای هر یک از آنها در محور عمودی قرار گرفته است.
خصوصیات متغیر تصادفی برنولی
از مهمترین خصوصیات متغیرهای تصادفی، امید-ریاضی و واریانس آنها است. در ادامه شیوه محاسبه این دو مشخصه متغیر تصادفی برنولی شرح داده میشود.
امید-ریاضی برای متغیر تصادفی برنولی به راحتی توسط تعریف و مفهوم آن قابل محاسبه است. کافی است مقدارهای متغیر تصادفی را در احتمال وقوع آنها ضرب کرده و جمع نتایج را محاسبه کنیم.
$$\large E(X)=p\times 1+ (1-p)\times 0 =p\times 1+ q\times 0 =p $$
همچنین برای بدست آوردن واریانس متغیر تصادفی برنولی خواهیم داشت:
$$\large Var(X)=E(X^2)-E^2(X)=(p\times 1^2+ (1-p)\times 0^2)-p^2=p(1-p)=pq$$
در نتیجه میتوان گفت که واریانس متغیر تصادفی برنولی با پارامتر 0.3 برابر با واریانس متغیر تصادفی برنولی با پارامتر 0.7 است و برابر است با 0.21.
مثال
در پرتاب یک تاس، اگر مشاهده شش، موفقیت باشد، تابع احتمال، امید-ریاضی و واریانس به صورت زیر محاسبه میشوند.
از آنجایی که مشاهده ۶ (موفقیت) با احتمال $$\tfrac{1}{6}$$ رخ میدهد، برای تابع احتمال داریم:
$$\large P(X=x)=(\tfrac{1}{6})^x(\tfrac{5}{6})^{1-x}\;\;\;x=0,1$$
امید-ریاضی نیز طبق رابطه گفته شده برابر با $$p=\tfrac{1}{6}$$ خواهد بود و واریانس نیز با $$\tfrac{1}{6}\times \tfrac{5}{6}=\tfrac{5}{36}$$ برابر است.
کابردهای متغیر تصادفی برنولی
اغلب از متغیر و توزیع برنولی در علوم پزشکی استفاده میکنند تا وضعیت سالم یا ناسالم بودن فرد را نشان دهند. در رگرسیون لجستیک (Logistic Regression) از توزیع برنولی برای مدلسازی وقوع بیماری استفاده میشود. همچنین براساس مجموع چند متغیر تصادفی برنولی مستقل و با پارامتر یکسان، میتوان یک متغیر تصادفی دو جملهای (Binomial Random Variable) ایجاد کرد.
اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزشهایی که در ادامه آمدهاند نیز برایتان کاربردی خواهند بود.
- مجموعه آموزش های آمار و احتمالات
- آموزش آمار و احتمال مهندسی
- متغیر های تصادفی – میانگین، واریانس و انحراف معیار – به زبان ساده
- متغیر تصادفی و توزیع هندسی — به زبان ساده
^^











از سایت و مطالب خیلی مفید تون متشکرم???
لطفا به دل نگیرید ولی اگر صدا دوستمون که ویدئو رو زحمت کشیدن ضبط کردن رو تغییر بدید فکر کنم خیلی بهتر شه ???