احتمال شرطی و قضیه بیز در علم داده – راهنمای کاربردی

این نوشتار قسمت پنجم و آخرین قسمت از مطالب دنباله‌‌دار در مورد نقش آمار در حوزه علم داده است که به موضوع و مبحث احتمال شرطی و قضیه بیز در علم داده می‌پردازد. البته در دیگر نوشتارهای فرادرس با عنوان احتمال شرطی (Conditional Probability) — اصول و شیوه محاسبه با احتمال شرطی آشنا شده‌اید. همچنین نوشتار قضیه بیز در احتمال شرطی و کاربردهای آن نیز مرتبط با این موضوعات است. با توجه به مفهوم احتمال و پیشامدها که در این مطلب، به آن‌ها خواهیم پرداخت، خواندن نوشتار آزمایش تصادفی، پیشامد و تابع احتمال نیز خالی از لطف نیست.

قسمت‌های مختلف این دنباله مقالات مطابق با فهرست زیر هستند.

• قسمت اول: شاخص‌های آمار توصیفی در علم داده — راهنمای کاربردی
• قسمت دوم: توزیع‌ های آماری مهم در علم داده — راهنمای کاربردی
• قسمت سوم: معیارهای مکانی و گشتاورها در علم داده — راهنمای کاربردی
• قسمت چهارم: وابستگی، کوواریانس و ضریب همبستگی — راهنمای کاربردی
• قسمت پنجم: احتمال شرطی، قضیه بیز (Bayes’s Theorem) — راهنمای کاربردی

احتمال شرطی و قضیه بیز در علم داده

قبل از شروع بحث در مورد احتمال شرطی و قضیه بیز در علم داده باید مقداری در مورد احتمال شرطی اطلاع حاصل کنیم. احتمال شرطی را می‌توان محاسبه احتمال رخداد یک پیشامد A به شرط رخداد پیشامد دیگر مثلا B در نظر گرفت. ممکن است رخداد پیشامد B روی احتمال رخداد A تاثیر گذار بوده و این اطلاعات شانس رخداد پیشامد A را افزایش یا کاهش دهد. از طرفی ممکن است اطلاع از رخداد پیشامد B هیچ تاثیری بر روی رخداد پیشامد A نداشته باشد.

محاسبه احتمال شرطی (Conditional Probability)

برای نمایش احتمال رخداد پیشامد A به شرط پیشامد B از نماد $$P(A|B)$$ استفاده می‌کنیم و آن را به صورت «احتمال A به شرط B» می‌خوانیم. به این ترتیب منظورمان این است که از پیشامد B مطمئن هستیم و حال می‌خواهیم احتمال رخداد پیشامد A را مشخص کنیم. شیوه محاسبه این احتمال به صورت زیر است:

$$\large P(A|B)=\dfrac{P(A \cap B)}{P(B)}$$

مشخص است که منظور از $$A\cap B$$ پیشامدی است که از اشتراک پیشامدهای A و B‌ تشکیل می‌شود. منظور از این پیشامد، رخداد هر دو پیشامد A و B است. برای نمایش این پیشامد از نمودار ون استفاده کرده و آن را به صورت زیر نشان می‌دهیم.

مثال

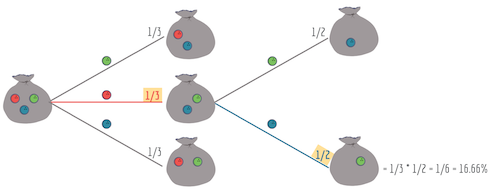
فرض کنید قرار است از یک جعبه سه مهره بیرون بیاوریم. درون جعبه، مهره‌هایی به رنگ قرمز، سبز و آبی است. احتمال آنکه در اولین انتخاب، مهره قرمز و در دومین انتخاب مهره آبی، خارج شود، چه خواهد بود؟ با طرح این پرسش، مشخص است که به دنبال احتمال $$P(A\cap B)$$‌ هستیم. اگر A پیشامد انتخاب مهره قرمز در اولین انتخاب و B نیز پیشامد مشاهده مهره آبی در انتخاب دوم باشد، احتمال $$P(A\cap B)$$ طی مراحل زیر محاسبه می‌شود.

ابتدا احتمال را برای پیشامد A محاسبه می‌کنیم.

$$\large P(A)=\dfrac{1}{3}=0.3333$$

از این جهت مقدار 0.3333 حاصل شده است که از بین سه مهره، احتمال مشاهده مهره قرمز برابر با است با $$\frac{1}{3}$$. از طرفی احتمال مشاهده مهره آبی در انتخاب دوم، با توجه به اینکه فقط دو مهره باقی مانده است با $$\frac{1}{2}$$ برابر است. یعنی داریم:

$$\large P(B|A)=\dfrac{1}{2}=0.5$$

حال برای محاسبه احتمال $$P(A\cap B)$$‌ از رابطه زیر کمک می‌گیریم.

$$\large P(A\cap B)=P(A)\times P(B|A)=0.33 \times 0.5=0.1666$$

محاسبه این احتمالات و ارتباط آن‌ها با یکدیگر را می‌توانیم به صورت یک نمودار درختی که در ادامه قابل مشاهده است، نمایش دهیم. هر شاخه در این درخت نشانگر محاسبه یک احتمال شرطی است.

نکته: احتمال شرطی را نمی‌توان به صورت رابطه علت و معلولی در نظر گرفت. ممکن است ارتباط بین دو پیشامد A و B‌ به صورت علّی نباشد و فقط در مقدار احتمال با یکدیگر ارتباط داشته باشند. این نکته را در قسمت چهارم از این سری مطالب، مورد تاکید قرار داده‌ایم.

پیشامدهای مستقل (Independent Events)

پیشامد A را نسبت به B‌ مستقل می‌نامیم، اگر رخداد B بر احتمال رخداد A تاثیری نداشته باشد. این واقعیت را می‌توان با نمادهای احتمال شرطی به صورت زیر نشان داد:

$$\large P(A|B)=P(A)$$

رابطه ۱

با توجه به رابطه بالا می‌توان به شکل ساده‌تری نیز استقلال پیشامد A را نسبت به B مشخص کرد.

$$\large P(B|A)=\dfrac{P(A\cap B)}{P(A)}\rightarrow P(A\cap B)=P(A)P(B)$$

به این ترتیب می‌توان استقلال پیشامد A نسبت به B‌ را به شرطی دانست که احتمال رخداد اشتراک دو پیشامد A و B برابر با حاصلضرب پیشامد هر یک باشد.

می‌توان نشان داد که اگر رابطه بالا برقرار باشد، آنگاه رابطه زیر نیز برقرار خواهد بود.

$$\large P(B|A)=P(B)$$

رابطه ۲

با توجه به رابطه‌های بالا می‌توان به گفت اگر پیشامد A مستقل از پیشامد B باشد، آنگاه پیشامد B نیز مستقل از پیشامد A خواهد بود. در نتیجه استقلال یک رابطه دو طرفه است.

پیشامدهای دو به دو مجزا (ناسازگار) (Mutually Exclusive Events)

موضوع دیگری که در احتمال شرطی و قضیه بیز در علم داده باید در نظر گرفت، مفهوم پیشامدهای ناسازگار است. منظور از دو پیشامد ناسازگار یا مجزا، پیشامدهایی مانند A و B هستند که رخداد یکی نشانگر عدم رخداد دیگری است. به بیان دیگر هیچگاه دو پیشامد A و B همزمان رخ نمی‌دهند. این واقعیت را می‌توان به زبان احتمالاتی به صورت زیر نوشت:

$$\large P(A|B)=0$$

$$\large P(‌‌B|A)=0$$

نکته: همانطور که دیده شد، اگر پیشامد A مستقل از پیشامد B باشد، می‌توان نتیجه گرفت که پیشامد B نیز از پیشامد A مستقل است. همین ارتباط را برای پیشامدهای ناسازگار نیز داریم. یعنی اگر A مجزا یا ناسازگار با B باشد، پیشامد B نیز ناسازگار با A است.

قضیه بیز (Bayes' Theorem)

حال که با احتمال شرطی آشنا شدید، به معرفی احتمال شرطی و قضیه بیز در علم داده می‌پردازیم. صورت این قضیه به صورت زیر است.

فیلم آموزش تحلیل های بیزی با نرم افزار وین باگز WinBUGS در فرادرس

کلیک کنید

«احتمال رخداد پیشامد A به شرط B برابر است با احتمال رخداد پیشامد B به شرط A ضرب در احتمال رخداد پیشامد A تقسیم بر احتمال رخداد پیشامد B»

این گزاره را می‌توان به صورت رابطه زیر با احتمال شرطی بیان کرد.

$$\large P(A|B)=\dfrac{P(B|A)P(A)}{P(B)}$$

همان طور که دیده می‌شود، این قضیه نشان می‌دهد که برای محاسبه احتمال شرطی، چگونه باید جای شرط‌ها را عوض کرد و برای بدست آوردن $$P(A|B)$$ از $$P(B|A)$$‌ استفاده کرد.

در حالت کلی اگر برای پارامتر توزیع احتمال جامعه آماری نیز یک تابع احتمال در نظر گرفته شود، به حوزه «آمار بیزی» (Bayesian Inference) برخورد کرده‌ایم. این شاخه از آمار در بسیاری از علوم دیگر بخصوص فارموکولوژی و علوم مالی کاربرد دارد. در اکثر اوقات کیفیت و کمیت هر دو در بحث قضیه بیز مطرح هستند. برای مثال فرض کنید که قرار است ریسک یک سرمایه‌گذاری در شرکت را محاسبه کنیم. این ریسک به عوامل زیاد دیگری مانند سابقه فعالیت شرکت، اعتبار و بدهی‌های شرکت و ... مرتبط است که می‌توانند به صورت تصادفی تغییر کنند. به این ترتیب وجود متغیرهای زیاد در مسئله می‌تواند با در نظر گرفتن احتمال شرطی، دقت برآوردها را افزایش دهد. در ادامه به ذکر مثال‌هایی در مورد احتمال شرطی و قضیه بیز در علم داده خواهیم پرداخت.

مثال

فرض کنید پزشکی براساس یافته‌هایی که از بیمارانش دارد، متوجه شده است که احتمال اینکه مراجعه کننده‌ای دچار مشکل کبدی باشد برابر با ۲۰٪ است. از طرفی احتمال این که این فردی سیگاری باشد نیز برابر با 5٪ گزارش شده. احتمال اینکه فردی که دچار مشکل کبدی است، سیگاری هم باشد برابر با 10٪ است. با توجه به این اطلاعات، احتمال اینکه فرد سیگاری دچار بیماری کبدی باشد چقدر است؟ این مثال نقش احتمال شرطی و قضیه بیز در علم داده را به خوبی نمایش می‌دهد.

ابتدا اطلاعات موجود را طبقه‌بندی می‌کنیم:

• پیشامد A، به معنی وجود مشکل کبدی در فرد است. پس $$P(A)=20\%$$
• پیشامد B، به معنی سیگاری بودن فرد است. پس احتمال سیگاری بودن فرد برابر است با $$P(B)=5\%$$.
• پیشامد اینکه فردی که دچار بیماری کبدی است، سیگاری هم باشد به صورت $$P(B|A)=10\%$$ خواهد بود.

به این ترتیب می‌توانیم احتمال اینکه فرد سیگاری، دچار بیماری کبدی باشد را محاسبه کنیم.

$$\large P(A|B)=\dfrac{P(B|A)P(A)}{P(B)}=\dfrac{10\% \times\ 20\%}{5\%}=40\%$$

پیشامدهای ناسازگار و قضیه بیز

اگر فضای نمونه یا $$\Omega$$ را به دو پیشامد +A و -A افراز کنیم، می‌توان حالت خاصی از قضیه بیز را در نظر گرفت. در اینجا منظور از -A‌ عدم رخداد و +A رخداد پیشامد A در نظر گرفته شده است.

نکته: مشخص است که دو پیشامد +A و -A ناسازگار هستند.

$$\large P(A+|B)=\dfrac{P(B|A+)P(A+)}{P(B|A-)P(A-)+P(B|A+)P(A+)}$$

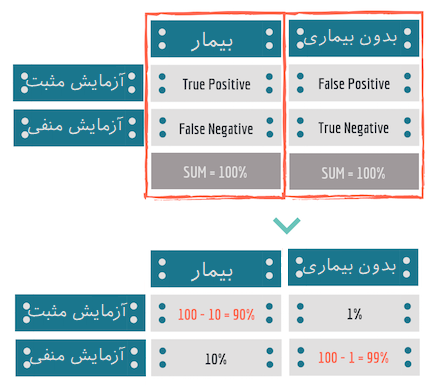
دقت (Accuracy)

در بحث علم داده، هنگام ایجاد مدلی که قادر به توصیف رفتار داده‌ها باشد، از اصطلاح «مثبت صحیح» (True Positive - TP) استفاده می‌شود. منظور از TP حالتی است که مدل به درستی عمل پیش‌بینی را برای گروه مثبت انجام داده است. همین کار را برای حالتی که مدل،‌مشاهده را در گروه نادرست قرار نداده می‌توان در نظر گرفت که به آن «منفی صحیح» (True Negative - TN) گفته می‌شود.

همچنین منظور از «مثبت کاذب» (False Positive - FP) حالتی است که مدل به نادرستی یک گروه مثبت را تشخیص داده است. به همین ترتیب می‌توان اصطلاح «منفی کاذب» (False Negative - FN) را به معنی تشخیص نادرست مدل برای گروه منفی تصور کرد. بر این اساس «حساسیت» (Sensitivity) و «تشخیص‌پذیری» (Specificity) مدل را می‌توان بوسیله روابط زیر تعیین کرد.

حساسیت بیانگر احتمال آن است که مدل مشاهده را درست گروه‌بندی کند. این حالت همان TP است. به این ترتیب احتمال TP میزان حساسیت مدل را نشان می‌دهد.

$$\large \operatorname{Sensitivity}=\dfrac{TP}{TP+FN}$$

تشخیص‌پذیری نیز براساس احتمال TN تعیین می‌شود. یعنی مشاهده را در گروهی که نباید باشد قرار نمی‌دهد.

$$\large \operatorname{Specificity}=\dfrac{TN}{TN+FP}$$

مثال

فرض کنید نرخ یک بیماری (اپیدمی) ۲٪ است. اگر نرخ منفی کاذب 10٪ (عدم تشخیص بیماری در حالیکه فرد بیمار است) و نرخ مثبت کاذب 1٪ (تشخیص بیماری در حالیکه فرد بیمار نیست) احتمال اینکه فردی دارای آزمایش مثبت برای بیماری است واقعا بیمار باشد چقدر است؟ در این حالت مشخص است که اگر +A را به عنوان پیشامد بیمار بودن در نظر بگیریم، و B را نتیجه مثبت برای آزمایش بنامیم، می‌خواهیم احتمال $$P(A+|B)$$ را محاسبه کنیم. این مورد بخصوص در احتمال شرطی و قضیه بیز در علم داده زیاد مورد توجه قرار می‌گیرد.

می‌توانیم فضای نمونه را به دو بخش افراز کنیم. یا فرد بیمار است +A یا فرد بیمار نیست -A. در نتیجه با اطلاعاتی که مسئله در اختیارمان قرار داده است می‌توانیم عبارت‌های زیر را برای محاسبه احتمالات بنویسیم.

$$\large P(A+)=2\%,\;\;\;P(A-)=100\%-2\%=98\%$$

در نتیجه احتمال اینکه فردی بیماری نداشته باشد ولی آزمایش نتیجه مثبت بدهد همان مثبت کاذب (FP) بوده، به صورت زیر نوشته می‌شود.

$$\large P(B|A-)=1\%$$

از طرفی، احتمال اینکه نتیجه منفی با وجود بیمار بودن همراه باشد مطابق اطلاعات مسئله همان منفی کاذب (FN) نامیده شده که برابر با 10٪ است.

$$\large P(B|A+)=10\%$$

حال از قضیه بیز استفاده کرده و محاسبات را به شیوه‌ای که در ادامه قابل مشاهده است، انجام می‌‌دهیم.

$$\large P(A+|B)=\dfrac{P(B|A+)P(A+)}{P(B|A-)P(A-)+P(B|A+)P(A+)}=\\ \large \dfrac{90\% \times 2\%}{1\% \times 98\% +90\% \times 2\%}=64.7\%$$

این قسمت‌ها را می‌توان مطابق ماتریس‌های زیر نشان داد.

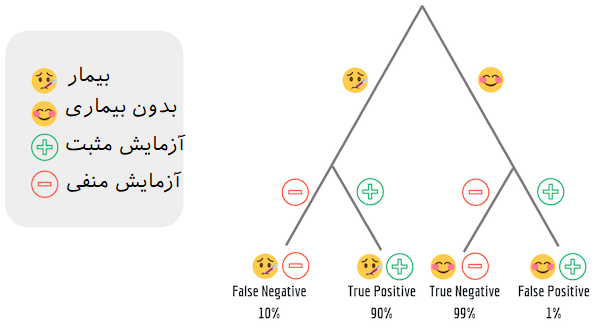
همچنین ارتباطات بین این مشخصات مطابق با نمودار درختی زیر به شکل واضح‌تری قابل مشاهده است.

خلاصه و جمع‌بندی

همانطور که در این نوشتار مطالعه کردید، ابتدا با مفهوم پیشامد و احتمال شرطی آشنا شدیم و از با استفاده از آن مفاهیم با قانون بیز آشنا شدیم. با توجه به قانون یا قضیه بیز بسیاری از مسائل مربوط به علم داده‌ که بر اساس احتمال شرطی تعریف می‌شوند، قابل حل هستند. به عنوان مثال می‌توان به روش دسته‌بندی به کمک بیز ساده (Naive Bayes) اشاره داشت. در نوشتارهای بعدی با کاربرد احتمال شرطی و قضیه بیز در علم داده آشنا شده و از آن در دسته‌بندی یا یادگیری با نظارت استفاده خواهیم کرد.

اگر مطلب بالا برای شما مفید بوده است، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش های SPSS
• مجموعه آموزش های Minitab
• احتمال شرطی (Conditional Probability) — اصول و شیوه محاسبه
•  قضیه بیز در احتمال شرطی و کاربردهای آن
• یادگیری ماشین به زبان قضیه بیز، بی نظمی شانون و فلسفه
• پیاده سازی الگوریتم های یادگیری ماشین با پایتون و R — به زبان ساده

^^