شاخص های آمار توصیفی در علم داده — راهنمای کاربردی

به عنوان یک حوزه میان رشتهای، «علم داده» (Data Science) بیشترین وابستگی را به مفاهیم و تکنیکهای آماری دارد. در یک سلسله مطالب دنبالهای با مفاهیم پرکاربرد آمار در علم داده آشنا خواهیم شد و به این ترتیب شناختی نسبی از تکنیکهای علم داده پیدا خواهیم کرد که به نوعی با آمار سر و کار دارند. دانشمند و آمارشناس بزرگ انگلیسی «کارل پیرسون» (Karl Pearson) که به عنوان پدر آمار مدرن شاخته میشود، در جمله معروف خود، “Statistics is the grammar of Science”، آمار را دستور زبان همه علوم میداند.
مشخص است که علم داده نیز از این قاعده مستثنی نیست. برای نمایش کاربردهای علم آمار در حوزه یادگیری ماشین، ۵ مقاله با عنوانهای زیر تهیه شده است.
- قسمت اول: شاخص های آمار توصیفی در علم داده --- راهنمای کاربردی
- قسمت دوم: توزیع های آماری مهم در علم داده --- راهنمای کاربردی
- قسمت سوم، معیارهای مکانی و گشتاورها در علم داده --- راهنمای کاربردی
- قسمت چهارم: وابستگی- کوواریانس و ضریب همبستگی --- راهنمای کاربردی
- قسمت پنجم: احتمال شرطی، قضیه بیز (Bayes's Theorem) --- راهنمای کاربردی
در این نوشتار به عنوان قسمت اول، به بررسی انواع داده (Data Type) میپردازیم.
اگر برای مطالعه این نوشتار نیازمند پیشزمینههایی هستید، بهتر است مطلب جامعه آماری — انواع داده و مقیاسهای آنها و مقایسه معیارهای تمرکز (میانگین، میانه، نما) و واریانس و اندازههای پراکندگی — به زبان ساده را مطالعه کنید.
آمار و انواع داده (Data Types)
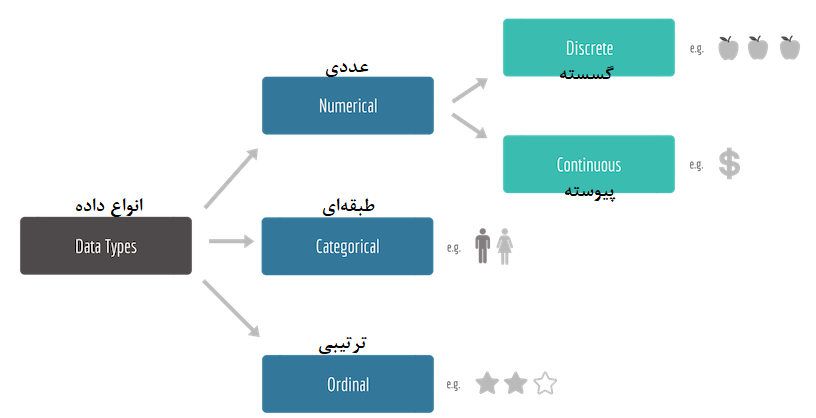
به عنوان یک طبقهبندی اولیه در علم داده، مقادیر و دادهها را به سه گروه تقسیم میکنند: دادههای عددی، دادههای طبقهای و دادههای ترتیبی.
در ادامه هر یک از این گروهها را معرفی کرده و اگر هر گروه نیز دارای زیر بخشی باشد، به آن نیز اشاره خواهیم کرد.
- دادههای عددی (Numerical): مقادیری که توسط روشهای اندازهگیری یا شمارش حاصل میشوند، از گروه دادههای عددی محسوب میشوند. معمولا این نوع داده را به دو زیر دسته با عنوان، دادههای گسسته و پیوسته طبقهبندی میکنند.
- گسسته (Discrete): این مقدارهای عددی زیر مجموعهای از اعداد طبیعی هستند. (برای مثال تعداد افراد، تعداد فرزندان و ...)
- پیوسته (Continuous): اگر مقدارهای حاصل از دادههای عددی، زیر مجموعهای از اعداد حقیقی (دارای اعشار) باشد، نوع داده را پیوسته در نظر میگیرند. (برای مثال وزن، مسافت و ...)
- دادههای طبقهای (Categorical): معمولا دادههای مربوط به صفتها یا ویژگیهای کیفی، از نوع طبقهای هستند. این گونه دادهها برای گروهبندی اعضای جامعه آماری مناسب هستند. اگر برای نمایش یا مشخص کردن هر طبقه یا گروه از اعداد استفاده کنیم، عمل کدگذاری عددی صورت گرفته و باید توجه داشت که این اعداد نباید مبنای محاسبات ریاضی قرار بگیرند. (برای مثال محل تولد، جنسیت، نوع خودرو و ...)
- دادههای ترتیبی (Ordinal): اگر مقدارهای ویژگیهای کیفی دارای ترتیب باشند، دادهها را ترتیبی میگویند. برای مثال صفتهایی که دارای رتبه یا اولویتهایی هستند میتوانند گروه دادههای ترتیبی باشند. به کمک چنین ویژگیهایی میتوان اعضای جامعه آماری را مرتب کرد. (برای مثال رتبه هتلها، میزان تحصیلات و ...)
آمار و معیارهای مرکزی (Measures of Central Tendency)
فرض کنید مسافت شهر تهران از ۵ شهر دیگر در یک مجموعه داده به صورت زیر ثبت شده است. میخواهیم معیارهای تمرکز را برای این مجموعه داده معرفی و محاسبه کنیم.
1{ 6, 3, 100, 3, 13 }میانگین (Mean)
معمولا میانگین را با نماد نشان میدهند. شیوه محاسبه آن همان معدلگیری است. به این معنی که همه مقادیر با یکدیگر جمع شده و حاصل بر تعداد تقسیم میشود. به این ترتیب، میانگین برای دادههای بالا به صورت زیر محاسبه خواهد شد.
1 6 + 3 + 100 + 3 + 13 = 125 →
2 μ = 125 ÷ 5 = 25میانه (Median)
میانه، نقطه وسط دادهها است. برای محاسبه میانه ابتدا باید همه مقادیر را به ترتیب (از کوچک به بزرگ) قرار داده، سپس مقدار وسط را مشخص کرد. بر این اساس میانه برای دادههای بالا به صورت زیر بدست میآید.
1 3, 3, 6, 13, 100 → 6نکته: اگر تعداد دادهها زوج باشد، میانگین دو مقدار وسطی را به عنوان میانه در نظر میگیریم.
میانه نسبت به میانگین کمتر تحت تاثیر «دادههای پرت» (Outlier) قرار میگیرد. بنابراین براساس توزیع دادهها، باید برای انتخاب معیار تمرکز از میانگین یا میانه استفاده کرد.
نما (Mode)
مقداری که بیشترین فراوانی را دارد، نما در نظر میگیرند. پس برای تعیین نما باید به کمک جدول فراوانی (Frequency Table) مقداری که دارای بیشتری فراوانی است به عنوان نما معرفی کرد.
محاسبه میانگین، میانه و نما برای دادههای عددی میسر است در حالیکه برای دادههای طبقهای فقط از نما به عنوان معیار تمرکز استفاده میشود. همچنین اگر دادهها از نوع ترتیبی باشند، میانه و نما را میتوان به عنوان شاخصهای تمرکز مورد محاسبه قرار داد.
آمار و معیارهای پراکندگی (Measures of Variability)
برای شناخت رفتار دادهها، علاوه برای مشخص کردن محل تمرکز آنها باید میزان پراکندگی نیز تعیین شود. برای سنجش پراکندگی دادهها از شاخصهای مختلفی که در ادامه معرفی میشوند، استفاده خواهیم کرد.
دامنه تغییرات (Range)
فاصله بین بیشترین و کمترین مقدار، دامنه تغییرات را تشکیل میدهد. این مقدار حداکثر میزان پراکندگی در دادهها را تعیین میکند. برای دادههای مورد نظر ما، دامنه تغییرات به صورت زیر محاسبه میشود.
1 100 – 3 = 97با توجه به شیوه محاسبه دامنه تغییرات، حساسیت آن به «دادههای پرت» غیرقابل انکار است.
واریانس (Variance)
اگر مرکز دادهها را میانگین در نظر بگیریم، واریانس متوسط پراکندگی یا فاصله اعداد نسبت به میانگین را محاسبه میکند. به این ترتیب اگر فاصله از میانگین را بوسیله مربع اختلاف مقدارها از میانگین در نظر بگیریم، واریانس میانگین این فواصل خواهد بود.
قبلا میانگین را برای دادههای فرضی، محاسبه کردیم که برابر با ۲۵ بود. حال طی مراحل زیر واریانس را بدست خواهیم آورد.
گام اول- محاسبه میانگین
1 6 + 3 + 100 + 3 + 13 = 125 →
2 μ = 125 ÷ 5 = 25گام دوم- محاسبه اختلاف از میانگین
فاصله هر یک از مقدارها را از میانگین دادهها محاسبه میکنیم.
16 - 25 = -19
23 - 25 = -22
3100 - 25 = 75
43 - 25 = -22
513 - 25 = -12گام سوم- محاسبه مربعات این فاصلهها
1(-19)^2 = 361
2(-22)^2 = 484
3(75)^2 = 5,625
4(-22)^2 = 484
5(-12)^2 = 144گام چهارم- محاسبه میانگین مربعات فاصلهها
براساس مقدارهای بدست آمده از گام سوم، میانگین را بدست میآوریم.
1361 + 484 + 5,625 + 484 + 144 = 7,098 →
27,098 ÷ 5 = 1,419.6به این ترتیب مقدار واریانس برابر با 1419.6 است که مقدار بزرگی به نظر میرسد.
سوالی که این جا مطرح میشود این است که چرا برای محاسبه واریانس از مربعات فاصلهها استفاده شده است؟ از آنجایی که میانگین مرکز ثقل دادهها محسوب میشود، متوسط فاصله اعداد از میانگینشان برابر با صفر است.
زیرا مقدار بعضی از این فاصلهها منفی و بعضی دیگر مثبت هستند. در نتیجه مجموع آنها صفر خواهد بود. برای اینکه مقدارهای منفی از بین بروند و فقط میزان فاصله (و نه جهت فاصله) در نظر گرفته شود، این فواصل در محاسبه واریانس به صورت مربع درآمدهاند. به همین علت نیز واریانس تحت تاثیر شدید دادههای پرت قرار دارد.
نکته: باید توجه داشت که اگر تعداد اعداد را در نظر بگیریم، هنگام محاسبه واریانس برای جامعه آماری مجموع مربعات فاصلهها از میانگین بر تعداد اعضای جامعه () تقسیم میکنیم ولی برای محاسبه واریانس یک نمونه از جامعه، مجموع مربعات بر تقسیم خواهد شد.
به این ترتیب اگر مجموعه داده مورد نظر ما مربوط به یک نمونه باشد، باید واریانس را به صورت زیر محاسبه کنیم.
17,098 ÷ 4 = 1774.5انحراف استاندارد (Standard Deviation)
اگر جذر واریانس را محاسبه کنیم، انحراف استاندارد حاصل میشود. معمولا انحراف استاندارد یا انحراف معیار را با علامت نشان میدهند. پس میتوان رابطه بین واریانس و انحراف استاندارد را به صورت زیر نشان داد.
برای دادههای ما نیز انحراف استاندارد مطابق محاسبه زیر بدست میآید.
1 σ = SQRT(1,419.6) = 37.68بر اساس انحراف استاندارد و میانگین میتوان تشخیص داد که چه دادهای پرت محسوب میشود. برای مثال دادههای فرض مطرح شده در این نوشتار، مقدار ۱۰۰ داده پرت (دور افتاده) به نظر میرسد زیرا از میانگین بیش از حدود ۳ انحراف استاندارد دور است.
1μ = 25
2σ = 37.68
3100 / 37.68 = 2.65اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزشهایی که در ادامه آمدهاند نیز برایتان کاربردی خواهند بود.
- مجموعه آموزش های SPSS
- مجموعه آموزش های Minitab
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- مفاهیم آماری – شاخصهای توصیفی
- توزیع فراوانی – به زبان ساده
- مفاهیم آماری: آمار و جامعه آماری – به زبان ساده
^^














خیلی خیلی خوب بود
ممنون
تو توضیحات واریانس قسمت نکته، غلط املایی وجود داره و دوبار واریانس رو به کار بردین
با سلام؛
نکته صحیح است، واریانس را میتوان برای تمام جمعیت یک جامعه آماری بهدست آورد یا قسمتی از جامعه آماری را انتخاب و واریانس را برای نمونههای انتخاب شده محاسبه کرد. بنابراین، به هنگام محاسبه واریانس برای تمام جمعیت باید مجموع مربعات فاصلهها از میانگین بر تعداد اعضای جامعه (N) تقسیم شود. در مقابل، برای محاسبه واریانس برای گروخی اط جامعه آماری باید مجموع مربعات فاصلهها از میانگین را بر N−1 تقسیم کنیم.
با تشکر از همراهی شما با مجله فرادرس
با سلام و تشکر بابت آموزش
آیا در انتها برای تشخیص داده پرت لازم نیست ابتدا 100 از 25 که میانگین است کم شود سپس با تقسیم بر انحراف معیار استاندارد یعنی 37 مقدار دور بودن آن از سایر داده ها سنجیده شود؟ لطفا توضیح بفرمایید.