متغیر تصادفی و توزیع پواسون – به زبان ساده

اگر یک آزمایش تصادفی به شکلی باشد که وقوع یک پیشامد، مرتبط با واحد مکان یا زمان باشد،‌ یک آزمایش پواسن تشکیل شده است. این نام به علت تحقیقات دانشمند فرانسوی، «سیمون پواسن» (Simone Poisson) در این زمینه انتخاب شده است.

آزمایش پواسن باید شرط‌های زیر را دارا باشد:

1. بین هر دو فاصله مجزای مکانی مثل $$(d_1,d_2)$$ و $$(d_3,d_4)$$ رخداد پیشامد مستقل از هم باشند. این قانون برای هر دو فاصله زمانی مثل $$(t_1,t_2)$$ و $$(t_3,t_4)$$ نیز باید وجود داشته باشد.
2. در هر واحد فاصله مکانی یا زمانی کوچک، وقوع بیش از یک پیشامد صفر است. یعنی اگر پیشامد مورد نظر ما A باشد، برای هر فاصله کوچک $$\Delta t$$ داشته باشیم: $$P(t$$
3. احتمال رخداد یک پیشامد با طول فاصله مکانی یا زمانی متناسب باشد. یعنی مثلا اگر طول یک فاصله مکانی برابر با d باشد، احتمال رخداد یک پیشامد در این فاصله برابر با $$\lambda d$$ باشد. $$P(D$$ که در آن $$\lambda$$ ضریب تناسب یک عدد حقیقی مثبت است.

فیلم آموزش تحلیل داده ها با نرم افزار مینی تب Minitab – مقدماتی در فرادرس

کلیک کنید

همانطور که دیده شد،‌ وقوع یا عدم وقوع یک پیشامد در این آزمایش ملاک است. پس می‌توان نتایج آزمایش پواسن را به شکلی مرتبط با آزمایش و توزیع دو جمله‌ای دانست. برای اطلاع از آزمایش دو جمله‌ای و توزیع آن می‌توانید به مطلب متغیر تصادفی و توزیع دو جمله‌ای --- به زبان ساده مراجعه کنید.

تعداد زدگی‌ها در یک قواره پارچه، تعداد قطعی در ارسال پیام‌های رایانه‌ای در یک فاصله زمانی و ... مثال‌هایی از فرآیند پواسن هستند، زیرا:

1. پیشامد وجود زدگی در هر متر مربع از پارچه مستقل از یکدیگر است. همینطور قطع ارتباط در میلی ثانیه اول از قطع ارتباط در میلی ثانیه‌ دوم هنگام ارسال پیام مستقل است.
2. در هر واحد مکان، پیشامد مشاهده بیش از یک زدگی پارچه یا قطع ارتباط بیش از یک بار در هر میلی ثانیه تقریبا صفر است.
3. تعداد زدگی‌ها به مساحت پارچه و تعداد قطع ارتباط با طول زمان ارسال پیام بستگی دارد.

فرض کنید در یک آزمایش دو جمله‌ای، احتمال موفقیت به تعداد آزمایش‌ها وابسته باشد یعنی توزیع به شکل $$B(n,p_n)$$ باشد. همچنین حالتی را در نظر بگیرید که با بزرگ شدن  n, مقدار $$p_n$$ کوچک شود. آنگاه می‌توان گفت که تعداد موفقیت‌ها از توزیع پواسن با پارامتر $$np_n=\lambda$$ پیروی می‌کند.

نکته: اگر احتمال موفقیت ثابت باشد، تعداد موفقیت‌ها دارای توزیع دو جمله‌ای است.

اگر متغیر تصادفی مربوط به تعداد موفقیت‌ها را در این حالت X بنامیم، خواهیم دید که:

$$P(X=x)\approx (^n_x)(\tfrac{\lambda}{n})^x(1-\tfrac{\lambda}{n})^{n-x}$$

در این حالت اگر n به سمت بینهایت میل کند، خواهیم داشت:

$$\lim_{n\to \infty}\dfrac{n!}{(n-x)!n^x}=1\; ;\;\;\;\; \lim_{n\to \infty} (1-\dfrac{\lambda}{n})^{n-x}=e^{-\lambda}\times 1= e^{-\lambda}$$

پس می‌توان نوشت:

$$P(X=x)=e^{-\lambda}\dfrac{\lambda ^x}{x!}$$

به این ترتیب با توجه به ویژگی‌های آزمایش پواسون،‌ متغیر تصادفی و توزیع پواسون معرفی می‌شوند.

متغیر تصادفی پواسون و توزیع احتمال آن

فرض کنید متغیر تصادفی X تعداد موفقیت در یک آزمایش پواسون باشد، آنگاه تابع احتمال آن به صورت زیر خواهد بود:

$$P(X=x)=e^{-\lambda}\dfrac{\lambda ^x}{x!};\;\;\;\;\lambda >0, \;\;\;x=0,1,2,\dots$$

به این ترتیب می‌نویسیم $$X\sim P(\lambda)$$ و می‌خوانیم X دارای توزیع پواسون با پارامتر لاندا است. مشخص است که تکیه‌گاه این متغیر تصادفی مقادیر نامنفی است زیرا از طریق شمارش تعداد موفقیت بدست می‌آید.

نکته: اگر متوسط تعداد رخدادها در و احد زمان برابر با $$\lambda$$‌ در نظر بگیرم، عاقلانه است که متوسط تعداد رخدادها را در t برابر واحد زمانی نیز $$t\lambda$$ محاسبه کنیم.

اگر تابع احتمال مربوط به متغیر تصادفی پواسون را برای $$\lambda = 1,4,10$$ براساس تکیه‌گاه آن ترسیم کنیم نمودار مربوطه به صورت زیر در خواهد آمد.

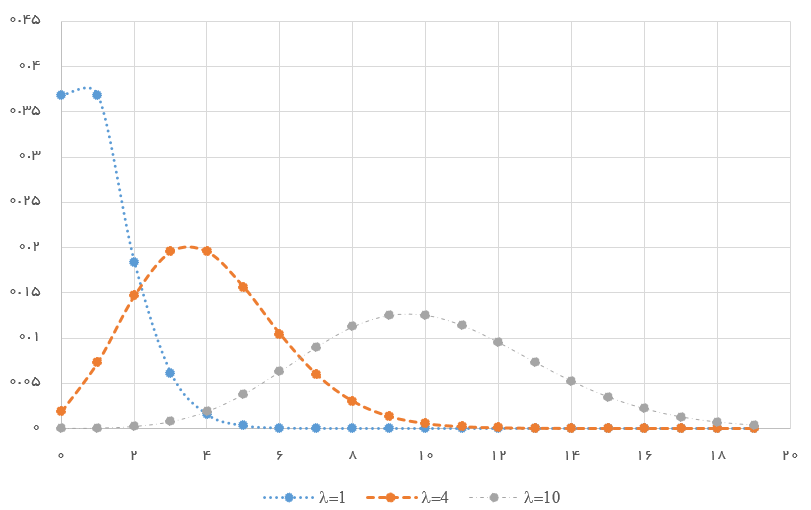
همانطور که دیده می‌شود با افزایش مقدار $$\lambda$$ منحنی به سمت توزیع نرمال با میانگین و واریانس $$\lambda$$ نزدیک می‌شود. مقدار نما (نقطه‌ای از تکیه‌گاه متغیر تصادفی با حداکثر مقدار برای تابع احتمال) برای هر یک از این حالت‌ها برابر با $$\lambda$$ و $$\lambda-1$$ است.

مثال ۱

در یک کارخانه تولید خودرو، احتمال اینکه خودرو به علت نقض فنی در قسمت کنترل کیفیت بازگشت داده شود،‌ برابر 1٪ است. احتمال آنکه در بین ۳۰۰ دستگاه تولیدی ۵ دستگاه برگشت داده شود چقدر است؟

در اینجا متوسط تعداد برگشتی‌ها همان پارامتر توزیع پواسون است. یعنی $$\lambda=300\times 0.01=3$$.

پس برای محاسبه احتمال به صورت زیر عمل می‌کنیم:

$$P(X=5)= \dfrac{e^{-3}3^5}{5!}=0.1008$$

مثال 2

یک کارگزار بیمه، به طور متوسط در هفته سه قرار داد بیمه نامه را با مشتری امضاء می‌کند. احتمال اینکه در طول یک هفته حداقل یک بیمه نامه بفروشد، چقدر است؟

از آنجایی که در هر واحد زمان بیش از یک بیمه نامه فروخته نمی‌شود و تعداد فروش بیمه نامه در هر واحد زمانی مستقل از زمان‌های دیگر است، کافی است که تعداد فروش بیمه نامه هم متناسب با زمان در نظر گرفته شود تا شرایط آزمایش پواسون برای کارگزار بیمه محقق شود.

برای محاسبه احتمال نیز کافی است، عملیات زیر را انجام دهیم:

$$P(X>0)=1-P(X=0)=1-\dfrac{e^{-3}3^0}{0!}=1-0.0498=0.9502$$

نکته: متوسط تعداد بیمه فروخته شده در هفته همان پارامتر توزیع پواسون است. یعنی $$\lambda =3$$.

امید-ریاضی و واریانس متغیر تصادفی پواسون

فرض کنید $$X\sim p(\lambda)$$. براساس تابع احتمال متغیر تصادفی پواسون می‌توان امید-ریاضی این متغیر تصادفی را به شکل زیر بدست آورد:

$$E(X)=\sum_{x=0}^{\infty} x\dfrac{e^{-\lambda}{\lambda^x}}{x!}=\lambda e^{-\lambda} \sum_{x=1}^{\infty} \dfrac{\lambda^{(x-1)}}{(x-1)!}=$$

$$\lambda e^{-\lambda} \sum_{y=0}^\infty \dfrac{\lambda^{y}}{y!}=\lambda$$

زیرا: $$\sum_{y=0}^\infty \dfrac{\lambda^y}{y!}=e^\lambda$$.

به طریق مشابه نیز می‌توان نشان داد که واریانس متغیر تصادفی پواسون به صورت زیر محاسبه می‌شود:

$$Var(X)=E(X^2)-E^2(X)=\lambda$$

پس امید-ریاضی و واریانس برای متغیر تصادفی پواسون با هم برابر هستند.

مثال ۳

در مثال 2، مسئول بیمه به طور متوسط در سال چند بیمه نامه را به قرار داد می‌رساند؟

نکته: با توجه به اینکه طول زمان در این مثال ۵۲ هفته است،‌ می‌توان گفت که توزیع پواسون با پارامتر $$52*3=156$$ خواهد بود.

$$E(X)=\lambda =156$$

مثال ۴

فرض کنید ۲ درصد جمعیت دارای گروه خونی AB هستند. یک نمونه ۶۰ تایی از جمعیت به طور تصادفی انتخاب شده است. اگر متغیر تصادفی X را تعداد افرادی که دارای گروه خونی AB هستند در نظر بگیریم، احتمال اینکه هیچ یک دارای گروه خونی AB‌ نباشند چقدر است؟

مشخص است که در اینجا X یک متغیر تصادفی با توزیع دو جمله‌ای با پارامترهای ۶۰ و 0.02 است، یعنی $$X\sim B(60,0.02)$$. برای محاسبه این احتمال از روی توزیع دو جمله‌ای باید محاسباتی نظیر !۶۰ را انجام بدهیم که زمان زیادی صرف خواهد شد. ولی اگر از تقریب پواسون استفاده کنیم، می‌توانیم به سرعت به جواب تقریبا مناسبی برسیم.

در این حالت برای تقریب توزیع دو جمله‌ای از توزیع پواسون استفاده می‌کنیم و می‌گوییم $$X\sim P(60 \times 0.02=1.2)$$. پس مقدار $$\lambda=1.2$$. حال احتمال (P(X=0 را بدست می‌آوریم.

$$P(X=0)=\dfrac{e^{-\lambda} \lambda^x}{x!}=\dfrac{e^{-1.2}\times 1.2^0}{0!}=0.3012$$

ولی اگر این محاسبات را براساس توزیع دو جمله‌ای انجام دهیم با صرف زمان زیاد به جواب زیر خواهیم رسید. این جواب با تقریب پواسون حدود 0.003 تفاوت دارد.

$$P(X=0)=(^{60}_0)0.02^00.98^{60}=0.2975$$

مثال ۵

با توجه به مثال ۴، اگر هدف پیدا کردن احتمال آن باشد که در نمونه ۶۰ تایی حداکثر ۵ نفر گروه خونی AB داشته باشند، محاسبه احتمال به صورت زیر خواهد بود:

$$P(X\leq 5)=\sum_{x=0}^5 P(X=x)=0.998$$

فیلم آموزش تحلیل داده های معدنی با نرم افزار مینی تب Minitab در فرادرس

کلیک کنید

برای پیدا کردن این احتمال می‌توان از جدول‌های توزیع احتمال پواسون کمک گرفت. در زیر یک نمونه از این گونه جدول‌ها دیده می‌شود:

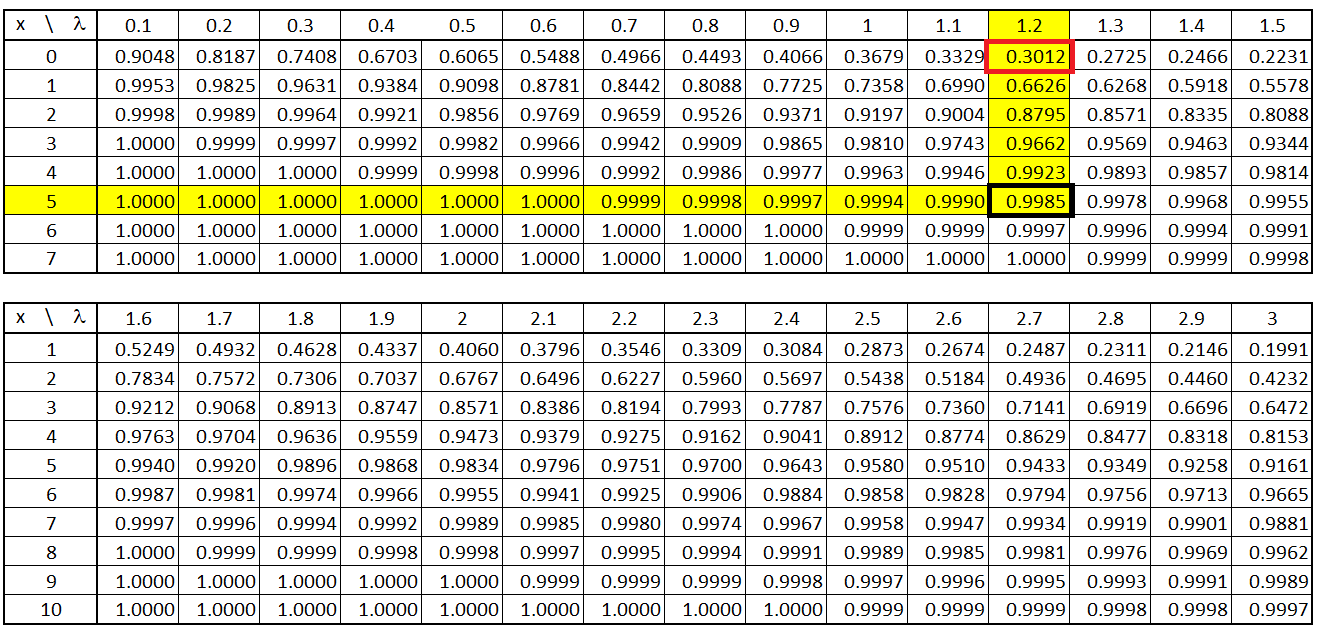
سطر اول این جدول بیانگر مقدار $$\lambda$$ و ستون اول نیز مقدار x را نشان می‌دهد. اعداد درون جدول نیز مقدار تابع توزیع احتمال متغیر تصادفی پواسون یعنی $$P(X\leq x)$$ را بیان می‌کنند.