مفاهیم آماری – شاخصهای توصیفی

در این نوشته قصد داریم برخی از مهمترین مفاهیم آماری که شامل شاخصهای توصیفی میشود را معرفی کنیم. برای توصیف جامعه یا نمونهی آماری به طور معمول از سه نوع شاخص یا معیار استفاده میشود.
- شاخصهای تمایل به مرکز
- شاخصهای پراکندگی
- شاخصهای تقارن توزیع
شاخصهای تمایل به مرکز
شاخصهای تمرکز: مقادیر (کمی یا کیفی) که بیانگر میزان تمرکز دادهها هستند، شاخصهای تمرکز (Centerl Tendency: معیارهای مرکزی) نامیده میشوند. از معروفترین شاخصهای تمرکز میتوان به میانگین (Mean: مرکز ثقل دادهها- برآیند مقادیر)، میانه (Median: مقدار میانی در صورتی که دادهها به ترتیب قرار گیرند) و نما (Mode: ویژگی با بیشترین فراوانی) اشاره کرد. در بررسیهای آماری عبارتهایی نظیر: میانگین (متوسط) درآمد در جامع، میانه (حد وسط) میزان تحصیلات و مدل خودرو با اکثریت میزان تصادفات (نما یا مد) صحبت به میان میآید. جدا از شیوه و نحوه محاسبه، هر یک از این شاخصها، کاربردهای متفاوتی نیز دارند و جنبهی خاصی از خصوصیات جامعه یا نمونه را نشان میدهند.
میانگین
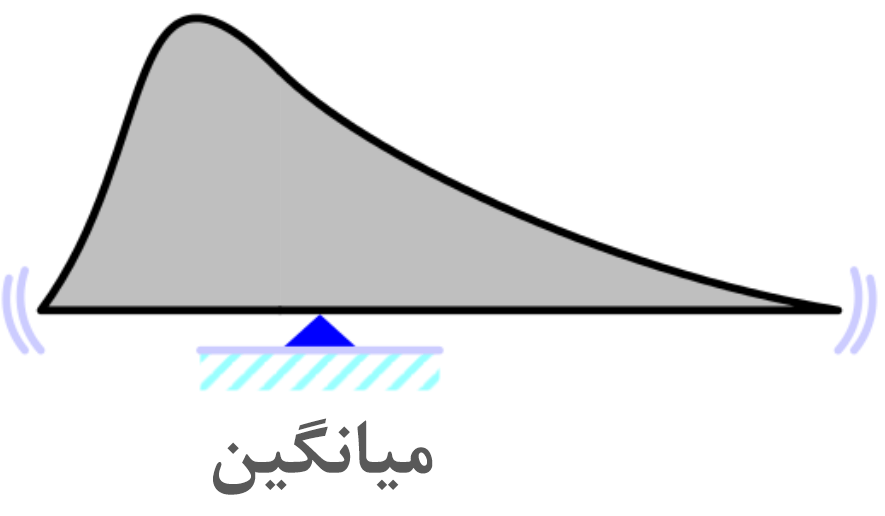
مقدار برآیند یا مرکز ثقل دادهها توسط میانگین بیان میشود. برای محاسبه آن کافی است که همه دادهها را با هم جمع کرده و بر تعدادشان تقسیم کنیم. متوسط فاصله میانگین از دادهها برابر صفر است. به این ترتیب میانگین، برآیند دادهها را نشان میدهد. میانگین برای دادههای کمی قابل محاسبه است. استفاده از میانگین و بهرهگیری از خواص آن، در بررسی و تحلیلهای آماری بسیار مقید است. زیرا در محاسبه آن همه دادهها نقش خواهند داشت.
میانه
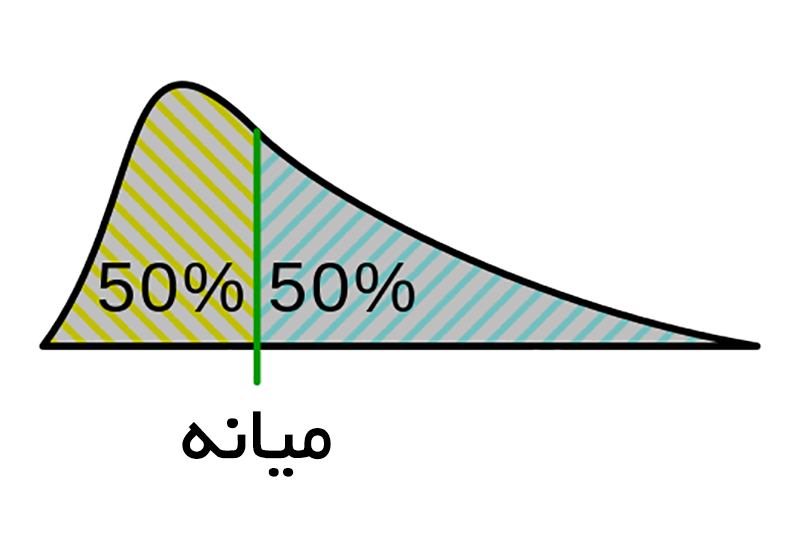
اگر دادهها را از کوچک به بزرگ مرتب سازیم، دادهای که در وسط قرار گرفته است، میانه خواهد بود. میانه را میتوان مقداری در نظر گرفت که 50% دادهها از آن کمتر با بیشتر هستند. میانه را برای دادههای کمی و کیفی ترتیبی میتوان محاسبه کرد. درحقیقت میتوان میانه را یک نقش متعادل بین تعداد دادهها در نظر گرفت. از نظر میانه بزرگی یا کوچکی دادهها مهم نیست، بلکه تعداد و ترتیب آنها در محاسبه میانه نقش دارد.
نما
نما برای دادههای کمی و کیفی قابل محاسبه است و دادهای است که بیشتری تکرار یا فراوانی را داشته باشد. در حقیقت نما را میتوان نماینده اکثریت جامعه دانست. از آنجایی که فقط تعداد تکرار (نه ترتیب و نه مقدار دادهها) در محاسبه نما نقش دارد، نسبت به مقادیر بزرگ و کوچک حساس نیست و مقدار نما تحت تاثیر مقادیر بزرگ و کوچک نخواهد بود.
شاخصهای پراکندگی
تغییرات و پراکندگی دادهها توسط شاخص یا معیارهای پراکندگی قابل اندازهگیری است. با انجام محاسباتی، معیاری عددی برای میزان پراکندگی دادهها به دست میآید. هرچه مقدار این معیار بزرگتر باشد، نمایانگر پراکندگی بیشتر دادهها خواهد بود. و برعکس با کوچک بودن این معیار، متوجه میشویم که دادهها به یکدیگر نزدیک هستند.
دامنه تغییرات
حداکثر میزان تغییرات توسط این شاخص محاسبه میشود. اختلاف بین بزرگترین و کوچکترین مقدار، دامنه تغییرات Range را نشان میدهد. این شاخص به راحتی قابل محاسبه است ولی فقط بر اساس دو مقدار از دادهها محاسبه میشود.
میانگین انحرافات نسبت به میانگین
برای سنجش پراکندگی بهتر است، بهتر است نقطهای را به عنوان نقطه اصلی در نظر گرفت و پراکندگی دادهها را نسبت به آن سنجید. در محاسبه میانگین انحرافات نسبت به میانگینAbsolute Difference to mean (A.D) ، نقطه تمرکز میانگین در نظر گرفته شده و از قدرمطلق اختلاف دادهها نسبت به میانگین، یک میانگین گرفته میشود. وجود قدرمطلق، محاسبه آن را کمی سخت میکند ولی در عوض همه دادهها در محاسبه شاخص پراکندگی نقش دارند.
واریانس و انحراف معیار
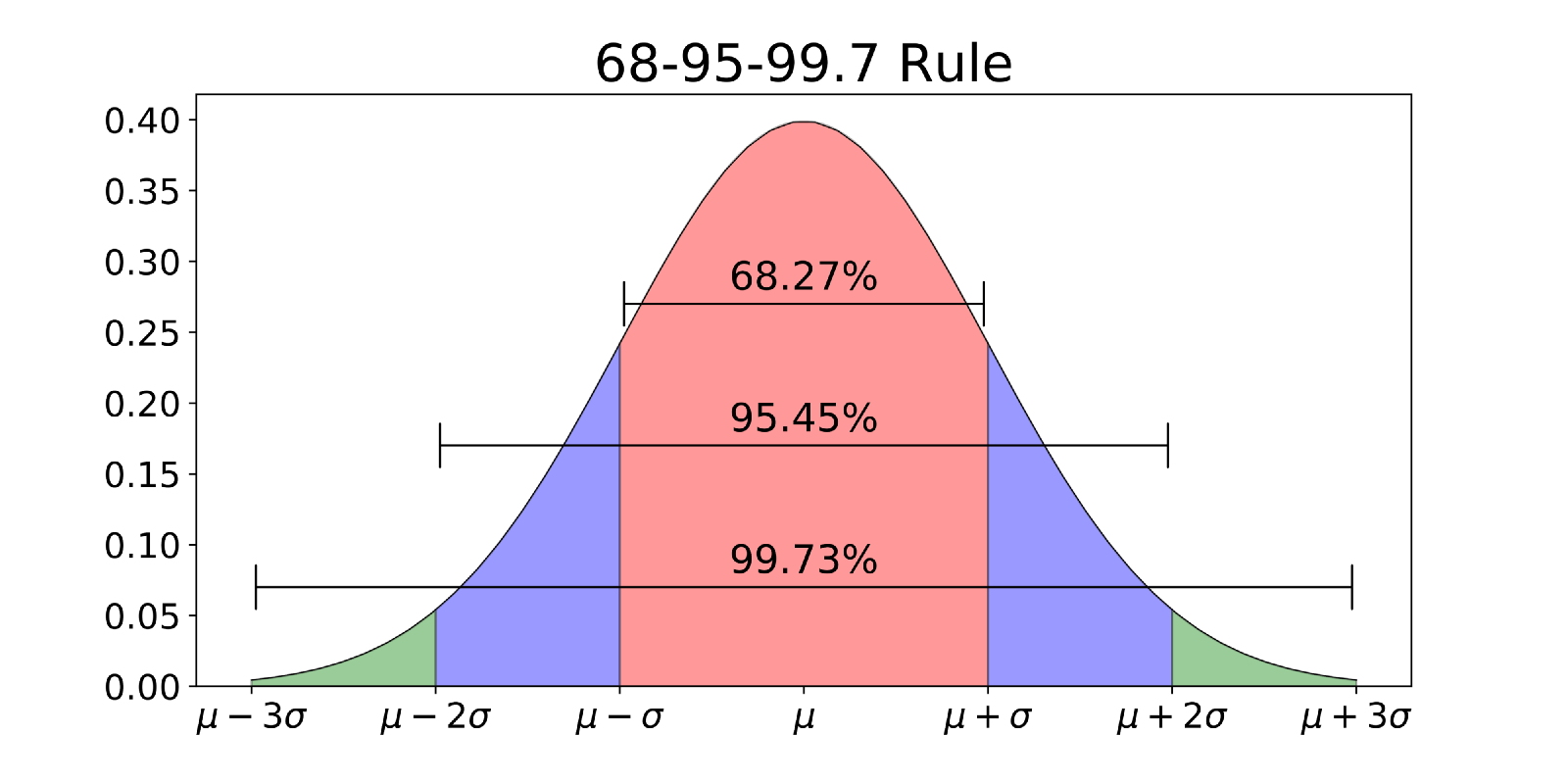
برای سنجش فاصله یا انحراف دادهها نسبت به میانگین، به جای قدر مطلق از مجذور فاصله نیز استفاده میکنند. به این ترتیب متوسط مجذور فاصله نسبت به میانگین، معیار دیگری برای پراکندگی نامیده میشود که به آن واریانس میگویند.
از آنجایی که محاسبه مشتق و انتگرال براساس مجذور (توان دو) راحتتر از قدرمطلق است، استفاده از واریانس بر میانگین انحرافات نسبت به میانگین ارجحیت دارد. واحد اندازهگیری واریانس به صورت مربع واحد اندازهگیری دادهها خواهد بود. برای مثال اگر دادهها برحسب متر باشند، شاخصهای تمرکز و پراکندگی به جز واریانس با واحد متر سنجیده میشوند. ولی واریانس با واحد متر مربع (به علت استفاده از توان 2) سنجیده خواهد شد. برای رفع این مشکل از جذر واریانس با نام انحراف معیار (Standard Deviation) استفاده میشود.
ضریب تغییرات
معیارهای پراکندگی معرفی شده قبل، همگی به واحد اندازهگیری دادهها بستگی دارند. اگر میخواهید میزان پراکندگی را بدون واحد اندازهگیری با به صورت درصدی بیان کنید، از ضریب تغییرات استفاده کنید. تعریف ضریب تغییرات برای دادههای نامنفی به صورت نسبت انحراف معیار به میانگین خواهد بود. به این صورت میزان پراکندگی به ازای یک واحد از میانگین محاسبه میشود. این معیار پراکندگی برای مقایسه بین دو جامعه یا دو متغیر که از لحاظ واحد اندازهگیری متفاوت هستند به کار میرود. برای مثال اگر میخواهید بین محصول دو کارخانه، کالای بادوامتر را انتخاب کنید، کالای با میانگین بیشتر و پراکندگی کمتر (ضریب تغییرات کوچکتر) را انتخاب خواهید کرد.
شاخصهای تقارن در توزیع
اطلاع از شاخصهای تمرکز و پراکندگی و تقارن در توزیع، به درک شکل و الگوی جامعه آماری کمک فراوانی میکند.
شاخصهای تقارن مقایسهای بین شکل توزیع دادهها با توزیع نرمال استاندارد ارائه میدهد. هرچه مقادیر شاخصهای تقارن از صفر دور باشند، وجود عدم تقارن در جامعه مورد بررسی مشهودتر است. عدم وجود تقارن به صورت افقی و عمودی با دو معیار چولگی و برجستگی اندازهگیری میشود.
میعار چولگی

میزان عدم تقارن افقی نسبت به منحنی توزیع نرمال استاندارد را چولگی مینامند و به صورت کسری است که صورت آن اختلاف میانگین با نما و مخرج آن انحراف استاندارد است. در نتیجه این معیار به صورت بدون واحد یا درصدی بیان میشود. مقدار مثبت نشانگر چولگی به راست و مقدار منفی نشانگر چولگی به چپ است. مقدار صفر نشانگر وجود تقارن افقی در دادهها است. در این حالت نما، میانه و میانگین بر یکدیگر منطبق خواهند شد.
- در حالتی که چولگی به راست باشد ترتیب معیارهای تمرکز از کم به زیاد – نما، میانه و سپس میانگین خواهد بود
- در حالتی که چولگی به چپ باشد، ترتیب معیارهای تمرکز از کم به زیاد- میانگین، میانه و سپس نما خواهد بود.
معیار برجستگی
میزان عدم تقارن عمودی نسبت به منحنی توزیع نرمال استاندارد، برجستگی نامیده میشود و به مرتبط با کسری است که صورت آن توان چهارم میانگین اختلاف دادهها نسبت به میانگین و مخرج آن توان چهارم انحراف معیار است. برای محاسبه معیار برجستگی این کسر را از عدد 3 که میزان برجستگی برای منحنی نرمال استاندارد است کم میکنیم. اگر این تفاضل منفی باشد عدم تقارن به صورت پخی برای دادهها در نظر گرفته میشود و در صورتی که معیار برجستگی مثبت باشد، نشانگر وجود عدم تقارن به صورت برجستگی نسبت به منحنی نرمال استاندارد خواهد بود.
برای مطالعهی بیشتر در این زمینه میتوانید از مطالب زیر استفاده کنید:
- مجموعه آموزشهای نرمافزار SPSS
- آموزش آمار استنباطی برای مدیریت و علوم انسانی
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- مجموعه مطالب آمار وبلاگ فرادرس ویژه مهندسین صنایع
- روش های نمونهگیری (Sampling) در آمار — به زبان ساده
- تقلب نامه (Cheat Sheet) آمار توصیفی و احتمال — راهنمای کامل و سریع
- مجموعه آموزشهای نرمافزارهای آماری
==












با سلام. ممنون از توضیحاتی که ارائه فرمودید.
ی سوال داشتم: در نرم افزار spss چطور میشه ضریب تغییرات رو بدست آورد و حساب کرد راهی هست که بشه ضریب تغییرات تمام تیمارها یا متغیرها رو نسبت به یک متغیر دیگر در آن واحد حساب کرد؟؟
برا جداول آنالیز واریانس لازم دارم.
با تشکر فراوان
با سلام و سپاس از همراهی شما با مجله فرادرس
به زودی نوشتاری با موضوع ضریب تغییرات و محاسبه آن در SPSS منتشر خواهد شد. ولی میتوانید متن انگلیسی مربوطه را از اینجا مشاهده کنید.
از اینکه به مطالب مجله فرادرس توجه دارید ممنون هستیم.
موفق و شاد و سلامت باشید.
بسیار سپاسگزارم. زبان متن بسیار روان و قابل فهم است. توفیقاتتان در پناه حق افزون باد.
فقط یه سوال: اگر ضریب تغییرات نسبت انحراف معیار به میانگین است، آیا میانگین بیشتر و پراکندگی کمتر منجر به ضریب تغییرات بزرگتر میشه؟
پیشاپیش بابت پاسخگویی شما سپاسگزارم.
با سلام تشکر از همراهی شما با مجله فرادرس!
همانطور که در متن اشاره شد، ضریب تغییرات به عنوان یک محک و معیار برای اندازهگیری پراکندگی است که به صورت نسبت انحراف معیار با میانگین بدست میآید. انحراف معیار در صورت کسر و میانگین در مخرج کسر قرار دارد. بنابراین هر چه میانگین بیشتر و پراکندگی کمتر باشد، ضریب تغییرات کوچکتر خواهد بود. در نتیجه جامعه حول میانگین کمتر پراکنده هستند و تمرکز روی میانگین بیشتر است.
متن با توجه به تذکر شما اصلاح شد.
با سپاس فراوان از اینکه همگام با فرادرس هستید!
بسیار سپاسگزارم. زبان متن بسیار روان و قابل فهم است. توفیقاتتان در پناه حق افزون باد.
سلام
از شما بسیار سپاس گزارم.
البته فکر کنم تصویر مرتبط با بحث میانه درست نباشد. این طور نیست؟
باسلام و احترام فراوان
خداوند خیر دنیا و آخرت رو بهتان بده … واقعا کارتون عالیست …