توزیع های آماری و رسم نمودار تابع احتمال — با کدهای R

بسیاری از پدیدههای تصادفی، دارای قواعدی برای تعیین احتمال رخداد پیشامدها هستند. الگوی رخداد پیشامدهای تصادفی را «توزیع آماری» (Distribution Function) برای آن پدیدههای تصادفی مینامند. به تابعی که احتمال رخداد یک پیشامد تصادفی را تعیین میکند، «توزیع احتمال» (Probability Function) یا «تابع چگالی احتمال» (Probability Density Function) گفته میشود.
از طرفی بیشتر پدیدههای تصادفی به کمک «متغیرهای تصادفی» (Random Variables) بهتر توصیف میشوند. همچنین بسیاری از متغیرهای تصادفی نیز دارای تابع احتمال یا تابع چگالی احتمال هستند. در این نوشتار به معرفی تابع احتمال برخی از متغیرهای تصادفی میپردازیم و نمودار آنها را رسم میکنیم.
برای آشنایی بیشتر با تابع احتمال به مطلب آزمایش تصادفی، پیشامد و تابع احتمال مراجعه کنید. همچنین برای آگاهی از تعریف و خصوصیات متغیرهای تصادفی، مطالعه نوشتار متغیر تصادفی، تابع احتمال و تابع توزیع احتمال پیشنهاد میشود.
توزیعهای آماری و نمودار تابع احتمال
بسیاری از توزیعهای آماری، به بررسی احتمال رخداد پدیدههای تصادفی میپردازند که اغلب در زندگی روزمره نیز با آنها مواجه هستیم. بنابراین آگاهی از توزیعهای آماری این پدیدههای تصادفی، شناخت ما را نسبت به آنها بیشتر کرده، قادر به درک آنها خواهیم شد.
در ادامه به بررسی برخی از توزیعهای آماری رایج پرداخته و نمودار تابع احتمال یا چگالی احتمال آنها را به کمک بسته «Stats» در زبان برنامهنویسی R محاسبه و رسم میکنیم. این بسته در نسخههای جدید این زبان به صورت خودکار نصب شده و احتیاجی به راهاندازی آن نیست.
برای انجام محاسبات براساس توزیعهای آماری، چهار نوع تابع در بسته Stats در نظر گرفته شده است. جدول زیر به معرفی عمومی این توابع میپردازد.
| ردیف | تابع | محاسبه | رابطه (فرمول) |
| ۱ | dxxx | محاسبه تابع احتمال یا چگالی احتمال (Density) | |
| ۲ | pxxx | محاسبه تابع توزیع احتمال تجمعی (Probability Distribution Function) | |
| 3 | qxxx | محاسبه چندکهای توزیع احتمال (Quantiles) | |
| 4 | rxxx | تولید عدد تصادفی از توزیع دلخواه |
اگر متغیر تصادفی از نوع گسسته باشد، تابع احتمال یا چگالی احتمال، همان مقدار احتمال در نقطه مورد نظر است. در این حالت داریم:
ولی برای متغیرهای تصادفی پیوسته، تابع احتمال، جرم احتمال در نقطه مورد نظر را نشان میدهد زیرا مقدار احتمال در تک نقطهها مانند y برابر با صفر است و فقط میتوان احتمال را برای یک فاصله عددی محاسبه کرد.
همچنین تابع احتمال تجمعی نیز مقدار احتمال تا یک نقطه را نشان میدهد. در حقیقت شیوه محاسبه آن برای متغیرهای تصادفی گسسته به صورت و برای متغیرهای تصادفی پیوسته به صورت است.
از طرف دیگر نیز منظور از چندک pام، نقطه یا مقداری از متغیر تصادفی مثل y است که مقدار احتمال تابع تا آن نقطه برابر با p است. به این ترتیب . در این حالت اگر را معکوس تابع توزیع بنامیم، میتوان نوشت:
در این نوشتار به معرفی توابع چگالی یا احتمال پرداخته و براساس تولید اعداد تصادفی از هر توزیع، نمودار تابع احتمال یا چگالی آنها را رسم میکنیم. ابتدا در مورد محاسبات توابع احتمال متغیرهای تصادفی گسسته بحث خواهیم کرد.
توزیعهای گسسته
در این بخش از توزیعهای گسسته «دوجملهای» (Binomial)، «هندسی» (Geometric)، «پواسون» (Poisson)، «فوق هندسی» (Hyper-Geometric) و «دوجملهای منفی» (Negative binomial) استفاده خواهیم کرد. برای آگاهی از پارامترهای هر یک از توزیعهای آماری کافی است که به مطالب فرادرس مراجعه یا روی لینک نام توزیعها کلیک کنید.
جدول زیر به معرفی توابع مربوط به این توزیعهای گسسته در R پرداخته است.
| توزیع | تابع احتمال | تابع توزیع احتمال | محاسبه چندک | تولید عدد تصادفی | نام انگلیسی |
| دوجملهای | dbinom | pbinom | qbinom | rbinom | binomial |
| هندسی | dgeom | pgeom | qgeom | rgeom | Geometric |
| پواسون | dpois | ppois | qpois | rpios | Poisson |
| فوق هندسی | dhyper | phyper | qhyper | rhyper | HyperGeometric |
| دو جملهای منفی | dnbinom | pnbinom | qnbinom | rnbinom | Negative Binomial |
برای رسم تابع احتمال این توزیعها از کدهای زیر استفاده کردهایم. با مشاهده این برنامه مشخص میشود که ابتدا به کمک تابع rxxx تعداد ۱۰۰۰ عدد تصادفی از توزیع مورد نظر تولید شده، سپس آنها را مرتب میکنیم تا روی محور افقی به ترتیب قرار بگیرند. از طرفی با استفاده از تابع احتمال که با تابع dxxx محاسبه میشود، برای هر یک از توزیعها محاسبات را انجام داده و در انتها نیز نمودار تابع توزیع برحسب دادههای تصادفی را با دستور plot ترسیم میکنیم. البته باید توجه داشت که تولید اعداد تصادفی و احتمال براساس پارامترهای هر توزیع صورت گرفته است.
1par(mfrow=c(3,2))
2y=rbinom(n = 1000,size = 20,prob = 0.2)
3d=dbinom(sort(y),size = 20,prob = 0.2)
4plot(sort(y),d,type = 'o',col='red',xlab = 'Values',ylab='Probability', main = 'Binomial Distribution')
5
6y=rgeom(n = 1000,prob = 0.2)
7d=dgeom(sort(y),prob = 0.2)
8plot(sort(y),d,type = 'o',col='green',xlab = 'Values',ylab='Probability', main = 'Geometric Distribution')
9
10y=rpois(n = 1000,lambda = 2)
11d=dpois(sort(y),lambda =2)
12plot(sort(y),d,type = 'o',col='lightgreen',xlab = 'Values',ylab='Probability', main = 'Possion Distribution')
13
14y=rhyper(nn = 1000,m = 10,n = 15,k = 5)
15d=dhyper(sort(y),m = 10,n = 15,k = 5)
16plot(sort(y),d,type = 'o',col='orange',xlab = 'Values',ylab='Probability', main = 'HyperGeometric Distribution')
17
18y=rnbinom(n = 1000,size = 10,prob = 0.2)
19d=dnbinom(sort(y),size = 10,prob = 0.2)
20plot(sort(y),d,type = 'o',col='blue',xlab = 'Values',ylab='Probability', main = 'Negative BinomialDistribution')نکته: فرمان باعث میشود که صفحه ترسیم نمودارها به سه سطر و دو ستون تقسیم شود.
نتیجه اجرای این برنامه به صورت زیر است.
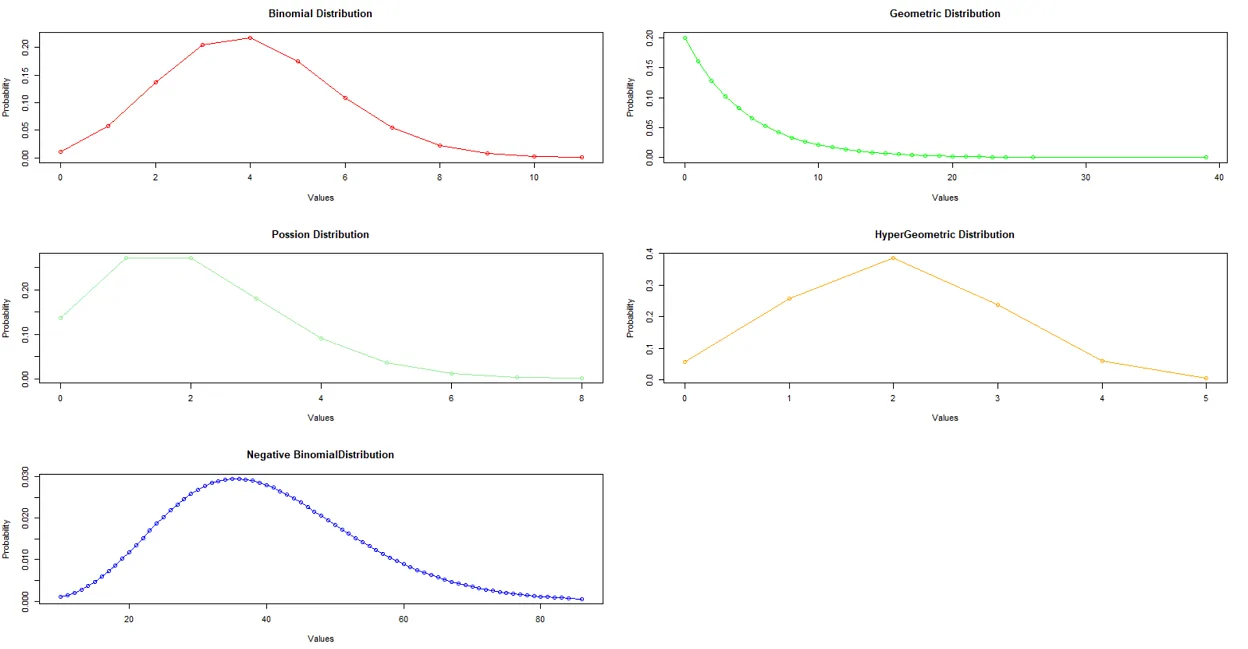
توزیعهای پیوسته
در این بخش از توزیعهای پیوسته «توزیع نرمال» (Normal Distribution)، «توزیع تی» (Student's Distribution)، «توزیع یکنواخت» (Uniform Distribution)، «توزیع نمایی» (Exponential Distribution)، «توزیع کای ۲» (Chi Squared)، «توزیع بتا» (Beta Distribution)، «توزیع گاما» (Gamma Distribution)، «توزیع فیشر» (F Distribution) و «توزیع کوشی» (Cauchy Distribution) استفاده خواهیم کرد.
جدول زیر به معرفی توابع مربوط به این توزیعهای پیوسته در R پرداخته است.
| توزیع | تابع احتمال | تابع توزیع احتمال | محاسبه چندک | تولید عدد تصادفی | نام انگلیسی |
| توزیع نرمال | dnorm | pnorm | qnorm | rnorm | Normal |
| توزیع تی | dt | pt | qt | rt | Student's t |
| توزیع یکنواخت | dunif | punif | qunif | runif | Uniform (Continuous) |
| توزیع نمایی | dexp | pexp | qexp | rexp | Exponential |
| توزیع کای ۲ | dchiq | pchiq | qchiq | rchisq | Chi-Squared |
| توزیع بتا | dbeta | pbeta | qbeta | rbeta | Beta |
| توزیع گاما | dgamma | pgamaa | qgamma | rgamma | Gamma |
| توزیع فیشر | df | pf | qf | rf | F |
| توزیع کوشی | dcauchy | pcauchy | qcauchy | rcauchy | Cauchy |
به منظور رسم نمودار تابع چگالی احتمال این توزیعها نیز درست به مانند روش قبلی عمل میکنیم. کدهای زیر برای ترسیم تابع چگالی احتمال این توزیعها نوشته شده است.
1par(mfrow=c(3,3))
2y=rnorm(n = 1000,mean = 0,sd = 2)
3d=drnom(sort(y),mean= 0,sd= 2)
4plot(sort(y),d,type = 'o',col='red',xlab = 'Values',ylab='Probability', main = 'Normal Distribution')
5
6y=rt(n = 1000,df = 2)
7d=dt(sort(y),df = 2)
8plot(sort(y),d,type = 'o',col='green',xlab = 'Values',ylab='Probability', main = 'Student\'s t Distribution')
9
10y=runif(n = 1000,min = 0,max = 1)
11d=dunif(sort(y),min = 0,max = 1)
12plot(sort(y),d,type = 'o',col='lightgreen',xlab = 'Values',ylab='Probability', main = 'Uniform Distribution')
13
14y=rexp(nn = 1000,rate = 1)
15d=dexp(sort(y),rate = 1)
16plot(sort(y),d,type = 'o',col='orange',xlab = 'Values',ylab='Probability', main = 'Exponential Distribution')
17
18y=rchisq(n = 1000,df = 10)
19d=dchisq(sort(y),df = 10)
20plot(sort(y),d,type = 'o',col='blue',xlab = 'Values',ylab='Probability', main = 'Chi-Squared Distribution')
21
22y=rbeta(n = 1000,shape1 = 1,shape2 = 5)
23d=dbeta(sort(y),shape1 = 1,shape2 = 5)
24plot(sort(y),d,type = 'o',col='blue',xlab = 'Values',ylab='Probability', main = 'Beta Distribution')
25
26y=rgamma(n = 1000,shape = 1,scale = 5)
27d=dgamma(sort(y),shape = 1,scale = 5)
28plot(sort(y),d,type = 'o',col='blue',xlab = 'Values',ylab='Probability', main = 'Gamma Distribution')
29
30y=rf(n = 1000,df1 = 1,df2 = 10)
31d=df(sort(y),df1= 1,df2 = 10)
32plot(sort(y),d,type = 'o',col='blue',xlab = 'Values',ylab='Probability', main = 'Fisher Distribution')
33
34
35y=rcauchy(n = 1000,location = 0,scale = 5)
36d=dcauchy(sort(y),location = 0,scale = 5)
37plot(sort(y),d,type = 'o',col='blue',xlab = 'Values',ylab='Probability', main = 'Cauchy Distribution')تصویر زیر خروجی این برنامه را نشان میدهد. در اینجا صفحه نمایش به سه سطر و سه ستون برای نمایش نمودارها تقسیم شده است.
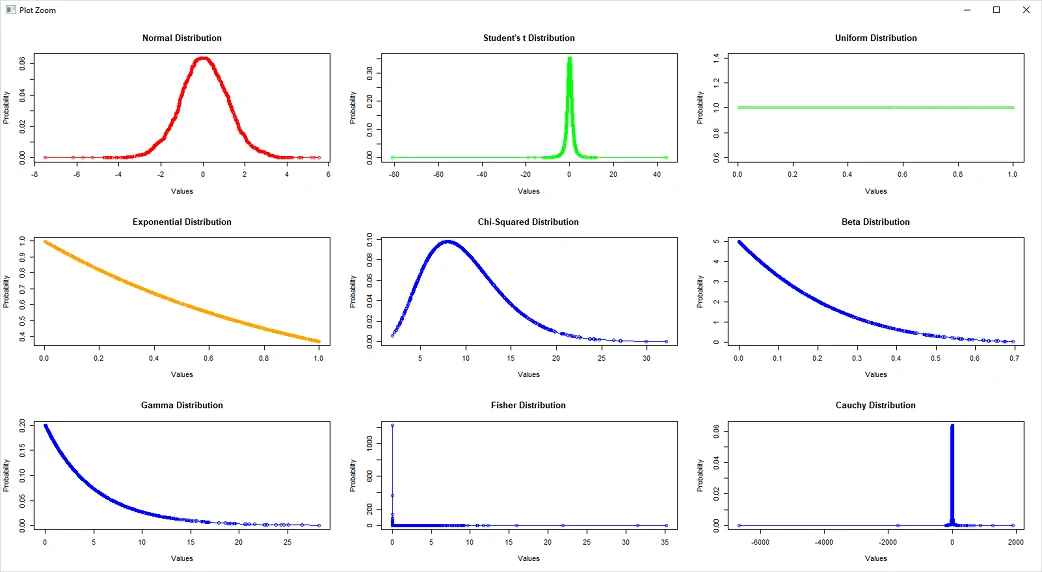
اگر میخواهید از پارامترها مربوط به هر یک از توزیعهای گفته شده اطلاع پیدا کنید، بهتر است از دستور str کمک بگیرید. به این ترتیب برای مثال اگر میخواهید پارامترهای تابع احتمال گاما (gamma) را بشناسید، بهتر است کد دستوری را وارد کنید. خروجی، پارامترهای این دستور خواهند بود که در شکل زیر قابل مشاهده است.

خروجی این تابع پارامترهای dgamma را نشان میدهد. پارامتر اول (x) مقداری است که باید چگالی در آن نقطه محاسبه شود، shape پارامتر شکل، rate پارامتر نرخ توزیع گاما و همچنین scale نیز پارامتر مقیاس است که میتواند به صورت عکس پارامتر rate معرفی شود. در انتها نیز پارامتر log که یک پارامتر با مقدارهای منطقی است، نشان میدهد آیا لازم است لگاریتم مقدار تابع چگالی احتمال محاسبه شود یا خیر. البته این دستور را میتوانید برای هر تابعی در R بکار ببرید.
کد مربوط به نمایش این نمودارها را میتوانید با کلیک روی این لینک دریافت کنید.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای نرمافزارهای آماری
- مجموعه آموزشهای آمار احتمالات و دادهکاوی
- آزمایش تصادفی، پیشامد و تابع احتمال
- آموزش آمار و احتمال مهندسی
- متغیر تصادفی و توزیع برنولی — به زبان ساده
- متغیر های تصادفی – میانگین، واریانس و انحراف معیار – به زبان ساده
- مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری
^^












